Generalized Surface Flows for Deformable Registration and Cortical Matching

Abstract

Despite being routinely required in medical applications, deformable surface registration is notoriously difficult due to large intersubject variability and complex geometry of most medical datasets. We present a general and flexible deformable matching framework based on generalized surface flows that efficiently tackles these issues through tailored deformation priors and multiresolution computations. The value of our approach over existing methods is demonstrated for automatic and user-guided cortical registration.

1 Introduction

Matching (or registration) of deformable surfaces is a fundamental problem in medical image analysis and computational anatomy. One particularly challenging instance of the problem arises in the field of human brain mapping, where deformable registration of two cortical surfaces is required for intersubject comparisons and intrasubject analysis of neuroanatomical surface data. Related studies include progression of disorders such as Alzheimer's disease, brain growth patterns, genetic influences [1] and the effects of drug abuse on the structure and function of the brain [2]. The challenge in registering two cortices lies in the wide inter-subject variability and the convoluted geometry of the cortical surface, representing a real “stress test” for any general deformable registration technique. Various landmark-based and landmark-free methods have been developed [3–8]. Parameterization-based techniques first find a mapping between the cortical surface and a plane or a sphere, then align in the parameter domain cortical features such as mean curvature [2, 5, 6] or sulcal landmarks [8, 9]. The often large change in metric due to the mapping needs to be accounted for while performing the alignment process in the parameter domain [9, 10], adding to the computational costs. Another class of techniques operates directly in the ambient space by finding a 3D warping field that aligns the cortical features. Most of these methods are volume-based, aiming to align image features such as intensities [11] or invariant geometric moments [12], rather than surfaces. As a result, their matching of the cortices often exhibits inaccuracies.

In this paper we present a new, general, and flexible computational framework for deformable surface matching, based on the notion of generalized flows of discrete surfaces. Generalized flows were introduced recently in [13] and [14] in the Eulerian setting (i.e., for implicit surface representations), and extended to the Lagrangian (mesh-based) case in [15]. The proposed method iteratively deforms a 3D template surface to match the target, until convergence criteria are met. As a result, the whole deformation trajectory is available as a by-product for evaluation and determination of the best fit.

The use of geometric flows in medical image analysis is not new: for instance, active contours (or snakes) and deformable models have been widely applied to reconstruct surfaces from volumetric images (e.g., [16]). The main drawback of these methods is their sensitivity to local minima, which can become particularly severe when matching of geometrically complex objects is sought. Here we show a way to systematically deal with this issue using problem-specific prior knowledge. The contributions of this paper are as follows:

• - We present a computational framework for surface matching based on generalized discrete geometric flows. By allowing custom deformation priors, the generalized approach significantly helps avoiding local minima and provides additional flexibility and control over the registration process, as well as robustness to noise.

• - The proposed framework uses a triangle mesh (Lagrangian) representation for surface matching. Compared to the Eulerian methodology, this approach is both topology-preserving by definition and efficient by nature, confining computations strictly to the object boundary. Moreover, this representation can provide point correspondences between two surfaces at any chosen resolution.

• - We formulate the alignment problem as a minimization process of a pseudo-Hausdorff distance and show a practical application of the method to cortical matching.

• - The basic algorithm is optimized using a surface multiresolution representation, allowing efficient handling of complex models and faster convergence.

2 Method

A typical shape matching problem considers two 3D models—a template and an instance—assumed to have some “meaningful” but unknown mapping between them. The matching problem is thus to find such a valid mapping between the two shapes, generally involving a non-rigid mapping in medical applications. We start with a brief overview of our approach to the problem of deformable shape matching, before proceeding to the specific (and challenging) case of cortical surface matching.

2.1 Object Alignment as a Geometric Optimization

The task of aligning two objects is often cast as a geometric distance minimization problem: a common approach to registration is to deform one of the shapes (typically, the template) so as to minimize its “distance” to the other shape. 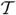Since an L²-type distance measure is known to be too forgiving in comparing two shapes, we opt instead for the symmetric Hausdorff distance which, for two surfaces and , is given by

$$d(\mathcal{S},\mathcal{T})=max\left[\underset{p\in \mathcal{S}}{max}\underset{q\in \mathcal{T}}{min}\Vert p-q\Vert ,\underset{p\in \mathcal{T}}{max}\underset{q\in \mathcal{S}}{min}\Vert p-q\Vert \right].$$

Since this expression is not differentiable, we adopt a pseudo-Hausdorff distance d_H(X,Y) between two distinct meshes X = {x_i}_i=1..P and Y = {y_j}_j=1..Q, based on a method introduced in [17] in the context of Level Sets, and adapted in [15] to handle irregularly shaped polygonal meshes. This allows us to formulate distance minimization as an iterative gradient descent procedure, where the template mesh X is evolved (or flowed) at each step in the direction of the negative gradient of d_H(X,Y), with Y being the instance mesh. This process is known as gradient flow, and can be written as the following PDE:

$$\frac{d\mathbf{\text{X}}}{dt}=-{\mathbf{\text{M}}}^{-1}\frac{\partial d_H}{\partial \mathbf{\text{X}}}(\mathbf{\text{X}},\mathbf{\text{Y}}),$$ (1)

where M is a finite element lumped (diagonal) mass matrix [18] associated with the mesh X to account for non-uniform sampling, and $\frac{\partial d_H(\mathbf{\text{X}},\mathbf{\text{Y}})}{\partial \mathbf{\text{X}}}$ is given by

$$\frac{\partial d_H(\mathbf{\text{X}},\mathbf{\text{Y}})}{\partial {\mathbf{\text{x}}}_i}=\frac{{(d_H(\mathbf{\text{X}},\mathbf{\text{Y}})+\epsilon )}^{1-2\alpha }}{P\cdot Q}{M}_{ii}^{\text{x}}\sum _j\frac{{\mathbf{\text{x}}}_i-{\mathbf{\text{y}}}_j}{d_{ij}^{\alpha +1}}{M}_{jj}^{\text{y}}(f_i^{-2}+g_j^{-2}),$$ (2)

$$\text{where}{d}_H(\mathbf{\text{X}},\mathbf{\text{Y}})={\left[\frac{1}{P}\sum _i{M}_{ii}^{\text{x}}{f}_i^{-1}+\frac{1}{Q}\sum _j{M}_{jj}^{\text{y}}{g}_j^{-1}\right]}^{\frac{1}{2\alpha }}-\epsilon ,$$

$$\text{and}{f}_i=\frac{1}{Q}\sum _j{M}_{jj}^{\text{y}}{d}_{jj}^{-\alpha },g_j=\frac{1}{P}\sum _i{M}_{ii}^{\text{x}}{d}_{ij}^{-\alpha },d_{ij}={\left|{\mathbf{\text{x}}}_i-{\mathbf{\text{y}}}_j\right|}^2+{\epsilon }^2,$$

with $M_{ii}^x$ and $M_{jj}^y$ are elements of the mass matrices of X and Y, respectively, and ε > 0, α ≥ 0 are parameters [15]. However, as illustrated by Figure 1 (right) such a naïve minimization is unlikely to yield relevant correspondences between two dissimilar shapes, as the energy landscape is too complex and non-linear to avoid getting stuck in one of the numerous local minima.

Fig. 1.

A white matter cortex and its corresponding Partially Flattened Surface (a), where the major sulci is still clearly present. A basic Hausdorff gradient flow applied on a rotated, smoother version (b) creates spurious deformations (c) due to lack of coherence and local minima, while with a quasi-rigid deformation prior (d), it successfully recovers the transformation.

2.2 Generalized Hausdorff Flow

One important detail is that the definition of the gradient in Eq. 1 is implicitly based on the L² inner product on the deformation space [13], which in fact can be replaced by any valid inner product. In particular, given the L² inner product and any self-adjoint positive-definite linear operator L : U → U (U being the deformation space), a new inner product can be defined by

$${\langle \mathbf{\text{u}},\mathbf{\text{v}}\rangle }_{\mathbf{\text{L}}}={\langle \mathbf{\text{u}},\mathbf{\text{Lv}}\rangle }_{L^2}={\langle \mathbf{\text{Lu}},\mathbf{\text{v}}\rangle }_{L^2}.$$ (3)

This is a special type of inner product, as it is defined with respect to the L² norm. The advantage is that, given the L²-gradient ∇_L2 of any surface energy functional 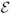, the generalized gradient [13] of 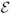can be defined by

$${\nabla }_{\mathbf{\text{L}}}\mathcal{E}(\mathbf{\text{X}})={\mathbf{\text{L}}}^{-1}{\nabla }_{L^2}\mathcal{E}(\mathbf{\text{X}}).$$ (4)

This leads to the definition of a generalized Hausdorff flow:

$$\frac{d\mathbf{\text{X}}}{dt}=-{(\mathbf{\text{ML}})}^{-1}\frac{\partial d_H}{\partial \mathbf{\text{X}}}(\mathbf{\text{X}},\mathbf{\text{Y}}).$$

The operator L should be chosen so as to reflect prior knowledge about the nature of a problem-specific deformation, and is therefore called a deformation prior (not to be confused with probabilistic priors used in Bayesian estimation). Thus, this procedure is of practical interest because it allows us to modify any existing L² gradient flow. Note that the energy itself is never altered by a prior—it is only the optimization path that is. We will now show two particular priors useful in many deformable registration contexts.

2.3 Deformation Priors

Sobolev Deformation Prior

As most conventional gradient flows are based on the L² norm of vector fields which disregards the spatial coherence of a deformation, they can produce highly irregular motion and are susceptible to noise and local minima. To address these flaws, Sundaramoorthi et al. [14] proposed a regularizing inner product, namely, a Sobolev norm, in the context of Eulerian (Level Sets) active contours. For meshes, the Sobolev norm H¹ derives from the following inner product:

$${\langle \mathbf{\text{u}},\mathbf{\text{v}}\rangle }_{H^1}={\int }_{\mathcal{S}}\mathbf{\text{u}}(\mathbf{\text{x}})\cdot \mathbf{\text{v}}(\mathbf{\text{x}})d\mathbf{\text{x}}+\lambda {\int }_{\mathcal{S}}\nabla \mathbf{\text{u}}(\mathbf{\text{x}})\cdot \nabla \mathbf{\text{v}}(\mathbf{\text{x}})d\mathbf{\text{x}}.$$

Using Eq. 3 and integration by parts, we can show that this inner product corresponds to the linear operator L_H1(u) = u − λΔu, where Δ is the discrete Laplace-Beltrami operator [19], and λ is an arbitrary weighting factor. Equipped with this deformation prior, we can define the H¹-gradient of the pseudo-Hausdorff distance (or any other surface energy 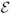), and perform an explicit integration of the corresponding gradient flow. This yields:

$${\mathbf{\text{X}}}_{t+dt}={\mathbf{\text{X}}}_t-dt{(\text{Id}-\lambda \Delta )}^{-1}\frac{\partial ℰ}{\partial \mathbf{\text{X}}}({\mathbf{\text{X}}}_t).$$

Thus, a step of Sobolev gradient flow is computed by solving the following linear system:

$$(\text{Id}-\lambda \Delta ){\mathbf{\text{X}}}_{t+dt}=(\text{Id}-\lambda \Delta -dt\frac{\partial ℰ}{\partial \mathbf{\text{X}}}){\mathbf{\text{X}}}_t.$$ (5)

Consequently, the solution of this linear system couples the motion of each vertex to the motion of the other vertices. This exemplifies the regularization effect: vertices that move independently in an L² flow will now move in concord.

For a stronger regularization effect, we can extend to above scheme to higher order Sobolev-type norms. For instance, we can define a higher-order prior L(u) = u+μΔ²u, where Δ² = Δ ∘ Δ. With a slightly higher computational cost, the resulting scheme is equivalent to regularizing the instantaneous deformation with a thin-plate spline energy term (see e.g. [20]). In practice, we stick to the H¹ prior in this work.

Quasi-rigid Deformation Prior

Since the two input shapes are generally given in separate coordinate frames, it is often desired to first bring them into a rigid alignment. For that purpose we can use the quasi-rigid deformation prior L_R (see [13, 15] for the Eulerian and Lagrangian derivations, respectively). Due to space constraints, we will not reproduce its formulation here. In essence, it can be seen as a linear filter that boosts the rigid component of a given motion field by a user-specified factor. As a result, an arbitrarily-rigid surface flow can be obtained. Figure 1 shows a successful quasi-rigid alignment of two cortices with this prior.

Note that since each of prior is given by a linear operator, we can also design a combined L_R,H1 prior which is a weighted combination of the two above operators, such that the rigid motion is prioritized and the non-rigid residual is smoothed. The result is a single prior that covers both phases of the registration process.

2.4 Matching Cortical Surfaces

Basic Algorithm

We are now ready to apply the Hausdorff flow approach to match a template cortical surface (e.g., a digital atlas of the cortex) to an instance surface, e.g., segmented from a MRI scan. One naïve solution would be to perform the minimization directly on the input surfaces, combined with the H¹ deformation prior for regularization. This process is still likely to get stuck in a local minimum due to the highly convoluted geometry of the cortex. Even if we managed to get the two surfaces into a complete alignment, the result would hardly be adequate, as intercortex correspondence is in general not well-defined due to extreme variability of the cortical structures. In practice, quality of match is measured by the alignment of the major sulcal patterns that can be consistently identified in all brains. Thus, minimum intersurface distance alone is not a sufficient condition for an acceptable solution. In view if this problem, the use of Partially Inflated Surfaces (PFS) has been advocated for cortical matching [6,21]. The idea is to smooth out excessive surface detail through, e.g., Mean Curvature Smoothing [22]); a limited amount of smoothing is performed in order to facilitate matching while preserving the principal sulcal patterns—see Figure 1(a) for an illustration. We adopt this approach, with one important difference. While correspondence between two PFSs is typically computed by matching their maps in a common parameter domain, we eliminate these intermediate mappings by aligning the PFSs directly. Our strategy is summarized below, and illustrated in Figure 2:

Fig. 2.

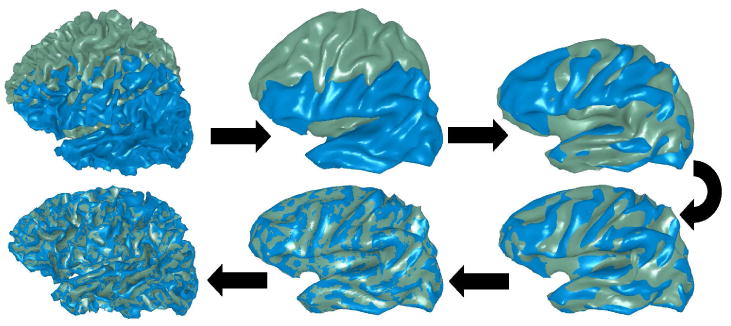
Automatically matching a template (grey) to the subject cortex (blue). Partially flattened representations of both surfaces are iteratively aligned using a Hausdorff flow with a smoothing prior. The obtained alignment yields a correspondence between the original surfaces. The final color mix is due the fact that the surfaces lie on each other.

Algorithm:

1. Partially flatten and 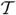obtaining and 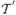respectively.

2. Apply Generalized Hausdorff Flow to achieve an arbitrarily close alignment of with 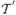, yielding a correspondence map φ between the two.

3. Return $\mathcal{S}\to {\mathcal{S}}^{\prime }\stackrel{\phi }{\to }{\mathcal{T}}^{\prime }\to \mathcal{T}$ as a bijective map between and .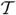

The first step can be done rapidly using Mean Curvature Smoothing (MSC), with implicit time integration allowing an arbitrarily large time step. Note that MSC is a classical example of gradient flow, so our whole approach fits nicely into the flow-based methodology. The crux of the algorithm lies in the second step, where the template PFS (which can be precomputed for repeated use) is iteratively deformed to match 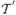. To regularize the flow, we use the L_R,H1 operator from Section 2.3. In practice, once the rigid component of the motion vanishes, L_R,H1 can be replaced with a simpler H¹ prior for efficiency. As the surfaces get closer, we switch to implicit time integration (Eq. 5) to avoid oscillations and accelerate convergence.

Finally, to make the process even more efficient for high-resolution models, the basic minimization algorithm is cast in a multiresolution framework, yielding a speedup of several orders of magnitude. A coarse match is first computed for simplified versions [23] of both PFSs, before refining them back to the original resolution (using pyramid coordinates [24]) for final alignment. Thus, our approach applies multiscale strategies to reduce both geometric and computational complexities: geometrically—using partial flattening to find a mapping, and computationally—employing coarser meshes to optimize performance.

Adding Constraints

As shown in Figure 3, the above procedure manages to automatically align most sulci, but cannot guarantee a correct match when a strong sulcal variability is present. A common remedy is to incorporate constraints, i.e., expert-specified sulcal curves, to control the mapping. In our case, adding constraints to the pseudo-Hausdorff energy is quite straightforward. Indeed, matching of two curves on opposite surfaces is just another distance minimization problem—this time, between sets of surface points that lie on the two curves. Thus, we can reuse the same Hausdorff distance approach, applying a separate, similar energy term to those mesh vertices that are incident on the curves (instead of the global Hausdorff potential). Adding point constraints, if needed, is even simpler. Note also that the constrained deformation is still kept smooth due to the use of the H¹ prior.

Fig. 3.

a. Automatic matching of PFSs yields a close alignment for most sulcal curves. b. Constraining only 7 out of the 23 available curves reduces most misalignments, further improved by using the full set of constraints (c). d. Corresponding sulcal alignment for the original cortical surfaces. For clarity, a single cerebral hemisphere is shown.

3 Results

The proposed cortical matching algorithm was tested with a dataset of six subject brains, segmented from MRI scans using the BrainSuite tool [25], each supplemented with a set of sulcal curves marked by an expert according to the LONI Sulcal Tracing Protocol [1]. As illustrated by Figure 2, the algorithm automatically computes a near zero-distance alignment for two partially inflated cortical surfaces, effectively yielding an intercortex correspondence. It results in a reasonably close alignment for most sulcal curves, further improved through the addition of constraints. Figure 3 shows that most sulci could be matched automatically, and constraining only a subset of the sulcal curves is sufficient, thus significantly reducing the amount of manual effort required.

Table 1 summarizes a limited evaluation of our algorithm (GHF), compared to HAMMER [12], based on six pairs of subject brain images. Although the two methods operate on different modalities, distances between corresponding subject and deformed template sulcal curves can be measured in both cases. Even without resorting to constraints (to make a fair comparison to the landmark-free HAMMER), our method demonstrates a comparable quality of match, with clearly superior computation times: under 5 min on a standard PC, as opposed to several hours. Note also that for PFS sulci, registration error is even lower, which illustrates the quality of the core deformable matching procedure.

Table 1.

Quality of match between deformed template and subject brains as average L² distances between corresponding sulcal curves.

Method / Data	Mean L2 Distance Per Case (mm)						Total Average
HAMMER / Original Sulci	4.67	4.62	4.79	5.05	5.13	4.90	4.87
GHF / Original Sulci	5.49	5.02	4.56	5.16	4.97	4.53	4.96
GHF / PFS Sulci	4.13	3.87	3.54	4.12	4.07	3.32	3.84

4 Discussion and Future Work

We have presented a practical and flexible multiresolution framework for deformable surface registration, based on generalized geometric flows. In the case of cortical matching, initial evaluation indicated quality comparable to state of the art methods, with near-interactive computation times. The presented solution is not without limitations: for instance, self-intersections may occur during the deformation, e.g., in presence of constraints (in fact, one can design constrained configurations not having any intersection-free solution). This shortcoming can be addressed through a special deformation prior added to the constraint energy term, e.g., a prior that prioritizes tangential motion. We are also investigating ways to generalize the definition of geometric distance and design new priors to improve automatic matching of sulcal features. Using generalized flows to compute continuous morphs that follow geodesics in shape spaces [26, 27] is another exciting avenue of future work.