Unbiased diffusion in tubes with corrugated walls

Abstract

This study is devoted to unbiased motion of a point Brownian particle in a tube with corrugated walls made of conical sections of a varying length. Effective one-dimensional description in terms of the generalized Fick-Jacobs equation is used to derive a formula which gives the effective diffusion coefficient of the particle as a function of the geometric parameters of the tube. Comparison with the results of Brownian dynamics simulations allows us to establish the domain of applicability of both the one-dimensional description and the formula for the effective diffusion coefficient.

INTRODUCTION

In many problems of practical and theoretical interest, motion of Brownian particles is spatially constrained.¹ When diffusion occurs in quasi-one-dimensional structures, it is intuitively appealing to introduce an effective one-dimensional description. In a three-dimensional tube of varying radius R(x) with the x-axis directed along the centerline of the tube, the one-dimensional concentration of point particles c(x,t) is related to their three-dimensional concentration C(x,y,z,t) by the relationship

$$c\left(x,t\right)={\int }_{A\left(x\right)}C\left(x,y,z,t\right)dydz,$$ (1)

where the integration is carried out over the position-dependent cross-section area A(x) of the tube. On condition that distribution of the particles in every cross section is uniform, the one-dimensional concentration obeys the Fick–Jacobs equation²

$$\frac{\partial c\left(x,t\right)}{\partial t}=D_0\frac{\partial }{\partial x}\left\{A\left(x\right)\frac{\partial }{\partial x}\left[\frac{c\left(x,t\right)}{A\left(x\right)}\right]\right\},$$ (2)

where D₀ is the particle diffusion coefficient in space without constraints.

The Fick–Jacobs equation was generalized by Zwanzig (Zw) who showed that when the tube radius is a slowly varying function of x,

$$\left|dR\left(x\right)∕dx\right|⪡1,$$ (3)

the diffusion coefficient entering into Eq. 2 becomes position dependent D(x) and the equation takes the form³

$$\frac{\partial c\left(x,t\right)}{\partial t}=\frac{\partial }{\partial x}\left\{A\left(x\right)D\left(x\right)\frac{\partial }{\partial x}\left[\frac{c\left(x,t\right)}{A\left(x\right)}\right]\right\}.$$ (4)

Zwanzig derived the following expression for D(x):

$$D_{\text{Zw}}\left(x\right)=\frac{D_0}{1+\left(1∕2\right){\left(dR\left(x\right)∕dx\right)}^2}.$$ (5)

This result was later generalized by Reguera and Rubi (RR) who suggested⁴

$$D_{\text{RR}}\left(x\right)=\frac{D_0}{\sqrt{1+{\left(dR\left(x\right)∕dx\right)}^2}}.$$ (6)

In a recent numerical study,⁵ it was demonstrated that the generalized Fick–Jacobs equation Eq. 4 with D(x) given by Eq. 6 is valid for

$$\left|dR\left(x\right)∕dx\right|\le 1.$$ (7)

This significantly extends the range of applicability of the generalized Fick–Jacobs equation as compared with the requirement in Eq. 3. A more general theory of reduction to the effective one-dimensional description was developed by Kalinay and Percus.⁶

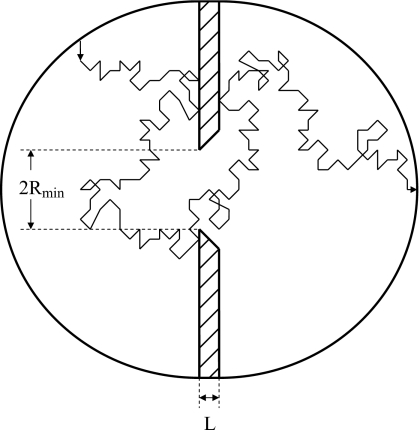
In Ref. 5, the authors studied long conical channels whose length L was much larger than the smallest radius of the cone L⪢R_min. It is intuitively clear, however, that the condition in Eq. 7 is not sufficient and the effective one-dimensional description may fail if the cone is not long enough. Figure 1 illustrates this point by presenting a cartoon of the two-dimensional projection of a three-dimensional trajectory of a particle passing through a conical channel, whose length is four times smaller than its diameter. It is seen that although the trajectory shows multiple interactions with the reflecting walls of the partition containing the channel, the particle does not interact with the channel walls. In the case when L⪡R_min, most of the particles passing through the channel will have only a small chance to interact with its walls. As a consequence, the effective diffusion coefficient of such particles in the channel will be equal to D₀ independently of the dR(x)∕dx value. Even if the particle distribution is close to the uniform one, the reduction to the one-dimensional description works only if most of the translocating particles are able to “probe” the reflecting walls of the tube. This requirement imposes an additional constraint on the domain of applicability of the generalized Fick–Jacobs equation.

Figure 1.

A cartoon of the two-dimensional projection of a three-dimensional trajectory of a particle passing through the channel.

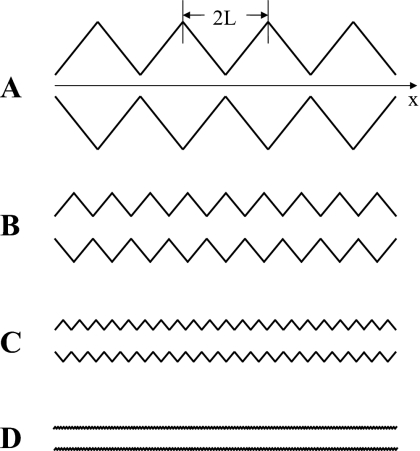
Another intuitively appealing example is given in Fig. 2. It shows a sequence of corrugated tubes with the same minimum radius R_min but with different periods l=2L of the radius variation. The sequence starts with a tube made of long conical sections L>R_min [Fig. 2A] and ends with a tube made of short conical sections L⪡R_min [Fig. 2D]. For all these tubes, the radius variation rate along the tube axis |dR(x)∕dx|=λ is the same. Moreover, the tubes are long so that diffusing particles multiply interact with the tube walls. However, as the period l gets smaller [going from Fig. 2A to Fig. 2D], the tube becomes more and more similar to a regular cylindrical tube. As a consequence, the effective diffusion coefficient of the particle approaches D₀ independently of the dR(x)∕dx value again.

Figure 2.

A sequence of corrugated tubes made of conical sections. All tubes have the same minimum radius R_min and the same radius variation rate λ=|dR(x)∕dx| but different periods l=2L. The period decreases from top to bottom: L>R_min in panel A and L⪡R_min in panel D.

The two examples above show that the domain of applicability of the one-dimensional description in terms of the Fick–Jacobs equation Eq. 4 has another restriction in addition to that given in Eq. 7. One of the two goals of the present paper is to establish this restriction. Another goal is to find the effective diffusion coefficient D_eff of a point Brownian particle in a corrugated tube made of conical sections.

In what follows, we first use Eq. 4 with D(x) given in Eq. 6 to derive a formula for D_eff. This formula, Eq. 14, shows how D_eff depends on the two dimensionless parameters that characterize the tube geometry: λ=|dR(x)∕dx| and L∕a, where a=R_min is the minimum radius of the tube. Then, we compare the theoretically predicted D_eff with the effective diffusion coefficient found in Brownian dynamics simulations. Such a comparison will tell us about the range of applicability of the formula for D_eff obtained on the basis of the generalized Fick–Jacobs equation, thus establishing a constraint on the ratio L∕R_min that guarantees the applicability of Eq. 4 on condition that the requirement in Eq. 7 is fulfilled.

THEORY AND SIMULATIONS

Let R(x) be the tube radius at given x with the most narrow cross sections of radius R_min=a located at x=2nL, n=0,±1,±2,…. Within one period dependence, R(x) is given by

$$R\left(x\right)=\{\begin{array}{cc}a+\lambda x,& 0<x<L\\ a+\lambda \left(2L-x\right),& L<x<2L\end{array}\phantom{\}}.$$ (8)

For this geometry |dR(x)∕dx|=λ and the RR formula for the local diffusion coefficient, Eq. 6 takes the form

$$D_{\text{RR}}\left(x\right)=\frac{D_0}{\sqrt{1+{\lambda }^2}}=D_{\lambda }.$$ (9)

Thus, in this case the local diffusion coefficient is position independent.

Introducing entropy potential U(x),

$$U\left(x\right)=-k_{B}T\text{\hspace{0.17em}ln}\frac{A\left(x\right)}{\pi a^2}=-2k_{B}T\text{\hspace{0.17em}ln}\frac{R\left(x\right)}{a},$$ (10)

where k_B and T are the Boltzmann constant and the absolute temperature and A(x)=π[R(x)]² is the tube cross section area. We can write the Fick–Jacobs equation as the Smoluchowski equation,

$$\frac{\partial c\left(x,t\right)}{\partial t}=D_{\lambda }\frac{\partial }{\partial x}\left\{\text{exp}\left(-\frac{U\left(x\right)}{k_{B}T}\right)\frac{\partial }{\partial x}\left[\text{exp}\left(\frac{U\left(x\right)}{k_{B}T}\right)c\left(x,t\right)\right]\right\}.$$ (11)

The zero energy count of the entropy potential is fixed so that U(x)<0 at all values of x except for x=2nL,n=0,±1,±2,…, where U(x)=0.

Since the entropy potential is periodic U(x+2L)=U(x), we can find D_eff by means of the Lifson–Jackson formula,⁷

$$D_{\text{eff}}=\frac{D_{\lambda }}{⟨\text{exp}\left(-U\left(x\right)∕k_{B}T\right)⟩⟨\text{exp}\left(U\left(x\right)∕k_{B}T\right)⟩},$$ (12)

where the angular brackets define the averaging over the period $⟨f\left(x\right)⟩=\left(1∕2L\right){\int }_0^{2L}f\left(x\right)dx$. In our case this formula takes the form

$$D_{\text{eff}}=\frac{D_{\lambda }{L}^2}{\left[{\int }_0^{L}A\left(x\right)dx\right]\left[{\int }_0^L(dx∕A\left(x\right))\right]}=\frac{D_{\lambda }{L}^2}{\left[{\int }_0^L{\left(a+\lambda x\right)}^{2}dx\right]\left[{\int }_0^L(dx∕{\left(a+\lambda x\right)}^2)\right]}.$$ (13)

Carrying out the integrations we obtain

$$D_{\text{eff}}=\frac{D_0}{\sqrt{1+{\lambda }^2}}\frac{1+\lambda L∕a}{1+\lambda L∕a+{\left(\lambda L∕a\right)}^2∕3}.$$ (14)

This is one of the main results of the present paper. The formula shows that D_eff monotonically decreases with L∕a at fixed λ. Its asymptotic behavior at λL∕a⪢1 is given by

$$D_{\text{eff}}=\frac{3a{D}_0}{\lambda \sqrt{1+{\lambda }^2}L}.$$ (15)

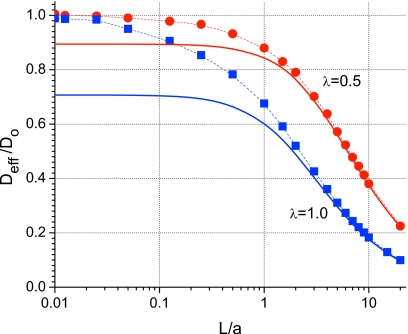
In Fig. 3, we compare D_eff predicted by Eq. 14 and found in Brownian dynamics simulations. This is done at two values of the radius variation rate: λ=|dR(x)∕dx|=0.5 and 1.0. One can see excellent agreement between the theoretical predictions and numerical results at L∕a=L∕R_min>2 for λ=0.5 and at L∕a=L∕R_min>3 for λ=1.0. However, the predictions fail at small values of L∕a. Here the formula in Eq. 14 predicts that D_eff tends to $D_{\lambda }=D_0∕\sqrt{1+{\lambda }^2}$, while the simulations show that the effective diffusion coefficient approaches its bulk value D₀, which is larger than D_λ. Based on a detailed numerical study (the results are not shown), we might suggest that the domain of applicability of the formula in Eq. 14 is given by

$$L>3a,\lambda \le 1,$$ (16)

where the second inequality is a consequence of the condition in Eq. 7.

Figure 3.

Effective diffusion coefficient D_eff normalized to its counterpart in space with no constraints D₀ as a function of L∕a, where L is the length of a conical section (half period of the structure) and a=R_min is the minimum radius of the tube. Symbols show the results found in Brownian dynamics simulations at λ=0.5 (circles) and λ=1.0 (squares). Dashed curves are drawn through the symbols to visualize the dependences. Solid lines are the dependences predicted by Eq. 14.

CONCLUSIONS

Thus, our analysis demonstrates that the requirement in Eq. 7 is not sufficient for a successful reduction of the three-dimensional diffusion in a tube of a varying cross section to the effective one-dimensional description: Eqs. 4, 6. One more factor should be taken into account, namely, the characteristic length of the radius variation should be large enough. This and the formula for D_eff in Eq. 14 are two major results of this paper. This formula extends the collection of analytical expressions for D_eff derived in recent years for periodic porous media of different geometry.⁸