Elastic, dielectric, and piezoelectric constants of Pb(In_1∕2Nb_1∕2)O₃–Pb(Mg_1∕3Nb_2∕3)O₃–PbTiO₃ single crystal poled along [011]_c

Abstract

Ternary single crystals xPb(In_1∕2Nb_1∕2)O₃–(1−x−y)Pb(Mg_1∕3Nb_2∕3)O₃–yPbTiO₃ (PIN-PMN-PT) poled along [011]_c showed remarkable electromechanical properties. We report complete sets of elastic, dielectric, and piezoelectric constants of PIN-PMN-28%PT and PIN-PMN-32%PT, measured by using combined resonance and ultrasonic methods. The electromechanical coupling coefficients k₁₅, k₃₂, and k₃₃ can reach 0.95, 0.90, and 0.92, and the piezoelectric strain coefficients d₁₅, d₃₂, and d₃₃ are as high as 3354 pC∕N, −1781 pC∕N, and 1363 pC∕N, respectively. These full matrix data sets provide the base for fundamental studies on domain engineering phenomena as well as urgently needed input data for the design of electromechanical devices using [011]_c poled PIN-PMN-PT single crystals.

[011]_c-poled relaxor-based ferroelectric single crystals (1−x)Pb(Zn_1∕3Nb_2∕3)O₃–xPbTiO₃ (PZN–xPT) and (1−x)Pb(Mg_1∕3Nb_2∕3)O₃–xPbTiO₃ (PMN–xPT) with compositions near the morphotropic phase boundary (MPB) exhibit ultrahigh transverse piezoelectric properties, which provides the base for much better transverse mode piezoelectric devices.^{1, 2, 3, 4, 5, 6, 7} However, the coercive field E_C (∼2.5 kV∕cm) of these binary crystals is too low for high-field driven devices. In addition, their relatively low Curie point T_c (∼130–170 °C) and low rhombohedral–tetragonal phase transition temperature T_R–T (∼75–95 °C) cause poor temperature stability and restrict device operating temperatures.

It was demonstrated that the ternary xPb (In_1∕2Nb_1∕2) O₃– (1−x−y)Pb (Mg_1∕3Nb_2∕3) O₃–yPbTiO₃ (PIN-PMN-PT) single crystal system has about 30 °C higher rhombohedral–tetragonal phase transition temperature than that of PMN-PT single crystals.^{8, 9, 10} The coercive field of this ternary single crystal has increased more than twice.^{11, 12} More importantly, this PIN-PMN-PT single crystal system has just as excellent piezoelectric properties as PMN-PT and PZN-PT single crystals. Recently, Liu et al.^{13, 14} have measured the complete sets of material constants for [001]_c- and [111]_c-poled rhombohedral PIN-PMN-PT single crystals with MPB composition using combined resonance and ultrasonic methods.

The PIN-PMN-PT ternary relaxor based ferroelectric single crystal has perovskite cubic structure above T_c, becomes tetragonal below T_c and transforms to rhombohedral below T_R–T with 3m point group symmetry. When the crystal is being poled along [011]_c direction, the domain pattern forms orthorhombic mm2 symmetry.^{15, 16} Following the convention, we take the [011]_c pseudocubic direction as the Z axis, the ${\left[0\overline{1}1\right]}_{\text{c}}$ and [100]_c as the X and Y axes, respectively. Based on such a coordinate choice, we report here two complete sets of material constants for PIN-PMN-28%PT and PIN-PMN-32%PT single crystals poled along [011]_c.

The PIN-PMN-PT single crystals used in our work were grown by the modified Bridgman method. The nominal composition of xPIN–(1−x−y)PMN–yPT crystals obtained are x∼0.25–0.35 and y∼0.30–0.32 but the composition along the growth direction varies due to the segregation of titanium in the crystal. Our crystal samples were cut from the bottom and middle part of the as-grown crystal boule, and the corresponding PT contents are 0.28 and 0.32, respectively.

All samples were oriented using the Laue x-ray machine with an accuracy of ±0.5°. Each sample was cut and polished into a parallelepiped with three pairs of parallel surfaces along ${\left[0\overline{1}1\right]}_{\text{c}}$, [100]_c, and [011]_c, respectively. Then, the samples were sputtered with gold electrodes on the pair of [011]_c surfaces, and poled with a field of 10–15 kV∕cm at room temperature. Because the [011]_c poled multidomain PIN-PMN-PT single crystals have macroscopic orthorhombic mm2 symmetry, there are total 17 independent material constants to be determined for each composition; nine elastic, five piezoelectric, and three dielectric constants.

It is nearly impossible to pole samples of different geometries to the same degree because the domain pattern formed depends on the geometry. Therefore, it is often very difficult to get self-consistency full matrix data by using the resonance method described in related textbooks. This is the main reason why some published data on [011]_c poled PMN-PT single crystals measured by using the resonance technique are lack of self-consistency.¹⁷ Therefore, we used combined resonance and ultrasonic methods together with capacitance and d₃₃ meter to obtain the maximum number of combinations from the least number of samples.¹⁸

For resonance measurements, the dimensions and geometries of samples used were specified by the IEEE standards on piezoelectricity.¹⁹ The resonance and antiresonance frequencies were obtained by an HP 4194 A impedance-phase gain analyzer. In ultrasonic measurements, a 5.0×5.0×5.0 mm³ cube was used and the orientations are ${\left[0\overline{1}1\right]}_{\text{c}}$, [100]_c, and [011]_c. A 15 MHz longitudinal wave transducer (Ultran Laboratories, Inc.) and a 20 MHz shear wave transducer (Panametrics Com.) were used for the ultrasonic pulse-echo measurements. The transducers were excited by a 200 MHz pulser∕receiver (Panametrics Com.) and the time of flight between echoes was measured using a Tektronix 460 A digital oscilloscope. The phase velocities of the longitudinal and shear waves were measured along the three pure mode directions, i.e., ${\left[0\overline{1}1\right]}_{\text{c}}$, [100]_c, and [011]_c. We can obtain eight elastic stiffness constants: $c_{11}^E$, $c_{22}^E$, $c_{33}^D$, $c_{44}^E$, $c_{44}^D$, $c_{55}^E$, $c_{55}^D$, and $c_{66}^E$ based on the Christoffel wave equations from this one sample alone.

From the measured resonance and antiresonance frequencies, we can calculate the corresponding piezoelectric strain coefficients d₃₁, d₃₂, and d₃₃, the elastic compliance constants $s_{11}^E$, $s_{22}^E$, $s_{33}^E$, and $s_{33}^D$, the elastic stiffness constants $c_{33}^D$ and $c_{33}^E$, and electromechanical coupling coefficients k₃₁, k₃₂, k₃₃, and k_t. The free and clamped dielectric constants ${\epsilon }_{11}^T$, ${\epsilon }_{22}^T$, ${\epsilon }_{33}^T$, ${\epsilon }_{11}^S$, ${\epsilon }_{22}^S$, and ${\epsilon }_{33}^S$ were determined from the low (1 kHz) and high frequency (2f_a) capacitance measurements. Overall, we obtained 27 independent measurements for the 17 independent coefficients. A program was developed to extract a reliable self-consistent matrix data set based on error analysis.

The measured and derived elastic, piezoelectric and dielectric constants of the PIN-PMN-28%PT and PIN-PMN-32%PT single crystals poled along [011]_c are given in Table 1. Material constants marked with a star (^*) were determined directly by the resonance or ultrasonic measurements while others were derived values. Compared with [001]_c poled PIN-PMN-PT single crystal, the main advantage of the [011]_c poled crystal is its super large shear piezoelectric coefficient d₁₅ (3354 pC∕N for PIN-PMN-32%PT), which is more than an order of magnitude larger than the d₁₅ [232 pC∕N for PIN-PMN-33%PT (Ref. ¹³)] of [001]_c poled single crystal.

Table 1.

Measured and derived material constants of PIN-PMN-28%PT and PIN-PMN-32%PT multidomain single crystals poled along [011]_c. [Directly measured constants are denoted by star (^*).]

	Elastic stiffness constants: $c_{ij}^E$ and $c_{ij}^D$ (1010 N∕m2)
	$c_{11}^{E*}$	$c_{12}^E$	$c_{13}^E$	$c_{22}^{E*}$	$c_{23}^E$	$c_{33}^E$	$c_{44}^{E*}$	$c_{55}^{E*}$	$c_{66}^{E*}$
28%PT	19.96	12.51	7.19	13.54	11.89	15.36	6.49	0.76	5.33
32%PT	21.45	15.01	8.01	17.37	14.10	15.26	6.37	0.48	4.56
	$c_{11}^D$	$c_{12}^D$	$c_{13}^D$	$c_{22}^D$	$c_{23}^D$	$c_{33}^{D*}$	$c_{44}^{D*}$	$c_{55}^{D*}$	$c_{66}^D$
28%PT	20.19	12.10	8.26	14.25	10.02	20.21	7.15	4.56	5.33
32%PT	21.50	14.86	8.46	17.94	12.39	20.35	7.30	4.59	4.56
	Elastic compliance constants: $s_{ij}^E$ and $s_{ij}^D$ (10−12 m2∕N)
	$s_{11}^{E*}$	$s_{12}^E$	$s_{13}^E$	$s_{22}^{E*}$	$s_{23}^E$	$s_{33}^E$	$s_{44}^E$	$s_{55}^E$	$s_{66}^E$
28%PT	18.27	−29.36	14.05	69.97	−40.37	31.23	15.41	131.58	18.76
32%PT	25.53	−45.13	27.87	101.45	−70.31	56.84	15.70	208.33	21.93
	$s_{11}^D$	$s_{12}^D$	$s_{13}^D$	$s_{22}^D$	$s_{23}^D$	$s_{33}^{D*}$	$s_{44}^D$	$s_{55}^D$	$s_{66}^D$
28%PT	10.07	−8.75	0.11	18.18	−5.33	7.59	13.99	21.93	18.76
32%PT	11.21	−10.84	1.63	19.37	−7.50	8.79	13.70	21.79	21.93
	Piezoelectric coefficients: eiλ(C∕m2), diλ(10−12 C∕N), giλ(10−3 Vm∕N), and hiλ(108 V∕m)
	e15	e24	e31	e32	e33	d15	d24	$d_{31}^{*}$	$d_{32}^{*}$	$d_{33}^{*}$
28%PT	16.74	7.39	3.43	−6.00	15.74	2203	114	460	−1156	782
32%PT	16.10	10.32	1.44	−5.50	16.47	3354	162	744	−1781	1363
	g15	g24	g31	g32	g33	h15	h24	h31	h32	h33
28%PT	49.79	12.51	17.80	−44.73	30.26	22.71	8.94	6.79	−11.89	31.20
32%PT	55.63	12.34	19.28	−46.15	35.32	25.51	9.01	2.72	−10.41	31.17
	Dielectric constants: εij(ε0) and β(10−4∕ε0)
	${\epsilon }_{11}^{S*}$	${\epsilon }_{22}^{S*}$	${\epsilon }_{33}^{S*}$	${\epsilon }_{11}^{T*}$	${\epsilon }_{22}^{T*}$	${\epsilon }_{33}^{T*}$	${\beta }_{11}^S$	${\beta }_{22}^S$	${\beta }_{33}^S$	${\beta }_{11}^T$	${\beta }_{22}^T$	${\beta }_{33}^T$
28%PT	833	935	570	5000	1030	2920	12.01	10.70	17.54	2.00	9.71	3.43
32%PT	713	1294	597	6814	1483	4361	14.03	7.73	16.75	1.47	6.74	2.29
	Electromechanical coupling factors kij and density
	k15	k24	$k_{31}^{*}$	$k_{32}^{*}$	$k_{33}^{*}$	$k_t^{*}$	Density (kg∕m3)
28%PT	0.91	0.30	0.67	0.86	0.87	0.49	8102
32%PT	0.95	0.36	0.75	0.90	0.92	0.50	8185

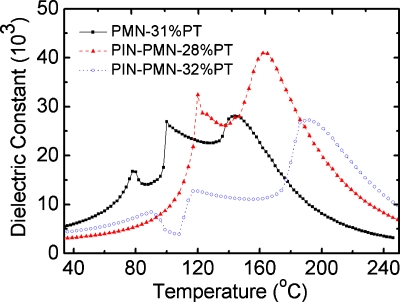
Some material constants for different relaxor-based ferroelectric single crystals poled along [011]_c are listed in Table 2 for comparison. We found that the electromechanical coupling coefficients and the piezoelectric strain coefficients of PIN-PMN-32%PT single crystal are comparable to that of PMN-30%PT, much better than PMN-28%PT and PMN-29%PT. The dielectric constants of PIN-PMN-PT system are lower than those of PMN-PT crystal system, making it a better candidate for ultrahigh frequency medical imaging transducers. The coercive field of PIN-PMN-28%PT and PIN-PMN-32%PT is around 5.5 kV∕cm, which is more than twice of the value of binary PMN-31%PT (∼2.6 kV∕cm). Figure 1 shows the temperature dependence of the dielectric constant ${\epsilon }_{33}^T$. It can be seen that the Curie temperatures of the PIN-PMN-28%PT and PIN-PMN-32%PT are 165 °C and 192 °C, respectively, which is more than 20 °C higher than that of PMN-31%PT (143 °C). Both the rhombohedral–orthorhombic and orthorhombic–tetragonal phase transition temperatures T_R–O and T_O–T of PIN-PMN-32%PT (93 °C and 118 °C) are more than 15 °C higher than that of PMN-31%PT (77 °C and 100 °C). For PIN-PMN-28%PT, there is only rhombohedral–tetragonal phase transition, which occurs at T_R−T=120 °C.

Table 2.

Comparison of some important material constants for different relaxor-based ferroelectric single crystals poled along [011]_c.

Single crystals	d15 (pC∕N)	d32 (pC∕N)	d33 (pC∕N)	k15	k32	k33	${\epsilon }_{11}^T∕{\epsilon }_0$	${\epsilon }_{22}^T∕{\epsilon }_0$	${\epsilon }_{33}^T∕{\epsilon }_0$
PMN-28%PTa	2816	−1761	1766	0.90	0.89	0.91	7466	4713	6366
PMN-29%PTb	1188	−1883	1020	0.83	0.94	0.78	3564	1127	4033
PMN-30%PTa	3262	−2116	1916	0.95	0.94	0.92	8783	5233	6966
PIN-PMN-28%PTc	2203	−1156	782	0.91	0.86	0.87	5000	1030	2920
PIN-PMN-32%PTc	3354	−1781	1363	0.95	0.90	0.92	6814	1483	4361

^aSee Reference ⁶.

^bSee Reference ⁷.

^cThis work.

Figure 1.

Dielectric constant ${\epsilon }_{33}^T∕{\epsilon }_0$ as a function of temperature for PMN-31%PT, PIN-PMN-28%PT, and PIN-PMN-32%PT single crystals measured in the poling direction [011]_c.

In summary, by using combined resonance and ultrasonic methods, we have measured the elastic, dielectric, and piezoelectric constants of relaxor-based ferroelectric PIN-PMN-28%PT and PIN-PMN-32%PT ternary multidomain single crystals poled along [011]_c. Due to higher phase transition temperature and much larger field endurance, [011]_c poled PIN-PMN-PT single crystals are much better candidates than PMN-PT and PZN-PT single crystals for shear and transverse piezoelectric devices. The two complete sets of material constants for two compositions of [011]_c-poled rhombohedral PIN-PMN-PT domain engineered single crystals can be used to perform fundamental theoretical analysis on domain engineering phenomena as well as being the input for finite element packages to design and optimize practical electromechanical device, such as transducers, sensors and actuators.