Enhancement of breast CADx with unlabeled data

Abstract

Purpose: Unlabeled medical image data are abundant, yet the process of converting them into a labeled (“truth-known”) database is time and resource expensive and fraught with ethical and logistics issues. The authors propose a dual-stage CADx scheme in which both labeled and unlabeled (truth-known and “truth-unknown”) data are used. This study is an initial exploration of the potential for leveraging unlabeled data toward enhancing breast CADx.

Methods: From a labeled ultrasound image database consisting of 1126 lesions with an empirical cancer prevalence of 14%, 200 different randomly sampled subsets were selected and the truth status of a variable number of cases was masked to the algorithm to mimic different types of labeled and unlabeled data sources. The prevalence was fixed at 50% cancerous for the labeled data and 5% cancerous for the unlabeled. In the first stage of the dual-stage CADx scheme, the authors term “transductive dimension reduction regularization” (TDR-R), both labeled and unlabeled images characterized by extracted lesion features were combined using dimension reduction (DR) techniques and mapped to a lower-dimensional representation. (The first stage ignored truth status therefore was an unsupervised algorithm.) In the second stage, the labeled data from the reduced dimension embedding were used to train a classifier toward estimating the probability of malignancy. For the first CADx stage, the authors investigated three DR approaches: Laplacian eigenmaps, t-distributed stochastic neighbor embedding (t-SNE), and principal component analysis. For the TDR-R methods, the classifier in the second stage was a supervised (i.e., utilized truth) Bayesian neural net. The dual-stage CADx schemes were compared to a single-stage scheme based on manifold regularization (MR) in a semisupervised setting via the LapSVM algorithm. Performance in terms of areas under the ROC curve (AUC) of the CADx schemes was evaluated in leave-one-out and .632+ bootstrap analyses on a by-lesion basis. Additionally, the trained algorithms were applied to an independent test data set consisting of 101 lesions with approximately 50% cancer prevalence. The difference in AUC (ΔAUC) between with and without the use of unlabeled data was computed.

Results: Statistically significant differences in the average AUC value (ΔAUC) were found in many instances between training with and without unlabeled data, based on the sample set distributions generated from this particular ultrasound data set during cross-validation and using independent test set. For example, when using 100 labeled and 900 unlabeled cases and testing on the independent test set, the TDR-R methods produced average ΔAUC=0.0361 with 95% intervals [0.0301; 0.0408] (p-value⪡0.0001, adjusted for multiple comparisons, but considering the test set fixed) using t-SNE and average ΔAUC=.026 [0.0227, 0.0298] (adjusted p-value⪡0.0001) using Laplacian eigenmaps, while the MR-based LapSVM produced an average ΔAUC=.0381 [0.0351; 0.0405] (adjusted p-value⪡0.0001). The authors also found that schemes initially obtaining lower than average performance when using labeled data only showed the most prominent increase in performance when unlabeled data were added in the first CADx stage, suggesting a regularization effect due to the injection of unlabeled data.

Conclusion: The findings reveal evidence that incorporating unlabeled data information into the overall development of CADx methods may improve classifier performance by non-negligible amounts and warrants further investigation.

INTRODUCTION

The rise of digital imaging followed by increased sophistication of image output and lowering cost of data storage has resulted in the accumulation of a substantial amount of clinical image information. This new reality provides ampleopportunity for enhancing the development of computer-aided diagnosis (CADx) algorithms.¹ More robust methodologies can now be implemented due to the simultaneous increase in the size of training, testing, and validation image databases and the availability of images with higher information content. However, the algorithmic training of CADx is commonly implemented via supervised classification, which requires that “truth” (i.e., actual biological disease status such as “malignant” or “benign”) be known for each image. Unfortunately, reliable truth labeling is seriously time and resource consuming and therefore acts as a limiting factor to databases’ sizes.² Even if the gathering of pathological, genetic, and radiological information associated with each clinical case is expected to become more efficient, a relative abundance of readily available unlabeled (UL) (i.e., “truth-unknown” or probability of disease equal to prevalence) or incompletely labeled (i.e., “truth-partially-known” or probability of disease higher or lower than prevalence for each specific case) images is likely to persist in most research contexts. For example, in the clinic, patients may be referred to an imaging follow-up rather than a biopsy. From a practical standpoint, it is wasteful to completely discard this information, as these images are likely to contain useful information as indicated, for example, by research suggesting that radiologists’ decision making processes might be endlessly refined by exposure to both labeled (L) (i.e., probability of disease equal to 0 or 1) and unlabeled image data, interpretable as a development of a general sense of familiarity with the structures contained in the image “space.”³

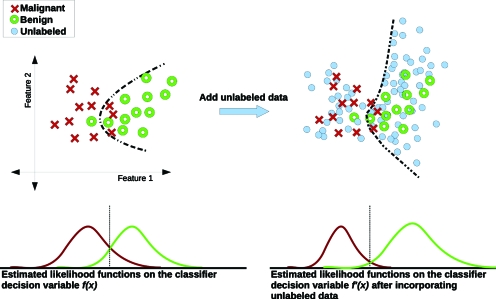
Unlabeled image data can be regarded as a sample drawn from the underlying probability distribution marginalized over the combined class-categories, e.g., all cases ignoring whether they are malignant or benign. A large and unbiased unlabeled database sample provides detailed knowledge of the inherent structure of the marginal distribution of the images, which can guide the subsequent design of supervised classification on labeled cases and perhaps improve performance.⁴ In other words, the unlabeled data may help “regularize” the training of CADx algorithms. Figure 1 illustrates these concepts.

Figure 1.

Simplified example illustrating how the use of unlabeled data might potentially improve CADx classifier regularization. The upper-left section displays a number of labeled samples from a hypothetical 2D feature space with a decision boundary (for likelihood ratio equal to 1) produced by a classifier trained on those data. The upper-right-hand section depicts the same data, plus unlabeled samples which provide additional structural information, therefore altering the classifier and decision boundary. The lower section illustrates the class-conditional density functions of the classifier output decision variables obtained by applying the two trained classifiers as described above to the population.

The possibility for meaningful integration of unlabeled and labeled image data have been provided by “transductive” methods such as the recently developed unsupervised, local geometry preserving, nonlinear dimension reduction (DR) and data representation techniques, including Laplacian eigenmaps (Belkin and Niyogi) and t-distributed stochastic neighbor embedding or t-SNE (van der Maaten and Hinton).^{5, 6, 7} Additionally, building on the DR conceptual foundations for preserving inherent data structure, manifold regularization (MR) establishes the possibility for “truly” semisupervised approaches, allowing for a natural extension to the immediate classification of out-of-sample test cases.⁸ The purpose of our study is to introduce these methods to breast CADx and to provide a preliminary exploration of the potential for leveraging unlabeled databases toward the design of more robust breast mass lesion diagnosis algorithms. Additionally, the experimental design considered here aims to mimic, within the constraints imposed by the available data set, clinically relevant scenarios involving potentially available unlabeled diagnostic data sets, specifically in terms of the expected cancer prevalence.

BACKGROUND

Current perspectives on breast CADx

A detailed discussion of past and present breast image CADx methods can be found in a number of reviews.^{1, 9} A quick recapitulation suggests that these methods are intended to improve the quality and consistency of radiologists’ clinical diagnoses and that they are usually designed following a supervised pattern recognition scheme constituted of segmentation, feature extraction, feature selection, and classifier training∕testing∕validation. The relative merits of these steps are partially confounded by the limitation of utilizing relatively small data sets. Critical to the success of such methods are the informative value of the extracted features toward the specific diagnostic task and the robustness of the classification algorithm employed to make use of the feature information. Feature selection (FS) is the final step of information evaluation and attempts to select the most discriminative input subpace from a possibly large array of potential feature candidates.^{10, 11, 12} An appealing alternative to explicit feature selection is to perform DR, which we have previously compared with FS for multimodality breast image CADx feature spaces including full-field digital mammography, ultrasound, and dynamic contrast enhanced magnetic resonance imaging (MRI).⁵ In this previous study, we evaluated classification performance and visualization of high-dimensional data structures. The methods investigated, t-SNE and Laplacian eigenmaps, are designed to discover the underlying structure of the data. Our analysis revealed that the DR methods, while not necessarily ready to completely replace FS, generally lead to classification performances on par with FS-based methods as well as providing 2D and 3D representations for aiding in the visualization of the original high-dimensional feature space.

Proposed incorporation of unlabeled data for training CADx

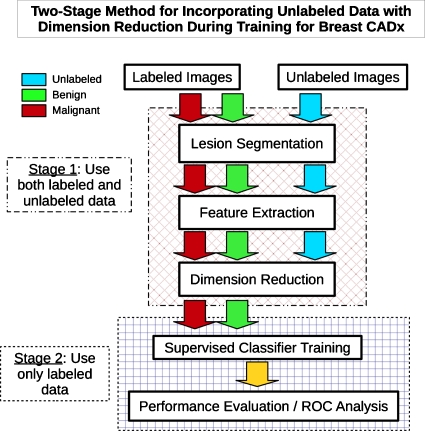
In the previous work, we did not consider DR’s capability of utilizing in a straightforward manner unlabeled data together with labeled data during the mapping from the higher to the lower-dimensional space. Since feature extraction is identical for labeled and unlabeled cases, instead of using supervised feature selection (such as automatic relevance determination), which is dependent exclusively on the labeled cases, unsupervised dimension reduction can use the high-dimensional feature vectors, including the unlabeled feature data, to construct a lower-dimensional representation.¹¹ Ideally, the unlabeled data can help to more accurately capture the underlying manifold structure associated with the population of the imaged objects, even if some of the structure might not relate directly to the diagnostic task, e.g., describe differences among benign cases. Figure 2 gives a broad outline of the proposed algorithm. We hypothesize that the labeled data subspace produced by this type of DR mapping (including unlabeled data) could allow a supervised classifier to achieve enhanced classification performance. We call this approach “transductive-DR regularization” (TDR-R). The TDR-R approach requires the potentially computationally intensive remapping step each time a new case is introduced. As differentiated from supervised learning which requires full knowledge of class categorization∕labeling for training data, and unsupervised methods which do not use any information related to class identity, semisupervised learning (SSL), in general, refers to a class of algorithms designed to make use of and learn from both labeled and unlabeled examples in a unified fashion for the task of classification.⁴ We thus also included a truly semisupervised learning algorithm known as MR, which is designed to explicitly incorporate unlabeled data information data during training and can be extended to classify new cases without the remapping and retraining of transductive.⁸

Figure 2.

Breast CADx algorithm work flow outline illustrating a two-stage method for incorporating unlabeled data with the use of dimension reduction.

Related work involving unlabeled data

To our knowledge, the use of nonlinear, local geometry preserving DR and manifold regularization to exploit unlabeled image feature data toward improving breast lesion CADx classification performance has yet to be investigated. However, methods involving unlabeled data have been briefly investigated in the area of computer-aided detection (CADe). Li and Zhou¹³ proposed to use unlabeled image data in conjunction with their algorithm “Co-Forest,” a modification of ensemble and cotraining based learning techniques, for a CADe application focused on microcalcifications in digital mammograms. In their paper, the authors provided limited results based on an experimental design using only 88 images total. In the broader field of computer analysis in medical imaging, others have investigated the use of k-means clustering with texture analysis for unlabeled liver MRI image regions toward diagnosis of cirrhosis; unfortunately, their conclusions were also limited because of their relatively small study size.¹⁴ The use of unlabeled data information for classification tasks is a growing research interest outside of the medical imaging arena as well, for example, in the analysis of protein sequences and speech∕audio recognition.^{15, 16} Additionally, research exists on full image-space input based approaches (as opposed to using fixed predetermined features), inspired in part by humanlike visual systems that are intimately associated with the use of unlabeled stimuli.¹⁷ Again, because of the relative abundance of unlabeled or incompletely labeled data in healthcare related fields, such as image processing and CAD research, we expect that the challenge of how to effectively use such information will likely remain highly relevant.

METHODS

Overview

Our experiments were based on sets of randomly selected cases from previously acquired retrospective data sets consisting of labeled cases. Each of the cases was represented by computer extracted features obtained from ultrasound (U.S.) images of breast mass lesions. Each set consisted of labeled and “mock” unlabeled samples (i.e., cases for which the truth was ignored in that specific experiment for the purpose of assessing the effect of unlabeled data). For each experimental run, cases were selected, on a by-lesion basis, according to specific sampling criteria, including clinically relevant cancer prevalence percentages with respect to both the labeled and unlabeled data, as well as varying the total number of labeled and unlabeled cases used. After generating these samples, the algorithms were trained and tested, with and without the unlabeled data. The subsections below review our approach in detail.

CADx breast ultrasound data set

The U.S. data characterized in this study consists of clinical breast lesions presented in images acquired at the University of Chicago Medical Center. Lesions were labeled according to pathological truth, determined either by biopsy or radiologic report and collected under HIPAA-compliant IRB protocols.

The U.S. image breast lesion feature data sets were generated from previously developed CADx algorithms at the University of Chicago.^{18, 19, 20, 21} Based on the manually identified lesion center, the CADx algorithm performed automated-seeded segmentation of the lesion margin followed by computerized feature extraction. Morphological, texture, and geometric features, as well as those related to posterior acoustic behavior, were extracted from the images. Further details regarding the previously developed features used here can be found in the provided references.^{18, 19, 20} Table 1 summarizes the content of the U.S. databases used, including the total number of lesion features extracted. The benign ultrasound lesions can be subcategorized as benign solid masses and benign cystic masses. This study only considered the binary classification task of distinguishing between cancerous vs noncancerous (termed malignant and benign) lesions. The empirical cancer prevalence for the first data set was approximately 14% and 50% for the independent testing data set. Again, all sampling and performance evaluations were conducted on a by-lesion basis, as multiple U.S. images may be associated with a single unique lesion. In such an instance, classifier output from all associated images for a single physical lesion case is averaged.

Table 1.

Feature database composition.

Data set	Total number of images	Number of malignant lesions	Number of benign lesions	Total number of lesion features calculated
Training and cross-validation set	2956	158	968 (401 mass; 567 cystic)	81
Independent test set	369	54	47 (34 mass; 13 cystic)	81

Frameworks for incorporating unlabeled data in CADx

General framework

The approaches considered here build on the geometric intuitions motivating the design and use of nonlinear DR techniques. This framework assumes that knowledge limited to the underlying marginal probability distribution P_x, i.e., without labeling, can contribute toward identifying better classification decision functions for the task of modeling the conditional probability P(y|x), where y is the target class label. This requires that if two points x₁ and x₂ are close according to the intrinsic geometry of P_x, the conditional probabilities P(y|x₁) and P(y|x₂) are likely to be similar.⁴ Algorithmic details applying this concept using two different techniques are provided below (Table 2). It is important to note that all these methods assume that the unlabeled data are from the same underlying population as the labeled data and that both are unbiased samples (possibly conditional on truth for the labeled data). Therefore, in the form described here, they are not designed to compensate for verification bias and similar sampling issues. Additionally, we note that for finite sample data sets, one cannot know with certainty if a sample satisfactorily represents the underlying population probability distribution. However, as the data set size increases, the quality of the underlying marginal distribution representation is expected to improve.

Table 2.

Summary of the four approaches explored for incorporating unlabeled data in breast CADx.

Method type		Stage 1	Stage 2
		Unsupervised DR	Supervised classifier
1	Transductive DR regularization	PCA (linear)	BANN
2	Transductive DR regularization	Laplacian eigenmaps (nonlinear)	BANN
3	Transductive DR regularization	t-SNE (nonlinear)	BANN
4	Manifold regularization	Combined stages using semisupervised algorithm: LapSVM

TDR-R approach

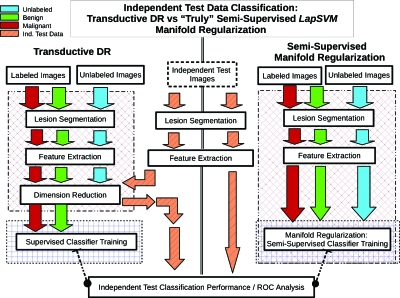
As previously stated, features are extracted in the same way for malignant and benign lesions as well as for and labeled and unlabeled lesions. Therefore unsupervised DR can be applied to data sets made of both labeled and unlabeled data in a straightforward manner (stage 1, Figs. 23). Next, a supervised classifier is trained using only the labeled samples, with feature information expressed in the reduced dimensionality representation (stage 2, Figs. 23). Conceptually, the DR mapping acts as the agent through which the transductive learning principle is accomplished. Specifically, because the structure of the DR-generated “point-cloud” is dependent on the presence of the unlabeled data, this influence acts as a regularizing force on the reduced-representation of the labeled cases, and hence the term TDR-R. Figure 3 provides an overview of the training and testing (on an independent test data set) of a breast CADx algorithm scheme incorporating TDR-R. It should also be noted that the TDR-R mappings considered here are, in general, nonparametric, reflected by the requirement that they must be recomputed with each new set of data. In practice, a potential computational limitation may be incurred due to the requirement to recompute the DR mapping for whenever new data needs to be analyzed. However, such concerns are expected to dissipate in time with the rapid, ongoing advance of computing technology, i.e., multicore processors and “grid” computing. Methods such as nearest neighbors (NN) approximations and the Nyström approximation can be used to estimate a lower-dimensional mapping directly on new test data without including them into the DR process.²² However, these approaches are not exact and often result in inconsistent performance. Thus, we decided to start exploring the potential of unlabeled data using transductive means. Because the test data must be introduced (albeit indirectly in an unsupervised fashion) during the training process, this approach is nonideal and computationally costly. New approaches are under development aimed at overcoming these potential weaknesses.²³

Figure 3.

Schematic diagram illustrating the side by side comparison showing how new independent test data are handled for the TDR-R (left side) and MR (right side) algorithm workflows that incorporate unlabeled data for breast CADx.

First stage: Combining labeled and unlabeled features in unsupervised dimension reduction

Mathematically, the general problem of dimensionality reduction can be described as: Provided an initial set x₁,…,x_k of k points in Rⁿ, discover a set $x_1^{\prime },\dots ,x_k^{\prime }$ in R^m, where m⪡n, such that $x_i^{\prime }$ sufficiently describes or “represents” the qualities of interest found in the original set x_i. For the specific context of high-dimensional breast lesion CADx feature spaces, ideally, such lower-dimensional mappings should help to reveal relevant structural information associated with the categorization of the lesion subtypes and disease status for a population of breast image data.

Described briefly below are three DR techniques, one linear, and two nonlinear, respectively: Principal component analysis (PCA), Laplacian eigenmaps, and t-SNE. The latter two methods were chosen because of their distinct approaches to nonlinearity and local structure. A brief description of these approaches is provided in the following, while a deeper discussion in the context of breast CADx can be found in our previous study.⁵ Using this previous study as a heuristic reference point, in these experiments, beginning with all 81 features as initial input, the output reduced dimension was set to 7D for PCA, 5D for t-SNE, and 7D for the Laplacian Eigenmaps. For the PCA and Laplacian eigenmaps, we simply use the first consecutive output embeddings up to the dimension desired. For the t-SNE, the output dimension is predetermined and all outputs are used. Details are described below.

PCA linearly transforms the input matrix of data into a new orthogonal basis set ordered according the fraction of global variance captured; in other words, it performs an eigenvalue decomposition of the data covariance matrix.²⁴ Lacking the ability to explicitly account for nonlinear and local structure, and hence assumed less likely to make efficient use of unlabeled data for regularizing labeled input used to train supervised classifiers, this linear dimension reduction method is included experimentally for comparison purposes only.

Building off of spectral graph theory, Laplacian eigenmaps, proposed by Belkin and Niyogi, utilize the optimal embedding properties of the Laplace–Beltrami operator on smooth manifolds and its theoretical connections to the graph Laplacian.^{25, 26} Specifically, after a weighted neighborhood adjacency graph is formed using the original high-dimensional data space, eigenvalues and eigenvectors are computed for the graph Laplacian. Acting as a discrete approximation to the Laplace–Beltrami operator, the Laplacian of the point-cloud graph can be shown to preserve local neighborhood information optimally for some criteria,^{25, 26} hence motivating the use of its eigenfunctions in embedding into lower-dimensional spaces.⁶ Two parameters are required to be set for Laplacian eigenmaps: First, the number of NN for constructing the connected graph, and second, the exponential heat kernel parameter, σ_heat. Based on our previous study,⁵ we chose NN=55 and σ_heat=1. Currently, no theoretical basis exists for univocal parameter selection.

The third method considered is t-SNE, proposed by van der Maaten and Hinton.⁷ Unlike the more theoretically motivated Laplacian eigenmaps, t-SNE attacks DR from a probabilistic framework. The basis of t-SNE is to carefully define and compute pairwise similarities between all points in the original high-dimensional space and then attempt to match this distribution in some lower-dimensional embedding by calculating a corresponding set of pairwise similarities. The algorithm begins by randomly initializing points according to a Gaussian distribution in the lower-dimensional space, and then iteratively updates point positions by way of a cost function and update gradient based on the Kullback–Leibler divergence. Although such iterative and statistically oriented approaches may require orders of magnitude more computational effort, greater flexibility and generality may be possible due to the easing of theoretical formalism, provided the system is well-conditioned. In the implementation used here, PCA is first applied to the data to accelerate convergence. In addition to the target embedding dimension, a single parameter called the Perplexity must be set which aids in the control of the local scaling used for the similarity calculations. This parameter was set to 30, following our previous paper.⁵

Second stage: Using DR mapped labeled cases in the training of a supervised classifier

In order to perform supervised classification on labeled cases in the reduced mappings as noted in Fig. 2, we implemented a Markov chain Monte Carlo Bayesian artificial neural network (BANN) classifier using Nabney’s NETLAB package for MATLAB.²⁷ Provided sufficient training sample sizes, a BANN can be shown to model the ideal observer and achieve optimal classification, given a data source.²⁸ The network architecture consisted of the input layer nodes, a connected hidden layer with one node more than the input layer, and a single output target as probability of malignancy.

Truly semisupervised learning with manifold regularization approach

Belkin, Niyogi, and Sindhwani⁸ introduced the idea of MR. Using “Representer” theorems and reproducing kernel Hilbert spaces (RKHS), their key theoretical accomplishment was to discover functional solutions capable of both explicitly incorporating information from the intrinsic geometric structure of the data (including unlabeled data) and also naturally extending to the classification of future out-of-sample cases, without having to rely on transductive means.⁸ Figure 3b illustrates a side by side comparison showing how new independent test data are handled by the respective TDR-R algorithm and the MR algorithm for CADx workflows. All 81 features extracted here are input into the MR algorithm. To briefly illuminate the nature of this latter approach, first we consider general supervised learning using only labeled data, which can be framed as the following problem:

$$f^{*}=\underset{f∊H_K}{\text{arg}\text{\hspace{0.17em}min}}\frac{1}{l}\sum _{i=1}^{l}V\left(x_i,y_i,f\right)+{\gamma }_A{\Vert f\Vert }_K^2.$$ (1)

Equation 1 contains two terms, the empirical loss function (V), which attributes penalty cost for incorrect classification [e.g., the hinge loss (1−y_if(x_i))], and the regularization term ${\Vert f\Vert }_K^2$, which constrains the complexity of the function solution (f^*), defined within the Hilbert space H_k. The relative penalty imposed on the “smoothness” of a function is controlled by the parameter γ_A. Notably, the penalty norm in Eq. 1 is defined in what is called the ambient space, or the space in which the original data (in this case high-dimensional breast image CADx features) exist. Solutions of the form

$$f^{*}\left(x\right)=\sum _{i=1}^l{\alpha }_{i}K\left(x_i,x\right),$$ (2)

where K is any positive semidefinite kernel can be found with the familiar convex optimization techniques used for RKHS-based support vector machines (SVMs).²⁹

Manifold regularization works by including an additional term ${\gamma }_I{\Vert f\Vert }_I^2$, which imposes a smoothness penalty on functions linked to the structure of the underlying lower-dimensional manifold geometry defined by the intrinsic structure of P_x,

$$f^{*}=\underset{f∊H_K}{\text{arg}\text{\hspace{0.17em}min}}\frac{1}{l}\sum _{i=1}^{l}V\left(x_i,y_i,f\right)+{\gamma }_A{\Vert f\Vert }_K^2+{\gamma }_I{\Vert f\Vert }_I^2.$$ (3)

Depending on whether the marginal distribution is known or unknown, Belkin, Niyogi, and Sindhwani⁸ provide a theoretical basis for expressing solutions in terms of RKHS-based functional forms. Note that in the context of empirical sample-based applications, the true underlying distribution is not known, and thus an approximation to the intrinsic (i.e., properties are local and thus variable from point to point) geometry is required. Building off of the utility of Laplacian eigenmaps for DR embedding, the intrinsic structure of the data is approximated with the graph Laplacian in a similar fashion as described above in Sec. 3C1. This approximation is shown to also admit solutions in the familiar and convenient functional form of a RKHS, allowing for a relatively simple algorithmic implementation, as done in this research effort. The optimization problem for the approximate case is provided here,

$$f^{*}=\underset{f∊H_K}{\text{arg}\text{\hspace{0.17em}min}}\frac{1}{l}\sum _{i=1}^{l}V\left(x_i,y_i,f\right)+{\gamma }_A{\Vert f\Vert }_K^2+\frac{{\gamma }_I}{{\left(u+l\right)}^2}{\mathbf{f}}^{T}L\mathbf{f},$$ (4)

where L is the graph Laplacian, f is the decision function, and 1∕(u+l)² is the scaling factor for the Laplace operator. The u unlabeled samples are explicitly incorporated into the optimization problem above as well as in the associated solution f^* of form

$$f^{*}\left(x\right)=\sum _{i=1}^{l+u}{\alpha }_{i}K\left(x_i,x\right),$$ (5)

where K is again any positive semidefinite kernel and α is the associated weighting coefficients. This solution can then be applied to classify independent test data.

Truly SSL classifier algorithm: LapSVM

Since the solution to the above optimization problem admits the same form as standard kernel based approaches,⁸ SVM algorithms can be extended to include intrinsic regularization, this is called LapSVM. Details of the algorithmic derivation can be found in the original publication.⁸ We employed a MATLAB implementation of the LapSVM algorithm using radial-basis function kernels and setting σ to 3. The graph Laplacian was built with nearest neighbors=25 and the heat kernel parameter set to 3.⁶ Each time the LapSVM was trained, γ_A and γ_I in Eq. 4 were adjusted according to the relative ratio of labeled and unlabeled cases. Note that when γ_I=0, LapSVM reverts to the SVM solution. Although a vital component, it is important to note again that no theoretical formalism exists for optimal selection of the aforementioned parameters. We selected “reasonable” settings based off heuristic observations. Due to the finite sample size of the data, if attempts are made to tweak the parameter space excessively the risk of overfitting may become significant. Because of this concern, we postpone a more thorough investigation of the parameter configurations to future simulation studies. Again, all 81 extracted features were input into the LapSVM algorithm.

Notably, the LapSVM can also be treated in a transductive fashion (similar to those schematics shown on the left in Fig. 3) by including the independent test set data into the graph Laplacian. This approach was investigated for comparison’s sake when testing the smaller ultrasound independent test data and will be referred to as T-LapSVM.

Experimental design and sampling protocol

Different experimental configurations were considered in order to explore the possible impact of incorporating unlabeled ultrasound image feature data into CADx classification algorithms. Within the context of this classification task, we hypothesize that the two most important factors influencing performance are the number of cases involved and the prevalence of cancer for both the labeled and unlabeled data sets used, respectively. We attempted to mimic clinically relevant situations to provide some guidance to the practical design and use of CADx systems.

Due to the finite size of the available ultrasound database used here, the scope of settings possible for our experimental design is restricted. Hence, beyond a point, scenarios involving a large number of labeled or unlabeled cases cannot be modeled reliably. Additionally, we were constrained by the inherent empirical cancer prevalence in our initial data set. The cancer prevalence is approximately 14% for the entire 1126 case (2956 ROIs) diagnostic U.S. feature data set (Table 1). For the labeled supervised training∕testing we focused on smaller set sizes of 50, 100, and 150 lesions. Because the calculations are highly demanding, we explored only a limited number of unlabeled data set sizes: Small, medium, and as large as practically possible (N_UL=900). The cancer prevalence was fixed at 50% malignant for the labeled case samples and 5% malignant for the unlabeled case samples (other prevalence configurations were considered but were not included in this article due to length constraints). The table below summarizes the configurations considered (Table 3).

Table 3.

Summary of the experimental run configurations according to the number of cases used for L and UL data sets.

Number of labeled cases (L)	Number of unlabeled cases (UL)
	Small	Medium	Large
50	50	500	900
100	100	500	900
150	150	400	900

For each experimental configuration, 200 independently randomly sampled subsets were drawn, by-lesion, from the entire ultrasound feature data set and identified to the algorithm as labeled or unlabeled according to the design specifications. For each sample set, the labeled and unlabeled subsets of cases were forced to be mutually exclusive. Sampling was performed without replacement. It is important to accumulate an adequate number of samples to boost statistical power for identifying trends and overcoming the noise produced by intersample variability in performance due to the small data set sizes, which is related to sampling distribution variability. Again, due to the finite data set size limitation, it is important to note that for the larger unlabeled data sets (900 UL), the case composition will be highly similar between the larger sample sets. This is consistent with using the original data set as the population because this limits feature values and their combinations in the sampled cases. On the other hand, this is a reasonably large data set and the purpose of this paper was to explore the new methods with empirical data.

Lastly, we tested the effect of using unlabeled data during training on the separate independent test set (Table 1), obtained independently from the original larger data set.

Performance evaluation methodology

The area under the receiver operating curve (AUC) was used to quantify classifier performance because it is not restricted to a specific and likely arbitrary operating point, sensitivity or specificity. Moreover, it usually provides larger statistical power. The AUC values were estimated using the nonparametric Wilcoxon statistic computed using libraries from the Metz’s group at the University of Chicago.³⁰ Classification performance was estimated by leave-one-out (LOO), for the 50L and 100L experiments, and 0.632+ bootstrap (632+) cross-validation (CV) for the 150 L experiments and the independent test set, all on a by-lesion basis.³¹ For a given experimental configuration, for each of the 200 runs, the difference in the estimated AUC, (ΔAUC=AUC_{with unlabeled}−AUC_{without unlabeled}), was found between classification performed with and without the use of unlabeled data. The paired, nonparametric Wilcoxon signed-rank test was applied to the ΔAUC values in each 200 run sets and to each of the subgroups defined by the original AUC (without unlabeled) quartiles, i.e., top 25th, top 25th–50th, bottom 50th–25th, and bottom 25th percentile. When necessary, p-values were adjusted for multiple comparisons testing using the Holm–Sidak step-down method.^{32, 33} Because of the considerable computational requirements, especially during cross-validation, the calculations were run on a local 256 CPU computing cluster. For example, while using an Intel Xeon E5472 CPU running at 3.0 GHz, although the Laplacian eigenmaps DR usually requires less than 15 s, the t-SNE DR can take over 15 min to complete on a 1000 case U.S. data set sample.

RESULTS

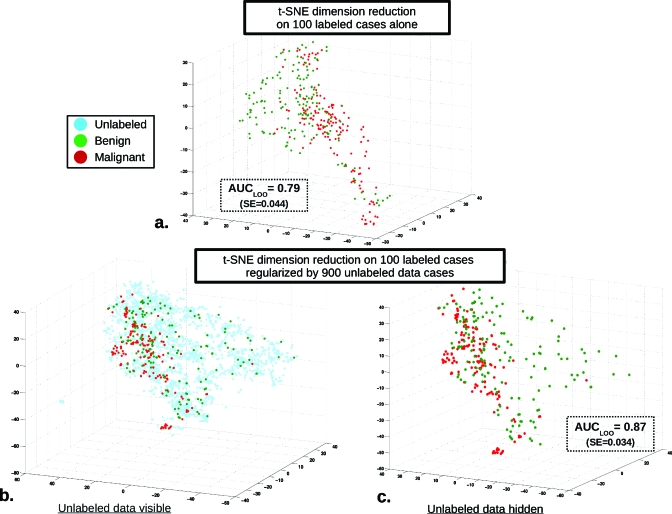
As an illustrative example, Fig. 4 displays the first three embedding dimensions produced (out of the 5D total) for the t-SNE DR mapping as well as AUC_LOO classification performance for a single data set run (out of the total 200 generated) with 100 L cases and 900 UL. The plot in Fig. 4a displays the t-SNE DR mapping produced with labeled data only, while for Figs. 4b, 4c, unlabeled data are incorporated during the mapping. For this particular single run, the estimated AUC_LOO increased from 0.79 (SE=0.044) without the use of unlabeled data to 0.87 (SE=0.034) when unlabeled data are included during the DR mapping (these standard errors refer only to the test set variability, i.e., we are analyzing the performance of the trained classifiers and not the training protocol). Importantly, this run is a single positive performance change example and is not representative of the entire set of runs or average performance.

Figure 4.

Example 3D visualization of the incorporation of unlabeled data for classifier regularization using t-SNE DR alongside the AUC_LOO classification performance for a single run data set (out of the total 200 generated) with 100 L cases and 900 UL. The three dimensions visualized are simply the first three embedding dimensions produced of the total 5D t-SNE DR. (a) Displays t-SNE DR mapping conducted with labeled data only, while for (b) and (c), unlabeled data are incorporated during the mapping. For this particular single run, classification performance as estimated by AUC_LOO increased from 0.79 (SE=0.044) without the use of unlabeled data to 0.87 (SE=0.034) when unlabeled data are included during the DR mapping. However, this single run is not representative of the entire set or average performance; rather, it is a single positive performance change example, a broad distribution of performances exists for the entire set of runs conducted (see Fig. 5).

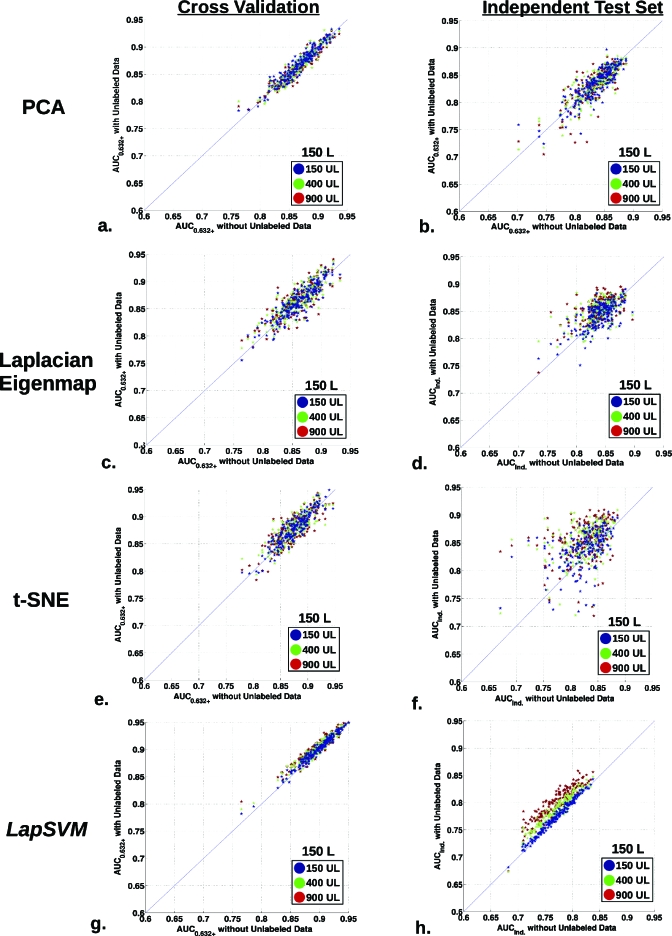
Estimated classification performance changes for the entire 200 runs and covers a wide range, as shown in scatter plots displayed in Fig. 5. Figure 5 displays the AUC_0.632+ performance for 150 L cases using 150 (blue), 400 (green), and 900 (red) UL cases for all 200 runs for each classifier. Both the CV and independent test results are shown for all methods, with the x-axis as the AUC without UL data and the y-axis as the AUC with UL data. The thin diagonal line indicates equivalence between the two estimates.

Figure 5.

Scatter plots summarizing the classification performance distribution for the entire set of the 200 generated runs. The plots display the AUC_0.632+ performance for training with 150 L cases using 150 (blue), 400 (green), and 900 (red) UL cases for all 200 runs. The CV and independent test results are shown for all methods, [(a) and (b)] PCA, [(c) and (d)] Laplacian eigenmap, [(e) and (f)] t-SNE, and [(g) and (h)] LapSVM, with the x-axis denoting the AUC without UL data and the y-axis as the AUC with UL data for each run.

A few observations can be made regarding these results. Overall, the t-SNE and Laplacian eigenmap DR methods, Figs. 5c, 5d, 5e, 5f, produced the largest variation (both positively and negatively) in AUC performance and, therefore, exhibited the noisiest distributions. For the cross-validation based performances, Figs. 5a, 5b, 5c, 5d, 5e, i.e., except the LapSVM, it is difficult to discern which side of the diagonal the majority of points lie with an unaided eye. It is possible that the cross-validation procedure counteracts or blurs out the changes produced by incorporating unlabeled data. Indeed, when using the independent test data for all the methods except the linear PCA TDR-R [Figs. 5b, 5d, 5f, 5h], it is clearer that the majority of points reside on the upper side of the equivalence diagonal, indicating that the average AUC estimate obtained with unlabeled data is higher than that obtained without unlabeled data. For the independent test data, LapSVM most evidently displays an improvement in estimated AUC increase with the use of unlabeled data even if the estimated absolute AUC performance is reduced, which might be an indication that, for this specific instance, the LapSVM algorithm was more prone to overfitting than the other three. Additionally, as indicated by the distinct layering of the blue, green, and red dots in Fig. 5h, it is clear that a higher amount of unlabeled data produces greater performance enhancement.

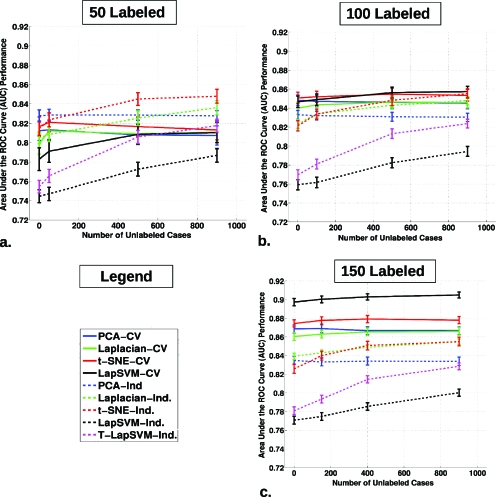
The AUC estimate distribution across the 200 generated runs can be condensed into a mean AUC and plotted according to the number of UL data included in the algorithm as shown in Fig. 6 for the use of 50, 100, and 150 L cases across all classifier methods with associated error bars, based on the variance of the sample mean for the distribution of points, such as shown in the scatter plots (i.e., we are considering the large data set as the population and ignoring validation-set variability because we are focusing on the effect this specific data set). Additionally, statistically significant differences from ΔAUC=0 for the average AUC are tabulated along with the rest of the results in Table 4, including associated p-values adjusted for multiple-hypothesis testing by employing the Holm–Sidak correction. Consistent with the scatter plots in Fig. 5, the influence of incorporating unlabeled data is most obvious for the independent set tests. For all the nonlinear approaches, Laplacian eigenmap, t-SNE, and LapSVM, the respective plots are positively sloped as more unlabeled data are added. Displaying this same trend most prominently, also included in Fig. 6, are the results for transductive LapSVM or T-LapSVM on the independent test data. Notably, the linear PCA TDR-R appears relatively flat for both the cross-validation and independent test set performance in Fig. 6. Also, as seen in Fig. 6, the mean AUC increases from approximately 0.78 at 50 L to 0.85 at 100 L, and finally close to 0.90 for 150L for the LapSVM CV. This trend clearly indicates the performance advantage of using more labeled data during training. For this data set, on a per case basis, unlabeled data appear to have less impact on average performance gains. This is to be expected because unlabeled data lack the variable that we are trying to predict: Whether a case is cancerous or not. However, as mentioned earlier, unlabeled cases are frequently less resource consuming to acquire and put to use, and often a collection of unlabeled or poorly labeled data is readily available besides the labeled data.

Figure 6.

The average AUC_{cross-validation} and AUC_independent classification performance, with associated error bars, for all 200 runs, plotted against the number of UL data incorporated in the given algorithm. Three plots are shown for (a) 50, (b) 100, and (c) 150 L cases including during the algorithm training, respectively.

Table 4.

Results for the average change in AUC due to the use of unlabeled data are shown using (a) cross-validation data and (b) independent test set data. Included are the 95% confidence intervals and statistically significant differences from ΔAUC=0 using a paired, nonparametric Wilcoxon signed-rank test, with consideration for multiple-hypothesis testing by employing the Holm–Sidak correction.

Method	Number of Cases		Mean ΔAUC	95% Conf. Int.		Adj. p-value	Stat. Sig.
	Labeled	Unlabeled		Lower	Upper
(a) Cross-validation results: Average ΔAUC
TDR-R: PCA	50	50	−0.0007	−0.0033	0.0031	1	NO
	100	100	−0.0009	−0.0026	0.0019	1	NO
	150	150	0.0003	−0.0014	0.0012	1	NO
	50	500	−0.0057	−0.0086	−0.0009	1	NO
	100	500	−0.0020	−0.0038	0.0011	1	NO
	150	400	−0.0014	−0.0028	−0.0004	1	NO
	50	900	−0.0055	−0.0093	−0.0011	1	NO
	100	900	−0.0037	−0.0060	−0.0002	1	NO
	150	900	−0.0019	−0.0031	−0.0006	0.4733	NO
TDR-R: Laplacian	50	50	0.0139	0.0081	0.0196	0.0017	YES
	100	100	0.0035	0.0013	0.0069	0.8847	NO
	150	150	0.0026	0.0008	0.0047	0.8513	NO
	50	500	0.0088	0.0022	0.0143	1.0000	NO
	100	500	0.0062	0.0028	0.0098	0.1432	NO
	150	400	0.0050	0.0031	0.0074	0.0012	YES
	50	900	0.0122	0.0054	0.0175	0.0549	NO
	100	900	0.0060	0.0024	0.0097	0.2089	NO
	150	900	0.0055	0.0040	0.0084	0.0001	YES
TDR-R:t-SNE	50	50	0.0044	−0.0005	0.0091	1.0000	NO
	100	100	0.0017	−0.0020	0.0048	1.0000	NO
	150	150	0.0033	0.0017	0.0051	0.0492	YES
	50	500	0.0002	−0.0073	0.0064	1.0000	NO
	100	500	0.0061	0.0022	0.0102	0.4308	NO
	150	400	0.0047	0.0023	0.0068	0.0234	YES
	50	900	0.0001	−0.0066	0.0072	1.0000	NO
	100	900	0.0052	0.0010	0.0089	1.0000	NO
	150	900	0.0036	0.0012	0.0059	0.5995	NO
MR: LapSVM	50	50	0.0084	0.0067	0.0097	3.43×10−18	YES
	100	100	0.0022	0.0018	0.0026	2.67×10−17	YES
	150	150	0.0030	0.0022	0.0035	5.56×10−11	YES
	50	500	0.0259	0.0208	0.0287	2.67×10−21	YES
	100	500	0.0105	0.0088	0.0119	4.65×10−22	YES
	150	400	0.0056	0.0046	0.0066	3.49×10−17	YES
	50	900	0.0287	0.0222	0.0314	1.40×10−20	YES
	100	900	0.0117	0.0094	0.0137	9.07×10−17	YES
	150	900	0.0070	0.0057	0.0080	3.71×10−19	YES
(b) Independent test set results: Average ΔAUC
TDR-R: PCA	50	50	0.0015	−0.0012	0.0028	1.00×1000	NO
	100	100	−0.0007	−0.0032	0.0012	1.00×1000	NO
	150	150	−0.0015	−0.0037	0.0009	1.00×1000	NO
	50	500	0.0002	−0.0032	0.0027	1.00×1000	NO
	100	500	−0.0020	−0.0050	−0.0005	1.00×1000	NO
	150	400	−0.0009	−0.0027	0.0018	1.00×1000	NO
	50	900	−0.0014	−0.0055	0.0004	1.00×1000	NO
	100	900	−0.0026	−0.0057	−0.0006	1.00×1000	NO
	150	900	−0.0012	−0.0031	0.0018	1.00×1000	NO
TDR-R: Laplacian	50	50	0.0046	0.0029	0.0093	4.80×10−02	YES
	100	100	0.0119	0.0089	0.0144	2.04×10−10	YES
	150	150	0.0048	0.0027	0.0078	1.61×10−02	YES
	50	500	0.0235	0.0207	0.0281	2.02×10−19	YES
	100	500	0.0207	0.0180	0.0244	2.19×10−18	YES
	150	400	0.0108	0.0073	0.0128	3.37×10−09	YES
	50	900	0.0333	0.0310	0.0385	2.62×10−23	YES
	100	900	0.0260	0.0227	0.0298	1.91×10−19	YES
	150	900	0.0169	0.0140	0.0198	2.21×10−17	YES
TDR-R:t-SNE	50	50	0.0094	0.0051	0.0131	2.16×10−03	YES
	100	100	0.0133	0.0082	0.0165	6.83×10−06	YES
	150	150	0.0149	0.0104	0.0187	9.79×10−08	YES
	50	500	0.0320	0.0264	0.0361	8.78×10−21	YES
	100	500	0.0286	0.0224	0.0330	3.05×10−14	YES
	150	400	0.0252	0.0193	0.0283	1.34×10−15	YES
	50	900	0.0351	0.0299	0.0389	2.29×10−20	YES
	100	900	0.0361	0.0301	0.0408	3.00×10−20	YES
	150	900	0.0304	0.0256	0.0345	1.43×10−18	YES
MR: LapSVM	50	50	0.0026	0.0017	0.0036	4.19×10−05	YES
	100	100	0.0033	0.0023	0.0038	1.24×10−10	YES
	150	150	0.0050	0.0041	0.0055	5.18×10−24	YES
	50	500	0.0309	0.0281	0.0346	1.74×10−27	YES
	100	500	0.0252	0.0224	0.0268	4.31×10−29	YES
	150	400	0.0177	0.0160	0.0190	1.43×10−30	YES
	50	900	0.0467	0.0428	0.0505	1.97×10−31	YES
	100	900	0.0381	0.0351	0.0405	2.39×10−30	YES
	150	900	0.0334	0.0311	0.0349	5.93×10−32	YES

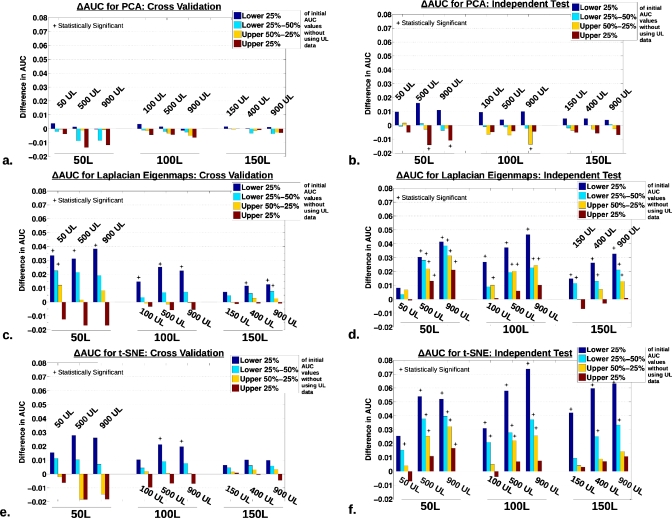
Only looking at the differences in average AUC ignores certain information, e.g., what is the effect of using unlabeled data on the variability of the resulting classifiers. As noted for Fig. 5, due to the relatively small number of labeled cases used, a wide distribution of performances estimates is produced. Dividing the 200 run sets according to their initial performance quartiles (without UL data), as described previously, allows one to observe how the use of unlabeled data appears to affect the relatively under-average, average, or above-average performing classifiers each of which was trained with a given labeled data set. The differential impact on performance caused by the incorporation of unlabeled data in these CADx schemes may consider classifier regularization effects in terms of whether differently performing classifiers tend to move closer to an average (and higher) performance after regularization. And while the restrictions of our finite data sets limit the generalizability of our results, we believe it is reasonable to assume that the overall trend in performance changes will reflect a more general property of this type of regularization.

Specifically, the initial AUC estimate performance distribution from the classifier without UL data was further decomposed in to respective quartiles: Top 25th, top 25th–50th, bottom 50th–25th, and bottom 25th percentile. Figures 78 displays the change in AUC (ΔAUC=AUC_{with unlabeled}−AUC_{without unlabeled}) according to the quartile decomposition across all classifiers for both cross-validation and independent test sets. In each plot, the quartile dependent change in AUC is ordered according to the use of 50, 100, and 150 L data moving left to right. Within each subset group, the triplet represents the use of a low (50, 100, and 150 UL), medium (400∕500 UL), and high (900 UL) number of unlabeled data. Statistically significant differences from ΔAUC=0 using a paired, nonparametric Wilcoxon signed-rank test, with consideration for multiple-hypothesis testing by employing the Holm–Sidak correction, are indicated by the ^* above the bars in Figs. 789. (Tests are again based on the distribution of points, as described previously.)

Figure 7.

Results for the TDR-R methods, highlighting classifier regularization trends due to the use of unlabeled data. The difference in AUC [ΔAUC=AUC(with UL data)−AUC(without UL data)] organized according to a quartile decomposition of the initial AUC performance without the use of unlabeled data (lower 25% in blue, lower 25%–50% in light blue, upper 50%–25% in orange, and upper 25% in dark red). In each plot, the quartile dependent change in AUC is ordered according to the use of 50, 100, and 150 L data moving left to right, during training. And within each subset group, the triplet represents the use of a low (50, 100, and 150 UL), medium (400∕500 UL), and high (900 UL) number of UL data. Statistically significant differences from ΔAUC=0 using a paired, nonparametric Wilcoxon signed-rank test, with consideration for multiple-hypothesis testing by employing the Holm–Sidak correction, are indicated by the ^* above the bars (setting α=0.05 or for adjusted p-values<0.05). The plots are organized by the respective techniques, [(a) and (b)] PCA, [(c) and (d)] Laplacian eigenmap, and [(e) and (f)] t-SNE, with cross-validation performance in the left column and the independent test set on the right.

Figure 8.

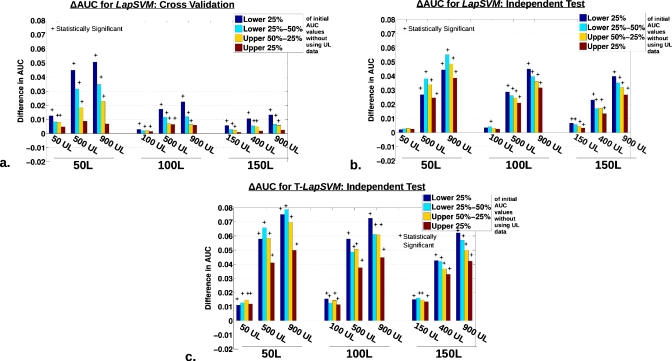
Results for the MR-based methods, highlighting classifier regularization trends due to the use of unlabeled data. The difference in AUC [ΔAUC=AUC(with UL data)−AUC(without UL data)] organized according to a quartile decomposition of the initial AUC performance without the use of unlabeled data (lower 25% in blue, lower 25%–50% in light blue, upper 50%–25% in orange, and upper 25% in dark red). In each plot, the quartile dependent change in AUC is ordered according to the use of 50, 100, and 150 L data moving left to right, during training. And within each subset group, the triplet represents the use of a low (50, 100, and 150 UL), medium (400∕500 UL), and high (900 UL) number of UL data. Statistically significant differences from ΔAUC=0 using a paired, nonparametric Wilcoxon signed-rank test, with consideration for multiple-hypothesis testing by employing the Holm–Sidak correction, are indicated by the ^* above the bars (setting α=0.05 or for adjusted p-values<0.05). The plots display (a) LapSVM for cross-validation, (b) LapSVM with the independent test, and (c) T-LapSVM on the independent test.

Figure 9.

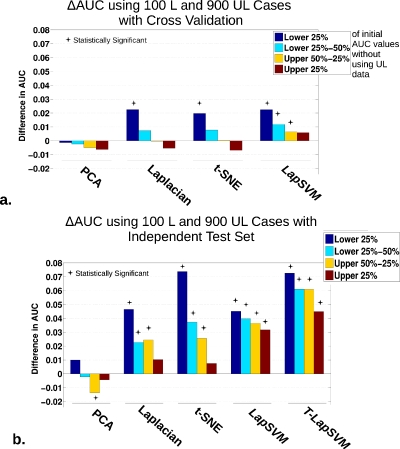
Using 100 L cases during training and highest number of UL cases (900 UL), displayed are the differences in AUC [ΔAUC=AUC(with UL data)−AUC(without UL data)] organized according to a quartile decomposition of the initial AUC_CV∕Ind performance without the use of unlabeled data (lower 25% in blue, lower 25%–50% in light blue, upper 50%–25% in orange, and upper 25% in dark red), highlighting classifier regularization trends. Statistically significant differences from ΔAUC=0 using a paired, nonparametric Wilcoxon signed-rank test, with consideration for multiple-hypothesis testing by employing the Holm–Sidak correction, are indicated by the ^* above the bars (setting α=0.05 or for adjusted p-values<0.05). The plots show (a) the cross-validation performance and (b) the independent test set performance.

The primary observation to be made from constructing the ΔAUC quartile decomposition is essentially that the use of unlabeled data most dramatically impacts the performance of the initially lower-than-average performing runs, suggestive of a potentially regularizing effect on the classifiers. As clearly indicated by the long dark blue bars in Figs. 78, the incorporation of unlabeled data provided the strongest performance boost to runs originating in the lowest 25th quartile (blue bars). Furthermore, moving from the lower quartile to the upper quartiles, respectively, the relative influence caused by including unlabeled data on classifier AUC performance is weakened. Interestingly, for a limited group of experimental configurations, such as for t-SNE and Laplacian eigenmap with 50 L data shown in Figs. 7c, 7e, the upper quartiles actually appear to trend in the negative direction.

For the CV results [Figs. 7a, 7c, 7e], it is apparent that the number of labeled data used to train impacts the consequent degree of change in AUC when UL data is added, with the largest differences appearing for when training with 50 L cases. However, with the independent data test, the effect of the number of labeled training cases was less pronounced, as seen in Figs. 7b, 7d, 7f. Turning to the impact of the number of unlabeled used overall, especially for the independent test set such as for the LapSVM in Fig. 8b, the magnitude of the ΔAUC trends upward as more unlabeled data is included.

Figure 8 displays the quartile decomposition in the comparison of all classifiers using 100 L cases during training and the highest number (900 UL cases) unlabeled data. Again, the independent data set reveal the largest changes in ΔAUC. Figure 9 also supports the idea that the linear PCA TDR-R is relatively ineffective in making use of unlabeled when assessed using AUC values, showing no indication of a sizable regularization effect.

Lastly, it is important to again emphasize the nature of the results analyzed here and the interpretation of the statistical significance reported. As noted above, the difference in AUC between classifiers incorporating unlabeled data and those which do not is based on 200 runs, each generated using samples from the same larger 1126 lesion U.S. data set. In the context of this experiment, the large data set is regarded as the “population.” Aside for the single independent test, experiments here do not (and could not) explicitly evaluate variability on expected performance changes by validation sets. Thus, statistically significant differences discovered here may not necessary generalize to other U.S. data sets at large.

DISCUSSION

General observations on the use of unlabeled data

Overall, the above results provide evidence that classification performance is potentially enhanced by incorporating unlabeled feature data during the training of breast CADx algorithms. In particular, while the change in the mean AUC due to adding UL data appeared modest relative to the impact of using more labeled data, statistically significant results were found for both the cross-validation and the independent test set evaluations. Interestingly, after further analysis of the results via the quartile decomposition, a more detailed understanding of the nature of the performance changes was developed. Specifically, chief among the observations presented above, is that classifiers trained with a labeled sample set producing lower than average performance (using cross-validation or independent test data) were more likely to be positively impacted consequently by incorporating unlabeled data via either the TDR-R or MR-based approaches. We interpreted this trend as a manifestation of the more general regularization properties one might expect to encounter by using unlabeled data in such a CADx scheme. We speculate that these observations may be consistent with the hypothesis that incorporating UL data via the use of structure-preserving DR techniques may help to more completely capture the inherent underlying distribution and thus render the classifiers trained on different samples more similar. Assuming such a theory to be true, the injection of UL data would most strongly impact sample sets which represent “poor” empirical estimations of the true underlying distribution and hence initially more likely to lead to trained classifiers with lower relative generalization performance. Consequently, the incorporation of the UL data, by aiding in more accurately capturing the inherent geometric structure of the data, could be construed as a beneficial regularizing influence on classifier performance. Conversely, for labeled sample sets which are more consistent with the inherent distribution, the introduction of additional UL cases would yield less enhancements, if any at all. Future investigations, and in particular simulations, are under way to answer these questions in more detail.

Performance comparisons of the different approaches

The PCA TDR-R based approach appeared least capable of using unlabeled data. This result was expected as PCA is linear and cannot make efficient use of local and nonlinear geometric qualities in the data structure, including when large amounts of UL data are present. Additionally, as suggested by the quartile decompositions (Fig. 789), PCA TDR-R did not appear to exhibit regularization trends present in the other methods. On the other hand, of the other approaches evaluated here, the MR LapSVM and T-LapSVM algorithms exhibited the most evident capacity for using unlabeled data to enhance classification performance. Specifically, as characterized in Figs. 5g, 5h, the classification performance of the LapSVM nearly always improved by incorporating unlabeled data. Furthermore, in addition to producing the “cleanest,” least noisy scatter plots, the LapSVM showed the clearest differentiation in the relative performance enhancement for different amounts of UL data added, as seen in the layering of the blue, green, and red points on Fig. 5h. These results are perhaps not totally unexpected as the LapSVM algorithm is more sophisticated and theoretically grounded in its design for the explicit use of unlabeled data compared to the more heuristic TDR-R based approaches considered here. It should also be noted that when only using labeled data (that is, 0 UL, e.g., the leftmost point on plots found in Fig. 6), the LapSVM mimics a plain SVM classifier using all 81 features as input. Along these lines, as mentioned earlier, we had previously shown that regularized classifiers using a large number of input features will perform similarly to classifiers trained on DR representations of the same features.⁵

However, while displaying a strong boost in estimated performance from the inclusion of unlabeled data, the LapSVM produced a lower absolute AUC performance on the independent test set compared to the other methods. It is not immediately clear why the LapSVM under-performed compared to the other methods with the independent test data. One possibility is that the kernel and Laplacian parameters used were not optimal for the independent data set. It is possible that the TDR-R methods partially avoided this dilemma by imposing stronger point-by-point regularization due to the requirement for generating a new reduced mapping when including the independent test data (which could also bias their performance evaluation making them look better on the independent test set because of that). In order to avoid further biasing the results and overfitting the algorithm to the data, we did not attempt to adjust or tweak any parameters during the performance evaluation on the independent test data set for any of the methods, and preserve the “one-shot” testing nature. This specific dilemma raises the more general and theoretically difficult problem of choosing appropriate parameters for techniques involved with manipulating and making use of unlabeled data or other unsupervised type tasks, such as clustering and DR. Moreover, this suggests that one should be very careful when assessing the performance of such an algorithm. These problems are active topics in machine learning research and we anticipate further advancements to be made in the near future.³⁴ Due to the current lack of adequate guidance on these issues, we identified this problem as beyond the scope of this manuscript. We are planning future simulation studies to more thoroughly investigate these theoretically oriented problems and how to possibly optimize the use of unlabeled data sets. We note that the primary objective of our effort here was to introduce these methods to breast CADx and provide a preliminary evaluation of the potential for using unlabeled data in the improvement of classification performance.

It should also be noted that in general, there is no reason to assume an independent test sample should necessarily produce high performance, even when classified by the optimal ideal observer. This is because the independent test set may simply consist of samples from a poorly separating subspace. In fact, as shown here in the independent test results, Fig. 5 (dotted lines), as the labeled training set size is increased (50, 100, and 150 L), although the variance decreases, the mean performance increased only slightly or not at all across all methods. This trend contrasts to the cross-validation results (Fig. 5, solid lines), in which the mean estimated AUC classification performance continued to rise considerably as the training set size is increased. This is expected as cross-validation methods, in addition to accounting for training and testing variability, attempt to estimate the expected performance of a classifier on the population. Thus, as more training cases are available both variability and expected classification performance on the population should improve.

Impact of cancer prevalence

In our experience, the cancer prevalence in the labeled training set has a limited effect on classifier performance, unless the data set is extremely unbalanced (very low or very high prevalence). The lower cancer prevalence in the unlabeled set reflects the fact that in clinical practice a “hard” truth based on biopsy or surgery is much more likely to be unavailable for benign appearing lesions than for malignant looking ones. If lesions appear sufficiently benign, they are often assigned for imaging follow-up and not all of these will be processed to be included in a clinical database (too expensive and time consuming), while those that appear to be cancerous will be biopsied and included. Of the lesions assigned to imaging follow-up, a few may be missed cancers, while of the biopsied lesions, a certain fraction will turn out to be benign. Hence, there is a “natural” division into how labeled (i.e., biopsied) cases and unlabeled cases are processed in clinical practice, which will produce a different prevalence (and might produce a bias if not done carefully). The majority frequently is unlabeled depending on the biopsy∕recall rate of a given institution. Although only results for a single cancer prevalence (50% and 5% malignant, respectively, for the labeled and unlabeled sets) were shown here, other cancer prevalence settings were investigated. Further results were suppressed for this article as the presented findings were representative of the general trends, i.e., performance characteristics were not found to change in any considerable between the different cancer prevalence configurations. While this study did not reveal any overwhelming and immediately obvious trend associated with variation in cancer prevalence and the use of unlabeled data, as a general and unavoidable limitation to the overall study conducted here, the restriction of working with a finite data set available may have limited the statistical power required to clearly observe underlying differences due to cancer prevalence. Despite these initial findings, we believe that cancer prevalence and more generally the composition of categorical lesion subtypes and structure of the population space (such as ductal carcinoma in situ, cystic, infiltrating ductal carcinoma, etc.) which make up a set of feature data, may be of fundamental importance and potentially of critical interest to understanding how to use most effectively make use of unlabeled data in future work, including practical∕clinical circumstances. Along these lines, it is of interest to consider how one might apply as additional input for training a potentially more robust classifier, the use of estimated prior, partial, or incomplete information (such as genetic, ethnic, and risk characteristics) associated with an unlabeled data distribution when coupled to an existing known labeled data set. Additionally, it is worth investigating whether certain types of CADx data may be more amenable to the usage of unlabeled than others.

Clinical relevance and future considerations

For the specific methods considered here, the MR LapSVM was currently the most practical candidate algorithm for clinical type situations, as it may be trained only once with inclusion of the unlabeled data and then later used to classify new independent test data without retraining. However, as the reality of affordable “desktop supercomputers” and scalable, real-time grid∕”cloud” computing emerges, computational demands may be of less concern.³⁵ In fact, there may be definite advantages to conducting more computationally intensive, full transductive-DR-based approaches when analyzing new test data. The use of TDR-R based techniques, such as those employing t-SNE or Laplacian eigenmaps (or other DR-based methods not considered here), may offer useful visualization, such as for the example in Fig. 4, of the comparative structure and relative geometric orientation of newly acquired UL or new test cases added along with the original known data structure. It should also be noted that because the t-SNE and Laplacian eigenmaps approach the DR problem via distinct algorithmic mechanics, complementary information may also be gathered by combining both techniques in some fashion. As hinted in our previous article, such an evaluation may provide at least qualitative, but also, as techniques continue to mature, potentially quantitative, insight into the nature of the new data sets.⁵ One such step in this direction is the recent proposal for a parametric t-SNE DR using deep neural networks.²³

Lastly, we wish to emphasize again an important point. For most realistic scenarios, labeled data will almost always be more effective at improving performance than the same amount of unlabeled data. However, even if the “per case” utility of unlabeled data is only a fraction of that for labeled data, we believe the abundance of unlabeled available data, due to modern radiology practice, will provide sufficient impetus, in many contexts, to motivate exploitation of such nascent information.

CONCLUSIONS

In summary, the incorporation of unlabeled feature data for the purpose of enhancing classification performance in the context of breast CADx was explored on four different algorithms. As discussed above, the results provide support for the hypothesis that including unlabeled data information during classifier training can act as a regularizing influence over cancer classification performance. The main limitation of this current study was the restriction of a finite, albeit relatively large, clinical database. However, we believe our results motivate future studies, both with simulations and using larger real clinical data sets. We expect a growing focus on such methods in the CADx research community with time.