Abstract
Purpose: The purpose of this work is to design a neuronal fiber tracking algorithm, which will be more suitable for reconstruction of fibers associated with functionally important regions in the human brain. The functional activations in the brain normally occur in the gray matter regions. Hence the fibers bordering these regions are weakly myelinated, resulting in poor performance of conventional tractography methods to trace the fiber links between them. A lower fractional anisotropy in this region makes it even difficult to track the fibers in the presence of noise. In this work, the authors focused on a stochastic approach to reconstruct these fiber pathways based on a Bayesian regularization framework.
Methods: To estimate the true fiber direction (propagation vector), the a priori and conditional probability density functions are calculated in advance and are modeled as multivariate normal. The variance of the estimated tensor element vector is associated with the uncertainty due to noise and partial volume averaging (PVA). An adaptive and multiple sampling of the estimated tensor element vector, which is a function of the pre-estimated variance, overcomes the effect of noise and PVA in this work.
Results: The algorithm has been rigorously tested using a variety of synthetic data sets. The quantitative comparison of the results to standard algorithms motivated the authors to implement it for in vivo DTI data analysis. The algorithm has been implemented to delineate fibers in two major language pathways (Broca’s to SMA and Broca’s to Wernicke’s) across 12 healthy subjects. Though the mean of standard deviation was marginally bigger than conventional (Euler’s) approach [P. J. Basser et al., “In vivo fiber tractography using DT-MRI data,” Magn. Reson. Med. 44(4), 625–632 (2000)], the number of extracted fibers in this approach was significantly higher. The authors also compared the performance of the proposed method to Lu’s method [Y. Lu et al., “Improved fiber tractography with Bayesian tensor regularization,” Neuroimage 31(3), 1061–1074 (2006)] and Friman’s stochastic approach [O. Friman et al., “A Bayesian approach for stochastic white matter tractography,” IEEE Trans. Med. Imaging 25(8), 965–978 (2006)]. Overall performance of the approach is found to be superior to above two methods, particularly when the signal-to-noise ratio was low.
Conclusions: The authors observed that an adaptive sampling of the tensor element vectors, estimated as a function of the variance in a Bayesian framework, can effectively delineate neuronal fibers to analyze the structure-function relationship in human brain. The simulated and in vivo results are in good agreement with the theoretical aspects of the algorithm.
Keywords: diffusion tensor imaging (DTI), Bayes decision rule, Hotelling transform
INTRODUCTION
Accurate estimation of structural connectivity in the human brain (in vivo) relies on effective segmentation of white matter pathways using diffusion tensor imaging (DTI). Analysis of images with diffusion weighting in multiple directions can characterize the anisotropy of water diffusion, which reflects the local axonal orientation and integrity of fibrous tissues. Fiber tracking, essentially a reconstruction of continuous curves from a direction field,1 relates the principal diffusion direction of water molecules to the orientation of major fibers. Principal component analysis of the tensor data is the basis of algorithms that track neuronal fiber pathways in the majority of reported works.2, 3, 4, 5, 6 However, noise and partial volume averaging (PVA) are the major reasons for erroneous fiber tracking as they deflect the estimated fiber from the true direction and its effect accumulates over the tracking process.7, 8 To minimize it, several smoothing techniques have been proposed,9, 10 including anisotropic smoothing and interpolation.11, 12
Quite a few probabilistic approaches have been proposed13, 14, 15, 16, 17 to address the problem of noise and PVA during fiber tracking. These methods can effectively track fibers in large regions of white matter since they are capable of tracking pathways in multiple directions. Uncertainty associated with fiber tracking is also modeled using Monte Carlo simulations, a nonparametric procedure for fiber tracking, with an assumption of normal noise distribution in the MRI signals.7, 18 In spite of this plethora of probabilistic fiber tracking methods, they are confined to track white matter pathways and have limited success in tracking fibers close to gray matter regions, where the fractional anisotropy (FA) is relatively low. We have previously developed a Bayesian regularization framework to track neuronal fibers in vivo.19 Uncertainty associated with tracking is modeled by optimizing a posteriori probability of the estimated tensor elements in this work. A stochastic Bayesian approach proposed by Friman et al.20 optimizes the cumulative probability over the fiber pathway unlike ours where the posteriori probability is maximized on each step. Experiments with synthetic and in vivo DTI data have shown that the above method can efficiently reduce the effects of noise and PVA. Recently, Correia et al.21 demonstrated that estimation of FA and contrast to noise ratio can be greatly enhanced after Bayesian tensor regularization.19 Encouraged by these results, we further improve the Bayesian framework by adding a probabilistic sampling to the fiber tracking process.
The purpose of the work is to analyze the structural connectivity in some vital pathways of the human language system in vivo. Language function, though sparsely observed by French surgeon Broca22 more than a century ago, has received considerable attention in cognitive neuroscience. Studies demonstrate that the structural connectivity pattern of a region in the brain determines its functional organization,23 such as connectivity between auditory cortex and prefrontal areas.24, 25, 26, 27 Recently, hemispheric functional dominance was analyzed in terms of structural connectivity between functionally active regions in the language circuit.28, 29 The former uses a non-Gaussian diffusion model,30 which does not specifically address tracking in low FA regions. Later, Powell et al.29 used a similar probabilistic streamline approach,31 where the uncertainty of fiber orientation is a function of FA. The structural connectivity is a map of connectivity based on statistical measure obtained from Monte Carlo simulations, rather than actual fiber pathways. The confidence measuring the existence of fibers is a function of distance from the initial seed regions. However, we will explicitly reconstruct fiber pathways that connect the important functionally active regions in the human language system.
We propose a novel deterministic tracking approach using stochastic sampling of the estimated tensors, based on its variance. The fiber tracking is performed multiple times from each seed location by calculating the tensors with a predefined value of mean and variance to reconstruct the fiber pathways. Functional activations in the human brain occur in gray matter regions, which overlap minimally with the white matter.32 These regions are characterized by low signal-to-noise ratio (SNR) and FA values, which may lead to erroneous estimation of the underlying fiber direction. A perturbation theory that modulates the random vector with local FA and adds it to the principal eigenvector in order to track the fiber pathway was used to analyze the structure-function relationship in our recent work.33 Though we could successfully delineate fiber bundles in language circuit, a robust estimation of major eigenvectors necessitates the development of this approach for accurate quantification of structural connectivity between functionally active regions. Briefly, we incorporate into the tracking process a stochastic sampling of the estimated major eigenvector that represents the dominant fiber orientation with maximum a posteriori probability. Synthetic data analysis demonstrates the robustness of the approach even when the SNR is low, hence offering the capability of delineating neuronal fibers connecting functionally activated regions in the gray matter.
The remainder of the paper is organized as follows. Section 2 describes the principle and the proposed probabilistic Bayesian tracking algorithm. Section 3 presents the results from synthetic images that mimic structural connections between functionally active regions and those from human DTI data acquired in vivo. Section 4 summarizes the major contributions and some of the technical issues, followed by the conclusion.
METHOD
Traditionally, fiber tracking is implemented as line propagation process, i.e., an integration of a position vector at discrete steps. Equation 1 below describes the simplest process of line propagation in tractography1
| (1) |
where si is the position vector at discrete step i, Δδ is the step size, and εi is the propagation vector. In the basic fiber tracking method (Euler method), εi is the principal eigenvector of the tensor matrix derived from the diffusion weighted image (DWI) data. This straightforward estimation of the propagation vector could be incorrect because noise and PVA (e.g., fiber crossing) can rotate the principal eigenvector relative to the true fiber orientation. To overcome this issue, εi has been estimated in numerous alternate ways, including improved methods that evaluate tensors at discrete steps (interpolation12 and estimation of the effect of tensors in voxels neighboring the point of interest). However, evaluation of the propagation vector could be based on a framework that is deterministic, probabilistic, or a combination of both. To reliably track the fiber pathway, we implemented a Bayesian principle that maximizes the posteriori probability. This involves deterministic calculation of tensor elements (assumed to be multivariate normal) from observed variables, followed by a stochastic sampling modulated with the variance of the estimated tensor. We will briefly describe the formulation of the Bayes decision rule to track the neuronal fibers.
Bayesian principle
The Bayesian decision rule is centered on a simple theory governed by the following formula [Eq. 2]:
| (2) |
P(μj) is the a priori probability of state μj where μj denotes a possible state of nature for j=1,…,n. Similarly, P(d|μj) is the conditional probability density of the variable d if the state is μj. The posterior probability P(μj|d) is the probability of being in the state μj given the observed variable d. Hence, Bayes decision is the process of determining the value of μ that maximizes the posterior probability P(μj|d). As the cumulative probability P(d) does not depend on μj, maximizing P(μj|d) is equivalent to maximizing the product of P(d|μj) and P(μj) [Eq. 3]
| (3) |
The true fiber direction is presumably the direction which maximizes the posterior probability by incorporating all available data and minimizes the error in the estimation. To find the true direction of the propagation vector, the prior and conditional probabilities are calculated in advance. In this model, these functions are not known a priori and hence should be modeled using the multivariate normal distribution. The Bayes decision rule is applied to the diffusion tensor instead of its major eigenvector. As the derived diffusion tensor matrix from the DWI data is symmetric in nature, six independent upper diagonal terms, called the tensor element vectors, d=(D11,D22,D33,D12,D13,D23)t, are assumed to be multivariate normal d∼N(μ,Σ), where μ represents the true unknown tensor element vector and ∑ is the covariance matrix. The variance of the measured tensor element vector is associated with the uncertainty due to noise and PVA. The prior probability P(μj), which is calculated from the tensor element vectors in the neighboring voxels of the point of interest, is also assumed to be multivariate normal, i.e., μj∼N(m,ϕ). Both conditional and prior probabilities can be explicitly described by the equations below. The posterior probability, being the product of 2, also possesses normal distribution P(μj|d)∼N(η,ψ). Readers interested in detailed analysis may refer to our previous work19 for the analytical solutions that maximize the posterior probability.
| (4) |
| (5) |
Consequently, the estimated mean value of the tensor element vector is the result of a one step analytical calculation, rather than a computationally expensive optimization procedure. The expected mean vector and covariance matrix that maximize posterior probabilities are as below [Eq. 6]
| (6) |
The covariance ψ of the estimated tensor element vector η in this case is smaller than the covariance of multivariate normal in both conditional and prior probability density functions as they are positive definite. This indicates that the optimal solution has reduced the uncertainty in estimating the tensor elements. The optimized six components of the mean vector are required to construct the symmetric tensor matrix and the dominant fiber orientation while tracking fibers. In this work, we focus on a tractography scheme that can delineate neuronal fibers more reliably in regions with relatively low FA. Uncertainty in estimating the dominant fiber direction increases when fiber pathways approach low FA regions, particularly when the SNR is low. Hence we proposed a probabilistic sampling technique to sample the mean vector at each step based on its covariance. At this point, we hypothesize that each point on the fiber pathway has an uncertainty associated with tracking, which is a function of noise, PVA, and the degree of anisotropy of water molecular diffusion as well. Regions of white and gray matter interface are less anisotropic; hence the covariance of the estimated tensor element vector is presumably higher than in white matter. Adaptive sampling of the estimated tensor elements, which is a function of the variance [Eq. 6], mitigates the effects of noise and PVA. Sampling of individual elements in the estimated vector is performed using the Hotelling transform.
Parameter estimation
The parameters associated with conditional and prior probability density functions, such as the covariance Σ of the tensor element vector, mean m, and covariance ϕ, are to be determined in advance. The conditional probability density function is defined on the basis of uncertainty of the measured tensor at every step in the tracking process. However, the prior probability is defined on the basis of the covariance within a volume surrounding the position where the principal eigenvector has to be evaluated. Accurate estimation of Σ and ϕ is important to calculate the variance at each step, which decides the degree of randomness to be added to the principal eigenvector. The parameter Σ depends on the DWI experimental setup in a pulsed gradient spin-echo experiment, acquired with 32 noncollinear directions. Parameter ϕ is evaluated by defining a uniform neighborhood to account for an unbiased estimation of the diffusion direction due to noise and PVA.
Estimation of Σ and d
The covariance matrix Σ of tensor element vectors can be estimated directly from the diffusion weighted data. The voxel signal intensity of a DW image assuming a normal distribution1, 7 of the zero mean noise can be described as
| (7) |
Taking the logarithm on both sides, we can have
| (8) |
A fixed number of experiments are performed, which is normally more than the number of elements in the diffusion weighting matrix . The multiple noncollinear gradient directions will generate a set of linear equations [Eq. 8]. A least-square solution for this overdetermined case [Eq. 9] can estimate the tensor element vector assigned to each voxel and the covariance Σ as mentioned below
| (9) |
| (10) |
| (11) |
Assuming noise in each experiment to be independent, Στ is a diagonal matrix with diagonal elements , where n indexes the experiment.
Estimation of m and ϕ
Theoretically, the prior probability of fiber orientation should be based on the knowledge of the fiber directions without experimental data. However, we evaluate this probability based on the knowledge about fiber orientations in neighboring regions. A relatively smaller region is included (eight voxels) in the neighborhood to evaluate these two parameters. Images may include multiple fibers, perhaps crossing fibers and regions containing both white and gray matter, if more voxels are included to calculate m and ϕ. The volume comprising eight voxels allows the model parameters to be estimated more reliably [Eqs. 12, 13]. FA is a measure of coherence of fiber orientation. Hence, calculating a weighted average of di over a smaller neighborhood suppresses the effect of noise and also PVA, unlike Lu et al.19 In fact, the eigenvectors corresponding to the mean tensor element vector m will be more biased by the neighborhood that has stronger anisotropic diffusion properties.
| (12) |
| (13) |
The vector m is the weighted mean value of the tensor element vector for k=1,…,8, where the covariance matrix ϕ is computed over the same volume and stored as a 6×6 matrix. To estimate the principal eigenvector at each step, the tensor element vector d and covariance Σ are calculated based on Eqs. 10, 11. Both of them are linearly interpolated to estimate their values at each location [Eq. 1]. The prior probability parameters (m and ϕ) are, however, estimated over a large volume and may be stored in advance to make tracking faster as these values do not change as long the tracking position is confined to the same voxel. Once a seed location is defined, the reconstruction of the pathway is performed in both directions until termination criteria are satisfied. In each iteration, the sampling volume is oriented with the propagation vector from the previous iteration [Eq. 1]. Both Σ and ϕ are calculated based on the DW experiment and should be an unbiased estimates of covariance associated with the tensor elements.
Probabilistic sampling
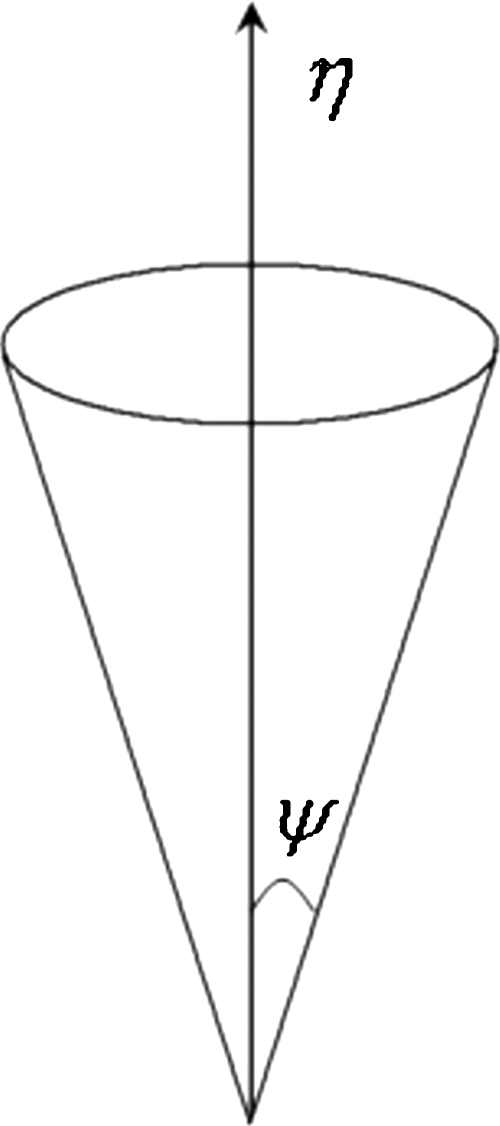
The fiber pathways are reconstructed multiple times from the same seed location. In each instance, the expected mean tensor element vector η is randomly sampled with a variance ψ, a function of covariance associated with conditional and prior probability density functions. Figure 1 gives an idea about how the mean vector η is allowed to vary within the solid angle in a controlled manner depending on the variance ψ. We applied the principle of the Hotelling transform to perform the probabilistic sampling. For example, if X is an N dimensional vector (in this case N=6, as there are six components of the tensor element vector), with an expected mean value η and covariance matrix ψ, we are free to create a new variable Y based on a linear combination of existing ones using a transformation matrix [Eq. 14]
| (14) |
The mean value of the new variable
| (15) |
Alternatively, Y can be defined as
| (16) |
yielding a mean value my=0 and covariance Cy=AψAT. The covariance matrix Cy is a diagonal matrix whose elements on the main diagonal are eigenvalues of the covariance matrix ψ. This property can be used to generate a random vector with mean η and covariance ψ. Thus we generated random vector X
| (17) |
with A=[v1,v2,⋯,v6] and . Here, v and λ are the eigenvectors and eigenvalues of covariance matrix ψ. Elements of vector y=[y1,y2,⋯,y6] are random numbers with zero mean and variance=1. Tracking multiple fibers from the same seed regions increases the possibility of delineating the fibers connecting or getting closer to the functionally active regions.
Figure 1.
Graphic representation of the tensor element vector η, randomly sampled with variance ψ.
Processing steps
After the required parameters are estimated, a seed region is defined and the tracking is performed in both directions to delineate fibers until any of the stopping criteria is met. Since an adaptive sampling strategy is suggested in a Bayesian framework, the likelihood of tracking true fibers improves with the number of times the fiber is tracked from the same seed location. The implementation of the fiber tracking procedure is described in the following steps:
-
(1)
Estimate the tensor element vector d and the covariance matrix ∑ from the experimental data in Eqs. 10, 11 (Appendix B).
-
(2)
Calculate the mean m and covariance ϕ based on the neighborhood information to estimate the prior probabilities in Eqs. 12, 13.
-
(3)
Compute the optimized mean tensor element vector η and corresponding covariance matrix ψ in Eq. 6 based on previously calculated parameters.
-
(4)
Generate the element vector X in Eq. 17.
-
(5)
Calculate the principal eigenvector εi by constructing the symmetric matrix with the elements in X.
-
(6)
Proceed to the next step with the dominant direction in Eq. 1 and repeat the procedure until any of the termination criteria is met.
We implemented simple linear interpolation to calculate the tensor element vector d and covariance ∑ during fiber tracking. Anisotropic interpolation12 is not used deliberately to have an unbiased comparison of the result with standard methods. Termination criteria, such as maximum allowable curvature and fiber length, are also implemented along with minimum FA value from the linearly interpolated FA map. As we are interested in implementing the algorithm to track the fibers in the language circuit, particularly to quantify fiber connections between functionally active regions, target specific termination criteria were implemented to delineate specific bundles that link functionally active regions.
Synthetic data analysis
We have constructed three synthetic fiber bundles to track fibers in a much similar fashion as in the language network. Tracking fibers multiple times from the same seed location is performed to increase the feasibility of locating fibers in regions where uncertainty due to noise and PVA often limits the tracking using conventional methods. To evaluate the performance of the Bayesian probabilistic approach, three synthetic data sets were constructed with high structural complexity that mimics the real fiber architecture in the human brain. The synthetic tensors were constructed for an eigenvalue trace of λ1+λ2+λ3=2.0×10−5 cm2∕s. The first synthetic data set is a 3D spiral [Fig. 2a] with a circular cross-section normal to the medial axis, where the FA is a function of the distance from the center. The FA value varies inversely with distance from the center, i.e., from 0.6 to 0.2 at the boundary. Both ends of the synthetic bundle are connected to spheres with diameter twice as large as that of the connecting bundle. However, the FA distribution is just opposite in the end spheres connecting the spiral, i.e., it varies linearly from 0.1 at the center to 0.15 at the surface. The FA value at both ends is made deliberately low to match the properties of gray matter regions.
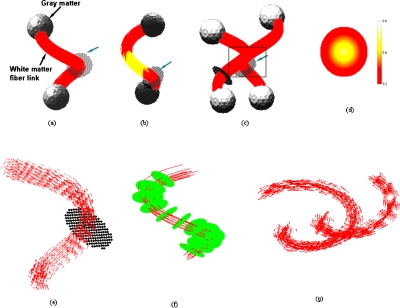
Figure 2.
Simulated data. (a) White matter spiral connecting gray matter regions at both ends. (b) Simulated fibers with a low FA region in the middle. (c) White matter pathways cross each other at the middle to simulate PVA. (d) FA distribution profile of the simulated fiber e in (a). The arrow indicates the seed planes. (e) The spirally shaped vector field representing the principal eigenvectors in the absence of noise. (f) Distances from the medial pathway are measured on uniformly spaced normal planes in a bundle where representative fibers are shown using streamline approach with SNR=60. (g) View of the direction fields associated with the principal eigenvector of each bundle [marked region in (c) expanded with direction fields].
The orientation of the principal eigenvector is parallel to the direction of the medial axis in the spirally shaped synthetic bundle. Tensors on the parallel tracts are identical to each other and are cylindrically symmetric (λ1>λ2=λ3). The eigenvalue contrast Δλ=λ1−λ2 is a complex function of FA (Appendix A). The principal eigenvectors in the end spheres are generated randomly to account for the absence of neuronal fibers that provide a guided anisotropic motion to the water molecules. The second set of data is also constructed in a similar manner where the FA is low in the middle of the spiral. The low FA region in the white matter bundle reflects a weak structural connection between regions [Fig. 2b], which may occur due to certain pathological conditions in patients. The third synthetic bundle is a combination of two spirals that cross at the middle to mimic crossing fibers and helps demonstrate the effectiveness of the algorithm to overcome partial volume averaging [Fig. 2c].
All the fiber bundles are placed inside a volume where the FA value is low (0.1). The tensor matrix is constructed with randomly generated eigenvectors (Appendix A) and any fiber leading out of the surface of the bundle will be terminated due to low FA criteria. The purpose of these experiments is to provide a comprehensive comparison between few well established methods used in tractography, such as Euler, Bayesian, and Friman’s approach, in terms of accuracy, precision, and robustness to noise and PVA.
Tracking accuracy and precision
Accuracy and precision of the proposed algorithm and comparisons with other methods were evaluated with the first synthetic data set. Due to a lack of any gold standard to perform quantitative evaluation, we demonstrate the relative variations of accuracy and precision while tracking the fibers in a bundle. First, fibers are tracked in both directions from a seed plane which is normal to the spirally shaped bundle at the middle. A Monte Carlo simulation of the fiber tracking is performed from 1000 seed locations on the seed plane ten times, each time with a different realization of noise. The addition of noise is performed by increasing the SNR from 10 to 80 in discrete steps of 10. Although the noise distribution with in vivo DTI data is Rician, Gaussian noise is a close approximation of Rician noise when the SNR is more than 5. Tracking accuracy is measured in terms of the number of successful fiber pathways that reach the regions of interests at both ends. Similarly, the precision is quantified by measuring the standard deviation of the distance from the true pathway and is measured by calculating the shortest distance on the plane normal to the medial axis.
Robustness to PVA and weak structural connectivity
Unlike the first synthetic data set, the other two sets are designed to closely resemble weak structural connectivity with a decline in fractional anisotropy toward the middle of the fiber bundle and PVA due to fiber crossing. The weaker structural connectivity is simulated by lowering the FA value in the middle portion of the spiral. The seed plane in this case is normal to the medial axis below the low FA region [Figs. 2b, 2c]. The PVA region is simulated by adding the eigenvectors of the two bundles. More specifically, we first determined the three eigenvalues based on the FA in the PVA region. Then the corresponding eigenvectors of the two separate bundles were added to generate the tensor as mentioned in Appendix A. The upper diagonal elements of the symmetric tensor matrix are considered as the tensor element vectors. Similarly, two seed planes were defined halfway between the crossing point and the center of the sphere at the lower end [Fig. 2c]. Zero mean Gaussian noise was added to the diffusion tensor matrix for both phantoms. The SNR was varied between 10 and 80 in discrete steps of 10. The fibers were tracked in either direction from the seed planes, and those reaching either end successfully are stored. The robustness of the algorithm is measured by comparing the number of fibers and the standard deviation of the distance vectors from the successful fibers to the medial axis.
The number of fibers reaching both ROIs is a reliable measure of robustness of the algorithm. However, the third data set has a common segment (PVA region) and addition of noise may lead fibers in the first bundle to terminate in the second. We therefore define a coefficient of misclassification [Eq. 18] to measure this uncertainty in tracking
| (18) |
q1 and q2: Number of fibers detected on the seed planes in bundles 1 and 2.
and : Number of fibers terminated in bundles 1 and 2 [upper gray matter regions, Fig. 2c].
The valid fibers stored for analysis purpose are those that terminate in the synthetic gray matter regions at both ends. Besides that, the other termination criteria are FA threshold (FA<0.12) and curvature limitation, i.e., if the angular deviation between two successive principal eigenvectors (curvature threshold θ) is greater than 60°. The step size used in the tracking is ∇δ=0.4 [Eq. 1] for both synthetic and in vivo data. The seed locations seen outside the bundle (Fig. 2) are prone to quick termination due to the low FA and curvature threshold criteria because eigenvectors outside the bundle volume are also randomly oriented.
Fiber tracking on in vivo DTI data
The in vivo data acquisition was performed on twelve healthy volunteers using a 3 T Philips Achieva MR scanner with a single shot echo planar pulsed gradient spin-echo imaging sequence. Diffusion weighting was performed along 32 noncollinear directions with b value of 1000 s∕mm2, repetition time TR=10 s, echo time TE=60 ms, and FOV 256×256×120 mm3. Sixty continuous slices having a matrix size of 128×128 were acquired with an isotropic spatial resolution of 2×2×2 mm3. These high resolution DWI data with SNR>50 were used for tensor calculation and diffusion tensor elements were fitted using a weighted least-squares approach. The FA maps are calculated from the tensor data. FMRI time series data were subsequently acquired (200 volumes) with the same imaging geometry while the subject performed a designated language task. The T2 weighted fMRI data with TR=1988.5 ms and TE=35 ms have lower spatial resolution of 64×64×30 with voxel size 3.5×3.5×3.5 mm3.
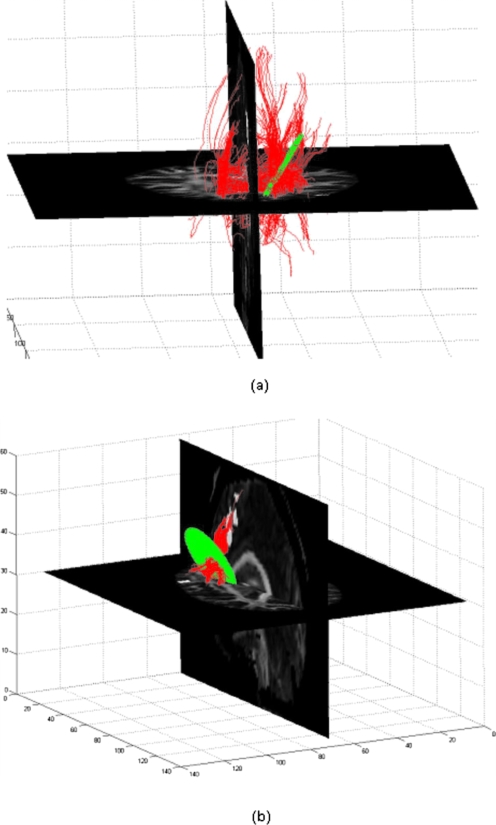
The above data underwent realignment and slice time correction to remove motion artifacts. A subjectwise analysis of the fMRI data was done using SPM5 to localize the high BOLD signal regions that corresponded to language related functional activation. The individual subjects were normalized with respect to SPM template and the transformations were applied to the corresponding binary activation maps, bringing all subjects to a common space. We then calculated the frequency of occurrence of activated voxels across the subjects and rejected those voxels which were not activated in at least three subjects. Three regions which usually are involved in language processing, namely, Broca’s, Wernicke’s, and the supplementary motor area (SMA), were localized manually as the global region of activation. The activated voxels in the individual data, which were present in the globally activated regions, were considered subjectwise functionally active regions. These regions were mapped back to the individual space by coregistering the fMRI data with respect to the DWI (b=0) data. The transformation was then applied to the binary activation maps to localize the functionally active regions in the individual subject space. All subjects except one demonstrated significant activation in all three regions of interest. We then defined a seed plane normal to the lines joining the centroids of Broca’s to the SMA (path 1) and Wernicke’s to Broca’s region (path 2). The diameter of the seed plane was 0.8 and 1.2 times the distance between the centroids of the functionally active regions connected by paths 1 and 2, respectively (all calculations were done in unit voxels). We deliberately made the seed plane larger in path 2 because dorsal and the ventral pathways connecting Broca’s to Wernicke’s region are well separated. The seed planes were uniformly sampled and the radius was defined to include all possible fiber pathways that connect the two regions, though they were masked out and were not considered for tracking. The step size and fiber termination criteria were exactly same as in case of synthetic data (step size=0.4, FA threshold <0.12, and curvature threshold θ>60°). We deliberately preferred lower FA and curvature threshold because we were interested in delineating fibers close to functionally active regions which usually are confined to gray matter region. Figure 4a shows all valid fiber pathways that cross the seed plane normal to the path joining Broca’s to the SMA region. Figure 4b has retained only those fibers which connect the functionally active regions in the concerned area. The fibers shown in Fig. 5 are plotted after tracking those five times from the uniformly sampled seed planes in both directions, each time from 2000 seed locations. However, the same seed plane was more finely sampled with 10 000 seed locations for fiber tracking using Euler’s, Friman’s, and Lu’s method. We have used our own code to delineate neuronal fibers, which was previously developed for our work12, 19 and was modified for this particular purpose.
Figure 4.
(a) An example of 3D view of all valid fiber pathways that cross the seed plane normal to the path connecting Broca’s and SMA region. (b) Shows the fibers that terminate in the concerned functionally active region. The grid shown is the seed plane.
Figure 5.
A 3D view of neuronal fibers connecting Broca’s to SMA region overlaid on FA map using (a) improved Bayesian algorithm, (b) Lu’s method, (c) Friman’s method, and (d) Euler’s method. (e) An individual case showing two separate pathways: (1) Broca’s to Wernicke’s area and (2) Broca’s to SMA. The volumes are the functionally active regions delineated based on a designated language task. The 3D view clearly shows both dorsal and ventral pathways of the arcuate fasciculus, i.e., arrow (dorsal pathway) and white (ventral pathway).
RESULTS AND DISCUSSION
Tracking accuracy and precision analysis (synthetic data)
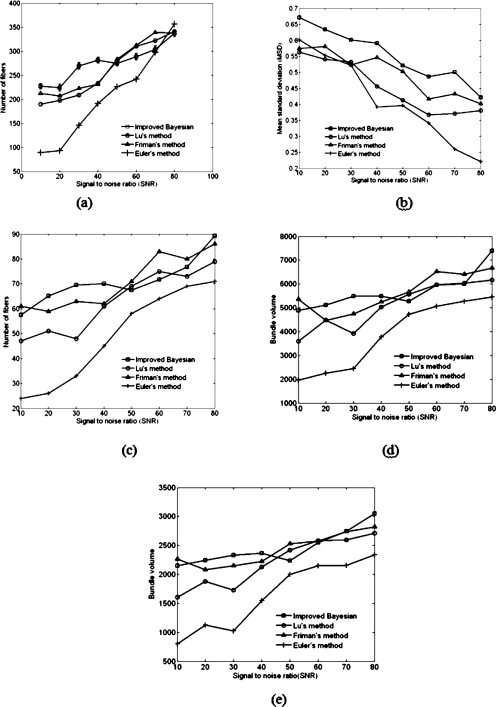
The first set of synthetic data was used in a tracking experiment to determine and compare the accuracy and precision of our approach with respect to other methods. The orientation of the principal eigenvectors are quite coherent in the noise free model unlike those found with in vivo data, and hence are easily trackable using Euler’s method [principal eigenvectors are shown in Fig. 2e on the fiber pathway]. Addition of noise, however, makes it more difficult to reconstruct the fibers, particularly when the FA is low. Our approach tracks the fibers ten times on the same seed plane, each time using 1000 seed locations for different realizations of noise. Tractography results using Euler, Friman and Lu et al. are compared with the mean number of fibers traced with our approach as we perform fiber tracking multiple times. Friman’s method was implemented to sample 10 000 points at a finer scale on the same seed plane for synthetic data, unlike what we did in our approach. The program rounds up the mean number of fibers to its nearest value as it was originally intended to compare the results to deterministic methods. It is shown that the mean number of successful fibers has an increasing trend when the SNR increases [Fig. 3a]. For high SNR, all the methods tend to have similar success rate; however, when the SNR is low, our method outperforms the other three.
Figure 3.
(a) Number of fibers vs SNR. The plot shows the mean number of fibers tracked ten times from each seed location for our method. The standard deviation for each set of measurements is also shown. (b) The standard deviation of the measured distance from the medial axis to ten representative fibers in the bundle using our approach and other three different methods. Standard deviations are plotted vs SNR. (c) Number of fibers vs SNR for the synthetic fiber bundle with a weak link between gray matter regions. Our approach shows the mean number of fibers tracked over ten simultaneous iterations from each seed position. (d) Bundle volume vs SNR calculated using different methods for the synthetic fiber bundle in Fig. 2a. (e) Similar calculation done for synthetic fiber bundle with a week structural link [Fig. 2b].
We have also randomly chosen ten fibers generated using each method and calculated the standard deviation of the distance vector from the medial pathway. The shortest distance is measured from the center of an intersecting plane, normal to the medial path to the intersecting fiber points [Fig. 2f]. The normal planes are drawn at 12 uniform intervals on the medial line. Figure 3b plots the mean value of standard deviations for each level of noise. It shows that the standard deviation in our method is higher than Friman’s and Lu’s method when the data are less noisy and almost comparable to other methods when the data are noisier. However, it decreases with increasing SNR and is minimal for the Euler method.
Tracking robustness to PVA and weak structural connectivity
Figure 3c presents the number of reconstructed fibers in a synthetic spirally shaped bundle whose middle region has low fractional anisotropy [Fig. 2b]. It can be observed that our approach performs better than other three methods in terms of number of fibers particularly when the level of noise is high and has comparable performance with less noisy data. Table 1 compares the robustness to PVA of the four algorithms quantitatively when noise is added to the data. The tensor in the PVA region is approximated by adding the eigenvectors associated with both the fiber bundles in the overlapping region; hence the resultant fiber orientation may not align with either of them. As a result, when noise is added to these data, the tracking produces erroneous fibers. The voxels in the overlapping region comprises of 132 voxels, which is shared by both fiber bundles. The calculated value of angular difference between the principal eigenvectors in these voxels varies between 52.32° and 88.05°. Each bundle is tracked from two different seed planes as shown in Fig. 2c. The vector field in Fig. 2g demonstrates the variation of direction field in both bundles. We believe this variation of angle between principal eigenvectors is a realistic simulation of fiber bundles.
Table 1.
Effect of PVA is analyzed by calculating the number of successful fibers that connect starting and terminating gray matter regions in the simulated bundles. q1 and q2 are the number of fibers that start from bundles 1 and 2. The results for the improved Bayesian approach are the mean value of the number of fibers over five runs. The terminated fibers at the other end of the respective bundle are presented in the second row. The coefficient of misclassification is in the third row and the best values for each case are shown in bold font.
| Method | SNR=10 | SNR=20 | SNR=30 | SNR=40 | SNR=50 | SNR=60 | SNR=70 | SNR=80 | |
|---|---|---|---|---|---|---|---|---|---|
| q1+q2 | q1+q2 | q1+q2 | q1+q2 | q1+q2 | q1+q2 | q1+q2 | q1+q2 | ||
| Improved Bayesian | Start | 55.8+61.4 | 70.9+73.4 | 66.9+74.8 | 64.8+70.5 | 65.6+62.5 | 75.4+82.1 | 64.6+83.0 | 86.7+94.4 |
| Terminate | 63.5+52.3 | 72.6+70.9 | 68.4+72.8 | 63.1+72.4 | 63.8+64.1 | 76.4+80.7 | 64.2+83.4 | 88.1+94.1 | |
| Mean Cmc | 0.1433 | 0.0291 | 0.0247 | 0.0266 | 0.0265 | 0.0152 | 0.0054 | 0.0094 | |
| Lu’s method | Start | 48+49 | 45+48 | 57+60 | 64+63 | 81+81 | 95+86 | 85+87 | 81+89 |
| Terminate | 50+47 | 50+43 | 51+66 | 62+65 | 79+83 | 91+90 | 80+92 | 78+92 | |
| Cmc | 0.0412 | 0.1075 | 0.1026 | 0.0315 | 0.0247 | 0.0552 | 0.0581 | 0.0353 | |
| Friman’s method | Start | 49+57 | 50+59 | 61+65 | 67+59 | 82+85 | 88+76 | 84+83 | 78+85 |
| Terminate | 56+40 | 53+56 | 57+69 | 60+66 | 79+88 | 86+78 | 79+88 | 76+87 | |
| Cmc | 0.1458 | 0.0550 | 0.0634 | 0.1904 | 0.0359 | 0.0243 | 0.0598 | 0.0245 | |
| Euler’s method | Start | 24+29 | 26+27 | 30+37 | 43+41 | 56+65 | 60+59 | 79+67 | 71+73 |
| Terminate | 28+25 | 30+23 | 27+40 | 47+37 | 58+63 | 59+60 | 76+70 | 72+72 | |
| Cmc | 0.1509 | 0.1509 | 0.0896 | 0.0952 | 0.0331 | 0.0168 | 0.0411 | 0.0139 |
The synthetic fiber bundle is simulated in a 128×128×192 image volume assuming each voxel to be isotropic. The bundle volume is calculated by summing up each voxel through which the each fiber in the bundle passes. The voxels that are common on multiple paths are considered once to avoid redundancy in calculating bundle volume. Hence the number of voxels in each bundle is a direct measure of bundle volume. We measured the bundle volume by varying the SNR, as in other analysis for two synthetic bundles shown in Figs. 2a, 2b. The overall bundle volume in both cases [(1) FA varies uniformly [Fig. 2a] and (2) low FA region at the middle [Fig. 2b]] are found to be higher in our approach. However, bundle volume using Friman’s approach is also significantly greater than Euler’s and slightly bigger than Lu’s approach for low SNR [Figs. 3d, 3e]. In some cases there were few fibers, which terminated in the gray matter area belonging to the other bundle. The metric defined in Eq. 18 quantifies the misclassification by calculating the ratio of the wrongly terminating fibers to the total number of fibers detected. Table 1 shows the number of fibers tracked successfully and the misclassification ratio. Interestingly the misclassification ratio for our approach is slightly high in comparison to Lu’s and Friman’s approach for low SNR but decreases rapidly as SNR increases.
Fiber tracking on in vivo DTI data
The in vivo tracking of neuronal fibers is performed on both pathways (path 1: Broca’s to SMA and path 2: Wernicke’s to Broca’s) in the language network in the left hemisphere because all the subjects have shown left hemispheric asymmetry while performing the language task. Figure 4a shows an example of all the fibers that could be traced on the circular grid defined normal to the path connecting Broca’s and SMA regions and Fig. 4b shows the fibers that terminate in the functionally active regions. Figures 5a, 5b, 5c, 5d shows fiber bundles in paths 1 and 2 delineated using our approach as well as other methods. For this particular case, our approach shows clearly a thicker bundle containing roughly 40% more than Euler’s method. The dorsal and ventral pathway for a particular subject is shown in Fig. 5e using our approach. The known arcuate fasciculus connecting Broca’s to Wernicke’s region was trackable in all 11 subjects using our and Friman’s approach (one subject was excluded due to undetectable activations in all three regions). The ventral path in the arcuate fasciculus could be tracked in six subjects only using our method, though there are less argument about the existence and function of this pathway in the human auditory system.34 However, Euler’s method was only able to track the dorsal connection of arcuate fasciculus in eight subjects and was unable to trace any of the ventral pathways.
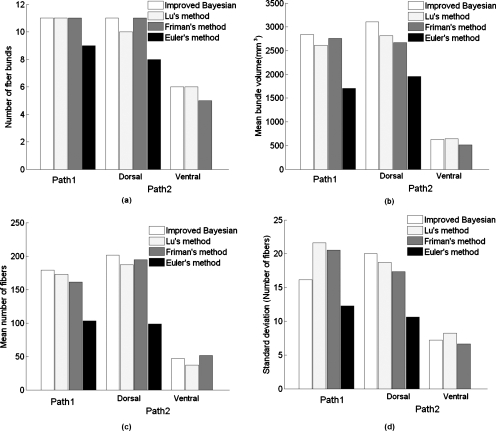
We calculated the mean bundle volume in individual pathways across subjects in each method using the following procedure. The isotropic voxel of the mean DWI data was used to calculate the bundle volume. Each voxel had a size of 2×2×2 mm3 and was subdivided in to eight subvoxels of 1×1×1 mm3 and the number of subvoxel inside which the fiber pathways lands up in each step were stored. The subvoxels that are common on multiple paths are considered only once to avoid redundancy. The number of voxels in each bundle is a direct measure of bundle volume in mm3. Figure 6 and Table 2 provide a quantitative and comparative presentation of ability of different algorithms to track fiber pathways using all the four methods, which clearly demonstrate the better performance of our method in terms of number of bundles tracked and the bundle volume. However, number of fibers, particularly in the ventral pathway connecting Wernicke’s to Broca’s region, and consistency in terms of STD of number of fibers across subjects is marginally superior in Friman’s approach, though it could track only five fiber pathways in this path.
Figure 6.
Bar plot that compares three vital parameters, i.e., (a) number of bundles tracked in two important pathways (including the dorsal and ventral part of arcuate fasciculus separately), (b) mean bundle volume, and (c) mean number of fibers, using four different approaches.
Table 2.
Quantitative presentation of the fiber path ways tracked using different methods. NFB: Number of fiber bundles, MBV: Mean bundle volume, MNF: Mean number of fibers, and STD: Standard deviation of the number of fibers.
| Method | Broca’–SMA (Path 1) | Wernicke’s–Broca’s (Path 2) | ||
|---|---|---|---|---|
| Dorsal | Ventral | |||
| Improved Bayesian algorithm | NFB | 11 | 11 | 6 |
| MBV | 2837.33 | 3109.21 | 626.06 | |
| MNF | 178.76 | 201.5 | 46.8 | |
| STD | 16.12 | 20.03 | 7.22 | |
| Lu’s method | NB | 11 | 10 | 6 |
| MBV | 2616.45 | 2819.2 | 643.17 | |
| MNF | 172.91 | 187.3 | 37.17 | |
| STD | 21.64 | 18.68 | 8.23 | |
| Friman’s method | NB | 11 | 11 | 5 |
| MBV | 2757.44 | 2672.4 | 516 | |
| MNF | 161.43 | 194.70 | 51.32 | |
| STD | 20.53 | 17.34 | 6.64 | |
| Euler’s method | NB | 9 | 8 | ⋯ |
| MBV | 1702.55 | 1958.37 | ⋯ | |
| MNF | 103.33 | 98.75 | ⋯ | |
| STD | 12.27 | 10.62 | ||
CONCLUSION
We have proposed in this work a novel method for adaptive tracking of neuronal fiber pathways in the human brain. Compared to the work we proposed earlier, there are two major contributions in the present work. First, this new framework extends the previous deterministic Bayesian tracking into an adaptive one that allows probabilistic tracking in the gray matter and performs closer to deterministic tracking in the white matter. Since brain functional regions reside in the gray matter, such an adaptive framework provides a useful tool for integrated studies of the structure-function relations in the human brain. Second, the proposed framework has been successfully applied to study the language circuits of eleven human subjects whose functionalactivations were detected. Experimental results with simulated and in vivo data are in good agreement with the theoretical aspects of the algorithm. Comparisons of the performance with conventional (Euler’s) method as well as Bayesian and Bayesian stochastic approaches indicate that a random sampling with a controlled variance can be helpful in overcoming difficulties to track fibers in such situations. Though the algorithm is computationally expensive in comparison to Lu’s method, due to the repeated tracking of the fibers from the same seed locations, the performance is superior due to its ability to delineate fibers in noisy and low FA regions. The random sampling of the estimated tensor element vectors is responsible for marginal increase in mean standard deviation using our approach. From the practical point of view, this approach can be used as a supporting tool for quantitative analysis of structure-function relationships in cognitive neuroscience as none of the methods proposed so far are able to fully quantify the structural connectivity in the language system, except few proposals to lateralize functional behavior in relation to structural connectivity. However, an effective and accurate integration of DTI and fMRI is beneficial to detailed analysis of distributed language network. Although such integrated studies are in beginning stage, we believe they will open up a new avenue for investigations into the structural basis of functional relations in human brain.
APPENDIX A: EIGENVECTORS ESTIMATION FOR SYNTHETIC FIBER BUNDLE
We have
where λ is the mean eigenvalue.
In case λ2=λ3,
Solution to the above quadratic equation if the principal eigenvalue is known
since the trace is assumed to be constant (C=2.0×10−5 cm2∕s).
Hence, λ2=(C−λ1)∕2.
If the unit principal eigenvector v1 is in the direction of the spiral, any two orthogonal unit vectors (v2 and v3⊥v1) generated randomly can construct the tensor element vector d for the synthetic data.
APPENDIX B: SIMULATION OF DTI DATA FROM IN VIVO DW DIRECTION INFORMATION
The pixel signal intensity, S in a pulse gradient spin-echo experiment is
where n=⌊nxnynz⌋ is the unit diffusion direction vector in the experiment (we considered 32 directions for the simulated data), b is the scalar diffusion weighting factor, and S0 is the signal intensity in the nondiffusion weighted data.
since the matrix D is symmetric. B is a 32×6 matrix made of direction information and Στ in Eq. 10 is a square matrix (32×32) . However, Σ is an identity matrix in case of synthetic data.
References
- Basser P. J., Pajevic S., Pierpaoli C., Duda J., and Aldroubi A., “In vivo fiber tractography using DT-MRI data,” Magn. Reson. Med. 44(4), 625–632 (2000). [DOI] [PubMed] [Google Scholar]
- Jones E. G., “Making brain connections: Neuroanatomy and the work of TPS Powell, 1923–1996,” Annu. Rev. Neurosci. 22, 49–103 (1999). 10.1146/annurev.neuro.22.1.49 [DOI] [PubMed] [Google Scholar]
- Conturo T. E., Lori N. F., Cull T. S., Akbudak E., Snyder A. Z., Shimony J. S., McKinstry R. C., Burton H., and Raichle M. E., “Tracking neuronal fiber pathways in the living human brain,” Proc. Natl. Acad. Sci. U.S.A. 96(18), 10422–10427 (1999). 10.1073/pnas.96.18.10422 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue R., van Zijl P. C., Crain B. J., Solaiyappan M., and Mori S., “In vivo three-dimensional reconstruction of rat brain axonal projections by diffusion tensor imaging,” Magn. Reson. Med. 42(6), 1123–1127 (1999). [DOI] [PubMed] [Google Scholar]
- Lazar M. and Alexander A. L., “An error analysis of white matter tractography methods: Synthetic diffusion tensor field simulations,” Neuroimage 20(2), 1140–1153 (2003). 10.1016/S1053-8119(03)00277-5 [DOI] [PubMed] [Google Scholar]
- Ding Z., Gore J. C., and Anderson A. W., “Classification and quantification of neuronal fiber pathways using diffusion tensor MRI,” Magn. Reson. Med. 49(4), 716–721 (2003). 10.1002/mrm.10415 [DOI] [PubMed] [Google Scholar]
- Anderson A. W., “Theoretical analysis of the effects of noise on diffusion tensor imaging,” Magn. Reson. Med. 46(6), 1174–1188 (2001). 10.1002/mrm.1315 [DOI] [PubMed] [Google Scholar]
- Lori N. F., Akbudak E., Shimony J. S., Cull T. S., Snyder A. Z., Guillory R. K., and Conturo T. E., “Diffusion tensor fiber tracking of human brain connectivity: Acquisition methods, reliability analysis and biological results,” NMR Biomed. 15(7–8), 494–515 (2002). 10.1002/nbm.779 [DOI] [PubMed] [Google Scholar]
- Westin C. -F., Maier S. E., Mamata H., Nabavi A., Jolesz F. A., and Kikinis R., “Processing and visualization for diffusion tensor MRI,” Med. Image Anal. 6(2), 93–108 (2002). 10.1016/S1361-8415(02)00053-1 [DOI] [PubMed] [Google Scholar]
- Chen B. and Hsu E. W., “Noise removal in magnetic resonance diffusion tensor imaging,” Magn. Reson. Med. 54(2), 393–401 (2005). 10.1002/mrm.20582 [DOI] [PubMed] [Google Scholar]
- Ding Z., Gore J. C., and Anderson A. W., “Reduction of noise in diffusion tensor images using anisotropic smoothing,” Magn. Reson. Med. 53(2), 485–490 (2005). 10.1002/mrm.20339 [DOI] [PubMed] [Google Scholar]
- Mishra A., Lu Y., Meng J., Anderson A. W., and Ding Z., “Unified framework for anisotropic interpolation and smoothing of diffusion tensor images,” Neuroimage 31(4), 1525–1535 (2006). 10.1016/j.neuroimage.2006.02.031 [DOI] [PubMed] [Google Scholar]
- Hagmann P., Thiran J. -P., Jonasson L., Vandergheynst P., Clarke S., Maeder P., and Meuli R., “DTI mapping of human brain connectivity: Statistical fiber tracking and virtual dissection,” Neuroimage 19(3), 545–554 (2003). 10.1016/S1053-8119(03)00142-3 [DOI] [PubMed] [Google Scholar]
- Parker G. J., Haroon H. A., and Wheeler-Kingshott C. A., “A framework for streamline-based probabilistic index of connectivity (PICo) using a structural interpretation of MRI diffusion measurements,” J. Magn. Reson Imaging 18(2), 242–254 (2003). 10.1002/jmri.10350 [DOI] [PubMed] [Google Scholar]
- Hosey T., Williams G., and Ansorge R., “Inference of multiple fiber orientations in high angular resolution diffusion imaging,” Magn. Reson. Med. 54(6), 1480–1489 (2005). 10.1002/mrm.20723 [DOI] [PubMed] [Google Scholar]
- Wedeen V. J., Hagman P., Tseng W. I., Reese T. G., and Weisskoff R. M., “Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging,” Magn. Reson. Med. 54(6), 1377–1386 (2005). 10.1002/mrm.20642 [DOI] [PubMed] [Google Scholar]
- Behrens T. E. J., Berg H. J., Jbabdi S., Rushworth M. F. S., and Woolrich M. W., “Probabilistic diffusion tractography with multiple fiber orientations: What can we gain?,” Neuroimage 34(1), 144–155 (2007). 10.1016/j.neuroimage.2006.09.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazar M., Weinstein D. M., Tsuruda J. S., Hasan K. M., Arfanakis K., Meyerand M. E., Badie B., Rowley H. A., Haughton V., Field A., and Alexander A. L., “White matter tractography using diffusion tensor deflection,” Hum. Brain Mapp 18(4), 306–321 (2003). 10.1002/hbm.10102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Y., Aldroubi A., Gore J. C., Anderson A. W., and Ding Z., “Improved fiber tractography with Bayesian tensor regularization,” Neuroimage 31(3), 1061–1074 (2006). 10.1016/j.neuroimage.2006.01.043 [DOI] [PubMed] [Google Scholar]
- Friman O., Farneback G., and Westin C., “A Bayesian approach for stochastic white matter tractography,” IEEE Trans. Med. Imaging 25(8), 965–978 (2006). 10.1109/TMI.2006.877093 [DOI] [PubMed] [Google Scholar]
- Correia M. M., Newcombe V. F., Carpenter T. A., and Williams G. B., “Regularization of fractional anisotropy using neighborhood information,” Proc. Intl. Soc. Mag. Reson. Med. 17, 3575 (2009). [Google Scholar]
- Broca P., “Sur le siege de la faculte du langage articule,” Bulletin de la Societe d’ anthropologie 6, 337–393 (1865). [Google Scholar]
- Passingham R. E., Stephan K. E., and Kotter R., “The anatomical basis of functional localization in the cortex,” Nat. Rev. Neurosci. 3(8), 606–616 (2002). [DOI] [PubMed] [Google Scholar]
- Jones D. K., Simmons A., Williams S. C. R., and Horsfield M. A., “Non-invasive assessment of axonal fiber connectivity in the human brain via diffusion tensor MRI,” Magn. Reson. Med. 42(1), 37–41 (1999). [DOI] [PubMed] [Google Scholar]
- Kaas J. H. and Hackett T. A., “‘What’ and ‘where’ processing in auditory cortex,” Nat. Neurosci. 2(12), 1045–1047 (1999). 10.1038/15967 [DOI] [PubMed] [Google Scholar]
- Romanski L. M., Tian B., Fritz J., Mishkin M., Goldman-Rakic P. S., and Rauschecker J. P., “Dual streams of auditory afferents target multiple domains in the primate prefrontal cortex,” Nat. Neurosci. 2(12), 1131–1136 (1999). 10.1038/16056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romanski L. M., Tian B., Fritz J. B., Mishkin M., Goldman-Rakic P. S., and Rauschecker J. P., “Reply to ‘what’, ‘where’ and ‘how’ in auditory cortex,” Belin and Zatorre,” Nat. Neurosci. 3(10), 956–966 (2000). 10.1038/79892 [DOI] [PubMed] [Google Scholar]
- Parker G. J., Luzzi S., Alexander D. C., Claudia A. M., Wheeler-Kingshott C. A., Ciccarelli O., and Ralph M. A. L., “Lateralization of ventral and dorsal auditory-language pathways in human brain,” Neuroimage 24(3), 656–666 (2005). 10.1016/j.neuroimage.2004.08.047 [DOI] [PubMed] [Google Scholar]
- Powell H. W., Parker G. J., Alexzander D. C., Symms M. R., Boulby P. A., Wheeler-Kingshott C. A., Barker G. J., Noppeney U., Koepp M. J., and Duncan J. S., “Hemispheric asymmetries in language-related pathways: A combined functional MRI and tractyography study,” Neuroimage 32(1), 388–399 (2006). 10.1016/j.neuroimage.2006.03.011 [DOI] [PubMed] [Google Scholar]
- Alexander D. C., Barker G. J., and Arridge S. R., “Detection and modeling of non-Gaussian apparent diffusion coefficient profiles in human brain data,” Magn. Reson. Med. 48(2), 331–340 (2002). 10.1002/mrm.10209 [DOI] [PubMed] [Google Scholar]
- Pajevic S. and Basser P. J., “Parametric and non parametric statistical analysis of DT-MRI data,” J. Magn. Reson. 161(1), 1–14 (2003). 10.1016/S1090-7807(02)00178-7 [DOI] [PubMed] [Google Scholar]
- Yarkoni T., Barch D. M., Garry J. R., Conturo T. E., and Braver T. S., “BOLD correlates of trial-by-trial reaction time variability in gray and white matter: A multi-study fMRI analysis,” PLoS ONE 4(1), e4257 (2009). 10.1371/journal.pone.0004257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan V., Mishra A., Newton A., Anderson A. W., Gore J. C., and Ding Z., “An integrated fMRI and DTI analysis of structure function relationship in the human language network,” PLoS ONE 4(8), e6660 (2009). 10.1371/journal.pone.0006660 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott S. K., Blank C. C., Rosen S., and Wise R. J., “Identification of a pathway for intelligible speech in the left temporal lobe,” Brain 123, 2400–2406 (2000). 10.1093/brain/123.12.2400 [DOI] [PMC free article] [PubMed] [Google Scholar]