Shear wave speed recovery in sonoelastography using crawling wave data

Abstract

The crawling wave experiment, in which two harmonic sources oscillate at different but nearby frequencies, is a development in sonoelastography that allows real-time imaging of propagating shear wave interference patterns. Previously the crawling wave speed was recovered and used as an indicator of shear stiffness; however, it is shown in this paper that the crawling wave speed image can have artifacts that do not represent a change in stiffness. In this paper, the locations and shapes of some of the artifacts are exhibited. In addition, a differential equation is established that enables imaging of the shear wave speed, which is a quantity strongly correlated with shear stiffness change. The full algorithm is as follows: (1) extract the crawling wave phase from the spectral variance data; (2) calculate the crawling wave phase wave speed; (3) solve a first-order PDE for the phase of the wave emanating from one of the sources; and (4) compute and image the shear wave speed on a grid in the image plane.

INTRODUCTION

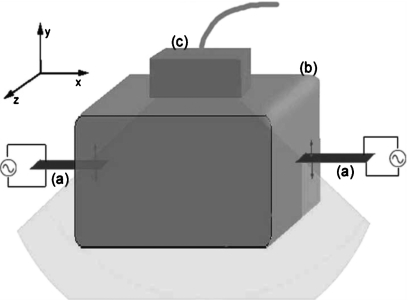
Shear stiffness imaging in tissue is a fast-moving research area inspired by the doctor’s palpation exam. Stiff regions indicate an abnormality. Experiments that are devised to create displacement that will yield tissue mechanical properties include: (1) tissue is compressed; stiff tissue compresses less; the displacement is measured using ultrasound or MR; the Lamé parameter, μ, is imaged, (Oberai et al., 2004; Barbone and Bamber, 2002; Konofagou et al., 2000; Thitaikumar and Ophir, 2007); (2) a time harmonic excitation is applied; the maximum displacement at each point in the image plane is measured using ultrasound and the displacement is imaged (Gao et al., 1995; Taylor et al., 2000; Wu et al., 2002); or the displacement, using MR, is measured at 4 to 8 equally spaced times in a period cycle, the shear wave speed or the Lamé parameter, μ, is imaged (Greenleaf et al., 1996; Kruse et al., 2000; Braun et al., 2001; Manduca et al., 2001, 2002, 2003; Ehman et al., 2006; Sinkus et al., 2007); (3) a traveling wave is created using: (a) a line source created by a sequence of interior radiation force pushes (Bercoff et al., 2002, 2004), and a primarily shear wave, with a front, travels outward from the source; the speed of the wave front is imaged (McLaughlin and Renzi, 2006a, 2006b; Tanter et al., 2008); a point source is created by an interior radiation force push and the local shear wave speed is determined by measuring the time to peak at a nearby location (Nightingale et al., 2001a, 2001b; Fahey et al., 2005; Palmeri et al., 2006); or (b) two harmonic sources that oscillate at different but nearly the same frequency; the traveling wave speed is imaged (Castaneda et al., 2009; Hoyt et al., 2006, 2007a, 2007b, 2007c, 2008a, 2008b; McLaughlin et al., 2007; Wu et al., 2004, 2006; Zhang et al., 2007, 2008). This latter experiment, termed the crawling wave experiment, provides the data for the shear wave imaging presented in this paper. Figure 1 shows a diagram of the experimental setup.

Figure 1.

Setup of the crawling wave experiment: (a) shear vibration sources, (b) biomaterial, and (c) ultrasound probe. The light gray area is the image plane.

In the crawling wave experiment, two sources with different but nearly the same harmonic excitations induce a moving interference pattern in the spectral variance imaged by a Doppler ultrasound machine, e.g., the GE Logiq 9. This moving interference pattern is termed a crawling wave (Wu et al., 2002, 2004, 2006), and the phase wave speed of this crawling wave is related to the shear wave speed of the tissue between the two sources. The phase of the crawling wave can be determined from the spectral variance and then, using, e.g., the Arrival Time algorithm (McLaughlin and Renzi, 2006a, 2006b), the crawling wave phase wave speed can be imaged; see e.g., McLaughlin et al. (2007). In phantoms, e.g., those utilized in McLaughlin et al. (2007); Hoyt et al. (2006, 2007a, 2007c, 2008a); Wu et al. (2004, 2006); Zhang et al. (2007), the crawling wave phase wave speed can be a good indicator of shear wave speed changes.

At the same time, it is possible for the inclusion to be positioned so that there are high-speed artifacts in a crawling wave phase wave speed image. These artifacts can distort the position of the inclusion and also suggest that the inclusion has a higher shear wave speed than is actually the case. This is particularly true when the harmonic sources are point sources, which is one of the cases targeted in this paper. It is less of a problem when the sources are line sources.

In this paper, we develop a new algorithm to recover the shear wave speed without such artifacts, and we test the algorithm on synthetic data. A major contribution is a derivation of a linear partial differential equation that enables calculation of the shear wave phase from both the crawling wave phase and the crawling wave phase wave speed.

MATHEMATICAL MODEL

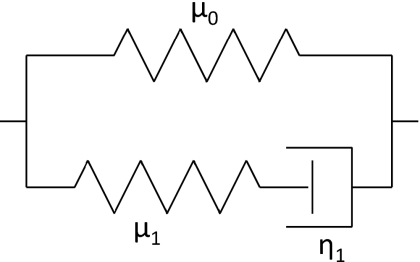
Tissue is viscoelastic. While in previous work (McLaughlin et al., 2007) we assumed that small displacements of propagating waves induced by the crawling wave experiment in tissues were governed by the equations of linear elasticity, here we choose a viscoelastic model. We have chosen the Standard Linear Solid Model (Zener Model) (Fung and Tong, 2001). This model can have several Maxwell elements in parallel. Here we have one Maxwell element in parallel with a spring element, as this model has been shown to match experimental data (Klatt et al., 2007). A diagram of our model is shown in Fig. 2.

Figure 2.

Standard linear solid model with spring (top) and Maxwell element (bottom) in parallel.

With the viscoelastic effect included only for the deviatoric part of the stress-strain relationship, the equations for this Linear Solid Model become

$$\rho {\mathbf{u}}_{tt}=\nabla \left(\lambda \nabla \cdot \mathbf{u}\right)+\nabla \cdot \left({\mu }_0\left(\nabla \mathbf{u}+\nabla {\mathbf{u}}^T\right)\right)+\nabla \cdot {\int }_0^t{\mu }_1{e}^{-\left(t-s\right)∕{\tau }_1}\frac{\partial }{\partial s}\left(\nabla \mathbf{u}+\nabla {\mathbf{u}}^T\right)ds,$$ (1)

where τ₁=η₁∕μ₁ is the relaxation time for the Maxwell element. We will denote the sum of the spring elements as μ=μ₀+μ₁.

We choose to include the viscoelastic effect for only the deviatoric part because our calculations with this model show good agreement with experimental data.

EQUATIONS FOR THE PHASE

Let ϕ₁ be the spatially-dependent phase of the solution u¹ due to the excitation from a source on the left side of the medium oscillating at a frequency ω₁. Similarly, let −ϕ₂ be the spatially-dependent phase of the solution u² due to the excitation from a source on the right side of the medium oscillating at a frequency ω₂. The Eikonal equations for ϕ₁ and ϕ₂ are derived as follows.

First, assume the geometric optics approximation (Ji et al., 2003) for u¹:

$${\mathbf{u}}^1\left(\mathbf{x},t\right)=\mathbf{A}{e}^{i{\omega }_1\left(t-{\varphi }_1\right)},$$

where

$$\mathbf{A}={\mathbf{A}}_0+\frac{{\mathbf{A}}_1}{i{\omega }_1}+\frac{{\mathbf{A}}_2}{{\left(i{\omega }_1\right)}^2}+\dots$$

is the asymptotic expansion of A. Substitute this expansion into the Linear Solid Model, Eq. 1 and write all terms of Eq. 1 in powers of ω₁. Assuming there is enough separation of scales, the coefficient of each power of ω₁ is separately set equal to zero. Here we consider only the coefficient of the term which has the highest power of ω₁. Setting this coefficient equal to zero yields

$$0=M{\mathbf{A}}_0,$$ (2)

where

$$M=\left[\left(\lambda +\mu \right)\nabla {\varphi }_1{\left(\nabla {\varphi }_1\right)}^T+\left(\mu {\left|\nabla {\varphi }_1\right|}^2-\rho \right)I\right].$$

This is the same form as in Ji and McLaughlin (2004), except here, consistent with the high-frequency approximation of geometric optics, μ=μ₀+μ₁. This also holds if we use several Maxwell elements in the viscoelastic model; in that case, $\mu ={\mu }_0+{\sum }_{\alpha =1}^N{\mu }_{\alpha }$. In order for Eq. 2 to have a nontrivial solution A₀, the matrix M must be singular. Therefore, we set det M=0, which implies that either

$$\left|\nabla {\varphi }_1\left(\mathbf{x}\right)\right|=\sqrt{\rho ∕\mu }=1∕c_s,$$ (3)

where c_s is the high-frequency limit of the shear wave speed, or

$$\left|\nabla {\varphi }_1\left(\mathbf{x}\right)\right|=\sqrt{\rho ∕\left(\lambda +2\mu \right)}=1∕c_p,$$

where c_p is the high-frequency limit of the compression wave speed. The experiment is designed so that the amplitude of the compression wave is small [see p. 2440, McLaughlin et al. (2007)], so we assume that the Eikonal equation in Eq. 3 holds.

Similarly, assuming

$${\mathbf{u}}^2\left(\mathbf{x},t\right)=\mathbf{B}{e}^{i{\omega }_2\left(t+{\varphi }_2\right)}$$

yields the same Eikonal equation, satisfied by ϕ₂; i.e.,

$$\left|\nabla {\varphi }_2\left(\mathbf{x}\right)\right|=\sqrt{\rho ∕\mu }=1∕c_s.$$ (4)

In the experiment, the Doppler spectral variance |u|² is imaged for the downward component u of u=u¹+u², which is the sum of the two shear waves propagating in opposite directions from the two sources. Under the geometric optics assumption, from the spectral variance, we obtain the phase ψ of the crawling wave (McLaughlin et al., 2007):

$$\psi \left(\mathbf{x},t\right)=\Delta \omega t-\widehat{\psi }\left(\mathbf{x}\right),$$ (5)

where

$$\widehat{\psi }\left(\mathbf{x}\right)={\omega }_1{\varphi }_1\left(\mathbf{x}\right)+{\omega }_2{\varphi }_2\left(\mathbf{x}\right)$$ (6)

is the spatially-dependent component of the phase, and Δω=ω₁−ω₂.

It is important to note that the geometric optics assumption is a far-field assumption, and we are actually in the near field. Also, this assumption models forward scattering. Therefore, we may have some artifacts due to backscattering that result from using the geometric optics assumption. We comment on artifacts due to backscattering in Section 8.

RELATIONSHIP BETWEEN THE CRAWLING WAVE SPEED AND THE SHEAR WAVE SPEED

Taking the time-derivative of Eq. 5, we obtain

$$\Delta \omega -\left(\frac{\nabla \widehat{\psi }}{\left|\nabla \widehat{\psi }\right|}\cdot \frac{d\mathbf{x}}{dt}\right)\left|\nabla \widehat{\psi }\right|=0.$$

The term in parenthesis is the time derivative of the phase in the direction normal to lines of constant phase $\left(\widehat{\psi }=\text{const}\right)$. Thus the phase wave speed $c_{\widehat{\psi }}$ of the crawling wave phase satisfies the Eikonal equation

$$c_{\widehat{\psi }}\left|\nabla \widehat{\psi }\right|=\Delta \omega .$$ (7)

Here we assume ω₁>ω₂. See also Osher and Sethian (1988); Sethian (1999); Osher and Fedkiw (2002).

We can derive a relationship between the shear wave speed, c_s, and the crawling wave speed, $c_{\widehat{\psi }}$, from Eqs. 3, 4, 7 as follows:

$$\frac{{\left(\Delta \omega \right)}^2}{c_{\widehat{\psi }}^2}={\left|\nabla \widehat{\psi }\right|}^2={\omega }_1^2{\left|\nabla {\varphi }_1\right|}^2+{\omega }_2^2{\left|\nabla {\varphi }_2\right|}^2+2{\omega }_1{\omega }_2\nabla {\varphi }_1\cdot \nabla {\varphi }_2=\frac{4{\omega }_1{\omega }_2}{c_s^2}\left({\text{cos}}^2\left(\theta ∕2\right)\right)+\frac{{\left(\Delta \omega \right)}^2}{c_s^2},$$

where cos θ=(∇ϕ₁⋅∇ϕ₂)∕(|∇ϕ₁|⋅|∇ϕ₂|). Then, with an error of order Δω∕ω₁, the relationship between c_s and $c_{\widehat{\psi }}$ is expressed as

$$c_s=\frac{2\sqrt{{\omega }_1{\omega }_2}}{\Delta \omega }\left|\text{cos}\left(\theta ∕2\right)\right|c_{\widehat{\psi }}.$$ (8)

We can see in Eq. 8 that the shear wave speed is almost a constant scaled factor of the crawling wave speed. If the two shear waves are propagating directly toward each other, and their lines of constant phase are parallel, then θ=0 and |cos(θ∕2)|=1, and the shear wave speed is exactly a scaled factor $2\sqrt{{\omega }_1{\omega }_2}∕\left(\Delta \omega \right)$ times the crawling wave speed. If we assume this estimate holds and estimate c_s by the linear relationship, we obtain

$$c_{\widehat{\psi },s}=\frac{2\sqrt{{\omega }_1{\omega }_2}}{\Delta \omega }{c}_{\widehat{\psi }}\approx c_s.$$

We call this estimate the scaled crawling wave speed. This is the imaging functional F in the preceding paper, McLaughlin et al. (2007).

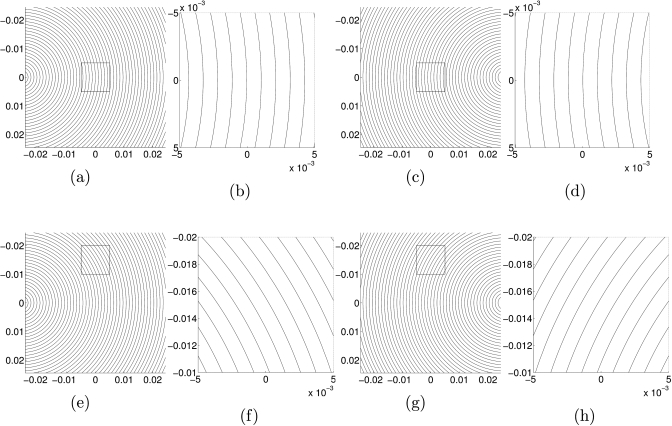
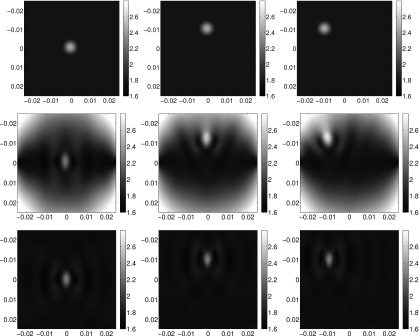
The lines of constant phase of one source may not be parallel to the lines of constant phase associated with the second source. We explain this further. First, consider a single shear wave propagating from a point source in a homogeneous medium. The wave begins by propagating away from the source in all directions at the same speed. Thus the only place where the wave would be propagating straight across the medium would be at points that lie on the horizontal line going through the point source. Now consider two shear waves in a homogeneous medium. At points that lie on the horizontal line between the two point sources, the two waves propagate in exactly opposite directions, so |cos(θ∕2)|=1. However, at any point above or below that line, neither wave is propagating directly across the medium, and so the two waves are not propagating in exactly opposite directions. See Fig. 3 for wavefront images in a constant medium.

Figure 3.

Wavefronts in a homogeneous medium. (a) and (e): wavefronts due to a single point source at (−0.025,0). (b) and (f): closeups of the regions outlined in (a) and (e). (c) and (g): wavefronts due to a single point source at (0.025,0). (d) and (h): closeups of the regions outlined in (c) and (g).

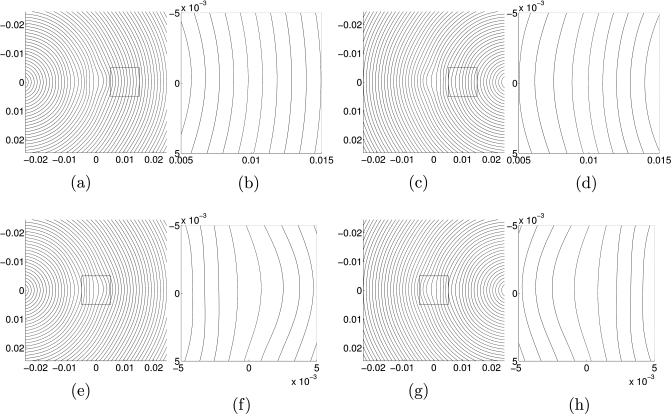
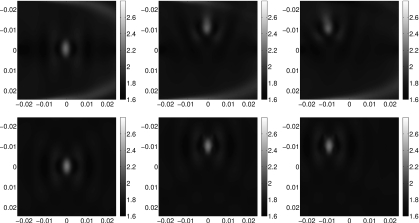
Second, consider just one shear wave in an inhomogeneous medium with an inclusion on the horizontal line through the point source. The shear wave propagates in a horizontal direction on that line, and nearly horizontal direction in a neighborhood about that line. When the wave reaches the inclusion, it travels faster through it than it does through the areas above and below the inclusion. Thus, after the wave has passed through the inclusion, the shape of the wavefront has changed. Before the inclusion, the front was nearly vertical in a neighborhood of the horizontal line from the source, whereas after the wave reaches the inclusion, the wave front is much more rounded. Therefore, the area in which the wave is propagating approximately straight across the medium is much smaller. When we have two shear waves propagating in opposite directions whose fronts both have a very round shape, the approximation θ≈0 is even less accurate. The approximation contains more error when the inclusion does not lie on the horizontal line between the two sources, because both waves enter the inclusion at directions that, even on initiation, are not horizontal. See Fig. 4 for wavefront images in an inhomogeneous medium.

Figure 4.

Wavefronts in an inhomogeneous medium with a polynomial inclusion located at the center of the image plane. (a) and (e): wavefronts due to a single point source at (−0.025,0). (b) and (f): closeups of the regions outlined in (a) and (e). (c) and (g): wavefronts due to a single point source at (0.025,0). (d) and (h): closeups of the regions outlined in (c) and (g).

These calculations suggest that: either (1) the point sources need to be sufficiently far from the region of interest; or (2) the point sources need to be replaced by sources that don’t induce these artifacts; and∕or (3) the artifacts are removed by adding a step to the algorithm that computes the shear wave speed from the crawling wave data. Note that line sources are utilized in Castaneda et al. (2009). As we show later, line sources do not produce the type of artifacts that point sources produce.

SIMULATING THE SPECTRAL VARIANCE

As discussed earlier, our model is described by the viscoelastic equations 1. Since the experiment is designed to have most of the information in one component, we make a simplification and use a wave equation model:

$$\rho u_{tt}=\nabla \cdot \left({\mu }_0\nabla u\right)+\nabla \cdot {\int }_0^t{\mu }_1{e}^{-\left(t-s\right)∕{\tau }_1}\frac{\partial }{\partial s}\nabla uds,$$ (9)

We create synthetic data by solving the viscoelastic wave Eq. 9. It is important to test the algorithm on spectral variance data obtained from the viscoelastic wave equation simulation because this data is a good representation of the data collected experimentally. To generate accurate synthetic data, we implement the following procedures.

We consider the case where μ₁ and τ₁ are constant. We write the modulus μ₀ as ${\mu }_0={\mu }_0^0+{\mu }_0^s$, where ${\mu }_0^0$ is the constant background and ${\mu }_0^s$ is the increase or decrease of μ₀ in the inhomogeneity. We write the solution u as u=u⁰+u^s where u⁰ is the homogeneous solution, solving

$$\rho u_{tt}^0=\nabla \cdot \left({\mu }_0^0\nabla u^0\right)+\nabla \cdot {\int }_0^t{\mu }_1{e}^{-\left(t-s\right)∕{\tau }_1}\frac{\partial }{\partial s}\nabla u^{0}ds.$$

Then the scattered wave u^s satisfies

$$\rho u_{tt}^s=\nabla \cdot \left({\mu }_0\nabla u^s\right)+\nabla \cdot {\int }_0^t{\mu }_1{e}^{-\left(t-s\right)∕{\tau }_1}\frac{\partial }{\partial s}\nabla u^{s}ds+f,$$

where $f=\nabla \cdot \left({\mu }_0^s\nabla u^0\right)$.

In the case of two point sources located at (x₁,y₁) and (x₂,y₂), the formula for u⁰ is:

$$u^0\left(x,y,t\right)=\frac{i}{4}{H}_0^{\left(1\right)}\left(k_1{r}_1\right)e^{i{\omega }_{1}t}+\frac{i}{4}{H}_0^{\left(1\right)}\left(k_2{r}_2\right)e^{i{\omega }_{2}t},$$

where

$$r_i=\sqrt{{\left(x-x_i\right)}^2+{\left(y-y_i\right)}^2},i=1,2$$

and

$$k_i=-{\omega }_i\sqrt{\frac{\rho }{G^0\left({\omega }_i\right)}},i=1,2,$$

where G⁰ is the homogeneous part of the complex modulus:

$$G^0\left(\omega \right)={\mu }_0^0+\frac{i\omega {\eta }_1{\mu }_1}{{\mu }_1+i\omega {\eta }_1}={\mu }_0^0+\frac{i\omega {\mu }_1{\tau }_1}{i\omega {\tau }_1+1}.$$

In the case of two line sources located at x=x₁ and x=x₂, the formula for u⁰ is

$$u^0\left(x,y,t\right)=\frac{1}{k_1}{e}^{i{k}_1\left(x-x_1\right)}{e}^{i{\omega }_{1}t}+\frac{1}{k_2}{e}^{i{k}_2\left(x_2-x\right)}{e}^{i{\omega }_{2}t}.$$

For better accuracy, we compute u⁰ using the exact formulas and we solve for only the scattered wave u^s numerically using a second-order numerical scheme. Then we compute the spectral variance:

$${\left|u\right|}^2={\left|u^0+u^s\right|}^2.$$

In addition, since u^s is an outgoing solution, we assume the Sommerfeld radiation condition for the scattering field. Since the simulation can only be performed in a finite computational domain, we need to implement appropriate absorbing boundary conditions to prevent numerical reflections of outgoing waves. Collino and Tsogka (2001) introduced the perfectly matched absorbing layer (PML) model by the split-field approach for a general hyperbolic system. Here we follow their idea and surround the interior domain of interest by artificial absorbing layers where waves are trapped and attenuated. The setup of the first-order system that is solved in the layer follows the derivation in Collino and Tsogka (2001).

The calculations here are in two dimensions, but correspond to a three-dimensional experiment. The oscillating point source in 2d corresponds to a line source oscillating perpendicular to the plane of interest in 3d. The line source in 2d corresponds to a planar source in 3d. The circular inclusion in 2d corresponds to a cylindrical inclusion in 3d.

CRAWLING WAVE SPEED IMAGES

Given the spectral variance |u|², we can recover the crawling wave speed by first computing the crawling wave arrival times by cross-correlation (Renzi, 2004; McLaughlin and Renzi, 2006a, 2006b), also including an optimization technique that encourages continuity in the arrival times, and then computing the crawling wave speed by Eq. 7. To calculate the derivatives of $\widehat{\psi }$, we use an averaging method (Anderssen and Hegland, 1999) which controls the noise in the derivatives.

We consider three examples, all with a polynomial inclusion in μ₀, but each with the inclusion centered in a different location. We solve the viscoelastic wave equation in a two-dimensional domain Ω={(x,y)∊R²:−0.025≤x≤0.025,−0.025≤y≤0.025}. We use frequencies ω₁=101∗2π and ω₂=100∗2π. We use point sources located at x=±0.025±2Δx, y=0 and line sources located at x=±0.025±2Δx. Recovered crawling wave speed images from both point sources and line sources are shown in Fig. 5, along with the exact wave speed images.

Figure 5.

Exact shear wave speed (top) and corresponding scaled crawling wave speed from 2d point sources (middle) and 2d line sources (bottom) for three polynomial inclusions.

With point sources, we see significant differences between the exact speed and the scaled crawling wave speed. In an image of the crawling wave speed, artifacts appear that do not appear in an image of the shear wave speed. The shape of the inclusion, which should be a perfect circle, becomes elongated. In some examples, depending upon the location of the inclusion in relation to the two sources, the inclusion appears to have a “tail.” This can be seen in the last two examples, which have the inclusion located close to the corner of the medium. This occurs because, as the two shear waves pass through the inclusion and into the area where the tail appears, their lines of constant phase are not parallel and their propagation directions make θ near π so that cos(θ∕2) is near zero. Given the relationship

$$c_{\widehat{\psi },s}=\frac{2\sqrt{{\omega }_1{\omega }_2}}{\Delta \omega }{c}_{\widehat{\psi }}=\frac{1}{\left|\text{cos}\left(\theta ∕2\right)\right|}{c}_s,$$

we see that having θ near π causes the scaled crawling wave speed to be much higher than the shear wave speed. It should be noted that the colorbar has been adjusted, so the high-speed artifacts are significantly higher even than the images show. With line sources, we have significantly less artifact, because θ≈0 is generally a more accurate assumption.

In these examples, with a single inclusion in a constant background, we notice that the artifact is smallest when the inclusion is halfway between the point sources. However, as we can see in the last two examples, when the inclusion is not directly in line with the two sources, the image of the crawling wave speed depicts its location to be closer to the edge of the medium than it actually is. This is a result of having point sources close to, or in, the region of interest. When we have line sources, the position of the inclusion relative to the sources does not have much effect.

RECOVERING THE SHEAR WAVE SPEED

Since the scaled crawling wave speed can give the type of artifact shown in the previous section, we now develop an algorithm to recover the true shear wave speed.

We cannot solve Eq. 8 directly without knowing the phases ϕ₁ and ϕ₂, because cos(θ∕2) depends on ∇ϕ₁ and ∇ϕ₂. An alternative possibility is to solve the following system of equations for ϕ₁, ϕ₂, and c_s:

$$\left|\nabla {\varphi }_1\right|=1∕c_s,\left|\nabla {\varphi }_2\right|=1∕c_s,$$

$$c_{\widehat{\psi }}=\frac{c_s\Delta \omega }{2\sqrt{{\omega }_1{\omega }_2}\left|\text{cos}\left(\theta ∕2\right)\right|}.$$

In this paper, we instead derive a first-order partial differential equation (PDE) for ϕ₁, where all that is needed is $c_{\widehat{\psi }},\nabla \widehat{\psi },\Delta \omega ,{\omega }_1$, and ω₂. We then solve the PDE and use the phase ϕ₁ to calculate the shear wave speed.

Derivation of the first-order PDE for the shear wave phase

We derive a first-order partial differential equation for the phase ϕ₁, beginning with the equation for the spatially-dependent phase of the crawling wave, which is given by

$$\widehat{\psi }={\omega }_1{\varphi }_1+{\omega }_2{\varphi }_2.$$

Let $\widehat{\widehat{\psi }}=\widehat{\psi }∕{\omega }_1$. We take the gradient of both sides,

$$\nabla \widehat{\widehat{\psi }}=\nabla {\varphi }_1+\frac{{\omega }_2}{{\omega }_1}\nabla {\varphi }_2$$

take the dot product of both sides with ∇ϕ₁,

$$\nabla \widehat{\widehat{\psi }}\cdot \nabla {\varphi }_1={\left|\nabla {\varphi }_1\right|}^2+\frac{{\omega }_2}{{\omega }_1}\nabla {\varphi }_2\cdot \nabla {\varphi }_1,$$

multiply the second term on the right-hand side by (|∇ϕ₂||∇ϕ₁|)∕(|∇ϕ₂||∇ϕ₁|)=1,

$$\nabla \widehat{\widehat{\psi }}\cdot \nabla {\varphi }_1={\left|\nabla {\varphi }_1\right|}^2+\frac{{\omega }_2}{{\omega }_1}\nabla {\varphi }_2\cdot \nabla {\varphi }_1\frac{\left|\nabla {\varphi }_2\right|\left|\nabla {\varphi }_1\right|}{\left|\nabla {\varphi }_2\right|\left|\nabla {\varphi }_1\right|}$$

and simplify, using the definition cos θ=(∇ϕ₂⋅∇ϕ₁)∕(|∇ϕ₂||∇ϕ₁|), where θ(x) is the angle between ∇ϕ₁(x) and ∇ϕ₂(x), giving

$$\nabla \widehat{\widehat{\psi }}\cdot \nabla {\varphi }_1={\left|\nabla {\varphi }_1\right|}^2+\frac{{\omega }_2}{{\omega }_1}\left|\nabla {\varphi }_2\right|\left|\nabla {\varphi }_1\right|\text{cos}\theta .$$

Substituting |∇ϕ₁|=1∕c_s and |∇ϕ₂|=1∕c_s, and using Eq. 8, we have

$$\nabla \widehat{\widehat{\psi }}\cdot \nabla {\varphi }_1=\frac{1+\left({\omega }_2∕{\omega }_1\right)\text{cos}\theta }{c_s^2}=\frac{\left(1+\text{cos}\theta \right)}{c_s^2}-\frac{\Delta \omega \text{\hspace{0.17em}cos}\theta }{{\omega }_1{c}_s^2}=\frac{{\left(\Delta \omega \right)}^2}{2{\omega }_1{\omega }_2{c}_{\widehat{\psi }}^2}-\frac{{\left(\Delta \omega \right)}^2}{2{\omega }_1{\omega }_2{c}_s^2}-\frac{\Delta \omega \text{\hspace{0.17em}cos}\theta }{{\omega }_1{c}_s^2}.$$

We neglect the last two terms, where the error in doing so is O(Δω∕ω₁), obtaining

$$\nabla \widehat{\widehat{\psi }}\cdot \nabla {\varphi }_1=\frac{{\left(\Delta \omega \right)}^2}{2{\omega }_1{\omega }_2{c}_{\widehat{\psi }}^2}.$$ (10)

Note that it is possible to derive and solve a PDE for ϕ₂ in the same way, letting $\tilde{\widehat{\psi }}=\widehat{\psi }∕{\omega }_2$, obtaining

$$\nabla \tilde{\widehat{\psi }}\cdot \nabla {\varphi }_2=\frac{{\left(\Delta \omega \right)}^2}{2{\omega }_1{\omega }_2{c}_{\widehat{\psi }}^2}.$$

While both ϕ₁ and ϕ₂ satisfy very similar PDEs, they have different boundary conditions on the left and right boundaries of the region of interest, and so the solutions are not the same.

Shear wave speed recovery algorithm

The shear wave speed recovery algorithm for wave equation data has the following outline:

• 1.Filter the spectral variance in time to remove all but the Δω frequency content;
• 2.Find the phase $\widehat{\psi }$ by interpreting the values of $\widehat{\psi }$ as arrival times and cross-correlating the time traces of |u|²;
• 3.Calculate $\nabla \widehat{\psi }$ and $c_{\widehat{\psi }}$, using averaging to compute the derivatives;
• 4.Solve the PDE 10 for ϕ₁;
• 5.Calculate ∇ϕ₁ and c_s, using averaging to compute the derivatives.

We note that the first step eliminates the effect of high-frequency noise in the data. For steps 2 and 3, our methods are the same as described in Section 6. Steps 4 and 5 are described in detail below.

Calculating ϕ₁ from the PDE

To find the phase ϕ₁ of the shear wave from the source on the left side of the medium, we need to solve the first order PDE:

$$\nabla \widehat{\widehat{\psi }}\cdot \nabla {\varphi }_1=\frac{{\left(\Delta \omega \right)}^2}{2{\omega }_1{\omega }_2{c}_{\widehat{\psi }}^2}.$$

To handle this equation in a stable and efficient manner, we adopt a first-order, fully-implicit upwind marching scheme which is unconditionally stable. The discretization of the PDE for the implicit upwind scheme is as follows.

If $\text{sgn}\left({\widehat{\widehat{\psi }}}_{x,i,j}\right)=\text{sgn}\left({\widehat{\widehat{\psi }}}_{y,i,j}\right)$:

$${\widehat{\widehat{\psi }}}_{x,i,j}{\delta }_{+}^x{\varphi }_{1,i,j}+{\widehat{\widehat{\psi }}}_{y,i,j}{\delta }_{-}^y{\varphi }_{1,i,j+1}=\frac{{\left(\Delta \omega \right)}^2}{2{\omega }_1{\omega }_2{c}_{\widehat{\psi },i,j}^2};$$

and if $\text{sgn}\left({\widehat{\widehat{\psi }}}_{x,i,j}\right)=-\text{sgn}\left({\widehat{\widehat{\psi }}}_{y,i,j}\right)$:

$${\widehat{\widehat{\psi }}}_{x,i,j}{\delta }_{+}^x{\varphi }_{1,i,j}+{\widehat{\widehat{\psi }}}_{y,i,j}{\delta }_{+}^y{\varphi }_{1,i,j+1}=\frac{{\left(\Delta \omega \right)}^2}{2{\omega }_1{\omega }_2{c}_{\widehat{\psi },i,j}^2},$$

where

$${\delta }_{+}^x{\varphi }_{1,i,j}=\frac{{\varphi }_{1,i,j+1}-{\varphi }_{1,i,j}}{dx};$$

$${\delta }_{-}^y{\varphi }_{1,i,j+1}=\frac{{\varphi }_{1,i,j+1}-{\varphi }_{1,i-1,j+1}}{dy};$$

$${\delta }_{+}^y{\varphi }_{1,i,j+1}=\frac{{\varphi }_{1,i+1,j+1}-{\varphi }_{1,i,j+1}}{dy}.$$

This scheme gives a diagonally-dominant linear system at every pseudo-time step x_j. The stability result follows from a von Neumann stability analysis. We choose initial conditions on the left side of the domain consistent with the source type, so that for a line source, the initial condition is

$${\varphi }_1=0,$$

and for a point source, the initial condition is

$${\varphi }_1=r_1∕c_s^0,$$

where r₁ is the distance from the source and $c_s^0$ is the high-frequency approximation of the background shear wave speed. If we have line sources, we adopt a zero Neumann boundary condition on the top and bottom boundaries. If we have point sources, then if the outflow condition is satisfied, the numerical scheme will automatically solve for values on boundary points, but if the inflow condition is required, we adopt a Dirichlet boundary condition; that is, we use the value of ϕ₁ which would be valid if there were no inclusion; i.e.,

$${\varphi }_1=r_1∕c_s^0.$$

For this simulation data, $c_s^0$ is known. For experimental data, we would have to use an estimate; for example, one could use as an estimate the results from compression tests on soft tissue similar to that being imaged, or alternatively, an average wave speed could be obtained from the time it takes for a wave initiated on one side of the tissue to propagate across the tissue.

To solve for the phase ϕ₂, we use a similar procedure except we specify initial conditions in the right side of the domain and solve from right to left.

SHEAR WAVE SPEED IMAGES

In Fig. 6, we show the recovered shear wave speed for the three cases introduced in Fig. 5, for both point and line sources.

Figure 6.

Recovered shear wave speed from 2d point sources (top) and 2d line sources (bottom) for three polynomial inclusions.

We can see in these images that the artifacts in the crawling wave speed using point sources have been significantly reduced in our shear wave speed images. The shear and crawling wave speeds using line sources are very similar. This is as we expect based on the previous analysis.

We note that the ring-like artifacts around the inclusion still appear in the shear wave speed images. These artifacts are a result of backscattering of the wave after it hits the inclusion. As the geometric optics approximation models forward scattering, we would not expect our algorithm to remove these artifacts.

In the case of point sources, we also see some artifacts propagating in from the upper and lower boundaries. These are a result of our using the high-frequency approximation of the shear wave speed on the boundary. These could be avoided by adapting the algorithm to take into account frequency-dependent wave speed; we will do this in the future.

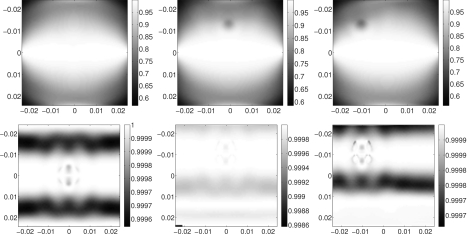
In Fig. 7, we show the term |cos(θ∕2)|. For point sources, the cosine term is significantly less than 1 in precisely the places where the scaled crawling wave speed had high-speed artifacts. For line sources, the cosine term is never significantly less than 1.

Figure 7.

Nonlinear term |cos(θ∕2)| calculated from recovered shear wave phases from 2d point sources (top) and 2d line sources (bottom) for three polynomial inclusions.

CONCLUSIONS AND FORTHCOMING WORK

Based on the foregoing calculations and numerical results, we suggest that (1) if the scaled crawling wave speed is to be used as an estimate of the shear wave speed, then an experimental setup with 2d line sources will yield a more accurate estimate; and (2) if 2d point sources are to be used, then (a) the scaled crawling wave speed images will have less artifact when the inclusion is close to the line between the two sources, and (b) an accurate image of the shear wave speed can be obtained by using the first-order PDE (10) and the Eikonal Eq. 3.

In summary, we have shown that it is possible to recover the shear wave speed, and the shape and location of an inclusion, from the data that is collected in the crawling wave experiment. We have done so by deriving and solving a partial differential equation for the phase of the shear wave.

We note that there are several advantages to using 2d line sources over 2d point sources. First, as mentioned above, the scaled crawling wave speed is a better approximation of the shear wave speed and thus a better indicator of tissue stiffness. Second, when solving the PDE for the shear wave phase, knowledge of the shear wave speed on the boundary is not required for line sources.

In a sequel paper, we apply the shear wave speed recovery algorithm to in vitro prostate data obtained in the crawling wave experiment, and compare our wave speed images to histology images.

In a future publication, we will consider the frequency-dependence of the shear wave speed and adapt the shear wave speed recovery algorithm accordingly, and compare the results of that algorithm to the results of the algorithm discussed in this paper, which is based on a high-frequency assumption. We will also calculate synthetic data in three dimensions.