Biased Feedback in Spatial Recall Yields a Violation of Delta Rule Learning

Abstract

This study investigates whether inductive processes influencing spatial memory performance generalize to supervised learning scenarios with differential feedback. After providing a location memory response in a spatial recall task, participants received visual feedback showing the target location. In critical blocks, feedback was systematically biased either 4° towards the vertical axis (Towards condition) or 4° further away from the vertical axis (Away condition). Results showed that the weaker teaching signal (i.e., a smaller difference between the remembered location and the feedback location) in the Away condition produced a stronger experience-dependent change over blocks than in the Towards condition. This violates delta rule learning. Subsequent simulations of the Dynamic Field Theory of spatial cognition provide a theoretically unified account of these results.

Spatial cognition research suggests that people divide regions of space into categories to enhance interactions with the local surrounds. Although this can lead to an increase in the precision of spatial memory (Huttenlocher, Hedges, Corrigan, & Crawford, 2004; Huttenlocher, Hedges, & Duncan, 1991), spatial categories also lead to systematic biases in location recall. For example, in one common task people reproduce the location of a dot in a circle following a short delay. Results show that recall estimates are biased away from the horizontal and vertical axes toward the centers of the quadrants within the circle. Two different spatial memory models have captured these ‘geometric’ biases—the Category Adjustment Model (CAM; Huttenlocher et al., 1991) and the Dynamic Field Theory (DFT; Schutte & Spencer, in press; Simmering, Schutte, & Spencer, 2008).

Several recent papers have investigated whether spatial cognition is also influenced by a second class of categorical effects—induced category biases. Inductive or experience-dependent processes, in which classification responses come to reflect the distribution of exemplars within a set of items, are an important component of category formation in multiple domains (Huttenlocher, Hedges, & Vevea, 2000). Although Huttenlocher and colleagues (2004) reported that spatial recall is not influenced by the target distribution, this contrasts with other reports. Spencer and Hund (2002), for example, reported that when a target 40° to the right of a vertical axis at 0° was paired with targets farther from the vertical axis (e.g., 60°), bias away from vertical increased. When the 40° target was paired with targets closer to the vertical axis (e.g., 20°), however, bias away from vertical decreased. In both cases then, geometric memory biases were adjusted towards the center of the target distribution. Spatial recall is also influenced by the frequency with which participants estimate each location (Spencer & Hund, 2003).

These findings indicate that experience-dependent processes influence spatial memory performance, contrary to claims of the CAM which lacks a mechanism to account for such effects. The DFT, by contrast, captures experience-dependent effects through a long-term memory (LTM) mechanism. In this theory, the maintenance of location information in working memory during short-term delays leaves a trace in LTM. Such traces can accumulate and create biases in working memory, including attraction toward an average remembered location (Simmering et al., 2008; Spencer, Perone, & Johnson, 2009).

To date, the LTM mechanism of the DFT has only been formally probed using data from unsupervised learning tasks, that is, tasks where there is not an explicit teaching signal that specifies the error on each trial. Unsupervised learning is often contrasted with supervised learning where an explicit teaching signal is present, and different learning rules have been proposed to account for findings from these two types of tasks (McLeod, Plunkett, & Rolls, 1998). Here we examine whether experience-dependent effects in spatial recall generalize to supervised learning contexts where a differential teaching signal is present and, further, whether the LTM mechanism of the DFT can account for participants’ performance. Note that the use of precise, metric feedback in spatial recall—re-displaying the target location after the participant has responded—opens the door to a new probe of supervised learning because previous studies have used categorical or forced-choice responses (Herzog & Fahle, 1997; Pashler, Cepeda, Wixted, & Rohrer, 2005) and discrete feedback. Precise, metric feedback allows for a finer-grained analysis of supervised learning mechanisms which are not yet fully understood (Pashler et al., 2005; Tsodyks & Gilbert, 2004).

Experiment 1

This experiment tests whether experience-dependent location memory processes generalize to supervised learning scenarios involving differential metric feedback. Although accurate feedback commonly increases response accuracy over time (e.g. Herzog & Fahle, 1997), systematically biased feedback can also decrease response accuracy (Herzog & Fahle, 1999). The current experiment builds on this idea to test whether systematically biased response feedback can produce metric distortions in spatial recall.

In our task, participants see a target, there is a 10s delay, and then they indicate the remembered target location by moving a cursor to the remembered location. Visual feedback indicating the “correct” target location is then given while the participants’ response is still visible, enabling participants to determine the error on each trial. To probe supervised learning processes, we biased the feedback participants received. In the Towards condition, feedback was biased 4° towards the vertical axis (e.g., feedback at 26° for a target 30° to the right of the vertical axis at 0°). In the Away condition, feedback was biased 4° further away from the vertical axis (e.g., feedback at 34° for a 30° target).

A common mechanism in models of supervised learning is the delta rule (McLeod et al., 1998). According to the delta rule, connection weights are adjusted based on differences between an external teaching signal (i.e. explicit feedback) and the current output (i.e., the response). Small differences lead to small weight changes and big differences lead to big weight changes and more dramatic learning. Because spatial recall responses are strongly biased away from the vertical axis, differences between the memory response (current output) and the feedback location (desired output) should be larger in the Towards condition where feedback is biased toward the vertical axis. According to the delta rule, large differences in the Towards condition should yield greater changes over learning relative to the Away condition.

Method

Participants

Thirty-two students (20 male, 12 female) participated in exchange for course credit or payment. All were native speakers of English with normal hearing and normal or corrected-to-normal vision. A participant who moved the cursor along “L”-shaped trajectories was replaced.

Materials and Apparatus

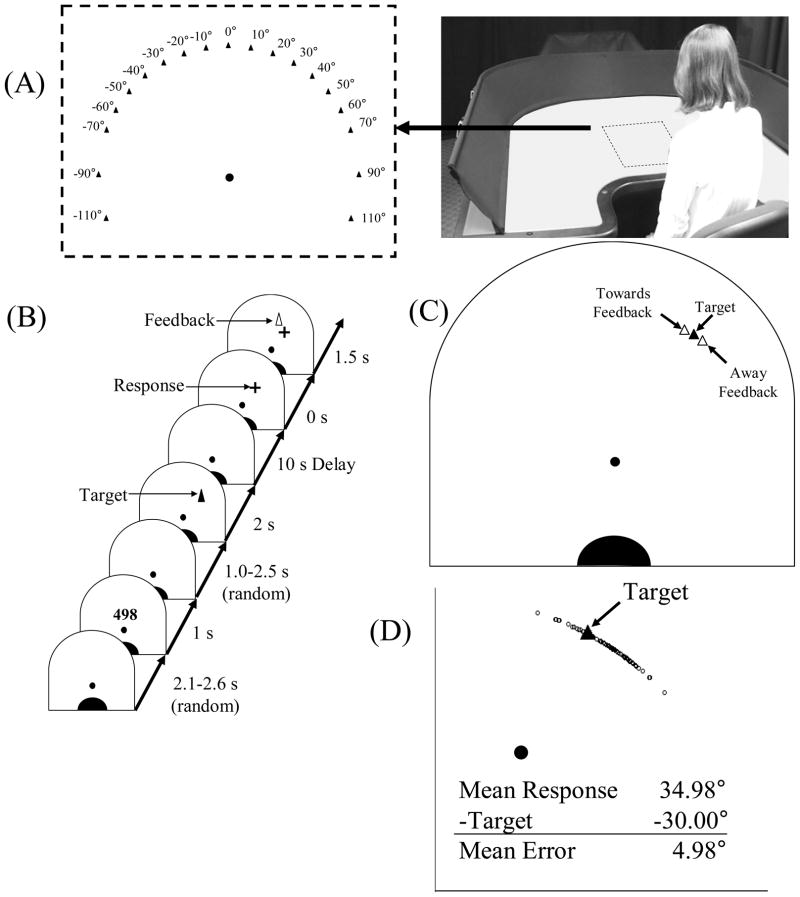
Participants sat at a large table (79cm (h) × 117cm (w) × 127cm (l)) with a homogeneous surface and no explicit landmarks (Figure 1A). Sessions were conducted in a dimly lit room with black curtains covering all external landmarks. Stimuli consisted of three images: a yellow three-digit number presented along the vertical midline axis of the table 46 cm from the participant, a yellow reference disc (15 mm diameter) located along midline 30 cm away from the participant, and a blue equilateral triangle “spaceship” (10 mm base). Stimuli were projected onto the table surface from below using a Sony VPL-PX LCD Projector. Participants responded by moving a mouse cursor that was projected on the surface of the table. The mouse was located on a pad to the right of the participant out of the field of view.

Figure 1.

(A) Target distribution (left panel) and apparatus (right panel) used for the spaceship task. The black disc at the origin of the target distribution corresponds to the yellow reference disc used in the experiment. Targets were projected onto the table from beneath. Lights were dimmed during the experiment and the table appeared black. (B) Time line of the experimental procedure. (C) Sample target location (30°) along with feedback biased either 4° towards the vertical axis (Towards condition) or 4° away from the vertical axis (Away condition). (D) Mean error calculation method demonstrated here using the response distribution for the ±30° target in the Away condition in Block 2 (all subjects) as an example.

Procedure

Each trial began with the appearance of the yellow referent disc which remained visible throughout the trial (Figure 1B). Then, a randomly chosen number between 100 and 500 appeared and participants began counting backwards from that number by 1s aloud until the recall response. This prevented verbal encoding of the spaceship position. Next, a blue spaceship target appeared for 2s. Participants looked up from the table when the spaceship disappeared and looked back when the computer said “Ready-Set-Go”. Once they heard “go” (10s after target presentation), participants moved the mouse cursor to the remembered location and clicked the button. After responding, a spaceship re-appeared and the computer said “Here’s where the ship was!” followed by a blank screen and the next trial.

Participants completed several demonstration trials (with accurate feedback) at the start of the session followed by three blocks of test trials. Blocks consisted of three responses to each of the following 19 targets in randomized order at a fixed 15cm radius from the yellow reference disc: 0° (vertical), ±10° ±20° ±30° ±40° ±50° ±60° ±70° ±90° ±110° (Figure 1A). In Block 1, participants received accurate feedback for all targets In Blocks 2 and 3, feedback was biased either 4° Towards the vertical axis or 4° Away from the vertical axis for the ±10° to ±70° targets (Figure 1C). Given that memory for locations along cardinal axes is quite accurate (see Spencer & Hund, 2002), targets at 0°, ±90°, and ±110° were presented with accurate feedback to reduce the possibility of participants detecting the feedback manipulation. All participants were debriefed after the session. There was no indication that participants detected the manipulation.

Methods of Analysis

Directional errors (°) on each trial were computed such that errors away from the vertical axis were positive (see Figure 1D for example). Responses to targets at mirror image locations on either side of the vertical axis (e.g., +30° and −30°) within the same experimental block were grouped together. Outlier trials—directional errors greater than 40° or exceeding the mean by 3 SDs for a specific target—were removed. There were few outlier (.5%); responses generally clustered around the actual target locations (see Figure 1D for example). Only responses to the biased feedback locations (±10° to ±70°) were analyzed.

Results and Discussion

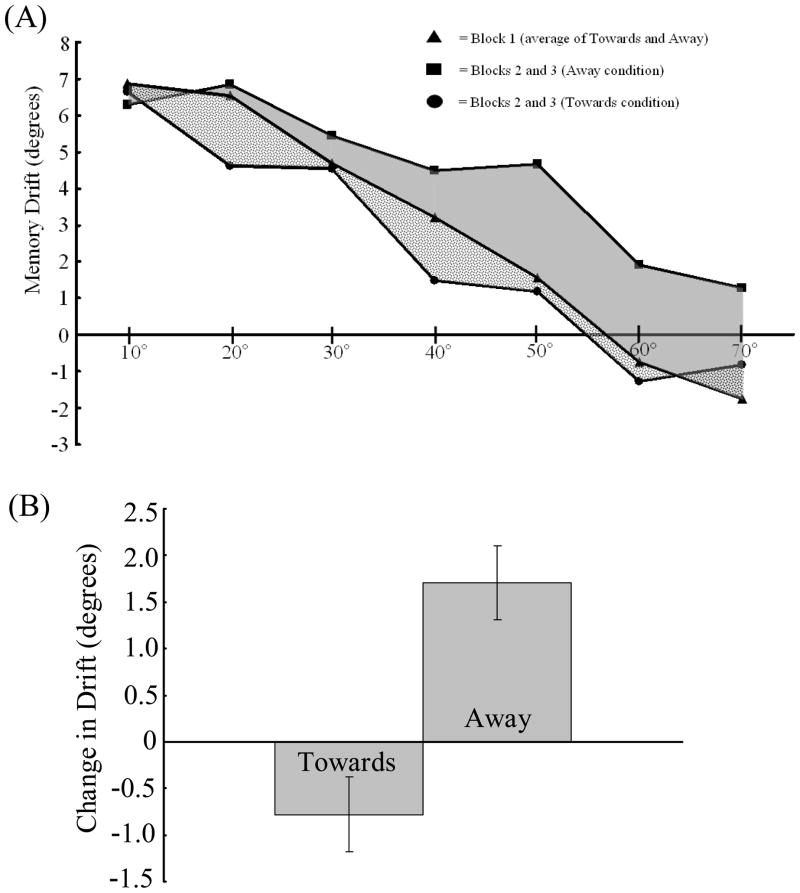
We first compared directional errors in Block 1 to determine whether performance was comparable across conditions before the introduction of biased feedback. A two-way analysis of variance (ANOVA) with Condition as a between-subjects factor and Target as a within-subjects factor revealed a main effect of Target, Wilk’s Λ=.21, F(6,25)=15.6, p<.001, η²_p=.79, but no significant Condition or interaction effects (ps>.14). Thus, performance across conditions was comparable in Block 1. Block 1 responses (Figure 2A) were generally biased away from the vertical axis, consistent with previous findings (e.g. Huttenlocher et al., 1991; Spencer & Hund, 2002).

Figure 2.

(A) Location memory performance. Positive errors indicate drift away from the vertical axis. Negative errors indicate drift towards the vertical axis. Block 1 performance is averaged across the Towards and Away conditions. The gray region reflects the change in memory performance from Block 1 to the average of Blocks 2 and 3 for those in the Away condition. The textured region reflects memory performance change from Block 1 to the average in Blocks 2 and 3 for those in the Towards condition. (B) Memory performance difference scores (collapsed across targets) for the Towards and Away conditions. Positive difference scores indicate an increase in drift away from the vertical axis over blocks. Negative difference scores indicate a decrease in drift away from the vertical. Error bars represent standard errors.

To obtain a within-subjects measure of performance change with the introduction of biased feedback, we computed difference scores by subtracting each participant’s mean error for each target in Block 1 from the mean error for each target in Block 2 and Block 3. A three-way ANOVA on these scores with Condition as a between-subjects factor and Target and Block Comparison (Block 2 - Block 1 or Block 3 -Block 1) as within-subjects factors revealed a significant main effect of Condition, F(1,30)=18.9, p<.001, η²_p=.39: difference scores for the Towards condition (textured region, Figure 2A) were significantly smaller than those of the Away condition (gray region, Figure 2A).

Subsequent analysis revealed that the mean Towards difference score (collapsed across targets) did not differ significantly from zero (t(15)=1.68, p=.11). The biased feedback in the Towards condition did not, therefore, alter spatial recall performance (Figure 2B). The Away condition difference scores, however, showed a significant overall mean increase in response bias away from the vertical axis (see Figure 2B; t(15)=5.17, p<.001). Moreover, follow-up analyses of difference scores (Block 3- Block 1) showed that the absolute magnitude of performance change for the Away condition was greater than that for the Towards condition (M_diff=1.3, SE= =.61), t(30)= 2.14, p=.04 (two-tailed).

The ANOVA also revealed a significant Target effect, Wilk’s Λ=.40, F(6,25)=2.79,p=.03, η²_p=.60. Difference scores in the Towards and Away conditions combined to produce means close to 0 at 10° (M=−.4°), 20° (M=−.83°), 30° (M=.31°), and 40° (M=−.23°). Targets at 50° (M=1.36°), 60° (M=1.07°), and 70° (M=1.98°), however, had higher average difference scores because the Away condition effects generally outstripped those of the Towards condition (see Figure 2A). All other effects were non-significant (ps>.11).

The larger effects for the Away condition appear to run counter to delta rule learning because the size of the teaching signal (i.e., the delta) should, on average, be smaller in the Away condition. To explore this, we conducted post-hoc analyses on the difference between each location memory response and the subsequent feedback location. This provides an index of the teaching signal magnitude. In Block 1 (where accurate feedback was given), the mean teaching signal for the Away (M=2.7; t(15)=5.5, p<.001) and Towards (M=3.1; t(15) = 5.2, p<001) conditions were both significantly greater than zero but did not differ across conditions (t(30)=.53, p=.58). By contrast, the introduction of biased feedback in Blocks 2 and 3 for the Towards condition significantly increased (t (15)= 7.3, p<.001) the mean teaching signal from 3.1 in Block 1 to 6.4 in Blocks 2 and 3. In contrast, the biased feedback for the Away condition in Blocks 2 and 3 significantly decreased (t(15)= 6.96, p< 001) the mean teaching signal from 2.7 in Block 1 to .43 in Blocks 2 and 3. Critically, the teaching signal in the Away condition was not only significantly smaller than in the Towards condition (t(30)=8.6, p<.001) but also did not differ significantly from zero, t(15)= 1.2, p=.24. Thus, participants showed the largest change over blocks in the condition where the teaching signal had a magnitude near zero.

We draw two conclusions from these results. First, experience-dependent changes in spatial recall generalize to supervised learning contexts. Second, the weaker teaching signal of the Away condition, whose average value was not statistically different from zero, produced a stronger experience-dependent location memory effect. This violates delta rule learning. In the following sections, we examine whether this learning asymmetry can be captured by the Dynamic Field Theory.

The Dynamic Field Theory

The DFT (Schutte & Spencer, in press; Simmering et al., 2008) is a formal theory of spatial cognition grounded in the principles of neural population dynamics (Erlhagen, Bastian, Jancke, Riehle, & Schöner, 1999) that captures experience-dependent changes in spatial memory performance (Simmering et al., 2008; Spencer et al., 2009). Here we probe whether this theory generalizes to a supervised learning scenario and captures the reported learning asymmetry.

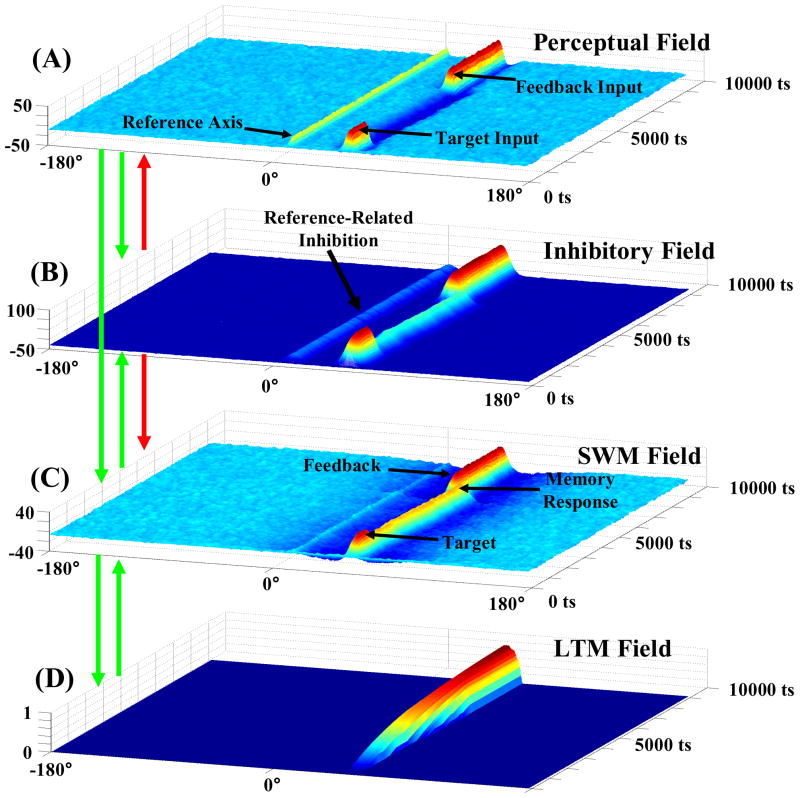
We first address how the model accounts for geometric spatial memory biases. Each of the four layers in the DFT (Figure 3) represents location (°) along the x-axis which is composed of aligned nodes, each preferentially tuned to a given spatial location. The z-axis of each layer represents the activation level of the nodes and the y-axis represents time (1 timestep = 2 milliseconds). Input enters the perceptual field (Figure 3A) strongly (with weak projections to working memory) and activates sites tuned to the input location. Perceptual field activation then propagates to the shared inhibitory field (Figure 3B) and the spatial working memory field (SWM; Figure 3C). Importantly, the nodes within the perceptual and SWM fields interact such that above-threshold nodes coding for similar spatial locations excite one another while nodes coding for strongly differing locations inhibit one another (via the shared inhibitory field). With sufficient activation input, local excitation and lateral inhibition can lead to a self-sustaining “peak” in SWM that is maintained over a delay even after stimulus removal.

Figure 3.

Simulation of the Dynamic Field Theory. Panel (A) represents the perceptual field, panel (B) the shared inhibitory field, panel (C) the spatial working memory (SWM) field, and panel (D) the long-term memory field. Green arrows indicate excitatory connections between fields. Red arrows indicate inhibitory connections. In each layer, spatial location (°) is represented along the X axis, time along the Y axis, and activation along the Z axis. The trial begins at the front of the figure and moves towards the back. See text for additional details.

The SWM field is continuously coupled to the perceptual field. Consequently, perceptual structure in the task space such as the vertical symmetry axis (Wenderoth, 1994) aligned with the reference disc can contribute to SWM dynamics. This can help keep spatial information anchored to perceived reference frames under some conditions (Simmering et al., 2008), but it can also systematically bias spatial recall under others. In particular, activation in the perceptual field associated with perceived reference frames (see Figure 3A) and its associated inhibition (see Figure 3B) can create a boost of inhibition in SWM near the vertical axis. Consequently, memory peaks near the vertical axis are “repelled” away from the axis over delay.

In addition to representing remembered locations, SWM peaks also leave activation traces in the long-term memory layer (see LTM, Figure 3D; see also Appendix). Because the LTM field is reciprocally linked to SWM, experience-dependent traces can, in turn, bias spatial working memory dynamics. Over time, LTM traces build up through this simple form of unsupervised Hebbian learning (Simmering et al., 2008).

How might this same system use feedback to alter spatial recall in a supervised learning task? One possibility is that feedback input, like target input, builds a second, localized peak in SWM that leaves traces at the corresponding sites in LTM. Given that location memories tend to drift away from the vertical axis over time, traces from these drifting memory peaks should overlap more with feedback traces biased away from the vertical axis than feedback traces biased towards the vertical axis. As a result, feedback in the Away condition should lead to a greater change in spatial recall because two influences conspire to impact LTM. By contrast, feedback in the Towards condition should lead to modest learning because two influences compete. Note that by this scenario, unsupervised and supervised learning occur within the same framework.

Simulation Method and Results

Our model exploration began with parameters from a recent paper by Schutte and Spencer (in press) who quantitatively modeled geometric biases in spatial recall from both children and adults. Critically, Schutte and Spencer did not include a LTM mechanism because their task limited possible LTM contributions. Thus, we took their parameters for the perceptual, inhibitory, and SWM fields and added a LTM mechanism (see, Simmering et al., 2008; Spencer et al., 2009). The question was whether we could qualitatively capture the present findings with this model, including the asymmetry in learning.

Three blocks of trials were presented in each simulation set. Block 1 feedback was presented at the true target location in both conditions. In Blocks 2 and 3, however, the feedback location was biased either 4° towards or 4° away from the vertical axis. Each target was presented three times in a randomized order within each of the three blocks. As in Schutte and Spencer (in press), we simulated only the five targets from 20°–60°. Each complete simulation run, therefore, consisted of 45 individual trials (5 targets X 3 trials per block X 3 blocks). We ran 100 complete simulation runs for each of the two feedback conditions to evaluate model performance in the presence of simulated neural noise. Note that a second set of 100 simulations replicated all findings reported below.

Block 1 simulations (averaged across conditions) exhibited a memory profile similar to the present experiment, with strong biases away from the vertical axis for targets near this axis (20° target=8.25° bias) followed by weaker biases (30° target=3.99° bias; 40° target=2.56° bias; 50° target=.17° bias) and an eventual reversal (60° target=−5.25° bias). A two-way analysis of variance (ANOVA) with Condition as a between-subjects factor and Target as a within-subjects factor for Block 1 revealed a main effect of Target, Wilk’s Λ=.02, F(4,195)=2137.3, p<.001, η²_p=.98, but no significant Condition or interaction effects (ps>.47).

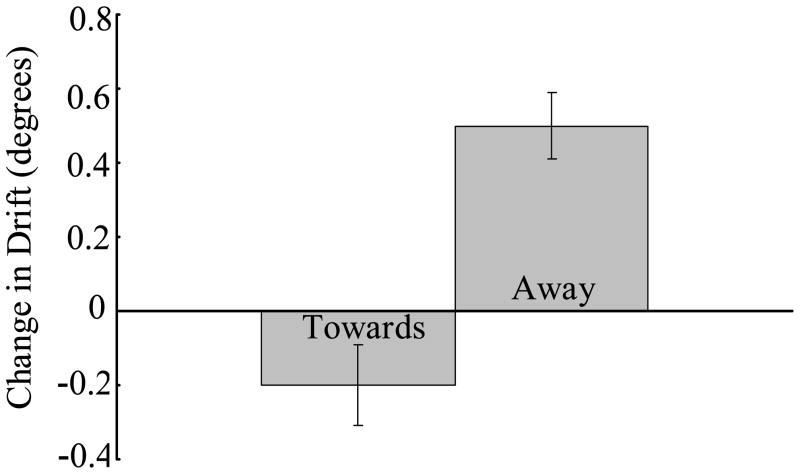
Difference scores were calculated to compare within-simulation performance change from Block 1 to Blocks 2 and 3 (see Figure 4). Difference scores collapsed across targets for the Towards condition were significantly smaller than those of the Away condition. The absolute magnitude of the bias effect in the Away condition was also stronger than in the Towards condition (t(198)=4.8, p<.001).

Figure 4.

Memory performance difference scores (collapsed across targets) for the Towards and Away conditions from simulations of the DFT. Positive difference scores indicate an increase in drift away from the vertical axis over blocks. Negative difference scores indicate a decrease in drift away from the vertical. Error bars represent standard errors.

These simulations thus capture the asymmetric feedback effect observed in the experiment. To determine whether the stronger Away condition effect was accompanied by a weaker teaching signal, we computed the magnitude of the teaching signal on each simulation trial. Block 1 (accurate feedback) mean teaching signals for the Away (M=1.88, t(99)=23.92, p<.001) and Towards (M=1.93, t(99) = 18.42, p<001) condition were both significantly greater than zero but did not differ across conditions (t(198)=.41, p=.67). For the Towards condition, however, the introduction of biased feedback significantly increased (t (15) = 7.3, p<.001) the mean teaching signal from 1.93 in Block 1 to 5.8 in Blocks 2 and 3. In contrast, the biased feedback for the Away condition significantly decreased (t(99)= 37.97, p< 001) the mean teaching signal from 1.88 in Block 1 to −1.62 in Blocks 2 and 3. Although this Away teaching signal differed significantly from zero (t(99)=38.96,p<.001), the absolute size of the teaching signal in the biased feedback trials was nonetheless significantly smaller than in the Towards condition (t(198)=71.6, p<.001). Thus, the weaker teaching signal for the Away condition produced a stronger learning effect, consistent with the reported empirical results.

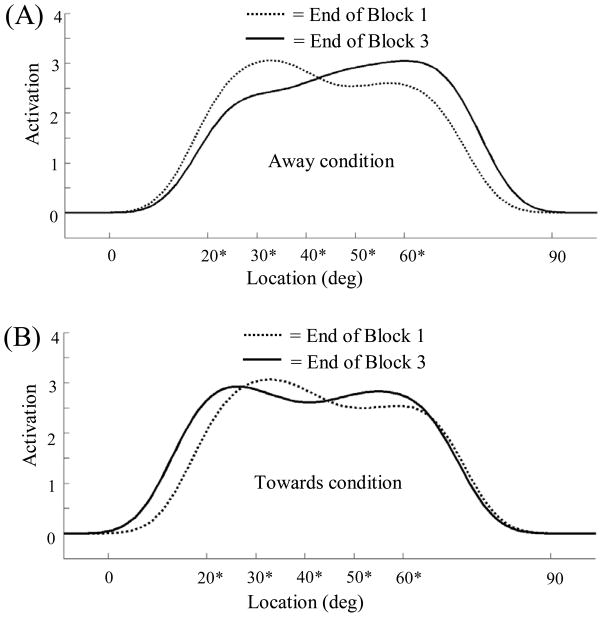
Figure 5 shows LTM activation in the model at different points in learning which explains the origin of the asymmetric learning across conditions. Both simulation sets show a comparable distribution of activation in LTM after the first block with a center of mass at 43.2° and a maximum activation near 30°. Critically, at the end of Block 3, the center of mass of LTM in the Away condition (Figure 5A) shifted substantially outward to 47.8° with a maximum activation near 60°. This major shift in LTM activation occurred because traces from memory peaks during the delay and traces built from feedback were biased in the same direction—away from the vertical axis. By contrast, the distribution of LTM in the Towards condition (Figure 5B) showed only a small shift in the center of mass to 41.2° with a maximum near 25°. This modest change occurred due to competition between LTM traces from memory peaks which were biased away from the vertical axis and traces built from feedback which were biased toward the vertical axis. In summary, these simulations show how the DFT generalizes to a supervised learning scenario to capture experience-dependent changes in spatial recall that violate delta rule learning.

Figure 5.

Comparison of long-term memory activation at the end of Block 1 (dashed line) and end of Block 3 (solid line) for the (A) Away and (B) Towards feedback conditions. Asterisks indicate target locations presented during simulation trials.

General Discussion

The experimental results show that inductive, experience-dependent influences on spatial recall (Spencer & Hund, 2002, 2003) generalize to supervised learning scenarios with differential feedback and can be formally captured by the DFT. This further delineates between two competing models of geometric spatial memory biases, the CAM and the DFT. While the CAM has no mechanism to account for these effects, the DFT incorporates a LTM mechanism that can capture key qualitative signatures of experience-dependent changes in spatial recall.

In this context, it is important to highlight the novelty of the proposed mechanism for the present results. Connectionist models of supervised learning typically use explicit error correction processes based on the delta rule. Instead, our dynamically integrated system, built using the same model and parameters from Schutte and Spencer (in press), processes feedback in the same manner as target input. This parsimonious account demonstrates how the fine-grained metric details of memory and feedback can account for the counterintuitive finding that a weaker teaching signal produces a larger change in memory performance. Thus, our work presents a novel empirical result in spatial cognition and it provides a new theoretical mechanism to explore behavioral changes in both supervised and unsupervised learning paradigms.

Appendix

Long-term memory field (LTM) activation is governed by

$$i_w(x,t)=\{\begin{array}{ll}\frac{1}{{\tau }_{\mathit{build}}}[-l_w(x,t)+{\mathrm{\Lambda }}_{lw}(w(x,t))]\hfill & \text{if}w(x,t)\ge 0\hfill \\ \frac{1}{{\tau }_{\mathit{decay}}}[-l_w(x,t)]\hfill & \text{otherwise}\hfill \end{array}$$

where l̇_w (x,t) is the rate of change of the activation for each node in the LTM field l_w across the spatial dimension, x, at time, t. The constants τ_decay and τ_build (with τ_decay > τ_build) sets the time scale of the dynamics for the decay and building of memory traces in LTM, respectively. Input is determined by the activation in the SWM field w at location x and time t.

The sigmoid $\mathrm{\Lambda }(w)=\frac{1}{1+exp[-\beta w]}$, where β is the slope, determines the extent to which the activation w of the given node contributes to the network dynamics.

The parameters were set as follows: τ_build =3000, τ_decay =100000, β=5.

The contribution of LTM field activation to location x in the SWM field is determined by the convolution ∫c_wl (x − x′)l_w (x′,t)dx′ where c is a Gaussian kernel with an amplitude of 0.2 and a width of 6.4.