Network mechanisms of theta related neuronal activity in hippocampal CA1 pyramidal neurons

Abstract

Although hippocampal theta oscillations represent a prime example of temporal coding in the mammalian brain, little is known about the specific biophysical mechanisms. Intracellular recordings implicate a particular abstract oscillatory interference model of hippocampal theta activity; the soma-dendrite interference model. To gain insight into the cellular and circuit level mechanisms of theta activity we implemented a similar form of interference using the actual hippocampal network in mice in vitro. We found that pairing increasing levels of phasic dendritic excitation with phasic stimulation of perisomatic projecting inhibitory interneurons induced a somatic polarization and action potential timing profile that reproduced most common features. Alterations in the temporal profile of inhibition were required to fully capture all features. These data suggest that theta-related place cell activity is generated through an interaction between a phasic dendritic excitation and a phasic perisomatic shunting inhibition delivered by interneurons; a subset of which undergo activity-dependent presynaptic modulation.

Introduction

Spatio-temporally correlated neuronal activity is commonly observed as network oscillations or rhythmic activity within neuronal circuits^1-5. One such rhythm is a relatively slow, 4-10 Hz oscillation of extracellular current that is found in the hippocampal formation of all mammals studied to date^1,4. This theta oscillation appears to provide a timing signal to hippocampal firing that is thought to be important for both spatial and non-spatial hippocampal functions during active exploration and REM sleep^1-4,7-11. Three characteristic firing^6-8,10,11 and subthreshold¹² membrane potential features have been reported to occur in place cells as the animal moves into and through the neurons place field. First, firing rate increases are associated with steadily increasing levels of intracellular depolarization, second the time of peak intracellular depolarization and action potential output both advance relative to the extracellular theta phase. Finally, as the animal leaves the place field the firing rate decreases back to baseline levels while the timing of the action potentials stays advanced. The available intracellular data suggests that the peak intracellular depolarization also stays advanced for this portion.

Generally, two forms of fairly abstract models have been proposed to account for the place related firing rates and phase precession. These include several forms of oscillatory interference models^7,13-18 as well as a more systems level model involving cell assemblies and asymmetric synaptic connections among the active neurons^13,19,20. Most of the above models are expected to produce characteristic intra- and extracellular signals that markedly differ from those described above¹². Yet, one particular interference model, the soma-dendrite interference model (SDI), has been proposed to account for many of the appropriate features^10,12,15,16. Here we sought to establish a physiological implementation of the SDI model using specific cellular and network level mechanisms to produce the characteristic features of theta related neuronal activity.

Results

The SDI model attempts to capture the flow of activity in the hippocampal network during theta states and has two main components, a phasic excitatory input to the dendrites that is simultaneous with a similarly phasic inhibitory input to the perisomatic regions^7,15-18. We have first used simultaneous whole-cell somatic and distal apical dendrite recordings in CA1 pyramidal neurons located in acute hippocampal slices from parvalbumin-Cre (PV-Cre) transgenic mice virally expressing a channelrhodopsin2-green fluorescent protein (ChR2-GFP, Supplementary Fig. 1a and Methods) in parvalbumin-expressing (PV+) interneurons^21-22, to compare the ability of two different versions of a SDI model to reproduce theta oscillation associated hippocampal activity. In both versions, dendritic excitation was provided by a progressively increasing depolarizing current injection in the shape of a 5 Hz rectified sine wave into the distal apical trunk (Fig. 1). In the first form of implementation the dendritic depolarization was paired with a 180° out of phase (i.e. hyperpolarizing) somatic current sine wave injection of constant amplitude (100-150 pA)^12-16. Current-voltage (I-V) relationships from the soma and dendrite showed that the form of inhibition produced by this SDI model was subtractive in that the slope of the relationship was only mildly altered (soma: 7 ± 1 % Δgain/gain, n = 7, dendrite: 9 ± 5% Δgain/gain, n = 4) while a large rightward shift was produced (soma: 104 ± 2 pA, n = 7, dendrite: 59 ± 5 pA, n = 4, Fig. 1d,e). In the second form of SDI a divisive form of phasic somatic inhibition was implemented. In order to achieve this, we used one-photon (Fig. 1a-c and Supplementary Fig. 1b,c) or temporally-focused two-photon (2pTeFo, see Methods and Supplementary Fig. 2a-c²³) ChR2-photostimulation confined to the cell body layer of the hippocampal CA1 region with a temporal pattern that produced a rectified 5 Hz sine wave of inhibitory conductance. This spatio-temporal pattern of input produced a divisive form of inhibition that originated predominantly around the soma. This was evidenced by a large decrease in the slope (soma: 48 ± 3% Δgain/gain, n = 7, dendrite: 19 ± 6 % Δgain/gain, n = 4, Fig. 1d,e) together with a relatively small rightward shift of the somatic I-V (soma: 19 ± 6 pA, n = 7, dendrite: 10 ± 4 pA, n = 4), as well as by the kinetics of the evoked unitary inhibitory responses (Supplementary Fig. 1d,e, n = 8). Similar effects were observed on the suprathreshold firing frequency-input (F-I) relationships where the stimulation of perisomatic inhibition reduced the slope of the relationship (Δgain/gain = 48%, shift = 170 pA, n = 7) to a much greater extent than the injection of hyperpolarizing currents (Δgain/gain = 13%, shift = 117 pA, n = 7, Supplementary Fig. 3). The rightward shift in the F-I relationship induced by an inhibitory synaptic conductance is likely due to the relatively low levels of synaptic noise present in the inputs ^24,25. These relationships demonstrated that for near threshold levels of excitatory input (∼250 pA), the dendritic arbor of CA1 pyramidal neurons would be relatively more depolarized in the presence of shunting perisomatic inhibitory input than with subtractive inhibitory input (shunt; 27 ± 2 mV, sub; 20 ± 2 mV; n = 4, p < 0.01), even though the somatic regions will be depolarized to similar levels (shunt; 9 ± 1 mV, sub; 11 ± 1 mV, n = 4, p > 0.05). Such elevated dendritic depolarization could increase the probability of dendritic plateau potential generation²⁶.

Figure 1.

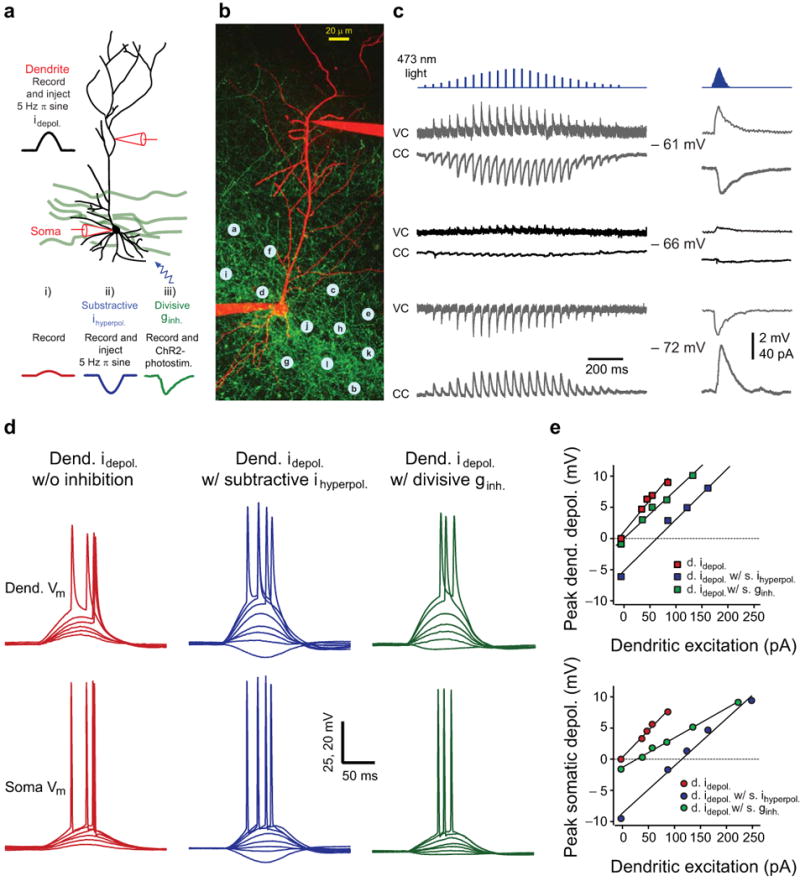
Experimental implementation of subtractive and divisive forms of inhibition. (a) Schematic of the experimental configuration. A dendritic whole-cell electrode was used to inject a depolarizing sine wave current while the corresponding somatic and dendritic voltage responses were recorded in the absence (i) or presence (ii) of a somatic 180° out-of phase hyperpolarizing sine wave current injection, or (iii) ChR2-photostimulation. (b) Two-photon image stack of a CA1 pyramidal neuron (red: Alexa 594) in a dense network of ChR2-GFP+ fibers (green) concentrated in the pyramidal layer in a hippocampal slice from a PV-Cre mouse injected with rAAV-FLEX-rev-ChR2-GFP. Blue dots: ChR2-photostimulation grid. (c) Individual (left, 1-25 locations, 100 ms interval) and synchronous (right, 1-25 locations, 3 ms interval) inhibitory postsynaptic currents (VC: voltage-clamp) potentials (CC: current-clamp) evoked by photostimuli corresponding to the locations indicated by letters on b (a: 1^st, 13^rd, 25^th; b: 2^nd 14^th; c: 3^rd 15^th;d: 4^th, 16^th;e: 5^th, 17^th; f: 6^th 18^th; g: 7^th, 19^th; h: 8^th, 20^th; i: 9^th, 21^st; j: 10^th 22^nd; k: 11^th, 23^rd; l: 12^th,24^th points) and recorded at three different membrane potentials. Blue tickmarks: timing and relative intensity of laser pulses (d) Dendritic (upper, Dend. V_m) and somatic (lower, Soma V_m) membrane potential responses obtained for dendritic current injection of increasing amplitude alone (left), plus in the presence of somatic hyperpolarizing current injection (middle) or with ChR2-photostimulation (right). (e) Subthreshold input-output curves recorded at the dendrite (upper) and at the soma (lower) for the three different input conditions.

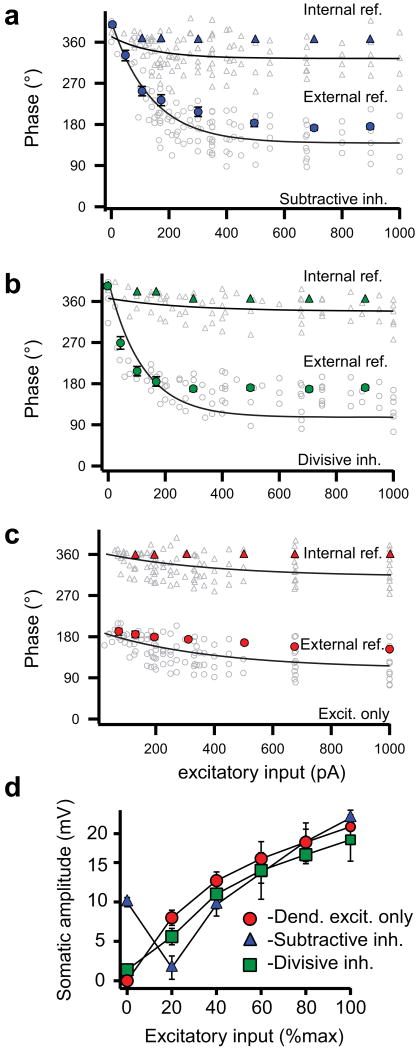
We next implemented the SDI model using either a subtractive or divisive form of somatic inhibition and compared the intracellularly recorded profile of spike timing and “subthreshold membrane potential” during progressively increased excitation. The subtractive inhibition form of SDI produced a pattern of action potential output that was characterized by a very controlled precession of spike times from ∼270° to ∼90° when referenced to the somatic hyperpolarizing sine wave (i.e. external reference, Fig. 2a; open circles in Fig. 3a, Supplementary Fig. 4a). The profile for the subthreshold potentials (3-8 Hz bandpass filtered traces with action potentials removed where applicable, see Methods) was very similar in that the peak of the depolarization gradually moved forward in time with increasing excitation (solid circles in Fig. 3a). Because the peak depolarization of the subthreshold potential advanced in time nearly as much as action potential latencies, there was very little phase precession of the spikes when they are referenced to the intracellular somatic potential waveforms (i.e. internal reference, solid and open triangles in Fig. 3a). Interestingly, the peak to trough amplitudes of the subthreshold potentials showed a biphasic relationship with excitation as they initially decreased for several cycles before finally increasing in amplitude as excitation enhanced (Fig. 2a, solid triangles in Fig. 3d and Supplementary Fig. 4a). Together these data indicated that in the subtractive form of the SDI model an interaction of the filtered dendritic excitatory input and the unfiltered somatic hyperpolarization produces an intrasomatic potential whose depolarizing peak smoothly advanced in time and phase driving action potential initiation to shorter and shorter latencies. The amplitude of the subthreshold somatic potential, initially determined by the size of the large somatic hyperpolarization (∼-10 mV), first decreased as the progressively increasing depolarization from the dendrite gradually removed the hyperpolarizing component and then increased as the depolarizing component dominates the subthreshold potential shape.

Figure 2.

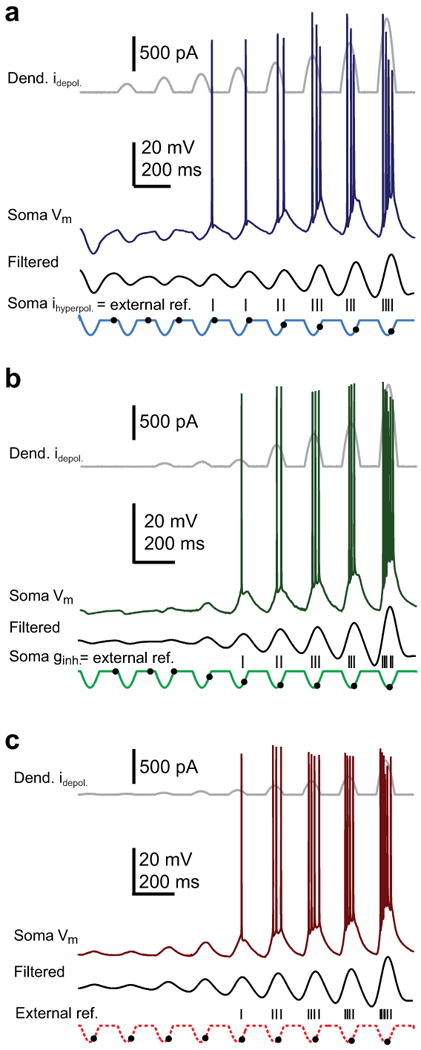
Soma-dendrite interference induces phase precession. (a) Dendritic excitation plus somatic current injection. Concatenation of dendritic current injection (upper gray, 0, 40, 75, 130, 200, 300, 500, 670, 1300 pA), soma membrane potential (soma V_m, dark blue), 3-8 Hz bandpass-filtered V_m (black) and soma current injection (light blue) waveforms. Hyperpolarizing 5 Hz sine wave-shaped somatic current injections (100 pA constant amplitude) are paired with depolarizing 5 Hz sine wave-shaped current injections into the distal apical dendrites. As the dendritic current amplitude is increased the spike latency (upper) and timing of the subthreshold peak depolarization (lower) advanced (grey dots: depolarization peak, black tickmarks: spike peak). (b) Dendritic excitation plus perisomatic conductance stimulation. Concatenation of dendritic current injection (upper gray, 0, 40, 75, 130, 200, 300, 500, 670, 1300 pA), soma V_m (dark green), bandpass-filtered V_m (black) and approximate perisomatic conductance (light green) waveforms. Increasing dendritic depolarizing current injection is paired with 5 Hz sine wave-shaped ChR2-photostimulation. Spike latency (upper) and timing of the subthreshold peak depolarization (lower) advances with increased dendritic current (grey dots: depolarization peak, black tickmarks: spike peak). (c) Dendritic excitation only. Concatenation of dendritic current injection (upper gray, 40, 75, 130, 200, 250, 300, 500, 670 pA), soma V_m (dark red), bandpass-filtered V_m (black) and missing soma inhibitory (light red dashed) waveforms. Increasing dendritic current injection is delivered alone without somatic inhibition. Spike latency (upper) and timing of the subthreshold peak depolarization (lower) advance only slightly with increased dendritic current (grey dots: depolarization peak, tickmarks: spike peak).

Figure 3.

Grouped data showing phase advance and subthreshold potential profiles. Action potential phase (open symbols) and mean subthreshold potential peak time (solid symbols, mean ± s.e.m, n = 6 cells) plotted versus dendritic current injection with reference to the dendritic or somatic input cycle (circles) or the peak of the intracellularly recorded subthreshold potential (triangles) for somatic inhibition delivered as somatic hyperpolarizing current injections (a, blue, n = 6 cells), synaptic conductance changes (b, green, n = 6 cells) or no inhibition (c, red, n = 6 cells). Spike times are fit by single exponential functions. d, Amplitude of somatic subthreshold potentials versus dendritic current injection (normalized to maximum) for somatic inhibition delivered as hyperpolarizing current injections (blue, n = 6), perisomatic conductance changes (green, n = 6) or no inhibition (red, n = 6).

The divisive form of SDI produced a different profile. As with the subtractive form, increasing dendritic excitation induced a gradual phase precession of action potential output that covered a phase range of ∼180° (∼270° to ∼90°) when referenced to the somatic hyperpolarizing current wave (external reference, Fig. 2b; open circles in Fig. 3b, Supplementary Figs. 2d,e and 4b). Again the depolarizing peak of the subthreshold somatic potential that drove the precession showed similar levels of phase advance (solid circles in Fig. 3b) and therefore very little action potential phase precession could be observed when the spike latencies were referenced to the intracellular potential waveform (internal reference, open triangles in Fig. 3b). However, with the inhibition now being generated by a predominantly perisomatic conductance, the subthreshold potential amplitude increased monotonically with the progressive increase in excitatory input (Fig. 2b, solid squares in Fig. 3d, Supplementary Fig. 4b). The reason for this is that with the inhibitory reversal potential near the resting membrane potential, there was very little hyperpolarizing current generated at the lowest excitatory input levels, even though there is a large inhibitory conductance. Thus a shunting or divisive form of inhibition produced enough perisomatic inhibition to allow both appropriate increases in firing rate and phase precession during periods of elevated dendritic excitation without also producing large membrane hyperpolarizations when excitation is weaker. This is a very similar profile to that recently recorded in behaving animals¹².

Dendritic excitation alone, without any form of inhibition, produced a subthreshold potential amplitude profile that, as above, increased monotonically with increased excitation (Figs. 2c and 3c; Supplementary Figs. 2f,g and 4c). Yet in contrast to the SDI models, the amount of phase precession observed for output action potentials or for the subthreshold potentials was markedly reduced to less than half of the range seen in either form of the SDI models (excit. alone: 58 ± 8°, n = 6; w/subtractive inh.: 172 ± 14°, n = 7; w/divisive inh.: 146 ± 21°, n = 7, p < 0.01), regardless to which waveform the spike times were referenced (open circles and triangles in Fig. 3c). Thus, in the end, only the SDI model using a divisive form of shunting perisomatic inhibition was able to capture the first two of the characteristic features reported recently for hippocampal theta activity¹², that is; 1) steadily increasing level of somatic depolarization that accompanies the increase in action potential rate, 2) time of peak subthreshold depolarization advances nearly as much as the evoked action potentials such that action potentials are observed to phase advance only when referenced to the cycle of the somatic input. It is important to note that the presence of either form of perisomatic inhibition caused spike timing to be delayed relative to that produced by excitation alone. Thus, perisomatic inhibition produced phase precession by spreading out spike timing over an entire theta phase, with the exact timing directly dependent on the level of phasic excitatory dendritic input.

A remarkable and poorly understood feature of theta-related place cell activity is that as an animal leaves the place field, the phase and rate of place cell firing become dissociated as the phase of firing stays advanced while the firing rate declines^27-29. Neither of the above implementations of the SDI model would be expected to capture this feature as the phase of firing and peak subthreshold depolarization simply shift back in time as the excitation level and firing rate decrease back to baseline levels. How could the SDI model be modified to produce a monotonic phase advance in the face of a biphasic firing rate profile? We reasoned that the temporal profile of perisomatic inhibition might become altered after a few theta cycles of high frequency action potential firing due to activity-dependent modulation of GABA release from inhibitory terminals. To test this we changed the symmetry of inhibition first by relatively delaying (Fig. 4a,b) the peak of inhibition as would be expected for a shift from short-term synaptic depression to facilitation. Indeed, we found that when decreasing levels of phasic dendritic excitation were paired with a phasic perisomatic inhibition whose peak was now relatively delayed in time (Δpeak g_inh.: 63 ± 5°, n = 9), the firing rate gradually declined while the peak phase of subthreshold polarization and the firing phase stayed constantly precessed (blue traces and symbols in Fig. 4c-e). The reason for this is that inhibition with a delayed peak conductance effectively shunted out the peak of the filtered dendritic depolarization at the soma and blocks spiking later in the cycle even for high levels of excitation (Supplementary Fig. 5). In contrast, phasic inhibition with peak relatively advanced in time (Δpeak g_inh.: 45 ± 4°, n = 4) moderately reduced the range of phase modulation (Supplementary Fig. 5) by confining spiking to later in the cycle. Together, we were able to successfully separate the firing rate from the firing phase and timing of peak subthreshold depolarization by delaying the peak of the perisomatic inhibition during periods of waning excitation.

Figure 4.

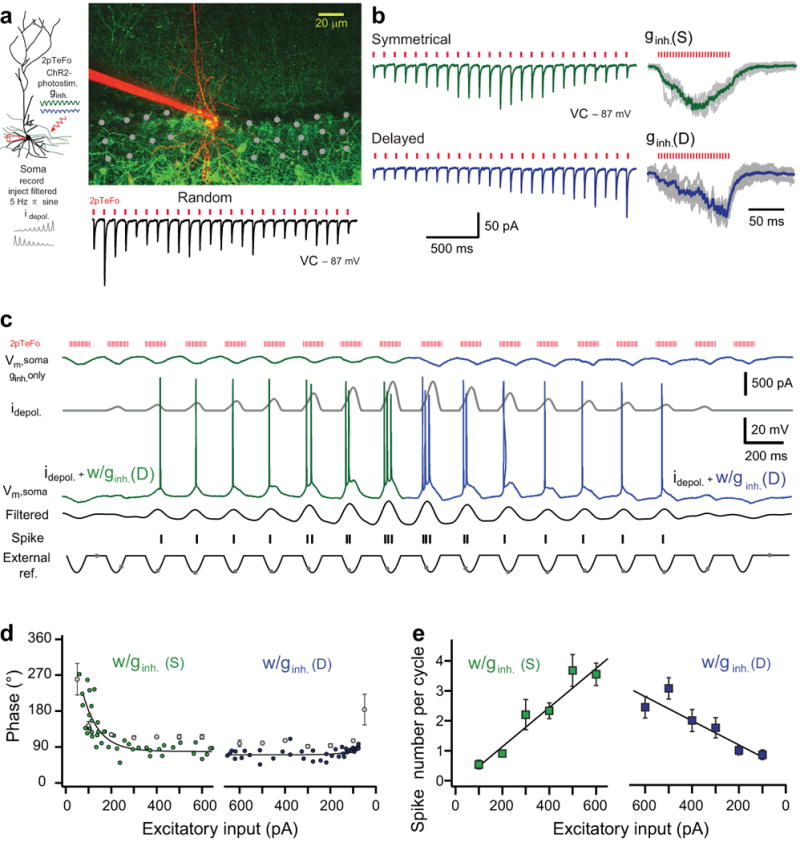
Delayed inhibition dissociates place cell firing rate and phase. (a) Left, experimental configuration: somatic filtered sine wave current injection paired with temporally-focused two-photon ChR2-photostimulation (2pTeFo) of inhibitory profiles. Right, two-photon stack of a CA1 pyramidal neuron (red) and ChR2-GFP+ profiles of PV-expressing interneurons. Grey dots: photostimulation grid. Individual inhibitory postsynaptic currents (VC: voltage-clamp) evoked by random pattern photostimulation (bottom right). Red tickmarks: 880 nm laser pulse timing. (b) Stimulation sequence arranged to evoke a bimodal (upper left, green) or an increasing (lower left, blue) amplitude sequence that generated a symmetrical (upper right; g_inh.(S), grey: individual traces, green: average) or a delayed (lower right; g_inh.(D); grey: individual traces, blue: average) inhibition profiles with synchronous photostimulation (3 ms interval), respectively. (c) Repeated 2pTeFo photostimulation: 1^st-9^th theta cycles with ramp-up depolarizing current injections (i_depol., dark grey) and symmetrical inhibition (V_m, soma g_inh. only, green); 10^th-18^th theta cycles with ramp-down current injections and delayed inhibition (V_m, soma g_inh. only, blue). V_m, soma: soma membrane potential, filtered: 3-8 Hz bandpass-filtered V_m, external reference: population inhibitory waveform. Black tickmarks: spike timing, grey dots: subthreshold peak. (d) Summary of mean spike phase (green and blue circles) and the mean phase of peak subthreshold potential (grey circles, mean ± s.e.m, n = 9) for increased and decreased levels of depolarization paired with symmetrical or delayed inhibition, respectively (n = 9). Solid lines: exponential fits. (e) Summary of mean number of spikes per cycle versus levels of current injections (mean ± s.e.m, n = 9). Solid lines: linear fits.

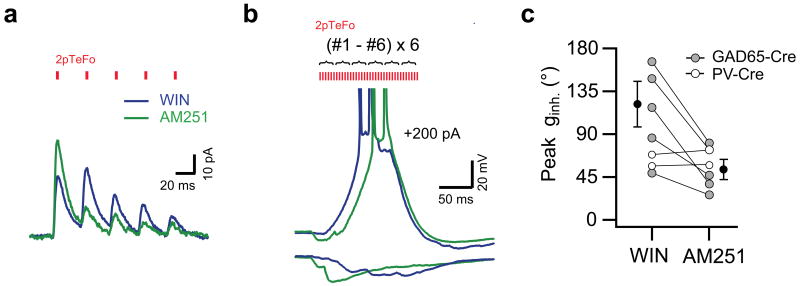
What mechanism could underlie such an activity-dependent and locally mediated shift in the timing of perisomatic inhibition? It is well established that GABA release from inhibitory terminals is modulated by a wide repertoire of presynaptic auto- and heteroreceptors. We tested the potential role of type I cannabinoid receptors (CB1Rs), which are present in the axon terminals of cholecystokinin-expressing (CCK+) interneurons^30-32. To recruit axon terminals of CCK+ interneurons and to avoid direct depolarization of perisomatic GABAergic boutons on the recorded pyramidal neurons, we used high spatial-resolution 2pTeFo photostimulation localized to the CA1 cell body layer in slices from GAD65-Cre knock-in mice virally expressing ChR2-GFP in GABAergic hippocampal interneurons. We found that repetitive 2pTeFo photostimulation²³ of CB1R agonist-sensitive inhibitory fibers (Fig. 5) evoked an inhibitory conductance with peak phase shifted to later in the cycle (peak g_inh.: 127 ± 27°, n = 5), due to the short-term synaptic facilitation present at these terminals in the presence of the CB1R agonist (1 μM WIN55,212–2). Subsequent application of CB1Rs antagonist AM251 (10 μM) reversed the short-term facilitation to short-term synaptic depression and this temporally advanced the peak of the inhibition (peak g_inh.: 53 ± 10°, n = 5, p < 0.05) on pyramidal cells from GAD65-Cre mice. In contrast, the short-term plasticity of GABA release and the temporal profile of photostimulation evoked inhibitory responses were insensitive to pharmacological manipulations of CB1Rs in the PV-Cre mice (n = 2, Fig. 5c). These data suggest that, an activity-dependent release of endocannabinoids from active place cells during later theta cycles may contribute to the pattern of theta related activity through the local modulation of the temporal profile of perisomatic GABA release^33,34. Together the results indicate that a shift in the relative timing of perisomatic inhibition paired with the waning of dendritic excitation can produce the dissociation of place cell firing rate and phase observed as an animal leaves the center of the field.

Figure 5.

Presynaptic cannabinoid receptor activations delays the time to peak of inhibition. (a) Type I cannabinoid receptor (CB1R) agonist-sensitive inhibitory postsynaptic currents evoked by repeated 2pTeFo ChR2-photostimulation at a single location in the pyramidal layer in a GAD65-Cre mice in the presence of CB1R agonist (1 μM WIN55,212-2, blue) and following CB1R antagonist (10 μM AM251, green) application. Red tickmarks indicate the timing of the 2pTeFo photostimulation pulses at 880 nm. (b) Representative membrane potential traces of CB1R agonist-sensitive inhibitory responses evoked by burst 2pTeFo photostimulation (36 stimuli; #1 - #6 non-overlapping locations repeated six times with a 1 ms duration and a 3 ms interval, ∼40 Hz cycle) alone (lower traces) and paired with depolarizing current injections (+200 pA, upper traces), in the presence of WIN55,212-2 (1 μM, blue) and following subsequent application of AM251 (10 μM, green). Note that the timing of APs is shifted forward in the presence of CB1R agonist. Red tickmarks indicate the timing and relative intensity of the 2pTeFo photostimulation pulses at 880 nm. c, Summary data of peak phase of inhibitory responses evoked by 2pTeFo photostimulation in PV-Cre mice (open circles, n = 2) and peak phase of CB1R agonist-sensitive inhibitory responses evoked by 2pTeFo photostimulation in GAD65-Cre mice (right, solid gray circles, n = 5, black: mean ± s.e.m), in the presence of WIN55,212-2 (1 μM) and following subsequent application of AM251 (10 μM).

Discussion

The data presented above provide new biophysical mechanisms for hippocampal theta related neuronal activity by demonstrating that many of the reported features of both intra and extracellularly recorded theta activity are captured by a soma-dendrite interference model implemented by a divisive or shunting form of perisomatic inhibition, whose temporal profile is modulated in an activity-dependent manner (Supplementary Fig. 6). Specifically, the above data support the following framework for the generation of hippocampal theta-related neuronal activity. As the animal moves into a place field of a particular CA1 pyramidal neuron, the increase in excitatory drive to the neuron, via the CA3 Schaffer collateral inputs, induces progressively more action potential firing (higher rate) with the timing of these spikes shifting forward with respect to the basket cell timing signal due to an interference between the dendritic and somatic oscillations as detailed above. Further, the prolonged activity of the place cell will result in the retrograde release of endocannabinoids^33,34. So that as the animal begins to leave the place field, now decreasing levels of excitation together with an endocannabinoid-mediated local modulation of the temporal profile of perisomatic inhibition, perhaps further aided by increased levels of asynchronous release from CCK+ terminals^35,36, result in a decrease in action potential firing rate while the timing of the spikes stays advanced. This proposed role of activity-dependent presynaptic modulation of GABA release is supported by recent reports of profound alteration in the coordination and phase precession of place cell spiking activity by cannabinoids in vivo^37,38. Our results further suggest that trial-to-trial fluctuations in the magnitude of presynaptic modulation of GABA release, perhaps related to running speed of the animal, might also contribute to the increase in spike phase variance in the last third of the place field for pooled-trial recordings observed in vivo³⁹.

From a neural computation point of view it appears that CA1 pyramidal neurons, as well as many others, may be functioning as a comparator for multiple classes of inputs^26,40,41. In the case of CA1 pyramidal neurons, an internal hippocampal representation provided by the CA3 Schaffer collateral (SC) input to the more proximal dendritic regions is compared with an external representation provided by the entorhinal cortical (EC) input to the dendritic tuft. When these inputs arrive with the proper timing within the same neuron, dendritic plateau potential initiation, burst firing action potential output and robust synaptic plasticity is produced²⁶. The present implementation of the SDI model using the highly compartmentalized form of shunting inhibition produces phase precession that advances action potential output without altering the integrative properties of the dendritic arbor. Given the requirement of backpropagating action potentials in these pathway interactions, the advance of up to 100 ms is an important feature of phase precession as it greatly enhances the temporal overlap of EC input and SC driven CA1 output⁴². The combination of these two elements, phase precession without dendritic shunting or hyperpolarization, allows only those neurons receiving the proper input levels to output bursts of action potentials and robustly potentiate the involved synapses²⁶. This potential “match signal” resulting from a positive input comparison may play a role in hippocampal novelty detection and sequence retrieval^43,44. Furthermore, as subcellular domain-specific innervation of the neuronal surface by co-aligned sets of GABAergic and glutamatergic inputs is a general organizing principle in cortical circuits⁴⁵, our results suggest that spatio-temporal interactions between excitatory and inhibitory inputs within and across different subcellular compartments may provide a general framework for cortical temporal coding.

The recent availability of accurate intracellular in vivo data has greatly aided the attempt to provide actual cellular and network mechanisms for behaviorally related neuronal activity¹². In turn, the current in vitro work produces several specific hypotheses that could be tested with future in vivo recordings. First, silencing of CA1 basket cells (particularly PV+) should remove phase precession by maximally advancing spike phase regardless of the location within the place field. Also, silencing studies may be able to determine if the overall levels of perisomatic inhibition are constant across the place field, as suggested by the current SDI model. Therefore, future studies combining high quality in vivo and in vitro recordings and manipulations in rodents will continue to advance our understanding of the link between neuronal circuit computations and specific behaviors⁴⁶.

Methods

All experiments were conducted in accordance with the National Institutes of Health guidelines and with the approval of the Janelia Farm Institutional Animal Care and Use Committee.

Virus and knock-in animal preparation

The ChR2-GFP fusion protein sequence was cloned into an adeno-associated viral cassette containing the mouse synapsin promoter, a woodchuck post-transcriptional regulatory element (WPRE), SV40 poly-adenylation sequence, and two inverted terminal repeats. Codon-optimized ChR2-GFP encoding the the amino acid substitution H134R was used for the study. rAAV-FLEX-rev-ChR2-GFP²¹ was assembled using a modified helper-free system (Stratagene, La Jolla, CA) as a serotype 2/7 (rep/cap genes) AAV, and harvested and purified over sequential cesium chloride gradients as previously described⁴⁷. PV-Cre knock-in mice have been described previously²². GAD65-Cre knock-in mice were generated using an IRES targeting construct to insert the Cre recombinase coding sequence into the 3′ UTR of the mouse GAD65 gene. The construct was electroporated into a hybrid C57BL/6-129/SV stem cell line. F1 progeny were backcrossed repeatedly to C57BL/6 to recreate the C57BL/6 genetic background. C57BL/6 content of the resulting mice was confirmed by microsatellite testing (Charles River Laboratory, Wilmington, MA).

Virus injection

Parvalbumin-Cre (PV-Cre) and GAD65-Cre knock-in mice (3-5 weeks old) were anesthetized with isoflurane and placed in a stereotaxic apparatus (David Kopf Instruments, Tujunga, CA). A small hole was drilled in the skull using a dental drill. Virus was delivered with a glass micropipette (tip size: 10 μm) using a microinjector (Nanoject II, Drummond Scientific Comp., Broomall, PA). Dorsal hippocampus was injected at three sets of coordinates: 2.2, 2.4 and 2.7 mm posterior from bregma, and 2.1 mm from midline. 20-30 nl of virus was injected every 150 μm from 1.55 mm to 0.95 mm below pia. The pipette was held at 0.95 mm for 3 min before being completely retracted from the brain.

Hippocampal slice preparation and electrophysiology

PV-Cre and GAD65-Cre mice were infected with Cre-dependent rAAV-FLEx-rev-ChR2-GFP, as above. 3-5 weeks post-injection the animals were deeply anaesthetized and decapitated. Coronal slices (350 μm) were prepared from the dorsal hippocampus⁴⁸ and visualized using an Olympus BX-61 epifluorescence microscope equipped with Dodt Gradient Contrast (Luigs and Neumann, Ratingen, Germany) under infrared illumination using a water-immersion lens (60× with 0.8 NA, Olympus, Melville, NY, USA) or with a Zeiss Examiner Z1, (Zeiss, Germany) epifluorescence microscope equipped with Dodt Gradient and with a 20× objective (W-Plan-Apochromat, 1.0 NA, Zeiss, Germany). Experiments were performed at 32-35 °C, in ACSF containing the following (in mM): NaCl 125, KCl 2.5, NaHCO₃ 25, NaH₂PO₄ 1.25, CaCl₂ 2, MgCl₂ 1, and glucose 25; and saturated with 95% O₂ and 5% CO₂. Simultaneous dual whole-cell patch-clamp recordings from distal dendrites and somata of hippocampal CA1 pyramidal neurons (Figs. 1-3 and Supplementary Figs. 1, 3 and 4a-c) or somatic whole-cell patch-clamp recordings (Figs. 4 and 5, Supplementary Figs. 2, 4d and 5) were performed using Dagan BVC-700 amplifiers (Dagan, Minneapolis, MN) in the active ‘bridge’ mode for voltage-clamp experiments, filtered at 1-3 kHz, and digitized at 50 kHz. The distance of the dendritic electrode (mean ± sem: 176 ± 8 mm, n = 14 recordings) was measured on stacked two-photon images collected at the end of recordings (ImageJ, NIH, Bethesda, MD). Series resistance for somatic recordings was 10-25 MΩ, whereas that for dendritic recordings was 20-50 MΩ.

Recording electrodes were filled with an internal solution containing (in mM): K-gluconate 120, KCl 6, HEPES 10, NaCl 4, Mg₂ATP 8, Tris₂GTP 0.6, phosphocreatine 28, and Alexa 594 (Molecular Probes, Eugene, OR) 0.1, pH = 7.25; and the membrane potential was kept close to the GABA-A reversal potential measured in voltage-clamp. Voltages were not corrected for the theoretical liquid junction potential (∼ 8 mV).

To isolate GABA-A receptor mediated responses, a GABA-B receptor antagonist (CGP55845A, Tocris, Ballwin, MO) was prepared in DMSO as 1 mM stock solution and used at 1 μM final concentration was used in most of the experiments. Under these conditions, GABA-A receptor antagonist SR95531 (20 μM, Tocris, Ballwin, MO) completely blocked the photostimulation evoked responses on pyramidal cells (n = 4, Supplementary Fig. 1b). CB1R agonist WIN 55,212-2-mesylate and CB1R antagonist AM251 (both from Tocris, Ballwin, MO) were prepared in DMSO as a 1 mM and 10 mM stock solutions and used at 1 μM and 10 μM final concentration, respectively.

One-photon and temporally focused two-photon (2pTeFo) ChR2-photostimulation

A dual galvanometer-based scanning system (Prairie Technologies, Middleton, WI) was used for 2pTeFo or one-photon ChR2-photostimulation and combined with two-photon imaging. For two-photon imaging, a 140 fs ultra-fast, pulsed laser beam at 920 nm center wavelength (Chameleon Ultra II; Coherent, Auburn, CA), controlled with electro-optical modulator (Model 350-50, Conoptics, Danbury, CT) was used to excite Alexa 594 and GFP.

For one-photon laser ChR2-photostimulation (Figs. 1-3, Supplementary Figs. 1, 4a-c and 5), a blue laser at 473 nm (DPSS, CrystaLaser, Reno, NV) was coupled to the uncaging path of the scan-head. Photostimuli consisted of light pulses of 1 ms duration and power levels in the range of 10-100 μW at the specimen. The timing, position and intensity of the light pulses were controlled using the lasers analog modulation circuitry in combination with a fast shutter (Uniblitz, LS2ZM2, Vincent Associates, Rochester, NY), via software written in LabView (PrairieView-TriggerSync, Prairie Technologies, Middleton, WI).

Experimental setup for two-photon temporal focusing was implemented as described in details^23,49. Briefly, a 140 fs ultra-fast pulsed laser beam at 880 nm center wavelength (Chameleon Ultra II, Coherent, CA) controlled with an electro-optical modulator (Model 350-50, Conoptics, Danbury, CT) was used as the source for temporal focusing. In order to be able to move the temporally focused spot in a few 100 μs time scale it was integrated into the scan-head of a two-photon scanning upright microscope (Examiner Z1, Zeiss, Germany and Prairie Technologies, Middleton, WI). The beam was first reflected towards a ruled diffraction grating with 300 lines/mm (Richardson, New York, NY) from which the first order diffraction was used. The illuminated spot on the grating was then imaged onto the space between X and Y scanning mirrors using an achromatic planoconvex lens (Thorlabs, Newton, NJ, f = 1000 mm). The scanning mirrors scanned the temporally focused beam on the back focal aperture of a 20× objective (W-Plan-Apochromat, 1.0 NA, Zeiss, Germany). The temporal focusing light was reflected and combined with imaging light by a dichroic mirror (900dcxxr-laser, Chroma, VT). The timing, position and intensity of the light pulses were controlled via software written in LabView (PrairieView-TriggerSync, Prairie Technologies, Middleton, WI). Temporal focusing ChR2-photostimulation consisted of light pulses of 0.1-1 ms duration and power levels in the range of 50-500 mW at the specimen. At non-saturated power levels (<50 mW), temporal focusing yielded two-photon excitation of a disc-shaped volume with a diameter of ∼ 5 μm and thickness of ∼ 2 μm²³. These values were measured by using a thin (∼100 nm) layer of fluorescence material on a microscope cover glass which was axially scanned through the temporally focused excitation volume. However as discussed in detail²³, mainly because of the out of focus excitation of ChR2 by the 2pTefo, the spatial resolution of excitation (axially and laterally) was slightly less confined when measured electrophysiologically using saturating power levels (∼50-500 mW). We found that using such a defocused excitation volume (diameter: ∼20 μm, thickness: ∼40 μm) increased the probability of suprathreshold bouton stimulation, while still significantly reduced the overlap and thus ChR2-desensitization when multiple closely placed stimulus locations were used in the cell body layer. The improved spatiotemporal resolution of ChR2-photostimulation by 2pTeFo allowed to (1) precisely manipulate the temporal profile of inhibition (Fig. 4), (2) to stimulate ChR2-expressing perisomatic inhibitory profiles at theta frequency repetitively (Fig. 4, Supplementary Fig. 2), and (3) to stimulate GABAergic (both PV+ and CCK+) profiles in the pyramidal layer in GAD65-Cre mice without directly depolarizing inhibitory terminals on the recorded pyramidal cell (Fig. 5).

In experiments with simultaneous dual whole-cell recordings, when a rectified 5 Hz sinusoidal depolarizing current was injected to the dendrite and paired with one-photon ChR2-photostimulation-evoked perisomatic inhibition (Figs. 1-3, Supplementary Figs. 1 and 4a-c), dendritic sinusoidal currents with different amplitudes (50-1000 pA) were injected during subsequent trials, interleaved with 30-60 second pauses to allow for ChR2 recovery from desensitization. In a subset of experiments to examine the effect of advanced and delayed inhibitory inputs on the range of phase modulation (Supplementary Figs. 4d and 5), and in those using 2pTeFo repeated photostimulation (Figs. 4 and 5, Supplementary Figs. 2), a single somatic electrode was used to inject a filtered depolarizing sinusoidal current (25-670 pA). The shape of the filtered rectified somatic current injection was set to reproduce the somatic depolarization profiles obtained with dual soma-dendrite recordings (Supplementary Fig. 5d).

To evoke CB1R agonist-sensitive IPSCs on CA1 pyramidal cells from GAD65-Cre animals, (Fig. 5), six non-overlapping locations in the pyramidal layer were selected (>20 μm from the recorded neuron), where the amplitude of 2pTeFo-evoked unitary IPSCs showed >20% reduction upon CB1R agonist application (data not shown). These “CB1R agonist-sensitive” IPSCs were subsequently used during high frequency 2pTeFo photostimulation (36 stimuli from six consecutive locations repeated six times with a 1 ms duration and a 3 ms interval).

Data analysis

To produce the subthreshold potentials shown in Figs. 2, 4, 6 and in Supplementary Figs. 2, 4 and 5, raw somatic voltage traces were run through a custom algorithm written in Igor Pro 6. Action potentials were first removed by blanking the traces from 2 ms before the AP peak to 5 ms after the peak, the traces were subsequently linearly interpolated and bandpass filtered using a linear phase finite impulse response (FIR) filter with a 1 ms Hamming window between 3-8 Hz. To produce the traces shown in Figs. 2, and in Supplementary Fig. 5; eight or nine individual traces, each for a different dendritic excitation level, were concatenated together and then the entire sequence of traces was run through the filter algorithm. Since the 5 Hz excitatory dendritic waves have the same time course as the somatic current or conductance waves we used either of these as a reference for the “extracellular reference” for the three experimental conditions. The phase of a spike occurring at time t, was calculated as 360 × (t/200 ms). When referenced to the intracellular depolarization we calculated the spike phase as 360 × (t/t_p) where t_p was the time of the peak of the filtered intracellular potential. Changes in gain for the I-V and F-I curves were calculated as (control slope-experimental slope)/control slope where the slope were determined from linear fits to the data. For F-I curves, input shifts were determined from the xhalf of sigmoid functions (base+max/1+exp(xhalf-x)/rate)) where base is the baseline frequency, max is maximum frequency and rate is the slope parameter. Significance of differences was tested with Student's t-test or ANOVA. P < 0.05 was considered as significant. Data are given in mean ± s.e.m.