The sedimentation properties of ferritins. New insights and analysis of methods of nanoparticle preparation

Abstract

Background

Ferritin exhibits complex behavior in the ultracentrifuge due to variability in iron core size among molecules. A comprehensive study was undertaken to develop procedures for obtaining more uniform cores and assessing their homogeneity.

Methods

Analytical ultracentrifugation was used to measure the mineral core size distributions obtained by adding iron under high- and low-flux conditions to horse spleen (apoHoSF) and human H-chain (apoHuHF) apoferritins.

Results

More uniform core sizes are obtained with the homopolymer human H-chain ferritin than with the heteropolymer horse spleen HoSF protein in which subpopulations of HoSF molecules with varying iron content are observed. A binomial probability distribution of H- and L-subunits among protein shells qualitatively accounts for the observed subpopulations. The addition of Fe²⁺ to apoHuHF produces iron core particle size diameters from 3.8 ± 0.3 to 6.2 ± 0.3 nm. Diameters from 3.4 ± 0.6 to 6.5 ± 0.6 nm are obtained with natural HoSF after sucrose gradient fractionation. The change in the sedimentation coefficient as iron accumulates in ferritin suggests that the protein shell contracts ~10% to a more compact structure, a finding consistent with published electron micrographs. The physicochemical parameters for apoHoSF (15%/85% H/L subunits) are M = 484,120 g/mol, ν̄ = 0.735mL/g, s_20,w = 17.0 S and D_20,W = 3.21 × 10⁻⁷ cm²/s; and for apoHuHF M = 506,266 g/mol, ν̄ = 0.724 mL/g, s_20,w = 18.3 S and D_20,w = 3.18 × 10⁻⁷ cm²/s.

Significance

The methods presented here should prove useful in the synthesis of size controlled nanoparticles of other minerals.

1. Introduction

Ferritin was first isolated from liver and spleen and crystallized by Laufberger in 1937 and identified as a protein containing unusually large amounts of ferric iron [1]. Soon thereafter, Granick and coworkers in a series of papers reported on the iron binding and magnetic properties of ferritin [2–4]. In the decades following this early work, ferritins have become one of the most investigated and widespread classes of proteins known. They are found in cells of nearly all animal tissues and in plants, fungi and bacteria [5–12]. A search in SciFinder Scholar results in over 30,000 articles related to ferritin. All canonical ferritins share the same basic structural features, an approximately spherical protein shell of M_r ~500,000 composed of 24 similar or identical subunits arranged symmetrically with 4:3:2 cubic symmetry about a hollow interior which encapsulates large amounts of iron in the form of a hydrous ferric oxide mineral resembling ferrihydrite [13], the structure of which is much debated [14–19]. In addition to ferrihydrite, iron oxide phases corresponding to hematite, magnetite/maghemite and wüstite have also been observed in lesser amounts as single phases in individual protein molecules [20,21].

In recent years there has been considerable interest in understanding the superparamagnetism, ferromagnetism, Mössbauer and quantum tunneling properties of the nanoparticle iron core of ferritin as well as the mechanism of water proton relaxation enhancement in magnetic resonance images of the iron laden tissues with high concentrations of ferritin and hemosiderin [23–29]. Additionally, the protein cage has proven useful as a reaction vessel, serving as a 3-D template for the synthesis of nanoparticles of magnetite/maghemite (e.g.[30]), various iron salts [31] and minerals of other metals such as gadolinium, lead, cadmium, nickel, cobalt, chromium and gold with interesting and useful properties [32–36]. Ferritin is increasingly finding use in nanotechnology as discussed in other chapters of this volume. Control or knowledge of the size of the nanoparticles within ferritin is important in many studies and applications. For example, uniform iron core sizes with a standard deviation within ± 1 nm are needed for the fabrication of memory devices [37]. In the case of metallic cobalt cores of ferritin, self capacitance is directly proportional to the diameter of the core particle [38] whereas the superparamagnetic relaxation time τ_s of the ferrihydrite nanoparticles depends exponentially on the volume of the particle [24,27,28].

While it is evident that good particle size control is desirable in most applications, this is not always easily achieved. The capacity of the protein cage in principle limits the maximum size of the nanoparticle but, in the case of iron, it is usually difficult to fill the cavity to capacity in vitro. Partially filled ferritin 24mer shells contain cores of varying size about some average which reflects the overall iron content of the protein. The subunit composition of the ferritin used strongly influences the size distribution which is obtained. Mammalian ferritins are composed of two types of subunits, H and L, with M_r ~ 21,000 and 20,000, respectively, which are structurally interchangeable within in the protein shell. Because these subunits have different functions, the H-subunit containing a ferroxidase site [39,40] and the L-subunit mineral nucleation sites [41], the protein shell is inherently polydisperse in subunit composition, resulting in polydisperse iron mineral cores as well (vide infra).

The mineral core is formed by three iron oxidation reactions [42] which further contribute to

$$2{\text{Fe}}^{2+}+{\mathrm{O}}_2+4{\mathrm{H}}_2\mathrm{O}\to 2{\text{Fe}}^{\text{III}}{\text{OOH}}_{(\text{core})}+{\mathrm{H}}_2{\mathrm{O}}_2+4{\mathrm{H}}^{+}$$ (1)

$$2{\text{Fe}}^{2+}+{\mathrm{H}}_2{\mathrm{O}}_2+2{\mathrm{H}}_2\mathrm{O}\to 2{\text{Fe}}^{\text{III}}{\text{OOH}}_{(\text{core})}+4{\mathrm{H}}^{+}$$ (2)

$${4\text{Fe}}^{2+}+{\mathrm{O}}_2+6{\mathrm{H}}_2\mathrm{O}\to 4{\text{Fe}}^{\text{III}}{\text{OOH}}_{(\text{core})}+8{\mathrm{H}}^{+}$$ (3)

its polydispersity in size. Depending upon how iron is added to the protein and the subunit composition of the ferritin, one or more of these reactions may dominate. When iron is added in small increments (low-flux ~ 50 Fe per addition), two irons are oxidized per O₂ at the ferroxidase center through the ferroxidase reaction [Eq. (1)]. When a large flux of iron is presented to the protein (1000 Fe per addition), the reaction largely occurs on the mineral surface and the stoichiometry of the reaction approaches 4 Fe(II) oxidized per O₂ consumed [Eq. (3)]. At intermediate fluxes, the H₂O₂ produced at the ferroxidase sites [Eq. (1)] oxidizes further Fe(II) by the detoxification reaction [Eq. (2)]. Each of these reactions is important under different experimental conditions of iron loading the protein. Essentially identical mineral cores are produced with either O₂ or H₂O₂ as the oxidant [(Eqs. (1) and (3) vs. Eq. (2)] under the same flux of iron into the protein (50 Fe/shell per addition) as demonstrated by Mössbauer spectroscopy [24].

Ferritins isolated from tissue or apoferritins reconstituted in vitro show that a significant fraction (10 – 30 %) of the sample remains relatively iron-free while another fraction is more fully loaded (approaching 4500 Fe/shell) [43–46]. The basis for these unusual iron distributions has been uncertain. Mineral growth models have related oxidation through Eq. (3) to the surface area of the growing mineral [44]. As the core grows in size, additional sites for oxidation and mineralization are created, allowing for increased capacity for deposition of additional iron by an autocatalytic mechanism. Under this scenario, those ferritin molecules that were able to first form a small core would have a greater likelihood of acquiring more iron than proteins that had not, leaving the latter proteins largely iron free. However, this model excludes any role for the protein in iron oxidation other than, perhaps, the formation of the initial iron cluster. An oxidation pathway directed purely by the ferroxidase site would seemingly allow for more uniform distribution of core sizes because all iron would be oxidized by the enzyme site and, therefore, in the same manner at the same rate. Such would be the case if all the protein shells in heteropolymer mammalian ferritins had the same number of H-subunits, i.e. they were uniformly distributed among the protein shells, which is not the case [5].

Analytical ultracentrifugation is well suited for studies of the heterogeneity of ferritin. The first detailed study was reported by Rothen in 1944 in his seminal work on horse, dog and human ferritins [46]. While the instrumentation available then was primitive compared to that today, the main conclusions of Rothen’s work still hold. Apoferritins were observed to be relatively homogeneous whereas iron containing horse spleen ferritin exhibited marked heterogeneity and broad sedimentation patterns in which both apoferritin (or low iron ferritin) and ferritin components were present.

Rothen [46] made the first molecular weight determination of apoferritin using sedimentation velocity measurements. The molar mass was calculated from the Svedberg equation [Eq. (4)]

$$M=\mathit{\text{sRT}}/D(1-\overline{\nu }\rho )$$ (4)

where s, R, D, ν̄ and ρ are the sedimentation coefficient, the gas constant, the diffusion constant, the partial specific volume of the protein and the density of the solution, respectively. The sedimentation coefficient of apoHoSF was determined to be $s_{20,w}^o=17.6$ in Svedberg units (10⁻¹³s). $s_{20w}^o$ corresponds to the sedimentation coefficient in pure water at 20 °C extrapolated to infinite dilution.) Rothen measured the diffusion coefficient $D_{20}^o=3.61\times {10}^{-7}$ cm²/s using a Tiselius apparatus and the partial specific volume ${\overline{\nu }}_{20}^o=0.747$ cm³/g of the protein using a quartz pycnometer. Given ${\rho }_{20}^o=0.99823$ g/cm³ for pure water, he calculated a molecular weight of 467,000. In 1973, Crichton and coworkers reported a value of M = 443,000 based on their measured value of $s_{20w}^o=17.12$ S for the apoprotein and using a value of ${\overline{\nu }}_{20}^o=0.731$ mL/g from the amino acid composition known at that time [47]. A more recent value of M_r ~ 450,000 by sedimentation equilibrium measurements has been reported [48]. Weight average molecular weights of 460,000, 480,000 and 515,000 have been published for horse spleen, liver and heart ferritins from sedimentation velocity measurements [49]. Other values reported for the horse spleen protein have ranged from 430,000 to 480,000 and are summarized in [50]. However, from the molecular weights of 19,978 and 21,269 from the cDNA sequences of the H- and L-subunits, respectively, a heteropolymer of 15% H and 85% L-subunit (a common composition of the horse spleen protein) would have a molecular weight of 484,120 only slightly larger than the molecular weight of 479,472 for the L-chain homopolymer and larger than the values predicted by the above referenced centrifugation measurements.

The Stokes diameter d of spherical particle (of which ferritin is a good example) is related to the diffusion coefficient D and viscosity of the solvent (η = 0.01002 poise for pure water at 20 °C) through the Stokes-Einstein equation [Eq. (5)] where k_B = 1.3807 × 10⁻¹⁶ erg-K⁻¹ is the

$$d=k_{B}T/3\pi \eta D$$ (5)

Boltzmann constant and T the absolute temperature. D has been measured for horse spleen ferritin and apoferritin by a number of other methods, including ultracentrifugation [49, 51], dynamic light scattering (DLS) [52], flow field flow fractionation (Fl-FFF) [53] and quasi-elastic neutron scattering (QENS) [54] under various solution conditions (buffer, salt, etc.), giving values of D ranging from 2.9 × 10⁻⁷ to 3.7 × 10⁻⁷ cm²/s. From the Rothen’s value of $D_{20w}^o=3.61\times {10}^{-7}$ cm²/s for apoHoSF in pure water at 20 °C, a Stokes diameter of an equivalent hard sphere of 11.9 nm is calculated from Eq. (5), which compares favorably with the nominally 12.5 nm diameter of the shell of horse spleen apoferritin from its x-ray crystal structure [55].

Historically, analytical ultracentrifugation has been used in studies of the heterogeneity and assembly properties of canonical ferritins [43–51,53,56–59] and, more recently, of Dps proteins [60–62]. AUC is well suited for examining the distribution of mineral core size in ferritin samples as well as detecting protein cross-linked species and measuring their hydrodynamic properties. During iron deposition, oxidative damage to the protein leads to minor amounts of dimers, trimers, tetramers and pentamers with sedimentation coefficients significantly larger than that of the monomeric protein [53,56,57,59]. Ferritin aggregates composed of two, three and four protein shells in clusters as well as chain-like assemblies of a dozen or so shells have been observed in transmission electron micrographs [63].

In the present study, we have employed analytical ultracentrifugation to study the heterogeneity of ferritin with regard to the polydispersity of the mineral core. The goals of the work were to develop a quantitative model for describing the observed sedimentation coefficient as a function of iron content of the protein and to evaluate methods for obtaining nanoparticles of reasonably uniform size. Sedimentation velocity measurements were used to monitor the iron distributions of native horse spleen ferritin and horse spleen and human H-chain ferritins reconstituted from the apoprotein under different conditions. Ferritin is unusual, and perhaps unique, in that as it acquires iron within its shell, its overall physical size and spherical shape remain relatively unchanged while its buoyant mass increases nearly two-fold. Hence, changes in sedimentation velocity patterns correlate directly with changes in the distribution of iron loading in ferritin, and can provide insights into the process of core mineralization within the protein as well as a measure of the degree of homogeneity of core size within a given sample preparation. Equations are developed for describing the effect of the change in iron content of the protein on the observed sedimentation coefficient and for assessing the distribution of core sizes from a linewidth analysis of g(s)* vs. s* curves. The data suggests that the protein shell is not rigid but contracts to some extent during core mineralization. Methods of addition of iron to the protein are assessed and procedures for improving core size homogeneity utilizing sucrose-gradient preparative ultracentrifugation are presented.

2. Materials and methods

2.1 Protein purification

Recombinant human liver ferritin (HuHF) was isolated from E. coli following a protocol similar to that described elsewhere [64]. Cells were lysed using a French press at pressures exceeding 10,000 psi. The lysate was centrifuged at 4 °C for 15 minutes at 14,400 × g to remove the cellular components. A heat precipitation step at 60 °C for 10 minutes was followed by another centrifugation step for 20 minutes at 4 °C at 14,400 × g. The supernatant was collected and brought to 80% saturation with 523 mg/mL (NH₄)₂SO₄. The suspension was allowed to stir for 2–3 hours at 4 °C and the precipitate was collected by centrifugation for 20 minutes at 4 °C and 3300 × g. Ferritin was resuspended in a minimal amount of 25 mM Tris, pH 7.4 buffer and dialyzed for 8 hrs. The protein solution was then treated with 1 mg/mL DNase, 1 mg/mL RNase and 100 mM MgCl₂ at 37 °C for 30 minutes to remove any contaminating nucleic acids. This mixture was centrifuged to remove any particulates, and the supernatant concentrated by ultrafiltration using a 100,000 MW cut-off Millipore membrane. The ferritin solution was run on a Superdex 200 or Sepharose CL-6B size-exclusion column equilibrated with 0.15 M NaCl, 25 mM Tris, pH 7.4, to remove any low molecular weight contaminating proteins. Fractions containing HuHF were collected, combined and run over a Q sepharose, fast flow Pharmacia anion exchange column with a 150 to 500 mM NaCl gradient. Peak fractions were collected, pooled, and dialyzed into buffer suitable for analytical ultracentrifugation.

Horse spleen ferritin (HoSF) was purchased from Calbiochem (San Diego, CA), MP Biomedicals (Irvine, CA) and Sigma (St. Louis, MO) and also isolated directly from horse spleen as follows: The tissue was blended in 1.5× its volume/weight (mL double deionized water/gram of tissue) and the homogenate subjected to heat denaturation at 70 °C for 10 minutes followed by centrifugation at 3300 × g for 30 minutes at 4 °C on an IEC MP4R centrifuge employing a swinging bucket rotor. After a second centrifugation step at 14,400 × g with a fixed angle rotor (IEC #854), β-mercaptoethanol to a concentration of 1 mM was added to the red-brown supernatant. The ferritin was precipitated with ~50% saturated (NH₄)₂SO₄ (313 mg/mL) with overnight stirring at 4 °C. The pellet was resolubilized in 20 mM sodium phosphate, pH 6.8 with stirring for 1 hour at 4 °C. Low molecular weight contaminants were removed by size-exclusion chromatography using a Superdex 200, 50 cm column. If necessary, the (NH₄)₂SO₄ step was repeated as needed to obtain a homogeneous ferritin solution as judged by size exclusion chromatography and PAGE. All isolated ferritins were run on a 15% SDS-PAGE and a 7% native PAGE gels to assess protein purity and to verify the absence of significant cross-linking between protein shells. The subunit composition of the HoSF used in this work was determined to be 15% H and 85% L by SDS-capillary gel electrophoresis as described [65].

2.2 Iron analysis

The iron content of native and reconstituted ferritins was measured by a modified colorimetric ferrozine assay [66]. Samples of known protein concentration were incubated at 90 − 95 °C in 10% trichloroacetic acid for 2 hours in 1 mL total volume followed by 10 min on ice. Denatured protein was removed by centrifugation. An aliquot of the supernatant was added to 100 µl of saturated ammonium acetate, 62.5 µl of 0.12 M ascorbic acid and 62.5 µl of 0.25 M ferrozine [3-(2-pyridyl)-5,6-diphenyl-1,2,4-triazine-p, p’-disulfonic acid, monosodium salt hydrate]. Samples were incubated at room temperature for 30 minutes. Absorbance at 562 nm was measured (molar absorptivity of the Fe complex at 562 nm = 27,900 M⁻¹ cm⁻¹) and the ratio of Fe to protein calculated.

2.3 Preparation of apoferritins

Ferritins, as purchased or isolated, contain varying amounts of iron. The HoSF generally was received or isolated with an average of ~ 2000 − 2600 Fe/shell whereas HuHF usually contained ≤ 50 Fe/shell. Iron was stripped from the protein by anaerobic dialysis using dithionite as the reductant [67]. Horse spleen ferritin was subjected to 5 changes with a ~50:1 volume ratio and 6 hours between changes against an anaerobic solution of 0.1 M sodium acetate, pH 5.2 to which dithionite had been added to a concentration of 3 g/100 mL. The procedure was repeated with the dithionite concentration reduced to 0.3 g/100 mL for the second cycle. A final anaerobic cycle of 5 changes was performed in the absence of dithionite with 1 mM of 2,2'-dipyridyl added to scavenge any remaining iron. Exhaustive dialysis to remove dipyridyl was performed using 10 mM Mops, 0.15 M NaCl, pH 7.1 (several changes). In the case of the more fragile HuHF, 50 mM MES, pH 6.0 was employed in place of acetate buffer [67]. The apoferritins were assayed for concentration either by UV (ε₂₈₀ = 19,500 M⁻¹ cm⁻¹ subunit⁻¹ for HoSF; ε₂₈₀ = 22,700 M⁻¹ cm⁻¹ subunit⁻¹ for HuHF) or using the BioRad Protein [68] and Better Bradford (Pierce Biotechnology, Rockland, IL, USA) assays. The Better Bradford assay was employed in all experiments reporting Fe/shell ratios because the presence of iron does not interfere with this method of determining protein concentration whereas the other assays showed some level of interference.

2.4 Reconstitution of ferritins

Ferritin was reconstituted by aerobic addition of Fe(II) to apoferritin (0.25 or 1.0 mg/mL) using either high (500 or 1000 Fe(II)/addition) or low (50 Fe/addition) flux conditions. Ferritins were reconstituted to final iron loadings of 500, 1000, 1500, 2000 or 2500 Fe/shell in both low and high iron fluxes or to a level where precipitation was observed. For the low iron flux samples, a series of additions at 50 Fe(II)/shell were made, allowing at least 10 minutes between additions for the complete oxidation of Fe(II) [69]. The 1 mL ferritin solutions were open to air and constantly stirred to maintain molecular oxygen in the sample. The high iron flux samples were made using a maximal single addition of 1000 Fe(II)/shell at a protein concentration of 0.25 mg/mL to keep the sample from going anoxic during the course of the experiment. Under these conditions about 50% of the dissolved O₂ would be consumed based on the known oxidation stoichiometry of 4 Fe(II)/O₂ [69,70].

2.5 Density and viscosity measurements

The density of the 0.1 M MOPS, 0.15 M NaCl, pH 7.5 buffer was measured at 20 °C with an Anton Paar DMA 02D densitometer, standardized with pure water and dry air. The dynamic viscosity was measured with an Anton Paar AMVn automated micro viscometer relative to air-saturated water at 20 °C.

2.6. Preparation of Sucrose Gradients

Sucrose solutions were made (w/w) in 0.15 M NaCl. Sucrose gradients were prepared using a two layer method (http://web-mcb.agr.ehime-u.ac.jp/english/methods/gradient.htm) in which 8 mL of 50, 60 or 70% sucrose was added to the bottom of a 16 × 22 mm ultracentrifuge tube (Beckman, 344061) and 8 mL of 0% sucrose solution gently layered on top. Tubes were covered tightly with parafilm and then slowly turned horizontal for 12 hours and then back to a vertical position. Gradients were also prepared by layering 4.8 and 23% (w/w) sucrose solutions (equivalent to 5 and 30% w/v) for 15 min, 30 min, 1 hr or overnight. Protein samples were gently layered on top of the gradient and spun on a Sorvall Ultra 80 centrifuge fitted with the AH-629 rotor at 25000 rpm (80,000 × g) at 4 °C for 8.75 hr with no braking. After centrifugation, sequential 1.5 ml fractions were taken from the top of the sucrose gradient and the percentage sucrose of each fraction measured with a Misco PA202 Palm Abbe digital refractometer to verify the integrity of the gradient. Each fraction was also analyzed for iron and protein. Fractions were then dialyzed into 0.1 M MOPS, 0.15 M NaCl, pH 7.5 buffer for the AUC measurements.

2.7. Sedimentation velocity experiments and analysis

Sedimentation velocity studies were carried out in 0.15 M NaCl, 0.1 M MOPS, pH 7.5, at 24,000 rpm and 20 °C on a Beckman Optima XLI analytical ultracentrifuge using Rayleigh interference optics, 12-mm double sector charcoal-epon centerpieces, and either a 4- or 8-hole titanium rotor, with ~8 seconds/scan. The apparent sedimentation coefficient distribution, g(s*) = dc/ds*, was calculated from the time derivative of the concentration profile with DCDT+ (uncorrected for the effects of diffusion) [71,72]. Although there are many other approaches available for analyzing sedimentation data (e.g. [73]), DCDT+ was determined to be most suited for the heterogeneous samples and broad sedimentation distributions encountered in this work. Because it is model independent, post analysis of the linewidths of the g(s*) curves can be carried out to obtain the dispersion in core size for different samples (vide infra). In all instances, care was taken to choose a sufficiently narrow time span of the data so as to avoid artificial boundary spreading.

2.8. Effect of iron loading of ferritin on its sedimentation coefficient

The partial specific volume of apo-HoSF was originally reported as ν̄_protein = 0.747 mL/g [46] but a more recent refined value is 0.738 mL/g [74]. A value of ν̄_protein = 0.735 ± 0.007 mL/g was used in this work as calculated using Sednterp [75] based on the amino acid composition of a protein of 15% H and 85% L subunits. The H and L homopolymers have Sednterp calculated ν̄_protein values of 0.727 and 0.736 mL/g, respectively. The partial specific volume ν̄_complex and, consequently, the sedimentation coefficient of the iron-ferritin micellar complex will change as iron is accumulated within the protein. The effect of iron loading on ν̄_complex can be estimated from equation (6) where g_protein is the gram mass of the protein;

$${\overline{\nu }}_{\mathit{\text{complex}}}=\frac{g_{\mathit{\text{protein}}}{\overline{\nu }}_{\mathit{\text{protein}}}+g_{\mathit{\text{core}}}{\overline{\nu }}_{\mathit{\text{core}}}}{g_{\mathit{\text{total}}}}$$ (6)

ν̄_protein = 0.735 mL/g; g_core is the gram mass of the accumulated iron core; ν̄_core is the specific volume of the iron core; and g_total is the gram mass of the protein plus its accumulated core.

The value of ν̄_core was estimated from published density measurements of ferrihydrite nanoparticles of various sizes ranging from 2.6 to 7.4 nm and containing from ~ 100 to ~ 3000 Fe per cluster [14]. A linear regression of the specific volume of the mineral as a function of cluster size for the larger iron clusters of n_Fe = 370 to 3000 Fe results in a reasonable fit (R= −0.991, N=3), giving ν̄_core = −7.7 × 10⁻⁶n_Fe + 0.286 mL/g. Thus, ν̄_core ranges in value from ~0.29 mL/g for small iron clusters to ~ 0.25 mL/g for a fully loaded ferritin of 4500 Fe/shell.

The expected sedimentation coefficient of the complex in 0.1 M MOPS, 0.15 M NaCl, pH 7.5 is given by Eq. (7):

$$s_{\mathit{\text{complex}}}=\frac{M_{\mathit{\text{protein}}}+n_{\mathit{\text{Fe}}}{M}_{\mathit{\text{core}}}/5*1-{\overline{\nu }}_{\mathit{\text{complex}}}\rho }{N_{A}f}$$ (7)

where M_protein = 484,120 g/mol is the molar mass of the HoSF used in the present study; n_Fe is the number of iron atoms in the core based on the reduced formula of ferrihydrite, Fe₅O₁₂H₉ [14]; M_core = 481 g/mol is the molar mass of the ferrihydrite unit cell; ν̄_complex is the partial specific volume of the protein/iron complex, calculated as described above; ρ = 1.0121 ± 0.0001 g/mL is the measured density of the 0.1 M MOPS, 0.15 M NaCl, pH 7.5 buffer; N_A is Avogadro’s number; and f = 1.34 × 10⁻⁷ g/s is the frictional coefficient of the protein calculated from the rearranged Svedberg equation [Eq. (8)] using the average value of s_protein = (15.4 ±

$$f=\frac{M_{\mathit{\text{protein}}}(1-{\overline{\nu }}_{\mathit{\text{protein}}}\rho )}{N_A{s}_{\mathit{\text{protein}}}}$$ (8)

0.6) × 10⁻¹³ s for the apoferritin (N = 7) in 0.10 M MOPS, 0.15 M NaCl, pH 7.5 (vide infra). In the model, the frictional coefficient is assumed unchanged by the presence of the mineral core.

By combining equation (6), (7) and (8) and setting g_protein = M_protein and g_core = n_FeM_core/5, a final expression relating $s_{\mathit{\text{complex}}}^{*}$ to n_Fe is obtained [Eq. (9)].

$$s_{\mathit{\text{complex}}}=s_{\mathit{\text{protein}}}·\frac{\left[M_{\mathit{\text{protein}}}+\frac{n_{\mathit{\text{Fe}}}{M}_{\mathit{\text{core}}}}{5}-\rho (M_{\mathit{\text{protein}}}{\overline{\nu }}_{\mathit{\text{protein}}}+\frac{n_{\mathit{\text{Fe}}}{M}_{\mathit{\text{core}}}{\overline{\nu }}_{\mathit{\text{core}}}}{5})\right]}{M_{\mathit{\text{protein}}}(1-{\overline{\nu }}_{\mathit{\text{protein}}}\rho )}$$ (9)

2.9. Correction of g(s^*) as a function of iron loading

Sedimentation velocity data were corrected for the change in refractive increment with concentration (dn/dc) as iron is loaded into the protein. The values for (dn/dc)_protein and (dn/dc)_core are 0.00173 and 0.00218 mL/g, respectively [46]. Under the assumption that dn/dc can be expressed as a weight average, a weighting function w(s) was applied to the g(s*) data to account for changes in refractive increment due to iron [Eqs. (10) and (11)]:

$$w(s)=\frac{c_{\mathit{\text{protein}}}{\left(\frac{dn}{dc}\right)}_{\mathit{\text{protein}}}+c_{\mathit{\text{core}}}{\left(\frac{dn}{dc}\right)}_{\mathit{\text{core}}}}{c_{\mathit{\text{Total}}}}=\frac{g_{\mathit{\text{protein}}}{\left(\frac{dn}{dc}\right)}_{\mathit{\text{protein}}}+g_{\mathit{\text{core}}}{\left(\frac{dn}{dc}\right)}_{\mathit{\text{core}}}}{g_{\mathit{\text{Total}}}}$$ (10)

and

$$F(s)=\frac{{\left(\frac{dn}{dc}\right)}_{\mathit{\text{protein}}}}{w(s)}$$ (11)

where c is in g/cm³, g_protein = M_protein and g_core = n_FeM_core/5 and F(s) is a function relating g(s*) to the fractional amount of iron loading that accounts for the increase in dn/dc due to iron. Therefore, g(s*)_corrected = g(s*)_raw · F(s) with F(s) ranging from 1.0 for apoferritin to 0.891 for ferritin having 4500 Fe/shell. Computed values of F(s) fit very well to a decaying exponential: F(s) = 0.137 · e ^{(−n_Fe/2883)} + 0.863, R = 0.9999 where n_Fe = (86.9±3.0) · s_complex −(1339±70) for HoSF and n_Fe = (86.9±3.0) · s_complex −(1443 ± 70) for HuHF (see below). Application of the F(s) correction to the g(s*)_raw data affects the integrated areas under the peaks by 5% or less for the samples in this work which typically contain ≤ 2500 Fe/shell.

2.10. Linewidth analysis

Individual peaks in the g(s*) vs. s* plots were fit to a Gaussian function of the form $g(s^{*})=A\text{exp}[-{(s_{\mathit{\text{peak}}}-s)}^2/2{\sigma }_{\mathit{\text{obs}}}^2]$, the area $A\sqrt{2\pi }{\sigma }_{\mathit{\text{obs}}}$ under the peak being proportional to the concentration of species present. The observed linewidth σ_obs has contributions from both the protein shell and the mineral core, i.e. ${\sigma }_{\mathit{\text{obs}}}^2={\sigma }_{\mathit{\text{shell}}}^2+{\sigma }_{\mathit{\text{core}}}^2$. σ_shell was determined from curve fitting of the peak for the apoprotein i.e. σ_obs = σ_shell, enabling σ_core to be calculated from σ_obs measurements of iron containing samples. However, σ_shell itself has contributions from both protein heterogeneity and diffusion of the protein, namely ${\sigma }_{\mathit{\text{shell}}}^2={\sigma }_{\mathit{\text{hetero}}}^2+{\sigma }_{\mathit{\text{diff}}}^2$. Because σ_diff can be calculated, the homogeneity of the protein can then be assessed from its σ_hetero value. The diffusion contribution to the linewidth was computed from the relationship ${\sigma }_{\mathit{\text{diff}}}=\sqrt{2\mathit{\text{Dt}}}/r_m{\omega }^{2}t$ where the diffusion coefficient D corresponds to that of the protein in buffer (D = 2.99 × 10⁻⁷ cm²/s for apoHuHF and D = 3.01 × 10⁻⁷ cm²/s for apoHoSF), t is the sedimentation time, r_m is the radius of the meniscus and ω is the angular velocity of the rotor. Because t and ω² t are different for each scan in the series used to compute g(s*) f or a given sample, their average values were used for the calculation of σ_diff [72]. Different sets of scans of narrow time range were used for calculation of g(s*) for different samples and therefore the computed value of σ_diff depend on the particular sedimentation run as well as on the identity of the sample.

3. Results

3.1. Sample calculation

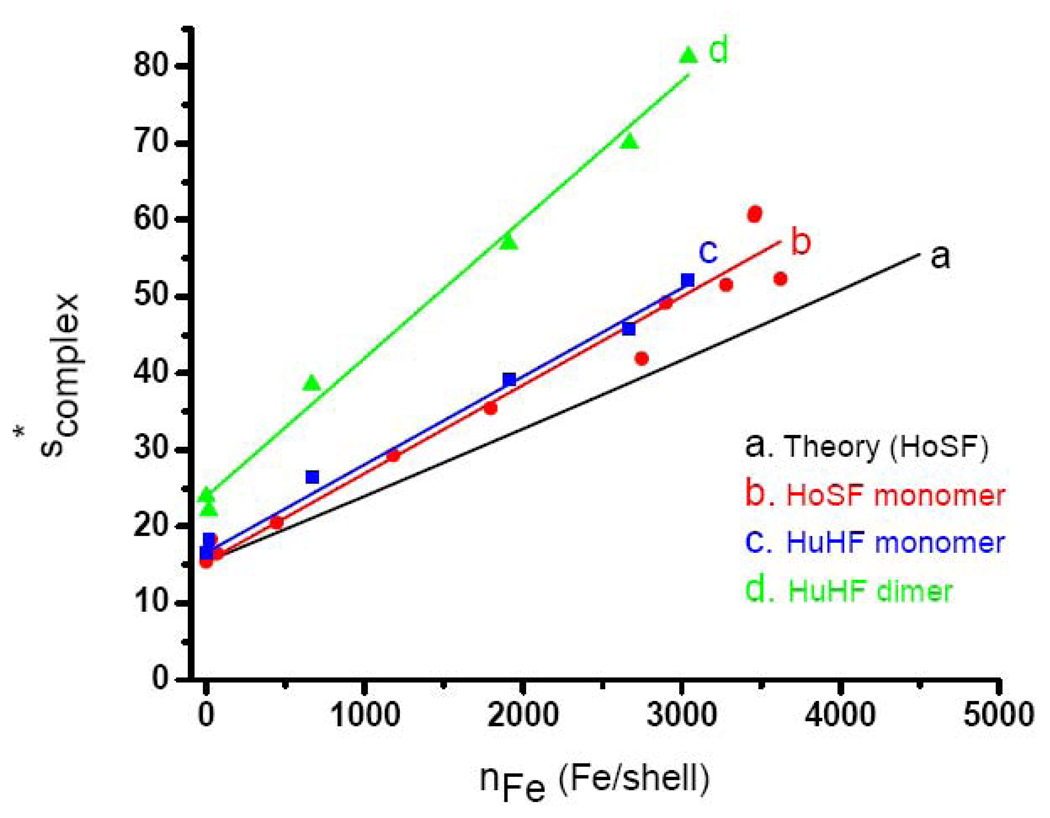
The calculated s_complex as a function of iron loading is shown in Fig. 1 (curve a). The predicted values of s_complex from equation (9) are remarkably linear with iron loading within the thickness of the line (linear regression: s_complex = 0.00882 · n_Fe +15.4, R = 0.999; or n_Fe =113.4 · s_complex −1746 ). Curve b is an empirical plot of the weighted average s_W of the sedimentation coefficient calculated by Eq. (12) as a function of n_Fe for a series of HoSF samples

$$s_W=\raisebox{1ex}{${\displaystyle \int s^{*}g(s^{*}){\mathit{\text{ds}}}^{*}}$}\!\left/ \!\raisebox{-1ex}{${\displaystyle \int g(s^{*}){\mathit{\text{ds}}}^{*}}$}\right.$$ (12)

obtained by preparative centrifugation on a sucrose gradient (linear regression: s_complex = (0.0115± 0.0004) · n_Fe+15.4 ± 0.6; or n_Fe =(86.9 ± 3.0) · s_complex −(1339 ± 70). The iron contents of the samples were measured by the ferrozine method and the protein concentration by the Better Bradford assay (Materials and Methods). The slopes of predicted curve a and experimental curve b differ by ~23%. This difference cannot be reconciled by any reasonable choice for the values of M_core and ν̄_core of ferrihydrite used in Eq. (9) [14–19], nor by using the corresponding values for the other minerals present in lesser amounts in ferritin cores [20,21]. These findings imply that the assumption inherent in Eq. (9) that the frictional coefficient of the protein is constant is not valid. Rather f appears to decrease to some extent as iron is accumulated within the protein shell, resulting in a further increase in s than that predicted on the basis of the buoyant mass of the core alone (more later). In subsequent analyses, we employed the empirical relationship between s_complex and n_Fe represented by the least-squares line of curve b in Fig. 1.

Fig. 1.

The variation in $s_{\mathit{\text{complex}}}^{*}$ with iron loading of HoSF and HuHF. Curve a: Calculated line for HoSF using equation (9) a described in Materials and Methods. The linear-regression is within the thickness of the line giving s_complex = 0.00882 · n_Fe +15.4 (R = 0.9999). Curve b: Data for sucrose gradient fractionated HoSF ferritin from MP Biomedicals. The linear regression through the 11 data points gives s_complex = (0.0115 ±0.0003) · n_Fe + 15.4 (R=0.982). Curve c: Data for monomeric HuHF reconstituted from apoHuHF with iron in 50 Fe²⁺ additions. The linear regression through the 5 data points gives s_complex (monomer) = (0.0115 ± 0.0003) · n_Fe + 16.6 (R = 0.995). Curve d: Data for dimeric HuHF reconstituted from apoHuHF with 50 Fe²⁺ additions as for curve c. The linear regression through the 5 data points gives s_complex (dimer) = (0.0181 ± 0.0005) · n_Fe + 23.9 (R = 0.996).

The y-intercept of curves a and b in Fig. 1 corresponds to the experimentally determined, uncorrected s = 15.4 S for apo-HoSF. Correction of s according to Eq. (13) for measured

$$s_{20,w}=s\frac{{\eta }^{*}}{{\eta }_{20,w}}\frac{(1-{\overline{\nu }}_{20,w}{\rho }_{20w}^o)}{(1-{\overline{\nu }}^{*}{\rho }^{*})}$$ (13)

buffer density and viscosity at 20 °C (ρ*= 1.0121 ± 0.0001 g/mL, η *= 0.01067 ± 0.00003 poise) to that of pure water at 20 °C ( ρ_20,w = 0.99823 g/mL, η_20,w = 0.01002 poise) with ν̄ * = ν̄_20,w = 0.735 ± 0007 mL/g gives s_20,w = 17.0 ± 0.6 S (N = 7, 95% confidence interval). This value compares with previously published values of s_20,w = 17.9, 17.6, 17.1, 16.6 and 16.5 S [46–49,74]. The relatively large error of ± 0.6 S associated with our value of s_20,w reflects the heterogeneity in the apoprotein and likely accounts for the range of values reported in the literature. In our work, s values ranged from 14.3 to 16.7 S for various apoprotein samples prepared from commercially supplied horse spleen ferritin and from protein isolated in our laboratory. This large range reflects oxidative damage to the protein, the tendency of the protein to cross-link to form dimers and higher order oligomers and the inherent heterogeneity associated with the variable subunit composition of the protein itself [49,53,56,57,59,65,76–78]. From s_20,w= 17.0 S, M = 484,120 g/mol and R = 8.3145 × 10⁷ erg-K⁻¹mol⁻¹, we calculate through

$$D_{20,w}=\frac{s_{20,w}·RT}{M·(1-\overline{\nu }{\rho }_{20,w})}$$ (14)

Eq. (14) a translational diffusion coefficient of D_20,w = (3.21 ± 0.15) × 10⁻⁷ cm²/s which compares well with the “best” published value of D_20,w = 3.24 × 10⁻⁷ cm²/s for apoHoSF [51,74]. From D_20,w = (3.21 ± 0.15) × 10⁻⁷ cm²/s, we calculate a Stokes diameter of 13.3 nm for the apoprotein (Table 1).

Table 1.

Sedimentation parameters for horse spleen and human H-chain ferritins.^a

Protein	M (g/mol)	s20,w (10−13s)	D20,w (10−7cm2/s)	d (nm)
apoHoSF (monomer)b	484,120	17.0 (0.6)	3.21 (0.15)	13.3
apoHoSF (dimer)c	968,240	25.1 (0.1)	2.37 (0.10)	18.0
apoHuHF (monomer)d	506,266	18.3 (0.1)	3.18 (0.09)	13.5
apoHuHF (dimer)d	1,012,532	26.4 (0.2)	2.29 (0.20)	18.7

^aEstimated errors in parentheses.

^bChemically prepared apoHoSF. Fractionated native HoSF (fraction # 1 of Fig. 9) gave s_20,w = 16.9 S and D_20,w = 3.19 × 10⁻⁷ cm²/s.

^cFractionated apoHoSF (fraction # 1 of Fig. 9)

^dapoHuHF as isolated and DTT treated (curve c, Fig. 5)

3.2. Examination of horse spleen ferritins from different sources

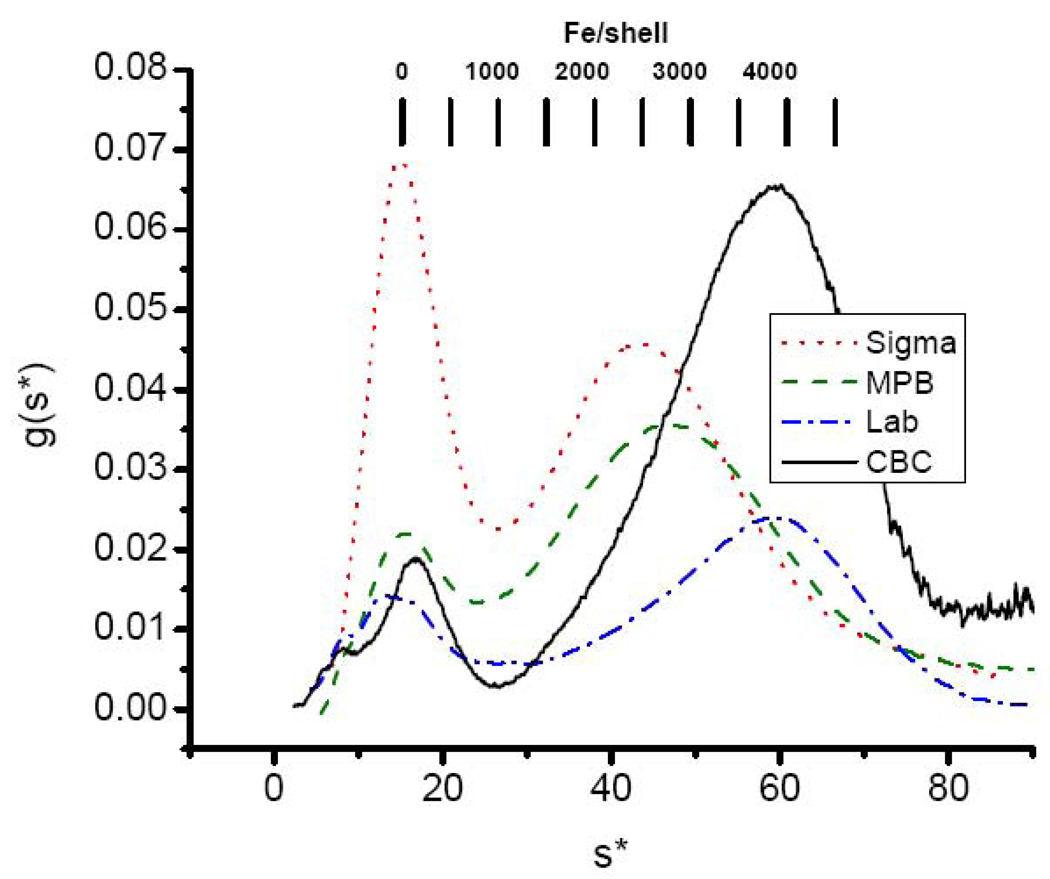
The sedimentation patterns of horse spleen ferritin from four sources are compared in Fig. 2. While they differ markedly from one another, they all show a largely iron free fraction and a heterogeneous iron containing fraction as originally observed by Rothen [46] and later by others [43,44]. The average Fe/shell ratio of each of the samples can be estimated from equation (15)

$$n_{\mathit{\text{Fe}},\mathit{\text{ave}}}=\frac{{\displaystyle \int n_{\mathit{\text{Fe}}}(s^{*})g(s^{*}){\mathit{\text{ds}}}^{*}}}{{\displaystyle \int g(s^{*}){\mathit{\text{ds}}}^{*}}}$$ (15)

where n_Fe(s*) is given by the linear relationship n_Fe = 86.9 · s_complex −1339 from the fit of curve b in Fig. 1. Substitution of s_W into the equation n_Fe,ave = 86.9 · s_W −1339 is mathematically equivalent to Eq. (15) and more convenient for calculations. Acceptable agreement is obtained between the iron contents n_Fe from AUC, which has an estimated relative standard deviation of ± 10% and those from ferrozine and Better Bradford analyses with measured relative standard deviation of ± 3.8% (Table 2), validating the use of Eq. (15) for determining the iron content of samples. We note that the presence of some intermolecular cross-linking would bias s_W to a higher value and would thus produce an artificially high result for n_Fe,ave. However, native PAGE showed no visual evidence of oligomeric species in any of the four HoSF samples in Table 2, indicating that cross-linked protein must represent less than ~ 5% of the total present and thus would not unduly affect the value of n_Fe from Eq. (15). However, some cross-linking is present as discussed below and, if desired, dimers, trimers and higher oligomers can be removed using size exclusion chromatography [79].

Fig. 2.

Sedimentation velocity profiles (g(s*) vs. s* curves) of commercially supplied holoHoSF from Calbiochem (black —), MP Biomedicals (green – –), Sigma-Aldrich (red ˙ ˙ ˙ ) compared to laboratory prepared holo-HoSF purified from frozen horse spleen as described in Materials and Methods (blue - ˙ - ). Sample conditions: 1.0 mg/mL ferritin in 0.1M MOPS, 0.15 M NaCl, pH 7.5. s* is defined as $s*(t_i,r_j)=\frac{1}{{\omega }^2{t}_i}\text{ln}(r_j/r_m)$ and is the transform of the radial axis of the centrifuge tube to the sedimentation coefficient axis where ω is the angular velocity, r_j is the radius in the solution and r_m is the radius of the meniscus and t_i is time. g(s*) is the concentration distribution function and is the concentration gradient on the s* axis, i.e. g(s*) = (∂c / ∂s*)_t. A detailed explanation of these quantities and their calculation can be found in reference [90].

Table 2.

Comparison of the iron contents (Fe/shell ratios) of horse spleen ferritin samples determined by AUC and ferrozine/Better Bradford analyses.

HoSF Preparation	Catalog Number	Fe/shella (ferrozine/Better Bradford)	Fe/shellb (AUC)	Percent Difference
CalBioChem	341476	2060	2250	9.2
MP Biomedicals	151119	2539	2480	2.3
Sigma	F4503	1990	1925	−3.2
Lab Prepared		2625	2690	2.5

^aRelative standard deviation in values is ±3.8%.

^bEstimated relative standard deviation in values is ±10%

3.3. Comparison of HoSF reconstituted at high and low iron flux

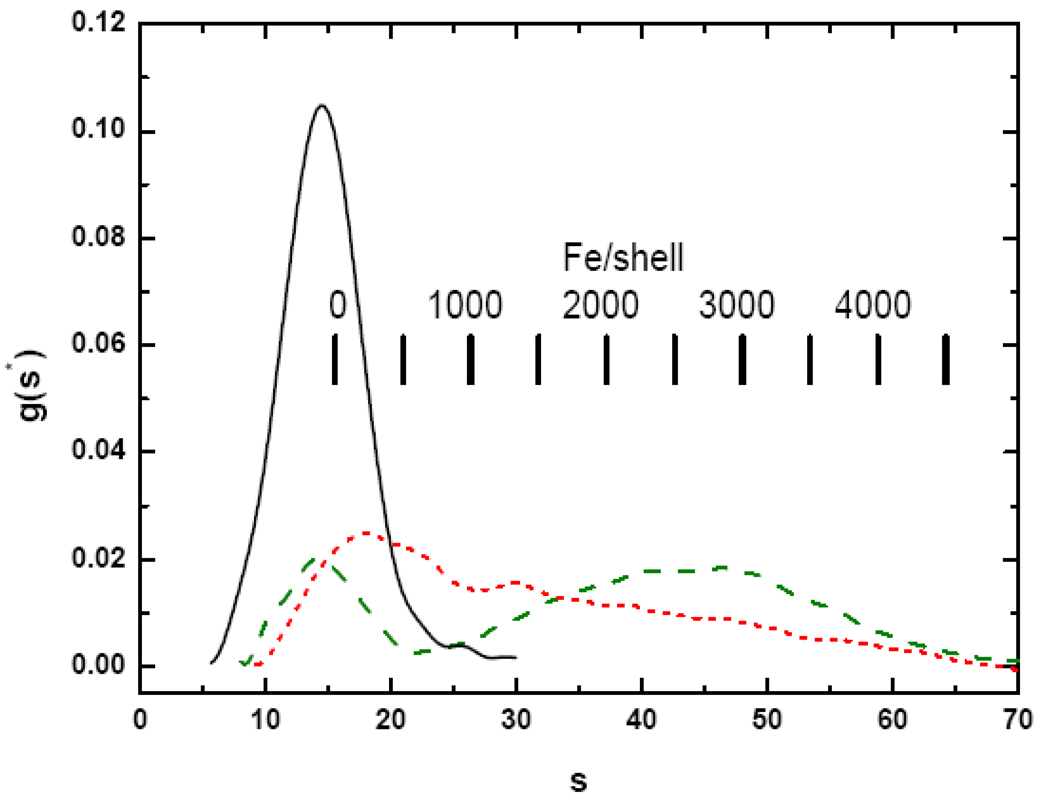
Solutions of apoHoSF and reconstituted HoSF containing an average of 500 to 2000 added Fe/shell were subjected to sedimentation velocity analysis to determine the distribution of core sizes. The apoHoSF sample yields a main peak centered at 14.4 S, with a small amount (~ 3%) of dimer at 24.9 S, the precise position being determined from a Gaussian fit (Fig. 3, black solid line). The dimer is predicted to occur at s₂ ~ 24.4 S based on the relationship s₂/s₁= (M₂ / M₁)^2/3 for same shaped molecules and using the average s₁ = 15.4 S for the monomer (vide supra). This type of sedimentation pattern has been reported previously for solutions of apoHoSF in which the higher molecular weight species at ~ 24 S have been determined to be apoHoSF dimers [56,57,59]. The Gaussian linewidth σ_obs = σ_shell = 6.5 G for the monomeric species in Fig. 3 is significantly larger than the calculated linewidth due to diffusion, σ_diff = 2.8 S. Consequently the observed linewidth is primarily due to structural heterogeneity in the chemically prepared apoprotein itself, namely ${\sigma }_{\mathit{\text{hetero}}}={({\sigma }_{\mathit{\text{shell}}}^2-{\sigma }_{\mathit{\text{diff}}}^2)}^{1/2}=5.9$ S (Materials and methods).

Fig. 3.

Sedimentation velocity profiles of Apo-HoSF (black —) and ferritins containing an average of 2000 Fe/shell added either in one bolus (red ˙˙˙) or in 40 additions of 50 Fe each (green – –). Sample conditions: 0.25 mg/mL apoferritin; 0.1 M MOPS, 0.15 M NaCl, pH 7.5. Iron addition to the samples and correction of g(s^*) for the effects of iron was performed as described in Materials and Methods.

HoSF was reconstituted from apoHoSF by addition of 2000 iron under either low- or high-flux conditions (Fig. 3). The protein was exposed to 2000 Fe/shell by either a single addition of 40 µL of 27 mM FeSO₄ in 0.01 M HCl to 1 mL of 0.25 mg/mL protein sample (red dotted line) or a series of forty 1 µL additions (green dashed line). The sedimentation coefficient distributions for low- and high-flux HoSF samples containing an average of 2000 Fe per protein are very different, indicating that the iron core size distributions are different. High-flux conditions result in a distribution that consists of a single peak at ~ 18 S which trails off slowly to higher s. In our experience the overall shape of the distribution is reproducible but minor features are not reproducible for different sample preparations. The irreproducibility of the distribution details suggests that the exact size distribution of the iron cores depends on the particulars of the sample and of its handling, even though every attempt was made to prepare the samples identically. Given this variability in minor features in the sedimentation pattern from sample to sample, there is little advantage in using a potentially higher resolution analysis, especially because oscillations in the pattern can result which could be erroneously interpreted as peaks [73].

The bimodal character of the sedimentation distribution for HoSF loaded under low-flux conditions is strikingly different from the high-flux distribution. For the low-flux sample, there appears to remain a significant amount of iron poor or apo-HoSF (~15 S) in addition to a broad distribution of HoSF centered ~ 45 S (~2550 Fe/shell). The s_W values for the high- and low-flux samples are 30.4 and 37.0 S, corresponding to an average iron content from Eq. (15) of 1290 Fe/shell and 1860 Fe/shell, respectively, compared to the 2000 Fe/shell added. Thus more effective loading of the apoprotein with iron occurs under the low-flux conditions.

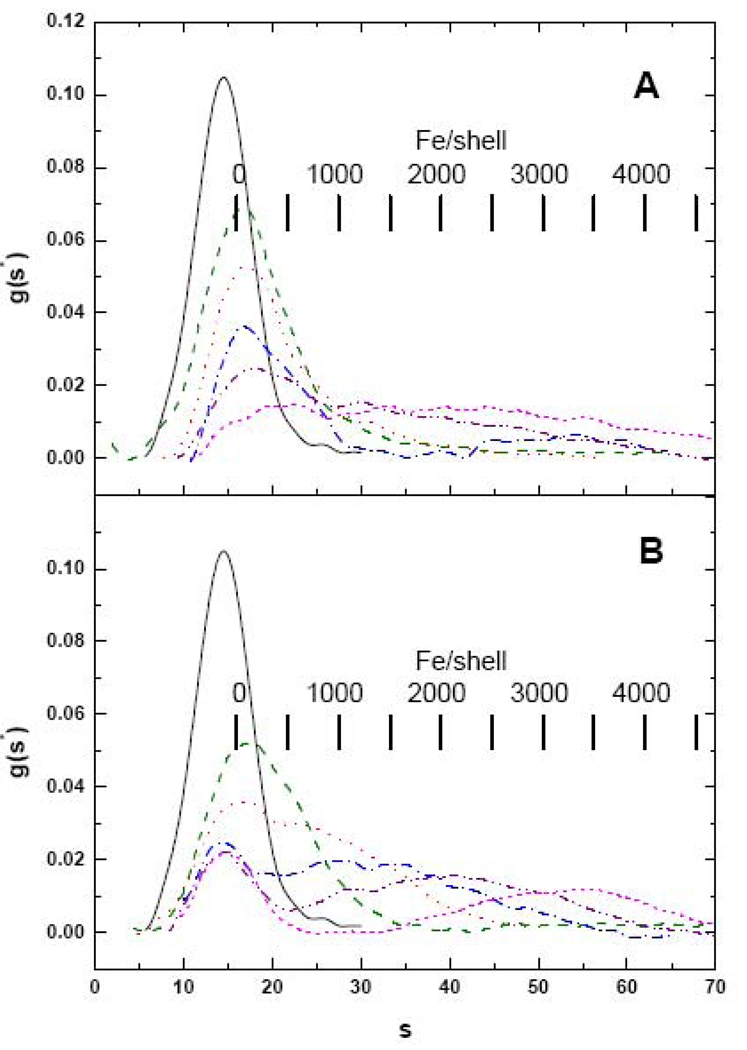
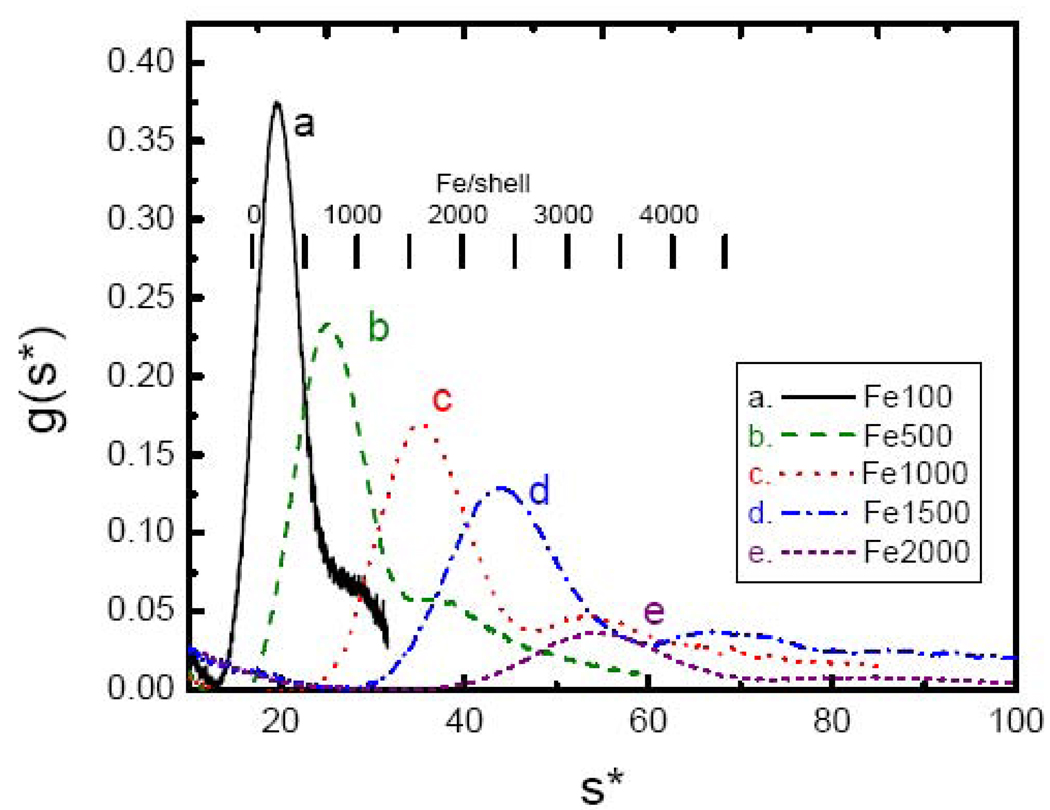
The results of additional iron loading experiments employing 500, 1000, 1500, 2000 and 2500 Fe/shell further reveal that very different iron core distributions develop depending on how apoHoSF is exposed to iron (Fig. 4). Under high-flux loading conditions (Fig. 4A), there is a progressive broadening of the distribution, until the distribution is nearly uniform over the range from ~ 20 to ~ 60 S (magenta dashed curve), and there is no distinct iron-poor fraction remaining, indicating essentially a continuum of iron containing species are present. s_W values range from 20.0 S for the 500 Fe sample to 40.6 S for the 2500 Fe sample, corresponding to iron contents n_Fe from AUC of 395 to 2175 Fe/shell, respectively. However, when HoSF is exposed to iron under low-flux conditions (Fig. 4B), there is a persistent peak in the distribution corresponding to apo-HoSF (~ 15 S), much like the holoprotein samples of Fig. 2, with a second peak that develops at iron loading levels exceeding 1500 Fe/shell. The iron-rich peak shifts to higher s with increasing levels of iron with peaks at s_peak ~ 35, 42 and 60 S for 1500, 2000 and 2500 Fe/shell, respectively. s_W values range from 21.6 S to 39.0 S, corresponding to n_Fe values from AUC ranging from 540 to 2030 Fe/shell for the 500 to 2500 Fe/shell samples. Additionally, both the low-flux and high-flux samples show the presence of a number of subpopulations within the iron-containing fractions.

Fig. 4.

Sedimentation velocity profiles of HoSF loaded either in one bolus (panel A) or in increments of 50 Fe/shell per bolus (panel B). In each panel data are shown for Apo-HoSF (black –) and for HoSF exposed to a total of 500 (green – –), 1000 (red ˙˙˙), 1500 (blue -˙-), 2000 (purple -˙˙-) or 2500 (magenta ---) Fe/shell. Sample conditions are as described in Fig. 3.

Under low-flux conditions, samples loaded to 2500 Fe/shell exhibited a small amount of precipitate. Under the conditions of these experiments, precipitated proteins will pellet prior to the onset of data acquisition. In order to determine the amount of protein lost to precipitation, integrals of the g(s*) curves were taken (Table 3). While no precipitation was observed by eye in samples with an iron loading of 2000 Fe/shell or less, it is clear from the integrals that loss of protein becomes significant at levels of 1500 Fe/shell and higher; i.e., in most instances there is a significant reduction in the relative values of the integrals compared to those of samples containing less iron. Precipitation of both protein and iron likely contributes to the observed differences in the expected Fe/shell ratios and those determined by AUC on spun samples.

Table 3.

Areas under the g(s^*)^a curves as a function of amount of iron and conditions of exposure.

Total ironb	Low flux	%Apo-HoSFc	High flux	%Apo-HoSFc
500	0.776	91	0.926	109
1000	0.804	95	0.705	83
1500	0.675	80	0.510	60
2000	0.635	75	0.662	78
2500	0.481	57	0.734	86

^aAreas reflect the correction for the effect of added iron on the refractive increment (Materials and methods).

^bAverage amount of iron added to the sample

^cRelative area of the iron-loaded samples to that seen with an identical concentration (0.25 mg/mL) of apo-HoSF, which resulted in an area of 0.851.

3.4. Human H-chain (H₂₄L₀) ferritin

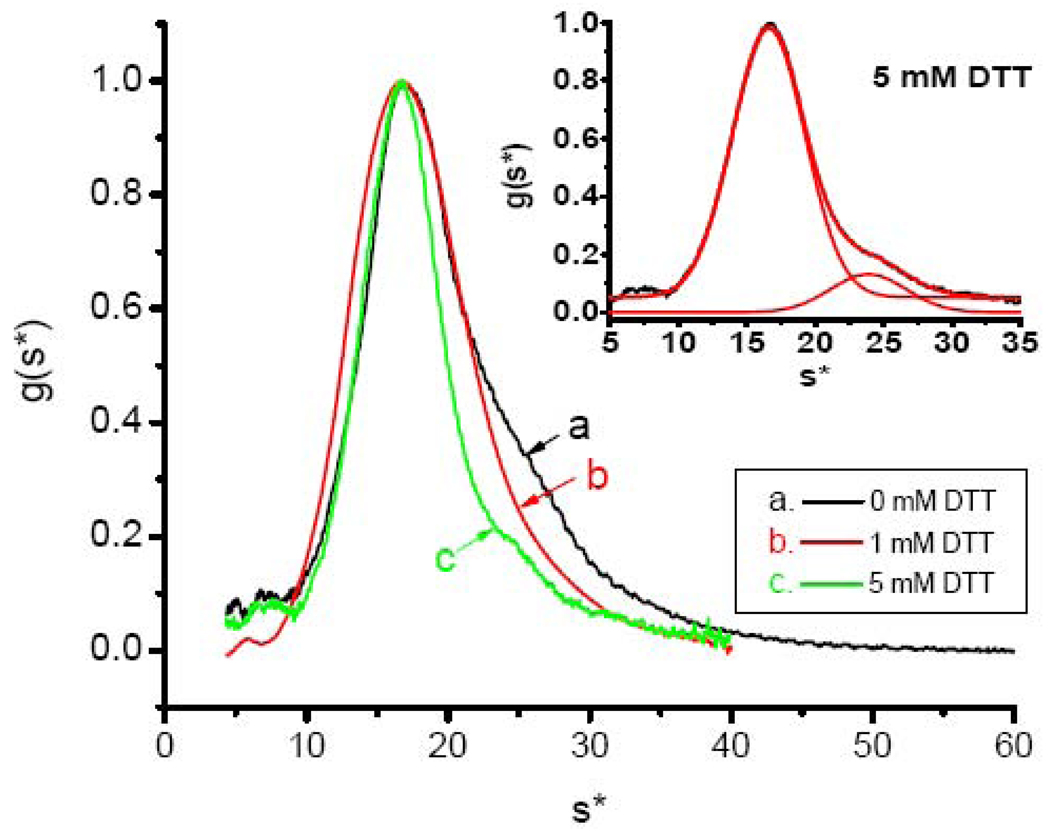
The inherent heterogeneity of HoSF shells with respect to their H- and L-subunit content likely contribute to the differences observed in iron deposition under low- and high-flux conditions and to subpopulations within the iron-containing fractions (Figs 3 and 4). Therefore, iron-distribution analyses were conducted using recombinant human H-chain ferritin homopolymer (HuHF, H₂₄L₀). The sedimentation profile of apoHuHF shows some dimerization of the protein (Fig. 5) as evident from the shoulder appearing at ~ 24 S. Treatment of the protein with dithiothreitol (DTT) reduces the amount of aggregated protein from 54% to 13% (curve a vs. curve c) as determined from fitting the respective g(s*) curves to a sum of two Gaussians and determining their relative areas. Dimerization of the HuHF through disulfide cross-links from oxidized Cys90 and to a lesser extent from dityrosine formation has been well documented [77,78]. The treated apoprotein sample can be curve fit to a sum of two Gaussians functions with fitting parameters for the monomer of s_peak = 16.59 ±0.02 S (σ_obs = σ_shell = 2.7 S) and for the dimer 23.9 ±0.1 S (σ_obs = σ_shell = 2.8 S) (Fig. 5, inset). The linewidth σ_shell = 2.7 S for the 5 mM DTT treated apoHuHF monomer is the same within fitting error as the calculated diffusion limited linewidth σ_diff = 2.8 S, indicating that the DTT treated apoprotein is homogeneous, i.e. σ_hetero ~ 0. The linewidth of the untreated monomer is 2.9 S, only marginally larger than that of the treated protein. For the dimer, σ_diff = 2.4 S, which in combination with σ_obs = σ_shell = 2.8 S, gives σ_hetero = 1.4 S, indicating the presence of a small amount of heterogeneity in this oligomer.

Fig. 5.

Sedimentation velocity profile of apoHuHF. Curves a, b and c correspond to the addition of 0, 1 and 5 mM DTT to the protein and demonstrate the presence of disulfide linkages. Inset: Fitting of 5 mM DTT sample (curve a of main figure) to the sum of two Gaussian functions with the parameters: A₁ = 0.9272 ± 0.0007, s_peak,1 = 16.59 ± 0.002 S, σ_obs,1 = 2.66 ±0.01 S, A₂ = 0.1312 ± 0.0019, s_peak,2 = 23.9 ± 0.1 S, σ_obs,2 = 2.8 ± 0.1 S and y₀ (offset) = 0.0519 ± 0.0008 with reduced χ² = 0.00002 and R² = 0.99588.

From the value of $s_{\mathit{\text{peak}}}^{*}=16.59$ S for the monomer and ν̄* = ν̄_20/w 0.724 ± 0.007mL/g based on the H-chain amino acid sequence, a value of s_20,w= 18.3 ± 0.1 S for apoHuHF is calculated [Eq. (13)]. A value of D_20,w(apoHuHF) = (3.18 ± 0.09) × 10⁻⁷ cm²/s is calculated from Eq. (14) using s_20,w(apoHuHF) = 18.3 S, M_HuHF = 506,266, ν̄_HuHF = 0.724 ± 0.007 mL/g and ρ_20,w =0.99823 g/cm³ from which a Stokes diameter of 13.5 nm is obtained [Eq. (5)]. Similarly, for the dimer, a value of s_20,w = 26.4. ± 0.1 S, D_20,w = (2.3 ± 0.1) × 10⁻⁷ cm²/s and Stokes diameter of d = 18.7 nm are calculated (Table 1).

Fig. 6 shows the sedimentation velocity profiles of a series of apoHuHF samples to which 100, 500, 1000, 1500 and 2000 Fe/shell were added in 50 Fe/shell increments. Subsequent ferrozine and protein analyses gave 16, 667, 1908, 2621 and 3042 Fe/shell, respectively, indicating that, with exception of the first sample, precipitation of protein relative to iron occurs, resulting in protein enriched in iron and exhibiting higher Fe/shell ratios. The traces all show considerably improved homogeneity over that seen with HoSF samples (c.f. Figs. 4B and 6); however, both monomer and dimer peaks are evident.

Fig. 6.

Sedimentation velocity profiles of apoHuHF loaded with 100, 5000, 1000, 1500 and 2000 Fe/shell under low flux, the data for which form the bases for curves c and d of Fig. 1. Final iron and protein analyses for the five samples gave 16, 667, 1908, 2621 and 3042 Fe/shell, respectively. Sample conditions: 1 mg/mL protein in 0.1 M MOPS, 0.15 M NaCl, pH 7.5.

The main peaks of the sedimentation profiles of the five samples were fit to a sum of two Gaussians. The values of $s_{\mathit{\text{peak}}}^{*}$ for the monomer and dimer components from curve fitting are plotted in Fig. 1 as a function of the iron content of the protein (curves c and d). The ratio of the slopes of curves c and d is 1.57 in accord with the expected value of 1.59 based on the 2^2/3 relationship between s values of monomers and dimers. The cores developed in both the monomer and dimer must have approximately the same amount of iron per protein shell otherwise the 2^2/3 relationship would not hold. Furthermore, the parallel lines observed for HoSF and HuHF (curves b and c) indicate that the core of each contributes the same to the buoyant mass regardless of whether the core is present naturally as in the HoSF samples or reconstituted as in the HuHF samples.

The diameter of a spherical particle is related to its iron content n_Fe and specific volume ν̄_core through the Eq. (16). Equation (16) and a linewidth analysis of the Gaussian peaks were

$$d={(6{\overline{\nu }}_{\mathit{\text{core}}}{M}_{\mathit{\text{core}}}{n}_{\mathit{\text{Fe}}}/5\pi N_A)}^{1/3}$$ (16)

used to estimate the size and polydispersity of the core. Given that σ_obs = σ_shell = σ_diff as noted above for apoHuHF, the value of σ_core was calculated, i.e. ${\sigma }_{\mathit{\text{core}}}={({\sigma }_{\mathit{\text{obs}}}^2-{\sigma }_{\mathit{\text{diff}}}^s)}^{1/2}$, and related to the standard deviation in the iron content of the core σ_Fe through the relationship σ_Fe = 86.9 · σ_core. The standard deviation in the diameter σ_d is given by σ_d/d = σ_Fe/3n_Fe. An analysis of the 667, 1908, 2621 and 3042 Fe/shell samples of HuHF gave diameters of 3.84 ± 0.32, 5.40 ± 0.18, 5.96 ± 0.22 and 6.21 ± 0.30 nm, indicating that all of the samples have low dispersion in their core sizes with relative standard deviations ranging from ± 3 to ± 8% with the larger cores having relatively less dispersion in size.

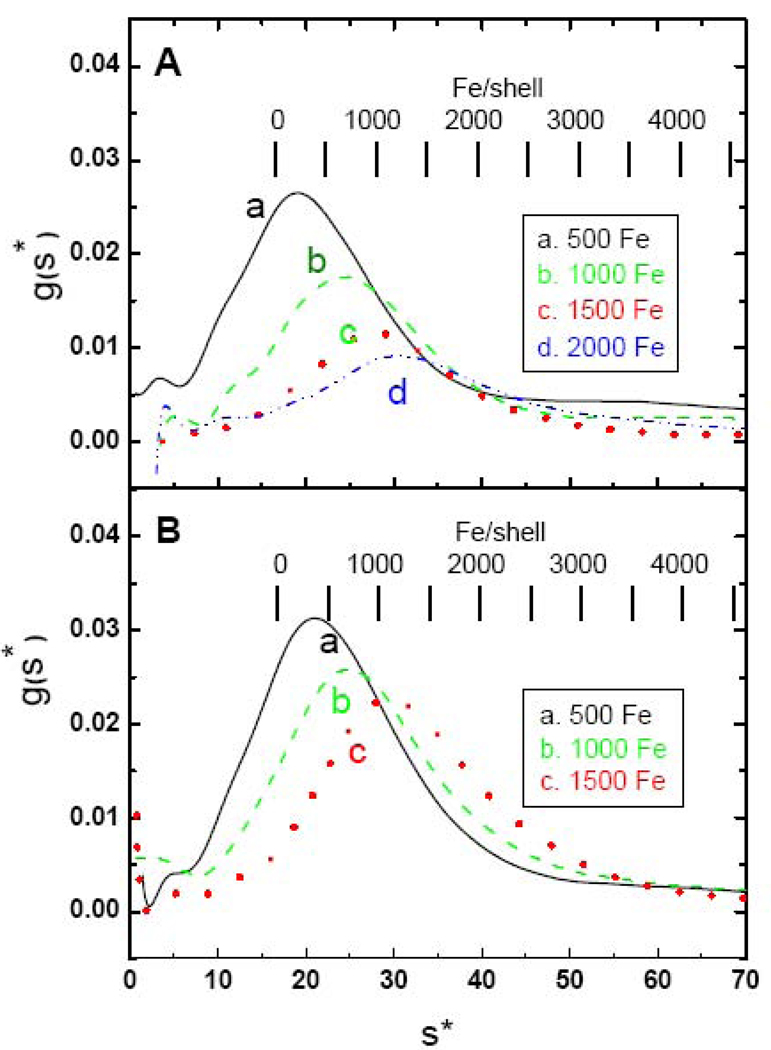
Fig. 7 illustrates the difference between high-flux (Fig. 7A) and low-flux (Fig. 7B) samples for another HuHF protein preparation. Significant precipitates are observed at levels over ~1000 Fe/shell, especially with the low-flux samples which is probably a consequence of hydrogen peroxide production through equation (1) and subsequent damage to the protein through Fenton chemistry [80]. These observations are in accord with previous reports that H-rich ferritins are less efficient at storing large iron cores than L-rich ferritins, resulting in aggregation and precipitation at higher iron levels [41]. For the high-flux samples, AUC measurements of iron content of the 500, 1000, 1500 and 2000 Fe/shell samples gave 575, 925, 1195 and 1495 Fe/shell, indicating that additions above 1000 Fe/shell result in less iron being acquired by the protein. For the low-flux 500, 1000 and 1500/shell samples (Fig. 7B), iron contents of 585, 990 and 1380 were obtained from AUC analysis. No population of iron-poor species is observed in Fig. 7 which contrasts with the data for HoSF (Fig. 4). Instead, the distributions shift to progressively higher s as more iron is loaded. Likewise, there is little evidence for subpopulations within the peak although some asymmetry is observed where dimers are expected to be present.

Fig. 7.

Sedimentation velocity profiles of HuHF loaded either in one or two boluses (panel A) or increments of 50 Fe/shell per bolus (panel B). In panel A data are shown for HuHF exposed to a total of 500 in one bolus (black —), for 1000 Fe in one bolus (green – –), 1500 Fe added in two boluses of 750 Fe/shell (red ˙˙˙), or 2000 Fe added in two boluses of 1000 Fe/shell (blue - ˙˙ -). In panel B data are shown for HuHF exposed to a total of 500 Fe/shell in 10 additions (black —), a total of 1000 Fe/shell in 20 additions (green – –) and a total of 1500 Fe/shell in 30 additions (red ˙˙˙) of 50 Fe/shell.

3.5. Sucrose gradients

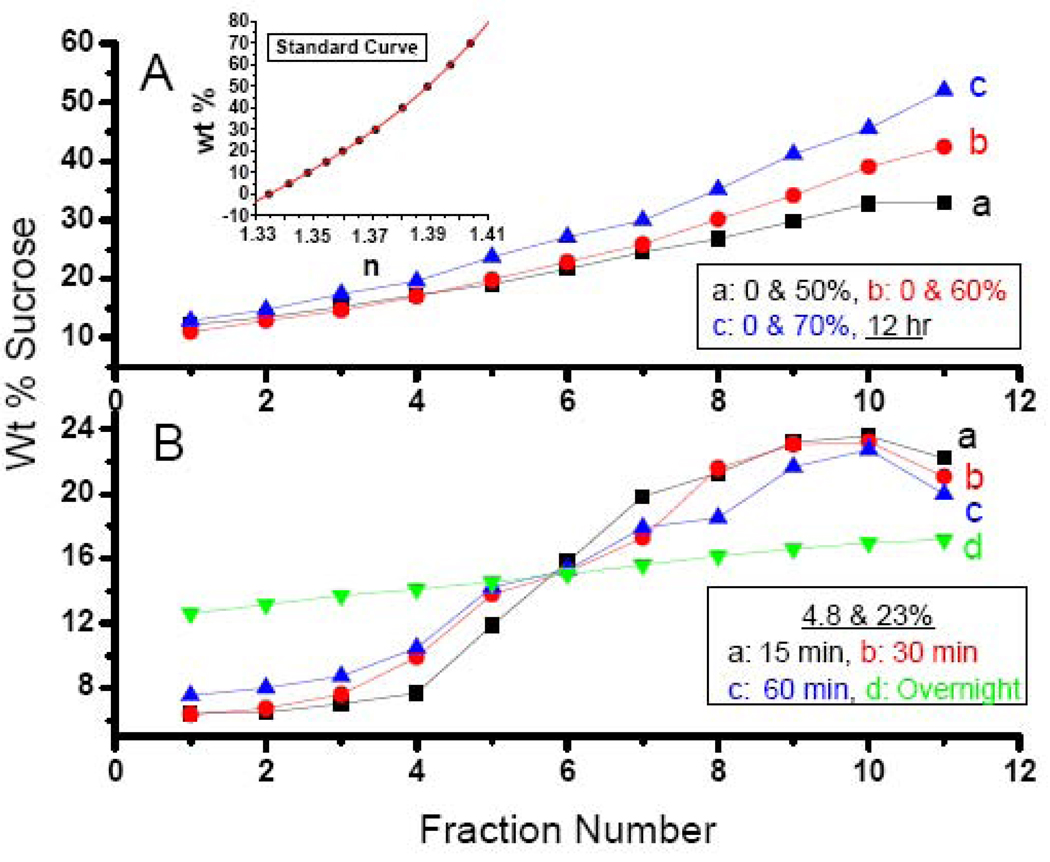
Sucrose gradients were prepared to improve the homogeneity in the cores obtained with HoSF. Sucrose gradients using the two-layer method are illustrated in Fig. 8. Gradients made with the starting solutions of 0 & 50, 0 & 60 and 0 & 70% w/v sucrose had ranges 12–33%, 11–43% and 13–52%, respectively (Fig. 8A), as determined by refractive index measurements employing the standard curve (Fig. 8A, inset). Gradients were also prepared from solutions of 4.8 & 24% sucrose incubated for 15, 30 and 60 min and overnight, producing more sigmoidal shaped gradients with ranges of ~ 6.4–23% (Fig. 8B).

Fig. 8.

Sucrose gradients obtained by the two layer method. Panel A: Curve a: Layering of 0 and 50% sucrose solutions resulting in a gradient from 12 to 33% sucrose; Curve b: Layering of 0 and 60% sucrose solutions resulting in a gradient from 11 to 43% sucrose; Curve c: Layering of 0 and 70% sucrose solutions resulting in a gradient from 13 to 52% sucrose. Inset: Standard curve of percent sucrose versus measured refractive index (n) of sucrose solutions of known composition and containing 0.15 M NaCl. A least-squares fit of the data yielded the following cubic equation from which the weight percent sucrose of the different gradients was calculated: wt% = 4.3398370×l0⁴ n³ − 1.7268340×10⁵ n² + 2.2975845×10⁵ n− 1.0222298×10⁵. Panel B: Layering of 4.8 and 23% sucrose samples for various times. (a) 15 min; (b) 30 min; (c) 60 min and (d) overnight. Gradients obtained for curves a, b, c and d were 6.4-22.6, 6.4-23.2, 7.5-22.7 and 12.7-17.3%, respectively. The weight percentage sucrose (w/w) of eleven 1.5 mL fractions from top to the bottom of the centrifuge tube was determined by refractometry.

3.6. Horse spleen ferritin separated on a sucrose gradient

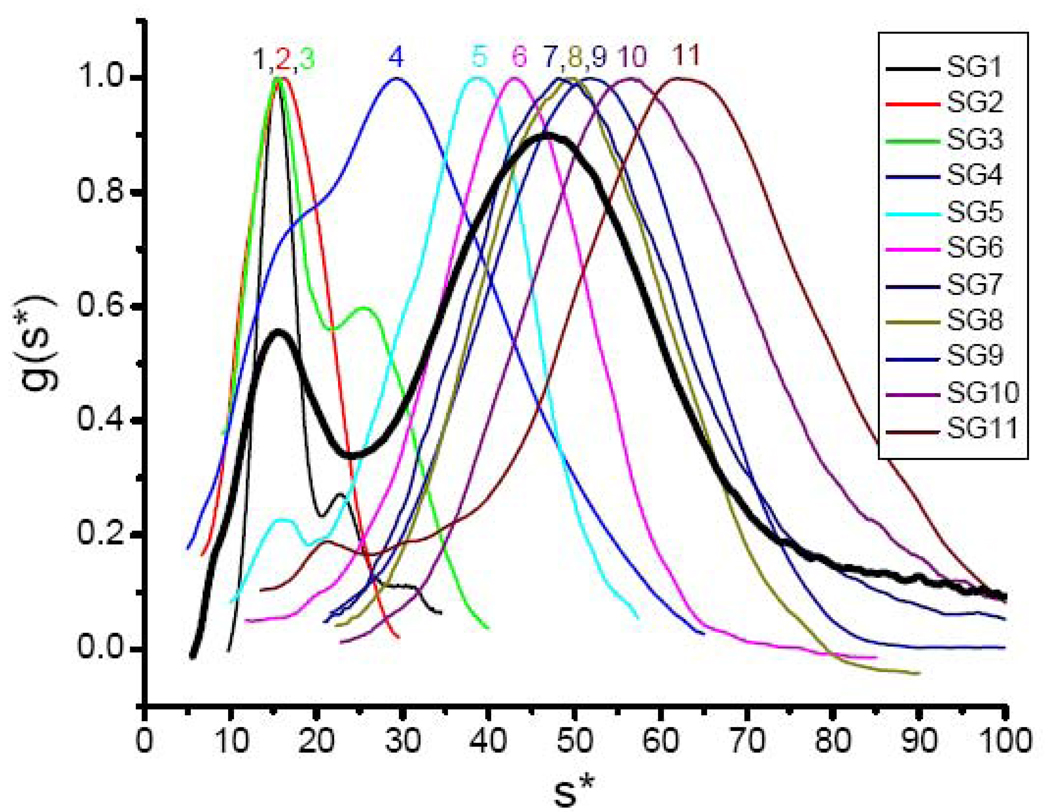
Fig. 9 shows the normalized g(s*) versus s* curves for eleven fractions of commercial HoSF from MP Biomedicals separated on a 6.4–23% w/w gradient (equivalent to 6.8 to 30% w/v), a gradient typical of those commonly used to fractionate ferritins. For comparison, g(s*) of the unfractionated protein is shown as a bold line in Fig. 9 at 90% of the amplitude of the others. The sedimentation profile observed differs markedly with each fraction and from the unfractionated protein. The 1.5 mL fractions have the following Fe/shell values determined by the ferrozine assay with the percentage of the total protein in the fraction given in parentheses: 1. 29 (10.6); 2. 68 (14.9); 3. 444 (11.0); 4. 1180 (10.3); 5. 1795 (10.6); 6. 2747 (10.8); 7. 3281 (9.5); 8. 2900 (9.1); 9. 3623 (6.0); 10. 3459 (4.0) and 11. 3465 Fe/shell (3.2%). The heaviest material (n_Fe > 3600) sedimented to the bottom of the tube. Use of a steeper gradient of 2.2 to 66.7% w/w resulted in significantly poorer resolution. However, the fastest sedimenting Gaussian component in fraction 11 of the steeper gradient appeared at s = 65.1 S, corresponding to n_Fe = 4320, a value close to the 4500 Fe/shell capacity of the protein. As expected, the relative order of the maximal s of the peaks in Fig. 9 approximates the iron contents of the samples. Most significant is the observation that no fraction contains protein in abundance (> 15%), illustrating the extreme polydispersity of the cores of natural horse spleen ferritin. Because of the wide range of iron contents among the subpopulations of HoSF samples, it is difficult to obtain any one component in large yield relative to the others.

Fig. 9.

Sedimentation velocity profiles of individual fractions of commercial HoSF obtained on a sucrose gradient. HoSF from M.P. Biomedicals was separated into eleven 1.5 mL fractions on a 6.4–23% gradient. The bold line shows the sedimentation profile of the unfractionated protein.

Fraction 1 is largely apoferritin (n_Fe = 29) and consists of 71% monomer (σ_obs = 2.3 S), 18% dimer (σ_obs = 2.3 S) and 11% trimer (σ_obs = 4.8 S), the relative amounts of protein being determined from the areas under the three Gaussians. The hydrodynamic parameters of the monomer and dimer are summarized in Table 1. The linewidth of the monomer (σ_obs = σ_obs = 2.3 S) is close to that predicted for diffusion alone (σ_diff = 2.5 S), indicating a homogeneous protein which contrasts with the heterogeneity noted above for chemically prepared apoprotein. Presumably this difference is due to the fact that the apoprotein isolated on a sucrose gradient has been exposed to very little iron and associated reactive oxygen species.

The contribution of σ_core to the observed linewidths of the iron containing fractions of Fig. 9 range from σ_core = 2.2 to 11.9 S for fractions 3 to 11, corresponding to dispersions in iron content of the particles ranging from σ_Fe ± 216 to + 1030 Fe/particle. Corresponding particle sizes range from 3.37 ± 0.55 to 6.50 ± 0.64 nm. Fraction 6 contains 2747 ± 670 Fe/shell (d = 6.04 ± 0.48 nm), which is the fraction closest in iron content to 2745 ± 1040 Fe/shell (d = 6.04 ± 0.76 nm) for the iron containing component at s = 47 of the unfractionated protein (Fig. 9). Thus, sucrose gradient fractionation resulted in a ~ 40% decrease of in polydispersity of the core. While a reasonably good separation of HoSF species according to core size with decreased dispersion was obtained using a sucrose gradient, the dispersion was still about twice that seen for the HuHF samples with cores of similar iron content.

4. Discussion

4.1. Contraction of the protein shell?

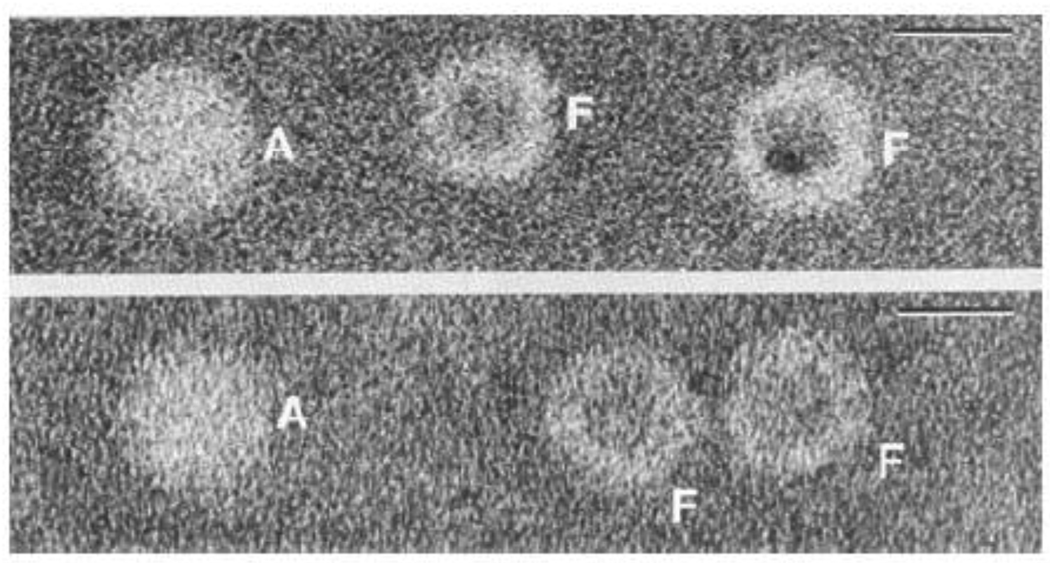
One of the most interesting observations of the present study is the apparent decrease in the frictional coefficient f of the protein as the mineral core develops within the cavity. Because f = 6πηr for a spherical molecule, this finding suggests that the protein shell contracts in size as it acquires iron. The average iron content of HoSF isolated from spleen is ~ 2300 Fe/shell (Table 2). According to curve b of Fig. 1, a HoSF molecule containing this amount of iron sediments at s = 41.8 S (M = 705,380 g/mol, ν̄ = 0.588 mL/g) and has D = 3.58 × 10⁻⁷ cm²/s [Eq. (14)] which corresponds to a Stokes diameter of 12.0 nm or a ~10% reduction over the value of 13.3 nm for the apoprotein. These findings are consistent with early published TEM images of shells of apoferritin and ferritin in the same micrograph [63,81] (Fig. 10). From Fig. 10, the diameter of the apoprotein shell is estimated to be ~ 12.6 nm, close to the Stokes value of 13.3 nm from this work. More importantly, the size of the protein shell in the micrograph is seen to decrease by ~ 12% in the presence the iron core. While it is conceivable that the observed reduction in the protein shell seen in the TEM image may be simply an artifact of drying of the sample, the fact that a similar reduction is suggested by the AUC data, and a reduction, albeit smaller, has been observed by DLS [73] warrants further study. Some contraction of the protein shell could occur through the binding of Fe³⁺ at glutamate nucleation sites on the inner surface of the protein cavity and at sites within the hydrophilic channels, reducing charge repulsions and giving rise to a more compact structure. In this connection, association between the core and protein shell has been seen in TEM images [63] and x-ray absorption and Mössbauer measurements have shown that iron in the early stages of development of the mineral core binds to carboxylate groups within the cavity [82]. In reconstituted HuHF, Fe³⁺ has been demonstrated to migrate from the twenty-four ferroxidase sites to the eight hydrophilic channels where it binds [83].

Fig. 10.

Transmission electron micrographs of horse spleen ferritin samples negatively stained with sodium silicotungstate. Upper: Micrograph of a natural ferritin sample showing both apoferritin (A) and ferritin (F) molecules. Lower: A chemically prepared apoferritin sample showing an apoferritin molecule (A) on the left and some ferritin molecules (F) on the right with some of the iron core removed. The diameter of the shell of the apoferritin (A) molecule is seen to be about 12% larger than that of the ferritin (F) molecule. Bar = 10 nm in the upper right hand corner. Adapted and modified from reference [81] with permission. Additional TEM images showing contraction of the protein shell can be found in reference [63].

4.2. The distribution of iron core sizes is dependent on iron presentation

The data demonstrate that the manner in which iron is presented to apo-HoSF results in distinct iron distributions in HoSF (Figs. 3 and 4). Under low-flux conditions, in which the iron is oxidized primarily at the ferroxidase site, a progressive fractionation of the HoSF sample into iron-poor and iron-rich fractions is observed (Fig. 4B), similar to that seen with native horse spleen ferritins (Fig. 2). The iron-poor fraction appears to reach a constant level when the average iron content is about 1500 Fe/shell and accounts for ~15% of the total protein in the sample. As more iron is added to the sample, the iron-rich fraction appears to sequester the additional iron preferentially. The iron-rich fraction is a broad distribution (from 35 to ~70 S in the 2500 Fe/shell sample) and consists of a number of subpopulations, as indicated by the unresolved shoulders and humps in the g(s*) distribution (Fig. 4B).

The high iron flux g(s*) distributions for HoSF (Fig. 4A) are quite different from low flux distributions (Fig. 4B). Under high-flux conditions the distributions become extremely broad as iron is loaded to 2500 Fe/shell, extending over the whole range of sedimentation coefficients accessible to HoSF shells (from 15.6 s to ~70 s). As increasing amounts of iron are presented to the protein, the center of the distribution shifts to higher s and broadens, indicating that iron is being loaded to produce a broad distribution of core sizes among the protein molecules present. This is in sharp contrast to the nearly bimodal distributions observed with low-flux additions. There is some remaining iron-poor ferritin, but its level is hardly distinct from the rest of the sample.

4.3. Subpopulations of iron-loaded species in HoSF

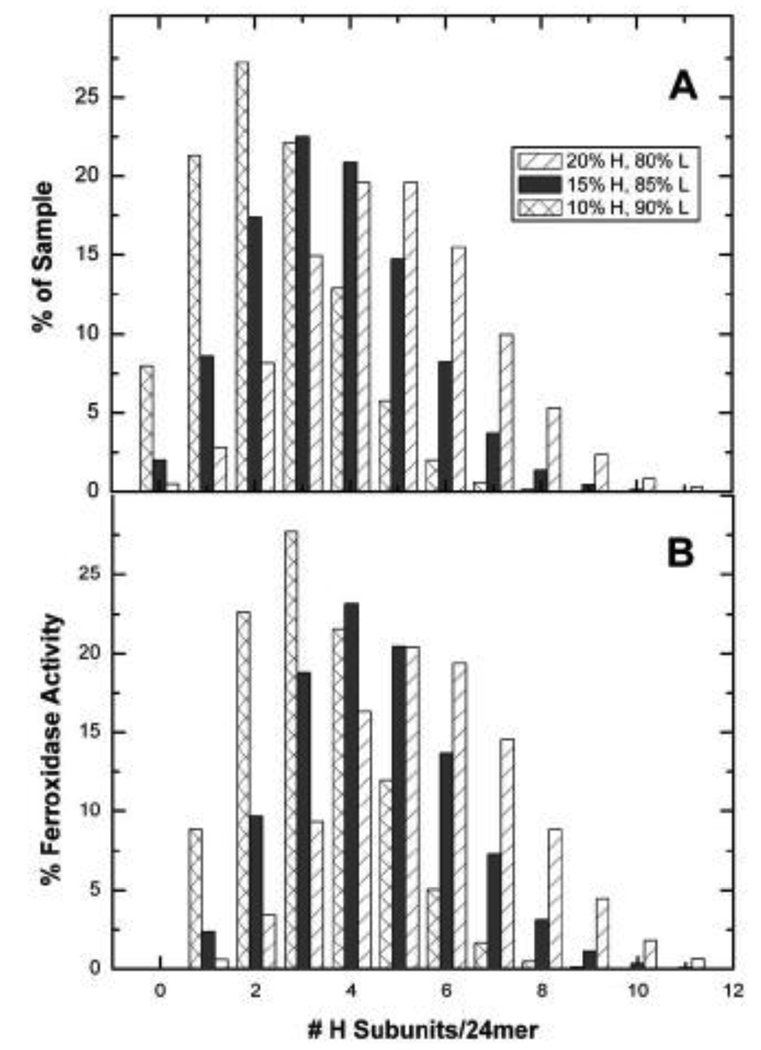
The subpopulations seen in the g(s*) vs. s* plots are likely due to different numbers of H-subunits in each shell of HoSF. The average composition of horse spleen ferritin is generally stated to be ~ 15% H-subunit and 85% L (~H₄L₂₀) as found in this work. However compositions ranging from 10% (~H₂L₂₂) to 20% (~H₅L1₉) have been reported [5,10]. If it is assumed that ferritin assembly is a stochastic process, the distribution of H and L subunits within a sample of given fractional population of each subunit is determined by the binomial probability distribution: $B(x,N,p)=\frac{N!}{x!(N-x)!}{p}^x{(1-p)}^{(N-x)}$, where B(x,N,p) is the probability of finding a given species having x L-type subunits out of the total, N, of 24 subunits, and p is the fractional population of L subunits in the sample. Separate calculations in which p was fixed at 0.8, 0.85 and 0.9 (i.e. 80%, 85% and 90% L-subunit) are shown in Fig. 11A. At least 10 different species are statistically possible for HoSF, assuming an average H composition of 15%. A dispersion (standard deviation) in molecular weight of ~ 2200 is predicted by the distribution in Fig. 11A which corresponds to a contribution of only 0.07 S to the linewidth of the apoprotein. Therefore, heterogeneity associated with subunit composition of individual ferritin shells is smaller than the precision of ± 0.1 S in the linewidth measurements.

Fig. 11.

The calculated binomial distributions of H-subunits for three different compositions of HoSF, assuming no cooperativity between subunits during assembly. A. Percent of composition. B. Relative ferroxidase activity.

The species in Fig. 11A will have vastly different ferroxidase activities. If one assumes that there is no cooperativity between H or L subunits with respect to the rates of iron oxidation (which is not strictly true [82,83]), then the relative activity of each species is proportional to its H-subunit composition. Hence, a shell with a composition of H₄L₂₀ would have the capacity to oxidize iron at a rate 4-fold that of an apoferritin with only a single H-subunit. If the fractional population of each species given by the binomial distribution is multiplied by its relative ferroxidase activity based on H-subunit composition, the resulting distribution then becomes normalized for differences in the population and H-subunit composition (Fig. 11B). This distribution predicts the likelihood of iron being oxidized by a particular subpopulation of a shell within the sample, assuming no enzymatic cooperativity between H and L subunits. Analysis of this figure shows that relatively small concentrations of an H-rich species can match or exceed the activity of another species present in somewhat higher concentration but of lower H-subunit composition. These differences are relevant to understanding the sedimentation patterns for HoSF shown in Fig. 4 which is composed of 15% H and 85% L subunits.

The distribution of the H-subunit within a sample (Fig. 11A) also provides an explanation for the presence of the iron-poor fraction seen under the low flux conditions. For samples having 15% H-chain, the fraction of material that contains one or no H-subunits accounts for over 10% of the protein in the sample, but only ~2% of the ferroxidase activity. Sedimentation velocity analysis reveals the presence of an iron-poor fraction accounting for ~15% of the initial apoferritin peak under the low flux conditions (Fig. 4B). Therefore, the iron-poor fraction observed under low-flux conditions is consistent with the anticipated fraction of shells composed almost entirely of L-subunits. The known cooperativity between H- and L-subunits in ferroxidase activity [84,85] would skew the distribution in Fig. 11B to the right, resulting in a prediction of even more iron-free protein.

Evidence linking subunit heterogeneity of HoSF with iron content has been reported previously, although prior to a full understanding of the subunit composition of HoSF [76]. This earlier study reported that the iron content of bands observed in isoelectric focusing correlated with the surface charge of the protein in the bands. In particular, the protein in the more acidic bands (i.e. having higher L-subunit content) had lower iron content than the more basic bands (having higher H-content). These results are in agreement with sedimentation results described here. It is interesting to note that the number of bands (~11) observed using isoelectric focusing of various samples [76] corresponds favorably with the number of species calculated from the binomial function (Fig. 11A). The relative populations of each band correlate less well to the binomial function. However, this may be due to the method of fractionation used in the earlier studies.

4.4. Homogeneity of iron loaded species in HuHF

The hypothesis that the presence of subpopulation in the core-size distributions may reflect heterogeneity in HoSF subunit composition is further supported by the results of the recombinant human H-chain experiments (Figs. 6 and 7). This homopolymer (H₂₄L₀) produced rather uniform distributions under both high-flux and low-flux conditions. In both cases, no significant shoulders or bumps in the distribution are seen. The lack of subpopulations like those seen in HoSF is likely due to the fact that the protein is truly homogeneous in structure (as indicated by the linewidth analysis) and activity. All the shells are identical and will therefore respond similarly to the iron-flux condition. The lack of fractionation of iron-poor and iron-rich species under the low-flux condition, as seen in HoSF, add further support to this hypothesis.

According to Eq. (16) the mineral cores of the reconstituted HuHF ferritins in Fig. 6 have predicted diameters ranging from 3.84 to 6.24 nm with relative standard deviations decreasing from 8% to 3%, respectively. For a 4500 Fe core, a maximal diameter of 7.0 nm is predicted by Eq. (16) in accord with the largest core particle size seen in TEM [63] and a value within the ~ 8 nm internal diameter of the protein cavity. A mean core, of 6.14 nm (range 4.11 to 8.27 nm) from TEM measurements has been reported for reconstituted HuHF containing 1074 ±99 Fe/shell [27] which is 35% larger than the calculated diameter of 4.50 nm using Eq. (16). Measurements of the diameters of the cores of reconstituted HoSF are also significantly larger than those predicted by Eq. (16) [28]. The differences between the TEM measured diameters and those predicted by Eq. (16) are likely a reflection of deviation from spherical geometry, especially for smaller nanoparticles, as evidenced by the irregular shapes of core particles in many micrographs [63,86,87]. TEM measurements of particle diameters also tend to be biased toward the largest dimensions of the particle. An additional complicating factor in some TEM studies [27,28] is that only the concentration of iron and not protein appears to have been measured following reconstitution of the protein. Because some protein precipitation, while not visually apparent (Table 3)), always occurs during reconstitution of ferritin, the reported Fe/shell ratios (n_Fe) may be significantly lower than the true values. A low value of n_Fe would account for the anomalously low density of iron predicted in the core by one study [28] and contribute to the difference between particle diameters measured by TEM and those calculated from Eq. (16).

The size and shape of nanoparticles greatly influence their properties. The fraction of the total Fe in a spherical nanoparticle that resides on the surface is quite large due to the high surface to volume ratio ($n_s/n_{\mathit{\text{Fe}}}=4n_{\mathit{\text{Fe}}}^{-1/3}$ [88]), ranging from 0.50 to 0.24 for particles containing 500 to 4500 Fe. A non-spherical particle has an even larger fraction of metal ions on the surface. Consequently, the magnetic behavior of ferritin nanoparticles of such high surface area is expected to be quite different from that of the bulk phase ferrihydrite, accounting for the superparamagnetism of the mineral core and contributing to its other interesting magnetic properties [15,22–30,88,89].

4.5. Strategies for preparing ferritin cores of uniform size

The results of the present study show that both native (as isolated from spleen) or reconstituted horse spleen ferritin are fairly heterogeneous in core size and may be unsuitable for certain studies in which the phenomena being investigated critically depend on core particle size and the number of surface Fe³⁺ ions. While the incremental addition of Fe to apoferritin results in a somewhat narrower core size distribution of the iron containing component than when Fe is added in a single bolus (Figs. 3 and 4), substantial heterogeneity still exists. The presence of subpopulations of core sizes appears to be an intrinsic property of the HoSF protein, as elaborated above. HoSF is best fractionated by preparative sucrose gradient ultracentrifugation and the fractions evaluated by analytical ultracentrifugation as detailed here. A reasonable strategy would be to load HoSF with various amount of iron under high-flux conditions where the mineral surface reaction [Eq. (3)] dominates and Fenton chemistry is minimized (reducing the amount of protein precipitation) followed by fractionation of the protein on a sucrose gradient. Dimers and trimers can be removed by size exclusion chromatography on a Sepharose 6B column prior to sucrose gradient fractionation [79]. Because iron is known to exchange between ferritin molecules with the iron rich ferritins gaining iron at the expense of iron poor ferritins (reviewed in [5]), it is prudent to stabilize samples immediately after ultracentrifugation analysis by either freezing with a glycerol/buffer mix or lyophilization.

In contrast to HoSF, the human H-chain protein, being a homopolymer, produces cores of reasonably uniform size (Figs. 6 and 7) that are suitable for direct study. However, it is difficult to load the protein much above 2000 Fe/shell because of precipitation and, moreover, the cores tend to be smaller and more irregular in shape compared to the L-chain homopolymer [87]. Precipitates, while not always visible, must be removed (e.g. by centrifugation) prior to using the sample. Cores produced with non-redox active metals that do not utilize the H-chain ferroxidase sites are not expected to be influenced by the same factors affecting the polydispersity of iron cores reported here where oxidation reactions [Eqs. (1) – (3)] play major roles.

4.6. Conclusion

In conclusion, the present work has provided a detailed analysis of the sedimentation properties of native and reconstituted ferritins. Heteropolymer ferritins exhibit an array of core sizes in vivo or when the apoprotein is reconstituted in vitro using Fe²⁺ and O₂. This property is attributed to the uneven distribution of the catalytically active H-chain subunits among the population of ferritin molecules, an idea supported by measurements with the H-chain homopolymer ferritin itself. Methods for obtaining cores of more uniform size and assessing their homogeneity are presented.

Abbreviations and symbols

AUC

analytical ultracentrifugation

DTT

dithiothreitol

HoSF

horse spleen ferritin

HuHF

recombinant human H-chain ferritin

MOPS

3-(N-morpholino)propanesulfonic acid

TEM

transmission electron microscopy

D

diffusion coefficient (cm²/s) under the specific conditions of protein concentration, buffer and temperature

c

concentration (g/cm³)

$D_{20,w}^o$

diffusion coefficient of infinite dilute protein in pure water at 20 °C (cm²/s)

D_20,w

diffusion coefficient of the protein at the stated concentration in pure water at 20 °C (cm²/s)

d

Stokes diameter (nm)

f

frictional coefficient (g/s)

g(s*)

concentration distribution function (see Fig. 2 legend)

η

viscosity (poise)

ρ

density (g/mL)

n_Fe

number of iron atoms per protein shell as determined by AUC or ferrozine assays

M

molar mass (g/mol)

M_r

relative molar mass (unitless)

r

Stokes radius (nm)

r_m

radius of meniscus (cm)

s

Svedberg constant for the protein at stated concentration and temperature in buffer (10⁻¹³s)

s_W

weighted average of s over the g(s*) curve

$s_{20,w}^o$

Svedberg constant for infinitely dilute protein in pure water at 20°C (10⁻¹³s)

s_20,w

Svedberg constant of protein at stated concentration in pure water at 20°C (10⁻¹³s)

ω

angular velocity (rad/s)

σ

linewidth of Gaussian function as defined in the text (svedbergs)

ν̄

partial specific volume (mL/g)