Two-Part Factor Mixture Modeling: Application to an Aggressive Behavior Measurement Instrument

Abstract

This study introduces a two-part factor mixture model as an alternative analysis approach to modeling data where strong floor effects and unobserved population heterogeneity exist in the measured items. As the names suggests, a two-part factor mixture model combines a two-part model, which addresses the problem of strong floor effects by decomposing the data into dichotomous and continuous response components, with a factor mixture model, which explores unobserved heterogeneity in a population by establishing latent classes. Two-part factor mixture modeling can be an important tool for situations in which ordinary factor analysis produces distorted results and can allow researchers to better understand population heterogeneity within groups. Building a two-part factor mixture model involves a consecutive model building strategy that explores latent classes in the data for each part as well as a combination of the two-part. This model building strategy was applied to data from a randomized preventive intervention trial in Baltimore public schools administered by the Johns Hopkins Center for Early Intervention. The proposed model revealed otherwise unobserved subpopulations among the children in the study in terms of both their tendency toward and their level of aggression. Furthermore, the modeling approach was examined using a Monte Carlo simulation.

This article considers modeling issues that arise from the latent variable analysis of items with two common types of complications—data exhibiting strong floor or ceiling effects, which produce highly skewed items, and data arising from several unobserved subpopulations, which produce unobserved heterogeneity. In such situations, conventional factor analysis can give strongly distorted results.

When the first complication—a strong floor effect—is present, a factor analysis measurement model is distorted due to the violation of the multivariate normality assumption and the linearity of the regressions of items on factors. A typical example of strong floor effects is seen in studies of early childhood behavior in which subgroups of children exhibit high levels of aggressive, hyperactive, impulsive, and inattentive behavior. It is common for items used to measure this type of behavior to show a preponderance of zeros, as the behavior has not yet emerged for many individuals in the population. Two-part modeling of longitudinal data, first introduced by Olsen and Schafer (2001) and applied to intervention studies by Brown, Catalano, Fleming, Haggerty, and Abbot (2005), addresses the problem of a preponderance of zeros when analyzing data from abnormal behavior studies. Two-part modeling, as the name suggests, decomposes the distribution of data into two parts—one part that determines whether the response is zero and the other part that determines the actual level if nonzero responses occur.

The second complication, unobserved heterogeneity, is often seen in general population samples that exhibit both normative and various types of nonnormative behavior. Factor mixture modeling, which combines factor analysis with a classification of individuals into types in line with latent class analysis, is a useful tool for exploring population heterogeneity (Muthén, 2008; Muthén & Asparouhov, 2006). In longitudinal intervention studies, factor mixture analysis on baseline data can uncover subpopulations that might respond differently to an intervention.

Given the limitations of conventional factor analysis, which often cannot handle these two complications properly, this study introduces a two-part factor mixture model as an alternative modeling approach to dealing with data that have strong floor effects for individual items of behavioral measurement and that show heterogeneity. In doing so, the aims are to (a) discuss three model building steps for two-part factor mixture models that combine the components of both two-part and factor mixture models, and (b) assess their viability through analyzing the results of the model in a Monte Carlo simulation study. Establishing two-part factor mixture modeling as an important tool for situations in which ordinary factor analysis produces distorted results can reap considerable rewards in practice. Particularly for intervention studies, two-part models hold the potential to allow researchers to better understand population heterogeneity within groups of at-risk children and better provide effective intervention techniques that can be tailored to subgroups that exist in a given population.

METHOD

Two-Part Factor Mixture Model

Two-part factor mixture modeling combines aspects of both factor mixture modeling, which attempts to discover latent classes, and two-part modeling, which has been developed to deal with semicontinuous variables. As an introduction to the methodology, a description of the factor mixture model as well as the two-part model is provided. This serves as the background to the later introduction of the combination of these two components into a single two-part factor mixture model.

Factor mixture models

Factor mixture models were originally proposed to detect unobserved population heterogeneity (Jedidi, Jagpal, & DeSarbo, 1997; McLachlan, Do, & Am-broise, 2004; McLachlan & Peel, 2000; Mislevy & Verhulst, 1990; Muthén, 2006; Muthén & Asparouhov, 2006; Yamamoto & Gitomer, 1993; Yung, 1997). Muthén (2008) provided an overview of these factor mixture models and described them as hybrid latent variable models that are categorized into two broad types, based on measurement invariance or noninvariance. Factor mixture analysis (FMA) models are classified in the noninvariant measurement branch of such hybrid latent variable models.

Muthén (2008) described how an FMA model presents a useful generalization for cross-sectional latent variable models and allows both the classification of subjects in the form of latent classes and the determination of continuous latent scores within these classes. Compared to the latent class analysis (LCA) that specifies that items are uncorrelated within each latent class, FMA allows the items to have nonzero correlations within each class because the factor in an FMA influences all items. Muthén (2008) points out that an LCA is a special case of FMA where the factor in an FMA is absent and that a variety of FMA models are possible by including measurement noninvariance in intercept differences and slope differences.

Based on these factor mixture models proposed by Muthén (2008), a factor mixture model for k = 1,…,K latent classes can be specified as follows:

$$\begin{array}{l}{\mathit{y}}_{ik}={\mathbf{\nu }}_k+{\mathbf{\Lambda }}_k{\mathbf{\eta }}_{ik}+{\mathbf{\epsilon }}_{ik}\\ {\mathbf{\eta }}_{ik}={\mathbf{\alpha }}_k+{\mathbf{\zeta }}_{ik},\end{array}$$ (1)

where for class k, y_ik are the individual i ’s responses on random variable y, which is a p vector of observed outcomes; ν_k is a p vector of measurement intercept; λ_k is a p × m (number of factor) matrix of factor loadings; η_ik is an m vector of factor scores and ε_ik is a p vector of residual errors. α_k is an m vector of the intercepts of the factors for each class k.

Factor analysis typically uses the maximum likelihood (ML) estimator. This method, however, can break down when the normality assumption is violated, a situation that yields distorted test statistics and standard errors that can lead to erroneous conclusions (Boomsma & Hoogland, 2001; Muthén & Kaplan, 1985, 1992; Powell & Schafer, 2001; Yuan & Bentler, 1998). Assessing the many robust methods that have been developed to handle such nonnormal data, however, Muthén (1989) pointed out that because robust approaches, such as the asymptotically distribution-free (ADF) estimation method, still maintain the linearity assumption, the application of ADF is not appropriate when the linearity of measurement variables are questionable, a situation that often occurs in censored data. In this context, the term censored refers to censoring from below, or left-censoring, a phenomenon that is the same as that observed in data containing a preponderance of zeros. Thus Muthén proposed a Tobit factor analysis approach for the censored data.

Two-part models

Two part models are particularly useful in dealing with semicontinuous variables. Similar to left-censored variables, semicontinuous variables have highly skewed distributions with a large portion of observations piled up at a single value—typically zero. According to Olsen and Schafer (2001), a semicontinuous variable is different from one that has been left-censored, or truncated, because the zeros are valid self-representing data values, not proxies for negative or missing responses. In practice, semicontinuous variables are frequently found in studies of abnormal behavior, adolescent substance use, and medical expenses.

When a Tobit model is applied to semicontinuous data, Olsen and Schafer (2001) discussed two possible problems. First, if a zero is a valid self-representing data point, the underlying distribution of the censored data does not exist. Thus, interpreting the parameters, which are the mean and the variance of censored data, can be problematic. Second, in a Tobit model, the censoring mechanism is jointly modeled with the outcome variable generation. When censoring mechanisms and outcome variable generations have separate processes that result in semicontinuous data, the restriction of a Tobit model is not appropriate. As an alternative, Duan, Manning, Morris, and Newhouse (1983) used a two-part regression modeling approach to handle data with such a piling up of zeros. Olsen and Schafer (2001) then extended the two-part regression approach to longitudinal settings.

Based on the definition by Olsen and Schafer (2001), a semicontinuous response ranging from zero to + ∞, y_ij, for an individual i = 1,…,I at occasion j = 1,…,J, can be written as follows:

$$\begin{array}{l}{U}_{ij}=\{\begin{array}{ll}1\hfill & \text{if}{y}_{ij}>0\hfill \\ 0\hfill & \text{if}{y}_{ij}=0\hfill \end{array}\\ V_{ij}=\{\begin{array}{ll}g(y_{ij})\hfill & \text{if}{y}_{ij}>0\hfill \\ \text{irrelevant}\hfill & \text{if}{y}_{ij}=0,\hfill \end{array}\end{array}$$ (2)

where g is a monotonically increasing function that will make V_ij approximately Gaussian. Olsen and Schafer (2001) modeled the semicontinuous responses by using a pair of correlated random-effect models, one for the logit probability of a nonzero response, U_ij = 1 and one for the mean of the continuous responses given that nonzero responses occur, E(V_ij|U_ij = 1). The first part of the model separated “no-use” from “any sort of use” by creating binary indicator variables that reveal any level of use within the previous time. In the second part of the model, continuous indicator variables represent the amount of the usage if “use” occurred. If there was “no-use” on the binary indicator variables, the continuous indicator variable that captures frequency of use was treated as missing. The random coefficients from the two parts were assumed to be jointly normal and possibly correlated.

In the application of the two-part model on abnormal behavior, the dichotomous part at any given time point concerns the engagement in the abnormal activity and the continuous part at any given time point concerns the amount of the activity when the engagement occurred. The engagement in the activity is usually positively correlated with the amount of activity; the higher the probability of engagement is, the higher the expected amount of activity and, conversely, the smaller the probability of engagement is, the lower the expected amount of activity. It is possible, however, for the amount of activity to be high even with a small probability of engagement, but this is a rare occurrence.

Two-part factor mixture analysis

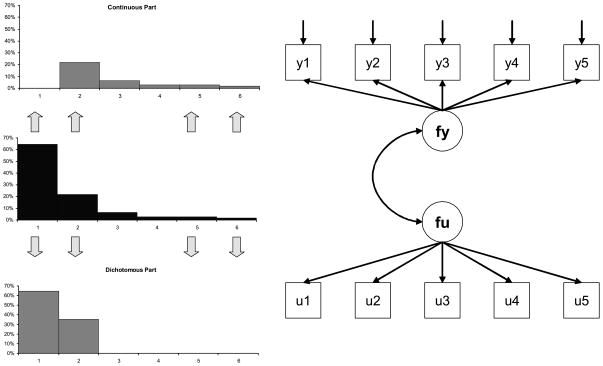
The two-part modeling approach can be combined with a factor model to deal with a situation in which multiple indicators have a preponderance of zeros and the rest of the observations are highly skewed. Thus, the combination of these two ideas takes into account the decomposition of the semicontinuous outcome measurements into a dichotomous response part (i.e., for zero versus nonzero responses) as well as a continuous response part. Figure 1 displays the process of decomposing the skewed distribution of the data into two parts and applying two-part modeling to a factor model to create a two-part factor model.

FIGURE 1.

Process of decomposing the skewed data into two parts and applying two-part modeling to a factor model.

Incorporating latent classes in a two-part factor model allows the two-part factor mixture model to explore qualitatively different subpopulations within the data set. The factor mixture model in Equation 1 can be decomposed into two parts—one to model the dichotomous response part and another to model the continuous response part. First, suppose (u)_ik denotes the individual i’s dichotomous response part for class k. The model for the dichotomous part can be written as follows:

$$\begin{array}{l}{\mathit{y}}_{ik}^{\ast }={\mathbf{\Lambda }}_{(u)k}{\mathbf{\eta }}_{(u)ik}+{\mathbf{\epsilon }}_{(u)ik}\\ {(\mathit{u})}_{ik}=\{\begin{array}{ll}1\hfill & \text{if}{\mathit{y}}_{ik}^{\ast }>\mathbf{\tau }\hfill \\ 0\hfill & \text{if}{\mathit{y}}_{ik}^{\ast }\le \mathbf{\tau }\hfill \end{array},\end{array}$$ (3)

where ${\mathit{y}}_{ik}^{\ast }$ is a set of latent response variables for class k; (u)_ik is a p vector of both zero and nonzero outcomes that vary depending on the threshold τ(u)_ik is 1 if ${\mathit{y}}_{ik}^{\ast }$ is greater than τ and 0 otherwise); Λ_(u)k is a p × m matrix of factor loadings for the dichotomous part for class k; and η_(u)ik and ε_(u)ik denote an m vector of factor scores and a p vector of residuals, respectively, for the dichotomous part for class k.

Second, similar to the factor mixture model in Equation 1, the model for the individual i’s continuous response part y_ik for class k where the observed ${\mathit{y}}_{ik}^{\ast }$ is greater than 0 can be written as follows:

$${\mathit{y}}_{ik}={\mathbf{\nu }}_k+{\mathrm{\Lambda }}_k{\mathrm{\eta }}_{ik}+{\mathbf{\epsilon }}_{ik}.$$ (4)

Because the continuous response part is usually skewed, the model can use a function g to make y_ik normal. Often in practice, logarithm functions are usually employed assuming a log-normal distribution on the continuous response part within each class (Olsen & Schafer, 2001).

The two-part factor mixture model was estimated using an ML estimator with robust standard errors in the Mplus program version 4.2 (Muthén & Muthén, 1998–2006). Numerical integration is necessary in ML estimation when a continuous latent variable has categorical indicators as is the case for the dichotomous part of the model.

Three Steps for Building a Two-Part Factor Mixture Model

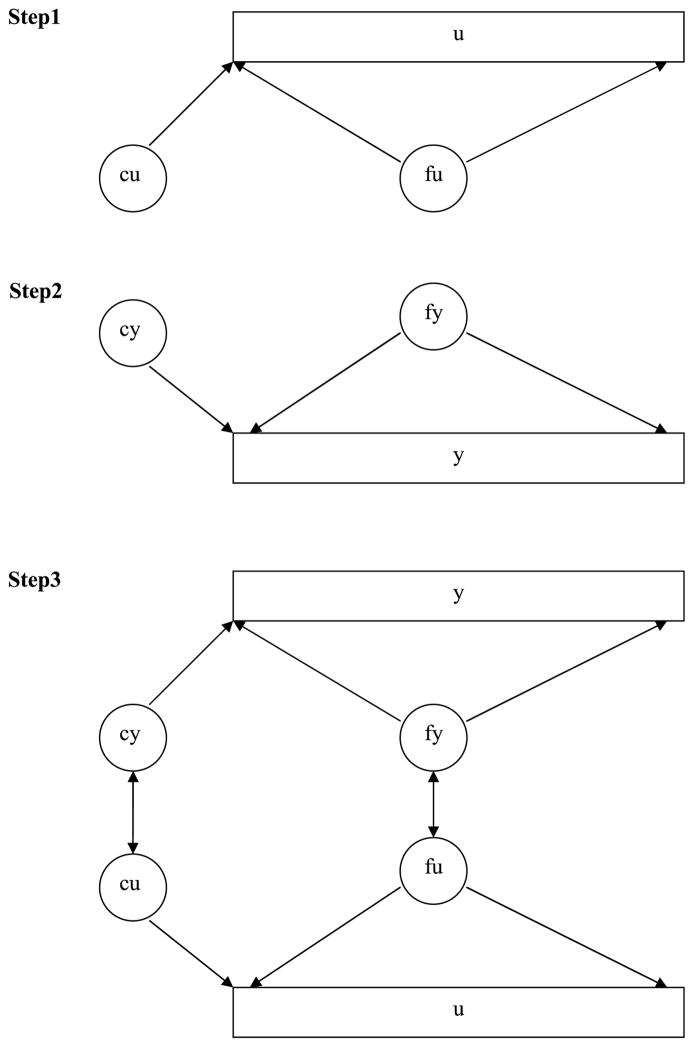
Because two-part factor analysis is a complex undertaking consisting of factor mixture modeling for both the dichotomous outcome part and the continuous outcome part, a stepwise approach should be utilized in constructing a two-part factor mixture model to help avoid model misspecification. This approach involves repeating the same model building strategy three times—once for the dichotomous outcome part by itself, once for the continuous outcome part by itself, and finally once for the combination of the two outcomes. Figure 2 illustrates this multistep process of building a two-part factor mixture model.

FIGURE 2.

Illustration of multistage strategy to build a two-part factor mixture model.

Components of each step

Each of the three steps toward building a two-part factor mixture model involves (a) conducting a conventional factor model analysis—either an exploratory factor analysis (EFA) or a confirmatory factor analysis (CFA)—to decide the number of factors, and (b) specifying a series of models and comparing fit information for each model considered to determine the number of latent classes that best captures population heterogeneity.

It is also possible to test models with either class-specific factor loadings or class-specific intercepts or thresholds. During model specification, models with class-specific or class-invariant variances can be compared. For model identification, however, both intercepts and factor means cannot vary across classes simultaneously. Next, the fit of the models with different numbers of classes is compared to determine how many classes are needed. Because regularity conditions are not met (McLachlan & Peel, 2000) when comparing mixture models that differ by one class, the traditional chi-square difference test in the form of the likelihood ratio test is not applicable. Instead, information criteria such as the Bayesian Information Criterion (BIC; Schwarz, 1978) as well as the Bootstrapped Likelihood Ratio Test (BLRT; Nylund, Asparouhov, & Muthén, 2007) have been used as the model selection tool that will determine the number of classes. Because there are no tests available among likelihood-based tests to compare models that differ in terms of the number of factors and classes (e.g., a two-factor model with two classes vs. a three-factor model with three classes), the models in this study were compared based on the BIC, the number of parameters, and the log likelihood values of the models.

Step 1: Dichotomous component

The first step is to fit a model for only the dichotomous component (i.e., the zero vs. nonzero responses), which is Step 1 in Figure 2. First, an EFA on the dichotomous outcomes is used to study the underlying structure of the data. Based on the results of an EFA, a CFA with a single class follows. Then, more latent classes can be added to the model obtained from the CFA. Given that both classes and factors capture heterogeneity, it should be expected that as the number of classes increases the number of factors needed might decrease. As mentioned earlier, fit indexes are used to decide the numbers of classes (e.g., BIC and BLRT).

Step 2: Continuous component

Step 2 in Figure 2 displays the model for the continuous part. In the second step, the same strategy—conducting an EFA, a CFA, and an FMA—can be applied to the continuous outcome component. This is conducted to understand the population heterogeneity of the frequency of use or level of activity in the continuous part of the data.

Step 3: Combination

The final step connects the models found separately in Steps 1 and 2. As displayed in Step 3 of Figure 2, this step connects these two modeling components by correlating the factors from the dichotomous component with the factors from the continuous component. Step 3 can start with correlating a single factor from the dichotomous part to a single factor from the continuous part. From there, the number of factors from both parts can be increased, a process that can serve as an EFA. Then, the latent classes can be added to the two-part model and correlated if necessary. Fit indexes from all the models under consideration are collected and compared to determine the best-fitting model. The number of factors and latent classes found at Step 1 and Step 2 can provide useful information about the number of factors and classes at Step 3. It should be cautioned, however, that results at Step 3, in terms of the number of factors and classes, might be different from the results of the prior steps because Step 3 is the final step connecting the separate two-part analyses done during the prior steps.

In Figure 2, the arrows from the latent class variable to the indicators (i.e., from cu to u and from cy to y) indicate that the item thresholds for the dichotomous part indicators and the intercepts for the continuous part indicators vary across classes. Alternatively, it is possible to allow factor means to vary across classes (i.e., allowing arrows from cu to fu and from cy to fy instead of allowing class-specific thresholds and intercepts in the model). For model identification, however, the latent class variables cannot affect both the items and the factors at the same time. In most applications of latent class analysis, the main objective is finding classes that differ with respect to their means or locations (Muthén, 2008). Thus, typical LCA allows either the thresholds of categorical indicators or the means of continuous indicators for the latent class variables to vary across classes. Furthermore, a previous study of an FMA on tobacco dependence data by Muthén and Asparouhov (2006) found that the approach of allowing latent class measurement parameters—thresholds and intercepts—to vary across classes fitted the data better. On the data for children’s aggressive behavior for this study, the model with class-specific factor means was also tested and rejected against the model with class-specific thresholds and intercepts. Therefore, this study chose the model with class-specific item thresholds (for the dichotomous part) and intercepts (for the continuous part).

Data

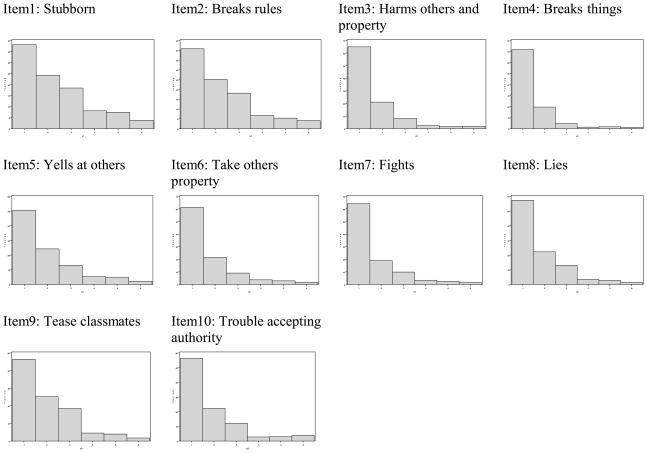
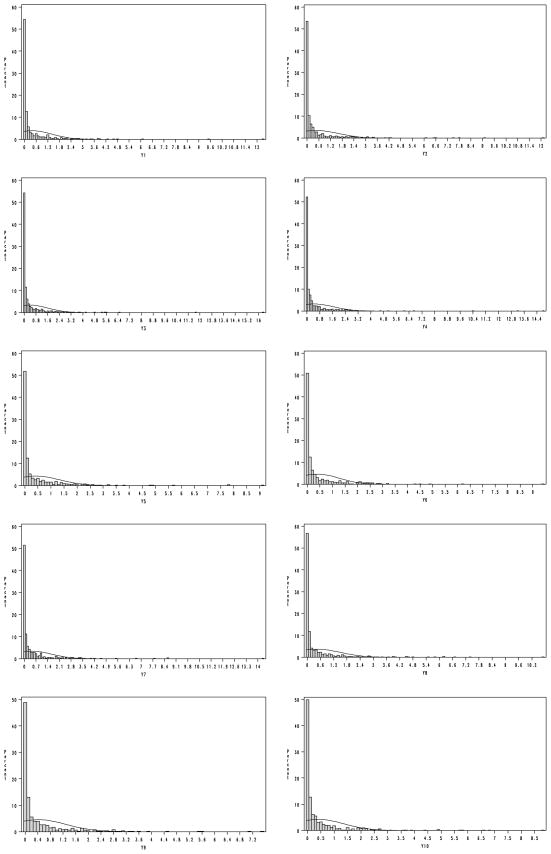
The data used in this study were obtained from a randomized universal preventive intervention trial in Baltimore public schools administered by the Johns Hopkins Center for Prevention and Early Intervention.¹ This trial is part of an ongoing research project that the Center has administered since 1985 and has provided the foundation for three generations of school-based preventive intervention field trials and their subsequent follow-ups. In these trials, teacher ratings of each child’s aggressive classroom behavior for Grades 1 through 7 were measured. The ratings were made using the Teacher’s Observation of Classroom Adaptation Revised (TOCA–R) scaling instrument (Werthamer-Larsson, Kellam, & Wheeler, 1991). This rating consists of 10 items,² each rated on a 6-point scale from almost never to almost always. This study focused on analyzing the pre-intervention data of Cohort 1—the TOCA–R ratings from the first grade—when the children first entered the intervention trial. Specifically, 527 male students in first grade in 1985 were analyzed. Figure 3 displays the distribution of items that clearly show a strong floor effect. On average, about 50% of children for each item were in the “almost never” category for each item. Thus, these items cannot be treated as if they were normally distributed.

FIGURE 3.

Distribution of 10 Teacher’s Observation of Classroom Adaptation Revised items.

RESULTS

Using the multistage strategy described earlier, a two-part factor mixture model was fitted to the TOCA–R data. For model estimation, an ML estimator with robust standard errors using a numerical integration algorithm was used. To avoid local solutions, a sufficient number of random starts was chosen for each step.³ The measurement intercepts (for the continuous part) and thresholds (for the dichotomous part) were allowed to be different across classes in the model. Also for identification purposes, the factor means were fixed at zero in all classes. Because the model estimation was computationally demanding, the factor loadings, variance, and covariance of factors were held equal across classes.

In Step 1, the dichotomous response part was examined (i.e., aggression vs. nonaggression). An EFA was conducted and a two-factor solution was found. Based on the EFA results in Step 1, a confirmatory factor model with two factors and one class was selected for the dichotomous part because the model has the lowest BIC compared to the other models included in Table 1.

TABLE 1.

Result of Factor Mixture Analysis, Step 1: Dichotomous Part

Model	Log Likelihood	No. of Parameters	Bayesian Information Criterion
CFA_1f1c	−2369.794	20	4864.932
CFA_2f1c	−2357.190	23	4858.525
FMA_1f2c with no class-specific variance	−2343.326	31	4880.935
FMA_2f2c with no class-specific variance	−2333.956	34	4880.996

Step 2 examined the continuous component of students’ level of aggression. It was found that a factor mixture with one factor and two classes was better than other competing models found in Table 2.

TABLE 2.

Result of Factor Mixture Analysis, Step 2: Continuous Part

Model	Log Likelihood	No. of Parameters	Bayesian Information Criterion
CFA_1f1c	−488.740	30	1160.152
CFA_2f1c	−462.092	34	1131.211
FMA_1f2c with no class-specific variance	−397.959	42	1051.657
FMA_2f2c with no class-specific variance	−393.512	45	1061.031

Finally in Step 3, the model with one factor and two classes for each part—the dichotomous component and the continuous component—was selected as the final model based on log likelihood values, BIC, and the number of parameters. Table 3 shows that the incorporation of the latent classes improved the model fit compared to the two-part factor model with a single class. Allowing latent classes from the dichotomous and continuous components to covary also seemed to improve the model fit. In the chosen model, therefore, the two latent class variables were allowed to covary. Although, in Step 1, the model with two factors and one class was found to be the best solution for the dichotomous part, for the joint step (Step 3), the model did not converge, most likely because the correlation between the two factors was close to one, which suggests that the two factors are not statistically distinguishable. This implies that the two-part modeling strategy of integrating both parts can provide results that are different from results obtained by the strategy of modeling only the dichotomous part.

TABLE 3.

Result of Factor Mixture Analysis, Step 3: Joint Analysis of Dichotomous and Continuous Parts

Model	Log Likelihood	No. of Parameters	Bayesian Information Criterion
Two-part factor model	−2769.178	51	5857.983
FMA_Y1f2c_U2f1c	NC	NC	NC
FMA_Y1f2c_U1f2c	−2669.339	73	5796.183
FMA_Y1f2c_U1f2c covarying cy and cu	−2665.564	74	5794.900

Note. NC = nonconverged; cy = latent class from the continuous part; cu = latent class from the dichotomous part.

The model in which the measurement intercepts and the factor loadings are class-invariant while the factor means are class-specific was also compared to the final model. The measurement invariant model for the continuous part estimated a lower log likelihood (−2776.306 with df = 56) and a higher BIC (5903.575) than the final model. This indicated that the measurement invariance for the continuous part did not hold.

Interpreting the results

Table 4 displays the estimated factor loadings of the 10 TOCA–R rating of children’s aggressive behavior for the dichotomous part and the continuous part. All factor loadings from the dichotomous part and the continuous part were positive and significant. Thus, the factor found in the dichotomous part can be interpreted as the “propensity to engage in aggressive behavior.” The factor from the continuous part can be interpreted as the “propensity to have high aggressive activity levels.” The correlation between the two factors was .935 and was significantly different from zero (p < .01).

TABLE 4.

Factor Loadings and Standard Errors for the Dichotomous Part and the Continuous Part

Part	Estimates	SE	Estimate/SE
Dichotomous
Stubborn	1.000	0.000	0.000
Breaks rules	1.598	0.261	6.124
Harms others and property	1.765	0.315	5.609
Breaks things	1.570	0.471	3.335
Yells at others	1.238	0.176	7.025
Take others’ property	1.387	0.224	6.187
Fights	1.308	0.246	5.323
Lies	1.389	0.274	5.076
Tease classmates	1.168	0.177	6.599
Trouble accepting authority	1.523	0.298	5.104
Continuous
Stubborn	1.000	0.000	0.000
Breaks rules	1.070	0.112	9.517
Harms others and property	0.808	0.126	6.395
Breaks things	0.233	0.065	3.572
Yells at others	1.035	0.121	8.526
Take others’ property	0.669	0.109	6.164
Fights	0.843	0.151	5.577
Lies	0.724	0.139	5.230
Tease classmates	0.819	0.127	6.437
Trouble accepting authority	1.016	0.101	10.055

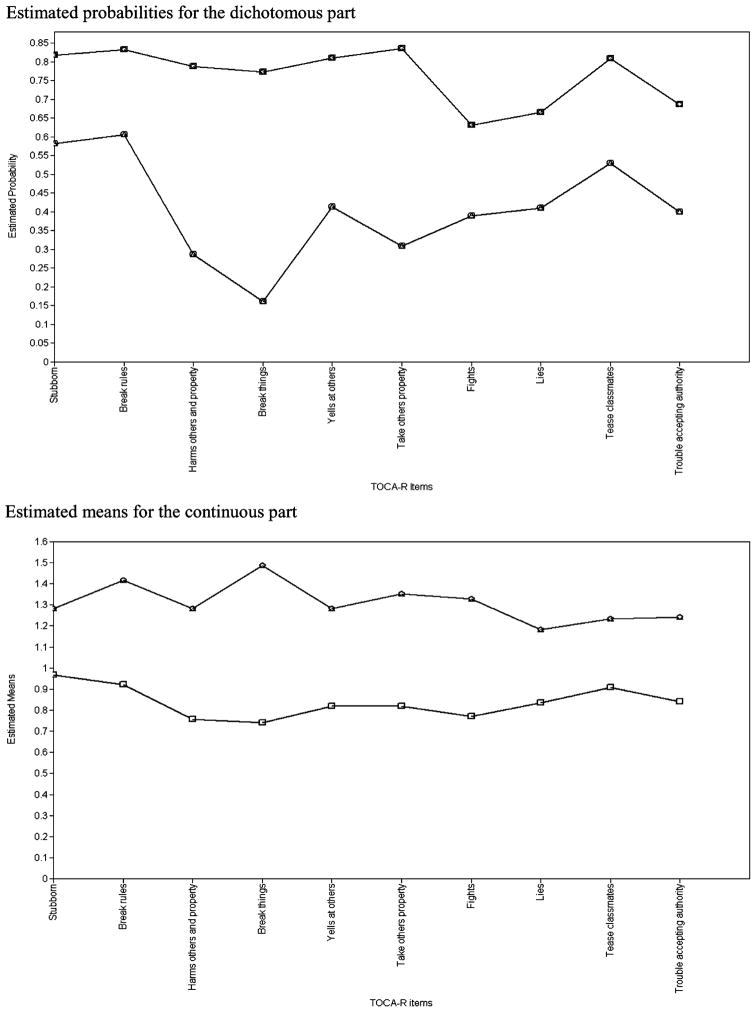
Figure 4 shows the estimated probabilities by latent class for the dichotomous component and the estimated means by latent classes for the continuous component. These plots clearly show the difference in the “propensity to engage in aggressive behavior” as well as the “propensity to have high activity levels” between the groups. The dichotomous component of the model provided the two classes that distinguished two groups of children in terms of their propensity to engage in aggressive behavior—a high engagement group and a low engagement group. The endorsements in the low engagement group for the dichotomous part were particularly low on Item 3 (Harms others and property) and Item 4 (Breaks things). This might suggest that membership in the low engagement group versus the high engagement group seems closely related to physical aggression.

FIGURE 4.

Estimated probabilities for the dichotomous part and the estimated means for the continuous part.

The continuous component of the model that considers the aggressive activity level identified two groups in terms of their propensity to have high activity levels—a high activity level group versus a low activity level group. In Figure 4, the estimated activity level means for the high activity level group are higher than the means for the low activity level group across all 10 items. Among these 10 items, the mean difference between the high activity level group and the low activity level group was the largest in Item 4 (Breaks things), Item 3 (Harms others and property), and Item 7 (Fights), indicating physical violence. As seen in the dichotomous component of the model, the items related to physical violence in the continuous component also might play an important role in making class distinctions.

After combining the two latent classes from each component of this two-part model, the following four types of latent class patterns emerged: (a) the low engagement/low activity level group, (b) the low engagement/high activity level group, (c) the high engagement/low activity level group, and (d) the high engagement/high activity level group. Table 5 presents the estimated intercepts and thresholds for the four latent class patterns. Compared to the high engagement/high activity level group, the low engagement/low activity level group had a lower probability of endorsing each item and lower intercepts for each item. Although the intercepts of the low engagement/high activity level group were the same as those in the high engagement/high activity level group, the two groups displayed different probabilities of endorsing the items. Similarly, although the high engagement/low activity level group had the same intercepts as the low engagement/low activity level group, the two groups had different probabilities of endorsing the items.

TABLE 5.

Estimated Intercepts and Thresholds of Four Latent Class Patterns

	Low Engagement/Low Activity Level			Low Engagement/High Activity Level
	Estimate	SE	Estimate/SE	Estimate	SE	Estimate/SE
Intercepts
Item 1	0.967	0.021	45.444	1.281	0.073	17.463
Item 2	0.922	0.022	42.542	1.416	0.062	22.977
Item 3	0.756	0.019	39.056	1.283	0.076	16.84
Item 4	0.740	0.014	53.404	1.488	0.054	27.727
Item 5	0.818	0.021	38.938	1.283	0.069	18.656
Item 6	0.818	0.023	36.052	1.353	0.066	20.627
Item 7	0.770	0.022	35.587	1.327	0.074	18.013
Item 8	0.836	0.024	34.263	1.182	0.101	11.719
Item 9	0.909	0.022	42.238	1.233	0.068	18.146
Item 10	0.841	0.026	32.688	1.242	0.081	15.289
Thresholds
Item 1	−	0.205	−2.649	−0.542	0.205	−2.649
Item 2	−0.999	0.384	−2.598	−0.999	0.384	−2.598
Item 3	2.252	0.636	3.538	2.252	0.636	3.538
Item 4	3.621	0.882	4.105	3.621	0.882	4.105
Item 5	0.673	0.414	1.627	0.673	0.414	1.627
Item 6	1.658	0.668	2.481	1.658	0.668	2.481
Item 7	0.893	0.295	3.026	0.893	0.295	3.026
Item 8	0.758	0.322	2.358	0.758	0.322	2.358
Item 9	−0.219	0.350	−0.624	−0.219	0.350	−0.624
Item 10	0.906	0.250	3.620	0.906	0.250	3.620

	High Engagement/Low Activity Level			High Engagement/High Activity Level
	Estimate	SE	Estimate/SE	Estimate	SE	Estimate/SE
Intercepts
Item 1	0.967	0.021	45.444	1.281	0.073	17.463
Item 2	0.922	0.022	42.542	1.416	0.062	22.977
Item 3	0.756	0.019	39.056	1.283	0.076	16.840
Item 4	0.740	0.014	53.404	1.488	0.054	27.727
Item 5	0.818	0.021	38.938	1.283	0.069	18.656
Item 6	0.818	0.023	36.052	1.353	0.066	20.627
Item 7	0.770	0.022	35.587	1.327	0.074	18.013
Item 8	0.836	0.024	34.263	1.182	0.101	11.719
Item 9	0.909	0.022	42.238	1.233	0.068	18.146
Item 10	0.841	0.026	32.688	1.242	0.081	15.289
Thresholds
Item 1	−2.421	0.636	−3.806	−2.421	0.636	−3.806
Item 2	−3.569	0.607	−5.884	−3.569	0.607	−5.884
Item 3	−3.209	1.152	−2.785	−3.209	1.152	−2.785
Item 4	−2.729	2.175	−1.254	−2.729	2.175	−1.254
Item 5	−2.692	0.693	−3.886	−2.692	0.693	−3.886
Item 6	−3.248	0.79	−4.109	−3.248	0.790	−4.109
Item 7	−1.063	0.327	−3.248	−1.063	0.327	−3.248
Item 8	−1.416	0.333	−4.246	−1.416	0.333	−4.246
Item 9	−2.573	0.613	−4.196	−2.573	0.613	−4.196
Item 10	−1.731	0.844	−2.052	−1.731	0.844	−2.052

Table 6 displays the counts and proportions of the four patterns. Of the approximately 32% of the students who were in the high engagement group, only 8% fell into the high activity level group. Thus, about 23% of the students who were in the high engagement group were assigned to the low activity level group in the continuous component of the model. Moreover, 68% of the remaining students fell into the low engagement group. Among these students, 64% showed a propensity to have low activity levels by being members of the low activity level group. On the other hand, 5% showed a propensity to have high activity levels because they also were members of the high activity level group. Thus the level of aggressive activity, even with a small probability of engagement, can be high (although unlikely to occur). This indicates that there was a certain group of students who did not show any engagement in aggressive behavior on most of the items. When this group did show engagement, however, the level of aggressive activity for those small number of items was very high. Based on the posterior probability of latent class membership, the model classified 13 students in the low engagement/high activity level group. The students in this group received almost never, which was the lowest rating, on an average of 5 items, whereas they received almost always or very often on only a few items.

TABLE 6.

Class Counts and Proportions for the Latent Class Patterns Based on the Estimated Model

Latent Class From Dichotomous Component	Latent Class From Continuous Component	Counts	Proportions
Low engagement	Low activity level	336.745	0.639
Low engagement	High activity level	25.131	0.048
High engagement	Low activity level	121.737	0.231
High engagement	High activity level	43.387	0.082

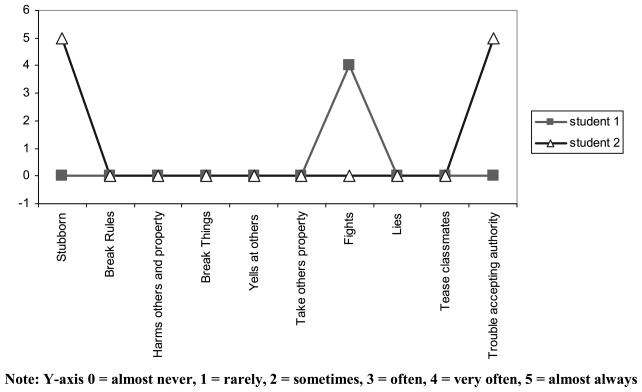
Figure 5 displays the rating pattern of two students classified in the low engagement/high activity level group. Although Student 1 received almost never for 9 items, he received very often for Item 7 (Fights). Student 2 received almost always for Item 1 (Stubborn) and Item 9 (Trouble accepting authority) and he received almost never for 8 items. Research on types of adolescent aggression has indicated that there is some asymmetry in the degree of association between types of aggression exhibited in adolescents (Munoz, Frick, Kimonis, & Aucoin, 2008). In other words, two groups of aggressive children are possible when two types of aggression exist: a group that is highly aggressive and shows two types of aggressive behavior and another group which is less aggressive overall and shows only one type of aggressive behavior. Thus, the results of the current study suggest that groups based on aggression type, including asymmetric combinations of aggression such as the low engagement/high activity level group and the high engagement/low activity level group, can be captured if the characteristics of the data with a preponderance of zeros were taken into account. It will be of great interest to see how the propensities to engage in aggressive behavior and the levels of aggression develop in each group over time.

FIGURE 5.

Teacher’s Observation of Classroom Adaptation Revised items for two students in the low engagement/high activity level group. Note. Y-axis 0 = almost never, 1 = rarely, 2 = sometimes, 3 = often, 4 = very often, 5 = almost always.

Comparison to a regular EFA

It is interesting to note that the BIC from the regular EFA suggested a two-factor solution (BIC for one-factor solution = 11315.696, BIC for two-factor solution = 11195.266, and BIC for three-factor solution = 11206.478). The factor loadings are shown in Table 7. The first factor can be interpreted as a verbal aggression factor because the items—Stubborn, Trouble accepting authority, Break rules, Yells at others, and Teases classmates—were loaded on the first factor. The second factor can be interpreted as a physical aggression factor because the items—Break things, Take others’ property, Harms others, and Fights—were loaded strongly on the second factor. It was found that the selected two-part factor mixture model with two classes fit the data better than a regular two-part factor model (i.e., a two-part factor model with a single latent class). Therefore, not only did the two-part factor mixture model capture the common content of observed variables (i.e., the aggressiveness factor) but it also revealed unobserved population heterogeneity that clustered the children in the study in terms of their propensity to engage in aggressive behavior and their propensity to have aggressive activity levels. By allowing item probabilities to vary across classes, however, the selected two-part factor mixture model found one factor and two classes, indicating that the two factors found by EFA should be seen as one factor with two classes. This shows how conventional factor analysis can give misleading results by ignoring the problem of a preponderance of zeros.

TABLE 7.

Factor Loadings from Exploratory Factor Analysis Two-Factor Solution

Item	Factor 1	Factor 2
Stubborn	0.909	−0.053
Break rules	0.605	0.332
Harms others and property	0.212	0.767
Break things	0.014	0.900
Yells at others	0.530	0.409
Take others’ property	0.165	0.772
Fights	0.381	0.551
Lies	0.450	0.446
Tease classmates	0.493	0.377
Trouble accepting authority	0.787	0.129

A Monte Carlo Simulation Study

To examine whether the multistage strategy used in this application was a reasonable choice or not, a small Monte Carlo simulation study was conducted. Using the Monte Carlo facility in Mplus version 4.2 (Muthén & Muthén, 1998–2006), data with semicontinuous variables were generated and then the simulated data were analyzed through the following three steps to examine how well each step identified the true model: (a) modeling only the dichotomous component, (b) modeling only the continuous component, and (c) modeling these two components together.

Data generation

Similar to the real-data analysis, data with a sample size of 527 and 10 semicontinuous variables were considered for the simulation study. As the data generation model of the simulation, a two-part factor mixture model with one factor and two classes for the dichotomous part and with one factor and two classes for the continuous part was considered. The data generation model had the same model specification as the final model for the TOCA–R data (i.e., the factor loadings and the factor variances for both the dichotomous and continuous parts were class-invariant). In addition, the factor correlation between the dichotomous and the continuous part was set to .9. Factor means for both were set to zero for purposes of model identification. The thresholds for the dichotomous part and the intercepts for the continuous part were specified as class-specific. With respect to the dichotomous part, two latent classes were set to have different item profiles. For latent Class 1, the thresholds of the first five items were set to −1.0 and those of the last five items were set to 1.0. For latent Class 2, the thresholds of the first five items and for the last five items were set to 1.0 and −1.0, respectively.

The intercepts for the continuous outcomes in the two latent classes were set as 1, 2, and 3 SD apart. Based on those three sets of intercept differences, therefore, the Mplus Monte Carlo facility generated three types of data—Data 1, Data 2, and Data 3—composed of 10 semicontinuous items with different means. Table 8 both presents the values of the three sets of intercept differences and summarizes the three types of data generation. All items were set to have log-normal distributions with a standard deviation of one but were set to have different means for the three types of the simulated data. One hundred replications were conducted for each data type. Approximately 50% of the overall responses to each item were zero. Figure 6 displays the distribution of each item from one of the simulated data sets that clearly shows the preponderance of zeros and the right-skewness with a long tail.

TABLE 8.

Summary of Data Generation for Simulation

	Data 1	Data 2	Data 3
Intercepts difference between two classes	1 SD difference	2 SD difference	3 SD difference
	Class 1: −2.5	Class 1: −2.5	Class 1: −2.5
	Class 2: −1.5	Class 2: −0.5	Class 2: 0.5
Distribution of items	Log-normal (μ = −2, σ= 1)	Log-normal (μ = −1:5, σ = 1)	Log-normal (μ = −1, σ = 1)
Model	Two-part factor mixture model: One factor two classes for both dichotomous part and continuous part
Sample size	527	527	527
Number of item	10	10	10
Number of replications	100	100	100

FIGURE 6.

Distribution of 10 items from simulated data.

Simulation results

The coverage values for the two-part factor mixture model with one factor and two classes for the dichotomous part and with one factor and two classes for the continuous part were found to be reasonable in all three types of data (between 0.79 and 0.99) although the coverage values for some of parameters in Data 1 were relatively small. The bias (between −0.06 and 0.07) and the mean square error (ranging between .003 and .095) for fits of the model to the simulated data were found to be fairly small, indicating that the parameters were well recovered. The average class proportions for each data type were about 0.5 and 0.5 for the two latent classes in both the dichotomous and continuous parts. The results indicate that the class sizes were well recovered because the population values for the class proportions for the two latent classes in both the dichotomous and continuous parts were 0.5 and 0.5 as well.

Table 9 displays the results of the model selection for each step of the multistage model building strategy. The first two steps (Step 1 and Step 2) toward constructing a two-part factor mixture model entail modeling the dichotomous and continuous parts separately. To determine the number of classes in these two steps, the BIC and a BLRT were used. For the dichotomous part of the model, overall BIC performance was good in all three types of data although it was better for both Data 2 and Data 3 than for Data 1. Whereas the lowest values of BIC occurred 100% of the time in the true model for both Data 2 and Data 3, they occurred 78% of the time for Data 1. In addition, the performance of BLRT was better in both Data 2 and Data 3 than in Data 1. Nonsignificant p values of BLRT occurred in the true model more than 90% of the time for both Data 2 and Data 3. On the other hand, BLRT selected the true model 76% of the time for Data 1.

TABLE 9.

Model Selection by BIC and BLRT: Percentage of Times the Lowest Value of BIC and Percentage of Times of a Nonsignificant p Value Selected for BLRT

	Data 1		Data 2		Data 3
	BIC	BLRT	BIC	BLRT	BIC	BLRT
Step 1: Dichotomous part
1fu_1c	0	0	0	0	0	0
1fu_2c	78	76	100	92	100	94
1fu_3c	22	24	0	8	0	6
Step 2: Continuous part
1fy_1c	100	26	100	5	0	0
1fy_2c	0	57	0	56	100	66
1fy_3c	0	17	0	39	0	34
Step 3: Joint part
1fu_1c 3 1fy_1c	0	—	0	—	0	—
1fu_2c 3 1fu_2c	0	—	100	—	100	—
1fu_3c 3 1fy_3c	100	—	0	—	0	—

Note. Bolded rows represent the true k-class model for the given model. BIC = Bayesian Information Criterion; BLRT = Bootstrapped Likelihood Ratio Test.

For the continuous part, the performance of BIC varied across the type of data and thus BIC seemed sensitive to the intercept difference between two latent classes. For Data 3, where the intercepts of the items in the two latent classes differed by 3 SD, BIC found the true model 100% of the time. In contrast to Data 3, for Data 1 and Data 2, of which the intercepts of the items in two latent classes differed by 1 and 2 SD, BIC failed to identify the true model and selected the model with one factor and two classes 100% of the time. Compared to BIC, BLRT seemed less sensitive to the intercept differences between two latent classes. For Data 1, Data 2, and Data 3, BLRT selected the true model in 57%, 56%, and 66% of the cases, respectively: BLRT performance seemed consistent across the level of intercept difference between latent classes.

In Step 3, BIC and log likelihood values were evaluated to decide the number of classes because BLRT is not available for a model with more than one latent class variable. In the joint step, the lowest values of BIC occurred 100% of the time in the true model for both Data 2 and Data 3. In contrast, the lowest values of BIC occurred 0% of the time in the correct model for Data 1. This result suggests that the true model can be correctly identified by BIC when the intercepts between latent classes differ by at least 2 SD.

The multistage approach to building a two-part factor mixture model indicates that it is possible to get model misspecification if only one part is modeled. The simulation study showed that the intercept differences between the latent classes affected the model selection by BIC. If the intercept difference between latent classes is smaller than 2 SD, BIC performance, especially in Step 2, which models the continuous part, might be poor. On the other hand, BLRT seems relatively less sensitive to the intercept differences between latent classes. When the intercept differences between latent classes are smaller than 2 SD, BLRT might provide better information in terms of identifying the true model in Step 2. Thus, caution should be taken when attempting to identify the correct model using only a single-step approach: The multistep approach is a way to confirm the correct model if several competing models are under consideration. The multistep approach can also provide further detail as to how well each model performs under each simulation.

DISCUSSION

This article introduces the two-part factor mixture model as a way to model data that have a preponderance of zeros and that exhibit group heterogeneity from unobserved subpopulations. The two-part factor mixture model suggests a more flexible framework by allowing the modeling of continuous outcomes and categorical outcomes simultaneously, a strategy not possible with either latent class models or factor models. This modeling approach breaks down a variable into two parts, one part that identifies an observed behavior and another part that describes the extent to which the observed behavior exists.

In the current study, the two-part factor mixture model identified group heterogeneity in terms of the aggressive behavior that exists among first-grade children. Results showed that there were four patterns: the low engagement/low activity level group, the low engagement/high activity level group, the high engagement/low activity level group, and the high engagement/high activity level group. Because these models involve several parts, a model building strategy was suggested as a way to specify a two-part factor mixture model and was replicated through a Monte Carlo simulation.

Clearly, there are more avenues for further study beyond the scope of this article. Covariates, such as family background, gender, and race, can be included in the model. The advantage of the two-part model is its ability to examine how differently these covariates affect the dichotomous part and the continuous part. In this study, because only the sample of students who were in the first grade in the fall were analyzed, the sizes of some latent classes were relatively small. Extending the sample, for example, to include spring first-grade data might help the model find unobserved subpopulations.

Moreover, although the multistage strategy was found to be reasonable in building a two-part model, there still are modeling questions that need to be investigated using simulation studies. First, given that this study used a limited type of a two-part factor mixture model, various types of two-part factor mixture models, such as a model with class-varying factor means and a model with class-varying intercepts of the items, should be compared to evaluate the performance of the model. Furthermore, these two-part factor mixture models should be compared to alternative and possibly less complicated latent class models as well. Second, when the log normality assumption, which was assumed in the continuous response part of the two-part factor mixture model, is violated, it is possible that class enumeration based on BIC can fail (Nylund et al., 2007). Therefore, a simulation study can examine the effect of the violation of the within-class log normality assumption and how it affects class enumeration. Third, although the current simulation study showed that the BIC would fail to identify the correct number of classes in the joint step when the intercept difference between two latent classes is not large, further simulation studies should be conducted to examine the performance of BIC at the joint step in more detail by looking at various conditions that affect class enumeration, such as sample size variation, number of items, different model settings, and so on. Fourth, the effect of model constraints, such as class-invariant factor variances that this study employed on the class enumeration, should be investigated by a simulation comparing other models without the constraints.

Ultimately, the furtherance of this model can help better understand how to treat at-risk children before their abnormal behavior becomes manifest, especially because signs of abnormal behavior in children can predict serious developmental problems that can afflict the later ability of children to adapt and adjust to society as adults. Studies have found that high levels of disruptive behavior during childhood are associated with such negative outcomes in adolescence and adulthood as academic difficulties or failure, juvenile delinquency, and so on. Thus, it is important that a methodology that accurately predicts the outcome of behavioral therapies on at-risk children be developed. This will allow for a more effective means of conducting the many widely employed interventions, such as peer and teacher-mediated behavioral interaction, that are aimed at reducing the level of disruptive behavior. Knowledge of the eventual trajectory of adult abnormal behavior can provide clearer insight into the proper treatment of an individual child at any point along his or her development path. Especially critical are the first stages of development because interventions can be adjusted or fine-tuned early on to match the specific trajectory of the child. As an advancement on existing modeling strategies, the proposed two-part factor mixture model can uncover these children that would have gone unnoticed. Based on the results of this study, it will be of great interest to further study a latent transition two-part FMA analyzing all of the time points beyond the baseline time point. This could help provide the most effective intervention methods for children and can ultimately lead to more successful interventions.