Estimation of percentage body fat by dual-energy x-ray absorptiometry: evaluation by in vivo human elemental composition

Abstract

Dual-energy x-ray absorptiometry (DXA) is widely applied for estimating body fat. The percentage of body mass as fat (%fat) is predicted from a DXA-estimated R_ST value defined as the ratio of soft tissue attenuation at two photon energies (e.g., 40 keV and 70 keV). Theoretically, the R_ST concept depends on the mass of each major element in the human body. The DXA R_ST values, however, have never been fully evaluated by measured human elemental composition. The present investigation evaluated the DXA R_ST value by the total body mass of 11 major elements and the DXA %fat by the five-component (5C) model, respectively. Six elements (i.e. C, N, Na, P, Cl and Ca) were measured by in vivo neutron activation analysis, and potassium (i.e. K) by whole-body ⁴⁰K counting in 27 healthy adults. Models were developed for predicting the total body mass of four additional elements (i.e. H, O, Mg and S). The elemental content of soft tissue, after correction for bone mineral elements, was used to predict the R_ST values. The DXA R_ST values were strongly associated with the R_ST values predicted from elemental content (r = 0.976, P < 0.001), although there was a tendency for the elemental-predicted R_ST to systematically exceed the DXA-measured R_ST (mean ± SD, 1.389 ± 0.024 versus 1.341 ± 0.024). DXA-estimated %fat was strongly associated with 5C %fat (24.4 ± 12.0% versus 24.9 ± 11.1%, r = 0.983, P < 0.001). DXA R_ST evaluated by in vivo elemental composition, and the present study supports the underlying physical concept and accuracy of the DXA method for estimating %fat.

Introduction

Quantifying body composition has many applications for phenotyping subjects as part of basic and clinical research. Among available methodologies, dual-energy x-ray absorptiometry (DXA) is an advanced technique for estimating body fat, lean soft tissue and bone mineral mass. The DXA approach involves minimal radiation exposure and is widely available and practical to apply.

The underlying concept of DXA estimation of body fat mass is relatively simple (Lee et al 2006). The DXA system first allows separation of the whole body into two compartments: bone mineral (Mo) and soft tissue (ST). When photons at two different energies (e.g., 40 keV and 70 keV for the GE Lunar DXA system) are passed through soft tissue, a heterogeneous absorber, a R_ST value is derived that represents the ratio of photon attenuation at the lower energy (e.g., μ at 40 keV) to photon attenuation at the high level energy (e.g., μ at 70 keV). R_ST can be expressed as follows (Pietrobelli et al 1996):

$$\begin{array}{cc}\hfill R_{\mathrm{ST}}& =\left(\mu \text{at}40\mathrm{keV}\right)∕\left(\mu \text{at}70\mathrm{keV}\right)\hfill \\ \hfill & =\left[\Sigma {(f_i\times {\mu }_{\mathit{mi}})}_{40\mathrm{keV}}\right]/\left[\Sigma {(f_i\times {\mu }_{\mathit{mi}})}_{70\mathrm{keV}}\right]\hfill \end{array}$$ (1)

where i is the component number; f_i is the fraction of soft tissue as the ith component and μ_mi is mass attenuation coefficient of each component.

On the molecular level, soft tissue can be separated into two components: fat and lean soft tissue (LST). When the two-component model (i.e. ST = fat + LST) is applied, the fraction of body mass as fat can be predicted from DXA-measured R_ST (Lohman and Chen 2005):

$$\text{Fraction of fat}=(R_{\mathrm{LST}}-R_{\mathrm{ST}})∕(R_{\mathrm{LST}}-R_{\mathrm{f}})$$ (2)

where R_f (i.e. R value of fat) is based on the mass attenuations of fat at 40 keV and 70 keV, i.e. R_f = μ_m at 40 keV/μ_m at 70 keV for fat (Pietrobelli et al 1996). Similarly, R_LST (i.e. R value of lean soft tissue) is based on the mass attenuation of lean soft tissue at the two energies (i.e. R_LST = μ_m at 40 keV/μ_m at 70 keV for lean soft tissue). Both fat and LST have characteristic mass attenuation coefficients at 40 keV and 70 keV. Previous studies reported R_f values (1.21–1.18) and R_LST value (mean ± SD, 1.399 ± 0.002) (Mazess et al 1990, Pietrobelli et al 1996). As both R_f and R_LST values are assumed constant, as equation (2) shows, fat fraction can be calculated from the measured DXA R_ST value and the assumed constant R_f and R_LST values.

On the other hands, elements are the fundamental building blocks of the human body. According to the five-level model of human body composition (Wang et al 1992), the general R_ST model (i.e. equation (1)) can be understood at the elemental level. However, the association between DXA R_ST and the corresponding elemental composition has never been fully evaluated, except for a few preliminary reports (Pietrobelli et al 1996, Testolin et al 2000). The major reason is the lack of complete information on in vivo body elemental composition. This represents a knowledge gap in confirming the underlying DXA physical concepts and in the estimation of body composition by DXA.

The aim of the present investigation was to evaluate the DXA R_ST value by elemental composition and the DXA %fat by the five-component (5C) model, respectively. The main concept is that the general R_ST model (i.e. equation (1)) can apply on the elemental level where f_i is the fraction of soft tissue as the ith element, and μ_mi is mass attenuation coefficient of each element. The R_ST values predicted from elemental composition will be applied to evaluate the DXA R_ST values.

Model development

Total body mass of major elements

There are ~50 elements in the human body. The content and distribution of the elements in the various tissues and organs are well documented in the Reference Man (Snyder et al 1975). Eleven major elements account for >99.5% of body mass and the other remaining ~40 elements account for less than 0.5% of body mass. The elemental composition of body mass (BM) can be expressed by the following model:

$$\mathrm{BM}=\mathrm{H}+\mathrm{C}+\mathrm{N}+\mathrm{O}+\mathrm{Na}+\mathrm{Mg}+\mathrm{P}+\mathrm{S}+\mathrm{Cl}+\mathrm{K}+\mathrm{Ca}+\text{others}.$$ (3)

In the present study, seven major elements can be measured in vivo: total body carbon (TBC) by inelastic neutron scattering (Kehayias et al 1987, 1991), total body nitrogen (TBN) by prompt-γ neutron activation, total body sodium (TBNa), phosphorus (TBP), chlorine (TBCl) and calcium (TBCa) by delayed-γ neutron activation (Dilmanian et al 1990, Ellis 2005, Ma et al 1993) and total body potassium (TBK) by whole body ⁴⁰K counting (Pierson et al 1982).

The remaining four major elements (hydrogen, oxygen, magnesium and sulfur) were not measured in this study. The elemental composition of the molecular level components, such as water, protein, bone mineral, carbohydrate and fat are given in table 1. These values are used to predict the four major elements, including total body hydrogen (TBH), total body oxygen (TBO), total body magnesium (TBMg) and total body sulfur (TBS).

Table 1.

Elemental composition of major molecular level components.

	H	C	N	O	Na	Mg	P	S	Cl	K	Ca
Water	11.2	–	–	88.8	–	–	–	–	–	–	–
Protein	7.1	53.1	16.1	22.7	–	–	–	1.0	–	–	–
Mo	3.5	16	4.2	44.5	0.3	0.2	9.5	0.3	–	–	21.5
Carbohydrate	6.2	44.5		49.3	–	–	–	–	–	–	–
Fat	12.2	75.9	–	11.9	–	–	–	–	–	–	–

Mo, bone mineral. Based on data summarized in ICRU (1992), ICRP (1995) and ICRP (2002).

Total body hydrogen (TBH)

The chemical stoichiometries of molecular level components are H₂Oforwater,C₁₀₀H₁₅₉N₂₆O₃₂S_0.7 for protein, (C₆H₁₀O₅)_x for carbohydrate and C₅₁H₉₈O₆ for fat (Heymsfield et al 1991, Wang et al 1992). Hydrogen mass fractions in these components are constant: 0.112 for water, 0.071 for protein, 0.035 for bone mineral (Mo), 0.062 for carbohydrate and 0.122 for fat. The additional molecular level component is the soft tissue mineral (Ms) component that contains a small amount of hydrogen as H₂PO₄⁻ and HCO₃⁻. The H amount in Ms can be calculated as 0.0357TBK + 0.007TBCl (Heymsfield et al 1991).

Fat is estimated as the difference between BM and the sum of total body water, Mo, protein, carbohydrate and Ms.

$$\text{fat}=\mathrm{BM}-(\mathrm{TBW}+\mathrm{Mo}+\text{protein}+\text{carbohydrate}+\mathrm{Ms}).$$ (4)

In equation (4), TBW and Mo are measurable by isotope dilution and DXA methods, respectively. Protein can be predicted from TBN as TBN/0.161 (table 1); carbohydrate is assumed to be present at a stable ratio to protein, 0.044 × protein (Kehayias et al 1991) and Ms is predicted as 2.76TBK + TBNa + 1.43TBCl − 0.038TBCa (Wang et al 2002). TBH can be predicted according to equation (4) and the information given in table 1 as

$$\mathrm{TBH}=0.112\mathrm{TBW}+0.035\mathrm{Mo}+0.071\mathrm{TBN}∕0.161+0.0062\times 0.044\mathrm{TBN}∕0.161+0.0357\mathrm{TBK}+0.007\mathrm{TBCl}+0.122\times [\mathrm{BM}-(\mathrm{TBW}+\mathrm{Mo}+\mathrm{TBN}∕0.161+0.044\mathrm{TBN}∕0.161+2.76\mathrm{TBK}+\mathrm{TBNa}+1.43\mathrm{TBCl}-0.038\mathrm{TBCa})].$$ (5)

Total body magnesium (TBMg)

Magnesium exists in both bone mineral and soft tissue tissues. Bone mineral magnesium can be predicted from total body calcium (=0.013TBCa). Soft tissue magnesium (as Mg²⁺) is almost entirely intracellular and occurs in a relatively fixed ratio to intracellular potassium (=0.06TBK). TBMg can be predicted as (Heymsfield et al 1991)

$$\mathrm{TBMg}=0.013\mathrm{TBCa}+0.06\mathrm{TBK}.$$ (6)

Total body sulfur (TBS)

As shown in table 1, sulfur exists almost entirely in protein and Mo with assumed constant ratios of S/protein = 0.010 and S/Mo = 0.003 (Heymsfield et al 1991). As protein is calculated from TBN, TBS can be predicted as

$$\mathrm{TBS}=0.010\mathrm{TBN}∕0.161+0.003\mathrm{Mo}.$$ (7)

Total body oxygen (TBO)

Oxygen is the most abundant element in the human body. In Reference Man oxygen accounts 61% of body mass (Snyder et al 1975). According to equation (3), TBO can be predicted as the difference between BM and the sum of the other ten major elements:

$$\mathrm{TBO}=\mathrm{BM}-(\mathrm{TBH}+\mathrm{TBC}+\mathrm{TBN}+\mathrm{TBNa}+\mathrm{TBMg}+\mathrm{TBP}+\mathrm{TBS}+\mathrm{TBCl}+\mathrm{TBK}+\mathrm{TBCa}).$$ (8)

In equations (5)-(8), body components (i.e. TBW, Mo, TBN, TBC, TBK, TBNa, TBP, TBCl and TBCa) are measurable and expressed in kilograms.

Fraction of soft tissue as elements

The DXA approach allows separation of body mass into two compartments: bone mineral (Mo) and soft tissues (ST). Bone mineral contains nine major elements, including H, C, N, O, Na, Mg, P, S and Ca (table 1). The content of each major element in Mo can be predicted from the fraction of Mo as elements (table 2). For example, C content in Mo = 0.160Mo.

Table 2.

Models for predicting elemental contents in bone mineral and soft tissue.

Element	Element contents in Mo	Element contents in ST
H	0.035Mo	TBH – 0.035Mo
C	0.160Mo	TBC – 0.160Mo
N	0.042Mo	TBN – 0.042Mo
O	0.445Mo	TBO – 0.445Mo
Na	0.003Mo	TBNa – 0.003Mo
Mg	0.002Mo	TBMg – 0.002Mo
P	0.095Mo	TBP – 0.095Mo
S	0.003Mo	TBS – 0.003Mo
Cl	–	TBCl
K	–	TBK
Ca	0.215Mo	TBCa – 0.215Mo

Mo, bone mineral; ST, soft tissue; TBC, total body carbon; TBCa, total body calcium; TBCl, total body chlorine; TBH, total body hydrogen; TBK, total body potassium; TBMg, total body magnesium; TBN, total body nitrogen; TBNa, total body sodium; TBO, total body oxygen; TBP, total body phosphorus and TBS, total body sulfur.

Soft tissue contains 11 major elements, including H, C, N, O, Na, Mg, =P, S, Cl, K and Ca (table 1), and the contents of each element in soft tissue can be predicted as shown in table 2. For example, C content in ST = TBC − 0.160Mo. The fraction of soft tissue as each major element can then be predicted. For example, the fraction of ST as carbon = (TBC − 0.160Mo)/(BM − Mo).

Attenuation of soft tissue at two energies

Soft tissues are further separated by DXA systems into fat and LST. Photons at two different energies pass through soft tissue. The mass attenuation coefficient (μ_m) of each element is characteristic at a given photon energy such as 40 keV and 70 keV and was reported in a few previous studies (Hubbell 1969, Rao and Gregg 1975, White et al 1980). In the present study, new μ_m values 40 keV and 70 keV is applied⁶. According to the corresponding μ_m values (table 3), the attenuation (μ) of soft tissue at 40 keV can be expressed as

$$\begin{array}{cc}\hfill \mu \text{at}40\mathrm{keV}=& \Sigma {({\mu }_{\mathit{mi}}\times f_i)}_{40\mathrm{keV}}=[0.346(\mathrm{TBH}-0.035\mathrm{Mo})+0.208(\mathrm{TBC}-0.016\mathrm{Mo})\hfill \\ \hfill & +0.229(\mathrm{TBN}-0.042\mathrm{Mo})+0.259(\mathrm{TBO}-0.445\mathrm{Mo})\hfill \\ \hfill & +0.397(\mathrm{TBNa}-0.003\mathrm{Mo})+0.488(\mathrm{TBMg}-0.002\mathrm{Mo})\hfill \\ \hfill & +0.810(\mathrm{TBP}-0.095\mathrm{Mo})+0.987(\mathrm{TBS}-0.003\mathrm{Mo})+1.12\mathrm{TBCl}+1.54\mathrm{TBK}\hfill \\ \hfill & +1.83(\mathrm{TBCa}-0.215\mathrm{Mo})]∕(\mathrm{BM}-\mathrm{Mo}).\hfill \end{array}$$ (9)

Table 3.

Mass attenuation coefficients at 40 keV and 70 keV and R values for 11 major elements found in the human body.

Element	Atomic number	Atomic weight	μm at 40 keV (cm2 g−1)	μm at 70 keV (cm2 g−1)	R
H	1	1.008	0.346	0.317	1.091
C	6	12	0.208	0.167	1.246
N	7	14	0.229	0.171	1.339
O	8	16	0.259	0.177	1.463
Na	11	23	0.397	0.198	2.001
Mg	12	24.3	0.488	0.218	2.239
P	15	31	0.810	0.275	2.945
S	16	32.1	0.987	0.312	3.163
Cl	17	35.5	1.12	0.332	3.373
K	19	39.1	1.54	0.413	3.729
Ca	20	40.1	1.83	0.472	3.877

μm at 40 keV, mass attenuation coefficient of element at 40 keV photon energy; μm at 70 keV, mass attenuation coefficient of element at 70 keV photon energy; and R, ratio of μm at 40 keV to μm at 70 keV for each element.

Similarly, the attenuation (μ) of soft tissue at 70 keV can be expressed as the following model:

$$\begin{array}{cc}\hfill \mu \text{at}70\mathrm{keV}=& \Sigma {({\mu }_{\mathit{mi}}\times f_i)}_{70\mathrm{keV}}=[0.317(\mathrm{TBH}-0.035\mathrm{Mo})+0.167(\mathrm{TBC}-0.016\mathrm{Mo})\hfill \\ \hfill & +0.171(\mathrm{TBN}-0.042\mathrm{Mo})+0.177(\mathrm{TBO}-0.445\mathrm{Mo})\hfill \\ \hfill & +0.198(\mathrm{TBNa}-0.003\mathrm{Mo})+0.218(\mathrm{TBMg}-0.002\mathrm{Mo})\hfill \\ \hfill & +0.275(\mathrm{TBP}-0.095\mathrm{Mo})+0.312(\mathrm{TBS}-0.003\mathrm{Mo})+0.332\mathrm{TBCl}\hfill \\ \hfill & +0.413\mathrm{TBK}+0.472(\mathrm{TBCa}-0.215\mathrm{Mo})]∕(\mathrm{BM}-\mathrm{Mo}).\hfill \end{array}$$ (10)

In equations (9) and (10), f_i is the fraction of soft tissue as the ith element; Mo is bone mineral mass and μ_mi is the mass attenuation coefficient of each element.

Soft tissue R (R_ST) value

At the elemental level, each element has a characteristic R value (table 3). Elements with low atomic numbers (e.g., H, C and N) have small R values, and elements with higher atomic numbers, such as P, K and Ca, have larger R values.

For a heterogeneous absorber such as human soft tissue the R value (i.e. R_ST) is defined as the ratio of attenuation at 40 keV to the attenuation at 70 keV. According to equations (9) and (10), a R_ST model (for the GE Lunar DXA system) can be derived as follows:

$$\begin{array}{cc}\hfill R_{\mathrm{ST}}=& \left(\mu \text{at}40\mathrm{keV}\right)∕\left(\mu \text{at}70\mathrm{keV}\right)\hfill \\ \hfill =& [\Sigma {(f_i\times {\mu }_{\mathit{mi}})}_{40\mathrm{keV}}]∕[\Sigma {(f_i\times {\mu }_{\mathit{mi}})}_{70\mathrm{keV}}]\hfill \\ \hfill =& [0.346(\mathrm{TBH}-0.035\mathrm{Mo})+0.208(\mathrm{TBC}-0.016\mathrm{Mo})+0.229(\mathrm{TBN}-0.042\mathrm{Mo})\hfill \\ \hfill & +0.259(\mathrm{TBO}-0.445\mathrm{Mo})+0.397(\mathrm{TBNa}-0.003\mathrm{Mo})+0.488(\mathrm{TBMg}-0.002\mathrm{Mo})\hfill \\ \hfill & +0.810(\mathrm{TBP}-0.095\mathrm{Mo})+0.987(\mathrm{TBS}-0.003\mathrm{Mo})+1.12\mathrm{TBCl}+1.54\mathrm{TBK}\hfill \\ \hfill & +1.83(\mathrm{TBCa}-0.215\mathrm{Mo})]∕[0.317(\mathrm{TBH}-0.035\mathrm{Mo})+0.167(\mathrm{TBC}-0.016\mathrm{Mo})\hfill \\ \hfill & +0.171(\mathrm{TBN}-0.042\mathrm{Mo})+0.177(\mathrm{TBO}-0.445\mathrm{Mo})+0.198(\mathrm{TBNa}-0.003\mathrm{Mo})\hfill \\ \hfill & +0.218(\mathrm{TBMg}-0.002\mathrm{Mo})+0.275(\mathrm{TBP}-0.095\mathrm{Mo})+0.312(\mathrm{TBS}-0.003\mathrm{Mo})\hfill \\ \hfill & +0.332\mathrm{TBCl}+0.413\mathrm{TBK}+0.472(\mathrm{TBCa}-0.215\mathrm{Mo})].\hfill \end{array}$$ (11)

equation (11) reveals that the R_ST value can be predicted from the total body masses of 11 major elements and the bone mineral mass (all units are in kg). In the present study, this elemental predicted R_ST value will be applied to evaluate the DXA-estimated R_ST value.

Subjects and methods

Protocol

Healthy adult subjects completed five tests within 2 weeks: DXA for R_ST and body composition (fat, Mo and lean-soft tissues), in vivo neutron activation analysis for total body masses of six elements (i.e. C, N, Na, P, Cl and Ca), whole body ⁴⁰K counting for total body potassium mass, underwater weighing for body volume and tritium dilution for total body water mass.

Subjects

The adult subjects were recruited through local sources including flyers posted in the medical center and by advertisements in newspaper. Each subject completed a medical history, physical examination and routine screening blood tests to confirm the absence of underlying disease. All subjects participated in recreational physical activities, and none was actively engaged in a competitive sports training program.

The subjects in the present investigation had participated in other large studies of body composition (NIH grant NIDDK PO1 42618). Although our database contains several thousands of subjects for different study purposes, there were only 27 subjects who were tested by all of the above body composition measurements. All subjects signed an informed consent form that was approved by the Institutional Review Board of St Luke's-Roosevelt Hospital Center.

Body composition measurements

Body mass was measured to the nearest 0.01 kg on a Weight Tronix Scale (Scale Electronics Development, New York) following a 12 h fast with the subjects wearing minimal clothing. Height was measured with a wall-mounted stadiometer (Holtain, Crosswell, Wales, UK) to the nearest 0.1 cm.

Dual-energy x-ray absorptiometry

The subjects were scanned using a whole body DXA scanner (DPX with software version 3.6, Lunar Radiation, Madison, WI). The Lunar DXA system uses a filtered x-ray source to provide peak energies at ~40 keV and ~70 keV. The system software divides pixels into bone mineral content (BMC)~and soft tissue~components. The soft tissue is then further separated by the system software into fat and lean soft tissue.

The BMC measured by DXA represents ashed bone (Friedl et al 1992). One gram of bone mineral yields 0.9582 g of ashed bone, because labile components such as bound water and CO₂ are lost during heating (Heymsfield et al 1989). The BMC thus needs to be converted to Mo as Mo = BMC × 1.0436 (i.e. 1/0.9582). The Lunar DXA system has a precision of ±1.28% for Mo, ±1.2% for lean soft tissue and 3–4% for fat (Russel-Aulet et al 1991). The radiation exposure from the DXA approach is minimal, 0.001 mSv with a range of 0.001–0.0035 mSv (Mettler et al 2008).

In vivo neutron activation (IVNA) and whole body ⁴⁰K counting (WBC)

The total body mass of six major elements (i.e. C, N, Na, P, Cl and Ca) was measured at the Medical Department, Brookhaven National Laboratory, Upton, New York (Dilmanian et al 1990, Ma et al 1993). TBN mass was measured by prompt-γ neutron activation analysis with a precision of 2.5%. TBNa, TBP, TBCl and TBCa were measured by delayed-γ neutron activation with precisions from ±1.2% to ±4.5%. Total body carbon (TBC) was measured by inelastic neutron scattering with a precision of ±3% (Ellis 2005). TBK was measured by whole body ⁴⁰K counting using the 4π whole-body counter at St Luke's-Roosevelt Hospital Center. This system has a reproducibility of ±3.2% (Pierson et al 1974). Detailed descriptions of the IVNA and whole body counting systems are provided in earlier reports (Dilmanian et al 1990, Ma et al 1993, Pierson et al 1974).

Underwater weighing (UWW)

This was the routine method for measuring body volume (BV) in the subjects in our laboratory. The BV was measured by underwater weighing in a stainless steel water tank, using a standard method with a technical error of ±0.0020 kg l⁻¹ (Going 2005). Residual lung volume was estimated after immersion of the subjects in a sitting position by means of the closed-circuit O₂ dilution method (Wilmore 1969). The BV was then applied to the five-component model for measuring body fat mass.

Tritium dilution

This was the routine method for measuring TBW in the subjects in our laboratory. Tritium dilution was performed at the Body Composition Unit of St Luke's-Roosevelt Hospital Center and was described in detail elsewhere (Schoeller 2005). The tritium space was determined with 200 μCi of ³H₂O, given intravenously. After a 3 h dilution, a blood sample was obtained to calculate the tritium space with the estimation precision of ± 1.5% (Pierson et al 1982). The tritium space (³H₂O in L) was then converted into TBW (in kg) by multiplying with a correction factor for non-aqueous hydrogen exchange and water density at the average body temperature of 36 °C (TBW = ³H₂O space × 0.96 × 0.994).

Five-component (5C) model

This was the criterion method for measuring total body fat mass in the subjects. Percent of body mass as fat (%fat) was measured with the 5C model as the criterion (Wang et al 1992):

$$\%\text{fat}=(2.748\mathrm{BV}-0.715\mathrm{TBW}+1.129\mathrm{Mo}+1.222\mathrm{Ms}-2.051\mathrm{BM})\times 100$$ (12)

where BM is body mass in kg; BV is body volume in liters; TBW is total body water in kg; Mo is bone mineral in kg and Ms is soft tissue mineral in kg. The soft tissue mineral can be predicted as Ms = 2.76TBK + TBNa + 1.43TBCl − 0.038TBCa (Wang et al 2002).

Statistical analysis

Simple linear regression analysis was applied to describe the relationship between R_ST values predicted from element masses and measured R_ST values by DXA. The mean differences between the R_ST values from element masses and from DXA were tested for statistical significance by paired t-tests. The difference between R_ST values predicted from elemental mass and measured by DXA was related to the mean of the two R_ST values (Bland and Altman 1986).

Similarly, a simple linear regression analysis was applied to describe the relationship between %fat by the 5C model and %fat by DXA. Mean differences between %fat by the 5C model and %fat by DXA were tested for statistical significance by the paired t-test. These differences were again analyzed by the Bland and Altman method (Bland and Altman 1986).

Data were analyzed using Windows and SPSS v12. Group results are presented as mean ±SD. P < 0.05 was considered statistically significant.

Results

Subjects' physical characteristics and body composition

The physical characteristics and body composition of the 27 adult subjects (21 males and 6 females; 14 Caucasians, 5 African Americans and 8 Puerto Ricans) are presented in table 4. The group had an age (mean ±SD) of 43.8 ± 16.8 years, body mass of 78.5 ± 13.2 kg and BMI of 26.6 ± 3.6 kg m⁻² The group body volume (75.3 ± 12.7 l), total body water (44.7 ± 9.9 kg), bone mineral (3.08 ± 0.80 kg) and soft tissue mass (75.5 ± 12.7 kg) were measured by underwater weighing, tritium dilution and DXA, respectively.

Table 4.

Subjects' physical characteristics and body composition.

	Mean	SD	Range
n	27		M 21, F 6
Age (year)	43.8	16.8	19–72
Body mass (kg)	78.5	13.2	53.9–105.9
Height (m)	1.72	0.12	1.51–1.94
BMI (kg m−2)	26.6	3.6	19.3–33.7
Body volume (l)	75.3	12.7	51.7–102.0
TBW by dilution (kg)	44.68	9.90	27.36–60.65
TBW/FFM (kg kg−1)	0.719	0.029	0.659–0.783
Mo by DXA (kg)	3.077	0.799	2.045–4.712
Ms (kg)	0.552	0.148	0.344–0.833
Soft tissue by DXA (kg)	75.47	12.71	51.26–102.07
Body fat by the 5C model (kg)	19.44	9.33	7.81–40.04
Body fat by DXA (kg)	19.12	10.20	4.91–39.35
%fat by the 5C model	24.9	11.1	11.0–46.3
%fat by DXA	24.4	12.0	6.9–47.4

5C model, five-component model; BMI, body mass index; DXA, dual-energy x-ray absorptiometry; Mo, bone mineral; Ms, soft tissue mineral; and TBW, total body water. TBW/FFM, hydration of fat-free mass where TBW and FFM are estimated by tritium dilution and DXA, respectively.

R_ST values by elements and DXA

The total body mass of 11 major elements was measured or predicted for the whole group as shown in table 5. The corresponding masses of the 11 elements in soft tissue were calculated according to the equations in table 2. The fractions of soft tissue as the 11 elements were then calculated as shown in table 6.

Table 5.

Subjects' total body mass of 11 major elements.

Element	Mean	SD	Range
TBH	8.19	1.40	5.64–11.14
TBC	19.44	6.44	9.3–33.9
TBN	1.90	0.43	1.19–2.83
TBO	47.14	10.45	27.82–67.73
TBNa	0.079	0.014	0.055–0.110
TBMg	0.020	0.005	0.013–0.030
TBP	0.567	0.128	0.367–0.811
TBS	0.127	0.029	0.082–0.190
TBCl	0.065	0.013	0.0457–0.0930
TBK	0.150	0.046	0.0845–0.2402
TBCa	0.869	0.204	0.552–1.289

TBC, total body carbon; TBCa, total body calcium; TBCl, total body chlorine; TBH, total body hydrogen; TBK, total body potassium; TBMg, total body magnesium; TBN, total body nitrogen; TBNa, total body sodium; TBO, total body oxygen; TBP, total body phosphorus; and TBS, total body sulfur. All units are in kg.

Table 6.

Subjects' element contents in bone mineral and soft tissue.

Element	In bone mineral (kg)		In soft tissue (kg)		Fraction of soft tissue as element
	Mean	SD	Mean	SD	Mean	SD
H	0.108	0.028	8.086	1.383	0.107	0.002
C	0.492	0.128	18.94	6.49	0.253	0.078
N	0.129	0.034	1.772	0.399	0.0235	0.0037
O	1.370	0.356	45.77	10.14	0.605	0.075
Na	0.0092	0.0024	0.070	0.012	0.0009	0.0001
Mg	0.0062	0.0016	0.014	0.004	0.0002	0.0000
P	0.292	0.076	0.275	0.061	0.0037	0.0009
S	0.0092	0.0024	0.118	0.027	0.0016	0.0002
Cl	–	–	0.065	0.013	0.0009	0.0001
K	–	–	0.150	0.046	0.0020	0.0004
Ca	0.662	0.172	0.207	0.065	0.0028	0.0010

Based on the soft tissue elemental composition (table 6) and models given in equations (9) and (10), we predicted the mean attenuation coefficients of soft tissue for the whole group: 0.2658 ± 0.0057 at 40 keV and 0.1914 ± 0.0008 at 70 keV (all units in cm² g⁻¹). The corresponding R_ST value was 1.3889 ± 0.0238 for the whole group with the range between 1.3389 and 1.4294. In contrast, R_ST estimated by DXA was 1.3409 ± 0.0241 with the range between 1.295 and 1.375 (table 7).

Table 7.

Subjects' R_ST values predicted from elemental composition and measured by DXA.

	Mean	SD	Range
μ at 40 keV	0.2658	0.0057	0.2540–0.2756
μ at 70 keV	0.1914	0.0008	0.1897–0.1928
RST from elements	1.3889	0.0238	1.3389–1.4294
RST by DXA	1.3409	0.0241	1.295–1.375

μ at 40 keV, subjects' soft tissue mass attenuation coefficient (in cm² g⁻¹) at 40 keV predicted from element composition of soft tissue; μ at 70 keV, subjects' soft tissue mass attenuation (in cm² g⁻¹) at 70 keV predicted from element composition of soft tissue; and R_ST from elements, soft tissue R value, i.e. R_ST = μ at 40 keV/μ at 70 keV.

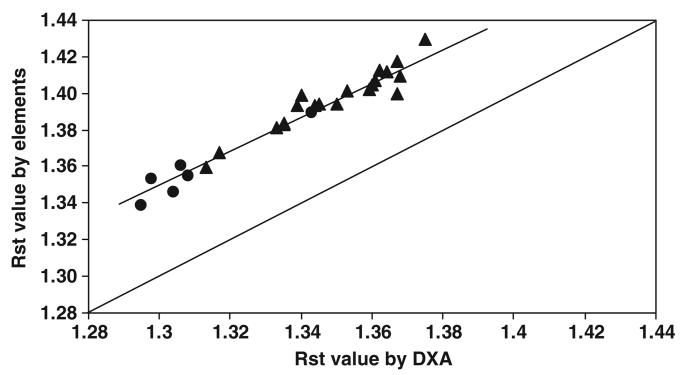
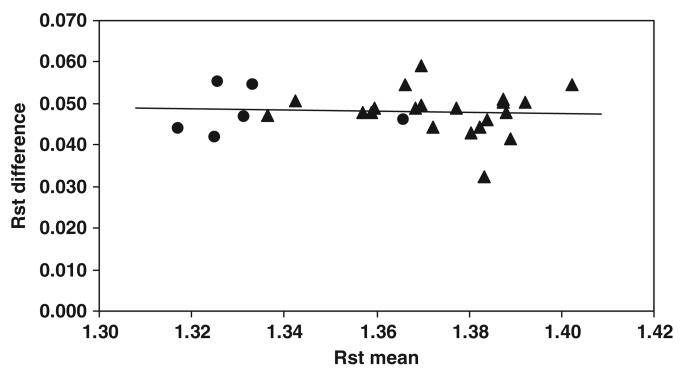
The R_ST values derived from elemental composition versus those provided by DXA for the subject group are plotted in figure 1. There was a strong correlation between the two R_ST values (r = 0.976; P < 0.001) and a significant difference (0.0481 ± 0.0054; paired t-test, P < 0.001) between the R_ST estimates. Bland–Altman analysis indicated that there was a significant bias between R_ST values by the two methods in relation to the mean R_ST values for the pooled group (figure 2; r =−0.557, P < 0.005).

Figure 1.

R_ST values by elemental composition versus R_ST values by DXA in adult subjects. R_ST by elements = 0.097 + 0.964 × R_ST by DXA; r = 0.976, P < 0.001; n = 27 (▲ men; ● women). The line of identity is shown.

Figure 2.

Difference between R_ST values by elements and DXA versus the corresponding mean R_ST values provided by elements and DXA in adult subjects. R_st difference = 0.0649 − 0.0123 × R_ST mean; r = −0.557. P < 0.005; n = 27 ▲ men; ● women).

Percentage of body mass as fat

The mean body fat mass measured by the 5C model and DXA were 19.44 ± 9.33 kg and 19.12 ± 10.20 kg, respectively. There was no significant difference (0.32 ± 1.78 kg; paired t-test, P = 0.35) between the two methods.

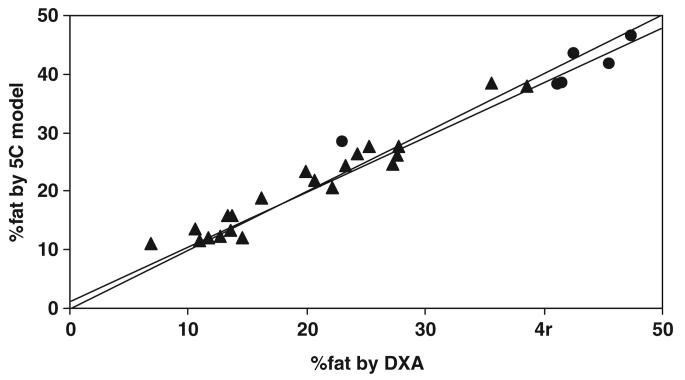
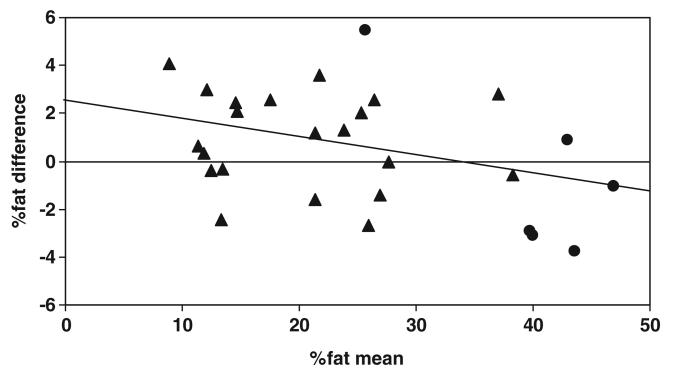
There was a strong correlation (r = 0.983, P < 0.001) between %fat by the 5C model and by DXA (figure 3). The mean %fat measured by the 5C model and DXA were 24.9 ± 11.1% and 24.4 ± 12.0%, respectively. There was no difference in %fat estimates (0.54 ± 2.41%, paired t test, P = 0.25) between the two methods for the pooled group, although Bland–Altman analysis indicated a bias for %fat between the two methods in relation to the mean values (figure 4; r = −0.400, P < 0.05).

Figure 3.

Percentage of body fat (%fat) measured by the five-component (5C) model versus %fat estimated by DXA in adult subjects. %fat by the 5C model = 1.259 + 0.912 × %fat by DXA, r = 0.983, P < 0.001; n = 27 (▲ men; ● women). The line of identity is shown.

Figure 4.

Difference between %fat by the five-component (5C) model and DXA versus the corresponding mean %fat provided by the 5C model and DXA in adult subjects. %fat difference = 2.61 − 0.084 × %fat mean; r = −0.400, P < 0.05; n = 27 (▲ men; ● women).

Relationship between the fraction of fat and R_ST values

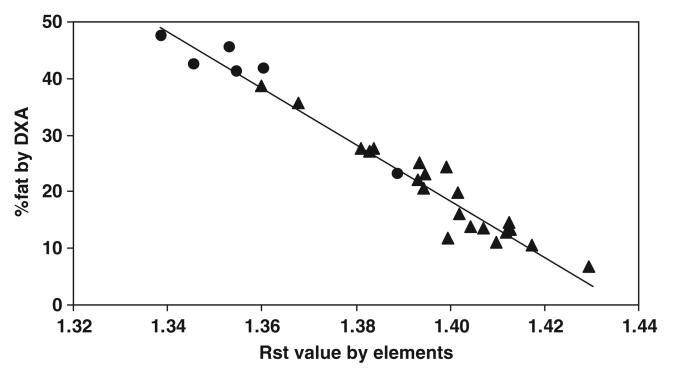
In the present study, the fraction of body mass as fat is measured by either the 5C model or DXA, and the R_ST value is measured by either elemental composition or DXA. There are four different combinations and each of them had strong correlation between the fraction of fat and R_ST value (figure 5):

$$\text{Fraction of fat by}5\mathrm{C}=6.429-4.449\times R_{\mathrm{ST}}\text{by elements}(r=0.957,P<0.001)$$ (13)

$$\text{Fraction of fat by}5\mathrm{C}=6.290-4.505\times R_{\mathrm{ST}}\text{by}\mathrm{DXA}(r=0.981,P<0.001)$$ (14)

$$\text{Fraction of fat by}\mathrm{DXA}=7.100-4.937\times R_{\mathrm{ST}}\text{by elements}(r=0.977,P<0.001)$$ (15)

$$\text{Fraction of fat by}\mathrm{DXA}=7.110-5.114\times R_{\mathrm{ST}}\text{by}\mathrm{DXA}(r=0.998,P<0.001)$$ (16)

Figure 5.

Percentage of body fat (%fat) estimated by DXA versus R_ST value predicted by elements in adult subjects. %fat = 710.0 − 493.7 × R_ST by elements; r = 0.977, P < 0.001; n = 27 (▲ men; ● women).

Discussion

The present study fully merges DXA %fat estimates with the most advanced in vivo analysis of major body elements. This investigation thus fills a gap in DXA methodology and provides a basis for a thorough understanding of the current DXA %fat estimation method.

Evaluation of DXA %fat estimation by the 5C model

Quantifying %fat is useful for phenotyping subjects in research and clinical settings. A major issue in the interpretation of %fat estimation is that different methods may yield different results in the same subjects (Testolin et al 2000). By using cadaver study as the criterion, several animal validation studies have been published using Lunar DXA instruments (Lohman and Chen 2005). For instance, the mean difference in fat content was 2.2% between carcass chemical analysis and DXA in pigs.

The currently available in vivo criterion for estimating %fat is the 5C model (i.e. equation (10)), which minimizes the need for assumptions of constancy between components (Wang et al 2002). However, the 5C model method is tedious, time consuming and therefore limited in its use and availability.

An alternative method for quantifying %fat is the DXA approach. Due to the importance of DXA %fat estimation in clinical applications, there is a need to establish agreement between the DXA and the 5C model methods. In the present study, we compared DXA %fat values with the 5C model as the criterion. Both our and previous studies demonstrate that the bias associated with DXA %fat is systematic (figure 4), with underestimation of %fat for leaner, and overestimation of %fat among obese subjects (Fields and Goran 2000, Gallagher et al 2000, Grant et al 2002, Lee et al 2006, Sopher et al 2004, Williams et al 2006). However, our results revealed that there is no difference in the pooled groups between DXA and the 5C model methods.

Evaluation of DXA R_ST value by elemental composition

The present study provides the first full evaluation of DXA R_ST estimates in the context of in vivo elemental composition. We observed a good overall correlation between R_ST values derived from elemental composition and those provided by the DXA system (figure 1), although the R_ST estimates from DXA and elements were not identical (figure 2). The small deviations or bias in the two R_ST values may be expected for two reasons. First, several assumptions are involved in predicting R_ST values from elemental composition. For example, we apply the mass attenuation coefficients of elements at 40 keV and 70 keV throughout the study, for simplicity. However, the actual photon energies in the Lunar DXA system may have a small difference from the assumed constants of 40 keV and 70 keV. Second, there are intrinsic measurement errors for the seven measured element contents (i.e. C, N, Na, P, Cl, K and Ca) and there are model errors for four predicted element contents (i.e. H, O, Mg and S). Propagated errors could thus be anticipated in the prediction of the R_ST value, and this might account for, in part, the difference between the elemental-predicted R_ST value and the DXA R_ST value.

The R_ST value is the key DXA measure used for predicting the fraction of body mass as fat (Lohman and Chen 2005). The prediction model of fat fraction from R_ST (i.e. equation (2)) can be converted to

$$\text{Fraction of fat}=R_{\mathrm{LST}}∕(R_{\mathrm{LST}}-R_{\mathrm{f}})-1∕(R_{\mathrm{LST}}-R_{\mathrm{f}})\times R_{\mathrm{ST}}.$$ (17)

As both the R value of lean soft tissue (i.e. R_LST) and R value of fat (i.e. R_f) are assumed to be constant, equation (17) demonstrates that the fraction of fat is a function of R_ST. In equation (17), R_LST/(R_LST − R_f) and 1/(R_LST − R_f) are the intercept and slope, respectively. Applying the intercept and slope values in equations (13)-(16), we are able to solve the R_LST and R_f values (table 8). The predicted R_LST values vary from 1.390 to 1.445, and the R_f values from 1.174 to 1.235. These values are close to the previous reports: 1.399 ± 0.002 for R_LST and 1.18−1.21 R_f (Mazess et al 1990, Pietrobelli et al 1996).

Table 8.

Characteristics of the prediction model of fat fraction.

Fat fraction by	RST by	RLST/(RLST – Rf)	1/(RLST – Rf)	RLST	Rf
5C model	Elements	6.429	4.449	1.445	1.220
5C model	DXA	6.290	4.505	1.396	1.174
DXA	Elements	7.100	4.937	1.438	1.235
DXA	DXA	7.110	5.114	1.390	1.198

The fat fraction prediction model (i.e. equation (17), fraction of fat = R_LST/(R_LST − R_f) − 1/(R_LST − R_f) × R_ST) is converted from equation (2): fraction of fat = (R_LST − R_ST)/(R_LST − R_f).

R_f, R value of fat; R_LST; R value of lean-soft tissue; R_ST, R value of soft tissue; R_LST/(R_LST − R_f), intercept of the prediction model; and 1/(R_LST − R_f), slop of the prediction model.

Study limitations

In addition to the limitations mentioned above that may lead to small errors in R_ST values, there are other limitations in the present study.

First, while elemental-predicted R_ST values were derived from measurements of whole body, DXA R_ST values are derived from the sum of lean soft tissue pixels, representing the part of the body not assigned as bone pixels, which include the major part of the head and substantial parts of the thorax and lower abdomen. Some assumptions have to be made about the lean soft tissue composition of bone pixels, and the algorithms used for this are proprietary to the DXA manufacturers. This may in part underlie the differences in body composition results obtained from different kinds of DXA equipment.

Second, the R_ST values predicted from elemental composition were based on two photon energies, i.e. 40 keV and 70 keV. Therefore, the derived R_ST prediction model (i.e. equation (11)) in this study can only be applied to DXA systems that use 40 keV and 70 keV, such as the Lunar or now GE Lunar system (Pietrobelli et al 1996). Other DXA systems may use different photon energies. The Norland XR DXA system (Norland Medical Systems, Fort Atkinson, WI, USA) applies 40 keV and 80 keV, while the Hologic QDR system (Hologic, Waltham, MA) applies 70 and 140 keV (Lohman and Chen 2005). Therefore, different R_ST models should be derived and applied for Norland and Hologic DXA systems (Testolin et al 2000).

Third, although IVNA is the only physics-based method for in vivo measurement of elemental composition in humans, this method is associated with a moderate level of radiation to the subject. As healthy adults, pregnant women and children present contraindications to radiation even at the moderate levels for research project, the range of subjects who can be studied is thus limited. Moreover, the IVNA system is costly to construct, and environmental controls are required for neutron radiation, so that very few centers have IVNA facilities and only Brookhaven National Laboratory (Upton, NY, USA) has all three INVA systems (Dilmanian et al 1990, Ma et al 1993). Our St Luke's research group has maintained a good collaboration with BNL since 1973, and therefore we were able to collect in vivo data of human elemental contents. The database applied in the present study is unique, including body composition on the elemental level and the molecular level (i.e. body fat, total body water and bone mineral mass). Unfortunately, however, the largest IVNA system in the world at BNL has been deactivated.

Fourth, this study used a database consisting of diverse levels of adiposity, gender, age and race. The rationale for including a large BMI range (19.7−33.7 kg m⁻²) is that inclusion of obese subjects might reveal limitations of R_ST estimation by DXA that are not evident in normal weight adults. However, the sample size (n = 27) of this study is too small to explore the potential influence of a wider range of adiposity, age and race on the accuracy of DXA-estimated R_ST values.

Conclusion

The present investigation provides the first full evaluation of the elemental and related physical basis for the DXA R_ST value that forms the underlying concept upon which DXA body composition estimates are based. This concept and its relationship with %fat estimates allow for a comprehensive understanding of DXA foundation models that can be applied when considered in the overall context of body composition research.