Breaking the computational barrier: a divide-conquer and aggregate based approach for Alu insertion site characterisation

Abstract

Insertion site characterisation of Alu elements is an important problem in primate-specific bioinformatics research. Key characteristics of this challenging problem include:

• Data are not in the pre-defined feature vectors for predictive model construction.

• Without any prior knowledge, can we discover the general patterns that could exist and also make biological insights?

• How to obtain the compact yet discriminative patterns given a search space of 4²⁰⁰?

This paper provides an integrated algorithmic framework for fulfilling the above mining tasks. Compared to the benchmark biological study, our results provide a further refined analysis of the patterns involved in Alu insertion. In particular, we acquire a 200nt predictive profile around the primary insertion site which not only contains the widely accepted consensus, but also suggests a longer pattern (T)₇AA[G|A]AATAA. This pattern provides more insight into the favourable sequence variations allowed for preferred binding and cleavage by the L1 ORF2 endonuclease. The proposed method is general enough that can be also applied to other sequence detection problems, such as microRNA target prediction.

1 Introduction

Retrotransposable elements are mobile DNA sequences that can cause diseases and shape genomes by integrating genetic information into chromosomes. These elements can be employed for functional genomics, gene transfer and human gene therapy. However, their insertion site preferences, which are critically important for these potential uses, are still far from being understood.

Alus are the primate-specific short interspersed non-autonomous retrotransposable elements whose active retrotransposition depends on reverse transcriptase encoded by autonomous long interspersed element-1 (L1). Full-length Alus are approximately 300 bps in length and are commonly found in introns and intergenic genomic regions. Throughout the evolutionary history of primates, Alu elements have amplified to more than one million copies, comprising roughly 11% of the human genome. Several distinct Alu subfamilies of different genetic ages have been identified. Compared to older subfamilies, the younger class Alu-Y is characterised by an increasing number of disease-causing insertion mutations, and higher proportions that exist in a polymorphic state. Because of their continued amplification and fairly random, non-specific insertional mutagenesis, Alu elements have a major impact on the human genome. A significant proportion of human genetic diseases have been ascribed to the disruptive Alu insertions and mutations (Deininger and Batzer, 1999; Belancio et al., 2008).

Characterising the preferences of Alu insertion sites has been a vital step to further understand the Alu insertion mechanism. The primary work concerning this issue is (Jurka, 1997). By locally aligning 400 sequences near the insertion site, Jurka identified the preferred primary insertion site is the 5′ TT-AAAA consensus sequence around the 5′ ends of flanking repeats of Alu. This consensus is a potential target for enzymatic nicking by the endonuclease domain provided by the L1 ORF2 product, and some variations in this consensus could also be used as targets. The above results are further validated through a larger scale sequence analyses using the Smith-Waterman local alignment algorithm (Gentles et al., 2005). Using sequences from different Alu subfamilies, Toda et al. (1998) analysed merely 5′ flanking regions of Alu elements by the information content calculation. Their results suggest: (1) the region between −20 and 5′ end of Alu elements is highly adenine-rich and shows significantly higher information content values compared to the rest of the region, and (2) younger subfamilies of Alu elements have higher information content values than older subfamilies. Although those studies hint at the involvement of sequence-specific enzyme specificity for Alu insertion, there is substantial computational cost in constructing these models. Yet, little is known whether any broader-scale patterns could exist that may also influence the insertion of Alus.

Recent progress in data mining techniques allows us to acquire this information from a new perspective. The derived knowledge, if available, would not only provide additional insight into the Alu insertion mechanisms, but also assist with the identification of which genes might be especially susceptible to these insertion mutations.

However, several biological specifications present in this application make the problem interesting and challenging. First, due to the costly and time-consuming laboratory studies it takes to enhance the recognition of the Alu insertion mechanism, biologists want to fairly ensure the certainty of a sequence being a target of Alu insertion when it is fed to the model. That is, the predictive precision needs to be maximised while the corresponding recall is maintained at a reasonable level. Unfortunately, the raw data is in the format of DNA sequences, and no pre-defined feature vectors can be directly presented to data mining algorithms to construct predictive models. Second, besides those significant discriminative patterns indicating the possible Alu insertion, biologists are very interested in identifying any potential proximal patterns in a relatively large scale of bases that may also affect the nicking. Nevertheless, without any prior knowledge of the existence of such patterns, it is nontrivial to design methods to catch them. The safest way to address this issue is to acquire a position reserved global predictive profile of the target sequences by aggregating the class exclusive discriminative patterns together, and then present it to biologists for further analysis.

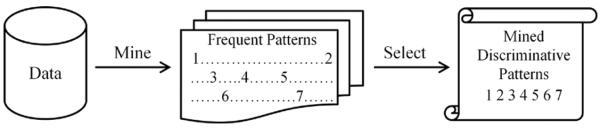
One promising approach to mine biological sequence data is discovering frequent patterns, i.e., patterns which occur in at least as many sequences as specified by a threshold. This approach is motivated by two fundamental biological observations: (1) similar sequences or structures are more likely to have the same or similar function, and (2) large portions of DNA or protein sequences are rather noisy. Thus, if a pattern occurs frequently, it ought to be important or meaningful in some way. The effectiveness of the frequent pattern discovery has been demonstrated by much work using both sequential and structured data (Han et al., 2007). On the other hand, a major obstacle faced by the frequent pattern mining research is how to efficiently discover those essential and discriminative frequent patterns. State-of-the-art frequent pattern mining algorithms (Cheng et al., 2007; Deshpande et al., 2005) usually employ a batch process, which first enumerates patterns above the given support and then performs pattern selection on this initial pool, as shown in Figure 1. Nevertheless, with these methods, there is still limited success in eventually finding those compact yet discriminative patterns. This is due to the four inherent problems of this process.

Figure 1.

Traditional two-step method

1. The number of candidate patterns can still be prohibitively large for effective pattern selection. One of the deteriorating factors is the routine of ‘ordered’ enumeration, that is, we cannot enumerate patterns of “min_sup = 10%” without first enumerating all patterns of ‘min_sup > 10%’. Another similar example exists in frequent sequence pattern mining. For example, to discover frequent patterns of length l from a set of DNA sequences, all possible pattern candidates of length l would be enumerated, resulting in 4^l(4¹⁰ ≈ 10⁶) strings in total. However, before 4^l patterns are obtained, up to ${\sum }_{i=1}^l{4}^i$ sequences of length ≤ l could be first generated, which obviously poses an intractable computational burden on this process.

2. If the frequency of discriminative patterns is below the support value chosen to enumerate the candidates, those patterns would not even be considered even if they have high discriminative information.

3. The discriminative power of each pattern is directly evaluated against the complete dataset, but not on some subsets of data that the other chosen patterns do not predict well.

4. The correlation among multiple patterns is not directly evaluated on their joint predictability.

In addition, a common problematic issue in the bioinformatics practice is that frequent patterns are only mined on the bio-data in question. It cannot guarantee that the discovered patterns are solely proprietary to the target data since they may also occur in other category of data of no interest.

In response to these considerations, we develop a systematic divide-conquer and aggregate based framework to tackle the above challenges as a whole. The proposed framework is a significant extension and generalisation of our prior work (Fan et al., 2008). Our main contributions are summarised as follows.

1. We introduce a divide-conquer and aggregate based framework to efficiently predict and characterise the primary Alu insertion site in a unified process. In this framework, the core is an improved frequent pattern classification algorithm coupled with two task-oriented modules for position reserved sequence mapping and target pattern aggregation. Algorithmically, this is the first probabilistic generative model developed for this issue. The concept of two-mode dynamic support, scalability and time complexity analyses are also provided for the proposed approach.

2. Compared to the benchmark biological study, our results provide a further refined analysis of the characteristic patterns involved in the mechanism of Alu insertion. Most importantly in biology, we acquire a 200 nt predictive profile around the Alu insertion which not only contains the widely accepted signal consensus, but also suggests a longer pattern (T)₇AA[G|A]AATAA. This pattern provides more insight into the favoured sequence variations allowed for preferred binding and cleavage by the L1 ORF2 endonuclease that is involved in initiating the insertion process.

3. For bioinformatics and data mining research, we have analytically and empirically shown that, (1) as the data is not in the pre-defined feature vectors, discriminative patterns are good candidates not only for prediction but general pattern approximation. (2) when compact yet predictive pattern discovery suffers from the intractable computation barrier, the proposed method can provide a general solution to similar sequential or structural pattern discovery problems.

4. Together with our previous work (Fan et al., 2008), we have demonstrated that the proposed divide-and-conquer framework is applicable to frequent patterns in general, not limited to any specific kind of frequent patterns.

The rest of the paper is organised as follows. Section 2 presents the proposed method. Each major component systematically integrated into the framework is described. We report the extensive experimental results in Section 3, and discuss the related work in Section 4. We conclude the paper and discuss the future directions in Section 5.

2 Methods

In this section, we first define the notions of frequent sequence pattern mining, and then present the design and analysis of the proposed method.

2.1 Notation

In the context of biological sequence mining, a sequence pattern is an ordered list of items defined on a specific alphabet. For example, the DNA alphabet consists of four nucleotides or bases, i.e., Σ={A, C, G, T}, and each can be viewed as an item. A subset of Σ is called an itemset. If not all positions in a pattern are precisely known, a wildcard symbol n can be included in Σ accordingly. The number of instances of items in a pattern is called the length of the pattern, and a pattern of length l is denoted as an l-mer pattern. A pattern t = {t₁ t₂, …, t_m} is a subpattern of p = {p₁ p₂, …, p_w} if and only if ∃ j₁, j₂, …, j_m such that 1 ≤ j₁ <j₂ < … < j_m ≤ w and t₁ ⊆ p_j1, t₂ ⊆ p_j2, …, t_m ⊆ p_jm. We also call p a superpattern of t. Given a sequence database D, a pattern p is frequent if at least a fraction of sequences within D contain p, i.e., Support_D(p) ≥ min_sup, where min_sup is the pre-defined support value. In general, frequent sequence pattern mining can be viewed as a special case of frequent itemset mining with the sequential constraint reserved among items.

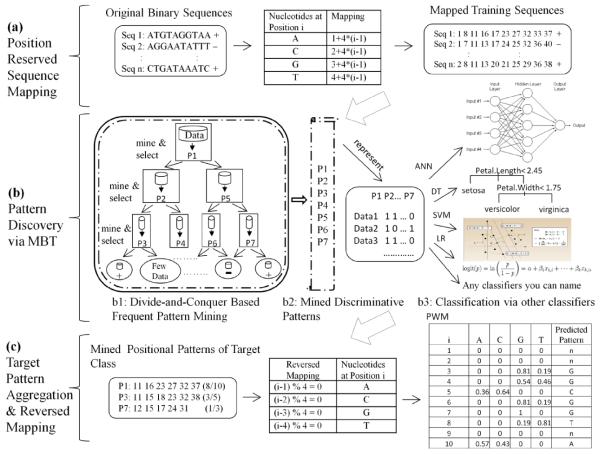
As shown in Figure 2, the proposed method contains the following three steps: position reserved sequence mapping, pattern discovery via Model Based search Tree (MBT) and target pattern aggregation.

Figure 2.

Overall flow of proposed method (artificial data for illustration purpose) (see online version for colours)

2.2 Position reserved sequence mapping

To identify the bases most-likely to receive Alu insertions, we implemented a positional mapping procedure for each nucleotide in a sequence. Without loss of generality, at a specific position i (1 ≤ i ≤ L), the probability of occurrence of each symbol in the alphabet is 1/|Σ| Therefore, |Σ| mapping formulas are needed at position i to uniquely represent a particular character. Figure 2(a) presents an example of this mapping schema if every position is known. According to this mapping, we can obtain the position-reserved numerical representations of the sequences in the dataset for MBT training.

2.3 Pattern discovery via MBT

MBT or ‘model-based’ search tree was initially proposed in our previous work (Fan et al., 2008). As shown in Figure 2(b1), the basic flow proceeds by constructing a depth-first search tree on the data from two classes. As each node in the tree is expanded, a frequent pattern mining algorithm is invoked only on the examples within that node to generate a pool of pattern candidates. Then based on some fitness criteria, such as gain ratio or Gini index, one pattern of the highest score among all candidates is chosen as the most discriminative feature and maintained in this node. Finally, depending on whether the examples contain the selected pattern (or whether the pattern is present in the examples), the data at the given node are divided into two disjoint subsets with each corresponding to a child node. The model tree grows by exploring each child separately and recursively. The search and tree construction terminates when (1) either every example in the given node belongs to the same class, or (2) the number of total examples at the node is smaller than a pre-defined threshold. After the algorithm completes, K discriminative frequent patterns are discovered and the corresponding model-based search tree is constructed. Algorithm 1 presents the detailed implementation.

Algorithm 1.

Build Model-based Search Tree

Input: A set of examples D from which patterns are to be mined A support threshold p normalized between 0 and 1 A pattern discover algorithm, such as a frequent pattern mining algorithm fp() m: minimum node size.

Output: A selected set of patterns, Fs A model-based search tree T.

Call the frequent pattern algorithm, which returns a set of frequent patterns FP = fp(D, p); Evaluate the fitness of each pattern α ∈ FP; Choose pattern αm as the most discriminative feature; Fs = Fs ⋃ (αm}; Maintain pattern αm as the testing feature in current node of the tree T; DL = subset of examples in D containing αm, and DR = D – DL; for ℓ ∈ {L,R} if |Dℓ| ≤ m or examples in Dℓ have the same class label, make Tℓ a leaf node; else recursively construct Tℓ with Dℓ and p; return Fs and T

Moreover, as illustrated in Figure 2(b2), once those K discriminative patterns are obtained, the original examples can be transformed into a K dimensional feature space through a binary representation. In this way, we successfully acquire the transformed ‘feature vectors’ that can be given to any data mining algorithms to build predictive models, which is shown in Figure 2(b3). Additionally, based on the divide-and-conquer tree structure, the MBT itself can also serve as an independent classification or probability estimation tree. Its performance has been demonstrated to be comparable to other popular data mining approaches, such as SVM (Fan et al., 2008).

Scalability of MBT and two-mode dynamic support

It has been theoretically proven that the number of frequent patterns ever enumerated by MBT can be upper-bounded by O(N^N(1–s)) during the tree construction process, where N is the number of examples in the dataset (>3) and s is the support in percentage. This enumeration scale can be also applied to the traditional frequent pattern algorithms (Fan et al., 2008). However, It is worth noting that in MBT, the support s is the unified local support at each node, i.e., the same support percentage s is used at each node to generate patterns. On the other hand, in terms of the entire dataset, a pattern with support s at a specific node also has a global support s’, which is much smaller than s. For example, assume that a node size is 10 and s = 20%, for a problem of size 10,000, the global support is 10 × 20%/10,000 = 0.02%. To discover such patterns, the traditional pattern mining algorithms will return an explosive number of candidates or fail due to resource constraints, since it will generate O(N^N(1–s’)) patterns. As s’ approaches 0, traditional frequent pattern mining algorithms could obtain up to N^N patterns. However, the recursive algorithm can identify such patterns without considering every candidate, thus it will not generate an explosive number of patterns. In particular, compared with traditional pattern mining approaches, the ‘scale down’ ratio of the patterns obtained by MBT will be approximately up to ≈ N^N(1–s)/N^N = 1/N^Ns. This demonstrates that the proposed recursive algorithm could conquer the barrier of explosive growth of frequent patterns and successfully identify discriminative patterns with very small support.

2.4 Target pattern aggregation

As shown in Figure 2(b), MBT is not only a frequent pattern based predictive model, but also a discriminative feature miner. The discovered features can be either further used to train other classifiers or be aggregated to provide a global solution to the target class. The rationale behind this aggregation is as follows. Enfolding the batch process of frequent pattern generation and selection at each decision node, the proposed algorithm is still a typical application of divide-and-conquer strategy. Once K discriminative frequent patterns are obtained via the tree construction process, each merely occurring in the target class and locally reflecting partial specific of this target class can be aggregated to acquire a large-scale pattern which captures the crucial ‘signatures’ distinguishing the target class from the class of no interest. This aggregation essentially corresponds to the generic ‘combine’ step of divide-and-conquer diagram, and is achieved by the accumulation and normalisation of the predicted nucleotide probability at a specific position.

To retrieve the patterns solely of the target class, for each selected pattern at a decision node in the tree, we also track how frequently this pattern occurs in the sequences of different classes within the region defined by this node. As shown in Figure 2(c), the patterns only contained in the target class are collected for aggregation. More specifically, let P_t be a discovered target sequential pattern consisting of a string of numerical positions. Associated with P_t is a frequency value which indicates the number of sequences in the target class at a specific node containing P_t. In general, this frequency value can be distributed to each numerical position within P_t to represent the frequency that we may have a specific nucleotide at this position via the reversed positional mapping. By accumulating and normalising the frequency value of a specific nucleotide at a particular position using all of the discovered target patterns, we can obtain an aggregated sequential pattern along with an L × 4 Position Weight Matrix (PWM) M, where L is the maximal sequence length. The ith row in M contains four probabilities, each indicating the probability we may have a specific nucleotide at the position i in the aggregated sequence. The nucleotide of the highest probability will be chosen as the predicted base at position i. It is this aggregation mechanism that allows us to acquire aglobal predicted probabilistic view of the target sequences, whereby making it possible to characterise the Alu insertion site on a relatively large-scale bases.

2.5 Time complexity of the proposed method

Given a set of N sequences, in the worst case, the computational complexity of the proposed method can be upper bounded by O(LN + logN(FP + dNlogN)), where L is the maximal sequence length, d is the number of frequent patterns generated at a node, O(FP) denotes the computational cost of the frequent pattern mining algorithm, and O(LN) represents the required computations by position reserved sequence mapping as well as target pattern aggregation and reversed mapping. It is evident that the major computational cost is primarily determined by the frequent pattern mining algorithm employed at each internal node of MBT, and it is ≤ O(logN(FP + dNlogN)). Because there are many efficient frequent pattern mining algorithms available (Cheng et al., 2007, 2008; Grahne and Zhu, 2003; Pei et al., 2001; Yan et al., 2008), the overall computational cost of MBT is acceptable compared to the primitive local alignment algorithm. Typically, the time complexity of applying the Smith-Waterman alignment algorithm to the same set of N sequences is $C_2^{N}O\left(L^2\right)$. As more sequences are involved into the study, simply aligning them using the Smith-Waterman algorithm is obviously impractical because its complexity can be factorial.

3 Experimental results

This section discusses the datasets used in the study, and three sets of experiments conducted to evaluate the efficacy of the proposed method. We term our method ‘MBT’ in the following descriptions and figures. To the best of our knowledge, there is no existing data mining algorithms proposed for Alu or other retrotransposable element insertion site prediction, therefore, we first summarise the MBT’s classification results on accuracy, precision, recall and the number of mined patterns, and then we present the characterised Alu insertion site contained in a 200 nt predicted profile. Finally, to study the scalability and quality of the patterns discovered by MBT, we compare its results to those of two benchmark approaches, one is the ‘Pattern Growth’ algorithm (Ye et al., 2007), and the other is what has been widely accepted in biology (Jurka, 1997).

3.1 Datasets

Two sets of Pre-Alu Insertion (PAI) sequences are generated from the human and chimpanzee genomes. For each sequence, we first identified five components as shown in Figure 3(a). Then each sequence is formed by the specifics illustrated in Figure 3(b). Typically, each sequence consists of 100 bases preceding the 3′ end of the 5′ flanking region, one copy of the Target Site Duplication (TSD) (i.e., flanking repeat) and some bases from the 5′ end of the 3′ flanking region. The total length of TSD and the sequence from 3′ flanking region is set to be 100, making each sequence 200 bases long. It is worth noting that, for both sets of PAI sequences, we only consider those from Alu Y family and of the perfect TSDs, that is, the 5′ TSD exactly matches the 3′ TSD. TSDs are indentified by applying TSDFinder (Szak et al., 2002) to the annotated human and chimpanzee genomes available at UCSC Genome Browser (http://genome.ucsc.edu/). In total, 5258 human and 3142 chimpanzee PAI sequences are involved in the study as the positive or target class. To train MBT, we also acquired four sets of 200 nt Non-Pre-Alu Insertion (NPAI) sequences by random sequence generation (Rouchka and Hardin, 2007) as well as random selection from three species which are known to not have Alu insertions. These species are S. pombe, chicken and mouse. We set the number of negative sequences to be 2000 since MBT is rather robust to the varied class distributions (Fan et al., 2008). As a result, eight datasets are generated by respectively combining one of the four sets of NPAI sequences with the human or chimpanzee PAI sequences. Table 1 summarises the statistics of each dataset.

Figure 3.

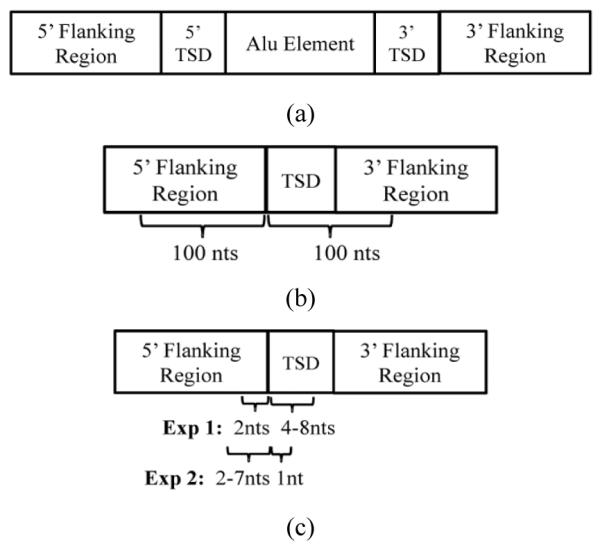
Structures of Alu sequences and PAI sequences used in experiments: (a) the structure of mutual orientation of Alu element, TSDs and flanking regions; (b) the composition of a PAI sequence with perfect TSDs used in our study and (c) illustration of sequences obtained for pattern verification presented in Section 3.4

Table 1.

Dataset description

	Datasets	PAI vs. NonPAI
Human (H)	Chicken (C)	5258 : 2000
	Mouses (M)	5258 : 2000
	Random	5258 : 2000
	S. pombe (Sp)	5258 : 2000
Chimpanzee (C)	Chicken (C)	3142 : 2000
	Mouses (M)	3142 : 2000
	Random	3142 : 2000
	S. pombe (Sp)	3142 : 2000

3.2 Classification results

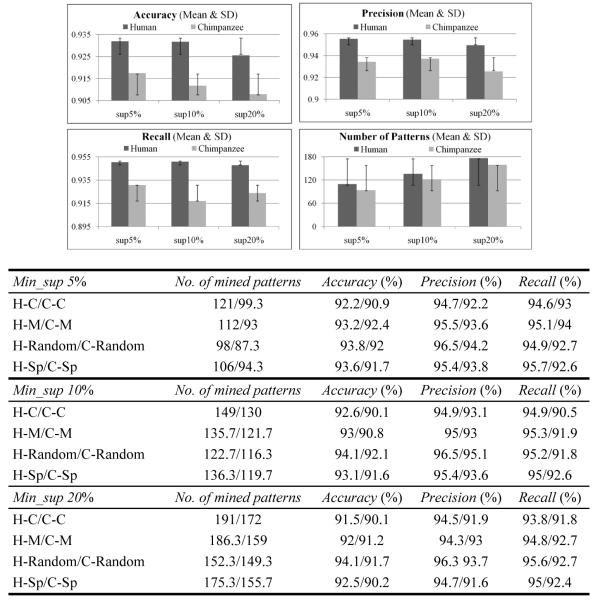
Standard 3-fold CV is employed to conduct classification study as well as the parameter selection for min_sup. Figure 4 summarises the average results over 3 runs for the human and chimpanzee when min_sup is respectively set to be 5, 10 and 20%.

Figure 4.

MBT performance on human (numbers before ‘/’) and chimpanzee (numbers after ‘/’)

In general, along with at least a 90.5% recall score, MBT achieves quite good performance on precision, i.e., over 94.3% for the human and 91.6% for the chimpanzee. This suggests that the frequent patterns discovered by MBT not only are very specific to PAI sequences, but also capture the characteristics of a large portion of PAI sequences and only reject a small number of other members in this class. In addition, MBT consistently performs better on the datasets containing the PAI sequences obtained from the human. This observation could be ascribed to the larger number of sequences acquired from the human, which enables MBT to discover more discriminative frequent patterns for the classification purpose.

As a further effort to study the sensitivity of MBT, we also respectively computed the means and standard deviations of the accuracy, precision and recall over the four datasets using the same category of PAI sequences as the positive class. The rather small range of the standard deviation for each evaluation metric ([0.6%, 1.1%] for accuracy, [0.7%, 0.99%] for precision, [0.2%, 0.86%] for recall) indicates that the performance of MBT is fairly stable with respect to different sequences as the negative class. Moreover, for both species, MBT achieves the overall highest accuracy, precision and recall, as well as the most compact set of discovered frequent patterns when it is trained at min_sup being 5%. As the value of min_sup increases from 5% to 20%, the performance of MBT tends to slightly decline with more frequent patterns obtained. This is because, compared to bigger min_sup thresholds, smaller ones can generate a larger pool of candidates from which MBT has a better chance of selecting optimal patterns with higher fitness scores. However, as demonstrated in Figure 4, the variation of each evaluation criterion is still limited regarding different thresholds of min_sup because those values are all correspondingly falling within the range of one standard deviation.

3.3 Characterisation of Alu insertion site through frequent pattern aggregation

Besides the classification study of the proposed algorithm, we carried out another set of experiments to directly mine the patterns proprietary to the PAI sequences. In particular, MBT is trained on all of the binary sequences in a dataset without conducting 3-fold CV, and only the patterns which occur in the PAI class are aggregated to characterise the potential Alu insertion site. We set min_sup to be 5% due to the overall better performance achieved in the above cross valiation study.

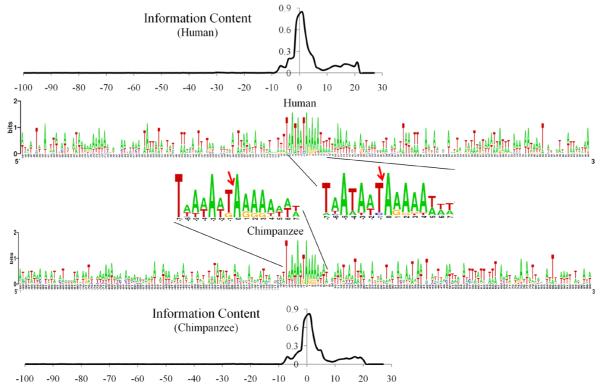
To graphically reveal the global predicted specifics around the Alu insertion site, for each species, we concatenated four aggregated predicted profiles together. Each profile is obtained by solely aggregating the target patterns mined from a data set of different negative (i.e., NAPI) but the same positive (i.e., PAI) sequences. By concatenating the multiple predicted profiles discovered from the varied pools of patterns, we can acquire a more complete and convincing forecast of the conserved subsequences. The logos (Crooks et al., 2004) over four different sequence datasets for the human and chimpanzee are presented in Figure 5. At each specific position, the logo letters are ordered from most to least frequent, and the height of each letter is in proportional to the predicted likelihood that this nucleotide could occur. Instead of no prediction at all, the letter vacancy at a position indicates the possibility of more than three bases. It is evident that the most remarkable signals are detected around the insertion site occurring between positions −1 and 0. To determine the maximum length of the statistically significant patterns contained in the predicted profile, we employ the information content criterion (Schneider et al., 1986) as defined below, where f_c,i is the observed frequency of base c at position i, and B_c the background or expected frequency of base c.

$$IC=\sum _{c\in \{A,C,G,T\}}{f}_{c,i}{\log }_2\frac{f_{c,i}}{B_c}.$$

For both species, the information content curves suggest that statistically significant patterns do exist in the peak regions surrounding the primary insertion sites, and the safest cutoff for the longest sequence pattern is from positions −7 to +7. It should be noted that, information content is computed on 100 bases from the 5′ flanking region and the TSD sequences of varied lengths because we are mainly interested in the primary insertion site in this study. As highlighted in Figure 5, the two discovered consecutive sequences are highly similar, and the super pattern of both can be generalised as 5′ [T|A][A|T|C][A|T][T|A][A|T][A|T][T|G|C][A][A|G][A|G][A|G|T][A|T|G][T|A|G][T|A|C][T|A|G] with the nucleotides at each position listed from most to least frequent. We underline the sequence in the 3′ end to distinguish it from the 5′ side. It is evident that the likelihood of the third base prediction at a particular position is essentially quite trivial, whereby dropping it would not damage the mined knowledge much. Thus we have a simplified pattern shown as follows [T|A][A|T][A|T][T|A][A|T][A|T][T|G][A][A|G][A|G][A|G][A|T][T|A][T|A][T|A]. Compared to the original search space, we already cut it more than half. The above sequence obviously comprises the reported primary candidates for the nick site (Jurka, 1997), e.g., 5′ TTAAAA, which is between −2 and +3. At the same time, more than one nucleotide prediction at most positions also suggests that alternative patterns very likely exist around the insertion site. Moreover, guanine is rather frequent between positions −1 and +3, and its frequency gradually decreases as the pattern extends towards 3′ end. Cytosine is seldom observed in the studied region, and most scattered low occurrence is often beyond positions −5 and +5. In addition, the nucleotide profiles of the predicted sequences are obviously A+T-rich, which demonstrate that Alu has a strong bias for insertion into A+T-rich endonuclease target sites. This is consistent with the observations for genomic Alu insertions (Jurka, 1997; Boissinot et al., 2000).

Figure 5.

Human and chimpanzee: 200 nt predicted profiles and statistically significant patterns identified via information content (arrows indicate primary Alu insertion site) (see online version for colours)

3.4 Pattern verification via algorithm comparison

Experimental design

‘Pattern Growth’ (Ye et al., 2007) is one of the state-of-the-art algorithms developed for protein databases without sequence alignment. It essentially employs the principles of pattern growth as PrefixSpan (Pei et al., 2001). To verify that the subsets of the simplified superpattern identified by MBT are also ranked highly by ‘Pattern Growth’ in terms of relative frequency, we implement the DNA version of this algorithm ‘DNAPG’ by revising the original code. Two experiments are conducted in this study, each focusing on the frequent pattern verification with the majority of bases obtained preceding or following the insertion site. Figure 3(c) illustrates the experimental procedures of sequence acquisition. Due to space limitations, we only report the detailed results of experiment 1. For each set of sequences of the specific length l (6 ≤ l ≤ 10), DNAPG is trained to discover the consecutive patterns containing the same number of bases. By doing this, we in fact considerably reduce the search space of DNAPG at least by 4¹⁹⁰, and we denote this DNAPG as “Shrunk DNAPG (SDNAPG)”. To mine all of such position-specific patterns without any prior knowledge, we have to set the absolute min_sup of SDNAPG to be 1. That is, an l-mer (6 ≤ l ≤ 10) pattern will be enumerated by SDNAPG as long as it occurs in at least one sequence of length l. On the other hand, l-mer patterns discovered by MBT are obtained via direct regular expression matching using the superpattern of length l. Typically, for MBT, the super pattern used in experiment 1 guiding the search is 5′ [A|T][T|G][A][A|G][A|G][A|G][A|T][T|A][T|A][T|A].

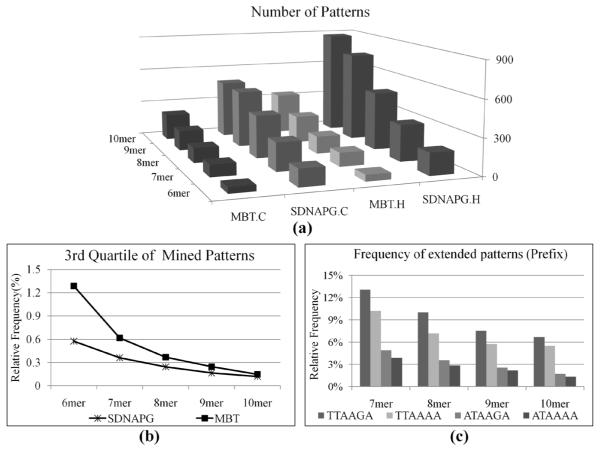
MBT vs. SDNAPG – scalability: Figure 6(a) summarises the number of patterns of varied lengths discovered by SDNAPG and MBT on each species.

Figure 6.

(a) MBT vs. SDNAPG: comparison of number of discovered patterns; (b) MBT vs. SDNAPG: comparison of pattern rankings and (c) prefix study: frequency of extended patterns

On average, the number of patterns identified by MBT is 37.5% of the patterns enumerated by SDNAPG regardless of the pattern composition. Compared to SDNAPG, MBT significantly reduces the cognitive domain from which insightful knowledge could be derived and interpreted by the biologists.

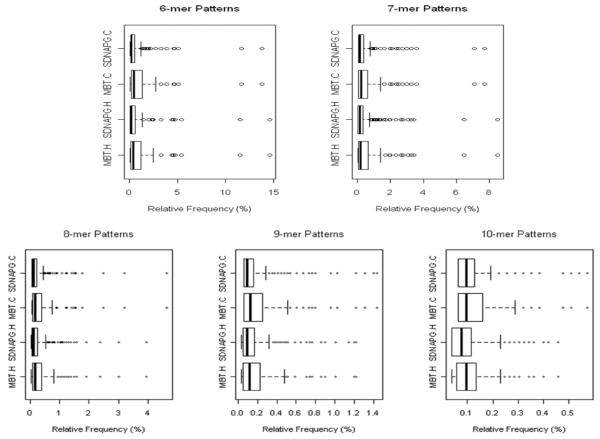
MBT vs. SDNAPG: pattern ranking

Using the patterns common to both species, we also studied the quality of mined patterns by looking into the distribution of the patterns’ relative frequency. The box plots of the relative frequency of the different patterns mined by two algorithms are presented in Figure 7. For each set of the specific composition, the patterns discovered by MBT consistently demonstrate much higher relative frequency compared to those enumerated by SDNAPG. At the same time, the patterns of the highest relative frequencies, as shown as the ‘extreme’ outliers in each plot, are always captured by MBT for both species. Because the distributions of the relative frequency are all rather skewed, median and 3rd quartile are essentially more reasonable statistical summaries than mean. In particular, the non-parametric Wilcoxon rank test showed that the difference between the medians of the relative frequency distributions of patterns obtained from two algorithms on the same species is constantly statistically significant at 95% confidence level. In addition, as presented in Figure 6(b), on average over two species, the 3rd quartile of the relative frequencies of patterns selected by MBT is respectively 130, 72, 52, 49 and 23% higher than that of SDNAPD as the patterns vary from 6 mer to 10 mer. A quartile study further reveals that, regardless of the pattern composition, the 75% quartile of the relative frequency of patterns selected by MBT corresponds to at least 83% quartile of the relative frequency of patterns generated by SDNAPG.

Figure 7.

MBT vs. SDNAPG: distributions of mined patterns’ relative frequencies

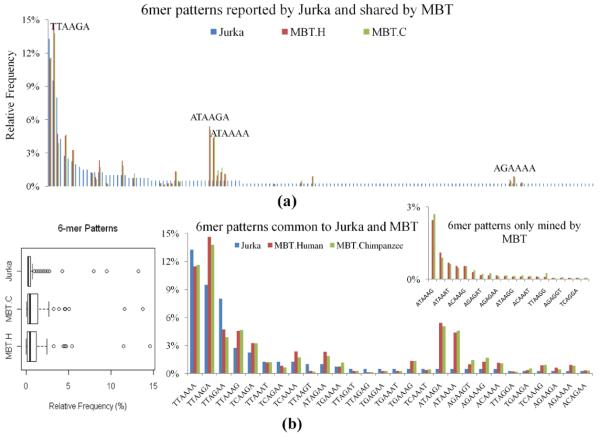
MBT vs. widely-accepted in biology – pattern refinement

As another way to study the quality of mined patterns, we also compared the relative frequencies of 6 mer patterns discovered by MBT to those 6 mer patterns reported by Jurka (1997) around primary insertion sites associated with 400 sequences. It is worth noting that, 6 mer patterns of MBT are mined from the same sequence region that Jurka used for consensus discovery, thus these two results are comparable. Figure 8(a) plots the relative frequencies of all of the 144 patterns reported by Jurka as well as those shared by MBT on the human and chimpanzee. Patterns in the plot are ranked by the relative frequencies of Jurka’s patterns in the descending order. In general, the pattern size of MBT is around 33% of that of Jurka’s, while the relative frequencies of patterns mined by MBT tend to be higher than those reported by Jurka, which can be observed from the box plot of Figure 8(b). A closer examination presented in the bar chart of Figure 8(b) further reveals that, most of the abundant patterns reported by Jurka are also ranked on the top by MBT, such as the signal consensus pattern TTAAAA and its variants TTAAGA, TTAGAA, TTAAAG, etc. They differ by only one base and share the same prefix character T. In a total of 8400 human and chimpanzee sequences, they represent around 39.1% of the 6mer patterns discovered in the sequence region of 2 nts preceding and 4 nts following the insertion site. However, inconsistency in the patterns’ ranking does exist between these two sets of results, and there are two most remarkable observations. First, the pattern of the highest frequency identified by MBT is TTAAGA, instead of TTAAAA, the most frequent pattern reported by Jurka. Among 8400 sequences, 14.3% contain TTAAGA while TTAAAA is associated with 11.5% of sequences. Typically, the relative frequency of TTAAGA reported by Jurka is about 4.8% lower than ours, while the relative frequency of TTAAAA reported by Jurka is 1.7% higher. If TTAAGA could be another signal pattern, together with its variants of the common prefix T and one base mutation, they exist in 30.1% sequences used in our study. Second, ATAAGA and ATAAAA occur much more often in our sequences compared to Jurka’s. If each of them is also treated as a signal sequence, along with its variants of the common prefix A and differing by one nucleotide, they respectively represent 17.1% and 11.6% of 6 mer consensus patterns surrounding the insertion site, which are summarised in Table 2. Therefore, [T|A]TAA[G|A]A and its variants could be a more general consensus which accounts for about 62.4% of 6mer patterns in this region.

Figure 8.

6 mer pattern comparison – MBT vs. widely accepted in biology (Jurka’s study) (see online version for colours)

Table 2.

Refined consensus analysis – MBT vs. widely-accepted in biology

Signal patterns	Variants with the same prefix character (T or A) and one base mutation	Total frequency (%)
TTAAAA (11.5%)	TTAAGA, TTAGAA, TTAAAG, TCAAAA, TTAAAT, TGAAAA	39.1
TTAAGA (14.3%)	TTAAAA,TCAAGA, TGAAGA, TTAAGT, TTAGGA, TTAAGG	30.1
ATAAAA (4.5%)	ATAAGA, ATAAAG, ATAGAA, ACAAAA, AGAAAA, ATAAAA	17.1
ATAAGA (5.3%)	ATAAGA, ATAAAA, ACAAGA, AGAAGA, ATAAGT, ATAAGG	11.6

Prefix study and brief results of experiment 2

Using each of the four 6 mer patterns as the prefix, we also calculated the total frequency of the corresponding extended patterns. As presented in Figure 6(c), for each pattern category, the patterns with TTAA[G|A]A as the prefix constantly dominate patterns with other 6 mer patterns as prefixes. In particular, the most frequent extended pattern would be TTAAGAATAA. The same experimental procedure is used in experiment 2 to compare MBT with SDNAPG, and we obtain the similar results. A further suffix study shows that the most abundant extended patterns can be captured by [T|A]T₃[T|A][T|A][T|G]A with T₇A ranked highest. Therefore, if we can assemble both groups of patterns together, the longer pattern of the highest frequency would be T₇AA[G|A]AATAA, which largely reflects the site-preference shown by the L1 ORF2-encoded endonuclease that initiates the insertion process in the genome.

4 Related work

In data mining research, the usage of frequent pattern in classification has been explored by many recent studies, and most of them focus on itemsets (Grahne and Zhu, 2003; Cheng et al., 2007, 2008) or subgraphs (Yan et al., 2008). This paper is an attempt to extend our newly proposed algorithm (Fan et al., 2008) to the biological sequence pattern mining, and it has been demonstrated that the proposed technique is applicable to frequent patterns in general, not limited to any specific kind of frequent pattern. In sequential pattern mining, seminal algorithms include (Srikant and Agrawal, 1996), PrefixSpan (Pei et al., 2001), etc. These methods can also be invoked at MBT’s internal node to mine candidate features to split data.

In bioinformatics, pattern discovery in sequence data is an active research area.Basically, most of the existing studies can be divided into two approaches (Jensen et al., 2006): exhaustive methods using simple pattern representations and nonexhaustive methods with more complex representations. This partitioning somehow reflects the computational trade-off: more descriptive pattern representations such as PWMs frequently make exhaustive searches computationally infeasible (Brejova et al., 2000). It is apparent that our method cannot be simply categorised into any group. Using the recursive divide-and-conquer schema and without specifying any pattern representation in advance, we actually directly mine and select the essential and discriminative patterns on gradually reduced data subspaces, and then obtain the large-scale predicted profile via the nature combination step of divide-and-conquer for further analysis. In this way, we not only effectively overcome the computational obstacle faced by the majority of sequence pattern discovery algorithms, but also discover the compact set of essential patterns by additionally utilising the two-mode support design.

Besides the primary work addressing Alu insertion, there is still some work exploring the insertion site selection of other retrotransposable elements. But most of them are based on the sequence alignment, statistical approaches or utilisation of the functional properties proprietary to specific elements (Geurts et al., 2006; Gilbert et al., 2008).

5 Conclusions

In this paper, we provide an integrated data mining based solution to the prediction of Alu insertion sites in primate genomes, a problem of primary interest for the overall recognition of Alu biology and genetic basis of human diseases. By simply aligning 400 sequences around Alu insertion sites, biologists identified the preferred, immediate consensus at the position of Alu insertion. It is well known that these methods are computationally costly, and are not portable from one retrotransposable element to another if biological properties pertaining to a specific element are utilised in the solution. At the same time, little is known whether any broader-scale patterns could exist that may also influence the insertion of Alu, and no existing methods can issue the probabilistic certainty of a sequence being a target of Alu insertion. To the best of our knowledge, this paper is the first attempt to use inductive learning techniques to address this issue. Our proposed method is divide-conquer and aggregate based MBT. The base line comparisons are two benchmark approaches, ‘Pattern Growth’ algorithm (Ye et al., 2007) and the study has been widely accepted in biology (Jurka, 1997). Using 8400 PAI sequences collected from the primate genomes, rather exhaustive classification study, large-scale insertion site characterisation as well as pattern verification via algorithm comparison, we have demonstrated that: (1) inductive learning can be a method of choice for insertions site prediction of retrotransposable elements. (2) In particular, both the predictive precision and recall on the target PAI sequences are over 90.5%; (3) compared to both standards, the proposed method is able to discover much more compact yet highly ranked patterns; and (4) most importantly, the obtained 200nt predictive profile around the Alu insertion not only contains the widely accepted signal consensus, but also suggests a longer pattern (T)₇AA[G|A]AATAA which indicates a broader surface of preferred binding sites of the L1 ORF2-encoded endonuclease. This is significant and important for biology studies.

For data mining research, we have shown that in general, (1) discriminative patterns are good candidates not only for classification but general pattern approximation as the data is not in the pre-defined feature vectors. (2) when compact yet predictive pattern discovery suffers from the intractable computation barrier, the proposed divide-conquer and aggregate based MBT can provide a common framework for similar sequential or structural pattern discovery problems, such as other biological sequence pattern mining, intrusion detection and system management.

More sophisticated sequence or structure mapping and reversed mapping techniques could be employed to achieve better performance. Studies of the second nick site of Alu on the other strand, as well as applying the proposed method to other retrotransposable elements are also on our agenda.