Molecular origins of fluorocarbon hydrophobicity

Abstract

We have undertaken atomistic molecular simulations to systematically determine the structural contributions to the hydrophobicity of fluorinated solutes and surfaces compared to the corresponding hydrocarbon, yielding a unified explanation for these phenomena. We have transformed a short chain alkane, n-octane, to n-perfluorooctane in stages. The free-energy changes and the entropic components calculated for each transformation stage yield considerable insight into the relevant physics. To evaluate the effect of a surface, we have also conducted contact-angle simulations of water on self-assembled monolayers of hydrocarbon and fluorocarbon thiols. Our results, which are consistent with experimental observations, indicate that the hydrophobicity of the fluorocarbon, whether the interaction with water is as solute or as surface, is due to its “fatness.” In solution, the extra work of cavity formation to accommodate a fluorocarbon, compared to a hydrocarbon, is not offset by enhanced energetic interactions with water. The enhanced hydrophobicity of fluorinated surfaces arises because fluorocarbons pack less densely on surfaces leading to poorer van der Waals interactions with water. We find that interaction of water with a hydrophobic solute/surface is primarily a function of van der Waals interactions and is substantially independent of electrostatic interactions. This independence is primarily due to the strong tendency of water at room temperature to maintain its hydrogen bonding network structure at an interface lacking hydrophilic sites.

Perfluorinated alkanes which have all the hydrogen (H) atoms of an alkane replaced with fluorine (F) atoms are known to have much lower water solubilities than the corresponding hydrocarbons (1, 2) while at the same time showing high lipophobicity (2) and an extraordinary affinity for carbon dioxide (3, 4). Enzyme inhibitors with fluorinated moieties show stronger binding than their nonfluorinated analogues (5), even in cases when the group on the inhibitor is not among those that bind to the active site (6)—consistent with the expectation from higher hydrophobicity. One intriguing observation regarding the greater hydrophobicity is that the free energy of hydration per unit hydrophobic surface area is similar for hydrocarbons and fluorocarbons (6). The puzzling aspect of this similarity is that, because the C-F bond has a much greater dipole moment than does the C-H bond, a stronger binding with dipolar water might be expected. Further, although the polarizability of F in the C-F bond is relatively low considering its position in the periodic table, it is not lower than that in the C-H bond (7), so that the dispersion interactions of C-F with water are reasonably expected to be more attractive than those of C-H with water. Therefore, a fluorocarbon surface could be argued to be more hydrophilic than that of the corresponding hydrocarbon. A plausible resolution could be that the fluorocarbon with a molecular cross-section of 28.3 Å² (8) occupies sufficiently more volume and surface area in water than the corresponding hydrocarbon with molecular cross-section of 18.9 Å² (9). Hence, the work done to form a cavity large enough to accommodate a fluorocarbon offsets the anticipated free-energy benefit from enhanced energetic interactions with water. However, if one considers the hydrophobic surfaces made via fluorocarbon coatings, these arguments related to cavity free energy do not pertain, and one might anticipate that such a surface would be more hydrophilic than a hydrocarbon surface, in contrast to experimental results (10). It is also not readily apparent whether there is an additional “polar hydrophobic” effect (5), i.e., whether the entropic penalty from restriction of solvent structure due to polar interactions offsets the energetic benefit of the same.

Given the great interest in quantitatively understanding hydrophobicity (11), we have undertaken calculations of the differences in water solvation between hydrocarbons and perfluorinated analogues using all atom molecular dynamics simulations. Although earlier quantitative simulations of simple fluorocarbon solutes (12, 13) and interfacial hydration (14) have been carried out, a universal principle for understanding fluorocarbon hydrophobicity has not been presented, and our goal here is to address this gap. First, for the prototypical example of n-octane, possessing all of the molecular elements of longer chains, we have transformed the hydrocarbon (state 0) into the perfluorocarbon (state 5) in water in stages: (i) “stiffening” the backbone (state 0 → 1), (ii) “lengthening” the C-H bonds to C-F bond length (1 → 2), (iii) “fattening” the H atom Lennard-Jones (LJ) diameter to match that of the F atom (2 → 3), (iv) “strengthening” the LJ energy parameter of the H atom to that of the F atom (3 → 4), and finally (v) “charging”—changing the electrostatic charges of the C and H atoms from those of the hydrocarbon to those of the fluorocarbon (4 → 5). The free- and interaction-energy changes calculated for each transformation yield considerable insight into the physics behind the hydrophobicity of fluorocarbons. Then, in order to isolate the effect of the surface and given the practical utility of hydrophobic surfaces (15), we have also conducted contact-angle simulations of water on a series of self-assembled monolayers (SAM) of hydrocarbon and fluorocarbon thiols.

Our results for solvation free energy as well as contact angle are consistent with experimental observations. We demonstrate a single unifying explanation for both solute and surfaces. The overriding reason that the fluorocarbon solute is more hydrophobic than hydrocarbon solute is due to its fatness, i.e., due to the relatively greater area/volume it occupies in water, leading to a greater free-energy penalty for hydration. The increased hydrophobicity of a fluorocarbon SAM compared to a hydrocarbon SAM is also because of the fatness of the fluorocarbons. In this case, it causes fluorocarbons to pack less densely (lattice spacing 5.9 Å) than the hydrocarbons (lattice spacing 4.97 Å) which is enough to offset their greater energetic affinity for water.

The article is organized as follows. We will first present the rationale for, validation, and results of the calculation of hydration free-energy changes in transforming n-octane to n-perfluorooctane. Next, we will present and validate the results of our contact-angle calculations. We will conclude by noting the striking features of the results and a comment on how they might be used to interpret a number of observations.

Hydration Free-Energy Calculations—Outline, Results, and Discussion

By “free energy of hydration” we mean the free-energy change that accompanies the passage of a single molecule from vapor (ideal gas) state into pure water. We calculate the difference in hydration free energies indirectly as illustrated in Fig. 1. The quantity we seek is the free-energy change accompanying the transformation of a hydrocarbon molecule to a fluorocarbon molecule in water at 1 atm and 298.16 K, in excess of the same quantity calculated in vacuum. Hydration free-energy change (ΔF) and hydration energy change (ΔU) for each stage of the transformation are obtained from the simulations and used to obtain hydration entropy change (-TΔS = ΔF - ΔU). For convenience, all the transformations are carried out first at constant volume, temperature, and particle number, and the result is corrected to a pressure of 1 atm. The computed difference in hydration free energy between perfluorooctane and n-octane is 2.54 ± 0.13 kcal/mol (ΔU = -5.46 ± 0.53 kcal/mol, -TΔS = 8.0 ± 0.58 kcal/mol). From data at 298.16 K and 1 atm for methane (16), ethane (17), propane (18), and for perfluoromethane, perfluoroethane, and perfluoropropane (19) we have, for the cases C1, C2, C3, ΔF = 1.13, 2.01, 2.85 kcal/mol, respectively, which fitting to a polynomial form gives a rough estimate of ΔF(C8) = 6.48 kcal/mol. Our simulation results appear to underpredict the value implied by these experiments, similar to ΔF(C1) = 0.44 kcal/mol calculated by Gough et al. (1). Nevertheless, the results will provide the desired insight into the physical phenomena.

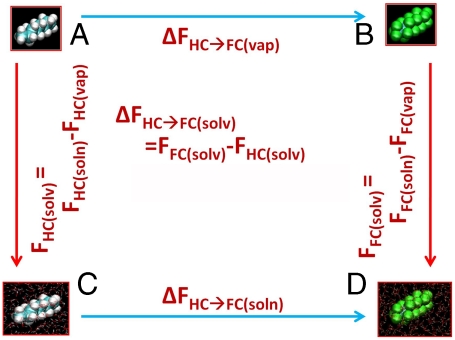
Fig. 1.

Scheme illustrating the thermodynamic cycle behind the simulation strategy to determine the difference in solvation free energy between n-octane (CH₃-CH₂-CH₂-CH₂-CH₂-CH₂-CH₂-CH₃, hydrocarbon, or HC) and n-perfluorooctane (CF₃-CF₂-CF₂-CF₂-CF₂-CF₂-CF₂-CF₃, fluorocarbon, or FC). This quantity is ΔF_{HC→FC(solv)}. The states A and B are the hydrocarbon and fluorocarbon, respectively, in vacuum, i.e., ideal vapor phase, denoted vap. The states C and D are the hydrocarbon and fluorocarbon, respectively, in solution by liquid water at ∼1 atm pressure, i.e., solution phase, denoted soln. The temperature is 298.16 K. The vertical transitions (A → C and B → D) show the transition from vapor phase to solution phase and the difference in free energies of these two transitions is the quantity of interest. The same value can be obtained with greater facility by taking the difference between the horizontal transitions ([C → D] - [A → B]) as we do here.

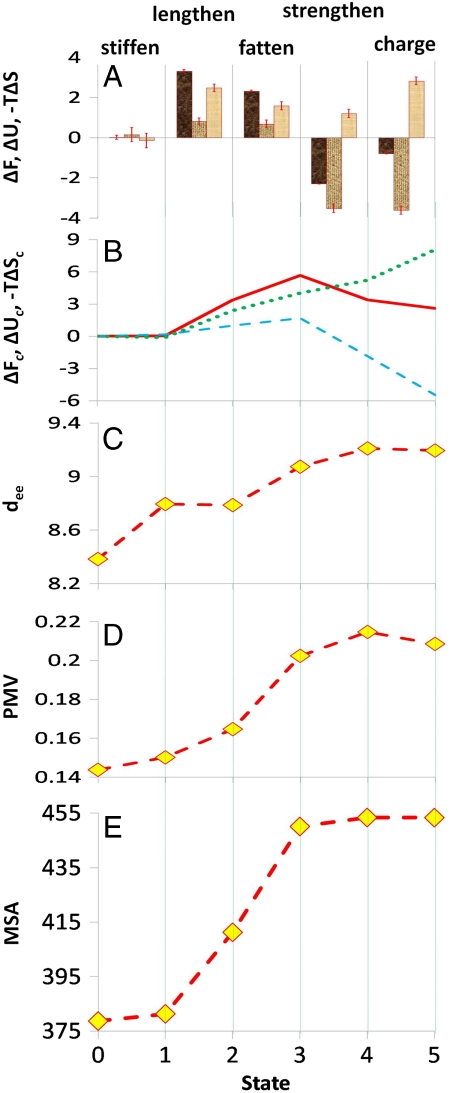
In Fig. 2 are depicted various thermodynamic and structural quantities associated with the transformations between states (state 0 being octane and state 5 perfluoroooctane). The dominant contribution to the final value is ΔF due to bond lengthening and fattening, which can be partly attributed to decreased solvent interaction with carbon backbone but much more so to the work of cavity formation associated with increasing molecular volume. This volume increase is evident in Fig. 2D. The energetic gain associated with the change in dispersion interactions (strengthening) is significant but notably less in magnitude. The orientational distribution of water about the terminal atoms of the alkane solute (Fig. 3) is consistent with the expected clathrate-like geometry (20–22) which allows water to substantially maintain its hydrogen bond network by straddling the surface. The resistance of this network to disruption is apparent from the fact that the net free-energy change associated with the last, charging, step is only ΔF = -0.8 kcal/mol with a favorable energetic benefit of only ΔU = -3.6 kcal/mol and concomitant decrease in entropy and decrease in the partial molar volume of the solute. The fact that the cumulative trends in ΔF_c (Fig. 2B), molecular surface area (Fig. 2E), and partial molar volume (Fig. 2D) are all similar is consistent with the remarkable observation that hydrocarbons and fluorocarbons have similar intrinsic hydrophobicity and that fluorocarbons are more hydrophobic because they offer a larger hydrophobic surface to water (6). This similarity in hydrophobicity is not, however, because the interaction potential with an individual water molecule would be similar, but rather a result of water’s collective hydrogen-bonded network which resists reorganization even in the presence of competing polar forces (22, 23).

Fig. 2.

Plots of various quantities of interest associated with solute transformation in water (298.16 K and ∼1 atm). (A) For the various transformations, ΔF (first column of each set) is the change in the hydration free energy. ΔU (second column of each set) and -TΔS (third column of each set) are the corresponding contributions due to changes in internal energy and entropy respectively. Also shown are standard-error bars calculated using the procedure of Hess (45). (B) Cumulative values of the change in free energy (ΔF_c, solid line), and the energetic (ΔU_c, dashed line) and entropic (-TΔS_c, dotted line) contributions to it for the various states. ΔF_c for each state i (i = 1,5) is the difference in solvation free energy between state i and state 0. (C) End-to-end distance (d_ee, Å), i.e., separation between the terminal carbon atoms for the various states, a measure of stiffness of the solute due to torsional and to steric effects. (D) Partial molar volume (PMV, m³/kmol) for each state. (E) Molecular surface area (MSA, Ų) for each state. All energies are in kcal/mol.

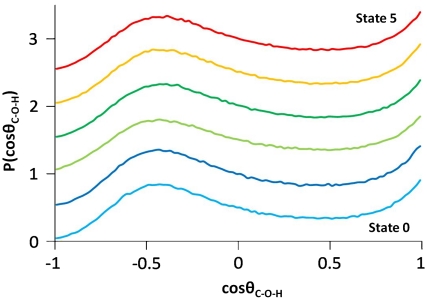
Fig. 3.

Probability density of cos(θ_C-O-H) in the proximal hemispherical solvation shell around the terminal carbon atoms (water O within a C-O separation 1.5 Å beyond the most probable) for the different states, where θ_C-O-H is the angle between the vectors C → O and O → H. Hence the cosine is +1 if the O-H is pointed away from the terminal C and is -1 if the vector points toward terminal C. There are two peaks—one at cos(θ_C-O-H) ∼ 1 (acute angle peak) and the other at cos(θ_C-O-H) ∼ -0.44 (obtuse angle peak). The distribution for each state i is shifted vertically by 0.5i for clarity.

Contact-Angle Calculations—Outline, Results, and Discussion

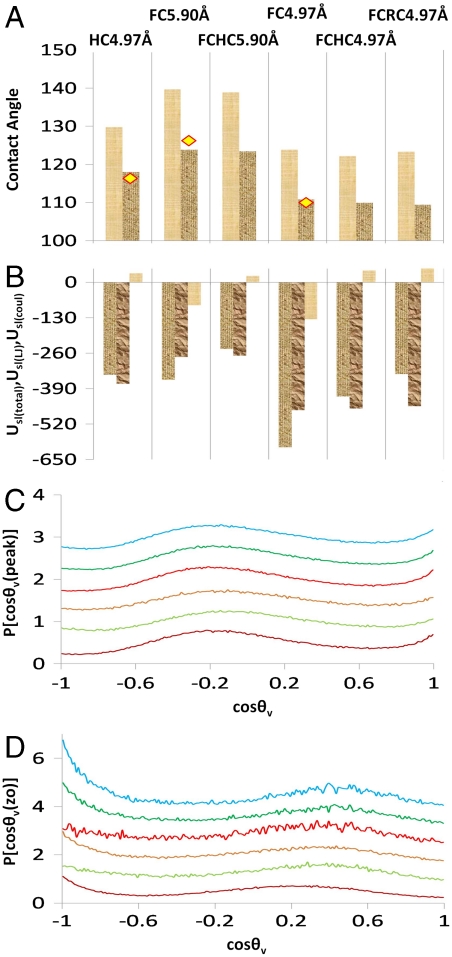
To investigate the isolated effect of a hydrocarbon/fluorocarbon surface with water, we carry out simulations of contact angles because the contact angle is a macroscopic, and hence easily measured, quantity. It is directly related to the interfacial free-energy change of wetting by Young’s relation: γ_SL - γ_SV = γ_LV cos θ. Here γ_LV is the liquid–vapor interfacial tension and θ is the contact angle (see Fig. 4), whereas γ_SL and γ_SV are the solid–liquid and solid–vapor interfacial tensions, respectively. The larger the contact angle, the less favorable is the wetting of the solid by the liquid. In order to compare with the experiments of Graupe et al. (10), which are relevant to our argument, we have simulated a droplet of water in contact with a SAM rather than with a crystalline polymer surface (24, 25). We are then essentially examining the isolated effect of the hydrocarbon/fluorocarbon tips with water; the tips are chemically similar to the lateral surfaces of the isolated molecules just considered. Hydrocarbons are represented by n-dodecanethiol and fluorocarbons by n-perfluorodecanethiol. To develop our understanding, we consider six surfaces among which the principal variable features are chain packing density and bond polarity. Specifically, we consider these SAMs: (i) HC4.97 Å, hydrocarbon thiols at hydrocarbon packing density taken to be that of alkanethiol on gold [i.e., lattice spacing of 4.97 Å (10, 26, 27)]; (ii) FC5.90 Å, fluorocarbon thiols at fluorocarbon packing density [i.e., lattice spacing of 5.9 Å (10)]; (iii) FCHC5.90 Å, fluorocarbon thiols at fluorocarbon density but with partial charges on C and F same as those on the C and H of hydrocarbon; (iv) FC4.97 Å, fluorocarbon but at hydrocarbon density; (v) FCHC4.97 Å, fluorocarbon but at hydrocarbon density and with hydrocarbon charges; and (vi) FCRC4.97 Å, fluorocarbon but at hydrocarbon density and with its partial charge signs reversed.

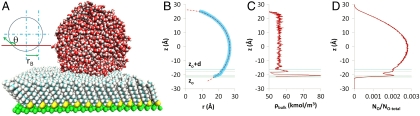
Fig. 4.

A set of figures to illustrate the calculation of contact angles. (A) A visual molecular dynamics visualization of a typical system setup. Here, using space-filling models, a water droplet is shown in contact with perfluorodecanethiol self-assembled monolayer (lattice spacing of 5.9 Å) after 3 ns of simulation time. Also shown is a sketch illustrating the meaning of contact angle (θ). (B) The profile of the liquid–vapor interface of the water droplet (about its center of mass averaged over 4,000 snapshots each 0.5 ps apart) is shown as shaded circles with the z position of a horizontal cross-section of the droplet plotted against the radius (r) of that cross-section. The broken line is the result of the points fitted to a circle. The lowermost solid horizontal line represents the height z_o at which represents the lowermost boundary of the water droplet. The uppermost solid horizontal line is the height (z_o + d) at which the water in the droplet can be said to have attained its bulk density. Hence we have two different ways of defining the contact angle. The broken horizontal lines in between represent the positions of the first and second peak in the density profile of water. (C) The profile of the density of water near the center of the droplet as a function of z position. It is structured at, and near, the solid–liquid interface but quickly attains its limiting value with increasing z. The horizontal lines are the same as for figure B. (D) The fraction of the number of O atoms in the droplet encountered in a z-direction slice 0.1-Å wide. The horizontal lines are the same as for figure B.

Interfacial tensions and corresponding contact angles can be evaluated computationally in alternative ways (28, 29). The contact angle is calculated in each case here by fitting the vapor–liquid interface of the droplet to a circle and taking the slope at the solid–liquid interface. We found no evidence in our droplet data of asphericity, although a highly anisotropic surface can induce such distortions (24). However, for a nanoscale system, as seen in Fig. 4, the macroscopic spherical droplet picture does have a limitation; liquid layering occurs near the interface and the bulk liquid density is attained at a distance d from the interface, which is significant compared to the system size. A macroscopic view would argue for taking the contact angle at a height where solvent bulk has been achieved. The two angles, i.e., θ (at z_o) and θ_d (at z_o + d) are related by cos θ = cos θ_d - d sin θ_d/r_B, where r_B is the radius of the circular liquid–vapor interface at z = z_o + d. It is interesting to note that the equation for line tension for a spherical drop, i.e., cos θ = cos θ_∞ - τ/γ_LV/r_B (30) has a parallel form, where τ is the line tension and θ_∞ is the macroscopic contact angle. We would then have τ = γ_LVd sin θ_d. Here, we take z_o + d at an increment past the second density peak of half the peak-to-peak spacing. The results for the contact angles for the various cases calculated both at z_o and at z_o + d appear in Fig. 5A along with experimental values from Graupe et al. (10) where applicable. Although either set of contact angles yield the same trend, only those calculated at z_o + d match experiment well. Further, using γ_LV = 0.073 N/m for water, or the similar value of 0.064 N/m for SPC/E (simple point charge/extended) (28), at 298.16 K, we have calculated the inferred line-tension values to be of the order 10^-11 N. This value is consistent with the simulated results for water on polyethylene surfaces (25) which is the closest analogue to our system for which we found data.

Fig. 5.

Results of contact-angle calculations. (A) Contact angles for the various cases. The left column is for contact angle taken at z_o and the right for that taken at z_o + d. The sequence of the graphs, from left to right is HC4.97, FC5.90, FCHC5.90, FC4.97, FCHC4.97, and FCRC4.97 Å (see text). The diamonds are centered on the experimentally reported contact angles (10). The reported experimental value for comparison for FC4.97 Å is that for an even carbon number alkyl chain terminating with CF₃, and hence with the dipole pointing outward (10). (B) Water–surface interaction energies (kcal/mol)-U_sl(total) (first column of each set) is the total interaction energy, U_sl(LJ) (middle column) is that due to Lennard-Jones interactions, and U_sl(coul) (third column) is the energy due to coulombic interactions with the surface. (C) Plots of orientational distribution of water O → H vectors’ angle with the vertical (i.e., surface outward normal) for water molecules at a z coordinate within 1 Å of the first density maxima from the solid–liquid interface. The bottommost data are for HC4.97 Å, the next for FC5.90 Å, and so on. (D) Plots of the orientational distribution of water O → H vectors’ angle with the vertical for water molecules at a z coordinate ∼z_o, i.e., very close to the solid–liquid interface.

We can also see from the interaction energy data in Fig. 5B that the contact angle correlates quite well with the LJ interactions of water with the surface and very poorly with the (small) electrostatic interaction. This observation is consistent with experiments that showed little response of contact angles of protic solvents to surface polarity, whereas for polar aprotic solvents, there was great sensitivity (10). We conclude that the only reason a fluorocarbon SAM is more hydrophobic than the hydrocarbon SAM is that the fluorocarbon ligands pack more sparsely (lattice spacing of 5.9 Å) on the surface than the hydrocarbons (lattice spacing of 4.97 Å), and the somewhat more attractive van der Waals interactions due to F atom over H atom cannot offset the reduction in interactions due to the lower density of interaction sites. Correspondingly, if the fluorocarbon were to pack with the same density as the hydrocarbons, the resulting contact angle would be lower than in case of the hydrocarbon; that is, the observed result is the contact angle increases as FC4.97 < HC4.97 < FC5.9 Å. From the solvent orientational distributions (Fig. 5 C and D), it is clear that the structure of water is again substantially independent of the nature of the surface for hydrophobic surfaces. We see that the orientation of water molecules closest to the solid–liquid interface (z ∼ z_o, Fig. 5D) is reversed from a clathrate-type geometry, with one O → H vector pointed straight into the surface [there is a peak at cos θ_v(z_o) ∼ -1] whereas the other vector is nearly tangent to it. This orientation is consistent with what would be expected from a planar hydrophobic surface (23). Also expected is the reversal in orientation for the layer centered on the first density maximum (Fig. 5C).

Conclusion

We have found that the greater hydrophobicity of fluorocarbons over hydrocarbons across geometries is determined by their size. It is generally appreciated that the dispersion forces associated with fluorocarbons are smaller than would be anticipated based on atomic size alone; we find that a fluorinated solute and a fluorinated SAM are then both more hydrophobic than a hydrocarbon solute and a hydrocarbon SAM simply because they are fatter, i.e., have greater molecular cross-sectional area. We have also found that due to the strong tendency of water to minimize disruptions to its hydrogen-bonded network, the structure of water is essentially refractory to the electrostatic nature of hydrophobic solutes/surfaces and free energy of hydration of these surfaces is much more responsive to changes in Lennard-Jones interactions than to electrostatic interactions. This insensitivity need not be the case for nonaqueous polar solvent. The lack of a hydrogen-bonded network also explains the CO₂-philicity of fluorocarbons. CO₂ has a much lower cohesive energy density (0.27 GJ/m³ at 298 K and 500 atm) than water (2.3 GJ/m³ at 298 K and 1 atm) (31), substantially reducing the work of cavity formation. Also, without a hydrogen-bonded network to maintain, quadrupolar CO₂ can benefit more from increased electrostatic interaction with fluorocarbons. It is also clear from the solvation calculations that a solute may have polar moieties and still be hydrophobic if its partial molar volume is large enough. Correspondingly, one strategy used for surfactants for water-in-CO₂ emulsions, which are important for a number of applications (32), can have the hydrophilic-CO₂philic balance in their tails adjusted by increasing polar moieties that convey CO₂-philicity while increasing solvent excluded volume for hydrophobicity (33).

Methods

All calculations are done using GROMACS 4.0 (34). Visualization is done using Visual Molecular Dynamics (35). The free-energy change accompanying a transformation is calculated using standard thermodynamic integration (36) employing 10-point Gaussian quadrature. Each point for the calculation involved 1 ns equilibration and 2 ns production run. For transformation in vacuum, a cubic cell of side 32 Å containing a single solute molecule was used. For transformation in water, a cell of side 34.061 Å containing 1311 SPC/E (37) waters and the solute is used. All solute molecular models are taken from Optimized Potentials for Liquid Simulation (OPLS) (38) except that the electrostatics on fluorocarbons are recalculated using GAMESS [electrostatic potential fitting with the native routine using 6-31G (p, d)] (39) to yield a charge of -0.17e on each F of CF₃ and -0.12e on each F of CF₂. The charge on C of each CF₃/CF₂ group is adjusted so that each group is neutral. Because the transformations are at constant volume, the endpoints of each transformation are at slightly different pressures (differing by at most tens of bars) and the work done to expand to 1 atm, 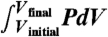, is calculated from V_final in a 1.5 ns production run using the Berendsen barostat (40). For the small change, we use P = aV + C where a and C are constants obtained from (P_initial, V_initial) and (P = 1 atm, V_final). These contributions are, in any case, quite small (≤ 0.1 kcal/mol) and have no impact on any of the discussion or conclusions.

The difference in volume between a cell at P = 1 atm and solute and one at P = 1 atm without solute is used to calculate partial molar volume. The hydrated end states at 1 atm are simulated, at their average volume obtained from the constant pressure simulation, for 1 ns equilibration and 5 ns production times with snapshots taken every 0.5 ps to get endpoint energies, structures, and distribution functions. Molecular surface area of the solute is calculated using the SURFCV code (41, 42). The probe radius used is r_probe = 1.4 Å. Atomic radius (r_atom) of C atoms is taken as 1.5 Å, of H atoms is 1.25 Å, and of F atoms is 1.475 Å. After the atom-fattening step, all H atoms are then considered to have F atom radii. For all calculations, temperature of 298.16 K is enforced using Nose-Hoover thermostat with 0.1 ps time constant, Lennard-Jones interactions are cut off at 10.0 Å, electrostatic contributions are calculated using particle mesh Ewald (PME) (43) with a direct interaction cutoff of 10.0 Å, fourth-order interpolation, grid spacing of 1.2 Å, and a tolerance of 10^-5. A time step of 0.001 ps is employed. The bond constraints for SPC/E water are implemented using the LINCS algorithm (44). The codes for implementing the PME and LINCS and for obtaining the derivatives required for thermodynamic integration at every step of a given simulation are all built into GROMACS 4.0. Convergence and error analysis are done by the method of Hess (45), also using a built-in script.

For contact-angle calculations, a substrate of hexagonally packed LJ particles (ε = 0.226828 kcal/mol, σ = 2.708 Å) with lattice spacing of 2.88 Å serves as a hard wall to anchor and constrain the ligands molecules. The substrate parameters (∼Ag) we use are those inferred from the results of ab initio calculations for silver atoms (46, 47) interacting with xenon (48). The parameters for the thiol are taken from OPLS—except that the charge of F on terminal CF₃ is -0.17e instead of -0.12e. The thiol root atoms (S) and the substrate atoms are rigidly fixed in place. The S atoms are distributed in a hexagonal monolayer ∼3.0 Å above the substrate atoms with lattice spacing that varies with the case. The water droplet is composed of 2,744 SPC/E water molecules. All cross-interactions are determined by Lorentz-Berthelot mixing rules, with arithmetic mean size parameters. The simulation cell is 80 Å in the x and y directions (i.e., along the plane of the substrate), whereas it is 200 Å in the z direction (perpendicular to the plane of the substrate). This periodicity enables use of 3D PME for calculation of electrostatics. The simulations are run in the canonical ensemble and use the same parameters for thermostat, PME, constraints, and LJ cutoffs, time step, etc. as the free-energy simulations. Each simulation is equilibrated for 1 ns followed by a production run of 2 ns. The contact angle is calculated according to a standard procedure (25).