Low-dose, simple, and fast grating-based X-ray phase-contrast imaging

Abstract

Phase sensitive X-ray imaging methods can provide substantially increased contrast over conventional absorption-based imaging and therefore new and otherwise inaccessible information. The use of gratings as optical elements in hard X-ray phase imaging overcomes some of the problems that have impaired the wider use of phase contrast in X-ray radiography and tomography. So far, to separate the phase information from other contributions detected with a grating interferometer, a phase-stepping approach has been considered, which implies the acquisition of multiple radiographic projections. Here we present an innovative, highly sensitive X-ray tomographic phase-contrast imaging approach based on grating interferometry, which extracts the phase-contrast signal without the need of phase stepping. Compared to the existing phase-stepping approach, the main advantages of this new method dubbed “reverse projection” are not only the significantly reduced delivered dose, without the degradation of the image quality, but also the much higher efficiency. The new technique sets the prerequisites for future fast and low-dose phase-contrast imaging methods, fundamental for imaging biological specimens and in vivo studies.

Over the last few decades X-ray imaging has experienced a true revolution. The most striking advancement has been the production of coherent X-ray beams with their intrinsic capability of generating interference signals and, as a consequence, providing access to phase information within the investigated sample. This fact has been very stimulating for the X-ray-imaging community, which had been continually challenged by the frustrating question of how to increase the contrast in X-ray images without increasing the dose imparted to a specimen. It is well known that, different from conventional visible light, the refractive index in X-ray optics is very close to and smaller than unity. In first approximation, for a small and negligible anisotropy in the medium, the index of refraction characterizing the optical properties of a tissue can be expressed—including X-ray absorption—with its complex form: n = 1-δ-iβ where δ is the decrement of the real part of the refractive index, responsible for the phase shift, while the imaginary part β describes the absorption property of the tissue. In conventional absorption-based radiography, the X-ray phase shift information is usually not used for image reconstruction. However, at photon energies greater than 10 keV and for soft tissues (made up of low-Z elements), the phase shift term plays a more prominent role than the attenuation term because δ is typically three orders of magnitude larger than β (1). As a consequence, phase-contrast modalities can generate significantly greater image contrast compared to conventional, absorption-based radiography. In fact, far from absorption edges, δ is inversely proportional to the square of the X-ray energy while β decreases as the fourth power of it. Consequently, phase signals can be obtained with much lower dose deposition than absorption, a very important issue when radiation damage has to be taken into account such as in biological samples or in living systems.

During the last 40 years, several methods have been developed to sense the phase variations induced by an object. They differ vastly in the nature of the signal recorded, the experimental setup, and the requirements on the illuminating radiation (especially its spatial coherence and monochromaticity). They can be classified into interferometric methods (2–4), free-space propagation techniques (5–9), setup using an analyzer crystal (10–12), or grating interferometers (13–15). The crystal interferometer uses a Bragg reflection as beam splitter, and the recorded signal measures the phase shift (Φ) directly. With the analyzer-based imaging method, the Bragg crystal selects the momentum, and therefore the first spatial derivative of the phase (or phase gradient) (∇Φ) is detected. For propagation-based phase imaging, where the measured quantity corresponds to the second derivative of the phase (ΔΦ), the in-line method is often used, where the effects of phase contrast become evident—due to the intrinsic coherent nature of the beam—as the sample-detector distance is increased. Although some of them yield excellent results for specific problems (4, 6, 11), none of them has so far found wide applications in medical or industrial areas, which typically require the use of a laboratory X-ray source, a large field of view (up to several centimeters), and a reasonably compact setup.

The use of gratings as optical elements can overcome the problems that have impaired the wider use of phase contrast in X-ray radiography and tomography so far. Momose et al. (14) first proposed and demonstrated the feasibility of two-grating interferometry in the hard X-ray region using a phase transmission grating and an absorption transmission grating made by gold stripes on glass plates. This work has been extended to achieve a 3D tomographic phase reconstruction using a hard X-ray two-grating interferometer (15). Recently, three-grating interferometry in the hard X-ray region with low-brilliance tube-based X-ray sources has been demonstrated (16). Such experiment can be considered a breakthrough in X-ray imaging because it demonstrated that phase contrast can be efficiently performed with a conventional, low-brilliance X-ray source with an enormous potential for applications in biology, medicine, nondestructive testing, food inspection, archaeometry, or security devices. In fact, a grating interferometer setup is mechanically robust, easy to align, and almost insensitive to mechanical drift. Its requirements on temporal coherence (ΔE/E ∼ 0.1–0.2) and spatial coherence (a few microns) are moderate, i.e., easily scaled up to large fields of view. In addition, because grating interferometry is particularly sensitive to shallow phase gradients, it is ideal technique for soft tissue studies in the fields of medical and biological imaging. These characteristics make grating interferometry superior to other phase-contrast approaches (2–12) and set the prerequisites for a broad use of phase-contrast X-ray radiography and tomography.

To separate the phase information from other contributions, a phase-stepping approach is normally adopted. One of the gratings is scanned transversely to the incident beam while acquiring multiple projections. The intensity signal at each pixel in the detector plane oscillates as a function of the displacement, and the phase of this intensity oscillation can be directly linked to the wave-front phase profile and to the decrement of the real part δ of the object’s refractive index (17). However, during phase stepping, the sample is supposed to be static, and the resulting poor time resolution is one of the major drawbacks of this method. Even more critical is the fact that phase stepping necessarily implies multiple exposures and, even though such exposures might be acquired each at very low dose (therefore exploiting the dose-fractionation effect), it is clear that a method that would extract the phase information without the need of multiple stepping would be a breakthrough enabling fast, low-dose, highly sensitive (phase-contrast) X-ray imaging.

In this work, we demonstrate such an alternative approach, which extracts the phase information without the need of a stepping procedure, thus overcoming limitations of both data acquisition speed and dose imparted to the specimen. The presented unique method bases its strength on a previously undescribed manipulation of the phase relation between different X-ray projections and does not require any additional constrain (e.g., coherence or monochromaticity) with respect to the phase-stepping approach. This means that the two major drawbacks (low speed and multiple exposures) of the phase-stepping technique are removed. For practical reasons, in this work, we used a synchrotron source to demonstrate our approach. However, we want to point out that the application of our method with conventional, low-brilliance X-ray sources is straightforward as soon as a third grating is placed close to the source (16). The source grating creates an array of slit sources, and the spatial coherence of each slit source is sufficient for the image formation process. The phase contrast of all slit sources will intensify each other on the condition that the period of the array source matches that of the analyzer grating. Furthermore, because our approach is as simple and fast as conventional (absorption-based) X-ray radiography and tomography, it can be readily implemented to currently existing X-ray imaging systems.

Results

The innovative approach presented here relies on the physical similarities between a crystal analyzer-based system and a grating interferometer. Both techniques record refraction angle signals and (analogously to the rocking curve of a crystal analyzer) the properties of the intensity curve (see Fig. 1) can be exploited to fully describe the performance of a grating interferometer. The refraction angle, i.e., the phase information of the sample, can be extracted by setting the gratings at the position where the intensity curve follows a linear behavior. In fact, according to the aforementioned analogy, the intensity recorded by a detector positioned after the grating interferometer can be expressed (see equation 1 in ref. 18) as:

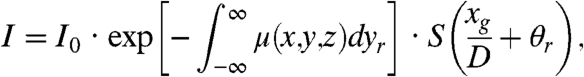[1]

where μ is the linear absorption coefficient, x_g denotes the relative displacement between the phase grating and the analyzer grating along the direction perpendicular to the incoming beam, θ_r is the refraction angle, D is the distance between the phase and the analyzer grating, S(x_g/D) is the shifting curve. For the sake of simplicity, the scattering contribution (19, 20)—which would induce a weak increment of the background noise—is neglected. (x_r,y_r,z) are the coordinates of the reference frame associated to the X-ray beam and (x,y,z) those associated with the sample. The two frames are linked by the rotation matrix

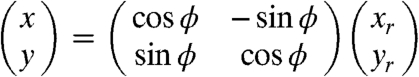[2]

being ϕ the rotation angle between the x_r the x-axis around the z-axis.

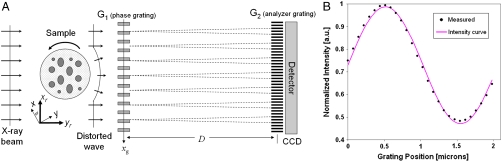
Fig. 1.

Working principle of the grating interferometer. (A) Through the Talbot effect, a periodic interference pattern is formed behind the phase grating (G1), in the plane of the analyzer grating (G2) (17). (B) Plot of the intensity oscillation (shifting curve) as a function of the grating position x_g for a detector pixel over one period of the analyzer grating. The dots correspond to the measured values (normalized to unit) while the gray line shows a sinusoidal fit.

With a good approximation, the behavior of the shifting curve near its half slope may be considered linear so that, if θ_r ≤ p₂/4D, p₂ is the period of the analyzer grating, S(x_g/D + θ_r)can be replaced by a first-order Taylor expansion.

According to equation 2 in ref. 18, we can write:

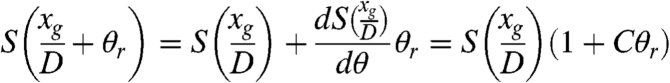[3]

where 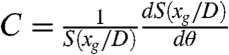is a constant.

The refraction angle in the X–Y plane (Fig. 1A) is determined by the line integral of the first-order derivative of the refractive index along the X-ray path (13), and it may be written as:

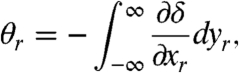[4]

where δ corresponds to the decrement of the real part of the refractive index of the sample as mentioned in the introduction. Substituting Eqs. 3 and 4 into Eq. 1, the projected image for a grating interferometer can be described by:

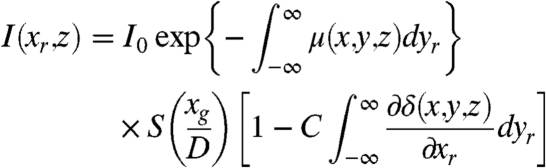[5]

where μ is a scalar and therefore rotational-invariant, while ∂δ/∂x_r strongly depends on the direction along which it is measured (21–22).

The projected image at the rotation angles ϕ and its corresponding reverse image at ϕ + π can be written as:

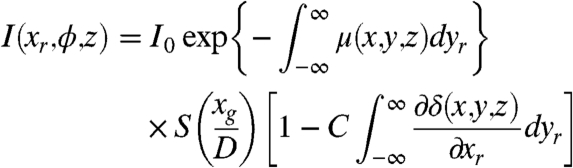[6]

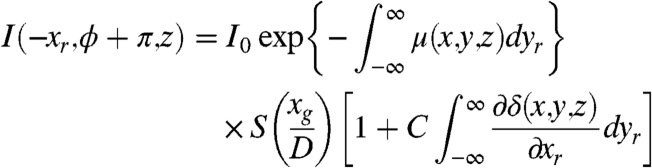[7]

The absorption signal can be obtained from the two projected images by the sum of Eqs. 6 and 7 and solving the Beer–Lambert relationship (19, 20), i.e.,

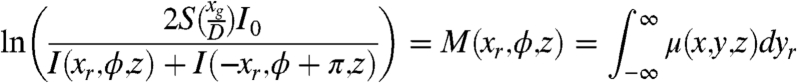[8]

In the same way, the angle of refraction can be obtained by a proper combination of Eqs. 6 and 7, as shown in the following expression (19, 20):

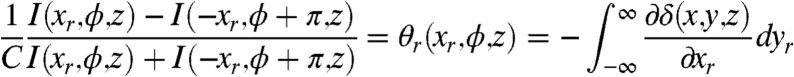[9]

According to fundamentals of computed tomography reconstruction, i.e., the Fourier Slice Theorem, the absorption coefficient as well as the refractive index can be easily obtained by the inverse Fourier Transform and a Hilbert filter:

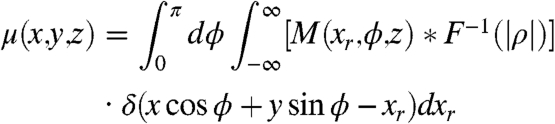[10]

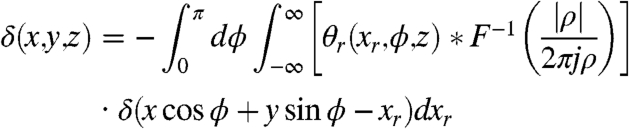[11]

where ρ is the spatial frequency and F^-1denotes the inverse Fourier transform.

Based on Eqs. 8 and 9, we introduce here an original acquisition protocol, dubbed the “reverse-projection” (RP) method. Before positioning the sample, we scan the phase grating or the analyzer grating along the transverse direction x_g over one period of the analyzer grating and record the normalized intensity I/I₀ on the detector versus the angle x_g/D. Actually, we collect the shifting curve S(x_g/D) and then set the grating interferometer at the center of the linear region of the shifting curve by positioning the phase grating or the analyzer grating at x_g = p₂/4 or x_g = -p₂/4. The experimental procedure can be described in three steps as follows:

1. place the sample in front of or behind the phase grating and collect m angular projections of the sample during a rotation of 360°,

2. extract M and θ_r according to Eqs. 8 and 9

3. reconstruct the absorption coefficient or the refractive index using the filtered back-projection. Therefore, the total number of acquired projection images is m.

On the contrary, the phase-stepping (PS) acquisition is based on four steps:

1. place the sample in front of or behind the phase grating, scan one of the two gratings along the transverse direction x_g, e.g., consider n points within one period of the analyzer grating and record one projection image at each point,

2. repeat the step (i) for a total of m/2 times within a sample rotation of 180°,

3. extract the gradient signal via the Fourier analysis of the intensity signal and

4. reconstruct the phase via a filtered back-projection.

Using the latter method, the total number of acquired projections images is n*m/2. As a consequence, if compared to the PS method the total number of projections required by the RP protocol is reduced by a factor of n/2. Even though the statistical noise can be reduced by averaging multiple images in the PS approach, the mechanical error induced by the phase-stepping procedure is increased, resulting in a deterioration of the image quality. Further, the signal recorded with the RP method is proportional to the refraction angle in the linear region of the shifting curve, no matter how small the refraction angle is. On the other hand, PS cannot detect a refraction angle that is smaller than one phase step.

We validated our method by performing both PS and RP experiments at the TOMCAT beamline of the Swiss Light Source at the Paul Scherrer Institut (23). We have operated the interferometer described in ref. 24 at 25 keV and in the third Talbot distance. In this configuration, the visibility of the interferometer has been measured to be 30%.

Imaging Weakly Absorbing Samples.

In a first case study, we investigated two different samples: a rat brain first fixed in 4% paraformaldehyde (PFA) and then embedded in paraffin and a demineralized mouse joint, fixed only in a phosphate buffer solution (PBS) (no embedding). We used the mouse joint and the rat brain to test the reconstruction method both on small (< 4 mm) and large (> 10 mm) samples. Both specimens are weakly absorbing objects and therefore ideal candidates for phase-contrast imaging. Reconstructions based on the two methods (PS and RP) are shown in Figs. 2 and 3, while experimental parameters are summarized in Table 1.

Fig. 2.

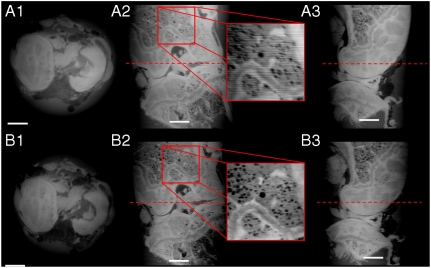
Tomographic reconstructions of a demineralized mouse joint, acquired at a voxel size of 3.5 × 3.5 × 3.5 μm³. A1 to A3 show the data obtained with the phase-stepping (PS) protocol, while B1 to B3 the reconstruction using the reverse-projection (RP) method. A1 and B1 shows an axial slice: B1 is sharper than A1, and there are no ring artifacts. A2 and B2 depict a coronal slice through the joint, clearly showing that the RP protocol is less sensitive to typical horizontal stripes artifacts observed with the PS method (see enlarged inset). A3 and B3 show a sagittal view through the joint. The dotted lines mark the locations where the axial views (A1 and B1) have been taken. Scale bar, 500 microns.

Fig. 3.

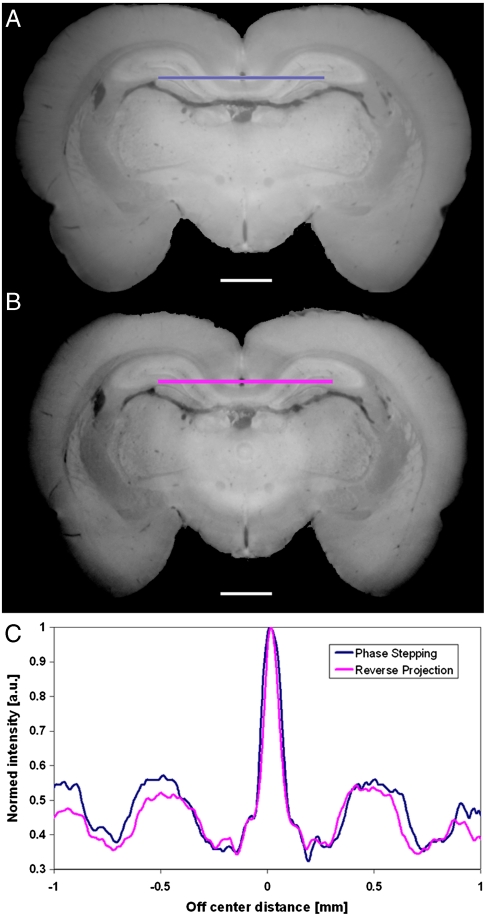
Coronal slice of a rat brain, obtained after tomographic reconstruction using PS (A) and the RP (B) protocol. Qualitatively, both reconstructions are very similar. In B the effects of the grating imperfection (ring artifacts), as expected, are more evident. The plot in C shows a quantitative comparison between two line profiles extracted at the position marked by the color bars (hippocampus region). Scale bar, 1 mm.

Table 1.

Experimental parameters for the tomographic scans of the three investigated samples: a rat brain (4% PFA, paraffin embedded), a (demineralized) mouse joint in PBS, and a rat paw (4% PFA)

	Mouse joint		Rat brain		Rat paw
	Phase Stepping	Reverse projection	Phase Stepping	Reverse projection	Phase Stepping	Reverse projection
Rotation	0–180°	0–360°	0–180°	0–360°	0–180°	0–360°
Pixel size [μm]	3.5 × 3.5	3.5 × 3.5	11.2 × 11.2	11.2 × 11.2	7.4 × 7.4	7.4 × 7.4
Field of view [mm]	3.58 × 3.58	3.58 × 3.58	11.45 × 3.6*	11.45 × 3.6	15.5 × 3.6	15.5 × 3.6
Angl. proj.	181	361	361	721	501	1001
Phase steps	9	1	9	1	9	1
Single exposure [ms]	200	200	200	200	60	60
Total exposure (s)	325	72	650	144	270	60

^*The optical system always produces field of views with a square shape. However, along the vertical direction the size of the field of view is reduced and limited by the vertical size of the beam (approximately 3.6 mm at 25 keV and at 25 m from the source).

Fig. 2 shows axial, sagittal, and coronal views of a mouse joint obtained with both PS and RP protocols (Table 1). The joint was immersed and fixed in an Eppendorf vial containing PBS to avoid any movements during the acquisition. A qualitative comparison of the images clearly shows that RP reconstructions are comparable to those obtained with the PS approach. Moreover, looking at the inset shown in Fig. 2 A2 and B2 the RP slice appears to be sharper than the PS reconstructions. This can be explained by the fact that the shifting curve is directly proportional to the refraction angle and that this—in the RP protocol—is obtained by a simple subtraction of a reference image (with no sample) from the paired images described in Eq. 9. In addition, because with the RP method no phase stepping is required, the system is less sensitive to mechanical instabilities.

However, a careful analysis of the reconstructed images reveals that the RP protocol imposes more stringent requirements on gratings, i.e., it needs better full-field uniformity and lower local grating imperfections than those used for the PS method. These imperfections may induce small ring-like artifacts in the RP-reconstructed slices that are less evident in PS reconstructions (see SI Text). However, recent improvements in microelectronic engineering resulted in novel methods for manufacturing periodic nanostructures (25, 26). With these novel techniques—in particular for large fields of view—a better control on the duty-cycle as well as on the uniformity of the grating can be obtained. With these nanofabrication advancements it will therefore soon be possible to overcome the aforementioned problems and achieve artifact-free RP-reconstructed slices.

Ring-like artifacts due to grating imperfections are not present in the images of Fig. 2, because the field of view is relatively small (3.58 × 3.58 mm²), and within such a small region the quality of the gratings can be considered highly homogeneous.

The largest investigated sample, a rat brain, was mounted vertically on the flat surface of the sample support to match the horizontal field of view of the detector system. The vertical sample arrangement also enabled a direct reconstruction of coronal slices through the sample, an approach very useful when trying to identify anatomical brain regions (Fig. 3). The height of the sample was larger than the vertical height of the beam and therefore four scans have been collected along the vertical direction to image the whole brain (Fig. S1). To achieve phase matching between sample and surroundings (24), we used an aquarium bath filled with room temperature liquid paraffin (chemical formula C_nH_2n+2 where n = 5–17, density ≈ 0.7 g cm^-3). For large samples too, a qualitative comparison of the images clearly shows that the RP reconstruction is as good as the one obtained with the PS approach. In addition, a line profile taken at the level of the hippocampus (see Fig. 3C) shows a quantitative good agreement between RP and PS approaches.

Imaging Strongly Absorbing Samples.

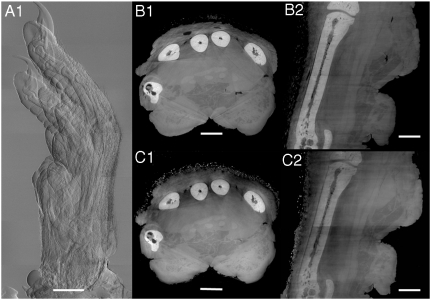
In the second case, the method has been validated using a more realistic sample, namely a specimen containing both soft and hard tissue. For this purpose, we investigated a rat paw (containing both bone and muscles) that was only fixed in 4% PFA. This fixation procedure is frequently used to maintain biological samples in a status as close as possible to their natural, original conditions. The rat paw was also mounted vertically in order to best match the horizontal field of view of the detector. Seven stacked scans were necessary to image the full sample volume.

The measurement of the rat paw was the most challenging experiment because the sample has been measured in air. This usually causes large phase jumps at the air-specimen interface and explains the “star” artifacts visible in Fig. 4B1 and, less serious, in Fig. 4C1. This is because the shifting curve is saturated when θ_r≥p₂/4D and, as a consequence, the RP method is not very sensitive to large refraction angles. This is not the case for the PS method, which has to cope with angles as large as θ_r ≤ p₂/2D. So far, no evidence in the literature reported that a realistic and complex biological sample (no special preparation, e.g. bone demineralization) has been investigated with grating interferometry at such a high resolution.

Fig. 4.

Imaging of a rat paw. (A) Differential phase-contrast radiography (7 stacks, RP protocol), (B1) axial and (B2) coronal slices through the paw acquired with the PS protocol, (C1) axial and (C2) coronal slices through the same sample obtained with the RP protocol. Structural details of both soft tissue (muscles, fat) and hard tissue (bone) are well visible. Scale bars, 2 mm (A), 1 mm (B1–2 and C1–2).

Discussion

In this manuscript we introduced a previously undescribed approach for fast and low-dose extraction of both the absorption coefficient and the refractive index of a sample using a grating interferometer. We demonstrated that this unique approach yields comparable information to the established phase-stepping technique but with a reduction factor of n/2 in the total dose released to the sample. This number might appear modest, but if one considers that, up to now, phase-stepping scans of acceptable quality have been reported only with n≥4, this means that, in the worst case, the RP method allows a dose reduction of at least 50%. For the X-ray imaging community, daily engaged in minimizing dose delivery to critical samples, this represents a significant step forward. Moreover, the RP approach makes high-sensitivity phase-contrast computed tomography (CT) as straightforward as conventional, absorption-based CT. We would like to underline that from Figs. 2, 3, and 4, it appears clear that such dose reduction does not come at the cost of image quality. Namely, according to the dose-fractionation theorem (27), the total dose required to achieve statistical significance for each voxel of a computed 3D reconstruction (tomogram) is the same as that required to obtain a single 2D image (projection) of that isolated voxel at the same level of statistical significance. Thus, a statistically significant 3D image can be computed from statistically insignificant projections, as long as the total dose distributed among these projections is sufficient to result in a statistically significant projection if the entire dose would be applied to only one image.

In this manuscript, we show that the RP method works well with parallel beam geometries, especially on a synchrotron beamline, where the illumination is almost ideal and only two gratings are used. However, we would like to underline that the method can also be well combined with laboratory X-ray sources, where an additional absorption grating G₀ is employed and positioned immediately in front of the source (16). The source grating G₀ splits the X-ray source into an array of slit sources. The width of the slit source is chosen approximately to provide sufficient spatial coherence for the image formation process. For each slit source, the principle of image formation and contrast generation is about the same as that of synchrotron sources, although the available flux is reduced by several orders of magnitude. To ensure a constructive contribution of each slit source to the final image formation, the geometry of the setup should satisfy the condition p₀ = p₂ × L/D, where L and D are the distances between G₀ and G₁ and between G₁ and G₂, respectively. The total source size s only determines the final spatial resolution, which is given by s × D/L. The source array decouples spatial resolution from spatial coherence and allows the use of X-ray illumination with coherence lengths as small as ξ_s = λL/s ∼ 10^-8 m in both directions (at a tolerated spatial resolution sD/L). Under these coherence requirements, differential phase contrast images can be easily obtained. Because the RP method essentially consists of a manipulation of such X-ray projections, it is obvious that its implementation on laboratory X-ray sources is straightforward.

Probably the most challenging application of the RP protocol will be in vivo phase-contrast imaging. With the advent of new highly efficient and high speed detectors (28), it will be possible to acquire the same amount of data within a fraction of a second. We estimate that it will be realistic to obtain a full tomographic dataset with the RP protocol with a total exposure time of 2–3 s. This, together with the ongoing efforts regarding robust and reliable iterative reconstruction algorithms (29), requiring a significant smaller amount of projections, can push the total acquisition time below 1 s and hence open the possibility of phase-contrast tomographic microscopy of small living animals. It is important to note here that fast, low-dose phase-contrast imaging can be performed only with the RP protocol.

Another very challenging application of the RP protocol will be the quantitative 3D description of the scattering signal. This image contrast is generated by small-angle scattering within the sample, and it provides complementary and otherwise inaccessible structural information at micrometer and submicrometer length scale (30). However, the signal is not rotational-invariant, and therefore it will be very challenging to quantitatively obtain such information in 3D.

Further developments will concern the manufacturing of optimized gratings for high X-ray energies leading to the implementation of the RP protocol in new medical X-ray CT scanners that would offer a significant increase in soft tissue sensitivity, a characteristic now provided (at much lower resolutions, however) only by much more expensive techniques such as magnetic resonance imaging.

Finally, we would like to point our that this approach is not limited to X-ray imaging and may be easily generalized to other methods such as grating based neutron phase imaging (31) and visible light differential interference contrast (DIC) microscopy (32), where a similar shifting curve is considered and a quantitative phase description appears possible.