Optimally designed nanolayered metal-dielectric particles as probes for massively multiplexed and ultrasensitive molecular assays

Abstract

An outstanding challenge in biomedical sciences is to devise a palette of molecular probes that can enable simultaneous and quantitative imaging of tens to hundreds of species down to ultralow concentrations. Addressing this need using surface-enhanced Raman scattering-based probes is potentially possible. Here, we theorize a rational design and optimization strategy to obtain reproducible probes using nanospheres with alternating metal and reporter-filled dielectric layers. The isolation of reporter molecules from metal surfaces suppresses chemical enhancement, and consequently signal enhancements are determined by electromagnetic effects alone. This strategy synergistically couples interstitial surface plasmons and permits the use of almost any molecule as a reporter by eliminating the need for surface attachment. Genetic algorithms are employed to optimize the layer dimensions to provide controllable enhancements exceeding 11 orders of magnitude and of single molecule sensitivity for nonresonant and resonant reporters, respectively. The strategy also provides several other opportunities, including a facile route to tuning the response of these structures to be spectrally flat and localization of the enhancement within a specific volume inside or outside the probe. The spectrally uniform enhancement for multiple excitation wavelengths and for different shifts enables generalized probes, wheras enhancement tuning permits a large dynamic range by suppression of enhancements from outside the probe. Combined, these theoretical calculations open the door for a set of reproducible and robust probes with controlled sensitivity for molecular sensing over a concentration range of over 20 orders of magnitude.

Surface-enhanced Raman scattering (1) (SERS)-based probes, consisting of nanostructured particles, are strongly emerging for biomedical applications. SERS-based probes (2, 3) are exceptionally attractive as they offer quantitative enhancement of signal with facile readout (4, 5), extensively multiplexed imaging (6), and ultrasensitive assays (7, 8)—but not all at the same time. The SERS effect is typically prominent in nanoscale metal-dielectric environments in which the signal of a proximal organic molecule can be rationally tailored (9) and enhanced to the extent that single molecules may be detected (10, 11). Hence, SERS probes typically contain nanoscale metallic structures and organic molecules (12) that act as a quantitative reporter for the presence of the probe. The signal of this reporter is greatly enhanced to transduce biochemical species of low concentration at the molecular (13), cellular (14), and tissue levels (15, 16) to measurable signals. The achieved enhancement depends on the reporters’ molecular characteristics as well as nanoscale size, shape, geometry, local aggregation state, and surface characteristics of the metal. These parameters can potentially be controlled to tune the reporters’ signal, especially to maximize sensitivity of detection. Controlling and tuning the enhancement of the reporter’s signal, however, is a major ongoing challenge. Given the large number of factors influencing enhancement, designing particles for specific enhancement levels remains an active theoretical challenge while simultaneously controlling variability in their response remains a practical hurdle. Both aspects are actually closely linked. Variability in SERS signal arises due to the synergistic effects of the metal’s atomic mobility (17), surface reorganization (18), and the reporter’s surface mobility. The net result is an unpredictable variation in enhancement, including blinking (19) or “hot spots” (20). Indeed, the intractability of controlling enhancement has led to theorization of a “SERS-uncertainty principle” (21) and a practical choice between (a) unstructured colloids providing an exceptionally large (22, 23) but uncontrolled enhancement [up to single molecule level (24)] and uncertain spatial localization or (b) well-defined and controlled probes using self-assembling monolayer reporters (25) but of lower enhancement and limited reporter diversity.

Variability in signal intensities (19) of a nanoparticle population (26) can be reduced, for example, by using self-assembled monolayers, whereas resonant dyes (27, 28) can be employed for ultrasensitive applications. These specialized remedies, however, are not conducive to designing a palette of reliable probes for high throughput and ultrasensitive multiplexing. Although the utility of controlled nanostructures on making the SERS effect usable (29) is now undisputed, a rational framework to design generalized SERS probes for a desired enhancement level, spectral selectivity, and size is lacking. In turn, this limits our capability to design assays in terms of both multiplexing and sensitivity based on theoretical models. In modeling probes to tailor SERS enhancement, two mechanisms—electromagnetic and chemical—are generally invoked. Electromagnetic enhancement (EE) is now well understood (30) and is usually larger compared to the chemical enhancement (CE) (31). CE mechanisms continue to be a subject of much research (32). Since the EE is larger, it is beneficial to focus on it in designing optimal structures. In general, high EE is observed for reporters confined between metal domains (33). It has been suggested that alternating dielectric and metal shells around a metal sphere could lead to a high EE effect at the core surface (34), and alternating metal and dielectric shells around a dielectric core could lead to a high EE effect at the shell surfaces (35). The potential of such multishell construct for designing and controlling SERS for sensing, however, has been surprisingly underappreciated though it has received attention as a method to tune scattering and plasmon-related absorption (36). Multishell spheres can be considered to be a spherically symmetric class of nanolayered alternating metal-dielectric probes (nano-LAMPs). Spherical nano-LAMPs are not only attractive for their directionally invariant response but also serve as a convenient model to study critical issues in designing SERS-based probes. Here, we propose the use of spherical nano-LAMPs as a means to designing SERS probes with controlled enhancement and exceptional multiplexing capability. A theoretical model is used to predict the limits of enhancement as a function of probe size and examine the spectral response of designed structures.

Results

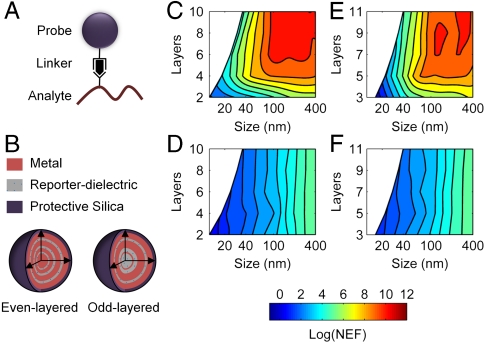
The schematic use of nano-LAMPs is illustrated in Fig. 1A. The SERS probe’s “tail” links to specific molecular analytes of biochemical interest and transduces its concentration. The SERS probe’s “head” consists of nanostructured metal, dielectric, and reporter components. The spectral response of the reporter is enhanced and recorded. The probe head (Fig. 1B) in our proposed configuration consists of dielectric layers with embedded reporter molecules alternating with metal layers. Several features of this configuration are important and help narrow the scope of the theoretical model. First, the dielectric embedment shields reporter molecules from direct contact with the metal surfaces and reduces CE to negligible levels. Second, probes are modeled with a protective outer silica shell for biocompatibility as well as shielding molecules outside the probe from enhancement (37). Since the outer layer is fixed, third, odd number-layered LAMPs will necessarily have a dielectric core, whereas even number-layered LAMPs will have a metal core. Finally, the probe’s spherical symmetry ensures enhancement uniformity with respect to the direction of illuminating radiation and likely simplifies fabrication. Hence, the analyte concentration can be directly related to the signal arising from the probe.

Fig. 1.

Structure and electromagnetic characteristics of nano-LAMPs. (A) Typical application of LAMPs. (B) Nano-LAMP configurations for odd and even number of layers. LAMPs with two layers have reporter embedded in protective outer layer, whereas all others have a protective, unlabeled outermost layer. The maximum NEF for even (C) and odd (E) layered silver-silica LAMPs of different sizes for 785-nm excitation (other wavelengths are shown in Fig. S2). (d, f) Purely numerical enhancement is significantly smaller; hence, the net amplification in signal arises from a couple of the NE and EE. The color bar code for C, D, E, and F is given below D and F.

If there were no SERS enhancement within the probe, a simple numerical enhancement (NE) would still result as a large number of molecules could be placed within the probe for every analyte molecule. The enhancement here, however, arises from the sum of the surface-enhanced signal arising from every reporter molecule in the probe. To quantify signal enhancement, hence, we define a net enhancement factor (NEF) as the ratio of a probes’ total Raman signal to that of a single analyte molecule. Without loss of generality, we can assume that the analyte and unenhanced reporter have equivalent spectra and do not consider resonance Raman enhancement (RRE). Assuming that the reporter is uniformly distributed in the dielectric layers at low concentration, the NEF is defined by the volumetric integral as

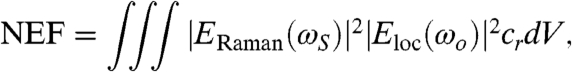[1]

where E_Raman is the electric field at the shifted frequency ω_s, E_loc is the field at the incident laser frequency ω_o, c_r is the concentration of reporter, and V is the volume of the dielectric reporter. The low concentration of the reporter reduces directly the NEF but is essential to prevent variability arising from surface adsorption. Following the treatment considered earlier (38), the EE for each reporter molecule scales as G = |E_Raman(ω_S)|²|E_loc(ω_o)|² ≈ |E_loc|⁴. Hence, the task is reduced to determining the local electric field at all locations within the probe, which is calculated using Mie theory for multilayered spheres as detailed in Methods (and Fig. S1). In this report, for the purposes of demonstrative calculations, we discuss the NEFs achievable with silver-silica nano-LAMPs. For a given nano-LAMP size, thinner metal shells allow larger dielectric shells (and higher reporter loading). Thin metal shells, however, result in a smaller mean free path for electrons that dampens and broadens the surface plasmon resonances (smaller EE). Thicker metal shells result in higher fields (larger EE) but smaller dielectric volumes (lower reporter loading) and higher metal absorption losses. The ultimate constraints on shell sizes, further, are determined by common fabrication limits of nanostructures (39, 40). The problem of determining enhancement for any LAMP structure is, thus, bounded. We systematically maximized and minimized the enhancement of probes of different diameters, at different excitation wavelengths, using genetic algorithms (GAs), as detailed in Methods (41).

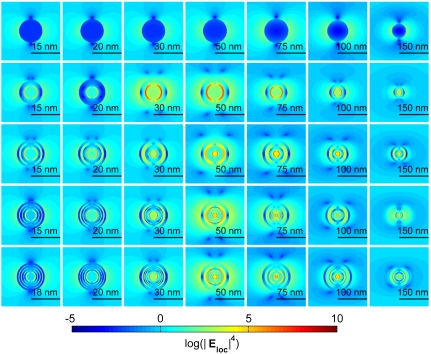
Each LAMP size can have even or odd layers. The thickness of any given layer in an optimized structure then depends on the overall configuration of the LAMP to maximize the counteracting effects arising from coupled plasmonic interactions and reporter loading. Optimized NEFs, hence, depend on both the total probe size (R) and the number of layers (L) for odd- or even-layered LAMPs, as shown in . 1 C and E. The contribution of reporter loading, or NE, is simply linear as shown in . 1 D and F and is much lower than the overall NEF. Hence, the enhanced probe signal arises primarily from the EE and not simply from more reporters per analyte. From . 1 C and E, it can be seen that the enhancement in signal achieves a plateau at ∼100 nm (for 785-nm excitation). A distribution of the enhancement within LAMPs (Fig. 2 and Fig. S3) indicates that the optimal structure reorganizes the surface plasmons to create local hot spots with a high NEF density at the core and appreciable contributions from elsewhere. This interplay of molecular and plasmon density determines the NEF. Interestingly, enhancement beyond a critical size is not predicted to improve by the complexity of additional layers or loading. The largest size of an optimal SERS probe, hence, is bounded by enhancement considerations, whereas the lower size limit is bounded by fabrication constraints. The desired probe size within this size range is likely dependent on the application and may be determined by considerations of fabrication, toxicity, or uptake. For example, in human cervical cancer cells (42), 50-nm sized gold spheres were found to be taken up more quickly compared to other sizes in 10- to 100-nm range. For a given size, then, SERS enhancement is bounded and depends on the number of layers. Hence, both complexity of potential nano-LAMPS and their sizes are predicted to be bounded, providing practitioners in this area an operating window for particles’ synthesis and use.

Fig. 2.

Enhancement distributions in the incident plane of illumination for even-layered silver-silica LAMPs of various configurations that are designed to maximize enhancements at an excitation wavelength of 785 nm. From top to bottom, the number of layers increases from 2 to 10. From left to right the total size increases as shown.

We also note that NEFs of ∼10¹² can be achieved for ordinary, nonresonant organic reporters. This availability is substantially higher than that encountered in using self-assembled monolayers (SAMs) for consistent CE or resonant dyes in simple geometries. The elimination of CE here is counterintuitive and would likely have been detrimental to enhancement, but structuring the probe balances the loss by enabling higher EE. Hence, consistency of probe response is freed of the constraints of using reporters that form SAMs. Further, as opposed to using resonant dyes in simple geometries, structuring of the particle can be used to obtain large enhancements. Hence, the probe is freed of the constraint of using a reporter resonant at the excitation frequency. The release of these two constraints considerably enhances the multiplexing capability of SERS probes as almost any organic molecule is now enabled to be used as a reporter and can be used to provide desired enhancements, subject only to the constraints in Fig. 1. Further increases beyond the upper limits of Fig. 1 are also possible following the conventional route of RRE. For example, a NEF of ∼10⁸ is attained at 785-nm excitation for a probe of size 50 nm by using four layers. Using a resonant dye at the same excitation frequency as a reporter would lead to NEFs of ∼10¹⁴, levels that allow for assaying up to single molecule levels. As opposed to the localization of molecules within nanoscale interstitial spaces, hence, the LAMP configuration can provide single molecule sensitivity for molecules outside the probe. Finally, most analytes can be tagged using existing linking mechanisms such as antibody-antigen, cDNA binding, and probe functionalization, thus generalizing the sensing capabilities of LAMPs.

While the capability required for single molecule assays and large-scale multiplexing will be possible with LAMPs, measuring multiple epitopes in biological samples often requires a large concentration range to be measured. Hence, tunable and large NEFs must be coaddressed with the challenge of devising a large dynamic range. Just as we enhanced the signal, we optimize the EE to quench (43) the Raman signal. Thus, the response of a particularly abundant analyte can be reduced, whereas a sparse analyte can be enhanced to measure both on the same platform and during the same experiment. Examining quenching as a function of size using GAs, we determined that quenching can be achieved using three-layered LAMPs by designing the structure to enhance E fields in the reporterless protective silica shell. Here, neither the reporter in the inner layers is enhanced, nor is the medium outside the probe. Three-layered LAMPs were found to be optimal because it becomes difficult to reorganize plasmonic interactions from several layers into the outer layer. Alternately LAMPs may be constructed with only a very low concentration in one of the inner layers. This possibility is not examined here for brevity. Quenching is illustrated in Fig. 3 (and Fig. S4), where distributions in minimized configurations are depicted in the plane of incident illumination. Finally, the enhanced and quenched probe pair for a given size and excitation wavelength provides the allowable dynamic range as shown in Fig. 4A (and Fig. S2). The shaded regions represent the viable tuning space of probe signals for any common organic used as a reporter. As noted above, using a lower concentration or weaker Raman scattering reporter, the total signal could be even lower. Similarly, the upper limit could be higher by using a resonant dye. For example, choosing LAMPs of size 100 nm, one could achieve a maximum NEF of ∼10¹¹ and quenched NEF of ∼10^-2 at 785-nm excitation laser for nonresonant molecules. By using resonant molecules and lowering dye concentrations, hence, analytes over 20 orders of magnitude in concentration may be measurable in a single assay. Finally, an interesting consequence of the interacting plasmons arises in the spectral behavior of LAMPs. The structuring of a particle into the LAMP configuration provides an opportunity to tailor the response of complex probes to be spectrally flat (Fig. 4B) compared to simpler structures. The spectral uniformity indicates that the same LAMPs can be excitable by multiple laser wavelengths, and enhancements at shifted frequencies do not experience a drop-off from the excitation laser frequency that is often selected to coincide with the spectral plasmon resonance peak of SERS probes. Hence, the LAMP configuration promises sensitive, tailored, reporter-independent, and spectrally consistent responses while being amenable to fabrication (44).

Fig. 3.

Enhancement distributions in the incident plane of illumination for even-layered silver-silica LAMPs of various configurations that are designed to quench internal enhancements at an excitation wavelength of 785 nm. From top to bottom, the number of layers increases from 2 to 10, whereas from left to right the total size increases as shown.

Fig. 4.

Allowable probe signal and multiple excitation capability. (A) Range of NEF attainable via silver-silica nano-LAMP configurations for 785-nm excitation as a function of probe size. (B) LAMPs can be made capable of excitation at multiple frequencies by tailoring the internal structure. Here, a six-layer LAMP provides similar signal at multiple frequiencies for the same size (50 nm) as a three-layered LAMP, while maintaining high enhancement.

Finally, we place in perspective the potential advance with LAMPs compared to several other notable and demonstrated probe technologies. The concept of a SERS probe-based assay was first demonstrated (using a SERS-active dye molecule) by immobilizing an antibody on an Ag surface and labeling the detection antibody with a SERS-active dye for a 10⁴-fold enhancement (45). Silica-coated SERS-active gold colloids with resonant reporters functionalized to gold surfaces were reported (3) to show SERS intensities with total enhancement factors on the order of 10¹³–10¹⁴. A SERS enhancement of 10⁶ has been reported (46) using nanoshells to enhance para-mercaptoanailine, and a SERS enhancement of 10¹² is calculated when reabsoprtion of Raman emission by surrounding nanoparticles is taken into account. Thus, the concept of interactions among particles is noted and shown to be very effective. High enhancements (10¹¹–10¹⁴) (47) have also been reported for RuBPy-embedded SiO₂-core-Au shell nanoparticles while using SAMs on Au nanoshells instead of spheres increases signal ∼176-fold (48). These enhancement levels are within the range of the structures proposed here and, indeed, the methods used to optimize geometries here will likely benefit these existing approaches.

Discussion

In summary, we have theoretically demonstrated the possibility of designing SERS probes (via nano-LAMPs) that possess designed enhancement that can be tuned over a permissible range, wavelength-tuning capability, and potential for multiwavelength excitation. The layered structure permits both the reduction of variance by shielding reporters from direct interaction with metal surfaces as well as being spherically symmetric. In principle, the configuration offers unlimited multiplexing using simple reporters, whose enhancements do not depend on their scattering cross-section but can be independently tuned by the probe. The use of any reporter, tailored enhancement, and reproducible response will open the possibility of measuring multiple molecular species in complex samples. A practical translation of this technology will facilitate the development of a large dynamic range and suppression of the signal from the surrounding media, which are both a limiting factor in the use of SERS probes. While the concept of enhancements in signal has been previously examined, the concepts of containing the enhancement within the particle for amplified signals and designing probes for quenching in the optimization makes this work especially practical. Just as we have enhanced the response of the reporter, the response of the probes may also be tuned to enhance or suppress out of probe enhancement to any desirable level. An enhancement of the region outside the probe, for example, has been recently used for sensitive measurements (49). In this case, the use of LAMPs will be more powerful and generally applicable than the use of solid substrates. The proposed structures are amenable to modern fabrication methods (50), and a number of biocompatibility and molecular targeting strategies are available for nanoparticles (51) that can be employed for the proposed structures. At the same time, strategies to use spectroscopic signatures for quantitative analyses via efficient computer algorithms (52) are available to analyze the data. Hence, the realization and use of nano-LAMP probes, as designed in this manuscript, can enable progress in a wide variety of fields ranging from clinical diagnostics, environmental sensing, to basic biomedical research.

Methods

Layered Mie Theory.

Owing to the symmetry of LAMPs (Fig. S1), the response due to a laser excitation can be simulated by evaluating the fields within the sphere when a plane wave is incident, without the loss of generality, by extending Mie theory. We consider here an L-layered nanosphere with embedding medium denoted by L + 1, the field in jth layer can be represented in terms of vector spherical harmonics as

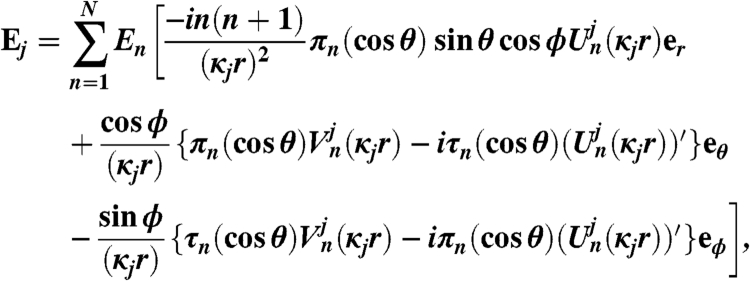[2]

[3]

where the functions U_n and V_n are given in terms of Ricatti-Bessel functions ψ and ξ as follows:

[4]

[5]

For the field in the core and the incident field, to be well defined at origin: 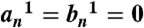and for the field in the embedding medium to be well defined at infinity: 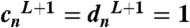. The other coefficients of expansion can be obtained using the following continuity conditions between j and (j + 1)th layer, for j = 1,…L.

[6]

[7]

Applying these boundary conditions and using orthogonality of the functions involved, a recursive formulation can be obtained. In the following logarithmic Bessel functions , 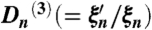and ratio function R_n( = ψ_n/ξ_n) are used for stability and accuracy of calculating higher order coefficients.

The coefficients A_n and B_n are obtained by upward recursion and the coefficients as follows:

[8]

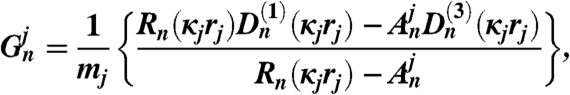[9]

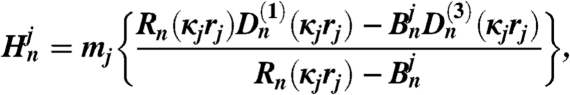[10]

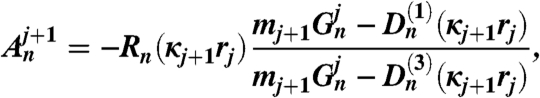[11]

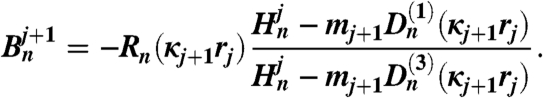[12]

The coefficients c_n and d_n are obtained by proceeding in a downward recursion as follows:

[13]

[14]

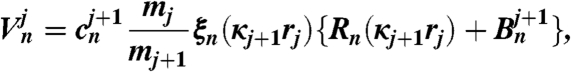[15]

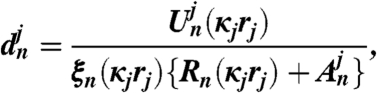[16]

[17]

Numerical integration of electromagnetic enhancement is performed with a weighted sum of integrand values using weights derived appropriate for spherical shells (53).

Probe Parameters.

Since the Raman enhancements observed so far are greatest for silver, it is chosen as the metal and silica is chosen as both the dielectric and protective layer. The core of LAMPs is constrained to be larger than 10 nm in diameter and shells to be thicker than 2 nm and 1 nm for the metal and dielectric material, respectively. A 1% loading and a molecular volume of 0.5 nm³ for the reporter are considered. Whole number shell sizes subject to size constraints are encoded using floating point numbers in [0, 1] interval.

Genetic Algorithm and Parameters.

The adapted operators for the algorithm are tournament selection without replacement (s = 4) (54), simulated binary crossover (SBX) (55, 56) with ηc = 10, crossover probability pc = 0.9, a polynomial mutation (57) with η = 20, and mutation probability p = 0.1. The GA was typically run for about 30–50 iterations after which all cases converged. In tournament selection without replacement and with tournament size s, s chromosomes (probe structures) are chosen at random without replacement and entered into a tournament against each other. The best (low error) individual in the group of s wins the tournament and is selected into a mating pool for evolving new solutions. In SBX, individuals in the mating pool are divided into random pairs, and each pair undergoes recombination with a probability pc. For each pair participating in the crossover, each gene (or shell size) undergoes a contracting or expanding crossover operation with a probability 0.5. Therefore, for each pair of chromosomes undergoing recombination, on average half of the genes are modified using either contracting or expanding crossover operations. The operations are designed to mimic crossover operator behavior on binary domains. The polynomial mutation is similar to SBX, and the only difference is in the computation of the polynomial probability. Instead of using genotypic distance between two parents as in SBX, the distance between a gene and its corresponding upper or lower bound, whichever is closer, is considered in computing the contracting and expanding probability distributions. In polynomial mutation, each gene (or variable) undergoes contracting or expanding operation with a probability p.