Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types

Abstract

A significant modification to the additive all-atom CHARMM lipid force field (FF) is developed and applied to phospholipid bilayers with both choline and ethanolamine containing head groups and with both saturated and unsaturated aliphatic chains. Motivated by the current CHARMM lipid FF (C27 and C27r) systematically yielding values of the surface area per lipid that are smaller than experimental estimates and gel-like structures of bilayers well above the gel transition temperature, selected torsional, Lennard-Jones and partial atomic charge parameters were modified by targeting both quantum mechanical (QM) and experimental data. QM calculations ranging from high-level ab initio calculations on small molecules to semi-empirical QM studies on a 1,2-dipalmitoyl-sn-phosphatidylcholine (DPPC) bilayer in combination with experimental thermodynamic data were used as target data for parameter optimization. These changes were tested with simulations of pure bilayers at high hydration of the following six lipids: DPPC, 1,2-dimyristoyl-sn-phosphatidylcholine (DMPC), 1,2-dilauroyl-sn-phosphatidylcholine (DLPC), 1-palmitoyl-2-oleoyl-sn-phosphatidylcholine (POPC), 1,2-dioleoyl-sn-phosphatidylcholine (DOPC), and 1-palmitoyl-2-oleoyl-sn-phosphatidylethanolamine (POPE); simulations of a low hydration DOPC bilayer were also performed. Agreement with experimental surface area is on average within 2%, and the density profiles agree well with neutron and x-ray diffraction experiments. NMR deuterium order parameters (S_CD) are well predicted with the new FF, including proper splitting of the S_CD for the aliphatic carbon adjacent to the carbonyl for DPPC, POPE, and POPC bilayers. The area compressibility modulus and frequency dependence of ¹³C NMR relaxation rates of DPPC, and the water distribution of low hydration DOPC bilayers also agree well with experiment. Accordingly, the presented lipid FF, referred to as C36, allows for molecular dynamics simulations to be run in the tensionless ensemble (NPT), and is anticipated to be of utility for simulations of pure lipids systems as well as heterogeneous systems including membrane proteins.

1. Introduction

This paper presents the CHARMM36 (C36) potential energy parameter set (or force field, FF) for lipids. C36 is an additive, all-atom model that replaces CHARMM27 (C27)^1,2 and CHARMM27r (C27r)^3,4 (a revision to C27 updating the acyl chain torsions, but leaving other parameters unchanged); it is consistent with CHARMM (Chemistry at HARvard Molecular Mechanics) parameter sets for proteins,^5,6 nucleic acids,⁷ ethers,⁸ carbohydrates,^9–12 and small molecules.^13,14 Accordingly, the C36 FF is applicable for simulation studies of heterogenous biomolecular systems.

Development of C36 was primarily motivated by two flaws in both C27 and C27r.^3,15–18 First is the large positive surface tension (30–40 dyn/cm) for fluid phase bilayers at the experimentally determined surface area per lipid. While there is not a direct measure of the surface tension, γ, of microscopic bilayers, theoretical considerations for self-assembled systems indicate that γ is identically zero^19–21 when the bilayer is flat, or only a few dyn/cm²² when undulations are taken into account. Experimental measurements on macroscopic black lipid bilayers also indicate a surface tension in the neighborhood of a dyn/cm.²³ The consequence of this positive surface tension with C27 and C27r is that bilayers shrink to near gel-phase areas when simulated at zero surface tension (as in the NPT, or constant number, isotropic pressure and temperature, ensemble).^17,18,24 The ad hoc solution of simulating with a large applied surface tension is unsatisfactory, given the good theoretical arguments for a much lower or vanishing surface tension.

The second flaw is that simulations carried out with these sets do not reproduce the experimental deuterium order parameters, S_CD, in the glycerol and upper chain regions.³ In particular, the splittings observed for a wide range of glycerophospholipids^25–29 for Carbon 2 (C2) of the aliphatic chains and Carbon 1 (CG1) of the glycerol are virtually absent. The inability of these FFs to reproduce the fine structure at the lipid water interface and the inequivalence of the acyl chains raises concerns that interactions of lipids with surface active agents would likewise be incorrectly described. Other flaws in the these FFs include underestimation of the area compressibility modulus, K_A,³⁰ underhydration of the head group region,³¹ underestimation of the electron density in the bilayer midplane,¹⁶ and overestimation of the frequency dependence of the ¹³C NMR T₁ of the acyl chains near the head group.²⁷

The strategy for the reparametrization was based on first reevaluating the partial atomic charges. Recent studies by different groups^17,24,32 indicated that changes in the partial atomic charges in the head group of C27 lead to substantial reductions in surface tension for 1,2-dipalmitoyl-sn-phosphatidylcholine (DPPC), 1,2-dimyristoyl-sn-phosphatidylcholine (DMPC), and 1-palmitoyl-2-oleoyl-sn-phosphatidylcholine (POPC) bilayers. The present reevaluation began with a determination of the validity of applying charges based on small model compounds (Fig. 1) in vacuum to DPPC in a bilayer using semi-empirical (AM1 level³³) quantum mechanical (QM) calculations. Based on the relative independence of charges with system size, application of the small molecule based optimization of non-bond parameters common to the CHARMM additive force fields was applied.³⁴ In addition, high-level ab initio calculations were carried out on model compounds representative of the lipid head group and glycerol linker region to act as the basis for optimization of selected torsion angle parameters. Optimized parameters were then tested on simulations single component lipid bilayers containing DMPC, DPPC, and POPC, 1,2-dilauroyl-sn-phosphatidylcholine (DLPC), 1,2-dioleoyl-sn-phosphatidylcholine (DOPC), 1-palmitoyl-2-oleoyl-sn-phosphatidylethanolamine (POPE). Simulations of DLPC, DMPC, DPPC, DOPC, POPC, and POPE bilayers were carried out at high hydration and DOPC was also subjected simulations at low hydration. Following several iterations of testing small molecule based parameters on DPPC bilayer simulations, the final parameter set was validated by comparisons with experimentally determined surface areas, compressibilities, deuterium order parameters, ¹³C NMR relaxation rates, and neutron/diffraction profiles on various bilayers.

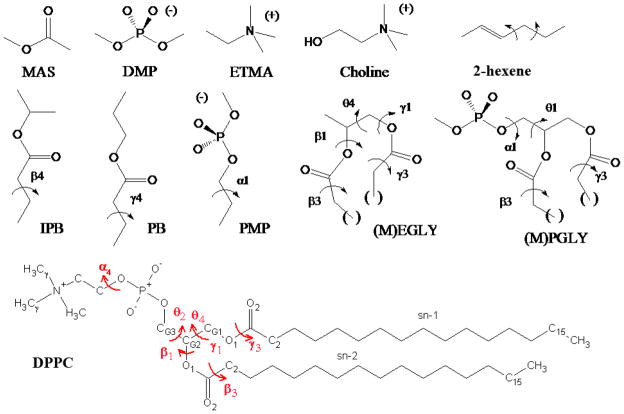
Figure 1.

Model compounds used in the present study including methylacetate (MAS), dimethylphosphate (DMP), ethyltrimethylammonium (ETMA), choline, 2-hexene, isopropylbutyrate (IPB), propylbutyrate (PB), propylmethylphosphate (PMP), an esterified glycerol analog ((M)EGLY), an esterified glycerol-phosphate analog ((M)PGLY) and the general structure of DPPC. For the esterified glycerol analogs, the parenthesis on the compound and the (M) indicate the extension of the aliphatic chain by a methylene as required to investigate the conformational energetics of the β₃ and γ₃ dihedrals using the model compounds MEGLY and MPGLY. DPPC is also shown with torsions labeled in red and corresponding labels for carbons used in comparison with NMR experiments.

Although the focus of this work is improving the all-atom CHARMM FF, it is important to review briefly the current pair-wise additive lipid force fields that are used in molecular simulations. These atomic- or near atomic-level FFs can be classified into either all-atom or united-atom models. In addition to the abovementioned CHARMM FFs,^1–4 the all-atom general AMBER force field (GAFF)³⁵ has the capability to simulate lipid membranes. GAFF has been successfully tested on pure fully-hydrated DMPC,³⁶ DOPC,^36,37 and POPC³⁸ bilayers with a decent description of structural and dynamical properties for a force field not fit to lipid experimental data. Notably, GAFF has been shown to be the only FF to capture the carbon-2 deuterium order parameter splitting,³⁷ but does result in lower surface areas per lipid and higher deuterium order parameters compared to experiment.^36–38 Recently, Hénin et al.³⁹ developed a united-atom acyl chain FF for CHARMM phospholipids, while maintaining an all-atom description of the lipid head group. This matches the C27r FF, while reducing the number of atoms, thus making it attractive for larger heterogeneous membranes. One of the main united-atom FFs for lipids are the GROMOS-based FFs, which have been optimized to reproduce condensed phase properties of alkanes.⁴⁰ One commonly used GROMOS-based FF was developed by Berger et al.,⁴¹ which included optimization of the LJ parameters to reproduce condensed phase properties of pentadecane. More recent modifications to the united-atom GROMOS FFs are 43A1-S3⁴² and 53A6.⁴³ Adjustments to the charges and LJ parameters of choline methyls and phosphate oxygens resulted in good agreement for surface area per lipid, density profiles, and deuterium order parameters for saturated and unsaturated acyl chain PC lipids with GROMOS-53A6.^43,44 However, the isothermal area compressibility modulus was found to be nearly twice that experimentally measured. Besides the GROMOS-based force fields, several research groups have developed their own united-atom lipid FFs, such as, Smondyrev and Berkowitz,⁴⁵ OPLS-UA,⁴⁶ and the adoption of the NERD FF to fatty acids by Sum et al.⁴⁷ Clearly there is a wide variety of united-atom force fields for lipids available, while only two all-atom models are available, GAFF and CHARMM, with CHARMM being the only FF parametrized directly for lipid molecules. Moreover, the different methodologies used to develop these individual FFs preclude the ability to combine two FFs from varying research communities.

By way of an outline, the Methods section initially describes the nomenclature used for the lipids and small molecules. Two additional subsections of the Methods describe the QM methods used in FF development and methods used in the molecular dynamics simulations. Section 3 provides a detailed description on how the FF parameters were fit to experimental and QM data, including adjusting partial charges to model the complex environment of a lipid bilayer (3.1), and conformational energy studies on small molecules representative of various lipid moieties (3.2). Section 4 describes the results from simulations with C36 for the model lipid DPPC (4.1), and other lipids (4.2). Section 5 examines two limitations of the new FF: the dipole potential drop (5.1); and inconsistencies of surface tensions of bilayers and monolayer (5.2). Section 6 presents the discussion and conclusions.

2. Methods

The Methods section is divided into three subsections. In the first, lipid molecule and atom names are briefly reviewed to avoid confusion among several commonly used conventions. Section 2.2 describes the QM methods used in justifying modifications to the partial charges for certain atoms in the head group of the lipid molecules along with the optimization procedure used to produce optimized non-bond parameters for the ester moieties in the glycerol linker region. This subsection also describes the QM methods used to obtain highly accurate torsional profiles for certain head group and alkene dihedrals. The Section 2.3 describes the methods used in the molecular dynamics (MD) simulations. The C36 additive all-atom lipid force field may be downloaded from the MacKerell group web page at http://mackerell.umaryland.edu/CHARMM_ff_params.html.

2.1. Lipid Nomenclature and Atom Naming Conventions

Lipid molecule names are in IPUAC sn nomenclature^48,49 (see http://www.chem.qmul.ac.uk/iupac/lipid/) throughout this document. For technical reasons, each atom of a molecule in a molecular mechanics FF must have a unique and simply expressed name, generally using the letters A–Z and numerals; standard sn nomenclature references do not address atom names in this level of detail. The CHARMM lipid FF uses atom and torsion names based on the Sundaralingam nomenclature:⁵⁰ a significant difference is the numbering of the glycerol carbon atoms, which is inverted with respect to the sn nomenclature. For glycerol-phosphate itself, 1-phospho-D-glycerol is the more correct name, while sn lipid molecule names are based on 3-phospho-L-glycerol, which is identical in terms of absolute configuration. To help clarify the equivalent names for a given atom, both sn and FF atom names are included in Tables 2 and 5. The sn atom nomenclature is used in the figures and text in the remainder of the document. The Supporting Information uses FF names in the tables, and sn names in the figures. For torsions, the Sundaralingam names will be used throughout; they are based on the chain names, which are the first three letters of the Greek alphabet, corresponding to the Sundaralingam glycerol carbon numbering. The polar chain is designated the α chain, the sn-2 chain corresponds to the β chain, and the sn-1 chain corresponds to the γ chain. Finally, the polar α chain atoms of both DOPC and POPC were renumbered in the C36 lipid FF release for consistency with other PC-based lipid descriptions.

Table 2.

AM1 CM2 partial atomic charges for the esters of the model compounds and differences in charges in the larger model compounds and in individual lipid molecules.

	Methylacetate			Glycerol-phosphate	Full lipids extracted from the bilayer (gas phase)	Lipids in the bilayer/water environment
sn	FF	q(average)	q(stddev)	Δq	Δq	Δq
sn-2 C2	C22	−0.209	0.026	0.033	0.075	0.073
sn-2 C1	C21	0.483	0.013	−0.015	−0.017	0.005
sn-2 O2	O22	−0.424	0.021	−0.039	−0.038	−0.042
sn-2 O1	O21	−0.355	0.015	0.023	0.032	0.032
CG2	C2	0.036	0.014	0.007	0.000	−0.001
sn-1 C2	C32			0.034	0.074	0.072
sn-1 C1	C31			−0.006	−0.018	0.005
sn-1 O2	O32			−0.048	−0.032	−0.046
sn-1 O1	O31			0.037	0.030	0.031
CG1	C3			0.018	−0.003	−0.001

Δq values calculated relative to the average charges for the small model compound (MAS). Calculation of average charges for MAS, Glycerolphosphate and the full lipids in both the gas and bilayer/water phases is described in the legend of Table S1 in the Supporting Information.

Table 5.

Comparison of selected charges and LJ parameters in the C36 and C27r force fields for the glycerol region. See Figure 1 for the sn atom nomenclature.

sn atom	FF atom	Charges		εi [kcal/mol]		0.5Rmin [Å]
		C27r	C36	C27r	C36	C27r	C36
CG2	C2	0.04	0.17	−0.020	−0.020	2.275	2.275
H2	HS	0.09	0.09	−0.022	−0.022	1.320	1.320
sn-2 O1	O21	−0.34	−0.49	−0.1521	−0.100	1.770	1.650
sn-2 C1	C21	0.63	0.90	−0.070	−0.070	2.000	2.000
sn-2 O2	O22	−0.52	−0.63	−0.120	−0.120	1.700	1.700
sn-2 C2	C22	−0.08	−0.22	−0.056	−0.056	2.010	2.010
sn-2 H2R	H2R	0.09	0.09	−0.024	−0.024	1.340	1.340
sn-2 H2S	H2S	0.09	0.09	−0.024	−0.024	1.340	1.340
CG1	C3	−0.05	0.08	−0.056	−0.056	2.010	2.010
H1R	HX	0.09	0.09	−0.024	−0.024	1.340	1.340
H1S	HY	0.09	0.09	−0.024	−0.024	1.340	1.340
sn-1 O1	O31	−0.34	−0.49	−0.1521	−0.100	1.770	1.650
sn-1 C1	C31	0.63	0.90	−0.070	−0.070	2.000	2.000
sn-1 O2	O32	−0.52	−0.63	−0.120	−0.120	1.700	1.700
sn-1 C2	C32	−0.08	−0.22	−0.056	−0.056	2.010	2.010
sn-1 H2R	H2X	0.09	0.09	−0.024	−0.024	1.340	1.340
sn-1 H2S	H2Y	0.09	0.09	−0.024	−0.024	1.340	1.340

2.2. Quantum Mechanics and Dihedral Parameter Fitting

To address the transferability of partial atomic charges based on small molecules to the larger head group in lipids, a series of semiempirical QM calculations on different compounds in different environments were undertaken. These calculations used the program DivCon,⁵¹ which applies a divide and conquer approach^52,53 to allow for full AM1 level calculations to be performed on systems with 10,000 or more atoms. Both the Mulliken and CM2 charges⁵⁴ were obtained and compared for the different compounds and environments to determine the impact of environment on partial atomic charges. DPPC was selected as the target lipid and corresponding small molecules were chosen, i.e., methylacetate (MAS), dimethylphosphate (DMP) and ethyltrimethylammonium (ETMA) (Fig. 1). These molecules were selected as they represent the compounds used for optimization of the non-bond parameters in the C27 FF, with DMP and MAS also being used in the present work. In addition, EGLY and PGLY (Fig. 1) were analyzed to determine the potential utility of larger model compounds. All model compound results were based on gas phase calculations and charges were averaged over multiple conformations as described in the legend of Table S1. For the full lipid, calculations were performed on the DPPC molecules individually in the gas phase and, importantly, on the fully solvated lipid bilayer. The charges for individual lipids used for averaging were based on lipids that were located near the central region of the bilayer to include realistic membrane interactions. The solvated bilayer was obtained from an NPAT MD simulation of 72 DPPC molecules at high hydration and the experimental surface area in periodic boundary conditions using the C27r FF.³ From this simulation, 13 time frames were extracted and individual lipid molecules in the central region of each leaf of the bilayer were identified, yielding a total of 64 lipid conformations. Each of these conformations was subjected to an AM1 calculation isolated in the gas phase and average charges were calculated. To evaluate the impact of the condensed phase environment on the partial atomic charges, AM1 calculations using DivCon on the full bilayer-solvent systems were calculated to obtain charges in a membrane environment. Though these calculations were performed in the absence of periodic boundary conditions used in the MD simulations, the conformations of the lipids in the gas phase and the bilayer/water phase calculations were identical; only the environment of the individual lipids changed.

The dihedral portion of the CHARMM FF is mostly from direct fits to vacuum QM-based conformational energies. This approach was not satisfactory for the glycerol torsions β₁θ₂, and θ₄, where solvent effects are expected to be complex such that gas phase potential energy surfaces may be inappropriate.^55,56 As described below, these torsions were adjusted slightly to match the experimental deuterium order parameters glycerol region for DPPC following new QM estimates. (Values of S_CD reported here are always positive; i.e., the absolute value sign is assumed.) The QM calculations follow the approach used for C27r where the acyl torsions were refined; see references 3,57 for details. Figure 1 shows the small molecules used to represent regions of the phospholipid to allow for high-level QM calculations. Second order Möller-Plesset perturbation theory (MP2)⁵⁸ is used to obtain global minimum energy geometries of these small molecules and a single dihedral constraint is used to obtain torsional energy scans. To obtain conformational energy at the coupled cluster level, CCSD(T),⁵⁹ with a large basis set, HM-IE (the Hybrid Method for Interaction Energies)⁶⁰ is used to estimate CCSD(T)/cc-pVQZ,

$$E[\text{CCSD}(\text{T})/\text{cc}-\text{pVQZ}]\cong E[\text{CCSD}(\text{T})/\text{cc}-\text{pVDZ}]+(E[\text{MP}2/\text{cc}-\text{pVQZ}]-E[\text{MP}2/\text{cc}-\text{pVDZ}])$$ (1)

which assumes that the effect of larger basis sets is additive. These conformational energies using HM-IE will be simply referred to as QM in this paper.

The following objective function was used initially to obtain all new torsional terms for C36,

$$\chi =\sum _i^{\#\text{of}\text{QM}\text{points}}{\left[U_i^{QM}-U_i^{\mathit{Model}}\right]}^2$$ (2)

where U_i is the energy for conformation i. The alkane torsions^3,4 were also refit to this function to maintain a consistent approach for fitting dihedral parameters (a higher weight was used for the trans and gauche minima in C27r). The alkene torsions adjacent to C=C doubles bonds were fit to conformations of 2-hexene at the RIMP2/cc-pVQZ//MP2/cc-pVDZ level using a Monte Carlo Simulated Annealing approach.⁶¹

2.3 Molecular Simulations

Small molecules used in the parametrization of the C36 were simulated at 298.15 K and 1 atm pressure using the new velocity Verlet integrator⁶² implemented in CHARMM. Standard procedures were used to include the influence of long-range electrostatics⁶³ and Lennard-Jones (LJ) forces.^64,65 Heats of vaporization and molecular volumes of MAS were calculated using a box of 128 molecules. Free energies of aqueous solvation of MAS and DMP were calculated via free energy perturbations (FEP)⁶⁶ using the staged protocol developed by Deng and Roux,⁶⁷ as previously described.⁶⁸ More details on these methods to obtain the heat of vaporization and free energies of solvation are provided in the supplementary material.

The CHARMM^69,70 and NAMD⁷¹ programs were used to simulate lipid bilayers and monolayers. The lipids studied, total simulation times, temperatures, and other conditions are listed in Table 1. A LJ switching function over 8 to 12 Å was used in MD simulations with CHARMM. For the NAMD simulations, a shorter LJ switching function was used (11 to 12 Å). Particle mesh Ewald (PME)⁶³ was used for the long-range electrostatic contribution for both CHARMM and NAMD. The LJ and PME contributions to the energy and forces were updated every step for the CHARMM simulations and every two and four steps, respectively, for the NAMD simulations (impulse-based Verlet-I/r-RESPA method).^72,73 The temperature was held constant with the Hoover thermostat⁷⁴ in CHARMM and by Langevin dynamics with a weak coupling constant of 1 ps⁻¹ in NAMD. Similarly the pressure was maintained anisotropically (NPT ensemble simulations) or in the direction perpendicular to the membrane (NPAT ensemble simulations) by the Nose-Hoover piston^75,76 (CHARMM) or a Nosé-Hoover-Langevin piston^77,78 (NAMD) at 1 bar. These differences between MD simulations with CHARMM and NAMD encompass typical approaches used by various research groups. Consistent for all of these simulations was the use of a 1 fs time step and constraining of the hydrogen atoms using the SHAKE algorithm.⁷⁹

Table 1.

Parameters and system details for the lipid bilayer and monolayer simulations. Time is given in total simulation time including equilibration.

Lipid	System	Program	Ensemble	# of lipids	water:lipid	T [K]	Time [ns]
DPPC	Bilayer	CHARMM	NPT	72	30.4	323.15	40
		CHARMM	NPATa	72	30.4	323.15	35/55
		NAMD	NPT	72	30.4	323.15	130
	Monolayer	CHARMM	NVTb	80	29.1	323.15	23
DMPC	Bilayer	CHARMM	NPT	72	25.7	303.00	40
DLPC	Bilayer	CHARMM	NPT	50	31.3	303.00	40
DOPC	Bilayer	CHARMM	NPT	72	5.4	296.00	45
		CHARMM	NPT	72	33.5	303.00	35
		NAMD	NPT	288	5.4	296.00	40
POPC	Bilayer	CHARMM	NPT	72	31.1	303.00	35
POPE	Bilayer	CHARMM	NPT	80	32.0	310.15	40

^aareas simulated were 60, 62, 66, and 68 Ų/lipid for 35 ns, and at 64 Ų/lipid for 55 ns

^bareas simulated were 54, 64, and 80 Ų/lipid.

Starting structures for DMPC,¹⁶ DPPC,³ POPE⁸⁰ and low hydration DOPC¹⁸ simulations were obtained from previous simulations with the C27 or C27r force field. For DPPC isotherm configurations other than 64 Ų area/lipid, two NPγT ensemble MD simulations starting from 64 Ų with applied surface tensions (γ) of −10 and 30 dyn/cm were used to contract and expand the system, respectively. The coordinate sets with unit cell edge lengths that most closely matched that for each target area were extracted from these simulations, and used as simulation starting points. The DLPC, POPC, and high hydration DOPC bilayers were built de novo from a library of single lipid conformations, as described previously.⁸¹ In this case, the library of conformations for each lipid was generated from eight 2-ns Langevin dynamics simulations in an orienting potential, with a different random seed for each replicate simulation. The P atom of the phosphate was tightly restrained to a position along the +z axis commensurate with the experimental bilayer thickness for each lipid. To prevent free rotation and limit whole molecule motions to wobbling in a cone, three restraint planes were used: the choline N atom was restrained to be 1 Å above the P atom, the ester O atoms were restrained to be 2 Å below the P atom, and the chain terminal C atoms were restrained to be within 4 Å of the z=0 plane. The restraint planes functioned as soft walls at the indicated z positions.

3. Deriving Force Field Parameters from vacuum QM

This section describes the procedure of adjusting certain parameters to the CHARMM FF,

$$V(\widehat{R})=\sum _{\mathit{bonds}}{K}_b{(b-b_0)}^2+\sum _{\mathit{angles}}{K}_{\theta }{(\theta -{\theta }_0)}^2+\sum _{\mathit{dihedrals}}\left[\sum _j{K}_{\varphi ,j}\left(1+cos(n_j\varphi -{\delta }_j)\right)\right]+\sum _{\begin{array}{l}\mathit{nonbonded}\\ \mathit{pairsi},j\end{array}}{\epsilon }_{ij}\left[{\left(\frac{R_{min,ij}}{r_{ij}}\right)}^{12}-{\left(\frac{R_{min,ij}}{r_{ij}}\right)}^6\right]+\sum _{\begin{array}{l}\mathit{nonbonded}\\ \mathit{pairsi},j\end{array}}\frac{q_i{q}_j}{{\epsilon }_D{r}_{ij}}$$ (3)

where the terms have their usual meanings. The bond and angle terms are left unchanged from previous modifications. As opposed to recent charge modifications to the CHARMM lipid FF by other workers,^17,24,32 the parametrization discussed in this section is consistent with the methods used in the CHARMM additive FF development strategy.²⁰ The first subsection justifies the need for changing the non-bonded parameters of the lipid head group (last two terms in Eq. 3). The choice of the final set of new lipid head group charges and Lennard-Jones (LJ) terms are also described in this subsection. The second subsection describes the dihedral changes to the CHARMM FF in C36.

3.1 Adjusting the Non-bonded Parameters of the Lipid Head Group

Optimization of lipid atomic charges depends on the size of the compound used to represent the full lipid molecule and its environment. A systematic test of this size dependence is illustrated in Table 2, which lists the average partial atomic charges based on the AM1/CM2 model of selected atoms in the model compounds and the differences in the partial atomic charges for the larger model compounds and the full lipid molecules. The average partial atomic charges and their standard deviations of all the compounds are presented in Table S1. The Mulliken and CM2 based charge schemes result in similar trends (Table S2). Overall, the charges for the model compound are similar to those for the larger compounds, i.e., differences are typically 0.05e or less. However, there are some significant differences for the ester charges (sn-2 chain C1, O1, and O2). For example, in the larger compounds the carbonyl oxygen (sn-2 O2) becomes more negative indicating local polarization, though the carbonyl carbon (sn-2 C1) and the ether oxygen (sn-2 O1) become more negative and more positive, respectively, which minimize this effect. However, upon going from the gas to the bilayer/water phase for the full lipid, the negative charge on the sn-2 C1 becomes more positive while that of the sn-2 O2 becomes more negative for both ester moieties. Thus, the present QM results (Table 2, S1, and S2) indicate that local charge induction occurs in the complex environment of the lipid bilayer, and that subtle differences observed as a function of model compound and environment should be considered when selecting the final non-bond models.

MD simulations of DOPC at low hydration indicated that the head group was not adequately hydrated.³¹ Such limitations may be probed by considering the free energy of aqueous solvation of model compounds representative of those regions of the lipids. Studies have shown that the free energy of aqueous solvation of tetraethylammonium is in excellent agreement with experiment,⁸² indicating that the quaternary amine parameters are satisfactory. This implies that the non-bond parameters in the linker region of the FF, including the phosphate and esterified glycerol moieties, may be problematic. Calculations were undertaken on the model compounds DMP and MAS, with respect to both QM and condensed phase calculations. Particular emphasis was put on MAS because that model had not been assessed since the original lipid force field was published in 1996,⁸³ whereas the phosphate parameters had been investigated in detail in 2000 in conjunction with nucleic acid FF development.⁷

A detailed analysis on the ability of the DMP FF model by Foloppe and MacKerell,⁷ showed that the model satisfactorily treated the interactions with water as a function of orientation as judged by QM calculations. Accordingly, emphasis in this study was placed on evaluation of the DMP model in the condensed phase, targeting the free energy of aqueous solvation, ΔG_S. A direct experimental value for ΔG_S of DMP is not available; as described in the Supporting Information it was estimated to be −76±4 kcal/mol using a thermodynamic cycle.^84,85 Calculation of ΔG_S of DMP for C27 and C36 was performed using a free energy perturbation methodology based on the Weeks, Chandler, Anderson decoupling approach (see supplementary material).^67,86 Error estimates were obtained by repeating the calculation three times with the individual simulations seeded with different initial velocities. From these calculations, −76.7±0.05 kcal/mole was obtained for C27, which is in excellent agreement in the estimated experimental value (Table 3). Based on this high level of agreement, the published DMP non-bonded parameters were maintained with the exception of LJ parameters for ester oxygens, which were modified during MAS optimization as described below. This change has only a small effect on DMP solvation energetics (cf. C27 and C36 values in Table 3), and the new value of −77.7 kcal/mol is within the statistical uncertainty of the experimental estimate.

Table 3.

Methylacetate and dimethylphosphate condensed phase properties.^a

Methylacetate		C27	C36
Pure Solvent	Exp.b	Calc	Calc.
Molecular Volume	132.7	135.2±0.1	135.6±0.1
Heat of Vaporization	7.72	8.55±0.01	7.97±0.01
Free Energy of Aqueous Solvation
	Exp.	Calc.	Calc.
Methylacetate	−3.32	−3.92±0.10	−4.84±0.10
Dimethylphosphate	−76±4	−76.68±0.05	−77.73±0.07

^aHeats of vaporization and free energies in kcal/mol and molecular volumes in ų. Averages and standard deviations over 10 independent pure solvent simulations of 150 ps with the average value from each simulation obtained over the final 100 ps. Free energies of solvation were obtained from 3 independent free energy determinations with 50 ps of equilibration and 100 ps of sampling for each value of the coupling/staging parameters.

^bSources of the experimental data are detailed in the Supporting Information.

The original optimization of the MAS non-bond parameters focused on the interactions with water, targeting QM data, and on the reproduction of its experimental pure solvent properties. ⁸³ In the present study, these target data were reanalyzed and the optimization was extended to include the dipole moment and the experimental ΔG_S. For the interactions with water, the QM MAS-water monohydrate interaction pairs were optimized at the HF/6-31G* level, in which the minimum interaction distances are offset by 0.2 Å and the interaction energies scaled by 1.16 as required to mimic local polarization effects in the condensed phase as well as limitations in the QM level of theory. Importantly, this level maintains consistency with the remainder of the CHARMM additive all-atom biological force field.⁵ These energies and dipole moments were used as target data to reoptimize the MAS partial atomic charges while reproduction of the pure solvent heats of vaporization and molecular volumes were used to adjust the LJ parameters. The new LJ parameters included the recently optimized oxygen LJ parameters for the ether oxygen in the ester linkage.⁸ The methyl LJ parameters were not adjusted. Once satisfactory models were obtained, free energy of solvation calculations were performed and used to select the final parameter set.

Table 4 lists the MAS dipole moments and interaction energies with water based on the QM calculations and C27 and C36. The C27 energies agree well with the QM target data. In contrast, the dipole moment, which was not previously included as target data, shows significant disagreement with the QM target values with respect to both the magnitude and the orientation. Accordingly, further optimization of the charges targeted the dipole moment along with the interactions with water. LJ parameters were simultaneously optimized to overcome the significant overestimation of the MAS pure solvent heat of vaporization with C27 (Table 3). This led to the development of several non-bond models for MAS. These models focused on accurate reproduction of the heat of vaporization and dipole moment with the level of agreement with the water interaction energies varied with respect to the magnitude of the energies, as compared to the QM data.

Table 4.

Methylacetate (MAS) dipole moments and interactions with water.

Dipole_moment		QM	C27	C36
X		−1.37	−2.38	−1.56
Y		−0.92	0.30	−1.02
Z		0.00	0.00	0.00
X/Y ratio		1.48	−7.83	1.52
Total		1.65	2.40	1.86

MAS-water interactions
	Interaction Energy, kcal/mol			Distance, Å
	QM	C27	C36	QM	C27	C36
1) C=O..HOH, along C=O bond, out-of-plane
	−5.15	−5.83	−6.71	2.08	1.78	1.75
2) C=O..HOH, 120° towards methyl, in-plane
	−6.63	−6.55	−6.92	2.03	1.78	1.76
3) C=O..HOH, 120° towards ester O, in-plane
	−3.15	−3.25	−3.53	2.64	2.54	2.53
4) O (ester)…HOH, out-of-plane
	−3.79	−2.71	−4.19	2.11	1.99	1.77
Average difference		0.10	−0.66
RMS difference		0.63	0.52
Average absolute error		0.49	0.66

From this effort a model was selected in which the experimental ΔG_S was overestimated, motivated by the QM charge analysis presented above and the need to obtain better agreement with the solvation of the head group and linker regions of DOPC at low hydration. The results indicated that a more favorable ΔG_S is necessary to properly hydrate the head group region (Table 3). Interestingly, application of the charges from a previous reparametrization of the DPPC parameters¹⁷ to MAS as part of the present study yielded ΔG_S =4.8 kcal/mol suggesting that the success of the previous model was also based on increased solvation of the glycerol linker region. This increased solvation was noted in the previous work with change attributed to differences in the charges of one of the methylene groups.¹⁷ At this stage several sets of ester non-bond parameters were used in MD simulations of DPPC bilayers from which the final non-bond model of the ester moiety was selected based on the surface tension of the simulation approaching zero (not shown). Table 5 compares the final lipid charges for C36 with those of C27r for the linker region. The final model yields good agreement with respect to the dipole moment, including its orientation, and the experimental pure solvent heat of vaporization and molecular volume (Table 3). This non-bond model of the ester moiety was used as the starting point for final optimization of the dihedral parameters and subsequent extensive testing in lipid bilayer simulations.

3.2. Adjusting the Conformational Energies

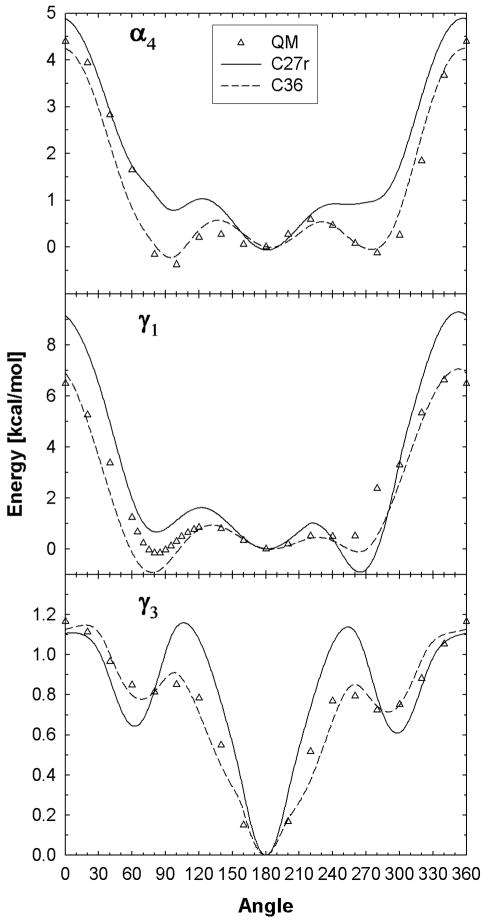
The conformational QM energies for the alkane model compounds, IPB (β₄), and PB (γ₄) (Figure 1) were previously calculated^3,57 and potential parameters were fit to these QM energies (Table S3). The alkane torsions were refit using an objective function consistent with that used for the other torsional fits performed in the present study (Eq. 3), but this had a minimal effect on the torsional profiles. 2-hexene was also used to refit the torsion parameters of the two C-C single bonds adjacent to C=C double bonds and C36 fits agree well with the QM data (Figure S1, Supporting Information). Conformational energies for γ₁ and γ₃ were calculated using the MEGLY model compound and PMP was use to calculate theα₄ torsional profile (Figure 2). There are significant improvements over C27r for the torsional barriers and gauche-like conformational energies, similar to previous alkane torsions. Specifically, C27r incorrectly predicts the trans state as the most stable conformation for the choline α₄ torsion, but the gauche⁺ conformation is the most stable. The C36 fit to the QM energies resolves the inaccurate relative conformational energies that exist with the C27r FF. This change substantially influenced the calculated deuterium order parameters for lipids, as discussed in the following section.

Figure 2.

Dihedral scans for the α₄, γ₁ and γ₃ torsions based on model compounds (MEGLY and PMP). The energy at 180° is set as the zero for γ₃ and α₄ and 60° for γ₁.

For β₁, θ₂, and θ₄, additional adjustments were based on MD simulations of DPPC bilayers to evaluate torsional populations that best matched deuterium order parameters for the glycerol and acyl chain C2 positions. A 27 state model, based on assuming 3 minima for each of the 3 dihedrals, was used to assist in the evaluation. Lipids were grouped into one of the 27 states based on the values of the 3 dihedrals, and the average S_CD from each group was computed. The experimental S_CD for a given C-H vector then could be calculated from a population weighted sum of the S_CD values for each of the states. While attempts to predict optimal populations by fitting were not successful, this exercise indicated that a major reduction in the population of the trans conformation for θ₂ was required, and that shifts in the conformer populations ofθ₄ should be considered. Four trial parameter sets were created and evaluated by 25-ns MD simulations of DPPC in the NPAT ensemble. The set with the best match to the experimental S_CD values was chosen. Comparison of QM and C36 potential energy surfaces for the β₁ and θ₄ surfaces based on the MEGLY model compound are shown in Figure S2 (left) of the Supporting Information. While final optimization of the associated dihedral parameters targeted the experimental S_CD values, the level of agreement between the QM and final empirical model is satisfactory. This indicates that the use of the experimental target data is not leading to the unphysical sampling of high-energy regions of the potential energy surfaces. In addition, the large discrepancy between QM methods (Fig. S2, left) suggests that the uncertainty for these two torsions is high.

4. Molecular Dynamics Simulations of Lipid Bilayers – Validation of the Force Field

4.1. Model Lipid DPPC

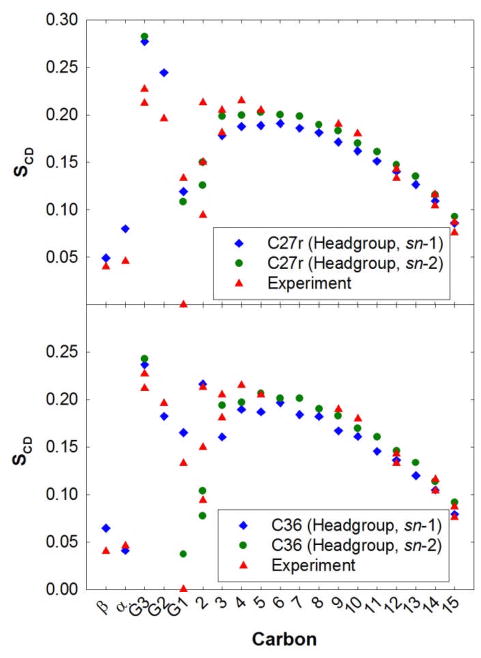
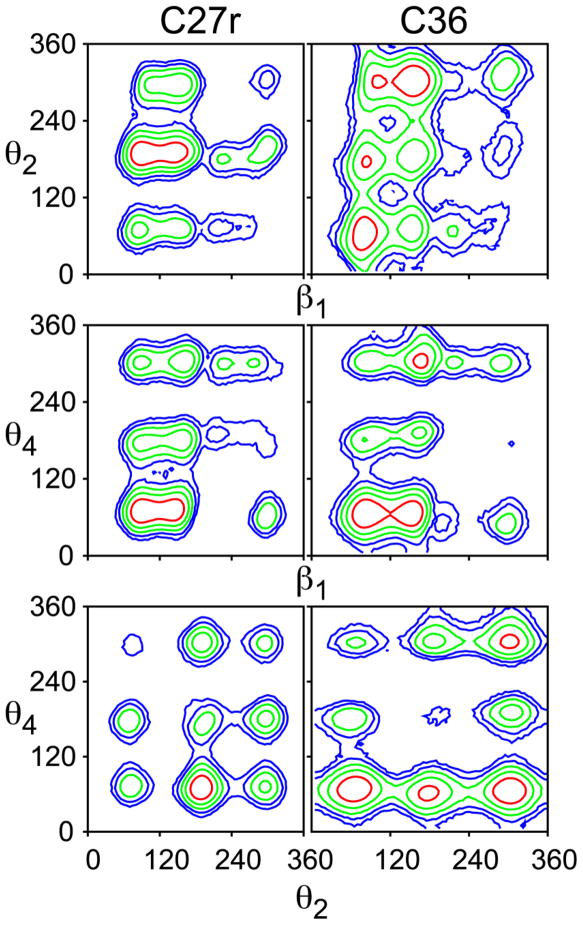
For the first stage of the validation of the force field parametrization, simulations of DPPC bilayers were performed at a constant surface area of 64 Ų/lipid (NPAT ensemble), which is close to the experimental value of 63±1 Ų/lipid.⁸⁷ As discussed in the introduction, the deuterium order parameters, S_CD, from the C27r simulations lack proper splitting of the first carbon on the aliphatic chain (sn-2 C2) and demonstrate large disagreement with the glycerol (CG1–CG3) carbons (Fig. 3, top). The results based on the C36 FF are a dramatic improvement for these carbons (Fig. 3, bottom). The S_CD for C2 of the sn-1 chain should be higher than those of the sn-2 chain and simulations with C36 agree with these measurments.^25,26 There is some splitting of the two C2 hydrogens of the sn-2 chain, albeit not to the extent of experiment. Order parameters for the CG1–CG3 carbons with C36 are substantially better than those from C27r. Since the three torsions that primarily control these order parameters (β₁, θ₂, and θ₄) were empirically optimized, this agreement is expected. However, to our knowledge this is the first FF to accurately capture the chain order splitting for all carbons. The contour plots in Fig. 4 highlight the complexity of the glycerol torsion surfaces, and the qualitative differences between C27r and C36. Moreover, the θ₄/β₁ torsional surface of C36 compares well with that of MP2/6-31g(d) scans (Fig. S2, right).

Figure 3.

NMR deuterium order parameters (S_CD) for a DPPC bilayer from experiment²⁵–²⁷ and NPAT simulations with A=64 Ų/lipid, which is close the experimental surface area.

Figure 4.

Contour maps of potentials of mean force from simulations for the glycerol torsions in hydrated DPPC bilayers for C27r and C36. Contours are at 1 kcal/mol intervals, with the red lines 1 kcal/mol above the global minimum for each surface.

The S_CD of the α carbon of the choline is reduced with C36 and is the result of ab initio-based torsional fits to the α₄ dihedral. The carbonyl C=O and ester C-O order parameters (0.26 and 0.15, respectively) for the sn-2 chain have been measured using infrared spectroscopy.⁸⁸ MD simulations with C36 agree well with these experimental values (0.26/0.14) and are an improvement compared to C27r (0.18/0.13). These torsional changes for the head group have a minimal effect on the aliphatic chain and these S_CD are nearly identical between DPPC bilayer simulations with C27r and C36.

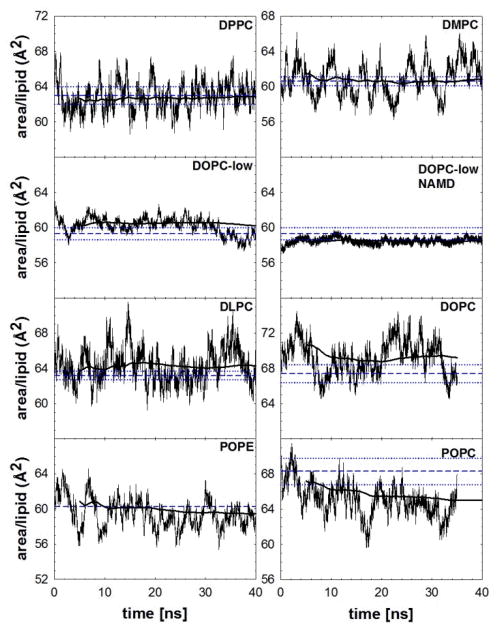
The main issue with previous versions of the CHARMM lipid FF was that NPT bilayer simulations with fully saturated lipids, such as DPPC, condensed to surface areas near that of the gel state above the transition temperature.^17,24 As shown in Fig. 5 and Table 6 for DPPC and the other lipids under study (discussed in detail below), this flaw is almost entirely rectified. MD NPT simulations for DPPC using two cutoff schemes (see Methods) also result in stable surface areas that are close to the experimental surface area for simulations up to 130 ns (Table 6 and Fig. S3). Since the tensionless bilayer has an average surface area close to experiment, the S_CD calculated from NPT C36 simulations are similar to the NP(A=64)T simulations and agree with experiment (Fig. S4).

Figure 5.

Surface areas versus time for the seven lipid systems considered in this study. Medium dashed lines show experimental values with dotted lines for mean ± standard error; heavy solid lines show the cumulative average beginning at 5 ns. Unless noted, all systems are at high hydration.

Table 6.

Average surface areas for the NPT ensemble bilayer simulations are reported based on values after area equilibration. The surface tensions are also reported for the NPAT lipid bilayer. Unless noted the simulations were based on the CHARMM program with standard cutoffs. For the DOPC simulations the low hydration (lo) was at a relative humidity (RH) of 66% and the high hydration was 100% RH.

Lipid	Ensemble	Area [Å2/lipid]	Surface Tension [dyn/cm/side]	Exp. Area [Å2/lipid]
DPPC	NPT	62.9±0.3		63.0±1.087
	NPTa	59.1±0.4
	NPAT	60	−5.8±0.9
		62	−2.3±0.7
		64	1.7±0.8
		66	5.2±0.7
		68	7.3±0.6
DMPC	NPT	60.8±0.2		60.6±0.516
DLPC	NPT	64.4±0.3		63.2±0.593
DOPC	NPT-lo	60.1±0.1		59.3±0.7105
	NPT-hi	69.0±0.3		67.4±1.087
	NPTa	58.5±0.3		59.3±0.7105
POPC	NPT	64.7±0.2		68.3±1.594
POPE	NPT	59.2±0.3		59.75–60.75b

^avalues from NAMD simulations with slightly different cutoffs

^bbased on reported volumes and phosphate-to-phosphate distances at 308 and 313 K⁹⁶

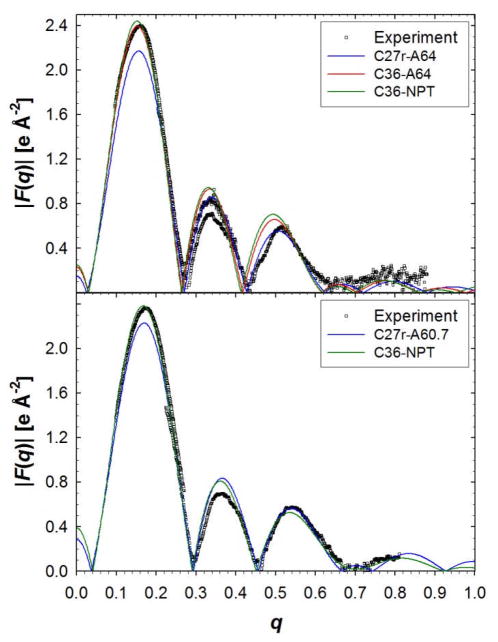
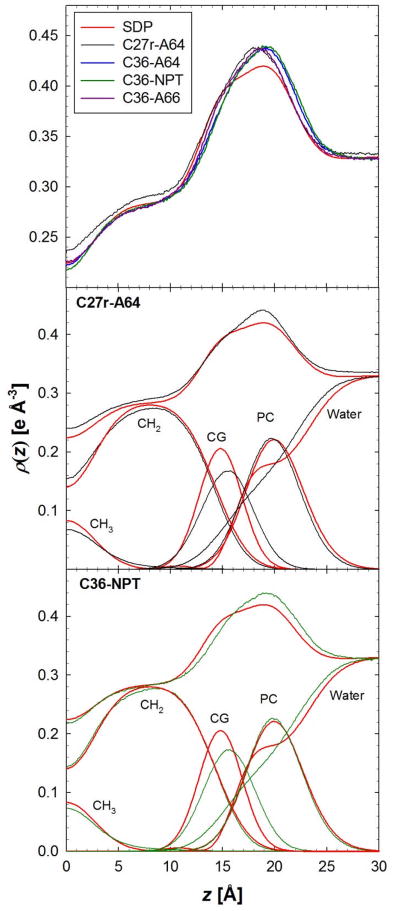
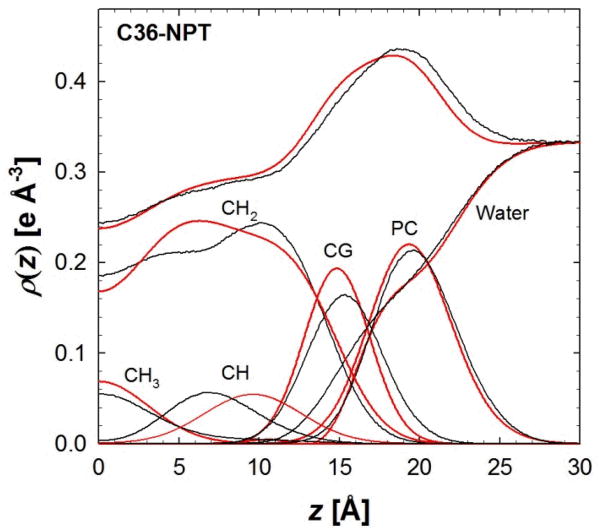
The order parameters are an excellent measure of molecular order but do not describe the overall structure of the bilayer. For this, the bilayer simulations are compared to x-ray diffraction data, i.e., form factors and electron density profiles as obtained by the SDP structural model ⁸⁷ (Figs. 6 and 7). The form factors offer a direct comparison with experiment that prevents errors that might be associated with structural models or inverse Fourier transforms.^16,18,89 There is excellent agreement between experimental form factors, F(q), and bilayer simulations with C36 (Fig. 6). The root mean squared deviation (RMSD) from experimental F(q) for simulations with the C27r FF is less than C36 with a surface area of 64 Ų/lipid. The minimum RMSD for C36 was for the 66 Ų/lipid, which is likely the result of a slight reduction of the electron-rich head group density (Fig. 7). There is a significant improvement in the electron density for the hydrocarbon region with C36 (Fig. 7). The density at the center of the bilayer is too high with C27r and is reduced with C36 with the NP(A=64)T and NPT simulations. The carbonyl-glycerol (CG) distribution is broader and slightly shifted with C36 compared to C27r, but the phosphate-choline (PC) distribution is improved.

Figure 6.

Form factors of DPPC (top) and DMPC (bottom) bilayers from experiment¹⁶,⁸⁷ and MD simulations. For DPPC, the NPAT simulations are labeled with A64 for 64 Ų/lipid. For DMPC, the C27r simulations were run in the NPAT ensemble with 60.7 Ų/lipid (A60.7) and the C36 simulations were run with the NPT ensemble.

Figure 7.

Electron density of a DPPC bilayer from an experimental structural model (SDP)⁸⁷ and MD simulations. NPT simulations with PME are labeled as NPT and constant surface area (64 Ų/lipid) is labeled as A64.

The excellent agreement between simulated and experimental surface areas for DPPC is borne out by the area isotherm at 323.15K where the zero surface tension lies between 62 and 64Ų/lipid (Table 6). This simulated data also allows estimation of the area compressibility modulus, K_A, from the relation³⁰

$$K_A=2A_0{\left(\frac{\partial \gamma }{\partial A}\right)}_T$$ (4)

where A₀ is the equilibrium area, here set to the experimental value of 63 Ų/lipid; the factor of 2 is required when surface tensions for bilayers are expressed in dyn/cm/side Using all 5 data points (60 to 68 Ų/lipid) and their standard deviations yields K_A = 207± 14 dyn/cm; K_A= 236 ± 31 dyn/cm when only the three middle points (62 to 66 Ų/lipid) are used. These are in substantially better agreement with the experimental value of 234 dyn/cm⁹⁰ than the 138 ± 26 dyn/cm obtained for C27r.³⁰

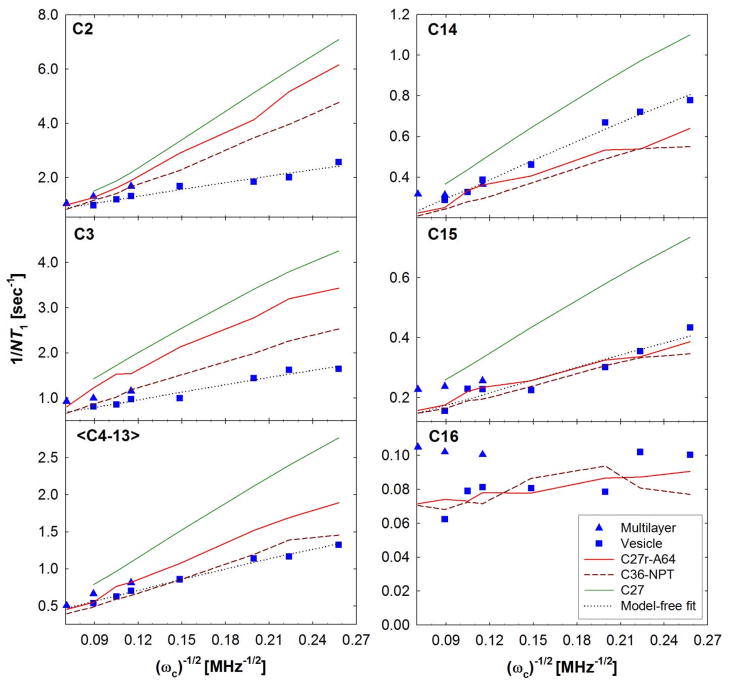
Fig. 8 compares the spin lattice relaxation rates from ¹³C NMR^27,91 experiments with those calculated with the C27,⁹² C27r²⁷ and C36 FFs. The C36 calculated NMR T₁ for the head group carbons (Fig. S5) are in excellent agreement with experiment and are similar to C27r (NPAT). As shown previously,²⁷ C27r is a significant improvement over C27 due to changes in the torsional barrier for alkanes. C36 is in similar agreement for C14 to C16. Although C27r and C36 both agree with the high frequency measurements for all aliphatic carbons, C36 significantly improves the frequency dependence at low Larmor frequencies for the center of the chain and those near the glycerol (C2 and C3).

Figure 8.

Lipid chain relaxation rates (1/NT₁) for a DPPC bilayer as a function of Larmor frequency (ω_c)^−1/2. Simulation relaxation rates for C36 are calculated using the NPT ensemble and compared to previous C27r (NPAT)²⁷ and C27 (NPAT) results.⁹² These are compared with measurements with multilayers²⁷ and sonicated vesicles.⁹¹

4.2 Lipids other than DPPC

Although the C36 FF was successful at reproducing many experimental observables for DPPC bilayers, additional lipid bilayers were simulated to test the transferability of these parameters to various systems. An experimental observable for fully saturated chains of lengths 12–16 carbons in PC-containing lipids is the surface area per lipid, which has a minimum when the aliphatic chain contains about 14 carbons (DMPC).^16,87,93 MD simulations with C36 and the NPT ensemble accurately capture this dependence of surface area per lipid on chain length (Table 6). Moreover, the agreement between experiment and simulation surface areas is excellent for the NPT simulations of DPPC, DMPC, and DLPC. The density profiles and experimental form factors are in similar agreement for the DMPC bilayers (Fig. 6, bottom) using both FFs. However, MD simulations with C27r require constant area simulations, whereas C36 does not.

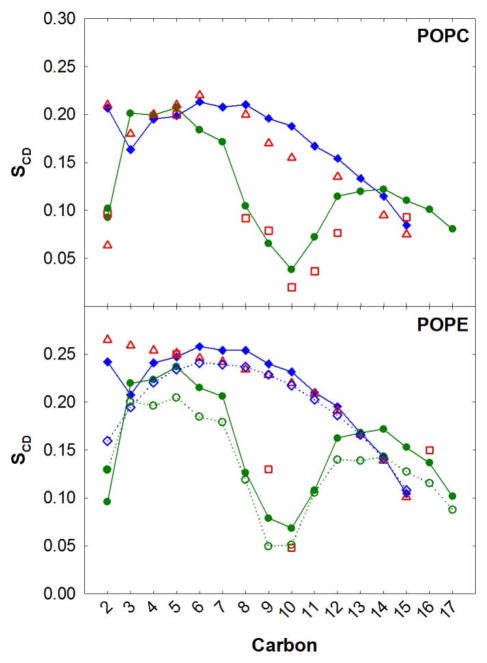
Saturated lipid chains are common in many cellular membranes, but lipids with unsaturated chains are also prevalent. Therefore, a successful FF should also reproduce experiments on these lipids. POPC contains one chain that is fully saturated and another chain with a single double bond. The surface area per lipid for POPC using C36 and the NPT ensemble (64.7±0.2Ų/lipid) is slightly lower than the experimental estimate 68.3±1.5 Ų/lipid.⁹⁴ The NMR deuterium order parameters with C36 NPT simulations are in excellent agreement with experiment^28,29 (Fig. 9, top). The agreement is nearly perfect for the fully saturated chain (sn-1), including the dip carbon position 3. C36 also reproduces the splitting of the order parameters at carbon position 2 for the sn-2 chain, and the characteristic drop large around the double bond.

Figure 9.

NMR deuterium order parameters (S_CD) for POPC and POPE bilayers. For the MD simulations the sn-1 and sn-2 chains are in blue and green, respectively. The solid lines are based on results from NPT simulations with C36 and the dashed lines based on NP(A=60)T with C27r for POPE. Experiment is shown in red: the sn-1 (308 K)⁹⁸ chain is in open triangles and sn-2 (310 K)²⁸ chain in open squares.

For a lipid bilayer with both chains unsaturated, i.e., DOPC, the C36 NPT simulations are in good agreement in the lateral and profile densities. The average surface area per lipid is slightly higher than experiment (Table 6), though within 2 standard errors of the experimental uncertainty. The overall density profiles of C36 agree favorably with the experiment (Fig. 10).⁸⁷ The density is slightly higher to the right of the peak and likely the result of a broader carbonyl-glycerol distribution and increase in water hydration. The overall density in the hydrocarbon region of the bilayer is in excellent agreement with experiment. However, the individual component densities disagree. The location of the carbons associated with the double bond (CH) is closer to the bilayer center than the SDP model. The SDP model is based on a combination of x-ray and neutron scattering measurements. Surprisingly, the simulation CH density is in better agreement with the neutron results,⁸⁷ where models fit to this data place the double bond closer to the bilayer center. This discrepancy between simulation and experiment will require a more detailed study to address whether this is a slight issue with simulation or the experimentally-based SDP model.

Figure 10.

Electron density of a DOPC bilayer from an experimental structural model (SDP)⁸⁷ and MD simulations. NPT simulations are in black and the SDP model is in red.

All of these abovementioned simulations were based on fully hydrated lipid bilayers. MD simulations of DOPC at 66% relative humidity (RH) or low hydration (lo) were used to further test NPT simulations with C36. Previous simulations using the C27 FF resulted in condensation and low surface areas per lipid for DOPC using the NPT ensemble (56.5±0.3 Ų/lipid),¹⁸ while using the C36 FF there is excellent agreement between simulation and experiment (Table 6).

The spatial distribution of selected moieties along the lipid normal can be determined using neutron scattering experiments. This is due to the ability of neutrons, in contrast to X-ray based methods, to detect hydrogen and to differentiate between hydrogen and deuterium. The extent of water penetration into the lipid bilayer normal can be probed using neutron scattering. The Gaussian water distributions from the experimental work of Weiner et al.⁹⁵ along with those from MD simulations of DOPC using C27 and C36 are compared in Figure 11. It is evident that the distribution is broader and is shifted to distances further away from the center of the lipid bilayer for C27r as compared to experiment. These differences highlight the limitations in the C27 FF associated with the solvation of the head group region, and led to the reevaluation of the ester non-bond parameters presented above. In the resulting C36 FF, the simulated distribution is narrower and shifts back towards the center of the lipid bilayer. The better agreement with the distribution obtained from the neutron scattering experiments with respect to both mean and width indicates that the optimized parameters lead to improved solvation of the phosphatidyl and acyl ester regions of the lipid, which, in turn, helps maintain the area/lipid near the correct values.

Figure 11.

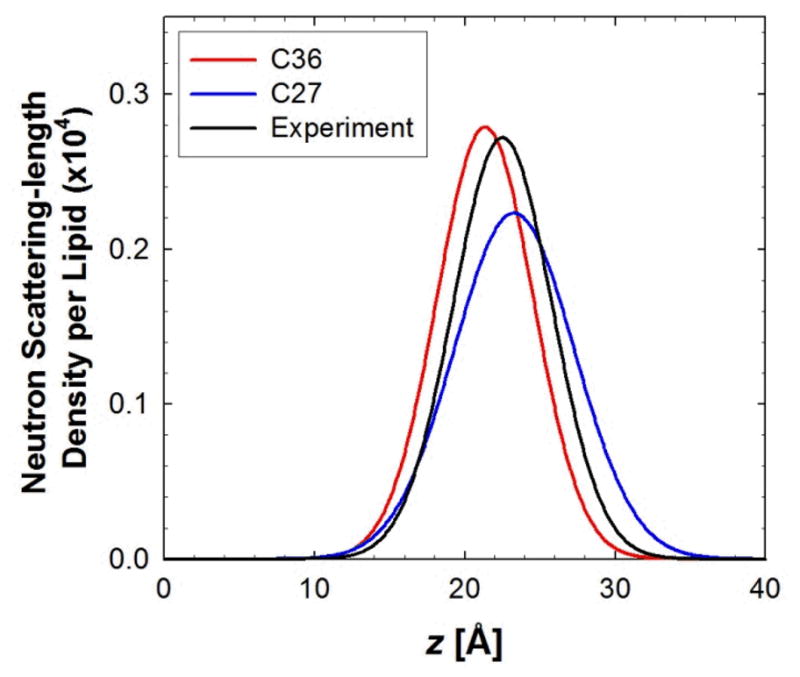
Water distributions in DOPC bilayers at low hydration from neutron diffraction experiments and NPT simulations. The experimental Gaussian distribution for a single bilayer leaflet⁹⁵ is compared to C36 and C27 simulations.

The last test of the C36 FF was on a lipid bilayer with a different head group, i.e., phosphatidylethanolamine (PE). The average lateral surface area per lipid for MD simulations with C36 and NPT was 59.2±0.3 Ų/lipid, which agrees with x-ray measurements (Table 6).⁹⁶ Since the experimental areas are at different temperatures than simulation and the resolution is lower than other lipids reported above, another way to test the validity of the lateral surface area is to compare with NMR deuterium order parameters, which are sensitive to the average area per lipid.⁹⁷ The agreement between S_CD values from experiment^28,98 and C36 NPT simulations is excellent for the sn-1 and sn-2 chains (Fig. 9, bottom). A dip in the S_CD is not observed for the carbon 3 position of POPE sn-1 chain,⁹⁸ but a slight lowering of the S_CD was calculated with the C36 NPT simulations. Since this non-monotonic decrease in chain order is measured for the POPC bilayers, the POPE measurement might be slightly in error for carbon 3. Aside from this slight discrepancy, C36 NPT simulations agree favorably with the S_CD values and do not require NPAT simulations that at 60 Ų/lipid would result in a bilayer surface tension of 27.8±1.2 dyn/cm with the C27r FF.

5. Limitations of C36

5.1. Dipole Potentials

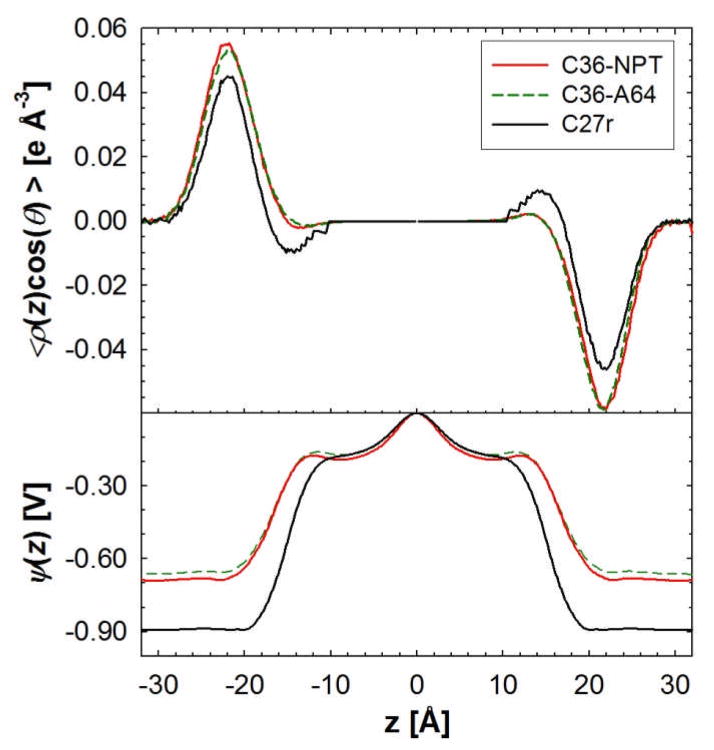
The precise experimental values of the dipole potential drop (Δψ) for bilayers and monolayers remain somewhat controversial,⁹⁹ and the simulated values are very sensitive to the definition of the charge distribution.¹⁰⁰ Nevertheless, evaluation of Δψ provides a useful comparison for parameter evaluation. Figure 12 compares the dipole orientation (top) and profile of the potential (bottom) for C36 and C27r. The location of the maximum of the water dipole in the choline region is identical for the C27r and C36 FFs. However, the angle of the dipole with respect to the interfacial plane is slightly larger at this location, i.e., 15.1° (C36) vs. 12.2° (C27r). Both sets show a similar approximate 200 mV Δψ from the bilayer center (z=0) to the head group region; this is expected because the acyl chains are unmodified (and nonpolarizable). The head group to water Δψ for C36 is approximately 500 mV, which is 200 mV smaller in magnitude than with C27r. These values are, nevertheless, substantially larger than the consensus experimental range of 225–250 mV.⁹⁹

Figure 12.

(top) The orientation of the water dipole with respect to the positive z-axis, scaled by the electron density for the DPPC bilayer at constant surface (64 Ų/lipid, A64) and NPT simulations. Simulations with the C27r FF were run at NP(A=64)T. The electrostatic potential drop for the bilayer simulations is shown in the bottom panel.

5.2. Inconsistent Surface Tensions of Bilayers and Monolayers

Simulation results presented so far have been carried out with PME and with a force switch on the Lennard-Jones terms. Hence, while long-range electrostatic interactions have been included, the long-range LJ interactions have been neglected. This is fairly standard methodology, and most simulation programs do not even contain provisions for including long-range LJ interactions. Hence, it is arguable that a parameter set that requires these terms is less generally useful that a set that does not.

However, alkane/air interfaces and lipid monolayers (which contain an alkane-like/air interface) are sensitive to long-range LJ forces.^15,101 Consequently, if a lipid FF is to be applied to monolayers, the impact of long-range LJ forces and consistency with bilayers must be considered. Such an analysis was recently carried out on DMPC for C27r using 3D-IPS/DFFT, a method developed by Wu and Brooks¹⁰² that can be applied to treat long-range electrostatic or LJ terms. While surface tensions of DMPC lipid monolayers agreed well with experiment when simulated with PME(r_c=12 Å), they increased by 8–10 dyn/cm when simulations were carried out 3D-IPS/DFFT. In contrast, the bilayer surface tensions were similar when simulated using the two methods; i.e., the DMPC bilayers did not appear to be sensitive to long-range LJ interactions for C27r. To determine if this trend holds for C36, the bilayers discussed earlier and DPPC monolayers were simulated with PME and 3D-IPS/DFFT.

Table 7 compares the calculated monolayer surface tensions with experiment. In contrast to previous results just described, results with 3D-IPS/DFFT used to treat both the electrostatic and LJ long-range contributions agree with experiment, and those with PME(r=12) are substantially lower than experiment. Some of the long-range LJ interactions that lowered γ for DPPC bilayers have also lowered it for the monolayers. This result implies that bilayer surface tensions for C36 will be too high when long-range LJ are included. This is indeed the case. Simulations of DPPC at areas of 60, 62, 64, 66, and 68 Ų/lipid with IPS-3D/DFFT yield surface tensions of 6.3±0.9, 11.0±1.0, 10.7±0.7, 14.1±0.8, and 16.6±0.7 dyn/cm/side, respectively. Similarly, the surface areas of DPPC and other bilayers contract when they are simulated at NPT and 3D-IPS/DFFT (data not shown).

Table 7.

Surface tensions in dyn/cm of the DPPC monolayer at 323 K (simulations) and 321 K (experiment).¹⁰⁶

Area [Å2/lipid]	IPS DFFT	PME rc=12 Å	Experiment
54	17.8±1.3	−7.0±1.2	17.9
64	43.9±0.8	26.4±1.0	40.9
80	59.5±0.5	43.8±0.4	54.9

6. Discussion and Conclusions

A CHARMM-FF consistent approach was used to modify the atomic charges and LJ parameters of the glycerol moiety of a phospholipid (Table 5). The modifications to the CHARMM FF were suggested by semi-empirical QM calculations of the full DPPC lipid in vacuum and in a realistic environment, and the incomplete hydration of the head groups observed in bilayer simulations³¹ This also agrees with a recent test on the CHARMM FF that suggested head group parameter modifications are needed.¹⁰³ The dipole moment of methylacetate was correctly described by the C36 charge modification (Table 4) and this resulted in an increase in the dipole moment of the carbonyl of both lipid chains. Consequently, there is an increase in hydration of lipid bilayers with C36 leading to good agreement with neutron scattering experiments on DOPC (Fig. 11). The location of the water distribution is shifted slightly inward compared to experiment and may be associated with the overestimation of the free energy of solvation of methylacetate as presented above. However, this overestimation was motivated by the QM charge calculations and facilitated the improved estimate in the DPPC surface area per lipid with NPT simulations.

A total of six lipids were simulated with the NPT ensemble and the surface areas are in very good agreement with experiment (Table 6 and Fig. 5). Deviations from experimental areas average 2%, with a maximum overestimate of 2.4% (DOPC) and a maximum underestimate of 5.3% (POPC). In contrast, C27r simulations with fully saturated chains condensed to values close to gel-like areas.^18,24,104 Although this is not the first effort to obtain a CHARMM-compatible lipid FF that can use a tensionless ensemble,^17,24,32 C36 is the only FF that obtains these charges in a CHARMM-FF consistent manner.²⁰ Moreover, the stability of the surface area from these simulations has been verified to 130 ns for DPPC (Fig. S3). The ability of C36 to reproduce the correct area for saturated and unsaturated chains implies that simulations with mixtures of lipids, cholesterol and proteins can be performed with the CHARMM family of FF without imposing a surface tension.

The deuterium order parameters for carbons in the glycerol and head group region of the lipid are well described using the C36 FF. Although the S_CD splitting is not perfect for carbons near the glycerol moiety (C2/CG1) (Figs. 3, 9, and S4), C36 is a substantial improvement over C27r, and demonstrates that C36 is fundamentally more sound in describing intramolecular conformations near the glycerol moiety. This splitting is not limited to the target DPPC lipid used to modify the C36 FF, but is also observed for other lipids, such as POPC and POPE.

Although the three abovementioned properties were initial targets for the lipid FF modifications, agreement with experimental measurements were also observed for several other properties. First, the lipid bilayer form factors and their real-space counterparts (electron densities) are in excellent agreement with experiment (Figs. 6, 7, and 10). The hydrocarbon density at the center of the bilayer is in near perfect agreement with experiment for both saturated and unsaturated bilayers, which was not the case for simulations for C27r. Moreover, the total density profiles of C36 match well with the experimental models. There is an increase in the width of the carbonyl-glycerol distribution compared to experiment and C27r and a slight increase in water hydration and penetration into the fully hydrated bilayers. However, these discrepancies are small and suggest a more detailed investigation of the source of these differences is needed, which is beyond the scope of this lipid parametrization.

Simulations with the C36 FF result in a significant increase in the rigidity of the membrane to respond to area changes. The C36 calculated area compressibility modulus for DPPC was increased by nearly 100 dyn/cm when compared to C27r. This resulted in a value that was within statistical uncertainty of experiment.⁹⁰

The calculated ¹³C NMR relaxation rates for the aliphatic chain and head group are improved with C36. The dependence on the Larmor frequency is better with C36 for aliphatic carbons near the head group (C2 and C3) and those at the center of the chain (Fig. 8). The slow relaxation times are decreased with C36 and thus lead to a decrease in the dependence of the relaxation rates on the Larmor frequency. Although the frequently dependent relaxation rates for C2 remain hard to obtain with simulation, values for the other aliphatic carbons agree well with the experiment.^27,91

A limitation of the C36 FF is the approximate treatment of long-range LJ forces. While the inclusion of long-range LJ with 3D-IPS/DFFT in simulations with C36 improves results for monolayers, the increased surface tension renders it unsuitable for bilayers. Hence, simulations of bilayers with C36 should be carried out with PME with r_c=10 or 12 Å and no long-range correction for the LJ term. These conditions, however, will lead to underestimates of the surface tensions of lipid monolayers. It is possible that a set of adjustments could be developed so that bilayers and monolayers can be treated consistently with all long-range forces included, though this is not necessarily practical given that most simulation programs do not support evaluation of long-range LJ terms.

In conclusion, C36 is a significant update to the C27/C27r lipid force field. This FF was developed in a CHARMM-FF consistent manner, assuring the utility of the model for the treatment of heterogeneous biomolecular systems. Simulations with C36 improve the hydration of lipids near the carbonyl-glycerol section of phospholipids and allow for the use of a tensionless ensemble (NPT) in MD simulations. Although there are some limitations with respect to the treatment of long-range LJ interactions, this is likely not a major concern for most applications. Future work is currently underway to add additional lipids to CHARMM, such as, sphingolipids, phosphatidylinositols, and those with branched aliphatic chains. Since C36 NPT simulations result in stable liquid crystalline bilayers, future NPT membrane simulations with peptides, membrane proteins, and lipid mixtures should not result in unrealistic gel-like structures above the gel-to-fluid transition temperature.