Abstract
The current state of the art for linear optimization in Flux Balance Analysis has been limited to single objective functions. Since mammalian systems perform various functions, a multiobjective approach is needed when seeking optimal flux distributions in these systems. In most of the available multiobjective optimization methods, there is a lack of understanding of when to use a particular objective, and how to combine and/or prioritize mutually competing objectives to achieve a truly optimal solution. To address these limitations we developed a soft constraints based linear physical programming-based flux balance analysis (LPPFBA) framework to obtain a multiobjective optimal solutions. The developed framework was first applied to compute a set of multiobjective optimal solutions for various pairs of objectives relevant to hepatocyte function (urea secretion, albumin, NADPH, and glutathione syntheses) in bioartificial liver systems. Next, simultaneous analysis of the optimal solutions for three objectives was carried out. Further, this framework was utilized to obtain true optimal conditions to improve the hepatic functions in a simulated bioartificial liver system. The combined quantitative and visualization framework of LPPFBA is applicable to any large-scale metabolic network system, including those derived by genomic analyses.
Keywords: Bioartificial Liver, Hepatocytes/Linear Physical Programming, Metabolic Networks, Multiobjective Optimization, Pareto Optimality
INTRODUCTION
Metabolic flux analysis (MFA) provides a framework for the estimation of intracellular metabolic fluxes at steady-state based on stoichiometric constraints of a metabolic pathway network. This technique, which has been extensively used for studying the metabolism of microorganisms (Antoniewicz et al., 2007a; Antoniewicz et al., 2007b; Stafford et al., 2002; Wong et al., 2004; Young et al., 2008), has been recently applied to characterize and compare different physiological states in mammalian systems (Banta et al., 2004; Chan et al., 2003a, b; Chan et al., 2002; Chan et al., 2003c; Ghosh et al., 2006; Lee et al., 2004; Nolan et al., 2006; Vo et al., 2004) . For validation of the MFA obtained intracellular metabolite fluxes, tracer based methods that commonly use 13-C labeling is used for quantifying invivo fluxes (Maier et al., 2008; Yoo et al., 2008). In order to obtain a unique solution for the flux distribution in a particular cell or tissue system, a minimum number of measurements of rates of uptake and release of extracellular metabolites by the system is needed. In cases where insufficient measurements are available, pathway fluxes have been predicted using linear optimization for one objective function, such as growth rate for unicellular organisms (Cox et al., 2006; Khannapho et al., 2008; Savinell and Palsson, 1992). Mammalian systems, such as hepatocytes, typically do not undergo cell proliferation, but rather perform an array of metabolic functions (protein secretion, detoxification, energy production), therefore different and multiple objectives need to be taken into account. Hepatocytes are the major cell type in the liver with multiple functions including efficient uptake and subsequent metabolic conversion of amino acids, carbohydrates, lipids, and vitamins. Subsequently, these nutrients are either stored or released after biochemical transformations. These biochemical processes make hepatocytes the epicenter of the metabolic modulation of intermediary metabolism in the body, and thus can play an important role in biotechnological applications that use liver cells, such as bioartificial liver (BAL) devices. A recent analysis concluded that several objectives were necessary to profile metabolic information from perfused livers (Lee et al., 2004). Another study (Nagrath et al., 2007), combined both energy and flux balance based nonlinear multiobjective framework for hepatic systems. Recently, Bayesian (Knorr et al., 2007) and optimization (Burgard and Maranas, 2003) based techniques have been developed for selecting objectives.
Multiobjective optimization strategies previously used for MFA, such as weighted optimization and goal programming, suffer from several limitations. For example, it is often unclear when to use a particular objective and how to combine and/or prioritize mutually competing objectives to achieve a true optimal solution. Furthermore, visualization of the results is not straightforward. Importantly, most of the existing MFA methods employ “hard constraints” for the estimation/distribution and optimization of intracellular fluxes in metabolic networks. Burgard and Maranas (Burgard and Maranas, 2003) had developed an optimization-based framework for testing whether maximization of a weighted combination of fluxes can explain a set of observed experimental data. Their approach is based on weighted-sum (WS) based optimization and utilizes weights defined as the coefficients of importance to quantify the additive contribution of a given flux to a objective function. The limitations of using WS based approach are: (1) weights are arbitrary and have no physical meaning; (2) the spacing of optimal soluions is largely dependent on relative scaling of weights thus often leads to ill-conditioned problems; (3) an even distribution of scalar weights in WS does not yield an even optimal flux solutions; and (4) WS fails to capture the Pareto optimal solutions where the Pareto frontier is non-convex. Here we introduce a multiobjective optimization based flux balance analysis approach, LPPFBA (Linear Physical Programming-Based Flux Balance Analysis), that employs Linear Physical Programming (LPP) (Maria et al., 2003; Messac, 2000)(Figure 1A), which enables the formulation of the optimization problem in terms of physically meaningful terms and parameters, and addresses the problems that exist in the previously used strategies by employing “soft constraints”.
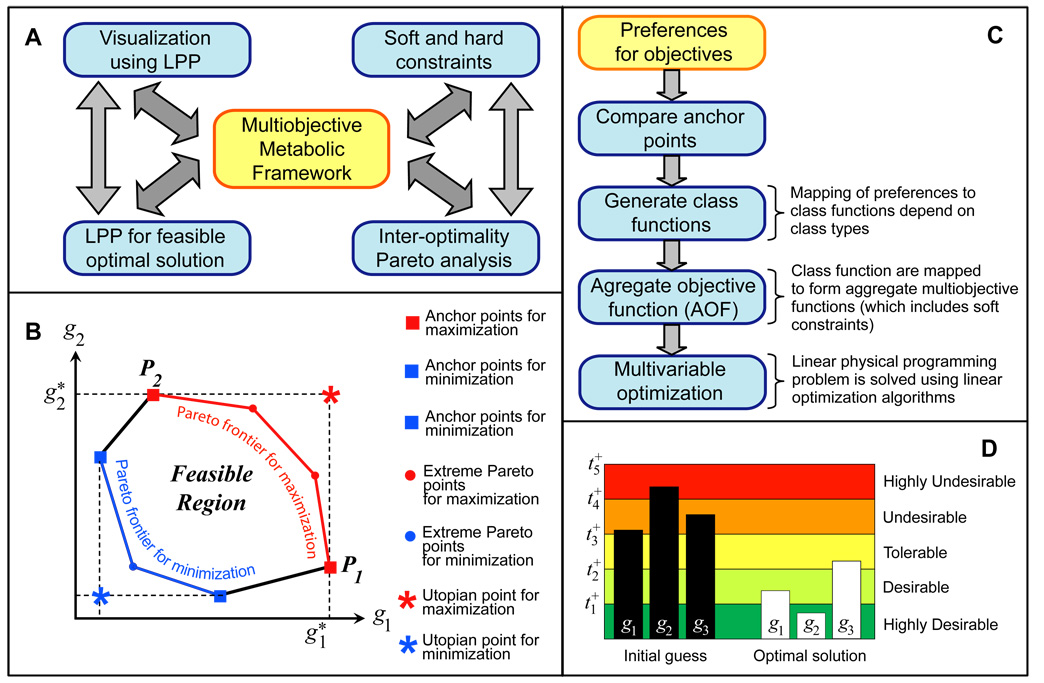
Figure 1.
A) Characteristics of Linear Physical Programming based multiobjective metabolic network. B) Pareto frontiers and extreme Pareto points shown for a bi-objective maximization and minimization problems. C) Strategy for Linear Physical Programming based multiobjective optimization. D) LPPFBA visualization window. Multiobjective optimal solutions are displayed as bar graph in color coded regions, with highly desirable solution being green and highly undesirable being red.
In LPPFBA approach, first a set of so-called Pareto-optimal solutions is generated. A solution is said to be Pareto-optimal if there are no other solutions that can better satisfy all of the objectives simultaneously (Nagrath et al., 2005). In other words, any improvement in one objective necessitates the worsening of at least one other objective. In our specific application, we generate Pareto frontiers of optimal metabolic fluxes to identify potential solution regions that provide a qualitative framework to assess the situation, and in particular, to determine the objectives that are conflicting. Second, we employ LPPFBA to prioritize the objectives and constraints. In LPPFBA, attributes of interest for each objective are defined to delineate degrees of desirability: unacceptable, highly undesirable, undesirable, tolerable, desirable, and highly desirable. Thus, LPPFBA completely eliminates the need for iterative weight setting, which is the object of the typical computational bottleneck in large optimization problems. Two key advantages of LPPFBA for metabolic flux optimization are: (1) once the preferences are articulated, obtaining the corresponding optimal fluxes is a non-iterative process – in stark contrast to conventional weight-based methods; and (2) it provides the means to reliably employ optimization with minimal prior knowledge thereof.
In this paper, we present a LPPFBA approach for analyzing the multiobjective flux analysis of metabolic networks. The developed approach was then utilized for optimizing the metabolism of liver cells in the context of bioartificial liver (BAL) development. BALs are being developed to provide hepatic support to patients with fulminant hepatic failure (Chan et al., 2003a, b; Chan et al., 2002; Chan et al., 2003c). One of the major design goals of BAL devices is to maintain viable hepatocytes that perform a high level of liver-specific functions (for example, albumin synthesis, urea secretion, cytochrome p450–mediated detoxification, etc.) (Berthiaume et al., 1996; Chan et al., 2002; Dunn et al., 1991). Obtained Pareto optimal metabolite fluxes were computed for various combinations of liver specific functions. Next, we obtained Pareto optimal solutions for tri-objective combinations of these hepatic functions. Lastly, we obtained the Pareto solutions for a simulated BAL system where the main goal was to operate the BAL at the highest possible level during human plasma exposure. This analysis exhibited that although lipid and carbohydrates fluxes may be similar but for hepatocytes amino acid synthesis, catabolism, is altered/rerouted in optimality analysis for maintaining hepatic functions
MATERIALS AND METHODS
Flux Balance Analysis
The stoichiometric coefficients of the metabolic reactions are collected into a matrix S , where each element sij is the coefficient of metabolite i in reaction j. S has dimensions of M × N, where M is the number of metabolites and N is the number of reactions. In matrix form the mass balance is written as:
| (1) |
where each element xi of x is the intracellular concentration of metabolite i and element Ji of J is the net rate of conversion in reaction j. External metabolite fluxes are generally measured (e.g., uptake of glucose, lactate, amino acids). Because of the very high turnover of the intracellular pools of most intracellular metabolites, the time scale of the intracellular metabolic reactions is short compared to other cellular reactions. Hence, the pseudo steady state assumption is generally applied to the metabolite mass balances, and thus
| (2) |
When the number of measured quantities is less than the number of measurements required for the system to be determined, the computation of unknown intracellular fluxes requires linear optimization (since infinite number of solutions exist) with linear bound constraints. Mathematically, this can be expressed as:
| (3) |
subject to
| (4) |
| (5) |
where the vector c specifies which unknown flux vector elements are to be maximized (or minimized); vectors Jlow and Jhigh provide the lower and upper bounds for the unknown fluxes; Jm and Ju indicate measured and unmeasured fluxes, respectively; and Sm and Su contain the stoichiometric coefficients of measured and unknown reactions, respectively.
Hepatocyte Metabolic Network
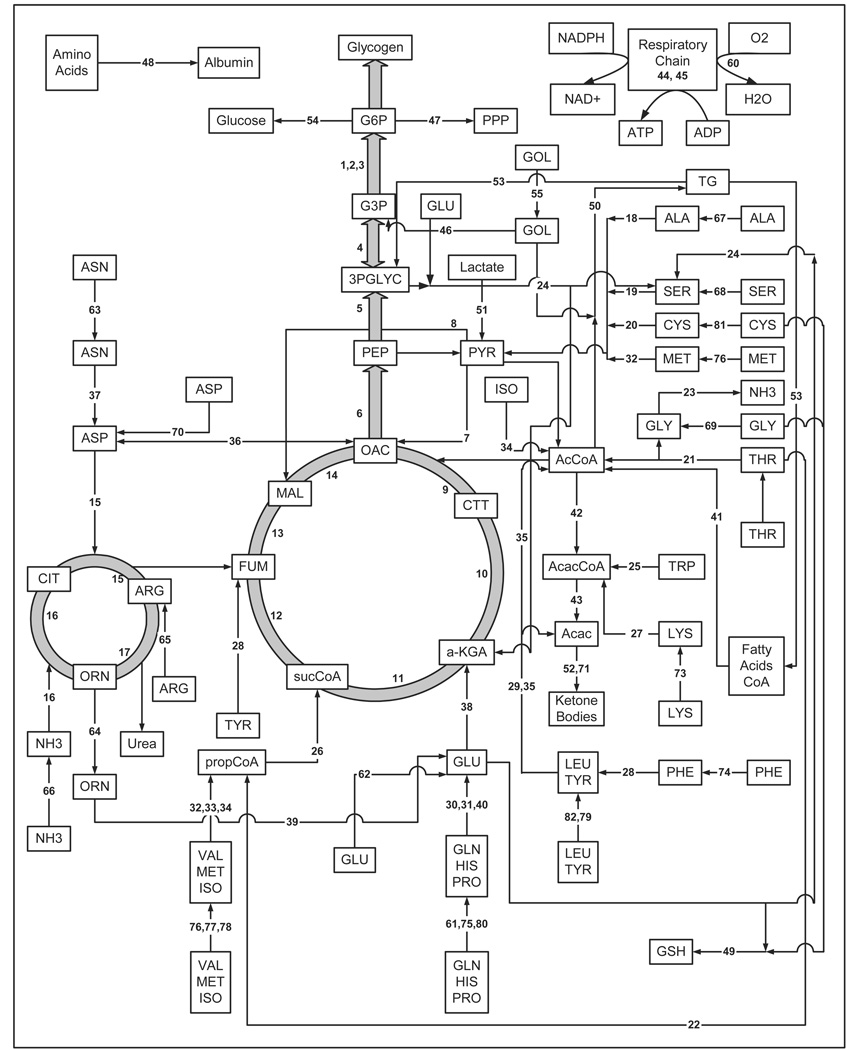
A previously described hepatic metabolic network (Chan et al., 2003b; Chan et al., 2002) includes all of the major intracellular pathways to account for the majority of central carbon and nitrogen metabolism found in hepatocytes, namely the tricarboxylic acid (TCA) and urea cycles, the gluconeogenic and glycolysis pathways, the pentose phosphate shunt, pathways of entry, transamination, and deamination of amino acids, protein synthesis, and the major components of lipid metabolism, including triglyceride synthesis and breakdown and β-oxidation of fatty acids, in addition to amino acid synthesis and apolipoprotein degradation. The current hepatic metabolic network model (Table S1) includes a few additional reactions, namely those of the 3-phosphoglycerate cycle as it is involved in glycerol production and glutathione synthesis, which results in a total of 81 reactions (as compared to 76 reactions in the previous model) and 47 metabolites (Table S2). Figure 2 presents the comprehensive hepatic metabolic network. The rationale for including glutathione synthesis is that glutathione is involved in several important detoxification functions of hepatocytes. The model assumes pseudo steady-state with no metabolic futile cycles. These assumptions are discussed in detail elsewhere (Chan et al., 2003a).
Figure 2.
Hepatic metabolic network showing the linkage of various metabolites.
Multiobjective Optimization
Definitions
Multiobjective Optimization
A multiobjective optimization is a problem involving several competing objectives and constraints. The solution of this problem is considered the best solution that satisfies the conflicting objectives. Other commonly used terms in the literature for multiobjective optimization are multicriteria optimization, multidecision optimization, and vector optimization.
Pareto Solution
A Pareto solution is one where any improvement in one objective can only take place at the cost of another objective. A Pareto set is a set of Pareto-optimal solutions.
Design Parameters
A design parameter is a parameter over which the designer has direct control. Other terms used in the literature for design parameters include decision variables, design variables or decision parameters.
Design Metric
A design metric refers to an objective measure of a design attribute. Other commonly used terms are objective functions, design criterion, figure-of-merit, goal and performance metric. In the current work, the variable g (x) denotes the vector of design metrics.
Design Constraint
A design constraint indicates the lower or upper bounds in the design metrics or design parameters.
Anchor value
The value obtained for a particular design objective if that design metric alone is optimized, given the bounds on the design parameters.
Mathematical Formulation of Multiobjective Problem P
Mathematically, the multiobjective problem can be stated as follows:
| (6) |
where D = {x ∈ Rn |h(x) = 0,f(x) ≤ 0,α ≤ x ≤ β}, h : Rn → Rr, f : Rn → Rs, α ∈ (R ∪ {−∞})n, β ∈ (R ∪ {+ ∞})n, m is the number of objectives, or criteria, m≥2, r and s the numbers of equality and inequality constraints, respectively. For any design parameter x = (x 1,…,xn), a design metric vector g = (g1,…,gm) is defined according to the function g :Rn→Rm. Z = {z ∈ Rm | z = g(x), x ∈ D} is the set of images of all points in D. D is called the feasible region in decision space and Z the feasible region in objective space; (g1(x)…,gm(x)) are the coordinates of the image of x in objective space.
Pareto Concept
For the multiobjective problem P, it is highly improbable to have a single optimal solution x* which minimizes every gi simultaneously; therefore, the solution is defined in terms of Pareto optimality in the following sense: a feasible solution for a multiobjective programming problem is Pareto optimal (noninferior, nondominated) if there exists no other feasible solution that will yield an improvement in one objective without causing a degradation in at least one other objective. So, x∈D is Pareto optimal if there does not exist y∈D, whose criteria vector, q=g(y), dominates the criteria vector of x, p=g(x), i.e. q≤p, p≠q. (For any vectors v and w, v ≤ w implies that vi ≤ wi ∀i).
Figure 1B presents a scheme of a Pareto set for a bi-objective linear maximization and minimization problem. If design metric g1 alone is optimized (maximized), then the optimal value is (shown as point P1). Similarly, if design metric g2 alone is optimized then the optimal value is (shown as point P2). Here and are the anchor values for design objectives g1 and g2, respectively. The ideal or Utopian solution obtained by the individual maximization of the objective functions is generally not a feasible solution of the multiobjective optimization problem. As seen in Figure 1B, lines joining points P1 and P2 defining the boundary of the feasible space are the efficient Pareto frontier. That is, for every point on arc P1-P2, it is not possible to improve both objectives simultaneously. If one objective is improved, it must be at the expense of the other. Points on the arc are often referred to as Extreme Pareto points. In view of their stated characteristics, Pareto points are usually the candidate of choice in the process of multi-objective optimization. Figure 1B shows Pareto frontiers for both maximization and minimization problems. It shows the shape of frontiers and tradeoffs involved between two objectives for two separate parameters and conditions of maximization and minimization.
Often several Pareto optimal points are available in cellular systems, representing alternative designs, from which one can select the one that offers the best trade-off among multiple objectives. This optimization generally involves forming an Aggregate Objective Function (AOF) (or, some functional aggregation of the many conflicting criteria). Implicit in this process is the assumption that this AOF has the ability to indeed yield all the potentially useful/desirable optimal solutions. The most common AOF structure is the weighted-sum approach, which involves forming a linear combination of objectives-minimized subject to the problem constraints. The algorithm for the Linear Physical Programming (LPP) based multiobjective FBA is shown in Figure 1C.
Linear Physical Programming Lexicon
The first step in the Linear Physical Programming (LPP) lexicon is to express the preferences with respect to each objective usingdifferent classes. Each class comprises two cases, soft and hard, referring to the sharpness of the preference. All soft class functions are integrated in the AOF (that will be minimized). The desired behavior of an objective function, during optimization, is described by one of sub-classes, soft (S) and hard (H). These classes are defined as follows:
Soft
Class-1S Smaller-Is-Better, i.e. minimization.
Class-2S Larger-Is-Better, i.e. maximization.
Hard
Class-1H Must be smaller, i.e., gi ≤ ti,max
Class-2H Must be larger, i.e., gi ≥ ti,min
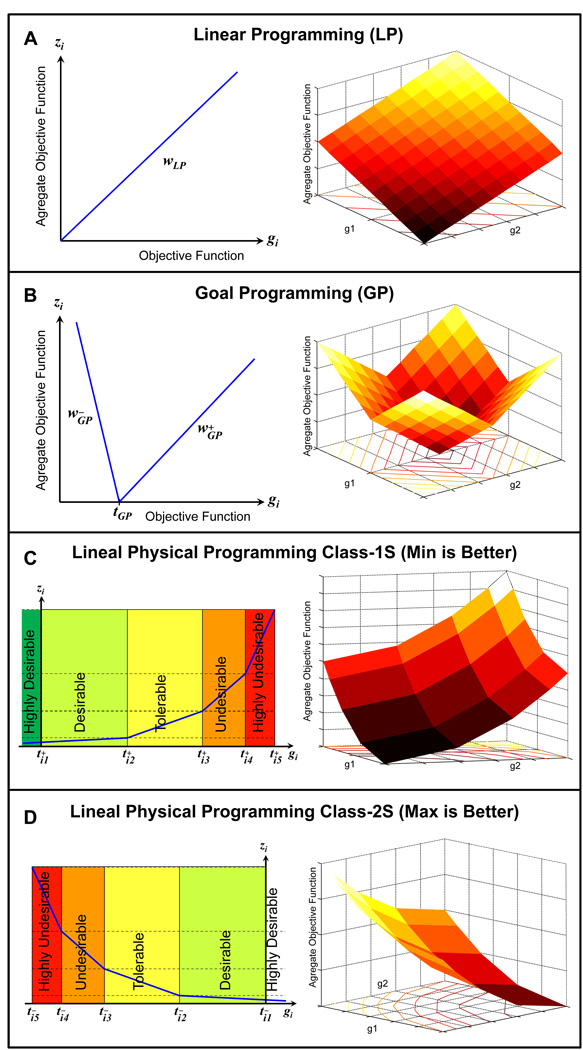
Figure 3 presents the relative capacity to express preferences using Linear Programming (LP), Goal Programming (GP), and LPP for a given objective function, gi. The vertical axis, zi , represent what is minimized in the optimization process. In the LP case, a single weight, wLP, can be increased or decreased to express preference relative to other criteria. In the GP case, there are two weights, and and a target value, tGP . In the LPP case, there is flexibility to choose up to ten target values, and it eliminates the need to deal with weights entirely, as seen in Figures 3C (Class-1S) and3D (Class-2S). The effectiveness of LPP comes from its ability to shape the class function (i.e. zi) to suite the typically complex structure of the preference. Compared to choosing weights which can be difficult and undesirable because they are physically meaningless, choosing target values is preferable because they are physically meaningful. In both LP and GP, it is usually not clear whether the weights should be increased by 10% or 100% in order to achieve the desired optimal result. This difficulty is compounded when there are several objectives involved. In this regard, LPP distinguishes itself by operating in a physically meaningful space.
Figure 3.
Relative capacity to express preferences using LP, GP and LPP for a given objective function, gi. zi is the actual quantity minimized in optimization. LP has a single weight wLP and no target value, GP has 2 weights and and 1 target value tGP. Soft classes-1S, 2S, 3S and 4S in LPP have 5, 5, 9, and 10 targets, respectively, and all LPP classes do not have any weights.
The behavior of the AOF, in the cases of LP, GP, and LPP are shown as a collection of indifference curves and their three-dimensional view (Figures 3A–D). For the LP case, the weighted sum of two objectives leads to a simple plane. In two-sidedgoal criteria for GP, there are four intersecting planes whose slopes depend on the weight-pair of each criterion. In contrast, the LPP case depicts a surface that comprises 40 intersecting planes.
Soft Classes
The soft class functions allow ranges of differing levels of preferences for each objective to be expressed (Figures 3C–D). Based on their classes, the class functions are generated for all the objectives. These class functions are then minimized for each objective using a linear programming algorithm. The qualitative and quantitative depictions of each class are shown in Figures 3C–D. Where, the value of the objective i under consideration, gi , is on the horizontal axis, and the corresponding class function, zi , is on the vertical axis. A lower value of the class function is better (i.e., more valuable than) than a higher value, and a class function of zero is ideal. As would be done in conventional mathematical programming formalism, preferences for each criterion are required in LPP, compared to using the terms minimize ormaximize For the soft case, this lexicon comprises terms that characterize the degree of desirability of up to eleven ranges. The LPP lexicon comprises terms that characterize the degree of desirability of six ranges for each generic criterion for classes 1S and 2S‥ As an illustration of the LPP lexicon, consider the case of class 1S (Figure 3C), where the ranges are defined, in order of decreasing preference. The parameters/targets through are physically meaningful values that are specified to quantify the preference associated with the i-th objective. These parameters delineate the desirability ranges within each objective. The shape of the class function depends on the numerical values of the range limits (targets). According to the definition of the ideal range, any two points of the ideal range are of equal value. The class function will be minimized only until the target value is reached. Below that point, class 1S expresses explicit indifference. If a smaller value of the objective is better, the ideal range does not apply. In this case, should be set to a value outside of the feasible space in order to exclude solutions in the ideal range. This will preclude the possibility of obtaining (incorrect) dominated solutions. A similar discussion would apply to the cases of class 2S.
Hard Classes
Constraints that are hard and have to be met are classified as hard. There are hard only two ranges defined for a hard objective, acceptable and unacceptable. All the soft class functions become part of the AOF to be minimized, and all of the hard class functions simply appear as constraints in the LPP model.
In the next section, the mathematical formulation of the class function for the soft objectives in a multiobjective setting is presented. The formulation includes implied intra-criteria and inter-criteria preferences.
Constrained Multiobjective Flux Balance Analysis Framework
This section first presents the procedure for forming the LPP problem model. The LPP application procedure entails four major steps:
Determining for each objective the appropriate class, i.e., which one of the four soft and hard classes applies.
Defining the limits of the ranges of differing degrees of desirability for each objective: the ‘target’-values (see Figure 3). For classes 1S and 2S, there are respectively fivesuch values. For classes 1H through 2H, these values are respectively ti,max and ti,min t i,max .
Generate weights based on the optimality requirement of cellular or physiological systems. Input in the form of range boundaries (or targets) for each objective are used in the Linear Physical Programming Weights (LPPW) algorithm to generate the weights (Table IA).
The following linear programming problem is then solved:
Table IA.
Linear Physical Programming Weights algorithm
| Steps | Action |
|---|---|
|
1. |
Initialize: i =0; s =1, nsc = # of soft criteria |
|
2. |
Set i = i + 1 |
| 3. | Evaluate, in sequence, |
|
4. |
Set s = s + 1 |
| 5. | If w̃min is less than some chosen small positive number (say, 0.01), then increase β, and go to step 2. |
|
6. |
If s ≠ 5, go to step 3. |
|
7. |
If i ≠ nsc, go to step 2. |
(‘i’ values correspond to soft criteria)
Piecewise Archimedean aggregate function
| (7) |
subject to
System Constraints
| (8) |
| (9) |
Goal Constraints
| (10) |
| (11) |
and
| (12) |
| (13) |
In the above formulation, x is the decision variable vector of the objective function gi (x), and nsc and nhc denote the number of soft and hard criteria, respectively. Next, we outline a simple algorithm for evaluating the weights that are used in the LPP model of the class functions. It is important to note that these weights are related to the class function slopes. Supplemental data S1 and Table IIA show the quantitative aspects of LPP. In the LPP implementation of this paper, the final value of the parameter β was kept constant for all criteria resulting in a more favorable numerical conditioning. The increase of β in the weight-algorithm loop above was set as 0.01. Then the weights obtained from the above LPPW algorithm are used to obtain expressions for the piecewise linear class function of each criterion. To maintain the linear programming framework, piecewise linear class functions were implemented using deviation variables . In the particular case of class-4S, for example, it can be shown that the LP model of the piecewise linear function is as follows:
Table IIA.
Mathematical Preliminaries
| CONCEPT | FORMULATION | |
|---|---|---|
| 1. |
|
|
| 2. | z̃s ≡ zs − zs−1 ; (2≤ s ≤5) ; z1 ≡ 0 | |
| 3. OVO rule enforcement |
z̃s > (nsc-1)z̃s−1 (3 ≤s ≤5) ; (nsc >1) (4) or, equivalently z̃s = β (nsc-1)z̃s−1 (3≤s ≤5) ; nsc >1 ; β > 1 where nsc denotes the number of soft criteria, and β will be used as a convexity parameter. |
|
| 4. convexity requirement |
Define The magnitude of the slopes of the class function of the i-th criterion is: where |
Piecewise Archimedean aggregate function
| (14) |
subject to
System Constraints
| (15) |
| (16) |
| (17) |
Goal Constraints
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
where Jm and Ju indicate measured and unmeasured fluxes, respectively; and Sm and Su contain the stoichiometric coefficients of measured and unknown reactions, respectively.
As discussed previously, the use of preferences for different degrees of desirability for each design metric also aids in simultaneous visualization of a large number of objectives. This facilitates the assessment of the effect of preference specifications on the objectives as well as the complex interplay of these objectives (Figure 1D). Each section is color coded according to the desirability level and labeled.
RESULTS AND DISCUSSION
Multiobjective optimization is a useful tool with applications to numerous disciplines and more recently for cellular systems (Nagrath et al., 2007; Vo et al., 2004) where simultaneous targeting of several objectives is vital. Therefore, we developed this approach to optimize hepatocellular function in the context of a BAL device, in which case the main goal is for the hepatocytes to function at the highest possible level. Here we focused on a limited set of critical representative hepatocellular metabolic processes: urea secretion, albumin synthesis, NADPH synthesis, and glutathione synthesis. Urea secretion (flux 16 in Table SI) is a critical detoxification reaction, and is primarily derived from ammonia and aspartate generated through transamination reactions. Albumin synthesis (flux 47) was used as a marker of liver specific protein secretion. NADPH is produced by the pentose phosphate pathway (PPP), and is primarily used in nonproliferating hepatocytes as a co-factor for cytochrome p450 dependent oxidation reactions, de novo synthesis of glutathione, as well as reduction of oxidized glutathione. To increase NADPH production, the NADPH-generating oxidative branch of the PPP represented in a lumped fashion as flux 46 was increased. The tripeptide glutathione (GSH, γ-Glu-Cys-Gly) is a free radical scavenger and is involved in many detoxification reactions. The synthesis of glutathione is represented by flux 48.
Using LPPFBA, we assessed the sensitivity and geometry of the optimal region and determined the optimal results using various preferences and/or prioritization of the four objectives (fluxes 16, 46, 47, 48) mentioned above. The constraints for the hepatic metabolic network are listed in Table SII. As described in the Methods, LPPFBA requires characterization of design metrics into different classes. Here, all four objective functions are maximized and hence fall in “Class 2S”. As part of this analysis, we first obtained Pareto frontiers between various bi-objective combinations of liver specific functions (albumin synthesis, urea secretion, NADPH synthesis, and GSH synthesis). Next, we obtained Pareto optimal solutions for tri-objective combinations of these hepatic functions. Lastly, we obtained the Pareto solutions for a simulated BAL system where the main goal was to operate the BAL at the highest possible level during human plasma exposure. The experimentally measured flux data for hepatocytes during plasma exposure were obtained from Chan et al. (Chan et al., 2002).
Analysis of Bi-objective Hepatic Metabolic Network
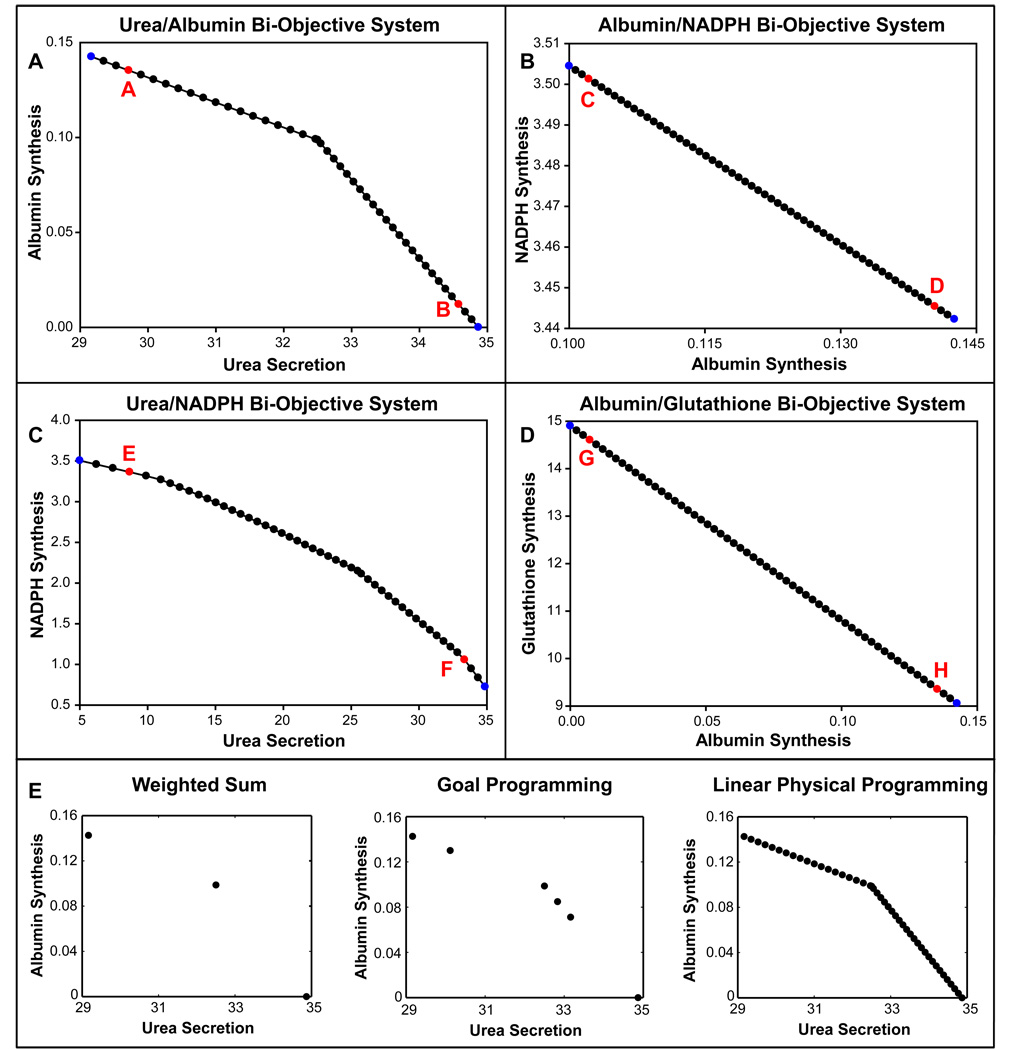
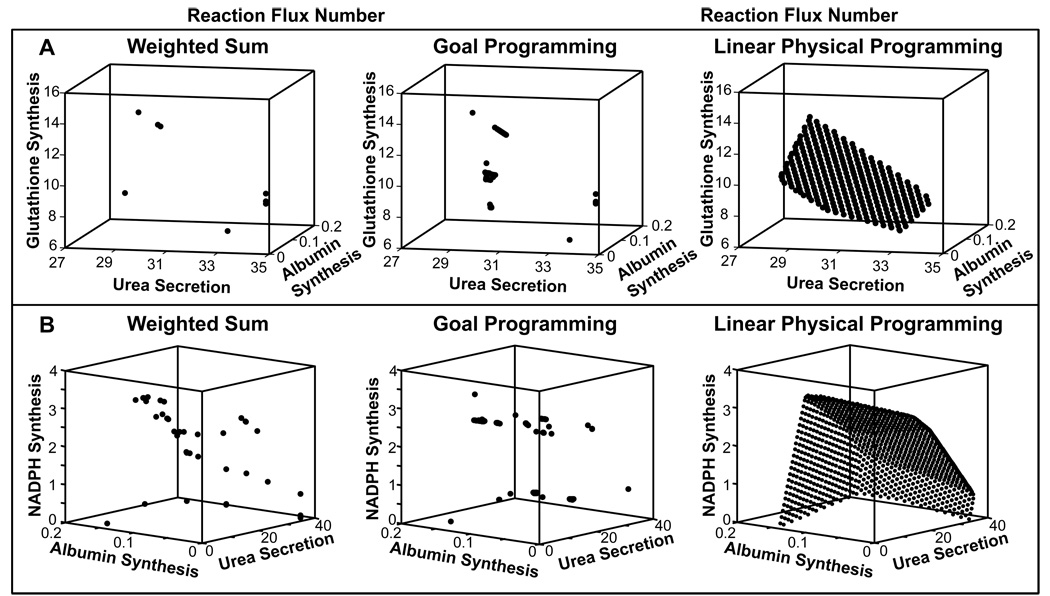
Pareto frontiers for various sets of bi-objectives were generated in this section to identify potential optimal solution regions. These optimal solutions can provide a qualitative framework to assess the tradeoffs and robustness of the hepatic metabolic network for a quad-objective scenario (albumin synthesis, NADPH synthesis, urea secretion and GSH synthesis). The representative results are shown in Figure 4. These Pareto optimal solutions were obtained by changing the preferences from higher desirable values to highly undesirable values. As seen in Figure 4, all of these objectives exhibited a tradeoff with each other; for example, albumin and urea synthesis could not be at their maximal values at the same time (Figure 4A). Similarly, there was a tradeoff between NADPH and albumin synthesis, NADPH synthesis and urea secretion, glutathione and albumin synthesis (Figures 4B, 4C and 4D, respectively). In addition, the impact of changing preferences (for example favoring albumin synthesis over urea secretion, and vice-versa) varied depending on the objective. In particular, the tradeoff region or range of Pareto optimal solutions (i.e., how far the optimal value is from the “anchor value”) for albumin synthesis was very high compared to NADPH synthesis and urea secretion. Several other combinations were also tested and all of them indicated Pareto optimality between various objectives (data not shown). Figures 4E compares the Pareto optimal solutions obtained between albumin synthesis and urea secretion using weighted-sum, goal programming and LPPFBA. For all three equal number of simulations were used. As seen in these figures LPPFBA has significant advantage over both weighted sum and goal programming. This is because mapping of preferences to form an AOF in LPPFBA results in piecewise smooth hyper surfaces which leads to an even spread of Pareto optimal solutions for a given even spread of input preferences without missing any Pareto optimal solution. This behavior of optimal solution with respect to change in preference is highly desirable in large-scale mammalian metabolic network analysis (where tradeoffs between objectives are ubiquitous). In conventional methods, the spacing of points is largely dependent on relative scaling thus may lead to ill-conditioned problems. Importantly, these methods fail to capture significant number of optimal solutions resulting in an uneven distribution for even distribution of weights.
Figure 4.
Pareto frontiers for bi-objective hepatic systems. Four major hepatic functions of albumin synthesis, urea secretion, NADPH and glutathione synthesis were used for bi-objective optimality in the combinations shown here: A) Pareto frontier between albumin and urea synthesis. B) Pareto frontier between NADPH and albumin synthesis. C) Pareto frontier between NADPH synthesis and urea secretion. D) Pareto frontier between glutathione synthesis and albumin synthesis. The blue circles are the Anchor points, black circles are Pareto optimal solutions for optimization and red circles are selected Pareto solutions for which complete set of optimal fluxes are shown in Table S4. A, B indicates Pareto points for albumin and urea bi-objective system; C, D indicates Pareto points for NADPH and albumin system; E, F indicates Pareto points for NADPH and urea bi-objective system.; and G, H indicates Pareto points for glutathione and albumin bi-objective system. E) Comparison of Pareto optimal solutions obtained by LPPFBA weighted-sum and goal programming for a bi-objective problem of maximization of albumin synthesis and urea secretion.
Figure S1 presents the distribution of Pareto optimal fluxes throughout the tradeoff region, which shows the changes required in flux values and direction (i.e. increasing or decreasing) as the objective preference is changed from one objective to another. The corresponding flux values are presented in Table S3. Figure S1A indicates the necessary change in fluxes when going from Pareto optimal solutions “A” to “B”, in other words, when going from higher albumin synthesis/lower urea secretion rates to lower albumin synthesis/higher urea secretion rates. This change requires increasing gluconeogenic fluxes (1–7), formation of pyruvate from amino acids (18) aspartate synthesis (37), formation of glutamic acid (30, 39), and increasing oxidation of triglycerides (52). Noticeably, higher urea secretion/lower albumin synthesis necessitates decreased uptake of both glucogenic (proline, 61; serine, 68; aspartate, 70; threonine, 72; phenylalanine, 74; methionine, 76; valine, 77; isoleucine, 78; glutamine, 80; tyrosine, 82) and ketogenic (lysine, 73; leucine, 79) amino acids over the lower urea secretion/higher albumin synthesis case. On the contrary, cysteine (81) uptake is increased when increasing urea secretion. Arginine (65) uptake rate was at maximum for both urea and albumin maximizations. Essentially, the uptake of pyruvate forming amino acids (alanine, 67; serine, 68; and threonine, 72), fumarate forming amino acids (phenylalanine, 74; and tyrosine, 82), and succinyl CoA forming amino acids (threonine, 72; methionine , 76; and valine, 77) was decreased in order to increase urea secretion since these amino acids play a major role in increasing albumin synthesis. Also, increasing urea synthesis resulted in increased gluconeogenesis, which was associated with an increased rate of glucose clearance and an increase in glycogen synthesis.
Figure S1B indicates the change in optimal fluxes from C to D Pareto solutions for the case when NADPH production and albumin synthesis are considered to be the main objectives and whose maximization was studied. Noticeably, TCA cycle fluxes (9 and 10) were higher for the case when albumin was maximized. Additionally, oxygen uptake and electron transport system flux (60 and 44) were significantly lower at higher NADPH production and lower albumin synthesis. Moreover, NADPH use for alanine synthesis in reaction 18 was significantly reduced for the case of NADPH maximization. Since the tradeoff region for NADPH synthesis is not large (3.5 to 3.44) there was not much change in gluconeogenic fluxes in this scenario. However, since the tradeoff region for albumin synthesis flux was high (from 0.1 to 0.14), increasing albumin synthesis required increasing the uptake rates of oxygen (60), proline (61), asparagine (63), arginine (65), serine (68), lysine (73), phenylalanine (74) and leucine (79). Interestingly, histidine (31), which produces glutamate, was decreased for increasing NADPH production because reaction 38 is proceeding in reverse direction, which utilizes NADPH.
Figure S1C presents the flux profiles for Pareto optimal solutions E and F for the NADPH synthesis/urea synthesis bi-objective scenario. There was an increase in the tradeoff region for NADPH flux (1.05 to 3.36) when compared to the previous bi-objective case of NADPH/albumin synthesis. As seen in Figure S1C and Table S3, higher urea flux necessitated upregulation of gluconeogenic fluxes (1–4), nonessential amino acid uptake (glutamate, 39), glucose release (54), asparagines uptake (63), arginine uptake (65), and aspartate uptake (70). On the contrary, increasing NADPH production required upregulation of the uptake of amino acids that produce succinyl CoA (methionine: 75) to increase electron transport chain flux (44) and uptake of amino acids that produce glutamate (histidine, 75). Interestingly, there is several fold increase in carboxylation of pyruvate (8) by malic enzyme when NADPH is maximized.
Figure S1D presents the flux profiles for Pareto optimal solutions G and H for the GSH synthesis/albumin synthesis bi-objective scenario. Higher glutathione production flux upregulated the urea cycle fluxes (15, 16 and 17), increased serine production (22, 23), increased glutamate synthesis (30), increased gluconeogenesis fluxes (5–6). Also, there is a significantly reduced synthesis of alanine by alanine aminotransferase through pyruvate (18). Noticeably, higher albumin requires increased catabolism of lysine (27), isoleucine (34), and ornithine (39) with an increased production of glutamate (39, 40), aspartate (37), and decreased ketone bodies (β-hydroxy butyrate, 52). Higher albumin flux also necessitates the increased uptake of amino acids (proline, 61; asparagine, 63; arginine, 65; alanine, 67; serine, 68; lysine, 73; phenylalanine, 74; valine, 77; isoleucine, 78; leucine, 79; glutamine, 80; tyrosine, 82).
As can be seen from the above results there is a significant re-routing of flux directions and cycle fluxes when switching from one objective to another within system constraints. In general, up regulation of gluconeogenesis was associated with higher urea secretion, which, in turn, was associated with higher arginine and aspartate fluxes. Increasing albumin synthesis required a significant increase in the uptake of various amino acids and the synthesis of some of the gluconeogenic amino acids. Interestingly, higher glutathione synthesis required an up regulation in glycine synthesis. It is important to note that the bi-objective cases analyses discussed in this section had preferences close to (although not exactly at) the anchor points.
Analysis of Tri-objective Hepatic Metabolic Network
Next, as part of this analysis, we demonstrate the use of LPPFBA to perform tri-objective optimization. We studied various preferences for two different tri-objective combinations: NADPH production, albumin synthesis, and GSH synthesis and urea secretion, NADPH production, and albumin synthesis. The optimal results are presented in Tables I and II, respectively, and the corresponding fluxes are in Table S4. For each combination, we examined three cases, each case favoring one of the three functions. Figures S2A–B show the metabolic profiling for change in fluxes for NADPH synthesis/albumin synthesis/GSH synthesis scenario and Figures S2C–D show the metabolic profiling for change in fluxes for urea secretion/NADPH synthesis/albumin synthesis when preferences are changed from one objective to another. The anchor points which are obtained by individual optimization of urea, albumin, glutathione, and NADPH are 34.579, 0.1404, 14.602 and 3.5014, respectively.
Table I.
Linear Physical Programming optimization results for a tri-objective system (NADPH synthesis, albumin synthesis and glutathione synthesis) for hepatic metabolic network. HUD is highly undesirable, UD is undesirable, T is tolerable, D is desirable and HD is highly desirable preference values of objective functions.
| Case # |
Priority | Flux | t1 (HD) |
t2 (D) |
t3 (T) |
t4 (UD) |
t5 (HUD) |
Optimal |
|---|---|---|---|---|---|---|---|---|
| 1 | High | NADPH | 3.504 | 3.242 | 2.979 | 2.716 | 2.453 | 3.324 |
| High | Albumin | 0.143 | 0.132 | 0.121 | 0.110 | 0.100 | 0.109 | |
| High | GSH | 14.900 | 13.782 | 12.665 | 11.547 | 10.430 | 10.430 | |
| 2 | High | NADPH | 3.504 | 3.242 | 2.979 | 2.716 | 2.453 | 3.442 |
| High | Albumin | 0.143 | 0.132 | 0.121 | 0.110 | 0.100 | 0.143 | |
| Low | GSH | 1.000 | 0.750 | 0.501 | 0.251 | 0.001 | 4.920 | |
| 3 | Low | NADPH | 0.100 | 0.078 | 0.055 | 0.033 | 0.010 | 0.100 |
| High | Albumin | 0.143 | 0.132 | 0.121 | 0.110 | 0.100 | 0.143 | |
| Low | GSH | 0.100 | 0.075 | 0.051 | 0.026 | 0.001 | 0.464 | |
| 4 | High | NADPH | 3.504 | 3.242 | 2.979 | 2.716 | 2.453 | 3.504 |
| Low | Albumin | 1.00·10−3 | 7.53·10−4 | 5.05·10−4 | 2.58·10−4 | 1.00·10−5 | 0.100 | |
| Low | GSH | 0.100 | 0.075 | 0.051 | 0.026 | 0.001 | 6.410 | |
| 5 | Low | NADPH | 0.100 | 0.078 | 0.055 | 0.033 | 0.010 | 0.532 |
| Low | Albumin | 1.00·10−3 | 7.53·10−4 | 5.05·10−4 | 2.58·10−4 | 1.00·10−5 | 1.00·10−3 | |
| High | GSH | 14.900 | 13.782 | 12.665 | 11.547 | 10.430 | 14.859 |
Table II.
Linear Physical Programming optimization results for a tri-objective system (NADPH synthesis, albumin synthesis and urea synthesis) for hepatic metabolic network. HUD is highly undesirable, UD is undesirable, T is tolerable, D is desirable and HD is highly desirable preference values of objective functions.
| Case # |
Priority | Flux | t1 (HD) |
t2 (D) |
t3 (T) |
t4 (UD) |
t5 (HUD) |
Optimal |
|---|---|---|---|---|---|---|---|---|
| 1 | High | Urea | 34.869 | 31.818 | 28.767 | 25.716 | 22.665 | 23.724 |
| High | NADPH | 3.504 | 3.198 | 2.891 | 2.585 | 2.278 | 2.278 | |
| High | Albumin | 0.143 | 0.130 | 0.118 | 0.105 | 0.093 | 0.130 | |
| 2 | High | Urea | 34.869 | 33.125 | 31.382 | 29.638 | 27.895 | 29.706 |
| Low | NADPH | 0.100 | 0.078 | 0.055 | 0.033 | 0.010 | 0.100 | |
| High | Albumin | 0.143 | 0.135 | 0.128 | 0.121 | 0.114 | 0.135 | |
| 3 | High | Urea | 34.869 | 33.125 | 31.382 | 29.638 | 27.895 | 34.845 |
| Low | NADPH | 0.100 | 0.078 | 0.055 | 0.033 | 0.010 | 0.311 | |
| Low | Albumin | 1.00·10−3 | 7.53·10−4 | 5.05·10−4 | 2.58·10−4 | 1.00·10−5 | 0.001 | |
| 4 | Low | Urea | 1.000 | 0.750 | 0.500 | 0.250 | 1.00·10−5 | 1 |
| High | NADPH | 3.504 | 3.329 | 3.154 | 2.979 | 2.804 | 3.442 | |
| High | Albumin | 0.143 | 0.135 | 0.128 | 0.121 | 0.114 | 0.143 | |
| 5 | Low | Urea | 1.000 | 0.750 | 0.500 | 0.250 | 1.00·10−5 | 4.39 |
| High | NADPH | 3.504 | 3.329 | 3.154 | 2.979 | 2.804 | 3.504 | |
| Low | Albumin | 1.00·10−3 | 7.53·10−4 | 5.05·10−4 | 2.58·10−4 | 1.00·10−5 | 0.100 | |
| 6 | Low | Urea | 1.000 | 0.750 | 0.500 | 0.250 | 1.00·10−5 | 1 |
| Low | NADPH | 0.100 | 0.078 | 0.055 | 0.033 | 0.010 | 0.100 | |
| High | Albumin | 0.143 | 0.135 | 0.128 | 0.121 | 0.114 | 0.143 |
Table I presents the multiobjective optimal solutions for 5 scenarios for the NADPH/albumin/GSH tri-objective case. Case 1 indicates the base case where preferences for all three hepatic objectives were given based on their anchor points, however, none of the objectives were given any specific priority, i.e., priority for each was set as equal to a high value. As seen from the Highly Desirable (HD) values for objective functions in Case 1, all objectives’ highly desirable values are close to their anchor points. The preference ranges in the LPP optimization for this case were selected as 3.504–2.45 for NADPH production, 0.143–0.098 for albumin synthesis, and 14.9–10.43 for glutathione synthesis. The optimal values of objective functions obtained for this case (Case 1) are 3.324 for NADPH synthesis (between highly desirable and desirable), 0.109 for albumin synthesis (between undesirable and highly undesirable) and 10.431 for glutathione synthesis (between undesirable and highly undesirable). Next, we present Cases 2–3, where higher priority is desired for albumin synthesis over objectives of glutathione and NADPH synthesis. In Case 2, preferences for preferences for glutathione synthesis were decreased significantly. This provides a higher priority for albumin synthesis and a lower priority for glutathione synthesis. In this case, we see that the optimal value of albumin (0.143) lies between desirable and highly desirable as compared to Case 1 where albumin was between undesirable and highly undesirable values. Inter-optimality or tradeoff between various objectives is clearly evident in Case 2 since albumin synthesis increased with a corresponding decrease in GSH synthesis. To further increase the albumin synthesis, in Case 3 preferences for both NADPH and GSH were decreased and of albumin increased. This sets the priority of albumin high compared to NADPH and GSH. The obtained Pareto optimal values of albumin synthesis from LPPFBA are now similar to the highly desirable (HD) preference and same as Case 2. As can be seen from the optimal values of NADPH (0.1) and GSH (0.464), the obtained values of NADPH and GSH decreased when compared to Cases 1 and 2 because of low preferences on their values. In Case 4, higher NADPH is desired and the priority for albumin and GSH synthesis is very low. To obtain multiobjective optimal solutions for this scenario compared to Case 1 a low preference range was assigned to both albumin and GSH synthesis. The preference ranges for the undesired objectives need to be lowered in order to achieve a higher value for the desired objective. This is because highly undesirable values act as a hard constraint for the objective. Interestingly, optimal values obtained for all three objectives were close to their highly desirable (HD) preference values; however, when compared to Case 2, optimal albumin synthesis was significantly decreased at the cost of a marginal increase in NADPH synthesis and significant increase in GSH synthesis. This shows that albumin synthesis is highly sensitive as compared to NADPH and requires a significant decrease in its synthesis for other hepatic functions to increase. In Case 5, higher glutathione synthesis was desired; hence, preference ranges for GSH were increased significantly towards HD values. As seen in the obtained optimal values from Table I, there was a significant decrease in optimal albumin synthesis (0.001) to increase GSH synthesis to the optimal value of 14.86. Table S5 presents the flux values for Cases 3, 4 and 5 with their corresponding profiling in Figures S3A–B. Cases 3, 4, and 5 present the scenarios where higher albumin is desired with lower preference for NADPH and GSH synthesis, higher NADPH is desired with lower preference for albumin and GSH synthesis, and higher GSH synthesis is desired with lower preference for NADPH and albumin synthesis, respectively. As seen in Figure S3A, going from Case 4 (higher NADPH) to Case 3 (higher albumin) requires up-regulation in the uptake of amino acid fluxes (59, 61, 63, 65, 67, 68, 70, 73, 74, 76–79), and catabolism of phenylalanine (28). Figure S3B presents the re-routing of fluxes from Case 4 to Case 5 (higher GSH). This requires up-regulation of catabolism of methionine (32), and higher electron transport chain flux (54) and oxygen uptake rate (60).
Table II presents the multiobjective optimal solutions for 6 scenarios for urea/NADPH/albumin tri-objective case. Case 1 indicates the base case where preferences for all three were given based on their anchor points, however, none of the objectives were given any specific priority. Hence, higher preferences for all three were given in the optimization, and as seen from the Highly Desirable value for objective functions, all objectives’ higher desirability is close to their anchor points. The preference ranges in the LPPFBA optimization for this case were selected as 34.87–22.67 for urea secretion, 3.5–2.21 for NADPH synthesis and 0.143–0.093 for albumin synthesis. The optimal values of objective functions obtained for this case (Case 1) are 23.724 for urea synthesis (between undesirable and highly undesirable), 2.28 for NADPH synthesis (between undesirable and highly undesirable), and 0.13 for albumin synthesis (between highly desirable and desirable). Next, we present Cases 2–3, where higher priority is desired for urea secretion over objectives of albumin and NADPH synthesis. In Case 2, the desirable preferences for NADPH synthesis were decreased and urea and albumin synthesis marginally increased over Case 1. The obtained multiobjective optimality results for Case 2 clearly indicate the inter-optimality or tradeoff and inter-play between objectives, since the optimal value of urea secretion (29.71) increased from Case 1 solution with a concomitant decrease in NADPH to 0.1 . Interestingly, Case 3 shows the case where preference for albumin secretion is decreased. In this case, urea secretion optimal values (between highly desirable and desirable) are close to the anchor point of urea secretion with a significant decrease in both NADPH and albumin synthesis. In Cases 4–5, the priority to achieve higher NADPH synthesis is desired over other objectives. As seen in the table, in Case 4 the preferences of urea were decreased (1–0.0) and both the NADPH and albumin synthesis preference ranges were increased to 3.5–2.81 and 0.14–0.11, respectively, resulting in higher optimal values for NADPH (3.442) and albumin (0.143) synthesis. In Case 5, still higher NADPH synthesis was desired with low priority for other objectives. All the objectives were similar to their highly desirable preference values. Case 6 presents the case where higher albumin synthesis was desired with low preferences for NADPH synthesis and urea secretion. Again, the higher optimal albumin synthesis was obtained at the cost of both urea and NADPH secretion. Table S5 presents the flux values for Case 3, 5 and 6 with their corresponding profiling in Figures S3C and S3D. As seen in Figure S3C, going from Case 5 (higher NADPH synthesis) to Case 3 (higher urea secretion) requires up-regulation of gluconeogenic fluxes (1–4), higher urea cycle flues (15–17), lower pyruvate to malate (8), and lower bypass reaction of 3-phosphoglycerate (24).
To further demonstrate the advantages of applying LPPFBA in metabolic systems, we compare the Pareto surface obtained using LPFFBA with weighted-sum (WS) and goal programming (GP) based MFA for two separate tri-objective systems: glutathione synthesis, urea secretion and albumin synthesis (Figure 5A); and NADPH synthesis, urea secretion and albumin synthesis (Figure 5B) of primary hepatocytes. We ran 50,000 simulations utilizing different sets of weights using WS and GP based MFA and only 1,000 simulations utilizing different set of preferences for LPPFBA. As seen in Figures 5A–B–F, even after using 50,000 set of weights using WS and GP based MFA very few Pareto optimal solutions could be obtained. This illustrates that the LPPFBA can predict all possible Pareto optimal solutions for large-scale metabolic network systems whereas existing methods can capture only limited optimal solutions on Pareto surface. This is a noteworthy advantage of LPPFBA.
Figure 5.
A–B) A–B) Comparison of Pareto optimal solutions obtained by LPPFBA, weighted-sum and goal programming for two tri-objective cases for hepatic metabolism.
Quad-objective Hepatic Metabolic Network
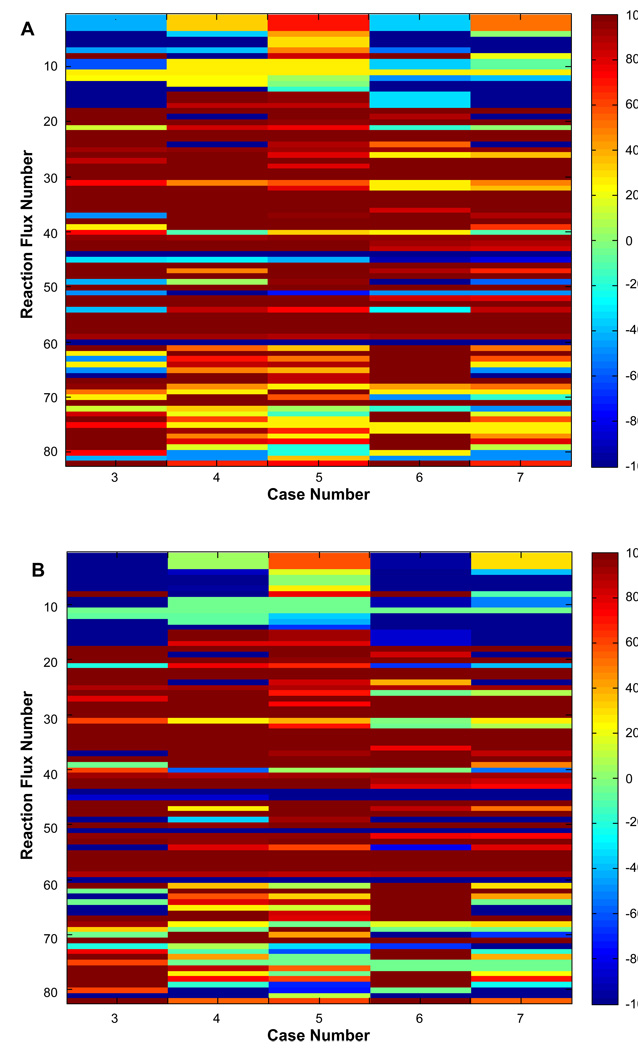
In the previous sections we presented the application of LPPFBA for bi-objective and tri-objective systems. In this section, we present the application of LPPFBA for improving current hepatic cellular systems using quad-objective (albumin synthesis, glutathione synthesis, NADPH synthesis and urea secretion) optimization. In BAL systems, when hepatocytes are exposed to human plasma they become steatotic and exhibit severe loss of hepatic function (albumin and urea synthesis, (Chan et al., 2002)). The experimental metabolic fluxes for simulated BAL condition of hepatocytes exposed to human plasma were obtained from the literature (Chan et al., 2003a; Chan et al., 2002). The goal was to determine optimal fluxes for the hepatic metabolic network under the simulated BAL condition considering all the objective functions simultaneously, leading to a quad-objective scenario (albumin, urea, NADPH and GSH). Table III presents the preferences assigned to the four objectives to create the different scenarios. The experimentally measured fluxes with their corresponding intracellular fluxes were used in the “base cases” for all comparisons. Two separate cases were used as “base case” to compare the changes in current fluxes from these “base cases” to the optimized scenarios where a variety of hepatic objectives were optimized. In one of the “base cases”, intracellular fluxes were obtained after optimizing for glutathione synthesis (in this case the other three hepatic objectives were used as measured fluxes obtained from (Chan et al., 2003a)). In the second scenario, all four hepatic objectives were simultaneously optimized, hence, all four objectives were treated as unmeasured fluxes and other fluxes were used for optimization to compute the intracellular fluxes. The corresponding fluxes for these four cases are presented in Table S6. These cases were a subset of 16 different scenarios presented in Table S7 (supplementary data). Various sets of preferences were changed for their corresponding objectives and the effect of changing preferences on the fluxes was investigated in the form of a “heat map”. Figures 6A–B show the distribution of flux changes for the cases shown in Table III in the form of a “heat map”. In Table III, the “base case” is indicated as Case 1. The experimental values of albumin, urea and NADPH secretion are indicated with GSH synthesis being computed from the available measured data. Case 2 of the quad-objective system includes all the measured fluxes of Case 1; however, all four hepatic objectives are unmeasured in this case. Hence, Case 2 is a scenario where we optimized the current measured hepatic flux data using a quad-objective system. Both Case 1 and Case 2 serve as base cases or present the fluxes of the current BAL systems. Again, two heat maps are shown to compare the changes in fluxes from the two “base cases” to the optimized scenarios for hepatic objectives.
Table III.
Linear Physical Programming optimization results for a quad-objective system (NADPH synthesis, albumin synthesis, urea synthesis and glutathione synthesis) for hepatic metabolic network. HUD is highly undesirable, UD is undesirable, T is tolerable, D is desirable and HD is highly desirable preference values of design metrics. The base cases consider 10 measurements to each 5 cases: flux 55 = 0.5; flux 57 = 0.38; flux 58 = 0.83; flux 61 = 0.12; flux 67 = 0.24; flux 68 = −0.13; flux 70 = 0.006; flux 71 = 0.13; flux 76 = 0.016; and flux 82 = 0.022. Base case 1 is obtained by optimizing GSH (flux 49). In addition to the 10 measurements, another 3 values were imposed as constraints based on experimental data: flux 17 (urea) = 0.57, flux 47 (NADPH) = 0.012, and flux 48 (albumin) = 9.4·10−5. Base case 2 is obtained by quad-objective optimization of urea, NADPH, albumin, and GSH using LPPFBA.
| Case # |
Priority | Flux | t1 (HD) |
t2 (D) |
t3 (T) |
t4 (UD) |
t5 (HUD) |
Optimal |
|---|---|---|---|---|---|---|---|---|
|
1 (base) |
Measured | Urea | — | — | — | — | — | 0.570 |
| Measured | NADPH | — | — | — | — | — | 0.012 | |
| Measured | Albumin | — | — | — | — | — | 9.40·10−5 | |
| Max | GSH | — | — | — | — | — | 9.912 | |
|
2 (base) |
Mid | Urea | 30.000 | 20.000 | 10.000 | 1.000 | 0.100 | 20.000 |
| Mid | NADPH | 2.500 | 1.500 | 0.500 | 0.100 | 0.010 | 2.444 | |
| Mid | Albumin | 0.100 | 0.050 | 5.00·10−3 | 5.00·10−4 | 5.00·10−5 | 0.001 | |
| Mid | GSH | 10.000 | 5.000 | 1.000 | 0.500 | 0.100 | 9.889 | |
| 3 | High | Urea | 34.869 | 31.818 | 28.767 | 25.716 | 22.665 | 34.845 |
| Low | NADPH | 0.100 | 0.078 | 0.055 | 0.033 | 0.010 | 0.100 | |
| Low | Albumin | 1.00·10−3 | 7.53·10−4 | 5.05·10−4 | 2.58·10−4 | 1.00·10−5 | 0.001 | |
| Low | GSH | 0.100 | 0.075 | 0.051 | 0.026 | 0.001 | 9.456 | |
| 4 | Low | Urea | 1.000 | 0.750 | 0.500 | 0.250 | 1.00·10−5 | 1.000 |
| High | NADPH | 3.504 | 3.198 | 2.891 | 2.585 | 2.278 | 3.504 | |
| Low | Albumin | 1.00·10−3 | 7.53·10−4 | 5.05·10−4 | 2.58·10−4 | 1.00·10−5 | 0.100 | |
| Low | GSH | 0.100 | 0.075 | 0.051 | 0.026 | 0.001 | 6.410 | |
| 5 | Low | Urea | 1.000 | 0.750 | 0.500 | 0.250 | 1.00·10−5 | 1.000 |
| Low | NADPH | 0.100 | 0.078 | 0.055 | 0.033 | 0.010 | 0.100 | |
| High | Albumin | 0.143 | 0.130 | 0.118 | 0.105 | 0.093 | 0.143 | |
| Low | GSH | 0.100 | 0.075 | 0.051 | 0.026 | 0.001 | 0.417 | |
| 6 | Low | Urea | 1.000 | 0.750 | 0.500 | 0.250 | 1.00·10−5 | 8.830 |
| Low | NADPH | 0.100 | 0.078 | 0.055 | 0.033 | 0.010 | 0.737 | |
| Low | Albumin | 0.001 | 7.53·10−4 | 5.05·10−4 | 2.58·10−4 | 1.00·10−5 | 0.001 | |
| High | GSH | 14.900 | 13.596 | 12.292 | 10.988 | 9.685 | 14.859 | |
| 7 | High | Urea | 34.869 | 31.818 | 28.767 | 25.716 | 22.665 | 22.724 |
| High | NADPH | 3.504 | 3.198 | 2.891 | 2.585 | 2.278 | 2.278 | |
| High | Albumin | 0.143 | 0.130 | 0.118 | 0.105 | 0.093 | 0.105 | |
| High | GSH | 14.900 | 13.596 | 12.292 | 10.988 | 9.685 | 10.589 |
Figure 6.
Metabolic profiling of percentage change in Pareto optimal fluxes for 16 solutions of the quad-objective optimization. The % change is taken from a referent optimal solution that consider 10 measurements to each 16 cases: flux 54 = 0.5; flux 56 = 0.38; flux 57 = 0.83; flux 60 = 0.12; flux 66 = 0.24; flux 67 = −0.13; flux 69 = 0.006; flux 70 = 0.13; flux 75 = 0.016; and flux 81 = 0.022. A) The reference is obtained by optimizing GSH (flux 48). In addition to the 10 measurements, another 3 values were imposed as constraints based on experimental data: flux 16 (urea) = 0.57, flux 46 (NADPH) = 0.012, and flux 47 (albumin) = 9.4·10−5. B) The flux of reference is obtained by quad-objective optimization of urea, NADPH, albumin, and GSH using LPP. The preferences for each variable are [30 20 10 1 0.1] for urea, [2.5 1.5 0.5 0.1 0.01] for NADPH, [0.1 0.05 0.005 0.0005 0.00005] for albumin, and [10 5 1 0.5 0.1] for GSH. Only changes up to 100% are shown.
In Case 3 of the quad-objective system, we examined the impact of choosing urea synthesis as a priority over the other liver specific functions of albumin, GSH and NADPH synthesis. For this purpose, the preference for urea secretion was increased close to a highly desirable value, while the preferences for albumin synthesis, GSH synthesis and NADPH synthesis were kept far lower than their corresponding anchor points. We found that the optimal value for urea secretion (34.85) increased from Case 1 (0.57) and was close to its anchor point. There was a concomitant increase in NADPH andalbumin andsynthesis from Case 1. However, compared to Case 2 there was an increase in urea secretion (34.86) in Case 3, however, with a significant decrease in NADPH synthesis. In Case 4, we prioritized NADPH synthesis. Hence, the preference for NADPH synthesis was increased closer to the anchor point and all other preferences were decreased. We found that NADPH synthesis optimal values were close to the anchor point for NADPH flux (between highly desirable and desirable) concomitant with a significant decrease in urea synthesis when compared to Case 2.
In Case 5, we prioritized albumin synthesis over other objectives. As seen in the table, in Case 5 the preferences of urea, NADPH and GSH synthesis were decreased and albumin synthesis preference range was increased to 0.1426, resulting in a higher optimal value of albumin (0.1426). In Case 6, we favored GSH synthesis over the other objectives. As seen in the table, preference for albumin synthesis has to be significantly decreased to achieve higher glutathione synthesis optimal values, whereas decreasing urea and NADPH synthesis is not necessary since it does not lead to any significant decrease in their optimal values. This is also confirmed in Figure 4D and Figure S2-D where going from Pareto optimal solution of higher glutathione synthesis (G) to higher albumin synthesis (H) does not require a significant change in urea and NADPH synthesis.
In Case 7, preferences for all four objectives were the same (highly desirable) and therefore none of them was given any specific priority. In this case, all objectives were close to their anchor points. The preference ranges in the LPP optimization for this case, were selected as 34.87–22.67 for urea secretion, 3.5–2.28 for NADPH, 0.143–0.09 for albumin, and 14.9–9.69 for glutathione syntheses. The optimal values of objective functions i.e., desired fluxes obtained for this case (Case 7) are 22.92 for urea synthesis (between undesirable and highly undesirable), 2.23 for NADPH synthesis (between highly undesirable and undesirable), 0.11 for albumin synthesis (between tolerable and undesirable) and 10.59 for glutathione synthesis (between tolerable and undesirable). All objectives optimal values were less than their individual priority case, thus clearly illustrating the inter-dependence and tradeoff among the various objectives.
Now, we quantitatively profile the fluxes of various metabolites under various optimal conditions in several cases based on the relative changes indicated in heat maps. Table S7 presents the flux values for Cases 1–7 with their corresponding profiling presented as a heat map in Figure 6A. The plasma exposed hepatic fluxes for the current BAL system are shown in Column 1 of Table S7. If high urea synthesis is desired (Case 3) in the BAL then this necessitates a significant increase in gluconeogenic fluxes (2–4), with a concomitant deccrease in TCA cycle fluxes (9–10, 12), increase in urea cycle fluxes (15–17), and an decrease in catabolism of glucogenic amino acid (serine, 19). Another key observation is that higher urea secretion in the simulated BAL requires a significant decrease in catabolism of ketogenic amino acids (leucine, 35). As seen in the table, the increase in fluxes is much higher when priority is more for urea secretion than the other objectives. Notably, there is a significant decrease in oxygen uptake (60) and electron transport chain fluxes (44, 45) when higher priority is for urea synthesis. The other evident factor is that uptake of glucogenic amino acids is higher (serine, 68;glycine, 69;histidine, 75) when higher priority is to achieve higher urea synthesis over other objectives. In Case 4 we give higher preference to NADPH synthesis over other objectives. This is achieved using an increase in conversion of pyruvate to malate (8), decrease in TCA cycle fluxes, an increase in uptake of ketogenic amino acids (lysine, 73; leucine, 79). The trends or changes in fluxes in moving from “Case 1 to Case 3” and “Case 1 to Case 4” in this quad-objective case are similar to the trends when moving from Case F to E in the bi-objective scenario (Figure C). However, there are some major differences because of constraints in other objectives (albumin synthesis and glutathione synthesis). In quad-objective Case 3 and Case 4 the preference of albumin synthesis is low and this results in differences in actual flux values. The other important differences are the decrease in oxygen uptake, lipid uptake (53), lipid stored (58) and fatty acid oxidation observed in Case 4 which were not significant in Case E of the bi-objective.
To move from “Case 1” to “Case 5”, i.e., to high albumin synthesis, requires glucogenic fluxes (2–4) and urea cycle fluxes (15–17) to be decreased significantly with a concomitant decrease in ketone body production (52, 71) and triglyceride lipolysis (53). There is also an decreased catabolism of essential amino acids which are both glucogenic and ketogenic (tryptophan, 25; phenylalanine, 28; and isoleucine, 34) and an increased uptake of glucogenic (61, 74–78) and ketogenic (lysine, 73; and leucine 79) amino acids. Notably, in Case 5, i.e. of high albumin synthesis, there is an increased uptake of pyruvateforming amino acid (alanine, 67) and α-ketoglutarate forming amino acids (proline, 61; arginine, 65) which is only evident under this condition of high albumin synthesis. In comparing Case 5 with 1-A of the bi-objective scenario (Figure 4A), again there is a decrease in urea secretion in Case 4, because of higher preferences for NADPH and glutathione synthesis over urea secretion. In Case 1-A, the values of two optimized objectives, urea secretion and albumin synthesis, were 29.7 and 0.136 respectively, and for the two non-optimized objectives, NADPH and glutathione synthesis, were 0.19 and 3.42, respectively. However, in Case 5, the values of optimized objectives for urea secretion, NADPH, albumin, and glutathione synthesis were 1.0, 0.1, 0.143 and 0.42, respectively. This results in decreased urea cycle fluxes, higher fatty acid oxidation (41), and decreased glucogenic fluxes in Case 5.
To move from “Case 1” to “Case 6”, i.e. to high gluathione synthesis, necessitates higher glucogenic amino acids (68, 72, 75, 76 and 80) and lower ketogenic amino acids (73, 79). Also, there is an increased uptake of amino acids relevant to urea cycle fluxes such as aspartate(70) compared to Case 1 but decreased arginine and asparagines uptake when compared to both Case 1 (base BAL case) and Case 5 (high albumin synthesis); but, there is a significant increase in amino acids involved in the synthesis of glutathione (glycine, 69; and glutamine, 80).
Case 7 presents the results where equal priority was assigned to all four objectives. As can be seen from the heat map, moving from Case 1 to Case 7 necessitates most of the fluxes to be increased. Significant increase in fluxes of amino acids forming pyruvate (serine, 19), acetoacetylCoA (tryptophan, 25), and α-ketogluatrate (glutamine, 40) is required to simultaneously increase the fluxes of various objectives. In summary, to increase the hepatic function in BAL from its current state of Case 1 to the Case where all four major hepatocyte functions are increased necessitates increases in glucogenic fluxes, TCA cycle fluxes, and increased uptake of both glucogenic and ketogenic amino acid fluxes. Interestingly, the increase in hepatic function also necessitates decreased lipid synthesis and storage fluxes. This is in concurrence with the experimental results of stimulated BAL where lipid storage and synthesis decreased hepatic function.
Figure 6B presents the profiling if Case 2 is used as the base case and metabolite changes are computed based on this base case. The difference between Base Cases 1 and 2 is essentially between the exclusion of measurements for urea, albumin and NADPH syntheses. Base Case 2 optimizes the hepatic function using the existing measurements of amino acids and lipid uptake. The respective values of equally prioritized optimal hepatic objectives for Case 2 using LPPFBA are urea synthesis (20.0), NADPH synthesis (2.44), albumin synthesis (0.001) and GSH synthesis (9.89). As seen in the heat map in Figure 6B, the flux changes to achieve various objectives when Base Case 2 is used as reference case both increased and decreased significantly from their current state. This is in contrast to Figure 6A where most of the changes were in the direction of increasing uptakes. Interestingly, to move from Case 2 to Case 7, i.e. to increase the hepatic functions in simulated BAL we need to decrease glucogenic fluxes (1–4) and increase the TCA cycle fluxes (12–15). Importantly, pyruvate is required to increase the synthesis of alanine (18) rather than using it directly as a substrate in the TCA cycle to compensate for the increased demand of alanine by other hepatic functions. Notably, TCA cycle flux from succinyl CoA to oxaloacetate is increased by increasing the synthesis of succinylCoA from methionine (net succinyl CoA flux is 4.37 in Case 7 compared to 0.012 in Case 2). There is net increase in uptake of various amino acids (proline, 61; serine, 68;glycine, 69; aspartate, 70; 73–80) required in Case 7 to increase the hepatic function in simulate BAL system.
Numerous studies abound in which biological systems have been shown to exhibit the property of optimality. Moreover it is a well known fact that mammalian systems perform an array of regulatory, metabolic, homeostatic, and phenotypic functions thus they exhibit a tradeoff between proliferation and differentiation, cellular functions and growth, and cellular functions and robustness, growth and proliferation. However, most of the current frameworks are not suitable for handling various biological objectives simultaneously. Thus, there has been a continued struggle in understanding the crosstalk and correlation of the cellular objectives in metabolic networks. We present a novel soft constraints approach which explains the effect of one objective over another and could decipher the basis behind the selection of optimal metabolic network fluxes for hepatic metabolic network system. Hepatic system in BAL is among the most complex metabolic network system because of the requirement of maintenance of several objectives (maximizing ketone body synthesis, minimizing triglyceride storage, maximizing fatty acid oxidation, maximizing albumin synthesis, maximizing urea secretion, maintaining anti-oxidative stress enzyme homeostasis, and bile transport). Using our approach we show the specific routing of fluxes needed for BAL systems for the cases where one or many of these objectives are desired to be maintained. The analysis presents an experimentally viable strategy for enhancing functionality of BAL systems.
CONCLUSIONS AND SUMMARY
Mammalian systems perform several different functions in nature and hence, optimization of such systems may involve more than one objective as the goal. For example, hepatocytes perform several different functions as the key component of BAL systems, and these functional objectives are potentially conflicting. As seen above, higher albumin synthesis changes the uptake of various metabolites in such a manner that necessarily decreases urea secretion. In order to investigate the trade-offs between these conflicting objectives and to explore available design options, one needs to formulate the optimization problem with multiple objectives (vector optimization). Vector optimization obtains a Pareto optimal solution that satisfies the strict constraints imposed by multiple objectives. However, most of the current algorithms suffer from several disadvantages, such as: requiring a priori selection of weights or targets for each of the objective functions which are inadequate in capturing desired preferences; providing a single Pareto solution; inability to generate proper Pareto points for non-convex problems (e.g., the weights method); inability to generate sensitivity information for trade-off and decision making; and no inherent capabilities for design exploration. LPPFBA captures the designer's preferences a priori in a mathematically consistent manner using preference functions. The application of LPPFBA does not require specifying weights for each objective function. Rather, the ranges of differing degrees of desirability for each objective function are specified. A clear advantage of the LPPFBA approach is that it is a strategy that allows one to obtain conditions where tradeoff of all the desired objectives could be observed in their physical space.
Another advantage of LPPFBA is its ability to deal with multiple objectives with ease. As seen in this paper, BAL systems have many objectives and as can be seen from the quad-objective scenario, working in physical space allowed us to analyze optimal conditions easily and obtain various desired optimal solutions. As seen in Figure 3, using linear programming for this quad-objective problem would have necessitated specifying four weights and no target values, using goal programming would have necessitated 8 weights and four target values; however, LPPFBA requires no specification of weights and only requires target values (20). Specifying the target values is much easier since these are specified in physical space which is always a known space for the designer. Another significant advantage of LPPFBA is that it facilitates optimization of poorly scaled problems. An example of such problems in metabolic networks is the maximization/minimization of two fluxes of different magnitudes, such as the minimization of albumin (on the order of 10−5) and NADPH synthesis (on the order of 101).
In summary, in this paper, a constrained multiobjective formulation LPPFBA to analyze large scale linear metabolic networks is presented. The LPPFBA approach provides a new effective tool to obtain Pareto optimal solutions. The incorporation of LPP into the standard Flux Balance Analysis method enables an unambiguous formulation of an aggregate objective function that facilitates effective multiobjective flux balance analysis for large-scale problems. The presented LPPFBA approach initiates a meaningful step towards analyzing optimality in natural and perturbed metabolic networks (Segre et al., 2002). Importantly, the presented methodology could be employed in various metabolic networks that invariably have multiple objectives (ranging from physiological to design objectives) to be optimized. The combined quantitative and visualization framework presented in this paper sets the stage for the development of true optimal solutions for large scale genomics based metabolic network systems. In the context of BAL, the results presented in this paper illustrate that BAL design using constraints based multiobjective optimization can result in an increase in overall hepatic functions by modifying various metabolite fluxes from its current simulated state during BAL operation. The results presented in this paper have the potential to improve the hepatic function by using optimal pre-conditioning medium in BAL devices. We are currently investigating the optimal fluxes obtained through multiobjective optimization experimentally by using hormonal supplements, inducers, and transfection of primary hepatocytes in our laboratory.
Supplementary Material
APPENDIX
Generation of Pareto points using LPPFBA
This section develops a simple Linear Physical Programming based Pareto frontier generation method. In LPPFBA approach, preferences regarding each cellular objective can be expressed by providing numerical values that are associated with ranges of differing desirability. In order to obtain the Pareto optimal solutions, preference values have to span the objective space, to generate all the combinations of actual preferences that can result in corresponding Pareto points. We generate Pareto points in a region where a particular objective function is small by simply expressing small pseudo-preference values for that objective function. In a similar fashion, we can generate Pareto points in a region where a certain objective function is large by simply choosing large pseudo-preference values for that design metric. The steps for Pareto genearation are presented below:
Step 1-Definition of the objective space of interest
First a hypercube that defines the region of interest in the objective space is generated. In particular, the minimum and maximum values associated with each design metric are defined. For the ith objective function, gi,min and gi,max respectively denote the associated minimum and maximum objective function values in the Pareto frontier, or in the desired region of investigation; where it is to be noted that the region of investigation must be a subset of the Pareto frontier. For the ith objective function, we also define
| (24) |
Step 2-Tradeoff matrix construction
Define the Tradeoff matrix G , as follows
| (25) |
where N is equal to the number of objective functions, nsc. In the tradeoff matrix G above, the ith row, ri , represents the set of objective function values that are obtained when gi = gi,min.
Step 3-Diagonal translation of AOF surface
The generation of the Pareto points involves translating the AOF surface across the objective space. A pseudo-preference translation vector is formed as
| (26) |
| (27) |
The parameter γi varies between 0 and 1, and the ith component of the translation vector varies between the minimum and maximum values of the ith objective function. The number of values of γi is dictated by the resolution with which we wish to generate the Pareto frontier. We let n, the point-density parameter (which represents the resolution of the Pareto frontier), denote the number of γi values for each objective function. Accordingly, the γi increments are 1/(n − 1). Figure S1 depicts the scenarios for two and three soft objective function cases, with n = 6. In the case of two design metrics, we have a total of 6 translation vectors, which will yield 6 Pareto solutions. In the case of three objective functions, we have 21 translation vectors yielding 21 Pareto solutions. The AOF surface is shifted through the objective space.With each shift, an optimization is performed resulting in a Pareto point. In essence, translating the AOF surface in the objective space generates the entire Pareto frontier.
Step 4-Offset in diagonal translation of AOF surface, and its magnification
In Step 3, we showed how the AOF surface could be translated, with the intent of generating the Pareto frontier. However, to avoid missing any Pareto solution if hypercube is too small we need following adjustments. First, we can offset the translation trajectory by replacing it with another that is parallel to the original. Alternatively, we can magnify the box size so as to overlap all regions of the objective space. First, we define the box size as
| (28) |
where nd is a real positive number that defines the relative size of the hypercube of interest and the AOF. By letting nd be a number less than or equal to two when there is no offset, we can ensure that all Pareto points can be generated. Second, we define the offset vector as
| (29) |
which is used to offset the translation trajectory, as discussed above.
Step 5-Formation of pseudo-preference vector
The pseudo-preference vector as follows. As discussed above, we directly use these values of preference input in the LPP algorithm to generate Pareto points. We define
| (30) |
and
| (31) |
which yield the pseudo-preference vector as
| (32) |
where
| (33) |
The variable is utilized to implement an additional offset of the translation trajectory. Also following constraints have to be satisfied in order for the pseudo-preferences to effectively impact the solution:
| (34) |
which leads to the requirement
| (35) |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
SUPPLEMENTARY DATA
Software containing the LPP based FBA algorithm will be available on the Center for Engineering in Medicine web site http://cem.sbi.org. The algorithm details for LPPFBA are presented as part of the supplementary data for the interested readers.
REFERENCES
- Antoniewicz MR, Kelleher JK, Stephanopoulos G. Elementary metabolite units (EMU): a novel framework for modeling isotopic distributions. Metabolic engineering. 2007a;9:68–86. doi: 10.1016/j.ymben.2006.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antoniewicz MR, Kraynie DF, Laffend LA, Gonzalez-Lergier J, Kelleher JK, Stephanopoulos G. Metabolic flux analysis in a nonstationary system: fed-batch fermentation of a high yielding strain of E. coli producing 1,3-propanediol. Metabolic engineering. 2007b;9:277–292. doi: 10.1016/j.ymben.2007.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banta S, Yokoyama T, Berthiaume F, Yarmush ML. Quantitative effects of thermal injury and insulin on the metabolism of the skeletal muscle using the perfused rat hindquarter preparation. Biotechnology and bioengineering. 2004;88:613–629. doi: 10.1002/bit.20258. [DOI] [PubMed] [Google Scholar]
- Berthiaume F, Moghe PV, Toner M, Yarmush ML. Effect of extracellular matrix topology on cell structure, function, and physiological responsiveness: hepatocytes cultured in a sandwich configuration. Faseb J. 1996;10:1471–1484. doi: 10.1096/fasebj.10.13.8940293. [DOI] [PubMed] [Google Scholar]
- Burgard AP, Maranas CD. Optimization-based framework for inferring and testing hypothesized metabolic objective functions. Biotechnology and bioengineering. 2003;82:670–677. doi: 10.1002/bit.10617. [DOI] [PubMed] [Google Scholar]
- Chan C, Berthiaume F, Lee K, Yarmush ML. Metabolic flux analysis of cultured hepatocytes exposed to plasma. Biotechnology and bioengineering. 2003a;81:33–49. doi: 10.1002/bit.10453. [DOI] [PubMed] [Google Scholar]
- Chan C, Berthiaume F, Lee K, Yarmush ML. Metabolic flux analysis of hepatocyte function in hormone- and amino acid-supplemented plasma. Metabolic engineering. 2003b;5:1–15. doi: 10.1016/s1096-7176(02)00011-3. [DOI] [PubMed] [Google Scholar]
- Chan C, Berthiaume F, Washizu J, Toner M, Yarmush ML. Metabolic pre-conditioning of cultured cells in physiological levels of insulin: generating resistance to the lipid-accumulating effects of plasma in hepatocytes. Biotechnology and bioengineering. 2002;78:753–760. doi: 10.1002/bit.10275. [DOI] [PubMed] [Google Scholar]
- Chan C, Hwang D, Stephanopoulos GN, Yarmush ML, Stephanopoulos G. Application of multivariate analysis to optimize function of cultured hepatocytes. Biotechnology progress. 2003c;19:580–598. doi: 10.1021/bp025660h. [DOI] [PubMed] [Google Scholar]
- Cox SJ, Shalel Levanon S, Sanchez A, Lin H, Peercy B, Bennett GN, San KY. Development of a metabolic network design and optimization framework incorporating implementation constraints: a succinate production case study. Metabolic engineering. 2006;8:46–57. doi: 10.1016/j.ymben.2005.09.006. [DOI] [PubMed] [Google Scholar]
- Dunn JC, Tompkins RG, Yarmush ML. Long-term in vitro function of adult hepatocytes in a collagen sandwich configuration. Biotechnology progress. 1991;7:237–245. doi: 10.1021/bp00009a007. [DOI] [PubMed] [Google Scholar]
- Ghosh S, Grossmann IE, Ataai MM, Domach MM. A three-level problem-centric strategy for selecting NMR precursor labeling and analytes. Metabolic engineering. 2006;8:491–507. doi: 10.1016/j.ymben.2006.05.001. [DOI] [PubMed] [Google Scholar]
- Khannapho C, Zhao H, Bonde BK, Kierzek AM, Avignone-Rossa CA, Bushell ME. Selection of objective function in genome scale flux balance analysis for process feed development in antibiotic production. Metabolic engineering. 2008;10:227–233. doi: 10.1016/j.ymben.2008.06.003. [DOI] [PubMed] [Google Scholar]
- Knorr AL, Jain R, Srivastava R. Bayesian-based selection of metabolic objective functions. Bioinformatics (Oxford, England) 2007;23:351–357. doi: 10.1093/bioinformatics/btl619. [DOI] [PubMed] [Google Scholar]
- Lee K, Hwang D, Yokoyama T, Stephanopoulos G, Stephanopoulos GN, Yarmush ML. Identification of optimal classification functions for biological sample and state discrimination from metabolic profiling data. Bioinformatics (Oxford, England) 2004;20:959–969. doi: 10.1093/bioinformatics/bth015. [DOI] [PubMed] [Google Scholar]
- Maier K, Hofmann U, Reuss M, Mauch K. Identification of metabolic fluxes in hepatic cells from transient 13C–labeling experiments: Part II. Flux estimation. Biotechnology and bioengineering. 2008;100:355–370. doi: 10.1002/bit.21746. [DOI] [PubMed] [Google Scholar]
- Maria A, Mattson CA, Ismail-Yahaya A, Messac A. Linear physical programming for production planning optimization. Eng Optimiz. 2003;35:19–37. [Google Scholar]
- Messac A. From dubious construction of objective functions to the application of physical programming. Aiaa J. 2000;38:155–163. [Google Scholar]
- Nagrath D, Avila-Elchiver M, Berthiaume F, Tilles AW, Messac A, Yarmush ML. Integrated energy and flux balance based multiobjective framework for large-scale metabolic networks. Annals of biomedical engineering. 2007;35:863–885. doi: 10.1007/s10439-007-9283-0. [DOI] [PubMed] [Google Scholar]
- Nagrath D, Bequette BW, Cramer SM, Messac A. Multiobjective optimization strategies for linear gradient chromatography. Aiche J. 2005;51:511–525. [Google Scholar]
- Nolan RP, Fenley AP, Lee K. Identification of distributed metabolic objectives in the hypermetabolic liver by flux and energy balance analysis. Metabolic engineering. 2006;8:30–45. doi: 10.1016/j.ymben.2005.08.004. [DOI] [PubMed] [Google Scholar]
- Savinell JM, Palsson BO. Network analysis of intermediary metabolism using linear optimization. II. Interpretation of hybridoma cell metabolism. Journal of theoretical biology. 1992;154:455–473. doi: 10.1016/s0022-5193(05)80162-6. [DOI] [PubMed] [Google Scholar]
- Segre D, Vitkup D, Church GM. Analysis of optimality in natural and perturbed metabolic networks. Proceedings of the National Academy of Sciences of the United States of America. 2002;99:15112–15117. doi: 10.1073/pnas.232349399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stafford DE, Yanagimachi KS, Lessard PA, Rijhwani SK, Sinskey AJ, Stephanopoulos G. Optimizing bioconversion pathways through systems analysis and metabolic engineering. Proceedings of the National Academy of Sciences of the United States of America. 2002;99:1801–1806. doi: 10.1073/pnas.032681699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vo TD, Greenberg HJ, Palsson BO. Reconstruction and functional characterization of the human mitochondrial metabolic network based on proteomic and biochemical data. The Journal of biological chemistry. 2004;279:39532–39540. doi: 10.1074/jbc.M403782200. [DOI] [PubMed] [Google Scholar]
- Wong MS, Raab RM, Rigoutsos I, Stephanopoulos GN, Kelleher JK. Metabolic and transcriptional patterns accompanying glutamine depletion and repletion in mouse hepatoma cells: a model for physiological regulatory networks. Physiological genomics. 2004;16:247–255. doi: 10.1152/physiolgenomics.00088.2003. [DOI] [PubMed] [Google Scholar]
- Yoo H, Antoniewicz MR, Stephanopoulos G, Kelleher JK. Quantifying reductive carboxylation flux of glutamine to lipid in a brown adipocyte cell line. The Journal of biological chemistry. 2008;283:20621–20627. doi: 10.1074/jbc.M706494200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young JD, Walther JL, Antoniewicz MR, Yoo H, Stephanopoulos G. An elementary metabolite unit (EMU) based method of isotopically nonstationary flux analysis. Biotechnology and bioengineering. 2008;99:686–699. doi: 10.1002/bit.21632. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.