Spatio-temporal oscillations of individual mitochondria in cardiac myocytes reveal modulation of synchronized mitochondrial clusters

Abstract

Mitochondrial networks in cardiac myocytes under oxidative stress show collective (cluster) behavior through synchronization of their inner membrane potentials (ΔΨ_m). However, it is unclear whether the oscillation frequency and coupling strength between individual mitochondria affect the size of the cluster and vice versa. We used the wavelet transform and developed advanced signal processing tools that allowed us to capture individual mitochondrial ΔΨ_m oscillations in cardiac myocytes and examine their dynamic spatio-temporal properties. Heterogeneous frequency behavior prompted us to sort mitochondria according to their frequencies. Signal analysis of the mitochondrial network showed an inverse relationship between cluster size and cluster frequency as well as between cluster amplitude and cluster size. High cross-correlation coefficients between neighboring mitochondria clustered longitudinally along the myocyte striations, indicated anisotropic communication between mitochondria. Isochronal mapping of the onset of myocyte-wide ΔΨ_m depolarization further exemplified heterogeneous ΔΨ_m among mitochondria. Taken together, the results suggest that frequency and amplitude modulation of clusters of synchronized mitochondria arises by means of strong changes in local coupling between neighboring mitochondria.

Mitochondria in cardiac myocytes under the influence of substrate deprivation or oxidative stress have a fundamental role as determinants of cell life or death, with implications that scale to affect the function of the whole heart (1, 2). Cardiac mitochondria are organized in a highly ordered network consisting of intermyofibrillar, subcarcolemmal, and perinuclear (3) mitochondria whose coordinated function controls the energy metabolism of the myocyte (4).

In cardiac myocytes, the localized perturbation of a few mitochondria within the overall mitochondrial network can trigger the transition from the physiological to the pathophysiological state by producing synchronized whole-myocyte oscillations of ΔΨ_m that can be monitored with the fluorescent dye tetramethylrhodamine ethyl ester (TMRE) (5). The imbalance between reactive oxygen species (ROS) generation and ROS scavenging capacity in a significant proportion of the network (∼60%) (5) is thought to destabilize ΔΨ_m beyond a critical point into a state of ROS-induced ROS release. Increased ROS overflow exceeding a threshold level results in the appearance of a spanning cluster of mitochondria oscillating in apparent synchrony throughout the cell as the mitochondrial network locks into a low-frequency, high-amplitude oscillatory mode (6, 7).

In many disparate examples of physically and chemically coupled oscillators, synchronization of the system generally arises from an initial nucleus of (spontaneously) synchronized oscillators that integrate neighboring oscillators, thereby increasing the size and signal amplitude of the initial oscillatory nucleus (8–11). When the cluster size passes a critical threshold, the whole network spontaneously self-organizes into a new state in a process resembling a phase transition; in the case of mitochondrial oscillators, this transition corresponds to the change from the physiological to the pathophysiological regime of the mitochondrial network. Aon et al. (6) found that this global phase transition occurs at a percolation threshold of the mitochondrial network, and further demonstrated that this global behavior, under normal conditions, obeys fractal, self-similar dynamics (7, 12, 13), with no inherent characteristic frequency, but rather displays a broad range of frequencies occurring over multiple time scales.

Finally, the observation that oscillating mitochondria may be spatially organized during myocyte-wide synchronized oscillations led us to explore the hypothesis that individual mitochondria within a cluster might oscillate at the same frequency and to examine whether the oscillation frequency of individual mitochondria influences the size and amplitude of the mitochondrial cluster oscillations and vice versa. Therefore, in the present work we aimed to establish a method for detecting and characterizing single mitochondrial ΔΨ_m oscillations and to examine the spatio-temporal organization of these oscillators as they interact with their nearest neighbors. The findings reveal significant correlations between mitochondrial cluster frequency and mitochondrial cluster size as well as between mitochondrial cluster amplitude and mitochondrial cluster size, indicating the strong influence of individual mitochondrial oscillators on the spatio-temporal organization and formation of mitochondrial clusters. The results shed light on understanding the behavior of the mitochondrial network.

Results

Time-Dependent Frequency Analysis of Individual Mitochondria Using Wavelet Analysis.

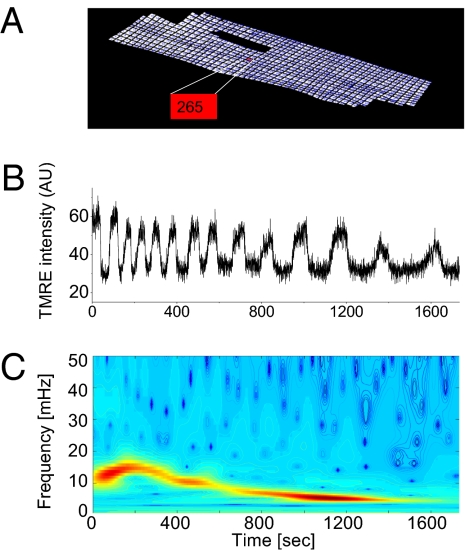
Single mitochondria of a cardiac myocyte were identified and labeled within a hand-drawn grid of a stack of frames averaged over time (Fig. 1A). Wavelet analysis was used to distinguish between an oscillating mitochondrion (Fig. 1 B and C) and a nonoscillating mitochondrion (SI Text). This unique approach allowed us to filter all mitochondria with similar dynamic frequency behavior in order to identify mitochondrial frequency clusters, and to examine their spatial correlates.

Fig. 1.

Wavelet analysis of single mitochondrial signals. (A) Single mitochondria of a cardiomyocyte are identified and labeled within a hand-drawn grid of an averaged stack of frames in time. TMRE signal for a single oscillating mitochondrion (B). (C) The absolute squared wavelet transform over frequency and time. The major frequency component in a cluster of mitochondria (see whole myocyte mean signal in SI Text), dropped from about 15 to 5 mHz during the recording.

Algorithm for the Selection of Mitochondria Belonging to a Major Cluster.

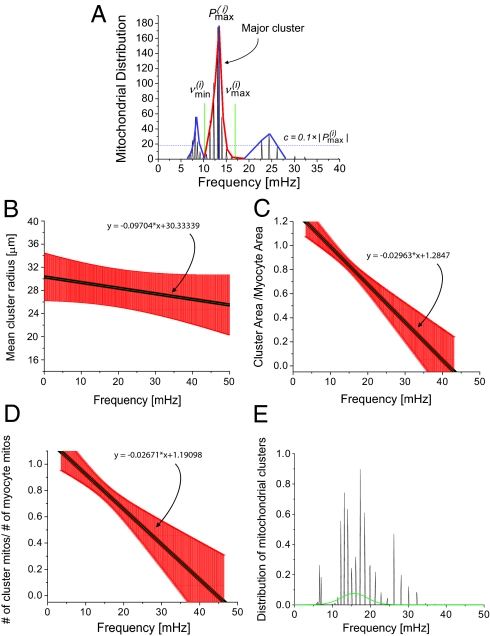
To determine the frequency distribution of oscillating mitochondria at each frame and their relationship to neighboring mitochondria, we have followed a procedure that is based on obtaining frequency histograms of all mitochondria for that frame. For each frame i, we obtained the instantaneous individual mitochondrial frequencies using the wavelet transform, as described below and by plotting their distribution we determined the maximum peak (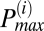) value as shown in Fig. 2A. We then identified all relevant histogram peaks as those frequencies whose histogram amplitude is above 10% of 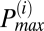(Fig. 2A).

Fig. 2.

Mitochondrial frequency distribution in clusters for different myocytes (n = 9). (A) Frequency histogram for a specific frame obtained from wavelet analysis. There are three apparent major clusters. The amplitude distribution cutoff (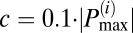) is marked with a horizontal dashed line and the relevant cluster peak 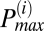(in red) extends to frequencies defined by 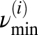and 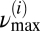(green lines). Because the correlation of the other two clusters peaks (in blue) with the major cluster peak is lower than 95%, the major cluster peak does not include these smaller clusters. (B) Mean cluster radius as a function of frequency. (C) Cluster area normalized by the full myocyte area as a function of frequency. (D) Cluster mitochondria count normalized by the total number of mitochondria for the major cluster as a function of frequency. SE bars are in red and the mean curve is in black. (E) Distribution of mitochondrial frequencies for all cluster mitochondria across all myocytes.

Additional adjacent peaks above 10% of 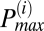were identified and considered as part of the same or different cluster as follows. For each such peak, we determined the mean TMRE signal as well as the lowest and highest frequencies of the peak by interpolating the nonzero frequency amplitudes within the peak. Thereafter, we obtained the correlation coefficient of the mean TMRE signal of mitochondria corresponding to the 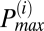peak, with the mean TMRE signal of mitochondria belonging to each of the adjacent identified peaks over a running window (T_w). To capture frequencies in the range of the largest period of oscillation in the mean TMRE fluorescence plot, the size of the running window was chosen such that it is equal to 1.1 times the duration of the period of that oscillation.

If the mean TMRE signal of an adjacent peak had a correlation coefficient that was greater than 95% with the mean TMRE signal of the 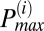peak, then the adjacent peak was incorporated into the 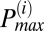peak. The procedure was repeated for both higher and lower frequencies with respect to 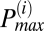until the correlation coefficient dropped below 95%.

At this stage, we have derived a frame-dependent distribution of frequencies that is likely to belong to a major cluster of oscillating mitochondria. Additionally, the mean TMRE signal of all mitochondria in the refined distribution of mitochondria around 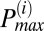was cross-correlated with the TMRE signal of each mitochondrion that did not belong to the major cluster. If the correlation coefficient of a single mitochondrion was above 95%, we further incorporated that mitochondrion into the major cluster, thus determining all oscillating mitochondria that belonged to the major cluster in a given frame. The latter approach was necessitated by the need to account for the case in which the cutoff 10% of 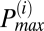was too strict and therefore could potentially reject mitochondria in which the TMRE signal was highly correlated with that of the major cluster.

Frequency and Cluster-Size Relationship.

To examine the relation between frequency and cluster size, we defined the mean radius of the cluster by measuring the distance of the pixel of the geometrical center of the cluster to each single mitochondrion's geometrical center and then by dividing it by the number of mitochondria in the cluster in each frame.

We then plotted the mean radius of the major mitochondrial cluster against the mean frequency of the cluster (Fig. 2B), the relative area of the major mitochondrial cluster (quotient of total cluster pixel-count and myocyte pixel-count) against the mean frequency of the cluster (Fig. 2C) and the relative number of the major mitochondrial cluster (quotient of the number of cluster mitochondria versus the total number of mitochondria) against the mean frequency of the cluster (Fig. 2D), for each frame. As can be clearly seen, there is an inverse relationship between mitochondrial cluster size, area, and number vs. the mean frequency of the cluster, which suggests that large clusters have a longer oscillation period than small clusters.

Subsequently, we sought to examine the frequency distribution of the mitochondria belonging to the major clusters. For each cardiomyocyte, we constructed a frequency histogram of all mitochondria belonging to a major cluster across all frames (Fig. 2E). Mitochondrial frequencies were counted in bins of width 0.1 mHz in the range of 0–50 mHz.

Specifically, to allow comparisons between myocytes, the counts of each frame were divided by the number of the mitochondria belonging to a major cluster in that frame, and the amplitude at each frequency in the frequency histogram was again divided by the total number of frames. Then, a final histogram was created and was fitted to a Gaussian function. The frequency bandwidth (mean ± std) of the Gaussian fit was determined to be: 8.73–22.3 mHz. Using Fig. 2B, this indicates that the mean radius of the oscillating cluster of mitochondria is between 27 and 30 μm. The relatively high SE in this region of the plot results from gaps in the major cluster of mitochondria. In fact, such a noncontiguous mitochondrial cluster, with mitochondria that oscillate close to the same frequency (a “frequency cluster”), shows a similar topology to that described for spanning clusters (2, 6). Specifically, we have observed that in some myocytes, the major frequency cluster shows many noncluster areas of mitochondria at the onset of oscillations, although during the course of recording more and more of these gaps between frequency cluster mitochondria are filled, yielding a more contiguous morphological cluster. Thus, from Fig. 2A, the rate of change of the mean radius with respect to the frequency has been calculated to be −0.0973 ± 0.13 μm/mHz.

However, it was observed that the percentage area of the cluster—defined as the quotient of the area of cluster mitochondria and the whole-myocyte area (Fig. 2C)—or the percentage number of cluster mitochondria—defined as the number of cluster mitochondria divided by the number of mitochondria in the cardiomyocyte (Fig. 2D)—are measures with less uncertainty of the cluster size. We have found that the percentage area of the cluster changes by −2.96 ± 1.11%/mHz and that the percentage number of cluster mitochondria changes by −2.67 ± 1.12%/mHz.

Cluster Oscillation Coherence.

To analyze the temporal properties of the cluster mitochondria, we investigated the temporal coherence properties of cluster mitochondria by estimating the average coherence of the TMRE signal of each cluster mitochondrion with its nearest neighbors. Coherence takes values between 0 and 1 at each frequency, indicating whether two signals oscillate in synchrony (“1”) at each frequency, or not (“0”).

The coherence of each cluster mitochondrion was estimated in Matlab with a running window of size T_w and a fixed Fast Fourier Transform (FFT) length of 2¹¹ dt. We took the frequency range for each myocyte from 0 to 100 mHz and divided that range into (2¹¹/2) + 1 segments; each segment therefore represented ≈0.1 mHz.

The coherence was then obtained for each major mitochondrial cluster in the specific running window by taking the average coherence at each frequency over all the nearest neighbors that belonged to the cluster. Subsequently, another averaging of the coherence was performed over all cluster mitochondria. We continued this process by shifting the running window by one frame at a time until the last frame of the current running window was equal to the last frame of the recorded signal. Finally, for each running window the value of the mean coherence at the mean frequency of all mitochondria belonging to the cluster was estimated, thus obtaining the coherence as a function of time. To further compare myocytes with unequal duration of recordings, we set each cardiomyocyte's duration of oscillations to 1.

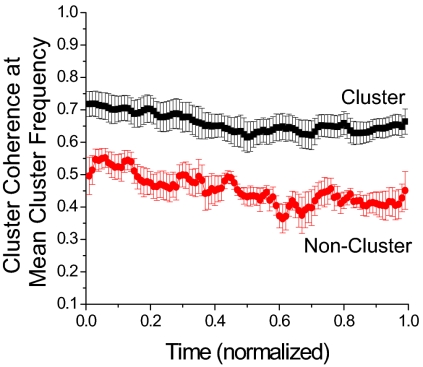
One observes that the coherence of the cluster mitochondria does not change significantly during the recording, indicating a high temporal stability of the coherence of the oscillating cluster mitochondria (Fig. 3, black markings). Averaging in time yields a coherence of 0.66 ± 0.04. In comparison, the coherence for noncluster mitochondria (Fig. 3, red markings) was determined to be 0.44 ± 0.04, which demonstrates, in a quantitative manner, that nonoscillating mitochondria are less correlated with each other than those within the cluster. Nevertheless, it should be noted that, despite the profound difference in coherence between cluster and noncluster mitochondria, the noncluster mitochondria still exhibited quite a high degree of coherence. This may be attributed to the fact that noncluster mitochondria might oscillate, too, although at a different inherent frequency from those within the cluster.

Fig. 3.

Coherence of mitochondria belonging to the major oscillating cluster, estimated at the mean cluster frequency (n = 9). To allow the statistical comparison among myocytes with unequal recording durations, the duration of the oscillations of each recording was normalized.

Mitochondrial Oscillation Amplitude vs. Cluster Size and Frequency.

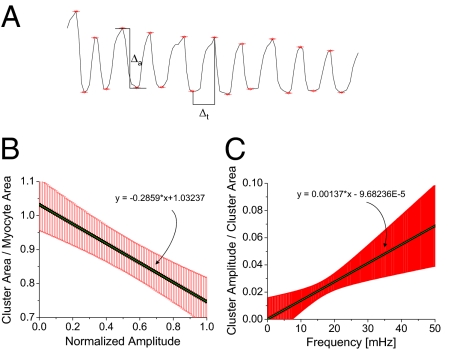
We next examined the relationship between oscillation amplitude and cluster size. We determined the mean TMRE signal of the mitochondrial cluster, manually identified each peak, and found the peak-trough time difference (Δ_t) and the peak-trough amplitude difference in TMRE intensity (Δ_a) of the TMRE intensity and vice versa (Fig. 4A). The mean frequency and area (in pixels) of the cluster mitochondria for all frames within Δ_t were then determined and averaged over Δ_t.

Fig. 4.

(A) Method for obtaining the amplitude of mitochondrial oscillations. After identifying the peaks of the mean TMRE signal of a major cluster of mitochondria, we determined the mean cluster area and frequency between consecutive peaks and determined the amplitude as the difference in their TMRE intensity. (B) The normalized cluster area is plotted against the oscillation amplitude values that have been normalized by the maximum amplitude value (n = 8). (C) Normalized mitochondrial cluster amplitude vs. normalized cluster area follows a linear pattern when plotted against the mean cluster frequencies (n = 6).

For each myocyte, and for each Δ_t, we plotted the mean cluster area normalized to the area of the full myocyte against the corresponding TMRE amplitude normalized to the maximum amplitude (Fig. 4B, slope: −0.29 ± 0.1). The quotient of cluster amplitude over the cluster area was found as a function of the mean cluster frequency in the same time range (Δ_t), suggesting that there is a negative correlation between cluster size and cluster amplitude (Fig. 4B). However, it should be noted that this result does not suggest that the extent of depolarization is smaller when the cluster size increases, but rather that it reflects a more prolonged and incomplete repolarization of the network between oscillations (see Fig. 4A). The rate of change of the normalized cluster amplitude (cluster amplitude divided by the maximum cluster amplitude) vs. frequency is larger than that of the normalized cluster area (cluster area divided by the whole myocyte area) vs. frequency (Fig. 4C, slope: 0.14E-2 ± 0.06E-2/mHz).

Isochronal Mapping.

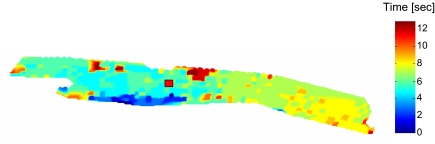
To further understand the spatio-temporal dynamics of mitochondrial ΔΨ_m at the onset of synchronized depolarizations for a myocyte subjected to a localized laser flash (indicated by a red square in Fig. 5), we created an isochronal map of earliest mitochondrial depolarization at the time of the maximum first derivative of the TMRE signal (Fig. 5).

Fig. 5.

Isochronal map of a canine cardiac myocyte at the onset of flash-triggered oscillations. The red square signifies the area of the flash. About 25 s after the flash, an initial critical mass of mitochondria in the left bottom area of the myocyte triggers mitochondrial depolarizations by exciting a critical number of mitochondria. The excitation penetrates the whole myocyte within ≈10–12 s, leading to a conduction velocity of about 32 μm/s.

Only mitochondria with a clear and distinctive depolarization slope were taken into account, and missing mitochondria were interpolated two-dimensionally using Matlab. The isochronal map was created by displaying the activation time of each mitochondrion with respect to the earliest activation time across all mitochondria.

As can be seen in Fig. 5, the first mitochondria depolarized at the bottom left of the myocyte, and the depolarization spread toward both ends of the cell along the longitudinal axis. It is remarkable that, in this myocyte (from a canine heart), it is not the flashed mitochondria (signified with a red square) that trigger the first depolarizations, but instead an initial nucleus of synchronized mitochondria slightly separated from the flashed region. This observation is in agreement with prior observations that suggest that myocyte-wide mitochondrial oscillations do not necessarily originate from a nucleus of mitochondria (2, 6, 7) that is fixed in only one place.

Assuming that the depolarization spreads uniformly from the geometrical center of the initiating nucleus of mitochondria to the farthest ends of the myocyte, which in this example took ∼10 s to complete, we obtained a longitudinal conduction velocity of ∼32 μm/s, which is close to that measured in flash-triggered guinea pig myocytes (22 μm/s) (6).

Longitudinal vs. Transverse Correlation of Mitochondrial Membrane Potential.

To quantitatively examine ΔΨ_m wave propagation differences in the longitudinal vs. transverse directions, we selected two axes: a longitudinal axis parallel to the cardiac myocyte myofilaments and a transverse axis perpendicular to the myofilaments (SI Text). For a single cluster mitochondrion {i} at each frame, we determined the neighboring mitochondria belonging to the major cluster along each axis. TMRE signals of the transverse or longitudinal neighbors of a mitochondrion {i} of the cluster were cross-correlated with that mitochondrion over a running window of length T_w, and the average correlation coefficient (CC) along each axis yielded a time- and mitochondrion-specific longitudinal and transverse CC.

In Table 1, we see that the values of the longitudinal and transverse correlations are significantly different from each other. Because the longitudinal correlation is stronger than the transverse one, this finding suggests that the longitudinal axis is the preferred axis of depolarization propagation. This is in keeping with the spatial organization of the mitochondrial network, where polarized mitochondria are usually distributed in rows along the longitudinal axis and very rarely along the transverse axis (with some deviation from this generalization for mitochondria located adjacent to the nuclei of the cell). This could be related to diffusional restrictions imposed by the spatial arrangement of the myofilaments that separate the mitochondria in the transverse direction (14).

Table 1.

Longitudinal and transverse correlation of cluster mitochondria

	Mean value	SE (±)
Longitudinal CC	0.8072	3.3494E-4
Transversal CC	0.7071	4.353E-4
Longitudinal CC/transversal CC	1.2657	0.0804

Correlation coefficients (CC) of direct cluster neighbors of cluster mitochondria are averaged along each axis and evaluated for all images in different myocytes (n = 7).

Discussion

Oxidative stress, which occurs as a result of an imbalance between ROS generation and ROS scavenging, forces the mitochondrial network of the cardiac myocyte into a high-amplitude, low-frequency oscillatory mode. It has been proposed that individual, weakly coupled, mitochondrial oscillators are present in the physiological state when ROS levels are low, but are strongly coupled in the pathophysiological state by mitochondrial ROS induced ROS release (12). This transition has a profound impact on myocyte electrical excitability and intracellular Ca²⁺ (1) and has been implicated in post-ischemic dysfunction of the heart (15).

The present study quantitatively characterizes the spatio-temporal organization of stress-induced mitochondrial oscillations of a heterogeneous mitochondrial network in the pathophysiological regime. The advances made by this study include (i) the development of a wavelet-based method for obtaining the time-dependent frequency of individual oscillating mitochondria; (ii) the development of an algorithm for identifying mitochondria that belong to a major cluster during the mitochondrial network oscillation; (iii) the finding that the frequency of oscillating mitochondria organized in a major cluster during synchronized ΔΨ_m oscillations is correlated with the size of that cluster; (iv) isochronal mapping indicates that the onset of myocyte-wide mitochondrial oscillations originates from a small nucleus of depolarized mitochondria that is different from the laser-excited mitochondria; and (v) the observations that ΔΨ_m correlations between neighboring mitochondria along the cardiac-myocyte longitudinal axes are stronger than between neighboring mitochondria in the transverse direction.

In this study, instead of selecting spanning clusters using a ROS-level threshold (7), we focused on major clusters of mitochondria to find the relationship between frequency and amplitude of oscillation or the actual size of the cluster. This procedure allowed us to uniquely identify closely connected clusters by their main frequency component while still taking into account smaller clusters with different frequencies. The mitochondria are therefore grouped into clusters solely by examining their frequencies in a narrow range, at a specific point in time, and should not be thought of as morphologically connected clusters.

In fact, cardiac myocytes possess mitochondria that may show static (morphology and biochemical properties) and dynamic heterogeneity. Static morphological distinctions include mitochondria in intermyofibrillar locations, subsarcolemmal mitochondria, and perinuclear mitochondria (16, 17). It has also been suggested that these differentially localized mitochondria may have different functional properties (18, 19).

These spatio-temporally organized networks underlie complex control mechanisms that influence oxidative phosphorylation and possibly lead to emergent macroscopic responses. Dynamic heterogeneity becomes especially significant under metabolic (20) or oxidative stress, and the scaling of network instabilities to whole-myocyte and even whole-organ function has been recently examined (6, 15, 21, 22). In these studies, it was shown that mitochondrial criticality—i.e., the abrupt and synchronous collapse of ΔΨ_m in individual cells or clusters of cells during ischemia-reperfusion injury—can contribute to the generation of fatal ventricular arrhythmias.

Recently, the application of network theory on mitochondrial networks has helped to understand the functional connectivity of mitochondria (23), especially the concept of scale-free mitochondrial networks (6, 7, 13, 24). These studies have provided evidence that mitochondrial morphology is linked to function [e.g., in the case of coupling between mitochondria and the L-type Ca²⁺-channel (25)] and that changes in metabolic fluxes may occur by altering the structure of the mitochondrial network and/or the topology of the mitochondrial membranes, which may be structural organizing centers for several intracellular signaling pathways (reviewed in refs. 26 and 27).

Some authors support the concept of a single reticular mitochondrial network that replaces the classic mitochondrion organelle (28). In this model, mitochondria are unipotential, and therefore synchronization of oscillations with different mitochondrial frequency spectra would not be possible. Thus, our findings do not support this concept of mitochondrial reticulum but are best understood with the classic view on mitochondrial structure.

It has also been shown that individual mitochondria can respond independently of the network (5, 29–31). In that context, observations of complete or chaotic synchronization (32–34) support the idea that cluster partitioning in networks of coupled oscillators can take place; the network splits into several clusters of mutually synchronized oscillators (35). In addition, a model using gradient coupling (36) exemplifies that around an optimal gradient, most oscillators can be synchronized to the same frequency; oscillators with large gradient coupling can be divided into synchronized clusters of oscillators with different frequencies that still maintain high system coherence.

It should be noted that mitochondrial coupling that starts from a nucleus of excited mitochondria (cf 7) is not an instantaneous process, but rather occurs in a finite time interval through diffusion-mediated processes within the coupling medium. Thus, this process appears to take more time to evolve in larger clusters and hence in such a case full synchronization of all mitochondria requires more time (Fig. 2 B–D). This effect alone leads to prolonged cluster depolarization and therefore to lower cluster frequency. Alternatively, one may reach the same conclusion by considering the more general theory that suggests that the frequency and phase of coupled oscillators adjusts to a common mode and that the larger the clusters, the longer it takes to synchronize as a group (37, 38).

In the present study, during synchronized oscillations we show that the percentage cluster size is inversely correlated with the percentage amplitude within the pathophysiological regime, which actually reflects the failure of the network to completely repolarize between oscillations (Fig. 4A). Therefore, this study provides insight into the behavior of the myocyte near death: the dying myocyte loses ΔΨ_m as the mitochondrial clusters grow larger, and the energetic and antioxidant deficiencies grow until recovery of the network is impossible.

In conclusion, our results show that in a cardiac myocyte the amplitude and frequency of a major cluster of oscillating mitochondria are correlated with the size of the cluster and that mitochondrial nearest-neighbor coupling is strongly influenced by the organization of mitochondria along the myofilaments. The findings highlight the importance of both spatial and temporal organization in defining how the mitochondrial network functions.

Materials and Methods

Experiments were carried out on freshly isolated adult guinea pig ventricular myocytes, at 37 °C, using protocols that were previously described (1). ΔΨ_m was monitored with the cationic potentiometric fluorescent dye, TMRE (5).

Images were recorded using a two-photon laser-scanning microscope (MRC-1024MP; Bio-Rad) with an excitation at 740 nm (Tsunami Ti:Sa laser; Spectra-Physics) and an emission band at 605 ± 45 nm.

Method to Analyze Mitochondrial Membrane Potential Signals.

Application of mitochondrial grid.

In each stack of frames (collected at a frame rate, dt, ranging from 0.5–3.5 s), we identified the onset of TMRE oscilations as the first frame with a significant mean TMRE intensity loss of more than 10% relative to the mean averaged TMRE intensity of all previous frames. All subsequent frames were then split into intervals of n frames each, where n was chosen such that n dt was smaller or equal to the duration of the smallest period of all TMRE oscillations.

From each sequence of n frames, an average frame was formed and each average frame was uploaded into Adobe Photoshop v7.0. Then we manually formed a grid, on a pixel-by-pixel basis, of the averaged frame with the highest fluorescence intensity and used it as a template. For each grid, we allocated a numerical identifier for each element of the mesh; i.e., each of these identifiers represents one mitochondrion within the myocyte (cf Fig. 1A).

Extraction of individual mitochondrial membrane potentials.

Further processing in ImageJ (v.1.40g) was used to mark the overall shift in x and y direction of the myocyte of each averaged frame. The template grid was then shifted accordingly as a whole, thus providing an interval-independent mesh for each mitochondrion. Finally, the TMRE intensity in each mesh was obtained by taking the average pixel TMRE intensity in that mesh.

Identification of mitochondrial nearest neighbors.

If meshes of the template grid of any two mitochondria could be connected with a straight line that did not cross more than one grid line, the corresponding mitochondria were considered to be nearest neighbors. For most mitochondria, this led to eight nearest neighbors, as in the case of a 2D lattice.

Method to Determine Clusters of Oscillating Mitochondria.

Although biological systems are usually nonstationary in time—i.e., they typically demonstrate complex irregular behavior and changing characteristics (39, 40)—application of standard methods of statistical analysis can often be used with the a priori assumption that they follow stationary processes. However, this approach is useful if the nonstationarity is associated only with the low-frequency portion of the power spectrum relative to the frequencies of interest. Because we had no prior knowledge that mitochondrial oscillations were stationary processes, we used the wavelet transform (41, 42) to determine the oscillation frequency of individual mitochondria within the myocyte.

As a form of time-frequency representation, the wavelet transform expands signals in terms of wavelets by breaking the signal down into different scale components. Starting from an analyzing wavelet function (“mother wavelet”), all wavelets are constructed from the analyzing wavelet via translations and dilations (“daughter wavelets”).

We employed wavelet analysis for each mitochondrion's TMRE signal by using wavelet software in Matlab, a typical example of which is shown in Fig. 1. Overall, we observed that the synchronized oscillations of mitochondria ranged from 4 to 40 mHz (which corresponded to 25- to 250-s periods of oscillation). To avoid time-consuming calculations, we therefore chose (i) a fixed value of dj = 0.1 for the spacing between scales; (ii) a starting point of s_o = 4 dt as the smallest scale of the wavelets that signified the smallest possible period for the detection of one oscillation, where dt is the sampling period; and (iii) the total number of scales, 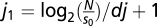, where N is the total number of the recorded frames. Therefore, the scales range from s₀ up to 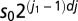, and each scale has dj suboctaves.

Furthermore, a lower cutoff frequency was chosen by looking at the mean TMRE intensity plot of the myocyte, by identifying the longest period T of a synchronized oscillation of the i^thframe, and by taking 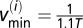as the minimum frequency; similarly, a maximum cutoff frequency was defined as .

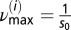In addition, each mitochondrial fluorescence signal was normalized by its SD, and the number of time series frames was padded with zeros to the next higher power of 2, thus preventing wraparound from the end of the time series to the beginning and also accelerating the Fast Fourier Transform that is used in the wavelet transform. For each frame and mitochondrion, we interpolated the power lineplot between 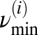and 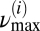for every scale using segments of 0.1 mHz. The frequency at maximum power for the interpolated plot was subsequently determined, and we arrived at a plot of maximal scale frequencies over time for each mitochondrion.

Statistics.

The wavelet analysis and fitting routines were obtained using Matlab v7.1.0.246 (R14). Further statistics were performed using OriginPro 8 SR0 v8.0724 (B724). Statistical significance (P < 0.05) was obtained using the Mann-Whitney test.