Robustness of Ancestral Sequence Reconstruction to Phylogenetic Uncertainty

Abstract

Ancestral sequence reconstruction (ASR) is widely used to formulate and test hypotheses about the sequences, functions, and structures of ancient genes. Ancestral sequences are usually inferred from an alignment of extant sequences using a maximum likelihood (ML) phylogenetic algorithm, which calculates the most likely ancestral sequence assuming a probabilistic model of sequence evolution and a specific phylogeny—typically the tree with the ML. The true phylogeny is seldom known with certainty, however. ML methods ignore this uncertainty, whereas Bayesian methods incorporate it by integrating the likelihood of each ancestral state over a distribution of possible trees. It is not known whether Bayesian approaches to phylogenetic uncertainty improve the accuracy of inferred ancestral sequences. Here, we use simulation-based experiments under both simplified and empirically derived conditions to compare the accuracy of ASR carried out using ML and Bayesian approaches. We show that incorporating phylogenetic uncertainty by integrating over topologies very rarely changes the inferred ancestral state and does not improve the accuracy of the reconstructed ancestral sequence. Ancestral state reconstructions are robust to uncertainty about the underlying tree because the conditions that produce phylogenetic uncertainty also make the ancestral state identical across plausible trees; conversely, the conditions under which different phylogenies yield different inferred ancestral states produce little or no ambiguity about the true phylogeny. Our results suggest that ML can produce accurate ASRs, even in the face of phylogenetic uncertainty. Using Bayesian integration to incorporate this uncertainty is neither necessary nor beneficial.

INTRODUCTION

The properties and evolution of ancient genes and proteins can seldom be directly studied because such molecules are rarely preserved intact over very long periods of time. Pauling and Zuckerkandl (1963) proposed that ancestral molecules could one day be “resurrected” by inferring their sequences and then synthesizing them. Decades later, the methods of ancestral sequence reconstruction (ASR) have emerged as important tools for examining the trajectory of molecular sequence evolution and testing hypotheses about the functional evolution of ancient genes (Thornton 2004; Dean and Thornton 2007; Liberles 2007). Among numerous examples, ASR has been used in the last decade to investigate the evolution of elongation factor proteins (Gaucher et al. (2003), Gaucher et al. (2007)), steroid hormone receptors (Thornton et al. 2003, Bridgham et al. 2006, Ortlund et al. 2007), visual pigments (Chang et al. 2002, Shi and Yokoyama 2004), fluorescent proteins (Ugalde et al. 2004), and alcohol dehydrogenases (ADHs; Thomson et al. 2005).

Although the first ASR practitioners used parsimony methods (e.g., Jermann et al. 1995), most modern studies use maximum likelihood (ML) (Yang et al. 1995, Koshi and Goldstein 1996, Pupko et al. 2000). ML begins with an alignment of extant gene sequences, a phylogeny relating those sequences, and a statistical model of evolution. For each internal node in the phylogeny and each site in the sequence, the likelihood of each possible ancestral state—defined as the probability of observing all the extant states given that ancestral state, the tree, and the model—is calculated. The ML ancestral state is the state with the highest likelihood. Confidence in any ancestral state inference is typically expressed as its posterior probability (PP), defined as the likelihood of the state (weighted by its prior probability) divided by the sum of the prior-weighted likelihoods for all states.

The ML approach to ancestral reconstruction assumes that the alignment, tree, model, and model parameters are known a priori to be correct. In practice, this assumption is often not valid; for many real-world data sets, alternatives to the ML tree and parameter values cannot be ruled out. To accommodate these sources of uncertainty, Bayesian methods have been proposed. Whereas ML assumes the most likely estimate of the tree and model parameters, Bayesian approaches incorporate uncertainty by summing likelihoods over a distribution of possible trees or parameter values, each weighted by its PP. Pagel et al. (2004) proposed a Bayesian method for integrating topological uncertainty into inference of ancestral states for binary and other discrete characters. Schultz and Churchill (1999) proposed a Bayesian method to integrate uncertainty about the parameters of the evolutionary model into discrete character reconstructions. For inference of ancestral DNA and protein sequences, Huelsenbeck and Bollback (2001) developed a Bayesian method to integrate uncertainty about the tree topology, branch lengths, and model parameters.

It is not known how Bayesian approaches affect the accuracy of reconstructed ancestral sequences. Here, we focus on the specific effects of one source of uncertainty—the phylogeny. There have been a few attempts to characterize the robustness of reconstructed ancestral sequences with respect to phylogenetic uncertainty in specific cases: Gaucher et al. (2003) reconstructed ancestral elongation factor proteins on two plausible phylogenies, and Bridgham et al. (2006) reconstructed the ancestral corticosteroid receptor on all trees within the 95% confidence interval from a Bayesian phylogenetic analysis. In both cases, the maximum a posteriori ancestral sequences changed very little when different phylogenies were assumed, and the functions of the reconstructed proteins in experimental assays were also unchanged. Huelsenbeck and Bollback (2001) used simulations to show that integrating uncertainty about the phylogeny, branch lengths, and model parameters can affect the PPs of ancestral states, but they did not study the effect of integration on the inferred maximum a posteriori state or the accuracy of those inferences.

To determine the causal effects of integrating over phylogenetic uncertainty on ASR accuracy, we implemented a topological empirical Bayesian method for ancestral reconstruction that is identical to the ML algorithm, except that it integrates over topologies. This approach allows us to directly infer the effects of incorporating phylogenetic uncertainty on ASR accuracy. We simulated and recorded the evolution of sequences under a variety of simplified and empirically derived conditions and inferred ancestral states from the evolved alignments; we characterized the accuracy of each approach to ASR by comparing inferred ancestral sequences to the “true” ancestors recorded during the simulation.

MATERIALS AND METHODS

Ancestral State Reconstruction Algorithms

The ML method for ASR, also called the empirical Bayes method (Yang et al. 1995), calculates the PP that some ancestral node contained state a at a sequence site of interest, given the observed sequence data d, an evolutionary model m, a topology 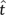, and a set of branch lengths and other model parameters 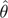; the topology and parameters are those that maximize the likelihood over all data columns in the alignment. The conditional likelihood of a is the probability of observing d given a, m, 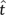, and 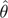. The prior-weighted conditional likelihood of a is the conditional likelihood of a multiplied by the prior probability of observing a, which is given by π_a, the equilibrium state frequency of a. The PP of a equals the prior-weighted conditional likelihood of a divided by the sum of the prior-weighted conditional likelihoods for all possible ancestral state assignments (4 for nucleotides or 20 for amino acids) (eq. 1).

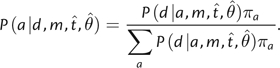(1)

The ML state assignment is the state with the highest prior-weighted likelihood (and necessarily the highest PP, as well). The ML sequence is the string of ML states. To reconstruct ML ancestral sequences, we used PAML v.4.1 (Yang 1997, Yang 2007).

The topological empirical Bayes (TEB) approach to ASR differs from ML only by integrating ancestral reconstructions over a distribution of trees (eq. 2). The TEB PP of ancestral state a is the weighted average of the PP of a over all possible trees, where the weights are given by the empirical Bayes PP of each tree t. The empirical Bayes PP P_EB of a tree assumes the ML estimate of branch lengths and other model parameters 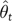on each tree (Kolaczkowski and Thornton 2008, Kolaczkowski and Thornton 2009):

(2)

Equation (2) takes a different form from but is equivalent to (see supplementary note 1, Supplementary Material online) the expression used by others (Huelsenbeck and Bollback 2001, Pagel et al. 2004) for ancestral state reconstructions integrated over topologies:

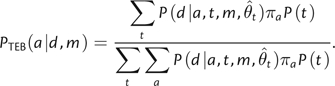(3)

The ML method also has an empirical Bayesian interpretation because equation (1) calculates a PP and uses priors on ancestral states. For simplicity, we will refer to the approach that uses only the ML tree as the “ML method” and the approach that integrates over trees as the “TEB method.”

One issue with estimating ancestral states from a distribution of trees is that every topology contains different ancestral nodes. We accommodate this problem by defining an ancestral node to be reconstructed as the most recent common ancestor of a specified set of descendants (Pagel et al. 2004). On any rooted tree, the clade descending from the specified ancestor will contain all members of this set; additional sequences may also be included in that clade, depending on the topology. A similar approach can be used to describe internal nodes on unrooted trees in relation to the split that places a specified set of terminal sequences into the smallest possible partition of the tree.

We implemented both the TEB and ML methods in our own software called Lazarus. This package spawns, manages, and then parses large batches of parallelized PAML jobs, one for each of a set of user-specified topologies. For each topology, branch lengths and model parameters are optimized by ML, the ML of the tree is calculated, and the PP of each ancestral state is calculated on that topology. Lazarus then parses these results to calculate the PP of each ancestral state integrated over topologies. Lazarus includes a modular Python API with object classes for quickly abstracting ancestral reconstruction data and is available at http://markov.uoregon.edu/software/lazarus/.

Simulations

We compared the ancestral states reconstructed by the ML and TEB methods on data simulated under both controlled and empirically derived conditions. The correct evolutionary model was assumed for all ancestral reconstructions.

Four-Taxon Phylogenetic Uncertainty

We simulated sequence evolution on four-taxon ultrametric trees of variable height and internal branch length (fig. 1A) and on four-taxon trees with randomly generated branch lengths. We examined ultrametric trees because they can be described by specifying only the total height of the tree and the lengths of the internal branches; the limited number of free parameters allows a detailed investigation of ancestral reconstruction methods as phylogenetic signal varies. Furthermore, ultrametric trees represent the most difficult conditions for ASR. For a pair of terminal branches with any given sum of lengths descending from an internal node, the ultrametric case represents the greatest total loss of character information about the ancestor; conversely, as some branches descending from an ancestral node become longer and others shorter, the information in the short branch has a more determinative effect on the inferred ancestral state. In the limit as one descendant branch length approaches zero, the ancestral state is inferred without ambiguity or error as the state in the sequence at the end of that branch.

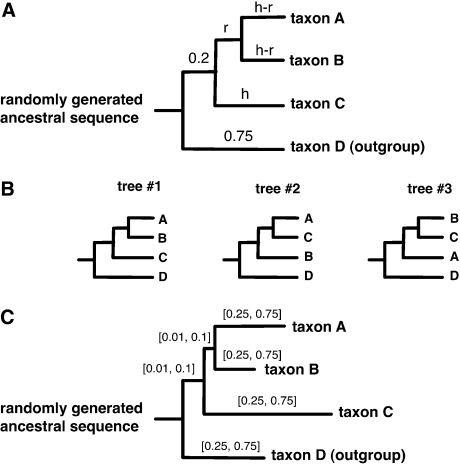
FIG. 1.

Four-taxon simulation conditions. (A) We seeded randomly generated amino acid sequences at the root of an ultrametric tree with four terminal branches. We simulated the ancestral sequences evolving across the branches to produce four descendant sequences (including one outgroup descendant). Simulations were performed under a variety of conditions by adjusting the internal branch length r and the overall height of the descendant clade h. (B) For each set of replicate sequences, we estimated the ML branch lengths and calculated the PP of all three possible topologies. (C) Sequences were also simulated using nonultrametric four-taxon trees with terminal branch lengths drawn from the uniform interval [0.25,0.75] and internal branch lengths from the interval [0.01,0.1].1

On ultrametric trees, the internal branch length (labeled “r” in fig. 1A) was varied from (0.01, 0.02, 0.03, 0.05, 0.1, 0.2), and the overall height of the descendant clade (labeled “h” in fig. 1A) was varied from 0.25 to 0.75 substitutions per site in intervals of 0.125. For each combination of r and h, we used Seq-Gen (Rambaut and Grassly 1997) to generate 100 sets of replicate descendant amino acid sequences of length 400 sites, using the JTT evolutionary model (Jones et al. 1991). For the nonultrametric simulations, 1,000 four-taxon trees were generated by randomly drawing an internal branch length from the uniform distribution U[0.01,0.1] and drawing four terminal branches from the uniform distribution U[0.25,0.75]. Seq-Gen was then used to simulate the evolution of sequences 400 amino acids long on each tree (fig. 1C).

For each replicate, we used ML and TEB ASR to infer the PP of reconstructed ancestral states in the most recent common ancestor of taxa {A,B,C}, of {A,B}, of {A,C}, and of {B,C}. Depending on the tree, some of these ancestors are the same. For example, on the tree ((A,B),C,D), the ancestor of {A,C} is the same node as the ancestor of {A,B,C}. However, on tree ((A,C),B,D), the ancestors for {A,B,C} and {A,C} are unique. We compared the maximum a posteriori ancestral state from TEB and ML to each other and to the true state, which was recorded at all nodes during the simulation. We analyzed the concordance and accuracy of TEB and ML ancestral states across all replicates and in relation to the values of r and h, the state pattern in descendant taxa, and whether the set of taxa in the clade descending from the ancestral node of interest in the ML tree is identical to that set in the true tree. With respect to the last criterion, the membership may be correct, a spurious taxon may be included as a descendant (mem+), or a taxon may be incorrectly excluded from the clade (mem − ).

Empirically Derived Phylogenetic Uncertainty

We also compared the accuracy of ML and TEB reconstructions inferred from sequences simulated on empirically derived trees. We used phylogenies inferred from the extant sequences of ADH proteins (Thomson et al. 2005), steroid hormone receptors (Bridgham et al. 2006), green fluorescent–like proteins (GFPs) (Kelmanson and Matz 2003, Ugalde et al. 2004), and Tu family elongation factor (EF-Tu) proteins (Gaucher et al. 2003). For each gene family, the phylogeny and branch lengths were calculated by ML using Phyml version 2.4.4 (Guindon and Gascuel 2003). The PPs of phylogenies in the 95% credible set (1,195 trees for ADH, 3,335 for steroid hormone receptors, 655 for GFP, and 544 for EF-Tu) were inferred using empirical Bayes Markov chain Monte Carlo, which integrates over topologies, each of which is assigned its ML branch lengths (Kolaczkowski and Thornton 2007). The ML phylogenies for ADH, GFP, and EF-Tu (fig. 2) differ only slightly from the original ML phylogenies shown in those data sets' corresponding publications. On each ML phylogeny, 100 replicates of protein sequences 400 amino acids long were then evolved by simulation, using the JTT model of evolution, to yield terminal descendant sequences. For each replicate, ancestral sequences at all internal nodes were then reconstructed using ML and TEB. We examined only the uncertain nodes (with Bayesian PP less than 1.0) and their immediate neighboring nodes; nodes with PP = 1.0 have no uncertainty over which to integrate, so the TEB and ML reconstructions are identical.

FIG. 2.

Empirical phylogenies used for simulations. Internal nodes are labeled with their empirical Bayes PP; circles indicate nodes at which ancestral sequences were reconstructed. Scale bars indicate mean per-site substitution probability. (A) Steroid hormone receptors (Bridgham et al. 2006). The tree and branch lengths were inferred from empirical protein sequences using the JTT + G model. (B) ADHs (Thomson et al. 2005). The tree and branch lengths were inferred from empirical DNA sequences using GTR + G. (C) GFPs (Kelmanson and Matz 2003). The tree and branch lengths were inferred from empirical DNA sequences using GTR + G. (D) EF-Tu (Gaucher et al. 2003). The tree and branch lengths were inferred from empirical protein sequences using JTT + G.2

State Pattern Analysis

To illustrate how integrating over topologies affects ancestral reconstruction for different data patterns under specific conditions, we performed ASR using ML and TEB and calculated the probability of each ancestral state for each of the possible state patterns of four nucleotides. We simulated DNA sequences 50,000 nucleotides long using the JC69 model on four-taxon ultrametric trees with high phylogenetic uncertainty (h = 0.3, r = 0.01) or virtually no phylogenetic uncertainty (h = 0.3, r = 0.2). We then examined the PP of each ancestral state inferred using ML and TEB for each of the possible state patterns for four-state data. Character state patterns are indicated using variables representing nucleotides of the same type: for example, pattern xyxy for the four-taxon case stands for the realizations ACAC, AGAG, ATAT, CACA, …, TGTG at that site in the four leaves, respectively.

Statistical Analysis

The correspondence between PPs and the frequency of correct inferences for TEB and ML were analyzed by binning inferences according to their PPs and calculating the mean PP(x) and the fraction of correct reconstructions (y) in each bin. The fit of the resulting points to the function y = x was evaluated using a chi-square distribution with degrees of freedom equal to the number of bins. The significance of the difference between ML and TEB in fit to the function y = x was assessed by evaluating the ratio of the chi-square statistics for the two methods using an F-distribution with degrees of freedom equal to the number of bins. To compare the differences in mean accuracy of the ML and TEB reconstructions, we conducted a paired two-sample t-test against the null hypothesis of no significant difference in accuracy between the two methods.

RESULTS

Effect of Incorporating Phylogenetic Uncertainty

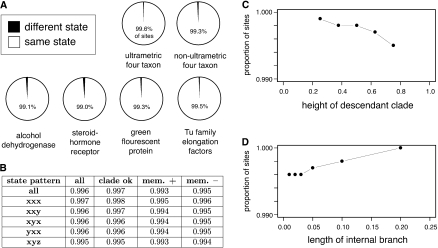
To determine how incorporating topological uncertainty affects ASR, we first examined the extent to which ancestors inferred using ML and TEB differ from each other under a range of conditions. We found that integrating over trees only rarely affected the inferred state at ancestral nodes (fig. 3A). In simulations on ultrametric four-taxon trees with varying levels of phylogenetic noise, the ancestral states inferred by ML and TEB differed at only 0.4% of sites. On nonultrametric trees, they differed at 0.7% of sites. On larger trees derived from empirical data sets of four gene families previously analyzed using ASR—steroid hormone receptors, ADHs, GFPs, and EF-Tu proteins—ML and TEB reconstructions differed by 1% or less (fig. 3A).

FIG. 3.

Integrating over phylogenetic uncertainty rarely changes ASRs. (A) Proportion of sites simulated under a variety of conditions at which ML and TEB methods inferred the same or different states. (B–D) Details of similarity between ML and TEB reconstructions for the ultrametric four-taxon simulations. (B) Proportion of sites at which ML and TEB infer identical states is shown in terms of descendant state patterns and types of phylogenetic error. Each row presents results for sites in which the descendant taxa A, B, and C have the specified state pattern (where pattern xxx corresponds to AAA, CCC, GGG, or TTT and xxy corresponds to AAC, AAG, AAT, …, or TTG). Columns indicate whether the set of taxa descending from the reconstructed node in the ML tree corresponds to those in the true tree: “clade ok” means the descendant membership is correct, “mem.+” means the ML descendant set spuriously includes an extra taxon, and “mem. − ” means the ML descendant set incorrectly excludes a taxon. (C) Similarity between ML and TEB reconstructions is plotted against the height of the descendant clade (“h” in fig. 1). (D) Similarity between ML and TEB reconstructions is shown versus the length of the internal branch (“r” in fig. 1).3

To determine whether certain phylogenetic conditions cause integrating over topological uncertainty to have a stronger effect on inferred ancestral states, we decomposed the results of the ultrametric four-taxon simulations according to the state patterns in the terminal sequences that descend from the reconstructed ancestor, the length of the branches on the tree, and the ways (if any) that the ML tree differs from the true tree (supplementary table S2, Supplementary Material online). There were no state patterns that resulted in differences between ML and TEB ancestors greater than 0.5%. The effect of integrating over uncertainty was slightly greater for divergent state patterns in which all ingroup descendants have different states (pattern xyz) than for patterns that contain phylogenetic signal (xxx or xxy; fig. 3B). Similarly, no branch length conditions examined caused ML and TEB to differ by more than 0.5%; ML and TEB ancestors differed least when the total root-to-tip branch length was short, and they differed to a slightly greater extent as the terminal branches became very long (fig. 3C). When the ML tree was correct (as it was in the majority of cases), integrating over uncertainty had a particularly weak effect on the inferred ancestor; however, even when the ML phylogeny erroneously inferred a spurious sequence as a descendant of the ancestor of interest or excluded a true descendant, the two methods still produced identical inferences at > 99% of sites (fig. 3B). Together, these data indicate that integrating over topological uncertainty per se does not strongly affect ancestral reconstructions; the effects are weak under conditions that cause the traces of the ancestral state to be lost in descendant sequences and virtually nonexistent under those that preserve phylogenetic signal about the ancestral state.

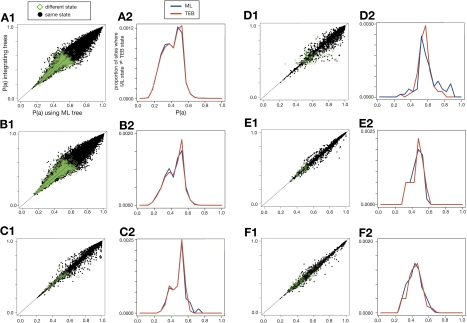
We next analyzed whether integrating over topological uncertainty tends to affect sites that are strongly or weakly supported by ML. Most ASR practitioners examine the support for ancestral state inferences and experimentally characterize the robustness of their inferences to alternate reconstructions that have PP above some defined plausibility cutoff (Chang et al. 2002, Ugalde et al. 2004, Thomson et al. 2005, Bridgham et al. 2006, Ortlund et al. 2007). We found that ML and TEB reconstructions disagreed only at sites that were already ambiguous in the ML reconstruction (fig. 4). In both ultrametric and nonultrametric four-taxon simulations, the ML and TEB reconstructions agreed at all sites at which the ML reconstruction had PP greater than 0.70. In the ADH, GFP, and EF-Tu simulations, the two methods agreed at all sites with PP greater than 0.76, 0.63, and 0.71, respectively. In the steroid hormone simulation, the methods agreed at all sites with PP greater than 0.87, and they disagreed at only 0.003% of all sites reconstructed with PP > 0.80. Over all four-taxon reconstructions, the maximum a posteriori ancestral state from TEB was different from the first- or second best state using the ML method at only 0.001625% of sites. These data indicate that integrating over topological uncertainty virtually never causes inferred ancestral states that are strongly supported by ML to be revised. Rather, TEB inferred a state different from the ML state only when that state was ambiguously reconstructed anyway, switching the favored state from one weakly supported possibility to another.

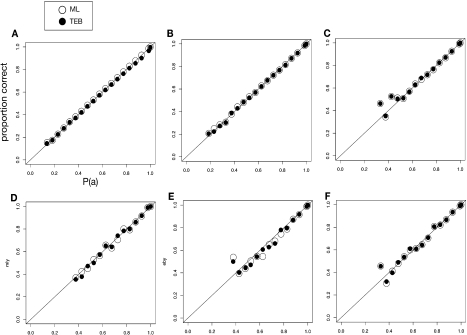
FIG. 4.

ML and TEB infer different ancestral states only when PPs are low. In each pair of plots, the left plot (A1, B1, etc.) compares the PP of the maximum a posteriori state inferred by ML to that inferred by TEB. Black points show sites at which ML and TEB methods inferred the same state; green diamonds indicate that the two methods inferred different states. The right plots (A2, B2, etc.) are histograms of the green points in the left plot: we grouped all ASR inferences into 5%-sized bins based on their PP and counted the proportion of sites at which ML and TEB inferred different states. Results are shown for simulations on ultrametric four-taxon trees (A1,A2), nonultrametric four-taxon trees (B1,B2), and the steroid hormone receptor (C1,C2), ADH (D1,D2), GFP (E1,E2), and EF-Tu phylogenies (F1,F2).4

Effect of Incorporating Phylogenetic Uncertainty on ASR Accuracy

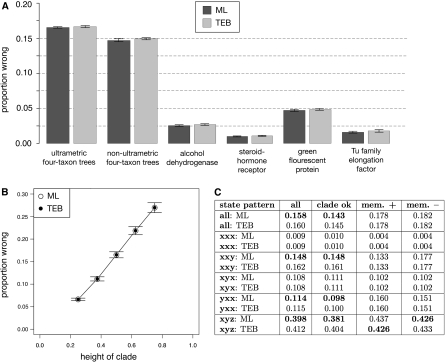
Although the ML and TEB methods inferred the same state at most sites, it is possible that TEB might produce more accurate reconstructions at the rare sites where the two methods differ. We measured accuracy as the proportion of sites at which the reconstructed state was identical to that of the true ancestor, which we recorded during each simulation. In the four-taxon and GFP simulations, ML was slightly, but not significantly, more accurate than TEB (fig. 5A and supplementary table S7, Supplementary Material online). In the ADH, steroid hormone receptor, and EF-Tu simulations, there was no difference in accuracy between the methods. The accuracy of both ML and TEB declined as terminal branch lengths grew longer, causing multiple substitutions to occur (fig. 5B). ML's superiority to TEB was greatest when the membership of the descendant clade was correct (fig. 5C), presumably because when the ML topology is the true tree, integrating phylogenetic uncertainty serves only to introduce error. Even when the ML tree was incorrect, however, TEB generally decreased accuracy; integrating over uncertainty improved accuracy only under the rare condition that the descendant state pattern was xyz and a spurious taxon had been included as a descendant of the node of interest. Under these conditions, both methods performed poorly because little or no phylogenetic signal of the ancestral state was retained in the descendants. For all other state patterns and forms of phylogenetic error, ML had accuracy equal to or slightly greater than that of TEB.

FIG. 5.

ASR error rates, measured as the proportion of sites at which the maximum a posteriori reconstructions differ from the true ancestral state. (A) Results from the four-taxon and empirically derived conditions are averaged over all replicates. None of the differences between ML and TEB are statistically significant. (B) Results from the ultrametric four-taxon simulation are shown versus the height of the descendant clade (where height equals “h” in figure 1. Error bars for ML and TEB are nearly identical. (C) Detailed results from the ultrametric four-taxon simulation. Each cell reports two values: the proportion of sites incorrectly reconstructed by ML (top) and TEB (bottom). Bold values indicate the method with higher accuracy. Data are sorted according to the same criteria in figure 3B.5

Effect of Incorporating Phylogenetic Uncertainty on ASR PPs

We next examined whether TEB or ML yielded more accurate estimates of statistical confidence in inferred ancestral states. For all simulations, we binned reconstructed ancestral states by their PP and counted the proportion of accurate inferences in each bin (fig. 6). If PP is an accurate predictor of the probability that an inferred state is correct, the mean PP in that bin should equal the proportion of correct ancestral state inferences. We observed that the ML and TEB methods generally produced similar PP values, and both types of PP were good predictors of mean accuracy. The major exception to this pattern was the four-taxon simulation on ultrametric trees in which integrating over trees slightly inflated support for reconstructions with PP > 0.5 (fig. 6A); a chi-square test indicates that ML's PPs fit the ideal better than TEB's PPs do, but the difference is small and does not reach statistical significance (P = 0.16, supplementary table S1, Supplementary Material online). When the ML tree was correct, ML's PPs were more accurate than TEB, but TEB was more accurate when the ML tree was wrong; because the former conditions are more frequent than the latter, however, ML's accuracy was higher overall. For the empirically derived conditions, ML's PPs were slightly more accurate, but the difference was again small and not statistically significant (supplementary tables S3–S6, Supplementary Material online).

FIG. 6.

Relationship of the PP of inferred ancestral states to the probability that those states are correct. For both ML and TEB, we grouped all ancestral state inferences by their PP into 5%-sized bins. Within each bin, we calculated the proportion of inferred states that match the true state. Bins with fewer than 50 members were excluded. Data are shown for simulations on (A) ultrametric four-taxon, (B) nonultrametric four taxon, (C) ADH, (D) steroid hormone receptors, (E) GFP, and (F) EF-Tu phylogenies.6

An Intrinsic Trade-off Explains Why Incorporating Uncertainty Does Not Affect ASR

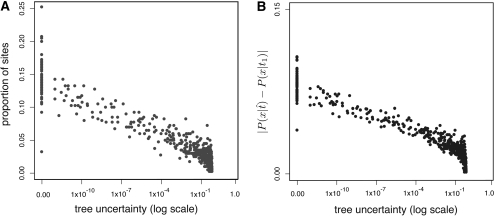
To understand why integrating over phylogenies has such a weak effect on ancestral reconstruction, we examined the relationship between the plausibility of alternate phylogenies and the dependence of the reconstructed state on the assumed phylogeny. We conjectured that as phylogenetic uncertainty increases, the same state will be reconstructed on the plausible trees. To test this hypothesis, we grouped all the replicates from our ultrametric four-taxon simulations according to the PP of their ML tree. For each replicate, we counted the proportion of sites at which the inferred ancestral state differs between the ML tree and the tree with the next highest PP (fig. 7A). We observed that when the ML tree was uncertain (PP < 1.0), the ancestral states among trees rarely disagreed. In contrast, when the ML tree was absolutely certain (PP = 1.0), the ancestral states on the ML tree and the second best tree disagreed at up to 25% of sites; however, because the PP of the second tree was so low, it contributed virtually zero weight to the TEB reconstruction. Support measures showed a similar trade-off: only when there was little or no uncertainty about the tree did the PP of an ancestral reconstruction differ among phylogenies. These results indicate that there is a trade-off between phylogenetic uncertainty and the extent to which ancestral state reconstruction depends on the phylogeny assumed.

FIG. 7.

Phylogenetic uncertainty versus alternate ancestral reconstructions. Each point corresponds to one set of replicate descendants in the ultrametric four-taxon simulation. Tree uncertainty for each replicate is measured as 1.0 minus the PP of the ML tree. (A) Tree uncertainty is plotted versus the proportion of sites at which the most likely ancestral state on the ML tree disagrees with the most likely ancestral state on the second best tree. (B) Tree uncertainty is plotted versus the average absolute difference between the PP of the most likely state on the ML tree (x) minus the PP of this same state on the second best tree.7

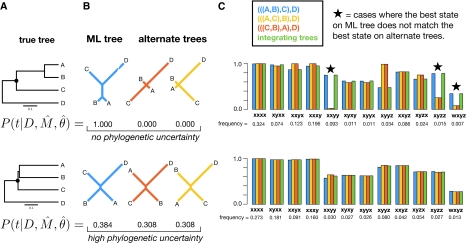
To understand this trade-off in detail, we examined ancestral reconstructions under two contrasting four-taxon conditions with different degrees of phylogenetic uncertainty (fig. 8). In one condition, the true phylogeny had a long internal branch, so the ML tree was inferred with no uncertainty (PP = 1.0); in the other, the true phylogeny had a very short internal branch, so the ML tree was inferred with considerable uncertainty (PP = 0.384). For each state pattern, we reconstructed the ancestral state on all three possible topologies. We found that when there was no phylogenetic uncertainty, the probability of an ancestral state can differ radically given different trees; for three of the state patterns, the maximum a posteriori ancestral state inferred on the ML tree differed from that inferred on alternate trees. Because the internal branch was long, however, these alternate trees had zero PP, so incorporating them into TEB reconstruction produces ancestral state inferences and PPs identical to the ML inference. In contrast, when the internal branch was short and the phylogeny was uncertain, all three topologies were close to being star trees. In this case, the probability of the ancestral state inferred on the ML tree was almost identical to the probability of that state given any other tree. Because the inferred ancestral state did not differ among phylogenies, TEB and ML again yielded the same reconstruction.

FIG. 8.

The conditions that produce phylogenetic uncertainty result cause ancestral state inferences to be identical across trees. (A) We simulated sequences on trees with long (top) and short (bottom) internal branches. On each, we randomly generated an ancestral sequence 50,000 nucleotides long and simulated sequence evolution. (B) From the descendant sequences, we inferred the empirical Bayes posterior distribution of the three trees, each with its ML branch lengths. (C) On each tree, we used the true model to reconstruct the common ancestor of descendants A, B, and C for all possible descendant state patterns (xxxx, xyxx, wxyz, etc.). Each bar corresponds to the PP of the best ancestral state on the ML tree (blue), the PP of the same state on the alternate trees (yellow and red), and the PP of that state integrated over all trees (green). Stars indicate state patterns for which the maximum a posteriori ancestral state on one of the alternate trees is different from that on the ML tree.8

DISCUSSION

Our results demonstrate that a Bayesian approach to incorporating uncertainty about the underlying phylogeny is not necessary for ancestral state reconstruction. By comparing two methods of ASR that differ only in that one assumes the ML phylogeny while the other integrates over phylogenies, we were able to determine the specific effect of incorporating phylogenetic uncertainty on ancestral state inferences, their statistical support, and their accuracy. We found that using TEB virtually never changes the inferred ancestral state; when it does, the reconstruction was already ambiguous using ML. ML has slightly higher accuracy, and its PPs provide a slightly better predictor of the probability that an ancestral state inference is correct.

Our analyses show that incorporating phylogenetic uncertainty only weakly affects ASR because the conditions that cause phylogenetic uncertainty also make the ancestral state the same across trees. This phenomenon occurs because when internal branches are short, the distance in tree space is small between the ancestor on the ML tree and the ancestor on the second best tree (Felsenstein 2004). At the limit, the true tree is a star tree with a zero-length internal branch, and all resolved topologies have equal PP, leading to maximal phylogenetic uncertainty; however, the ancestral nodes on the different topologies are identically located in tree space. In contrast, under the conditions that cause inferred ancestral states to differ among trees, there is typically no phylogenetic uncertainty to integrate over.

Prior work has shown that ASR is generally most accurate on star-like trees because the descendant sequences contain maximum mutual information about the ancestral state when those descendants are completely independent phylogenetically (Blanchette et al. 2004, Lucena and Haussler 2005). Those studies, however, assumed that the true phylogeny was known a priori, which is particularly unlikely for star-like trees with short internal branches. Our work shows that phylogenetic uncertainty, which is inevitable under these conditions, is not expected to undermine the accuracy of ancestral state reconstruction on star-like trees. These results underscore the potential to accurately reconstruct ancestral sequences at the base of rapid phylogenetic radiations despite phylogenetic uncertainty, such as the ancestors of all mammals (Blanchette et al. 2004) or all metazoans (Rokas et al. 2005).

Previous work by Huelsenbeck and Bollback, like ours, showed a close relationship between ancestral PPs estimated using the ML tree and integrating over trees (Huelsenbeck and Bollback 2001). Those authors did suggest, however, that uncertainty in the phylogeny might lead to significantly different interpretations of the ancestral state. This suggestion was illustrated using trees with arbitrarily assigned branch lengths and PPs; for all topologies in the illustration, the internal branch lengths were of significant length and the PPs were substantial. In reality, it is unlikely that any data set would support such a distribution of PPs over this set of tree/branch length combinations because nontrivial PPs on “next best” trees typically arise only when internal branches are short. Our results show that when the PPs on trees are derived from sequence data rather than arbitrarily assigned, integrating over uncertainty has a negligible effect on ancestral sequence inference and a negative impact, if any, on accuracy.

Our results should not be interpreted as an endorsement for sloppy analysis. Although incorporating phylogenetic uncertainty does not improve the accuracy of ancestral reconstruction, this does not mean that the phylogeny is unimportant. Because ancestral reconstructions can vary across trees under some conditions, arbitrarily choosing an incorrect and implausible phylogeny could yield inaccurate reconstructions. Our results indicate that when the true tree is well-resolved, assuming the wrong topology can change the inferred ancestral state for some state patterns (fig. 4). This finding is consistent with a prior study, which found that an arbitrary topological error on a tree with long internal branch lengths can slightly reduce ASR accuracy at some nodes (Zhang and Nei 1997).

Our findings should not be taken as evidence that ancestral reconstruction never errs. There are numerous potential sources of error that we did not evaluate, including use of incorrectly parameterized evolutionary models, which could yield incorrect (and strongly supported) inferences of phylogeny (Kolaczkowski and Thornton 2004) or incorrect ancestral state reconstructions even when the true tree is assumed. ASR practitioners should continue to use rigorous statistical practices, such as formal evaluation of a wide range of models that incorporate evolutionary heterogeneity (Posada 2001, Lartillot and Philippe 2004, Kolaczkowski and Thornton 2008) and dense targeted taxon sampling (Hillis 1998, Pollock et al. 2002, Heath et al. 2008). Our experiments specifically addressed phylogenetic uncertainty caused by a lack of phylogenetic signal. Whether integrating over phylogenetic uncertainty might improve ASR accuracy in the face of model violation or other causes of phylogenetic error warrants future study. Our analyses were specific to Bayesian integration over uncertainty about the underlying phylogeny: we did not address the effect on ancestral reconstructions of integrating over uncertainty about branch lengths, the substitution model, or its parameters. Whether a Bayesian approach to these sources of uncertainty would improve or degrade ASR accuracy warrants further research.

In summary, incorporating phylogenetic uncertainty by integrating over topologies does not improve the accuracy of ASR because the conditions that cause phylogenetic uncertainty make the ancestral state the same across trees. Using the ML tree will typically yield the best ancestral reconstruction, even when the ML tree is uncertain. A Bayesian approach to phylogenetic uncertainty is intuitively appealing but computationally demanding and, in this case, unnecessary.

SUPPLEMENTARY MATERIAL

Supplementary note 1 and tables S1–S7 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).