Effect of tidal volume, sampling duration, and cardiac contractility on pulse pressure and stroke volume variation during positive-pressure ventilation

Abstract

Introduction

Both pulse pressure variation and stroke volume variation during intermittent positive-pressure ventilation predict preload responsiveness. However, because ventilatory and cardiac frequencies are not the same, increasing the number of breaths sampled may increase calculated pulse pressure variation and stroke volume variation because larger (max) and smaller (min) pulse pressure and stroke volume may occur. Tidal volume and contractility may also alter pulse pressure variation and stroke volume variation. We hypothesized that the magnitude of pulse pressure variation would increase with sampling duration, and that both tidal volume and contractility would independently alter pulse pressure variation and stroke volume variation.

Methods

In seven pentobarbital-anesthetized intact dogs arterial and left ventricular pressure (Millar) and left ventricular volume (Leycom) were measured over 8 intermittent positive-pressure ventilation breaths at tidal volume of 5, 10, 15, and 20 mL/kg (f = 20/min, 40% inspiratory time) under baseline, esmolol (2 mg/min), dobutamine infusions (5 μg/kg/min) and following volume loading (500 mL NaCl). Stroke volume variation was calculated using pulse contour method (PiCCO, Pulsion Medical Systems, Munich, Germany) averaged over 12 secs. Pulse pressure variation was calculated as 100 × (PPmax − PPmin)/PPmean and calculated over 1, 2, 3, 4, 5, 6, 7, or 8 breaths.

Results

Pulse pressure variation increased progressively with increasing sampling duration up to but not exceeding five breaths. The effect on sampling duration was increased by greater tidal volume. Esmolol infusion decreased both pulse pressure variation and stroke volume variation as compared with baseline (p < 0.05) at all tidal volume levels. However, dobutamine did not alter either pulse pressure variation or stroke volume variation.

Conclusion

Sampling duration, tidal volume, and beta-adrenergic blockade differentially alters pulse pressure variation and stroke volume variation during intermittent positive-pressure ventilation. Thus, separate validation is required to define threshold pulse pressure variation and stroke volume variation values used to drive resuscitation algorithms.

Recently, physicians have developed a renewed interest in the hemodynamic effects of positive pressure ventilation. This interest focuses on the use of ventilation-induced changes in left ventricular (LV) stroke volume (SV) and arterial pulse pressure (PP) (the difference between diastolic arterial pressure and the subsequent systolic pressure) that occurs during a positive-pressure breath when no spontaneous respiratory efforts occur and heart rate is constant (1). Numerous reports from several institutions studying diverse patient groups have all documented the utility of estimates of this PP variation (PPV) and LV SV variation (SVV) (reported as a percent change) to predict the subsequent increase in cardiac output in response to a volume challenge (reviewed in Michard and Teboul [2]). However, the relationship between both PPV and SVV and cardiac function is often complex and influenced by ventilation-associated changes in LV diastolic compliance, through the process of ventricular interdependence, and LV filling, although phasic changes in venous return (3) and pulmonary venous capacitance (4), and LV afterload. In support of these complex interactions, the actual PPV observed do not mirror changes in either LV end-diastolic volume or SV in either animal (5) or human studies (6).

Importantly, the method of calculating either PPV or SVV is not uniform across studies. We originally proposed sampling 3 breaths to identify the largest PP (PPmax) and smallest PP (PPmin) for the calculation of the PPV using the formula PPV = (PPmax − PPmin)/([PPmax + PPmin]/2), where PPmax and PPmin need not occur during the same breath (7). However, because heart rate and ventilatory frequency are usually not synchronous, the actual PPmax and PPmin values can vary widely from breaths to breath. As the number of breaths increases, the likelihood of creating the maximal and minimal PP possible increases. Thus, it is not clear what impact varying the sampling duration relative to the number of respiratory cycles pooled would affect PPV and what the minimal sampling frequency is needed to ensure its reproducible and meaningful quantification. Furthermore, because PPV and SVV values are increasingly being used to drive resuscitation protocols, we reasoned that it would be important to define the impact of varying not just sampling duration, but also tidal volume (Vt) and contractility state on PPV and SVV. We hypothesized that sampling interval, Vt, and contractile state would all independently alter PPV and SVV.

METHODS

Surgical Preparation

After approval of the institutional Animal Care and Use Committee, we studied seven mongrel dogs (20.2 ± 1.2 kg body weight) following an overnight fast. Anesthesia was induced with a bolus of 30 mg/kg sodium pentobarbital and maintained with a continuous infusion of 0.1 mg/kg/min sodium pentobarbital. All medications were administered intravenously. After endotracheal intubation, we instituted positive-pressure ventilation (Harvard Apparatus, Cambridge, MA) with room air. Arterial blood gases were measured periodically. Acid-base status was adjusted with intermittent boluses of sodium bicarbonate solution, as needed, to maintain arterial blood pH between 7.35 and 7.45, and the ventilator was adjusted to maintain arterial PCO₂ between 35 and 45 mm Hg. Body temperature was maintained between 36°C and 38°C by using a heating blanket.

We placed fluid-filled catheters in the femoral artery for arterial blood gas analysis and in the femoral vein for drug and fluid infusion. A 7.5F pulmonary artery catheter (Swan-Ganz Thermodilution Catheter, Edwards Life-Sciences, Irvine, CA) was placed in the pulmonary artery for cardiac output and pulmonary artery pressure measurements. We placed a 5F high-fidelity micromanometer catheter (MPC-500, Millar, Houston, TX) into the thoracic aorta via femoral artery to measure aortic pressure. We also placed a second high fidelity micromanometer catheter and conductance catheter into the left ventricle from a carotid arterial site for use in an unrelated study.

Protocol

The protocol was initiated after at least 30 mins of hemodynamic stability following the insertion of the last catheter. Mechanical ventilation was begun using a Vt of 10 mL/kg, frequency of 20/min, and inspiratory ratio of 40%. After steady state data recorded, we changed Vt of 5, 15, and 20 mL/kg in a randomized order without changing frequency or inspiratory time. Animals were allowed to stabilize at each new Vt for 20 secs before data collection. This short interval was chosen to minimize arterial blood gas changes induced by varying Vt and minute ventilation. We recorded all measured variables over eight consecutive respiratory cycles for each Vt. These data are referred to as baseline data. We then made identical data collections during esmolol infusion (20 mg intravenous bolus followed by 2 mg/min continuous), dobutamine infusion (5 μg/kg/min) and following volume loading (500 mL of 0.9% NaCl). At each step, we allowed the preparation to stabilize for 20 mins before collecting data. Following these studies, the animals were studied in unrelated experiments. Following all studies the animals were killed using a sequential dose of sodium pentobarbital (100 mg intravenous bolus) followed by supersaturated potassium chloride (10 mL intravenous bolus) to induce ventricular fibrillation. A limited necropsy thoracotomy was performed and the tips of all intravascular catheters were dissected free from tissue to measure their hydrostatic zero pressure. All pressure data were referenced to their hydrostatic zero reference pressures.

Data Collection and Analysis

LV pressure, aortic pressure, pulmonary artery pressure, right atrial pressure, continuous cardiac output, and airway pressure data were digitized at 150 Hz and stored on disk for off-line analysis (Ponemah System, Gould, Cleveland, OH). Arterial PP was measured from thoracic aorta pressure as the diastolic to systolic pressure difference. PPV(%) was calculated as 100 × (maximum PP − minimum PP)/mean PP, where maximum and minimum PP are an extreme value of PP during a period of one through eight consecutive respiratory cycles, and mean PP is the average value for this time period. Cardiac output, LV SV, and SVV were measured using pulse contour analysis (PiCCO, Pulsion Medical Systems, Munich, Germany). SVV (%) was calculated as 100 × (maximum SV − minimum SV)/mean SV, the algorithm used during this study uses a continuously sliding time window of 30 secs to calculate mean SV. The time window is derived in four 7.5-sec periods; for each 7.5 secs the highest (SVmax) and the lowest values (SVmin) of SV were determined, and the average of the four 7.5-sec intervals were used to calculate SVV. We calculated PPV for a sampling frequency of from one through eight consecutive respiratory cycles for each Vt during baseline. Values for PPV for the entire eight-breath sequence were averaged over that same interval. Thus, the one respiratory cycle values reflect the average values of eight single breaths values, two breaths seven averaged values, etc. Whereas SVV was estimated by the PiCCO device over the entire eight respiratory cycles. To address the issue of sampling bias in the grouping of PPV data, we also compared the first breath to the first two, first three, etc., up to eight breaths to see if the single sample measured PPV was different.

Statistical Analysis

Three-way analysis of variance was used to evaluate the effects of sampling period, Vt, and either contractile state or volume loading on PPV and SVV. A post hoc Dunnet's test was used to define specific differences when significance was found. Significance reports a difference corresponding to a p value <0.05. Results are reported as mean ± SD.

RESULTS

Hemodynamic data under different conditions and Vts are shown for all seven dogs in Table 1. The heart rate and mean arterial pressure in baseline at Vt of 10 mL/kg were 135 ± 23 bmp and 125 ± 31 mm Hg, respectively.

Table 1.

Heart rate and mean arterial pressure for different conditions and tidal volumes^a

Tidal Volume (mL/kg)	Heart Rate (beats/min)	Mean Arterial Pressure (mm Hg)
Baseline
5	134 ± 23	127 ± 28
10	135 ± 23	125 ± 31
15	132 ± 21	121 ± 27
20	131 ± 23	113 ± 25
Volume loading
5	125 ± 18	122 ± 9
10	130 ± 13	123 ± 10
15	128 ± 13	121 ± 11
20	126 ± 16	116 ± 7
Dobutamine
5	140 ± 14	128 ± 19
10	141 ± 16	131 ± 20
15	141 ± 16	132 ± 19
20	142 ± 18	124 ± 17
Esmolol
5	114 ± 14	104 ± 15
10	114 ± 13	104 ± 16
15	116 ± 14	104 ± 17
20	115 ± 15	99 ± 17

^aData are mean ± so: n = 7.

Effect of Sampling Duration on PPV

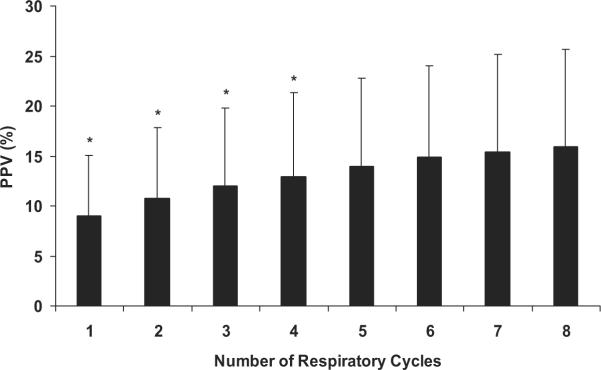
Measured PPV increased significantly with increasing the sampling duration (Fig. 1). However, measured PPV did not increase further above a sampling duration of five breaths, which represented a 15-sec sampling duration. For the remainder of the analysis we report only on the mean PPV values from five breaths.

Figure 1.

The effect of varying the number of respiratory cycles used in the calculation of pulse pressure variation (PPV) for all conditions and all animals. Data are means ± SD; n = 6. *p < 0.05 vs. eight respiratory cycles.

Effect of Tidal Volume

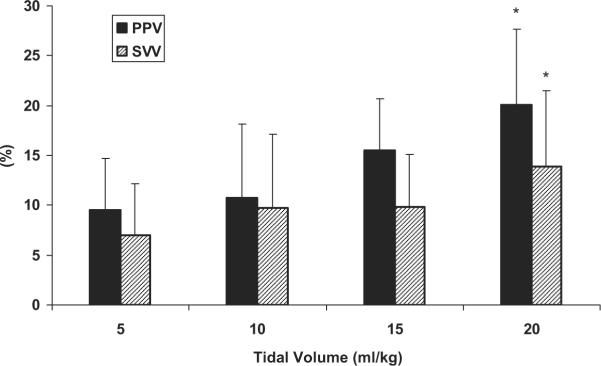
Mean values for five-breath sampled PPV and eight-breath sampled SVV as Vt varied are shown in Figure 2. As compared with Vt of 10 mL/kg both PPV and SVV decreased at Vt 5 mL/kg (10.7 ± 5.0% and 9.7 ± 7.4% to 9.5 ± 5.4% and 7.0 ± 5.2%, 10 to 5 mL/kg, respectively). Although both PPV and SVV tended to increase at Vt of 15 mL/kg (15.5 ± 9.1% and 9.9 ± 5.2%) and 20 mL/kg (20.1 ± 10.8% and 13.9 ± 7.5%) compared with Vt of 10 mL/kg, the increase was significant only at Vt of 20 mL/kg.

Figure 2.

The effect of varying tidal volume (Vt) in the calculation of pulse pressure variation (PPV) and stroke volume variation (SVV) for all conditions and all animals. Data are means ± SD; n = 7. *p < 0.05 vs. Vt of 10 mL/kg.

Influence of Esmolol and Dobutamine Infusion, and Volume Loading

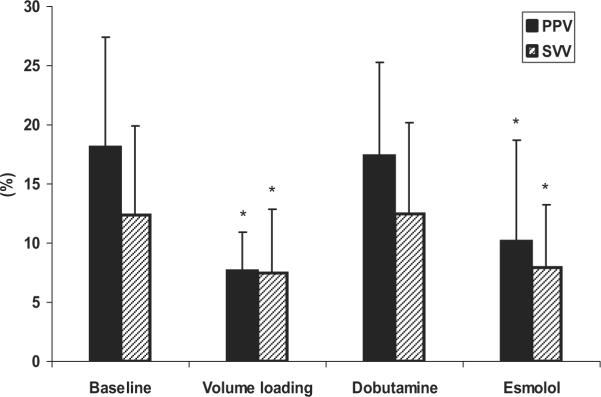
Figure 3 displays the mean values for five-breath sampled PPV and eight-breath sampled SVV as cardiac contractility and volume were varied and Figures E1 and E2 (online data supplement) display the individual animal data for these same conditions. Esmolol infusion was associated with a significant decrease in both PPV and SVV (10.2 ± 8.5% and 8.0 ± 5.2%) compared with baseline (18.2 ± 9.3% and 12.4 ± 7.5%) at Vt of 5, 10, 15, and 20 mL/kg (p < 0.05). However, dobutamine infusion did not influence either PPV (18.2 ± 9.3% and 17.4 ± 7.9%) or SVV (12.4 ± 7.5% and 12.5 ± 7.7%) as compared with baseline. As our positive control, volume loading was associated with a significant decrease the PPV and SVV after volume loading (7.7 ± 3.2% and 7.5 ± 5.3%, respectively) compared with baseline, but still displayed the same Vt and for PPV sampling duration influence as baseline conditions.

Figure 3.

The effect of esmolol infusion, dobutamine infusion, and volume loading in the calculation of pulse pressure variation (PPV) and stroke volume variation (SVV) for all tidal volumes and all animals. Data are means ± SD; n = 7. *p < 0.05 vs. baseline.

DISCUSSION

This study has four primary findings. First, that increasing the sampling duration to include more positive-pressure breaths increases the magnitude of calculated PPV but to an asymptote of five breaths. Second, the measured PPV and SVV are directly influenced by Vt. Both PPV and SVV increase for the same cardiovascular state as Vt increases from 5 mL/kg incrementally to 20 mL/kg. Third, that impaired contractility decreases both PPV and SVV but increased contractility does not influence either PPV or SVV. Finally, that although these sampling duration, Vt, and contractile state-specific changes alter both PPV and SVV their specific impact of both PPV and SVV can be different and may be either cumulative or counteract each other. These data are important for several reasons. First, both PPV and SVV have been shown to be highly predictive of preload responsiveness in a large series of clinical studies. Thus, knowing how these clinically relevant perturbations alter these parameters is important. Second, changing Vt, sampling duration relative to breaths and contractile state often vary in critically ill patients, especially during resuscitation and may alter the threshold values predicting volume responsiveness.

Michard et al. (7) used three breaths as their sampling duration to calculate PPV in patients with acute lung injury and septic shock (8). Similarly, Slama et al. (9) also used three breaths to estimate SVV in their patients with circulatory shock. However, several groups relied on proprietary calculations of SVV for arterial pulse contour analysis that do not identify specific breaths but rather sample a defined time interval. The PiCCO™ device by Pulsion measures SVV from the arterial pressure waveform analysis using a 20-sec moving window of data (10). Similarly, the LiDCO pulseCO™ device reports both directly measured PPV and calculated SVV from the power transfer equation for arterial pressure using a similar 20 secs moving window of data. For respiratory frequencies of >15 breaths/min these devices sample five to six breaths and thus should give consistent PPV and SVV values over time if hemodynamic conditions are also constant. However, if respiratory rates decrease to <10 breaths/min, then these devices may report inherently unstable values. Thus, our data suggest that investigators need to report on the respiratory rate of their sample population when describing PiCCO and pulseCO derived PPV and SVV data. Furthermore, in a fashion analogous to estimates of cardiac output by the bolus thermodilution technique, it might be necessary to average repetitive measures of PPV and SVV to minimize sampling bias if the respiratory rate is ≤10 breaths/min, although this specific issue was not addressed in our study.

Both PPV and SVV occur because phasic changes in venous return, pulmonary blood flow and LV filling are induced by intermittent positive-pressure ventilation (11). The phasic relation between intermittent positive-pressure ventilation and LV output is dependent of the changes in right atrial pressure, biventricular volume responsiveness, pulmonary transit time, and the respiratory rate (12). If both ventricles are preload responsive, then one will see both PP and LV SV vary with the same frequency as the ventilatory cycle. Both PPV and SVV thresholds are used to predict volume responsiveness. As mentioned above, PPV values >13% and SVV values >10% are highly predictive of volume responsiveness when patients are ventilated at a Vt 6 to 8 mL/kg and a frequency of between 10 and 20 breaths/min. We refer to this state as preload-responsive (13). Instantaneous venous return varies in a phasic inverse fashion as right atrial pressure varies (14). Because the primary determinants of changes in right atrial pressure are Vt (15) and chest wall compliance (16) it follows that varying Vt must also vary PPV and SVV. Indeed, DeBacker et al. (17) demonstrated that SVV co-varied with Vt changes in ventilator-dependent patients. Thus, one must hold Vt constant if changes in PPV and SVV are to be used to assess preload responsiveness. Interestingly, we recently showed that in fluid resuscitated patients immediately after cardiac surgery, that the increased intraabdominal pressure induced by diaphragmatic descent during positive-pressure inspiration mitigated the increased right atrial pressure's effect on the pressure gradient for venous return (18). Although not reported in that article, subsequent analysis revealed that those patients also did not display significant baseline PPV, suggesting that PPV remained a robust predictor of preload response even in resuscitated postoperative cardiac surgery patients. Potentially, PPV and SVV will be confounded if ventilation also alters ventricular interdependence. Common conditions in which ventilation usually alters the level of ventricular interdependence include spontaneous ventilation, acute cor pulmonale, hyperinflation, and tamponade (19). Previous studies revealed that systolic pressure variation, as a substitute for PPV is a poor predictor of preload responsiveness if spontaneous ventilation concomitantly occurs (20).

Finally, our data show that if contractility is reduced then both PPV and SVV will also be less for a given circulating blood volume, Vt and sampling duration. These findings should not be surprising because marked beta-adrenergic blockage often decreases volume responsiveness. The data do not allow us to identify why we did not see a lower SVV than PPV with all conditions except volume loading. Ventriculoarterial coupling defines the change in arterial PP to LV SV relationship, such that the PPV to SVV relation is determined by central arterial elastance (i.e., vascular stiffness). If the PPV to SVV ratio decreases then central arterial elastance must have decreased, as would occur with reduced sympathetic tone. In support of this hypothesis, we see that with volume loading PPV and SVV values become similar whereas with baseline and both esmolol and dobutamine infusion PPV is greater than SVV by 3% to 5%. Presumably, volume loading in a previously nonhypovolemic subject induces a hypervolemic vasodilation decreasing arterial elastance. Potentially, PPV to SVV ratio changes minor changes in vascular elastance. Whatever the reason, these data are consistent with our understanding that PPV is a mark of volume responsiveness and the PPV to SVV ratio reflects central arterial tone.

Our study has three major limitations. First, we used anesthetized canine preparation, not humans. The vascular responsiveness and contractile reserve of the dog is greater than that of humans. We used the PiCCO device to assess SV and SVV. This device was calibrated based on human vascular impedance (21), whereas the canine vascular impedance characteristics different (22). Thus, caution needs to be maintained in the direct extrapolation of these data to critically ill humans. Second, we used esmolol to induce transient impaired contractility. Esmolol is a selective beta adrenergic blocking agent. Thus, in the setting of increased sympathetic tone, esmolol might unmask an already existent increased vascular tone causing volume responsiveness to decrease out of proportion to the reduction in contractile reserve and not reflect accurately chronic heart failure. Still our hemodynamic responses to esmolol and dobutamine were in line with the known effects of these two agents in critically ill patients. Thus, our model of esmolol-induced decreased contractile reserve, although artificial, behaves in a fashion similar to that seen in patients with heart failure. Finally, we estimated LV SV and SVV from the PiCCO pulse contour method; we did not measure LV SV directly. If errors in its algorithm exist, then our data might also become inaccurate. However, in support of our findings, Slama et al. (9) measured LV SV directly using transesophageal echocardiography and showed that, like our data, SVV rested in the 10% to 20% range in volume responsive subjects. However, we measured arterial pressure directly, thus the PPV data remain valid. We conclude that as measures of volume responsiveness, PPV is independently influenced by Vt, sampling duration and contractile state, and SVV is influenced by Vt and contractile state.