High resolution lung airway cast segmentation with proper topology suitable for computational fluid dynamic simulations

Abstract

Developing detailed lung airway models is an important step towards understanding the respiratory system. While modern imaging and airway casting approaches have dramatically improved the potential detail of such models, challenges have arisen in image processing as the demand for greater detail pushes the image processing approaches to their limits. Airway segmentations with proper topology have neither loops nor invalid voxel-to-voxel connections. Here we describe a new technique for segmenting airways with proper topology and apply the approach to an image volume generated by magnetic resonance imaging of a silicone cast created from an excised monkey lung.

1. Introduction

A common prerequisite for computational analysis and simulations of models generated from biomedical datasets is performing appropriate image processing to reconstruct the data in a way that best represents the original specimen [1, 2]. One set of such specimens are airway lung casts. Reconstructing computational representations of the airways with additional detail enables simulations with greater accuracy and can assist in validation simulation boundary conditions. New airway casting approaches and modern imaging equipment have greatly increased the potential detail, but also present new image processing challenges. In the case of lung airways, it is critically important for the resulting reconstruction to be free of loops—as airways loops are not found in actual lungs—and to be absent of invalid voxel connections, i.e., edge-to-edge or corner-to-corner voxel connections that may be misinterpreted by surface extraction methods. This can present a challenge as airway branches may physically touch each other during the imaging processes due to a non-rigid cast material, or may appear to touch due to limits on the resolution of imaging. A previous lung cast imaging approach has avoided these topological pitfalls by under-segmenting, focusing on the data structure rather than the actual airway shape, and characterizing only a few hundred branches [3]. However, when acquiring airway information from over 10³ airway branches (from the trachea all the way down to the respiratory bronchioles) for fluid dynamic simulation purposes and other biomedical applications, topological issues must be handled. Simply applying an intensity threshold to separate the airways from the background may result not only in fused airways that were in fact separated by tissue in situ, but also in invalid voxel connections. To address this challenge, we present a series of image processing steps that accurately reconstruct structures free of loops and ambiguous voxel connections, and demonstrate the applicability of this process using a non-rigid monkey lung cast containing thousands of airways that was imaged using MRI. We compare our result to a reconstruction generated using a method described in [4] which utilizes erosion and dilation to remove loops. In addition, we demonstrate the general applicability of our approach for reconstructing lung airway casts by applying the method on a previously published imaged rat lung cast [5].

2. Method

2.1. Lung casting

A silicone rubber cast of a monkey's lungs (Figure 1) was obtained using the negative pressure injection procedure previously described [6]. The monkey used for this study was born and raised at the California National Primate Research Center under the provisions of the Institute of Laboratory Animal Resources conforming to practices established by the American Association for Accreditation of Laboratory Animal Care (AAALAC). Briefly, the 6 month old male Rhesus monkey was weighed (1.74 kg body weight), sedated with Telazol (8mg/kg IM), and anesthetized with Diprivan (0.1-0.2 mg/kg/min, IV), with the dose adjusted as necessary by the attending veterinarian. The monkey was euthanized with an overdose of pentobarbital followed by exsanguination through the abdominal aorta. The lungs were immediately inflation-fixed via tracheal cannula for four hours at 30 cm fluid pressure with 1% glutaraldehyde/1% paraformaldehyde in cacodylate buffer (adjusted to pH 7.4, 330 mOsm). The total lung volume was measured by fluid displacement after fixation, and the lungs were stored in fixative at 4°C until casting. Before casting, the lungs were removed from the fixative and rinsed in phosphate buffered saline. Dow Corning® 734 Flowable Sealant (Dow Corning, Midland, MI) and Dow Corning 200® Fluid, 20cs (Dow Corning) were mixed in a heat-sealed bag until a homogenous, bubble-free mix was obtained. The lungs were suspended by the tracheal cannula in a modified desiccator attached to a vacuum pump. The silicon mixture was pulled into the lungs by negative pressure (-100 mmHg) until the first sight of silicone at the pleural surface (10-20 minutes). The desiccator was then slowly brought back to atmospheric pressure. The silicone was allowed to polymerize overnight, and then excess tissue was removed by soaking in bleach. The resulting silicone cast of the airways was rinsed thoroughly in water and air-dried.

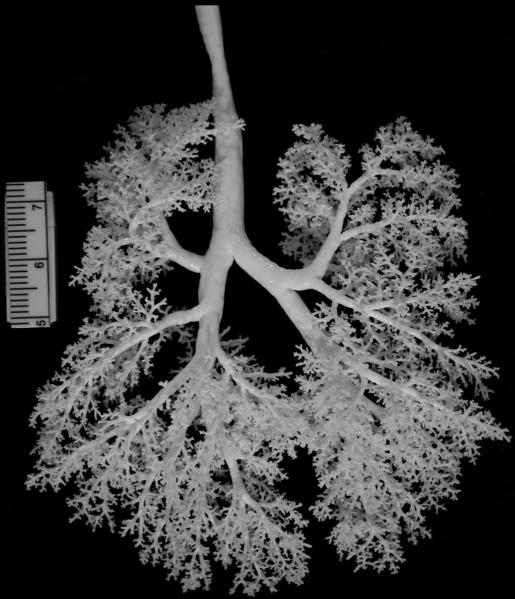
Fig. 1.

Photo of a silicone monkey lung cast lying flat, approximately 10 cm top to bottom.

2.2. MRI imaging

The silicone cast of the airways was prepared for imaging by submersion in 0.25% agar with 1 part magnevist for every 500 parts water. Imaging was performed using a 2 Tesla (84.991 MHz) Varian UnityPlus MRI spectrometer. Total imaging time for the 3D acquisition was 14 hours. The result was 256 transverse image slices each depicting a square field of view 10 cm on a side. The in-plane resolution was 391 microns, and each slice was 391 microns thick. After image reconstruction, the raw image data was in a floating point format. To store images as 8-Bit TIFFs, floating point values between 0.006 and 0.15 were linearly scaled to span 256 grayscale levels, with all values below 0.006 black, and all above 0.15 white. Thus, all 256 slices were stored as 256 greyscale (8-Bit) TIFFs containing 256 × 256 pixels. An example image is shown in Figure 2A.

Fig. 2.

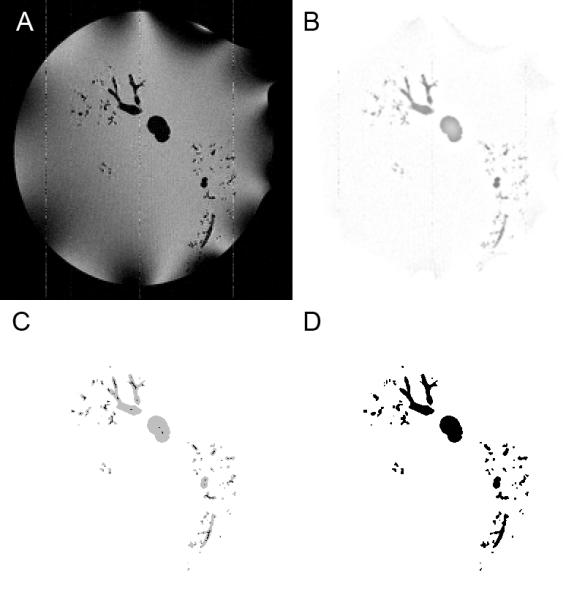
Segmentation steps. A. Sample original TIFF image (magnified 2x to match B,C,D). B. The same image after background normalization and interpolation preprocessing steps have been performed. C. The image after performing the connected threshold segmentation and skeletonization, shown here with cast as grey and cast skeleton in black. D. The final image after detecting and removing loops and handles.

2.3. Image pre-processing

Two pre-processing steps were implemented in Python and applied to the images to prepare for threshold-based segmentation: background signal normalization and 3D interpolation.

2.3.1. Background signal normalization

First, background signal normalization was employed to remove signal intensity artifacts from the image that result from the data collection method. Using the MRI imaging methods described above, the water outside the cast was the main signal source, with the absence of signal indicating the cast. The TIFF images produced using MRI generally exhibited a low amount of noise. However, a significant impediment to connected segmentation existed due to the dark artifacts due to RF inhomogeneity that in some places overlapped the dark cast in the images, demonstrated in the bottom right region of Figure 2A. To remove these artifacts, the background of each image was normalized. This was accomplished by creating a background image by blurring the original image with a 5 pixel radius Gaussian average. The background image was then subtracted from the original image.

2.3.2. 3D interpolation

The second pre-processing step, 3D interpolation, was employed to improve pixel connectivity for segmentation. A 3D bilinear interpolation algorithm was applied to the set of images to create 512 image slices, with each image being 512×512 pixels in size. Expanding the size of the image volume leads to a better utilization of the information stored in the 256 grayscale images during the next step – segmentation – which creates a binary image set. The result of the two image pre-processing steps upon an example image is shown in Figure 2B.

2.4. Segmentation

Connected-threshold segmentation was applied to convert the series of grayscale pre-processed images into a binary volume by associating each point in the series of images with either cast or not-cast. By this approach, the set of cast voxels would include every voxel both meeting the threshold criterion and also connected to a user-provided seed point known to be in the cast. Connectedness was restricted to face connectivity (see Figure 3) to prevent ambiguous representations of the surface between cast and not-cast. Face connectivity was accomplished by restricting the region growing algorithm to faces and by a post-segmentation connectivity check that reassigns voxels found to possess either vertex or edge connectivity. These segmentation steps were implemented in Python, and the threshold criterion used for this dataset was that intensity values below 230 greyscale qualify as cast.

Fig. 3.

Examples of different voxel-to-voxel connectivity. Connections by vertices (left), edges (middle), and faces (right). Vertex and edge connections are invalid due to ambiguously indicating if the material represented by the voxels is in fact continuous.

2.5. Loop removal

Loops were removed to bring the face-connected cast segmentation into proper topology using an approach similar to the handle removal step in [7]. A lung airway naturally has a genus of 0, which means a representation should also be free of all loops, handles, and self-connectedness. Loop removal took place by way of four automated steps – skeletonization, loop detection, loop cutting, and clean-up.

2.5.1. Skeletonization

For the first step – generating a face-connected skeleton – a topology-preserving erosion function was applied to the segmented volume. This approach is similar to [8], but with modifications to ensure that face-connectivity was maintained in the skeleton. To accomplish skeletonization, all cast voxels were initially assigned to be skeleton voxels. Then, an algorithm was applied using a set of four criteria upon each skeleton voxel to determine whether the voxel should remain a skeleton voxel or be returned to a cast voxel. These criteria were based upon the voxel itself, referred to now as the center voxel, and the eight voxels touching it. To simplify description, the criteria described in Table 1 are for the plane advancing from the top of the volume. The criteria were rotated accordingly to properly match other directions of advancement.

Table 1.

List of criteria for applying topology-preserving erosion

Center voxel and middle voxel above the center represent a boundary

The center voxel must be a skeleton voxel, and the voxel directly above must be either cast or not-cast.

This ensures that the erosion is taking place on the boundary of the current form.

Center voxel is not an endpoint of a line

If the number of neighbors that are also skeleton voxels is 1, then the center voxel represents a linear endpoint and should be left alone.

Do not create invalid edges or point connections between materials

The center voxel must remain a skeleton voxel if assigning it to be a cast voxel would create an edge or a point connection between voxel types (see Figure 3).

Do not change genus

The center voxel must remain a skeleton voxel if assigning it to be a cast voxel would either connect cast voxel neighbors that were previously completely separated by skeleton voxels in this neighborhood, or disconnect previously connected skeleton voxel neighbors in this neighborhood.

The erosion queried pixels in a plane, with the plane iteratively advancing from one side of the cube towards the opposite side. The directionality of the plane and its advancement alternated in order from the top, bottom, front, back, left, and right sides of the cubic image volume. This erosion was repeated until no voxels met the criteria for reassignment, leaving a skeleton that was a single-voxel thick and face-connected. (Figure 2C).

2.5.2. Loop detection

After skeletonization, the next step performed was detecting loops in the skeleton. A breadth-first search of branches in the skeleton was applied, starting at the top of the bronchus. When an explored branch ended at an already explored location in the skeleton, that point was marked as belonging to a loop. Then, for each loop-point marked, the entire loop was detected using a breadth-first search.

2.5.3. Loop removal

To find the optimal cutting location within the loop (see Figure 4), a test cut was performed separately for each skeleton voxel belonging to the loop. For a test cut, the plane perpendicular to the skeleton at that voxel was selected, and all adjacent cast pixels within that plane were counted to calculate the cross-sectional area of the test cut. In addition, the number of skeleton voxels within the test cut were counted. Of all the test cuts containing only one skeleton voxel, the test cut containing the smallest area to be cut was assigned to be the cut location. In the case of a tie, the test cut with the greatest path distance from the skeleton point at the top of the bronchus was selected. In the few instances where all test cuts for a loop contained more than one skeleton voxel, the test cut with the fewest number of skeleton voxels was selected as the cut location. After detecting all of the cut locations, all skeleton voxels were reassigned to be cast voxels, and then the cuts were performed at each cut location by reassigning adjacent cast voxels in the cut plane to be not-cast voxels.

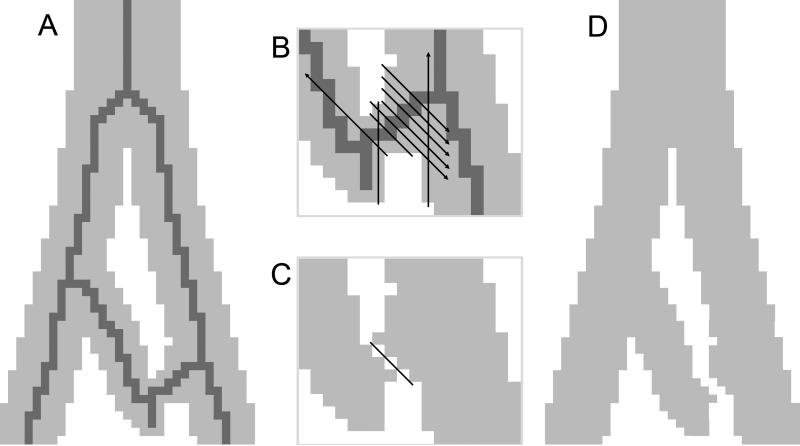
Fig. 4.

Automated loop detection and removal steps are illustrated here in two dimensions (2D) with pixels instead of voxels. A. A section of a lung airway demonstrating a loop is simplified into 2D. The skeleton generated is displayed in dark grey. B. Inset focusing on an airway branch displays black lines indicating test cuts for each pixel in the branch. Note that arrowheads on lines indicate continuance until no longer encountering airway pixels. Note also that test cuts are actually made for every branch that is part of the loop. C. The test cut which removes the least number of pixels is selected, and cutting is then performed. D. After cutting, a repair step reassigns pixels to eliminate invalid, ambiguous connections between pixels.

2.5.4. Clean up

As a final step in removing loops from the segmentation, the segmentation required a clean up. Cutting the loops in some instances separated small bits of the cast from the main segmentation, and it also created invalid edge or point connectivities between voxels in the cast when cutting along a diagonal plane. The post-segmentation connectivity check used previously before loop removal was reapplied to remove all edge and point voxel connections. Then a connected material algorithm was applied, reassigning all cast voxels not connected to the main cast to be not-cast. After this, the skeletonization and loop detection algorithm was re-run to validate the segmentation. Any detected loops at this point were a result of the voxel connectivity repair step. The small number of these and local nature of these loops made them simple to manually repair (Figure 2D).

2.6. Topology validation

The critical criterion in determining if the approach was successful is the number of airway loops in the final segmentation being equal to zero. To verify that a proper geometric topology was achieved, a triangle-mesh was generated by applying a marching tetrahedra algorithm [9] to the cast segmentation dataset. The resulting mesh was iteratively smoothed using volume-preserving smoothing [10]. Then the Euler characteristic of the mesh was calculated, i.e. χ = V - E + F where V, E, and F are the number of vertices, edges, and faces, respectively, of the surface mesh. A Euler characteristic of 2 indicates an airway surface with no loops.

2.7. Method validation

To demonstrate that the segmentation and loop removal process works on other sets of image data of this type, the procedure was repeated on another lung cast dataset. Steps 2.3 through 2.6 were applied to rat lung cast 66, a previously acquired dataset described in detail in [5].

2.8. Comparison with alternative approach

In order to illustrate the advantage of the approach described in prior steps for lung airway cast segmentation with proper topology, the volumetric techniques of Nooruddin and Turk for repairing models [4] were applied to the monkey lung cast dataset. As their approach is designed for an existing polygon model or segmentation, we used the monkey lung cast segmentation generated by step 2.4 and replaced step 2.5 with the Nooruddin and Turk method. Briefly, this method first performs an erosion, followed by 26-connected segmentation of the main object, and finally a dilation. The amount of volume eroded and dilated is determined by a user-defined distance from surface value, where the surface is the boundary between the segmented airway cast and the non-cast region of the volume. To minimize the amount of disruption to the final segmentation generated by this method, we used the lowest distance value of 1 voxel thickness for the erosion and dilation.

3. Results

The volumetric image dataset collected via MRI was 512³ voxels (~134 million voxels) in size. After applying the connected-threshold segmentation, 1,016,436 voxels were assigned as part of the lung cast. The skeletonization step reassigned 79,074 of these cast voxels to the skeleton. The final segmentation consisted of 938,515 voxels, indicating that less than 8% of the initial segmentation was removed through the loop removal process.

During loop removal, 337 loops were initially detected. After cutting these loops, the invalid voxel-to-voxel removal step reintroduced 9 small loops, which were automatically identified and manually repaired. A Euler characteristic of 2 was calculated for the resulting surface mesh (Figure 5 and Figure 6C), indicating a single surface with no loops or intersections. The final segmentation therefore achieved the necessary goals of having zero loops and no same-material voxel connections by only edges or points. The inset to Figure 5 shows an example of one of the 337 loops removed. The number of airway outlets was determined to be ~7300 and the resulting mesh (Figure 6C) matches well visually with the original cast (Figure 6D).

Fig. 5.

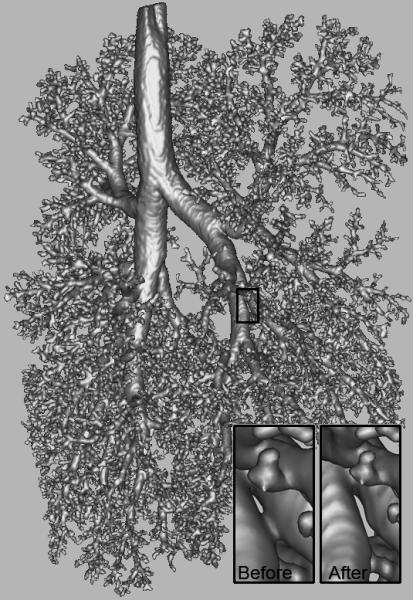
Mesh generated from final segmentation. The inset highlights the effect of automated removal of a loop from the mesh.

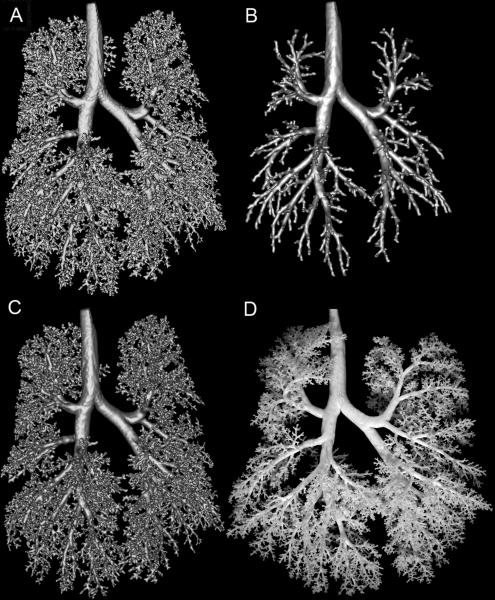
Fig. 6.

Visual comparison of segmentation methods. A. Segmented monkey lung cast prior to loop removal operations. B. Loops removed from A via volumetric erosion and dilation method described in [4]. C. The monkey lung cast surface mesh generated by removing loops from A using our approach detailed in this manuscript. D. Photo of actual lung cast. Differences in orientations of branches are due to gravity, as the non-rigid cast is lying flat in the photo, while during MRI, the cast is neutrally buoyant in fluid.

For comparison, the final mesh (Figure 6C) is illustrated alongside the surface mesh of the segmentation prior to application of the loop removal step (Figure 6A). In addition, the surface mesh generated by the loop removal method of Nooruddin and Turk [4] is shown (Figure 6B). This latter approach also resulted in an Euler characteristic of 2, indicating a surface suitable for computational simulations of airflow. However, much of the detail of the airway has been lost by this approach. Applying an erosion of even the minimum distance of 1 voxel thickness (as in this case) effectively chops the segmentation at any airway branch with a diameter less than ~500 microns. Visually, the diameters and lengths of the branches for both methods are comparably equivalent to that of the lung cast (Figure 6D). A detailed analysis of the accuracy and reproducibility of the image preprocessing and segmentation steps in comparison to manual measurements of branch length and branch diameter can be found in [5].

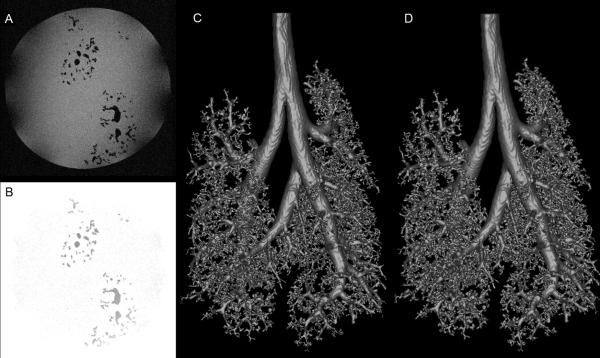
Figure 7 details the application of the methods 2.3 through 2.6 to the cast of a rat lung airway. Shown are original image data (Figure 7A), image data after preprocessing (Figure 7B), the segmented volume mesh prior to loop removal (Figure 7C) with 492 loops, and the final mesh of the rat lung airway with all loops removed (Figure 7D). The Euler characteristic of this surface was calculated to be 2, again indicating a single surface with no loops or intersections.

Fig. 7.

Segmentation and automated loop removal applied to rat lung cast. A. Sample original TIFF image. B. The same image after background normalization and interpolation preprocessing steps have been applied. C. The segmented rat lung cast prior to loop removal operations. D. The rat lung cast surface mesh generated by removing loops from C using the method described here.

4. Discussion

The intent of this method is to provide a reliable automated system for creating topologically valid representations of the mammalian lung in support of multiple potential applications. Using an automated approach is necessary because manually removing hundreds of loops in complex branching 3D object is prohibitively challenging [11]. There are two key characteristics of this approach. The first is a segmentation relying on face-connectivity between voxels of the same type rather than vertex-connectivity (see Figure 3). Face-connectivity in segmentation is important for eliminating connection ambiguity for the subsequent step of generating a surface mesh. Performing linear interpolation of the dataset established face-connectivity between voxels that were connected only by edges or vertices in the originally acquired image. The second characteristic is the final geometric topology of the segmentation matching that of the biological lung, specifically the nonexistence of loops in the airways. By achieving these goals, the resulting surface mesh can be utilized for different biomedical applications. These include generating a volumetric mesh [12] for performing CFD simulations of airflow and particle deposition in the lung [13-16], morphological self-similarity characterization of the lung airways [5], and generating atlases of lung airway branching patterns across multiple species. Beyond the lung, this approach would work on any complex branching biomedical structure, such as is found in the vasculature [17]. While this approach is successful in achieving its goals, future research may lead to optimal solutions for loop removal that minimize the total number of voxels removed during topological correction. As imaging technology improves and the resolution of the image increases, some of the topological issues will disappear. However, in the case of non-rigid casts, topological issues remain due to cast airway branches physically touching. We note that our method is best suited for imaged structures with well defined boundaries, such as is permitted by imaging a cast. Automated segmentation of common clinical images of lung airways generally suffers from the inability to distinguish airway boundaries due to low resolution and poor contrast, particularly for the smallest airways. This method is not designed to address these issues.