Probing Pore Constriction in a Ligand-gated Ion Channel by Trapping a Metal Ion in the Pore upon Agonist Dissociation

Abstract

Eukaryotic pentameric ligand-gated ion channels (pLGICs) are receptors activated by neurotransmitters to rapidly transport ions across cell membranes, down their electrochemical gradients. Recent crystal structures of two prokaryotic pLGICs were interpreted to imply that the extracellular side of the transmembrane pore constricts to close the channel (Hilf, R. J., and Dutzler, R. (2009) Nature 457, 115–118; Bocquet, N., Nury, H., Baaden, M., Le Poupon, C., Changeux, J. P., Delarue, M., and Corringer, P. J. (2009) Nature 457, 111–114). Here, we utilized a eukaryotic acetylcholine (ACh)-serotonin chimeric pLGIC that was engineered with histidines to coordinate a metal ion within the channel pore, at its cytoplasmic side. In a previous study, the access of Zn²⁺ ions to the engineered histidines had been explored when the channel was either at rest (closed) or active (open) (Paas, Y., Gibor, G., Grailhe, R., Savatier-Duclert, N., Dufresne, V., Sunesen, M., de Carvalho, L. P., Changeux, J. P., and Attali, B. (2005) Proc. Natl. Acad. Sci. U.S.A. 102, 15877–15882). In this study, the interactions of Zn²⁺ with the pore were probed upon agonist (ACh) dissociation that triggers the transition of the receptor from the active conformation to the resting conformation (i.e. during deactivation). Application of Zn²⁺ onto ACh-bound open receptors obstructed their pore and prevented ionic flow. Removing ACh from its extracellular binding sites to trigger deactivation while Zn²⁺ is still bound led to tight trapping of Zn²⁺ within the pore. Together with single-channel recordings, made to explore single pore-blocking events, we show that dissociation of ACh causes the gate to shut on a Zn²⁺ ion that effectively acts as a “foot in the door.” We infer that, upon deactivation, the cytoplasmic side of the pore of the ACh-serotonin receptor chimera constricts to close the channel.

Introduction

Eukaryotic pLGICs³ (also called Cys-loop receptors) constitute a superfamily of transmembrane receptors located at the cell surface of excitable neuronal and muscle cells. There, they mediate rapid transport of ions, such as Na⁺, K⁺, Ca²⁺, or Cl⁻, down their electrochemical gradients to alter the membrane potential or to enable a rise in intracellular Ca²⁺. The five subunits of pLGICs are radially aligned around the axis of ion permeation pathway to form a channel activatable by neurotransmitters such as ACh, serotonin, γ-aminobutyric acid, glycine, glutamate, or histamine that bind to an extracellular ligand-binding domain (LigBD) (Fig. 1A) (1–7).

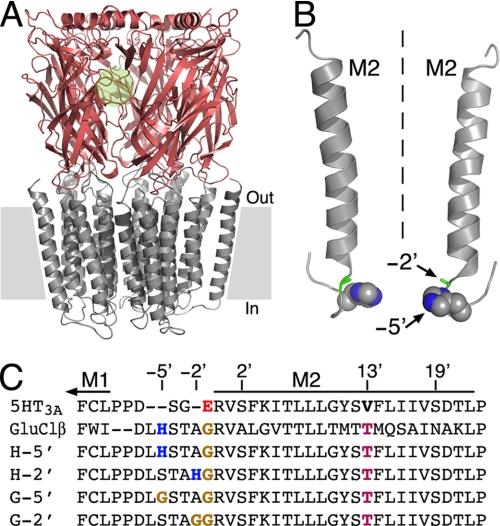
FIGURE 1.

Structural properties of the chimeric pLGICs used here. A, side view of a three-dimensional homology model of chimera H-5′, which consists of the extracellular LigBD of the α7 nAChR (reddish) and the transmembrane channel domain of the 5HT_3A serotonin receptor (gray). One of five intersubunit ACh-binding pockets is depicted by a green circle. The channel domain consists of 20 helices (4 from each subunit). Gray rectangles depict the lipid bilayer. The three-dimensional structure of the intracellular domain (assembled from five M3-M4 connecting sequences) is absent because most of it does not have a counterpart template structure. In various eukaryotic pLGICs, this domain was shown to interact with cytoplasmic proteins to mediate receptor clustering and trafficking (85, 86). B, shown are two of five transmembrane M2 segments that line the ion channel pore. Dashed line indicates the 5-fold axis of symmetry, which is also the axis of ion permeation pathway. A space-filling model of the histidines at position −5′ is shown with carbon and nitrogen atoms colored in gray and blue, respectively. The alanines at position −2′ are shown as green sticks. Hydrogens were removed for clarity. C, amino acid sequence alignment of the M2 segments of the chimeras studied here and the receptors whose channel-forming sequences were utilized for the chimeric design. 5HT_3A, a subunit of 5-hydroxytryptamine (serotonin)-activated cationic channel from mouse (Swiss-Prot accession number P23979); GluClR-β, β subunit of a glutamate-activated chloride channel from C. elegans (Swiss-Prot accession number Q17328). Positions are numbered relatively to the first amino acid of M2 (R0′).

Although it is well accepted that loops located at the LigBD-channel interface mediate movements of the pore-lining helices (M2s) (8–16), the specific M2 motions that open and close pLGICs are widely debated. Cryo-electron microscopy images of open and closed conformations of the nicotinic ACh receptor (nAChR) from Torpedo marmorata gave rise to the concept of gating motions, in which rotations along the longitudinal axis of the M2 segments open or close a mid-pore hydrophobic barrier (17, 18). State-dependent accessibilities of cysteines, histidines, or lysines substituted along the M2s to methanethiosulfonates, Zn²⁺ or protons, have excluded channel gating via rotations (19–23). It was further suggested that rigid body tilting (21) or small scale dilation (23) motions of the M2s gate the pore of an ACh-serotonin receptor chimera or a muscle nAChR, respectively. Several computational simulations suggested that the opening and closing of pLGICs depend on “global quaternary twist” motions (24, 25), rotations (26, 27), or rotations combined with either tilting (28) or bending vibrations (29) of the M2s. In contrast to these computational simulations, recent x-ray crystal structures of two different prokaryotic pLGICs, one displaying a closed pore conformation (30) and another with a potentially open pore conformation (31, 32), suggest that the pore-lining helices rigidly tilt to gate the channel. Yet, a major difference between the tilting gating motions suggested for the prokaryotic channels and those suggested for a eukaryotic pLGIC (21) emerges. In the case of the prokaryotic channels, the putative gating process involves the opening of a barrier to ions at the extracellular side of the pore (30–32), whereas functional studies in eukaryotic pLGICs indicate that activation involves opening of a barrier located at the cytoplasmic side of the pore (19–21, 33).

Here, we used eukaryotic pLGICs that have an engineered capacity to coordinate a metal ion at the cytoplasmic side of their pore (21). In a previous study the accessibility of the engineered histidines to Zn²⁺ ions was probed before or after activation (21), but in this study we detect Zn²⁺ ion trapping inside the pore upon agonist dissociation. This allows us to infer about a constriction motion that takes place during deactivation of a eukaryotic pLGIC.

EXPERIMENTAL PROCEDURES

Single-Channel and Macroscopic Patch-Clamp Recordings

For recordings, HEK-293T cells were seeded on glass coverslips (13-mm diameter) that had been coated with poly-l-lysine (20 μg/ml). Coverslips were placed in 35-mm plates, and the cells were transfected (by the calcium phosphate technique) with pIRES-CD8 (0.5 μg), as a marker for successful transfection, together with the pcDNA3-receptor (1.5 μg) per plate. Transfected cells were visualized using beads coated with anti-CD8 antibodies (Invitrogen). Recordings were performed 48–72 h following transfection. The cell-attached configuration of the patch-clamp recording technique was used for single-channel recordings. The patch pipettes were prepared from borosilicate glass (Warner Instrument Corp.) using a PC-10 puller (NARISHIGE Group). The electrodes were coated with Sylgard to reduce pipette capacitance, and their resistance was 6–10 megohms when filled with the pipette solution. The bath solution contained (in mm) the following: 140 NaCl, 2.8 KCl, 2 CaCl₂, 2 MgCl₂, 10 glucose, 10 HEPES, adjusted to pH 7.35 with NaOH (310 mosm). The pipette solution contained (in mm) the following: 1 ACh, 140 sodium isethionate, 2.8 KCl, 10 glucose, 10 HEPES, adjusted to pH 7.35 with NaOH (310 mosm). Zinc acetate (10 μm) was added to the pipette solution whenever the effect of Zn²⁺ was examined. Single-channel currents were recorded using an Axopatch 200B patch clamp amplifier and a Digidata 1440A interface (Molecular Devices). Acquisition of recording data were performed at 10 kHz, and recordings were low-pass filtered at 1 kHz through a four-pole Bessel filter on the Axopatch 200B amplifier.

Data acquisition and analysis were performed using the pClamp 10.0 software package (Molecular Devices). Single-channel events were detected by the half-amplitude threshold criterion using the Clampfit 10.0 program implemented within pClamp 10.0. The distributions of open and closed times were fitted with a single or two exponentials. Single-channel current amplitudes were measured as the mean of a Gaussian distribution fitted to the amplitude distribution.

Measurements of macroscopic currents were performed basically as in Sunesen et al. (34). The bath solution contained (in mm) the following: 140 NaCl, 2.8 KCl, 2 CaCl₂, 2 MgCl₂, 10 glucose, 10 HEPES, adjusted to pH 7.35 with NaOH. Patch pipettes had 6–10 megohm resistance when filled with a solution containing (in mm) the following: 130 CsCl, 4 MgCl₂, 4 Na₂ATP, 1 EGTA, 10 HEPES, adjusted to pH 7.35 with CsOH. ACh was applied onto the cell by using the VC-77SP fast step system (Warner Instruments) combined with N₂ pressure of 3–4 p.s.i.

Computer-assisted Homology Modeling

An oligomeric model of the LigBD of chimera H-5′ was built by using the carbachol-liganded ACh-binding protein (35) (AChBP, Protein Data Bank code 1UV6) as a quaternary structure template. To this end, the N-terminal sequence of the chimeric subunit was threaded throughout the atomic coordinates of each AChBP chain, according to the sequence alignment shown in supplemental Fig. S1. The resulting three-dimensional alignment was submitted for oligomeric modeling to the SWISS-MODEL Repository, a data base for theoretical protein models. After energy minimization with GROMOS96, the best three-dimensional structural alignment between the pentameric LigBD and the AChBP gave a root mean square difference of 0.38 Å for 3880 backbone atoms of 970 counterpart amino acids. Note that the modeled LigBD and the AChBP have 1030 and 1025 amino acids, respectively. Thus, 60 amino acids from the LigBD and 55 amino acids from the AChBP are not included in this root mean square difference calculation. The final model was then docked onto the structural model previously published for the transmembrane channel domain of chimera H-5′ (21). Hence, the backbone carbon atom (C′) of Arg-206 of each LigBD subunit was positioned 1.35 Å away from the backbone nitrogen atom of Pro-207 of the counterpart subunit in the channel domain (see supplemental Fig. S1 for amino acid numbers). The backbone was then ligated in silico to obtain an oligomeric receptor-channel structure, and energy minimization was performed once again with GROMOS96. No clashes have been observed between amino acids or between the backbone and amino acids, within the individual subunits or at the intersubunit interfaces. The models of the closed and open conformations built by Paas et al. (21) were used for Zn²⁺ docking.

Data Analysis and Computation

Data analysis and computation relating to dissociation constants, EC₅₀ values, and Hill coefficients were carried out using GraphPad Prism.

In the case of ³H-αBTx binding assays, curves were fitted to the data points by a nonlinear regression using Equation 1,

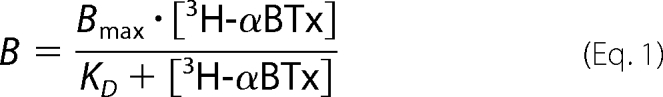where B is the bound ³H-αBTx; B_max is the maximal binding of ³H-αBTx; [³H-αBTx] is the concentration of radiolabeled toxin; and K_D is the dissociation constant, which equals the concentration of toxin required to reach half-maximal binding.

In the case of inhibition of ³H-αBTx binding by small agonists (ACh or nicotine), curves were fitted to the data points by a nonlinear regression using the Hill Equation 2,

where B is the bound [³H]α-BTx; B_max is the maximal binding of [³H]α-BTx; K_i is the agonist inhibition constant; [agonist] is the ACh or nicotine concentration and n_H is the Hill coefficient.

In activation experiments where EC₅₀ values were determined electrophysiologically, curves were fitted to the data points by a nonlinear regression using the Hill Equation 3,

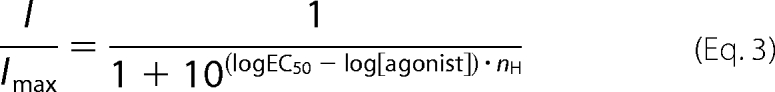where I is the current response; I_max is the maximal current response; EC₅₀ is the agonist concentration necessary to obtain 50% of maximal current response; [agonist] is the ACh concentration, and n_H is the Hill coefficient.

For the two-state allosteric model, Equation 4 was used,

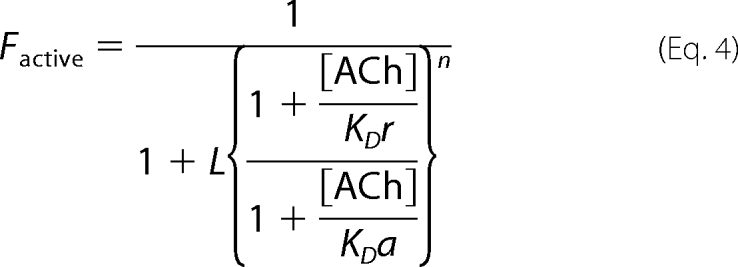where F_active is the fraction of the total receptor population in the active state; [ACh] is the concentration of the activator (ACh) for which there are “n” equivalent binding sites, each binds ACh with a microscopic dissociation constant K_Dr in the resting state, and K_Da in the active state. L is the equilibrium constant of the two states in the absence of ACh; it is equal to the total resting/active receptor ratio. The L value was determined based on functional experiments, as described in the legend to supplemental Fig. S2, E–H. Note that Equation 4 is equivalent to Equation 1 in Ref. 36, where the resting state is called the “T” state and the active state is called the “R” state.

To determine the activation time constants, the current rise of the traces (like those shown in Figs. 4 and 5) was best fitted with a single exponential time course by using Equation 5,

where A is the current amplitude; t is the time; τ is the time constant, and C is the constant y offset.

FIGURE 4.

Blocking of open channels by Zn²⁺ in a reversible manner. A and B, indicated chimeric receptors (expressed in Xenopus oocytes) are activated by saturating concentrations of ACh (300 μm) for 9 s. 3 s after onset of activation, 1 mm Zn²⁺ is added for 6 s to block the open channels (left side of the red traces). Then, following a 6-s-long wash of both ACh and Zn²⁺ simultaneously (1st red wash), the chimeras were reactivated with ACh (300 μm; 2nd red ACh) for 3 s, and washed again (2nd red wash). The black traces are unblocked currents activated by 300 μm ACh for 9 s; they show the maximal nondesensitizing current amplitudes. Recordings were performed at−80 mV and room temperature.

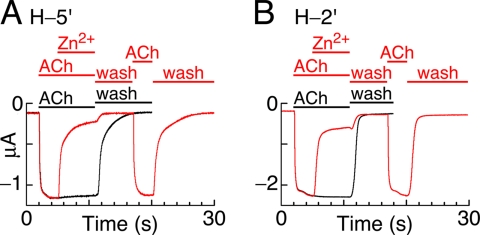
FIGURE 5.

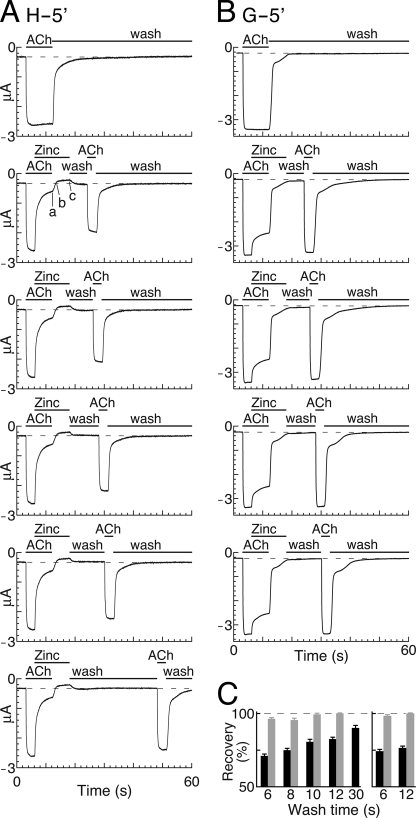
Induction of receptor deactivation in the presence of Zn²⁺ ions. A, six representative current episodes recorded from Xenopus oocytes expressing chimera H-5′ are lined up vertically. The 1st episode corresponds to activation by a saturating ACh concentration (300 μm) for 9 s, which shows the maximal nondesensitizing current amplitude. Dashed line shows the base line. 2nd to 6th episodes show application of an ACh-containing solution (300 μm) for 3 s, which was replaced by a solution that contains both ACh (300 μm) and Zn²⁺ (1 mm) for a further 6 s. The addition of Zn²⁺ led to inhibition of the steady-state current (decline to point a). Then, the solution containing both ACh and Zn²⁺ was replaced by a solution containing 1 mm Zn²⁺ without ACh, for further 6-s-long application to remove ACh while leaving Zn²⁺ in the application bath. This step led to further decline of the current to the base line (point b) and then to the inhibition of the leak current (from b to c). The oocyte was then washed with a physiological solution devoid of both ACh and Zn²⁺ for varying time periods (under 1st wash); within this washing time, the current trace returned from point c to the base line. Then, ACh (300 μm) was reapplied for 3 s (under 2nd ACh), followed by a second wash. Note that after each 60-s-long episode, the oocyte was briefly stimulated for a few times by ACh alone (and washed) until the maximal (primary) amplitude recovered. Recordings were performed at −80 mV at room temperature. B, same as in A but with a glycine-containing control chimera (G-5′). C, histograms of experiments performed as in A and B. Shown are percentages of current recovery (after the indicated washing times) of the chimeras as follows: H-5′ (left, black columns), G-5′ (left, gray columns), H-2′ (right, black columns), and G-2′ (right, gray columns). The recovery of the H-5′ channels significantly differs from that of the G-5′ channels; for 6, 8, 10, and 12 s of wash, p < 0.0001; for a 30-s wash of H-5′ compared with a 12-s wash of G-5′, p < 0.0007 (N = 5). The recovery of the H-2′ channels significantly differs from that of the G-2′ channels: for a 6- and 12-s wash, p < 0.0001 (N = 5).

The zinc association rate constant shown in Scheme 1 (see text) was calculated according to the explanation provided under “Results” (under “Single-Channel Recordings Show Fast and Slow Zn²⁺-blocking Events”), as in Equation 6,

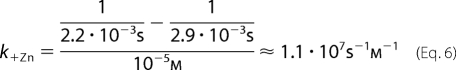Statistical Analysis

Unless stated otherwise, p values correspond to two-tailed paired t tests.

The following methods are provided in the supplemental material under supplemental Experimental Procedures: Chimeras and Mutants, Transfection of Cultured Cells and Cell Harvesting, Membrane Preparation, Ligand Binding Assays, and Electrophysiology in Xenopus Oocytes.

RESULTS

Structural Properties of the Chimeric Receptors Used Here and Their Capability to Interact with Zn²⁺

The receptors employed here assemble as homopentamers, and each subunit is a fusion polypeptide that consists of the extracellular N-terminal segment of the nAChR α7 subunit fused to the transmembrane and intracellular C-terminal segment of the serotonin receptor 5HT_3A subunit (37). Therefore, this chimeric α7–5HT_3AR responds to ACh, which binds to the LigBD to open a channel of a serotonin receptor. The chimeric α7–5HT_3AR was further mutated as follows. (i) Following Dang et al. (38), a V13′T mutation was introduced in the M2 pore-lining segment to eliminate the desensitization capacity of the chimera. (ii) The M1-M2 connecting sequence was replaced by the homologous sequence of the β subunit of the Caenorhabditis elegans glutamate-gated ion channel (21). A homology model of this chimera (H-5′) is shown in Fig. 1A. The replacement of the M1-M2 sequence resulted in a histidine residue at position −5′; thus, upon receptor assembly, five histidines have become organized around the ion permeation pathway (Fig. 1B) (21). Note that the replacement of the M1-M2 segment also removed a glutamate residue from position −1′, because the replacing M1-M2 segment naturally contains a glycine residue at this position (Fig. 1C). As such, the negatively charged ring at position −1′ was neutralized and could not serve as a potential metal-binding site, whereas the cytoplasmic (bottom) side of the ion channel pore has been equipped with a metal-binding ring consisting of five imidazole groups. Moving the histidine downstream, along the replacing M1-M2 segment, provided a metal-binding ring slightly higher in the pore (chimera H-2′) (Fig. 1, B and C, and Fig. 6, right side). We further designed control mutants that contain the aforementioned changes, with one exception being a glycine instead of a histidine at either position −5′ (chimera G-5′) or position −2′ (chimera G-2′) (Fig. 1C). We have used these Gly-containing control chimeras to determine whether the effects of Zn²⁺ are specific to the presence of the engineered histidines.

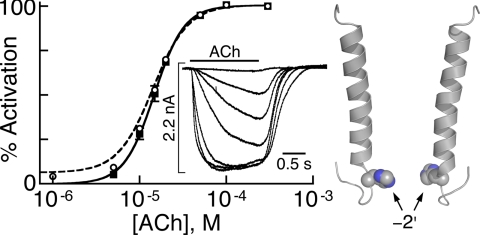
FIGURE 6.

Analysis of macroscopic currents in HEK293T cells expressing chimera H-2′^(RRR→QDA). Dose-response curve for chimeras H-2′^(RRR→QDA) (continuous black line) fitted by the Hill equation (Equation 3) to data points obtained from ACh-elicited currents (black squares) (N = 13 cells). The inset shows representative macroscopic currents that increase with the increase in applied ACh concentration (in μm): 5, 10, 15, 20, 50, 100, and 300 (performed at −70 mV at room temperature). The dashed curve was fitted to data points that include the ACh-elicited currents plus Zn²⁺-inhibited leak currents (open circles). Fitting of the dashed curve was performed by using a two-state allosteric model (Equation 4 under “Experimental Procedures”) with n = 5 binding sites, microscopic ACh-dissociation constants for the resting (K_Dr) and active (K_Da) states as provided in Table 2, and an equilibrium constant L = 22.6 that was determined (with S.E. = 2.3; N = 12) using the experimental procedure applied for chimeras H-2′ and H-5′ (explained in the legend to supplemental Fig. S2, E–H). On the right side, two helical M2 segments of opposite subunits are shown with a space-filling model of histidines at position −2′ (carbon and nitrogen atoms are colored in gray and blue, respectively).

In a previous article, Paas et al. (21) determined the capacity of the aforementioned chimeras to interact with Zn²⁺ ions before and after activation. For clarity, supplemental Fig. S2, A and B, shows again the dose-dependent inhibitory effect that externally applied Zn²⁺ ions have on the open state of chimeras H-5′ and H-2′, respectively. The Zn²⁺ inhibition constants (K_i) at −80 mV were (in μm) as follows: 30 ± 4.8 and 80 ± 12 (mean ± S.D., N = 8 and 6) for chimeras H-5′ and H-2′, respectively (21). The supplemental Fig. S2, C and D, shows that the glycine-containing control chimeras, G-5′ and G-2′, were inhibited to much lesser extent (inhibition of 27 ± 2% and 19 ± 5.6% at 1 mm Zn²⁺ (mean ± S.D., N = 5 and 4), respectively (21)). We do not know what is the origin of this weak inhibition; however, we do not exclude a weak inhibitory effect by Zn²⁺ interacting with the LigBD. Indeed, it was recently shown that a pentameric glycine-gated ion channel is strongly inhibited by Zn²⁺ that binds to the underlined amino acids of the HFHEIT sequence in the LigBD (39). Notably, at the homologous positions of the nAChR-α7 subunit (the donor of the LigBD in our chimeras), there are four side chains that could potentially interact with divalent metal cations (RFDATF; see sequence alignment in Ref. 40). In any event, based on supplemental Fig. S2, A–D, and other results by Paas et al. (21), it was concluded: (i) in the open conformation, a ring of five histidines at either position −5′ or −2′ is accessible for interactions with externally applied Zn²⁺ ions, and (ii) binding of Zn²⁺ blocks the open pore, presumably because a bound Zn²⁺ ion sterically interferes with the flow of other ions through the ion permeation path.

Ligand Binding Properties of the Chimeric Receptors

αBTx belongs to a family of α-neurotoxins that stabilize ACh receptors in a nonconducting state (41–43) by interacting with the ACh-binding pockets to sterically interfere with agonist binding (5, 44–49). αBTx binds to the brain α7 nAChR with nanomolar affinities (50). Our chimeras have the LigBD of the α7 nAChR, which binds small agonists like ACh or nicotine with low affinities (K_D of tens or few micromolars, respectively) (50, 51). Here, we characterized the binding affinity of the chimeras for αBTx (K_D values) and the capacity of ACh and nicotine to competitively inhibit ³H-αBTx binding (K_i values).

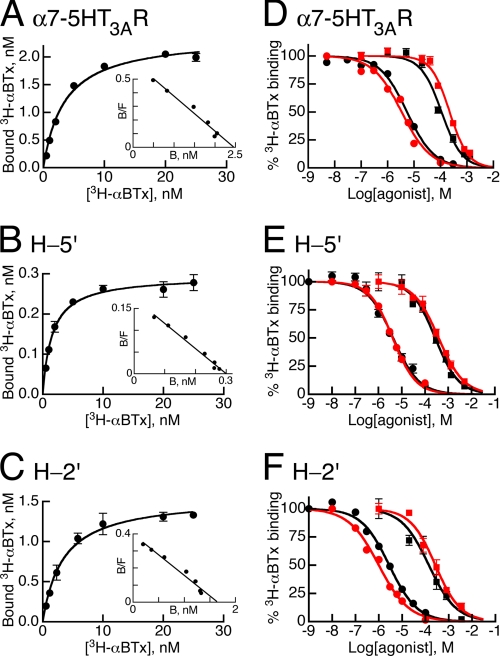
Fig. 2, A–C, shows saturation curves of ³H-αBTx binding to the α7–5HT_3AR and chimeras H-5′ and H-2′. The resulting dissociation constants (K_D) are shown in Table 1. The similar K_D values indicate that the three receptors bind αBTx with virtually the same affinity. The linear fits of the Scatchard plots (small insets) indicate that in each chimera the binding sites that do accommodate αBTx are identical.

FIGURE 2.

Ligand binding properties of the chimeric receptors α7–5HT_3AR, H-5′, and H-2′. A–C, saturation curves of ³H-αBTx binding to the chimeras indicated in the panels. Insets correspond to Scatchard analyses showing maximal αBTx binding (B_max in nm) of 2.5 ± 0.3, 0.3 ± 0.02, and 1.65 ± 0.2 (mean ± S.D.) for chimeras α7–5HT_3AR, H-5′, and H-2′, respectively. D–F, ³H-αBTx binding to the indicated chimeras in the presence of increasing concentrations of ACh (squares) or nicotine (circles). Throughout D–F, the competitive binding assays were performed in the absence (black curves) or presence (red curves) of 1 mm Zn²⁺. The ³H-αBTx concentration was 4–5 nm, which approximates the toxin dissociation constants (K_D values in Table 1).

TABLE 1.

Ligand binding properties of the α7–5HT_3AR and chimeras H-5′ and H-2′

K_D, K_i, and n_H are the dissociation constant, inhibition constant, and Hill coefficient, respectively. Data are means ± S.D. of at least three independent experiments, each performed in triplicate. Two-way analysis of variance between the affinities of the agonists for the three chimeras in the absence and presence of Zn²⁺ gave p = 0.67 and p = 0.27 in the case of ACh and nicotine, respectively.

Receptor	αBTx, KD	ACh				Nicotine
		−Zinc		+Zinc		−Zinc		+Zinc
		Ki	nH	Ki	nH	Ki	nH	Ki	nH
	nm	μm		μm		μm		μm
α7–5HT3AR	4.2 ± 0.7	143 ± 41	1.2 ± 0.1	201 ± 57	1.3 ± 0.1	3.2 ± 1.6	1.3 ± 0.3	3.8 ± 0.4	0.9 ± 0.1
H-5′	3.3 ± 2.4	201 ± 53	1.1 ± 0.2	324 ± 101	0.9 ± 0.1	3.2 ± 0.9	0.8 ± 0.1	2.9 ± 1.0	0.8 ± 0.1
H-2′	5.0 ± 2.8	182 ± 69	0.8 ± 0.1	224 ± 56	0.7 ± 0.1	3.7 ± 1.2	0.9 ± 0.1	1.8 ± 0.8	1.0 ± 0.2

As a next step, equilibrium binding assays were employed to determine the K_i values of ACh and nicotine. Fig. 2, D–F (black curves), shows binding of ³H-αBTx (at its K_D concentration) in the presence of increasing concentrations of ACh or nicotine. Evidently, the α7–5HT_3AR and chimeras H-5′ and H-2′ display similar ACh- and nicotine-K_i values (Fig. 2, D–F, and Table 1, under headings ACh or Nicotine, −Zinc), indicating that these three chimeric receptors share similar affinities for their agonists, ACh and nicotine.

We repeated the competitive binding assays in the presence of Zn²⁺ ions, because Zn²⁺ was used in electrophysiological experiments as a probe that interacted with the ring of five histidines engineered in the channel (described further below). Fig. 2, d–F (red curves), and Table 1 (under headings ACh or Nicotine, +Zinc) show that Zn²⁺ does not change the binding affinities of ACh or nicotine significantly. The Hill coefficients of ACh or nicotine binding were also not affected by the presence of Zn²⁺ ions in the ligand binding reactions.

In the α7–5HT_3AR, the ACh-K_i value (Table 1, under −Zinc) is ∼2 times higher than the ACh-EC₅₀ value derived from electrophysiological experiments (Table 2), in agreement with the ratio obtained previously for this chimera (51). In contrast, for chimeras H-5′ and H-2′, dividing the ACh-K_i values (Table 1, under −Zinc) by the ACh-EC₅₀ values in Table 2 gave mean ratios of ∼20 and ∼36, respectively. This significant difference between the α7–5HT_3AR and chimeras H-5′ and H-2′ motivated us to explore the allosteric properties of chimeras H-5′ and H-2′, as described below.

TABLE 2.

Affinity constants derived from channel activity

K_Dr, K_Da, and K_Dd are the microscopic ACh dissociation constants of the resting, active, and desensitized states, respectively. For the α7–5HT_3AR, these constants were previously determined based on a three-state allosteric model (indicated by asterisks (55)); they are compared with the constants determined here for chimeras H-5′, H-2′, and H-2′^(RRR→QDA) that, unlike the α7–5HT_3AR, do not undergo desensitization.

Receptor	Fitting by the Hill equation		Microscopic constants (allosteric models)
	ACh-EC50	nH	KDr	KDa	KDd
	μm		μm	μm	μm
α7–5HT3AR	68 ± 24 (7)a	1.4 ± 0.2a	88.0*	2.25*	1.6*
H-5′	10 ± 2.8 (6)a	2.2 ± 0.3a	96.0	9.40
H-2′	5 ± 0.5 (5)a	2.4 ± 0.2a	98.5	4.40
H-2′(RRR→QDA)	15 ± 2.6 (13)b	2.7 ± 0.5b	104	12.2

^a ACh-EC₅₀ is the ACh concentration that gives half-maximal current response; n_H is Hill coefficient of activation (mean ± S.D.; number of cells is in parentheses). Data were determined in Xenopus oocytes by Paas et al. (21).

^b Data were determined here in HEK293T cells.

Chimeras H-5′ and H-2′ Display Two Main Conformations

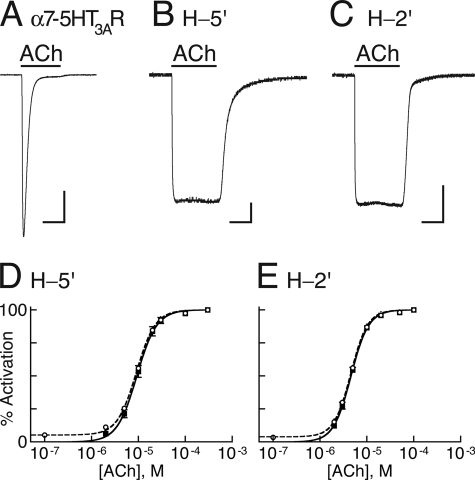
The α7–5HT_3AR is capable of desensitizing (Fig. 3A), i.e. its activation is followed by channel closing, but the receptor retains a high affinity for the agonist. In contrast, chimeras H-5′ and H-2′ were engineered not to desensitize, so that the pore remains open as long as an agonist is bound (Fig. 3, B and C). Elimination of desensitization was essential to ensure that any current decline due to interactions of Zn²⁺ with the histidines could not be attributed to desensitization.

FIGURE 3.

Channel activity and allosteric modeling. A–C, representative inward currents measured at −80 mV and room temperature in Xenopus oocytes expressing the indicated chimeras, as a response to saturating concentrations of ACh (300 μm). In each panel, the horizontal bar at the bottom corresponds to 3 s, and the vertical bar corresponds to 0.5 μA. D and E, dose-response curves (continuous black lines) for the indicated chimeras fitted by the Hill equation (Equation 3) to data points obtained from ACh-elicited steady-state currents (black squares). The dashed curves were fitted to data points that include the ACh-elicited currents plus the Zn²⁺-inhibited leak currents (open circles). Fitting of the dashed curves was performed by using a two-state allosteric model (Equation 4 in “Experimental Procedures”) with n = 5 binding sites, microscopic ACh dissociation constants for the resting (K_Dr) and active (K_Da) states as provided in Table 2, and equilibrium constants L = 18 and L = 28 for H-5′ and H-2′, respectively. L values were determined as explained in the legend to supplemental Fig. S2, E–H.

Previous studies performed with two different pLGICs have shown that mutations at the mid-pore 9′ position stabilize a so-called “pathologically opened desensitized state,” which was permeable to ions and displayed a drastic increase in apparent affinity (i.e. ∼160-fold decrease in ACh-EC₅₀) (52, 53). In these mid-pore mutants, the Hill coefficient of activation also changed significantly; it decreased from values ranging from 1.5 to 2.0 toward a value of 1 (52, 53). In contrast, the ACh-EC₅₀ values of chimeras H-5′ and H-2′ decreased moderately (by ∼7 and ∼14 respectively, compared with the α7–5HT_3AR), and their Hill coefficients of activation significantly increased (Table 2). These observations suggest that the open state of our chimeras potentially reflects the active state rather than a pathologically opened desensitized state. To ascertain that the chimeric H-5′ and H-2′ receptors indeed isomerize between two dominant states and that their conducting conformation corresponds to the active state, we have employed a two-state allosteric model based on the Monod-Wyman-Changeux theory (54) as applied also by Karlin (36) to the nAChR.

A two-state allosteric model postulates that the receptor interconverts between two distinct states as follows: a resting state, having a closed channel conformation, and an active state, having an open channel conformation. The equilibrium constant (L), which describes the resting₀ ↔ active₀ isomerization in the absence of an effector, was determined by analyzing Zn²⁺-blockable leak currents that we measured in oocytes expressing chimeras H-5′ and H-2′ (red traces in supplemental Fig. S2, E and F; see legend). Because Zn²⁺ had a very little effect on the leak currents recorded from oocytes expressing chimeras G-5′ and G-2′ (supplemental Fig. S2, G and H), we attribute the Zn²⁺-blockable currents (supplemental Fig. S2, E and F) to ions flowing specifically through spontaneously opened H-5′ and H-2′ channels. Assuming five identical ACh-binding sites, activation curves simulated based on this two-state allosteric model closely matched the activation Hill curves (Fig. 3, D and E). The microscopic ACh dissociation constants derived from the two-state allosteric model for the resting state (K_Dr) of chimeras H-5′ and H-2′ were very close to the microscopic dissociation constant characterized previously for the resting state of the α7–5HT_3AR chimera (55) (Table 2). The microscopic ACh dissociation constants derived for the active state (K_Da) of chimeras H-5′ and H-2′ were, respectively, ∼6 and ∼3 times higher than the microscopic ACh dissociation constant characterized previously for the desensitized state (K_Dd) of the α7–5HT_3AR (Table 2) (55). These ratios are clearly greater than the K_Da/K_Dd ratio characterized previously for the α7–5HT_3AR based on a three-state allosteric model (∼1.4 in Ref. 55) (Table 2). It is therefore most likely that chimeras H-5′ and H-2′ do not adopt a desensitized state with higher affinity for agonists than the open state. We conclude that the conducting channel conformation of chimeras H-5′ and H-2′ corresponds to the active conformation; so, the transition of these chimeras from the open state to the closed state corresponds to the active → resting transition typical of the deactivation process.

Triggering Receptor Deactivation Leads to Zn²⁺ Ion Trapping at the Bottom of the Shutting Pore

Fig. 4 (red traces) shows that following block of opened channels by a high Zn²⁺ concentration (1 mm), wash out of both ACh and Zn²⁺ simultaneously allows for reactivation of the entire channel population by ACh with similar amplitudes and activation time constants: τ = 84 ± 26 ms versus 72 ± 16 ms (mean ± S.D.; N = 6) for the first versus second ACh application in H-5′ (p = 0.36), and τ = 86 ± 29 ms versus 103 ± 32 ms (mean ± S.D.; N = 5) for the first versus second ACh application in H-2′ (p = 0.40).

Because Zn²⁺ blocks the active open conformation reversibly, the following question may be asked. Will the ring of five histidines trap Zn²⁺ upon pore closure? To answer this question, we induced deactivation of receptors having open, Zn²⁺-blocked channels. Fig. 5A shows a series of current traces (lined up vertically) obtained from a continuous experiment done in an oocyte that expresses chimera H-5′. Fig. 5A, upper trace, corresponds to the activation by saturating concentrations of ACh followed by a wash. This current response corresponds to the full capacity of activation, where the current reaches a steady state and does not decline as long as ACh is present. The 2nd to 6th traces in Fig. 5A indicate application protocols where ACh was applied at saturating concentrations until the channel population reached a steady state, and then a high Zn²⁺ concentration (1 mm) was added to the ACh solution. The addition of Zn²⁺ caused current decline to point a (2nd trace in Fig. 5A), which corresponds to ∼90% inhibition of the ACh-elicited currents. This indicates that Zn²⁺ blocked most of the open channels. Subsequently, the ACh plus Zn²⁺ solution was replaced by a zinc-containing solution devoid of ACh to remove ACh and to trigger receptor deactivation in the presence of a high Zn²⁺ concentration. This step led to further decline of the current to the base line (dashed line in Fig. 5A; denoted by b in the 2nd trace), which demonstrates the deactivation of the remaining ∼10% unblocked channels. Further reduction in the leak current from b to c in Fig. 5A is attributed to pore blockage of spontaneously opened H-5′ channels (as elucidated above).

Then a solution devoid of both ACh and Zn²⁺ was applied for varying washing periods as indicated by the first “wash” throughout Fig. 5A. The return of the current from point c in Fig. 5A to the base line indicates that during this wash Zn²⁺ dissociated from the spontaneously open channels, and it was washed out of the application bath together with all the free Zn²⁺ ions before ACh reapplication. Reapplication of ACh alone (2nd ACh application in Fig. 5A) resulted in currents that were significantly weaker than those elicited by the first ACh application, i.e. after a 6-s-long wash (2nd trace in Fig. 5A), ∼70% of the channel population reopened with an activation kinetics (τ = 87 ± 32 ms) similar to that of the first activation (τ = 81 ± 24 ms) (mean ± S.D., N = 5, p = 0.75), but ∼30% of the channel population did not conduct current. After a 30-s-long wash (6th trace in Fig. 5A), ∼8% of the channels were still nonconducting. In contrast to the strong inhibitory effect of Zn²⁺ on chimera H-5′, Zn²⁺ weakly inhibited the ACh-elicited currents in the control chimera, which has glycines instead of histidines at position −5′ (Fig. 5B). Also, Zn²⁺ did not inhibit the leak currents through the G-5′ mutant. Most importantly, currents have fully recovered upon reactivation of the G-5′ control chimera (Fig. 5B).

Together, our observations indicate that, under this experimental protocol (Fig. 5A), Zn²⁺ becomes trapped in the pore of chimera H-5′ and stabilizes a nonconducting conformation; this is probably due to strong interactions of Zn²⁺ specifically with the five-imidazole ring inserted at position −5′. Similar results were observed with chimera H-2′ and its G-2′ control mutant (supplemental Fig. S3). Fig. 5C provides quantitative analyses for the recovery of the currents; it shows that significant H-5′ and H-2′ channel subpopulations lost their capability to recover when ACh is washed away prior to Zn²⁺ (unlike the case of the control G-5′ and G-2′ chimeras, which were mostly unaffected).

Single-Channel Recordings Show Fast and Slow Zn²⁺ Blocking Events

Chimera H-2′ has the intracellular domain of the 5HT_3AR. It was previously shown that receptors having a channel domain assembled from the 5HT_3A subunit must carry three specific mutations (RRR → QDA) within the intracellular domain to conduct (with a yet unknown mechanism) detectable single-channel currents (9, 56). These three QDA substituents had no effect on the EC₅₀ and apparent dissociation constant for ACh when introduced in the chimeric α7–5HT_3AR, showing that they do not affect macroscopic activation properties (57). Notably, the RRR→QDA mutations were further applied for studying (by single-channel recordings) mechanisms of activation and desensitization in chimeric α7–5HT_3A receptors, without or with additional sets of mutations in other regions of the receptor (11, 57, 58). Hence, we decided to introduce the improving mutations in chimera H-2′ and concomitantly replaced Arg-404, Arg-408, and Arg-412 by Gln, Asp, and Ala residues, respectively. We chose chimera H-2′ for this step because its expression level in HEK293T cells (which we used for single-channel recordings) was ∼5-fold higher than that of chimera H-5′ (Fig. 2, B_max values); and thus, the likelihood of getting a channel-containing patch was higher.

Because the effect of the additional three mutations on the chimeric receptors used here was not known, we analyzed whole-cell current responses in HEK293T cells expressing chimera H-2′^(RRR→QDA). Fig. 6 (inset) demonstrates that the H-2′^(RRR→QDA) channel population does not desensitize in the presence of saturating ACh concentrations. The ACh-EC₅₀ and Hill coefficient determined for chimera H-2′^(RRR→QDA) were somewhat higher than those for chimera H-2′ (Table 2). However, like chimera H-2′ (and H-5′), chimera H-2′^(RRR→QDA) displayed significantly lower ACh-EC₅₀ and higher Hill coefficients than the “parent” chimeric α7–5HT_3AR, showing that the three “daughter” chimeras share common macroscopic activation properties (Table 2). A two-state allosteric model (Fig. 6) indicates that the microscopic ACh dissociation constant derived for the resting state of chimera H-2′^(RRR→QDA) (K_Dr) is very similar to that of chimera H-2′ (Table 2). Nevertheless, the microscopic ACh dissociation constant derived for the active state (K_Da) of chimera H-2′^(RRR→QDA) was ∼3-fold higher than that of chimera H-2′ and, more importantly, ∼8-fold higher than the microscopic ACh dissociation constant derived previously for the desensitized state of the α7–5HT_3AR (K_Dd) (55) (Table 2). Together, these observations strongly indicate that the conducting channel conformation of chimera H-2′^(RRR→QDA) corresponds to the active conformation but not to a (“pathologically opened”) desensitized state that should have had severalfold higher affinity for ACh. As such, single-channel closing events of chimera H-2′^(RRR→QDA) could not be attributed to desensitization.

Recordings of single-channel currents from cell-attached patches were performed here at −70 mV using 10 μm Zn²⁺, a concentration that is 10 times lower than the Zn²⁺ inhibition constant (K_i) previously determined for the open state of chimera H-2′ (100 μm at −70 mV; see Supporting Information of Ref. 21). Using such a low Zn²⁺ concentration (with 1 mm ACh) inside the recording pipette aimed at minimizing the likelihood of blocking the channel for long durations in a nonconducting conformation.

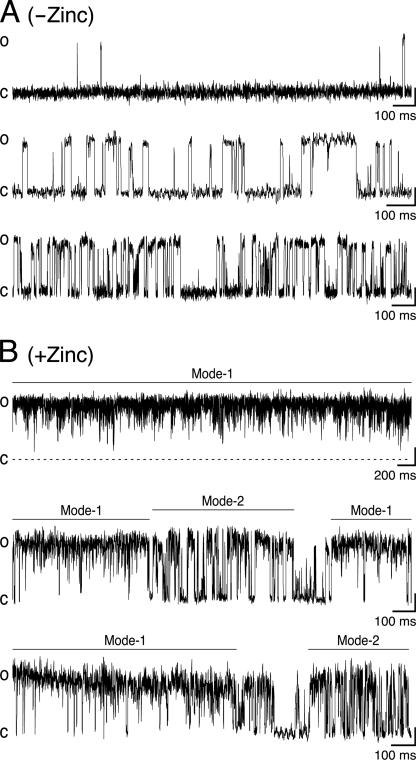
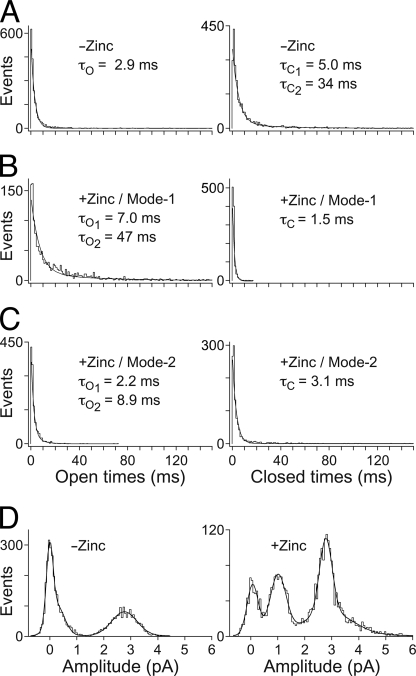
Fig. 7A shows single-channel openings from chimera H-2′^(RRR→QDA) that appear, in the absence of Zn²⁺, as isolated openings (upper trace), bursts of brief and long openings spaced by relatively long closing periods (middle trace), and long bursts with shorter closing times (lower trace). The distribution of open times within the bursts was fitted with a single exponential, whereas the distribution of closed times was best described by the sum of two exponential components (Fig. 8A, decay time constants τ_O, τ_C1, and τ_C2). In the presence of Zn²⁺, the channel behaved much differently (Fig. 7B); the single-channel currents showed bursts with an increased open channel noise, rapid fluctuations (flickers) in the open channel currents, and a bimodal behavior. One behavioral mode (“Mode-1”) displayed prolonged channel openings, which were interrupted by many flickers that could not be fully resolved as rectangular steps at the filtration bandwidth that we used (1 kHz) (e.g. Fig. 7B, upper trace). The second behavioral mode, “Mode-2,” displayed openings that were frequently interrupted by transitions to a nonconducting state, which probably indicate fully resolved blocking events that reached the base line (e.g. Fig. 7B, middle and lower traces). Mode-2 could sometimes be observed within the same burst together with Mode-1 (e.g. Fig. 7B, middle trace) or as separate bursts (e.g. lower trace). The distribution of open times in Mode-1 is best described by the sum of two exponential components, whereas the distribution of closed times in this mode is best fitted with a single exponential (Fig. 8B). Likewise, the distributions of the open and closed times in Mode-2 were best fitted with two and single exponential components, respectively (Fig. 8C). Note that in all the cases where the fit included two exponentials, the contribution of the component that provided longer times did not exceed 10% (legend to Fig. 8). A simple two-state model describes the blocking process in kinetic terms as shown in Scheme 1,

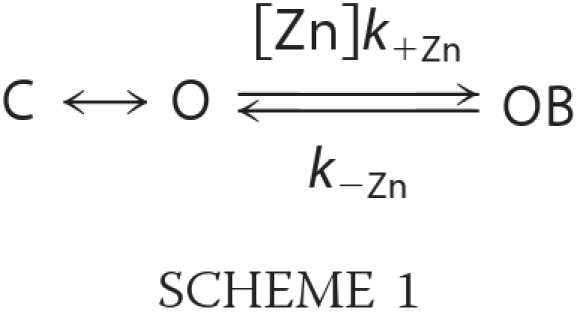where C is the closed state, O is the open state, OB is the open-blocked state, [Zn] is the concentration of Zn²⁺, and k_+Zn (s⁻¹ m⁻¹) and k_−Zn (s⁻¹) are the association and dissociation rate constants for Zn²⁺, respectively. As the rate of open-channel blocking depends on the concentration of Zn²⁺, [Zn]k_+Zn is the actual transition rate for the forward reaction. The equilibrium dissociation constant, K_D, for the blocking reaction (59) is provided by the k_−Zn/k_+Zn ratio. We have used the methodology of Lester and co-workers (60) to determine the values of the rate constants based on a single concentration of an open-channel blocker. As such, k_+Zn = Δ(1/t)/[Zn], and t is the mean open time that is equal to the decay time constants, τ_O or τ_O1, in the absence or presence of 10⁻⁵ m Zn²⁺, respectively (Fig. 8). Therefore, in the case of Mode-2, k_+Zn = 1.1·10⁷ s⁻¹ m⁻¹ (calculation detailed under “Experimental Procedures”). The average residence time of Zn²⁺ in the pore throughout Mode-2 is provided by the mean closed time, τ_C, which is equal to 1/k_−Zn. So, k_−Zn = 1/τ_C = 323 s⁻¹, and the K_D of Zn²⁺ binding to the pore during Mode-2 is thus ∼29 μm. This value is ∼3.5 times lower than that measured previously for the open state of chimera H-2′ (100 μm at −70 mV; see Supporting Information of Ref. 21). We could not employ this calculation in the case of Mode-1, which displays flickery behavior attributed to fast blocking events. This is because, within the recording limitations, many blocking events did not pass the half-amplitude threshold, and thus the long recorded “openings” mask a large number of potential rapid openings and blocking events. Yet, we analyzed the distributions of open and close times of Mode-1 taking into account the resolved and unresolved blocking events that did pass the 50% amplitude. As such, the mean open and closed times of Mode-1 are actually overestimated (τ_O1, τ_O2, and τ_C, in Fig. 8B), but nevertheless, they have a heuristic value as discussed below.

FIGURE 7.

Effect of Zn²⁺ ions on the single-channel activity of chimera H-2′^(RRR→QDA). Representative recordings from cell-attached patches in the absence (A) or presence (B) of 10 μm Zn²⁺ (in the pipette solution). In both cases, the pipette also contained 1 mm ACh. The closed state level is indicated by c; the open state level is indicated by o. Recordings were performed at −70 mV at room temperature.

FIGURE 8.

Single-channel properties of chimera H-2′^(RRR→QDA). A–C, histograms of distributions of open (left) and closed (right) times measured without or with Zn²⁺ as indicated in the panels. The conditions of single-channel recording are detailed in the legend to Fig. 7. The best fit decay constants are provided within the panels; these τ_O and τ_C values correspond to the mean open and mean closed times, respectively. Note that the long time exponential components τ_C2 (under −Zinc), τ_O2 (under +Zinc/Mode-1) and τ_O2 (under +Zinc/Mode-2) are 5.5, 9, and 6.5% of the contribution (fit span), respectively. D, event amplitude histograms for currents recorded in the absence of Zn²⁺ (left; N = 3 patches) or in the presence of Zn²⁺ (right; N = 4 patches). The event amplitude histograms were fitted with three Gaussian functions.

Gaussian fit of amplitude distribution measured in the absence of Zn²⁺ indicates a dominant conducting state with current amplitude of 2.8 pA (Fig. 8D, left). We did not observe any current fluctuations in a stepwise fashion between different levels (steps) of equal size, which indicates that only one channel was present in each patch. Under the same recording conditions but in the presence of Zn²⁺, two conducting states dominate as follows: one having a current amplitude of 2.9 pA and another has an amplitude of 1.0 pA (Fig. 8D, right). As mentioned above, many flickers in Mode-1 are unresolved due to our filtration conditions. Hence, the reduced amplitudes of these unresolved events were not taken into account in the analysis of amplitude distribution, which therefore includes only fully resolved events.

DISCUSSION

It is shown here that the nondesensitizing H-5′ and H-2′ pLGICs interconvert between two dominant conformations, a resting state and an active state (discussed under “Results”). In these pLGICs, the cytoplasmic side of the transmembrane channel domain was equipped with metal-binding sites organized around the ion permeation pathway as a ring that consists of five imidazole groups. As this five- imidazole ring is accessible to water in the pore, Zn²⁺ applied externally onto activated (opened) channels interacts with the ring and thus is capable of blocking the open pore of chimeras H-5′ and H-2′ (Figs. 4 and 5A and supplemental Fig. S3A and Fig. S2, A and B). Such a blockage (∼90% of the population) is not seen in chimeras that contain glycines instead of histidines (Fig. 5B and supplemental Fig. S3B and Fig. S2, C and D). It indicates that Zn²⁺ blocks the opened channels of chimeras H-5′ and H-2′ by interacting specifically with the inserted five-histidine ring.

Washing of ACh from open-blocked channels removes it completely from its binding sites and triggers receptor deactivation, regardless of the presence of zinc (Fig. 5 and supplemental Fig. S3). One may argue, however, that ACh could not readily be removed from open-blocked receptors when perfusing the oocyte with a Zn²⁺-containing solution; this is because stabilization of the channel in an open conformation by an open-pore blocker might “lock” the agonist in its binding pockets. If so, ACh could potentially remain bound to its binding pockets at the end of the application of the Zn²⁺-containing solution (Fig. 5A and supplemental Fig. S3A). However, we exclude this possibility because bound Zn²⁺ does not allosterically increase the binding affinity of chimeras H-5′ and H-2′ for ACh or nicotine (Fig. 2; Table 1). We thus conclude that the loss of current seen upon ACh reapplication after the first wash in Fig. 5A (and supplemental Fig. S3A) cannot reflect a channel subpopulation that is still blocked in the active (ACh-liganded) open state. This conclusion is strongly supported by the fact that Zn²⁺ could readily dissociate from open-blocked channels and be removed to allow for full recovery of the response upon ACh reapplication (Fig. 4). It is apparent that upon washing out both ACh and Zn²⁺ simultaneously, Zn²⁺ dissociates from the pore faster than ACh does from its binding sites, thereby allowing the channels to deactivate completely and to enter a reactivatable (resting) state. This conclusion well coincides with the findings that the microscopic ACh dissociation constant characterized for the active state of chimeras H-5′ and H-2′ (K_Da values of 9.4 and 4.4 μm, respectively; Table 2) is lower than the Zn²⁺ inhibition constant determined for the open state of these chimeras (K_i values of 30 and 80 μm, respectively) (21), i.e. the active open state has higher affinity for ACh than for Zn²⁺.

One may also argue that the macroscopic currents actually reflect a population of states through which the channel could transit, so spontaneously opened channels that become blocked by Zn²⁺ might contribute to the unrecovered subpopulation (i.e. to the reduced amplitude in Fig. 5A and supplemental Fig. S3A). We argue against the latter possibility because the inhibitory effect of Zn²⁺ on spontaneously opened channels completely disappears within less than 3 s of wash (e.g. Fig. 5A, current trace returns from point c to the base line). Because in these experiments Zn²⁺ was washed out of the application bath for at least 6 s before reactivation (by ACh), it is clear that the channel population did not contain Zn²⁺-blocked spontaneously opened channels at the time of ACh reapplication. It is also evident that channels having spontaneous activity do not become stabilized by trapped Zn²⁺, otherwise the leak currents would not have returned to the base line after 3 s of wash (Fig. 5A and supplemental Fig. S3A and Fig. S2, E and F). Furthermore, no progressive accumulation of spontaneously active channels in the open-blocked state or in any other potentially blocked state was observed when exposing H-5′ channels to Zn²⁺ for 3 min (21). Notably, the inability to reopen is specific to the five-histidine ring introduced at the intracellular side of the pore, because no loss of current was observed in similar experiments performed with the control Gly-containing chimeras (G-5′ and G-2′) (Fig. 5, B and C and supplemental Fig. S3B).

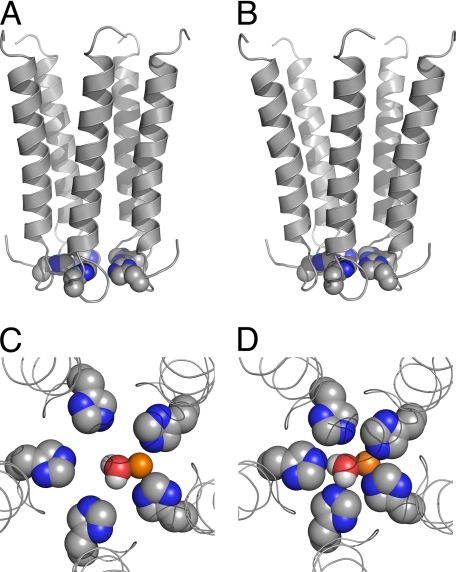
Because ACh could dissociate from opened Zn²⁺-blocked channels (as discussed above), washing of ACh away from active H-5′ or H-2′ channels prior to Zn²⁺ removal most likely triggered the process of receptor deactivation even when Zn²⁺ was still bound within the pore. As such, the currents that are missing upon reactivation with ACh (Fig. 5A and supplemental Fig. S3A) reasonably correspond to channels that could not reopen because of strong Zn²⁺ binding in a state reached during the process of deactivation. We infer that in these unrecovered channels, a Zn²⁺ ion interacts with the five-histidine ring on the way of the channel to close. Shutting the cytoplasmic side of the transmembrane pore on the Zn²⁺ ion would reasonably lead to Zn²⁺ ion trapping and stabilization of a nonconducting state. Such a process is feasible because of the following: (i) upon deactivation, the intracellular side of the pore-lining segments most likely moves toward the axis of ion permeation pathway to constrict the ring of five imidazoles, and (ii) the orientation of the histidines is preserved during the deactivation process. The constriction of the pore is illustrated in Fig. 9, A and B, and the effect of pore constriction on Zn²⁺ ion coordination within the pore is illustrated in Fig. 9, C and D. Zn²⁺ binding in the open active state probably involves electrostatic interactions with two adjacent histidines (Fig. 9C). Upon deactivation, the distances between the histidines and the axis of ion permeation pathway as well as between adjacent histidines get smaller; i.e. the histidines come together. The subsequent decrease in the diameter of the five-imidazole ring enables stronger Zn²⁺ ion coordination (Fig. 9D). Such a metal ion coordination is yet largely different from that seen in metallo-enzymes (61, 62) because of the channel pentagonal geometry, which allows a Zn²⁺ ion to directly interact only with two histidines concomitantly.

FIGURE 9.

Putative Zn²⁺ ion coordination within the ion channel pore. A and B, side views of the five pore-lining helices (M2s) of the putative active (A) and deactivated (B) channel conformations of chimera H-5′. C and D, top views of the putative activation/deactivation gate of chimera H-5′, which consists of five histidines organized around the axis of ion permeation pathway as a ring that accommodates a Zn²⁺ ion with an equatorially bound water molecule; shown are the putative active (C) and deactivated (D) gate conformations. Space-filling model of the histidines, Zn²⁺, and water are shown with the following colors: carbon, gray; nitrogen, blue; oxygen, red; hydrogen, white; Zn²⁺, orange. In the open pore model (C), the center-to-center distance between docked Zn²⁺ and the Nϵ atoms of the imidazole groups is 3.2 Å, whereas in the closed pore model (D) it is 2.3–2.4 Å. In both models the water oxygen is 2.3 Å away from the Zn²⁺ ion (center-to-center). Note that in water a Zn²⁺ ion is surrounded by a first hydration shell of six water molecules (87), so additional water molecules are probably bound to the Zn²⁺ ion above and below the shown plane. Notably, the models depicted here probably represent one of several possible different conformations that histidines may adopt, whereas Zn²⁺ itself can presumably induce changes in the histidine conformation.

The flickery behavior of the single channel seen under Mode-1 (Fig. 7B) is reminiscent of the flickers observed when the activity of a single muscle nAChR was measured, at <1-kHz filtration bandwidth, in the presence of the local anesthetic compounds QX-222 (63) or benzocaine (64). These compounds are well characterized open-channel blockers of nAChRs (60, 65, 66). Likewise, the flickers induced here by a low Zn²⁺ concentration (Mode-1) imply fast blocking events that coincide with the short mean closed time for Mode-1 (1.5 ms). Interestingly, the mean open times of Mode-1 (7.0 and 47 ms) are considerably longer than that observed in recordings without Zn²⁺ (2.9 ms). As stated under “Results,” these mean closed and open times of Mode-1 are probably overestimated. Yet, they indicate that at a low Zn²⁺ concentration, chimera H-2′^(RRR→QDA) fluctuates between the open (O) and open-blocked (OB) states (O ↔ OB), and Zn²⁺ interferes with channel closing. Because the channel continues to conduct between fast blocking events, we argue that the low Zn²⁺ concentration (one-tenth of Zn²⁺-K_i of chimera H-2′) prolongs the lifetime of the open state. Such prolongation of open times by an open-channel blocker (tetraethylammonium) was also observed in ATP-sensitive potassium channels (67). In line with this conclusion, the single-channel open probability in Mode-1 is very high (P_o ≈0.96) compared with Mode-2 and recordings without Zn²⁺ (P_o ≈0.42 and P_o ≈0.3, respectively). Note that the high P_o of Mode-1 is somewhat overestimated due to many fast blocking events that were filtered out by our recording conditions. Taken together, Mode-1 behavior corroborates previous inferences that were made on the basis of macroscopic current measurements (21), i.e. a large population of H-2′ channels could be shifted from a nonconducting OB state to long lasting O ↔ OB fluctuations accompanied with high conductance. This process was reflected by large macroscopic tail currents seen when the external Zn²⁺ concentration was rapidly reduced under very negative membrane potentials that increased the driving force for Zn²⁺ ion movement toward the five-histidine ring (21).

The mean closed time of Mode-2 (3.1 ms) is shorter than that measured without Zn²⁺ (5 ms), indicating that the channel openings in Mode-2 are interrupted by fully resolved slow blocking events that render the channel nonconducting. The time constants τ_C of Mode-1 and Mode-2 correspond to the average residence time for Zn²⁺ in the pore, and it is longer during Mode-2. Hence, in analogy to the macroscopic currents, we suggest that Mode-2 reflects the process of Zn²⁺ ion trapping upon deactivation. Yet, it appears that the co-presence of a very low Zn²⁺ concentration together with high ACh concentration in the single-channel recording pipette prevented the channel from entering into a sustained nonconducting blocked state.

The induction of a subconducting state by Zn²⁺ (Fig. 8D, right) implies that Zn²⁺ not only blocks the “fully” opened channel but also allows the channel to assume an open-blocked state having a smaller pore diameter. Relief of the latter state from the block probably causes the appearance of a subconductance. Taken together with the analysis of time distributions, we infer that Zn²⁺ acts as a “foot in the door” that does not let the single channel enter a completely deactivated-closed conformation and delays the eventual closing of the gate. This Zn²⁺-stabilized partially open/partially closed conformation might be analogous to the pre-open state recently shown to occur in the muscle nAChR (68, 69).

Notably, the results presented here are in full agreement with earlier studies of Karlin and co-workers (19, 20, 33) who showed that the activation gate of the muscle nAChR is located at the cytoplasmic side of the channel pore. Our current results also corroborate the previous conclusions of Paas et al. (21) regarding the location of the activation gate in the chimeric ACh-serotonin receptor, although one may still argue that the histidines created a second gate additionally to the native gate whose activity is masked by Zn²⁺ blockage. We exclude this possibility because the inserted histidines were accessed by external Zn²⁺ ions even before activation (21), indicating that in the resting state of our chimeras there is no interference for Zn²⁺ ion movement all the way to the bottom of the pore. It is also not likely that there is a gate below the five-histidine ring because the sequence upstream to position −5′ is located farther away from the ion permeation pathway, as it needs to connect to M1 (Fig. 1B). On the other hand, the substituting histidines most likely created a gate instead of the native gate, nearly at the same place. Reasonable candidates for creating a native gate at the bottom of the pore of the donor receptor (5HT_3AR) are five glutamates at positions −1′, whose side chains are organized as a ring around the axis of ion permeation pathway (70). Note that in our chimeras, glycine residues replace these glutamates (Fig. 1C). Because the van der Waals volumes of Glu and His are quite close (109 versus 118 ų, respectively) (71), it seems that there is sufficient space at the bottom of the pore of the chimeras to accommodate a ring of five histidines without altering the orientation of the M2 helices significantly, if at all.

Recently, the x-ray crystal structures of two different pLGICs from distantly related prokaryotes were determined at atomic resolution. The first, ELIC (from Erwinia chrysanthemi, a Gram-negative bacillus belonging to the family Enterobacteriaceae), displays a closed pore conformation in the crystal (30). The second, GLIC (from the cyanobacterium Gloeobacter violaceus), displays a potentially open pore conformation in the crystal (31, 32). It appears that the funnel-like structure of GLIC is reminiscent of the open pore shape previously suggested for eukaryotic pLGICs based on functional studies (19, 21–23, 33, 72). Superimposition of the crystal structures of ELIC and GLIC suggests that rigid-body tilting of the pore-lining helices gate the channel (31, 32), in accordance with previous inference based on functional studies done with a eukaryotic pLGIC (21). However, the crystal structure of ELIC shows that the upper (extracellular) side of the channel pore is too narrow to allow ions to pass, and the bottom (intracellular) side of the pore is much wider (30). Based on the assumption that ELIC and GLIC share a similar gating mechanism, it was inferred that closing of these prokaryotic pLGICs is accompanied by widening of the intracellular side of the pore (see supplemental movies in Hilf and Dutzler (31)). Conversely, agonist dissociation, which triggers the deactivation process in the eukaryotic pLGICs explored here, is accompanied with narrowing of the intracellular side of the pore. It should be emphasized that the affinity of the constricted state of the chimeras studied here for Zn²⁺ is not less than the affinity of their open state for Zn²⁺. This finding supports our plausible inference that the diameter of the five-histidine ring does not increase upon closing of chimeras H-5′ and H-2′, unlike an ELIC-like closing that should have increased the diameter of the five-histidine ring and weakened the interactions with Zn²⁺. One may argue, however, that if Zn²⁺ ions flow into the cell, a high concentration of Zn²⁺ would remain in the vicinity of the five-histidine ring upon an ELIC-like pore closing. In such a case, upon re-activation, a GLIC-like opening might result in trapping of Zn²⁺ and inability of the channel to conduct. We exclude these possibilities in the case of our eukaryotic chimeras because an increase in the intracellular Zn²⁺ concentrations during the single-channel recordings should have gradually increased the portion of Mode-2 over Mode-1 and prolonged the nonconducting periods. The single-channel recordings show that such processes did not occur. Moreover, if Zn²⁺ ions were flowing into the cell, the channel population in Fig. 4 would not have recovered entirely because of Zn²⁺ acting from the cytoplasm. This did not happen (Fig. 4) even at very negative membrane potentials that increase the driving force for Zn²⁺ inflow (21).

Two possible explanations may account for the difference between the eukaryotic and prokaryotic pLGICs. According to the first possibility, the crystallization conditions may have forced ELIC into a desensitized-like low energy conformation, so the constricted ring of five phenylalanines that line the extracellular end of the ELIC pore may actually corresponds to a desensitization gate rather than an activation/deactivation gate. This possibility coincides with Wilson and Karlin (20) who localized a desensitization gate topologically above the activation gate in the muscle nAChR, and with Purohit and Grosman (73) who suggested that the activation and desensitization gates are distinct entities. According to the second possibility, both the location of the activation/deactivation gate and the direction of the tilting motions that open and close this gate in eukaryotic pLGICs may be different from those of ELIC and GLIC. Various functional and affinity-labeling studies support this possibility. When applied externally at low concentrations in functional (electrophysiological) experiments, the local anesthetic tetracaine acts as a noncompetitive antagonist by blocking the pore of both the open and resting states of muscle-type (74) and neuronal (75) nAChRs. In the absence of an agonist, tetracaine binds to the muscle-type Torpedo nAChR with 100-fold higher affinity than in the presence of an agonist, i.e. tetracaine preferentially binds to the resting state of the Torpedo receptor (76). The high-affinity binding site for tetracaine in the resting Torpedo nAChR was identified by photoaffinity labeling experiments, which were performed in the absence of an agonist using either [³H]tetracaine (77) or unlabeled tetracaine to inhibit the photoincorporation of other pore blockers, analogs of 3-trifluoromethyl-3-(m-¹²⁵I-iodophenyl)diazirine (78). It was found that residues located at positions 13′, 9′, and 5′ in various pore-lining segments of the Torpedo nAChR contribute to a specific site for tetracaine. These positions in the Torpedo nAChR are respectively located two, three, and four helical turns below position 20′ (Protein Data Bank code 1OED) (18). Position 20′ appears to be at the same topological level of the ring of five phenylalanines that was implied to constrict and close the ELIC pore (see sequence alignment in supplemental Fig. S1a of Ref. 30 and Protein Data Bank code 2VL0). It thus appears that to block the pore of resting nAChRs, externally applied tetracaine should pass through position 20′ of the pore. This excludes the presence of an ELIC-like steric hindrance in the resting conformation of the aforementioned eukaryotic nAChRs.

Notably, differences in gating motions of pore-lining helices exist in potassium channels, despite the high tertiary and quaternary structural conservation of their pore domain. Crystal structures of two bacterial potassium channels, KcsA (in a closed conformation) (79) and MthK (in an open conformation) (80), imply that channel opening involves a hinge bending motion at a conserved glycine in the middle of the inner pore helices (81). In contrast, in eukaryotic Shaker family Kv channels, both functional studies and x-ray crystallography suggest that opening involves bending of the inner pore helices at a proline motif (Pro-Xaa-Pro) that is not found in bacterial K⁺ channels and is located closer to the intracellular side of the inner pore helices (82–84). These differences lead to variations in the open pore diameter, which is narrower in the Shaker Kv1.2 channel.

As to the gating mechanism of prokaryotic pLGICs, this still has to be functionally probed to ascertain the relevance of the structural states seen in detergent (and crystallization substances) to function of the receptors in the membrane.

In conclusion, here we have provided functional evidence that agonist dissociation, which triggers the receptor transition from the active open conformation to the resting closed conformation, causes the intracellular end of the pore-lining segments of an ACh-serotonin receptor chimera (a eukaryotic pLGIC) to move toward the 5-fold axis of symmetry so as to constrict the pore at its cytoplasmic side. We infer that such a constriction motion ultimately results in deactivation and obstruction of the ion permeation pathway.