Was Wright Right? The Canonical Genetic Code is an Empirical Example of an Adaptive Peak in Nature; Deviant Genetic Codes Evolved Using Adaptive Bridges

Abstract

The canonical genetic code is on a sub-optimal adaptive peak with respect to its ability to minimize errors, and is close to, but not quite, optimal. This is demonstrated by the near-total adjacency of synonymous codons, the similarity of adjacent codons, and comparisons of frequency of amino acid usage with number of codons in the code for each amino acid. As a rare empirical example of an adaptive peak in nature, it shows adaptive peaks are real, not merely theoretical. The evolution of deviant genetic codes illustrates how populations move from a lower to a higher adaptive peak. This is done by the use of “adaptive bridges,” neutral pathways that cross over maladaptive valleys by virtue of masking of the phenotypic expression of some maladaptive aspects in the genotype. This appears to be the general mechanism by which populations travel from one adaptive peak to another. There are multiple routes a population can follow to cross from one adaptive peak to another. These routes vary in the probability that they will be used, and this probability is determined by the number and nature of the mutations that happen along each of the routes. A modification of the depiction of adaptive landscapes showing genetic distances and probabilities of travel along their multiple possible routes would throw light on this important concept.

The Canonical Genetic Code was Selected for Minimizing the Effects of Point Mutations and Translational Errors

The five main points of this article are: the canonical genetic code is a rare empirical example of an adaptive peak in nature; the alternate genetic codes in mitochondria, chloroplasts, and certain organisms are all on adaptive peaks, and evolved from the canonical code by the mechanism of crossing adaptive bridges from one adaptive peak to another; the evolution of these alternate codes represents an empirical example in nature of the crossing from one adaptive peak to another by adaptive bridges, which are similar, but not identical, to neutral networks; adaptive bridges represent a general mechanism by which populations cross over maladaptive valleys from one adaptive peak to another; and the adaptive landscape needs modification to reflect the multiple routes, which vary in length and probability of being taken, by which peaks shifts occur. However, to demonstrate that the standard and alternate codes are on adaptive peaks, one must first demonstrate what selection maximized in the evolution of the code. Otherwise, it will be impossible to test the hypothesis that the genetic code is on an adaptive peak.

The error minimization hypothesis postulates that the canonical genetic code evolved as a result of selection to minimize the phenotypic effects of point mutations and errors in translation. There is a great deal of convincing evidence to support this hypothesis. Arguments supporting it date back to Sonneborn (1965) and Zuckerkandl and Pauling (1965), both of whom argue that the adjacent nature of synonymous codons within the code is an adaptation against point mutations having negative phenotypic effects. Synonymous codons are almost always fully adjacent to each other, differing by but one base, usually the third one. The only exceptions are the six serine and three stop codons. Most codons in both these families are fully adjacent to each other, while a minority is close to being so.

However, these arguments fail to take into account that it is likely that the code in its early evolution had few or even a minimal number of tRNAs that decoded multiple codons through wobble pairing, with more amino acids and tRNAs being added as the code evolved. The code could thus have evolved from very high degeneracy to the degree of degeneracy that it has today. This would cause synonymous codons to occur one point mutation from each other, without invoking error minimization.

Because of this counter-argument, the argument for an adaptive code based on error minimization has shifted to whether adjacent, non-synonymous codons specify chemically similar amino acids; this would support the error minimization hypothesis. Authors supporting this argument include Alff-Steinberger (1969), Epstein (1966), Goldberg and Wittes (1966), Woese (1965, 1973), Woese et al. (1966), and Haig and Hurst (1991), whose findings illustrate the idea. Haig and Hurst found that among 10,000 randomly generated codes, only two were more conservative than the standard code as regards polarity distances between amino acids. Freeland and Hurst (1998a) extended this work to show that the perceived efficiency of the standard code increases when the method of quantification is adjusted to include recognized biases in both mutation and mistranslation, indicating that the code was selected for error minimization, even if error biases are taken into account. Trinquier and Sanejouand (1998) proposed simple procedures to quantify how much an effective property embodied in a given ranking of the 20 amino acids can be affected by random point mutations at nucleotide bases. Of the various orderings tested, rankings based on most hydrophobicity scales showed low scores, thus offering better immunity toward such single-base mutations. Freeland et al. (2000a) showed convincingly that the standard code is very close to optimal with respect to minimizing the phenotypic effects of point mutations and translational errors, when other objections to the error minimization hypothesis are taken into account, including the consideration of a multitude of properties of amino acids, not just polarity. Yarus et al. (2005) presented convincing evidence suggesting the code’s stereochemical basis is consistent error minimization. Torabi et al. (2007) found support for error minimization in that aminoacyl-tRNA synthetases are optimized for distinguishing the correct amino acid and selection pressure for translational fidelity is responsible for the occurrence of 20 coding amino acids. Najafabadi et al. (2007) found that the codons of highly expressed genes are selected such that mistranslation would have the minimum effect on protein structure and function. For a good summary of much of the evidence favoring the error minimization hypothesis, see Freeland and Hurst (2004), and references therein.

Some authors have alternative interpretations or have found evidence supporting alternative hypotheses to this, and fairness dictates the following brief sampling of these interpretations and studies. It has been suggested that the pattern of adjacent codons coding for chemically similar amino acids could be accounted for by the alternative hypothesis that it is a historical artifact (Pelc and Welton, 1966; Dillon 1973; Wong 1988; Wong and Bronskill 1979; Taylor and Coates 1989). Such arguments typically posit that the code increased the number of amino acids it coded for by splitting existing synonymous codon blocks into subsets coding for the original amino acid and another one, which would be chemically related to it (Hartman 1975; Wong 1980; Wong and Bronskill 1979; Szathmary 1993; Bashford et al. 1998). Di Giulio and Medugno (2000) found the statistical foundations on which the co-evolution theory of the code are based, are robust. Szathmary (1999) suggested the code might have preceded the existence of translation, and that a stereochemical relationship between some amino acids and cognate anticodons/codons is likely to have been important in the earliest codon assignments. Knight and Landweber (1998) provided evidence that the origin of the code involved an intrinsic affinity between any given amino acid and its codon(s). Judson and Haydon (1999) constructed a genetic algorithm from which they concluded that the genetic code is far from minimized with respect to mutational effects or translational errors. Knight et al. (1999) revisited arguments that the current code is either somehow optimal, reflects the expansion of a more primitive code to include more amino acids, or is a consequence of direct chemical interactions between RNA and amino acids. They argued that such models can be reconciled by an evolutionary model whereby the code was optimized through codon reassignment. Alternatively, all three forces might have acted in concert to assign the 20 “natural” amino acids to their present position in the code.

However, in spite of the above arguments, the bulk of the evidence with respect to similar codons coding for similar amino acids favors error minimization. The evidence presented in the previous paragraph, e.g., is not as convincing as that of Freeland and Hurst (1998b), who showed clearly that historical features do not account for the error minimization properties of the natural code, but that these properties are indeed due to selection. Moreover, Di Giulio’s (2000) arguments against optimization for error minimization as tested by similar polarities of amino acids are convincingly refuted by Freeland et al. (2000a, b).

The Canonical Genetic Code is Almost, But Not Quite, Optimal With Respect To Error Minimization

The fact that synonymous codons tend to be adjacent to each other, with a tendency to differ by only the third base, and that this supports the error minimization hypothesis, has been mentioned above. I also pointed out that there are three exceptions to this rule. Two of the six serine codons differ from the other four at two bases (the first two), and one stop codon (UGA) differs from another stop codon (UAG) by two bases (the last two) and differs from UAA at the second base. This shows clearly that the genetic code is not optimal with respect to error minimization, although it is very close.

Another form of evidence for error minimization is the correlation between the number of codons for a given amino acid in the genetic code and the frequency that the amino acid is used in proteins throughout the various taxa of organisms. This is a correlation that one would expect if the code evolved for error minimization, as I will illustrate with a hypothetical example. Consider a hypothetical genetic code with one stop codon, 99 codons that code for arginine, one that specifies serine, and no other codons. Then any point mutation in a serine codon will have a phenotypic effect, while the vast majority of the point mutations in the arginine codons will have no effect on the phenotype. If a species with such a code used serine 99% of the time in its proteins, and arginine only 1%, any given point mutation or translational error would have a very high probability of expressing itself in the phenotype. Since most mutations and errors in translation are deleterious, this species would have a low probability of persisting for any length of time. Such a code would be very poorly adapted for minimizing the effects of errors in the organism. Conversely, a perfect correlation between the frequency of usage of each amino acid in proteins by an organism and the number of codons coding for it in the genetic code would be the case in a code optimally adapted for error minimization. Jukes et al. (1975) summarized the composition of 68 completely sequenced proteins containing 12,170 amino acid residues. The compilation included 47 eukaryotic, 17 prokaryotic, and 4 virus proteins. Only one representative of each family of proteins, such as the globins, was included. Although the overall correlation of frequency of any given amino acid’s usage in proteins with the number of codons that code for it in the code is high enough to support the error minimization hypothesis in a general way, statistical analysis by the authors forced them to reject the null hypothesis that the distribution of frequency of any given amino acid’s usage does not deviate from that expected from its proportion of codons in the genetic code. For example, lysine and alanine are present at levels significantly higher than expected, given the genetic code, while arginine, histidine, cysteine, proline, serine, and leucine, are at levels significantly lower. There are less basic amino acids than expected from the number of codons. This keeps the pH at about 7, so charge neutrality is selected for in spite of codon numbers to the contrary. Thus, this study of Jukes et al. shows strong evidence that the genetic code was selected for error minimization, but is not optimal for it.

Antezana and Jordan (2008) showed that, in vertebrates, nucleotides adjacent to and just up-stream or down-stream from dinucleotides or trinucleotides affect which mutations occur, thus causing a mutation bias. This could be one mechanism, though not necessarily the only one, by which the correlation between codon frequency and usage was decreased, and hence the genetic code became sub-optimal, at least in vertebrates. Further research is needed to determine if this would apply to other taxa than vertebrates. It is interesting that this mechanism does not involve natural selection, but mutation bias, in causing the code to become sup-optimal in vertebrates.

Now let us address the question of whether the standard genetic code has the optimal number of stop codons. By the same argument as above, the optimal number of termination codons would be roughly the total number of codons in the code (64) divided by the average number of amino acids in a protein. If the average protein were 64 or more amino acids long, the optimal number of termination codons would be one, since it is necessary to have at least one stop codon. Though the range in protein length is considerable, from 50 or less to over 1,000 amino acids, the average protein is about 500 amino acids in length, and this applies to everything from mitochondria to bacteria to vertebrates (Rine J, 2000, Personal communication). Thus, the optimal genetic code has no more than one termination codon. Hence, with respect to the number of termination codons, the standard genetic code is not optimal with respect to error minimization, having two termination codons more than the optimum.

In summary, the canonical genetic code has near, but not quite, one hundred percent adjacency of synonymous codons; more importantly, adjacent, non-synonymous codons are chemically similar; and the number of codons per amino acid and frequency of use of the same amino acid are correlated, but with a correlation coefficient less than one. All this indicates the code was selected for minimization of phenotypic effects of point mutations and translational errors, and that the code is well adapted, but not optimal, for this.

The Canonical Genetic Code is on an Adaptive Peak

Crick (1968) proposed the frozen-accident theory of the genetic code, which states that once organisms reached a threshold of genome size and complexity, the genetic code could not change, because any change in the code would then result in a new amino acid at every site coded by the codon with the new meaning. Of course, this would be lethal, or at least strongly selected against. It is an “accident” because it became frozen before reaching optimality, and thus the allocation of specific codons to specific amino acids resulted partly from chance. I would add that the code seems to have come close to being optimal at minimizing the effects of point mutations and errors in translation. However, it did not make it to optimality at these functions before the organisms had increased the sizes of their genomes too much to allow further change in the code.

Thus, the canonical genetic code is at a local optimum that is not at the global optimum. This is equivalent to saying the standard genetic code is on an adaptive peak, and this is precisely the case. Sewell Wright (1932) originated the concept that a population occupies a point on an adaptive landscape of allele frequencies and fitnesses. This may be represented as a multidimensional graph of the entire field of the possible gene combinations of a population, graded one gene combination at a time, plotted against adaptive value (reproductive fitness) under a specified set of conditions, so that each point on the surface is the fitness of a particular genotype. Wright estimated a population might have a thousand or more dimensions in its field of gene combinations. Wright thought that there would be a huge number of peaks, perhaps 10⁸⁰⁰, of varying height. Thus, as average fitness increases, the population will come to rest on the nearest adaptive peak, from which it is difficult to move to a higher peak, if one exists, because selection acts only to increase fitness. Wright pointed out that the population cannot move from a lower to a higher peak by selection alone, because this would require moving downhill (in a direction of lower fitness), since all areas around a peak are below it. Adaptive landscapes are considered one of the most important metaphors for evolution, and for over 60 years the majority of evolutionary biologists have considered Wright’s (1932) diagrams of them to be the most heuristically valuable diagrams in all of evolutionary biology. However, it is important to bear in mind that authors disagree on the value of the adaptive landscape concept, since the theses presented in this article depend on its validity. Kaplan (2008) finds the concept confusing, incoherent, and inadequate to the point where it is misguided to attempt to reform the metaphor. He thinks it is time to give up the pictorial metaphor entirely in favor of formal models. McGhee (2007) finds the concept very important in understanding evolution, allowing one to take a spatial approach to the concepts of natural selection, evolutionary constraint, and evolutionary development. Provine (1986) thinks that evolutionary biologists have generally overestimated its heuristic value. Most importantly, empirical examples of adaptive peaks in nature are rare. And generally, the data from nature are chosen so that two loci, each with two alleles, are under consideration, requiring two gene frequencies to construct a three-dimensional surface (Provine 1986). This generates adaptive landscapes, but not necessarily adaptive peaks. Lewontin and White (1960) provided the most famous example of this taken from a natural population, in their study of the grasshopper, Moraba scurra. They concluded all ten populations that they tested were on saddle points, not adaptive peaks. But, using different assumptions, Allard and Wehrahn (1964) and Wright (1978) himself found the populations examined by Lewontin and White to be all on adaptive peaks, and Turner (1972) found them to be about equally on peaks and saddle points. Hence, the fitness surface depends on the way that the mean fitness is calculated from the set of gene frequencies, so empirical cases of adaptive peaks in nature that have clearly been demonstrated in an unambiguous way, not open to an alternative interpretation, are rare if they exist at all.

Since the genetic code is very effective at maximizing the probability that point mutations or translational errors will have little to no phenotypic effect, it is a very good, adaptive code; since it is not the best possible code for these functions, it is slightly sub-optimal. Any change in the code would be highly deleterious if not lethal, even to the simplest autonomous extant organisms (not viruses or cellular organelles, but eubacteria and archaebacteria), even those with the smallest genome size, because every amino acid coded by the changed codon would be different than the one originally coded for. So the canonical code, being sub-optimal and selectively highly resistant to change, is on an adaptive peak, and it is extremely difficult for it to move to a higher adaptive peak, i.e., to a better code at minimizing the effects of point mutations and translational errors. The fact that the genetic code is a clear, unambiguous empirical example of an adaptive peak in nature is profound in itself, because of the rarity and importance of examples of adaptive peaks in nature. Equally important is the fact that this example is of something as fundamental as the genetic code, the “alphabet” of life. The fact that something as fundamental as the genetic code is on an adaptive peak indicates that it could be fruitful to look for more empirical examples of such peaks in nature, and that they may be more common than thought to be.

This also raises another important point. Molecular biologists have been very familiar with Crick’s idea and terminology of the code being a frozen accident for a long time. However, Wright’s idea of adaptive landscapes is an idea they tend to be unfamiliar with; at least, it is not have in forefront of their minds. Evolutionary and population biologists, on the other hand, are very familiar with adaptive landscapes, but are not focused on the fact that the genetic code is stuck on a local, adaptive, but sub-optimal point with respect to this function. It is the combining of these two ideas that gives the important insight that the genetic code is a rare empirical example of a sub-optimal adaptive peak in nature. This argues strongly for more communication and cross-fertilization between disparate fields of science, in particular between evolutionary/ecology/population biology and molecular biology. Researchers in different levels of biological research, from the molecular to the population level, need to communicate more.

Deviant Mitochondrial Genetic Codes Demonstrate the Mechanism of Crossing from One Adaptive Peak to Another: By Redundancy and Building Adaptive Bridges That Connect Adaptive Peaks

The genetic code is not universal; mitochondria and chloroplasts of various taxa, and certain unicellular taxa, have codes different from the standard code. All the alternate codes differ only in minor ways from the standard code; only a few of their codons have different meanings than the canonical code. Thus, all the alternate genetic codes appear to have ultimately evolved from the standard nuclear code. Knight et al. (2001a) convincingly argued that this is the case.

Changing the standard code to any of the deviant codes in mitochondria, chloroplasts, and the organisms with alternate codes has the same problem of disruption of the genetic system discussed above that occurs when any sufficiently complex genetic code is changed, so the changes from the standard code to these deviant codes all required the crossing of or over a maladaptive valley from one adaptive peak to another. This is significant, because there are very few empirical examples of crossing from one adaptive peak to another in nature. Here, we have a handful of examples of such crossings represented by each of the alternate codes, each having the standard code as the original adaptive peak that it crossed from, and the current alternate code as the peak it is now on. Although this is significant in its own right, it has further importance in that it allows us to study the mechanism of these code changes in the hopes of discovering the general mechanism by which populations move from one adaptive peak to another in the natural world.

Mayr (1963), then Eldredge and Gould (1972) proposed a mechanism by which a valley is crossed from one adaptive peak to another, arguing that co-adapted gene pools resist genetic change, and that a shift from one adaptive peak to another is facilitated by the destabilizing effect of small population size. This is the founder effect. Random factors play a greater role in small populations, allowing the crossing of a valley of lower fitness, if the less fit members of a population are favored by chance for a sufficient time period. However, these arguments have been strongly and effectively opposed by Lande (1980) and Barton and Charlesworth (1984), who pointed out that the founder effect is usually ineffective in shifting populations to new adaptive peaks. More recently, Gavrilets (2003) has shown that the classical hypotheses of speciation by peak shifts across maladaptive valleys driven by random genetic drift run into trouble, even showing the specific kind of trouble they run into. These arguments for peak shift by genetic drift are weak in that they rely on chance to cause the less fit to prevail, and hence for the population to go against the grain of natural selection, when it is descending from the original adaptive peak into the valley of lower fitness. Also, relying on small populations to cross from one adaptive peak to another is tenuous, because the smaller the population, the higher its probability of extinction from environmental challenges.

To understand the general mechanism by which a population gets from one adaptive peak to another, one must understand the mechanism by which the standard genetic code gave rise to the novel ones. This will answer the question of whether the novel codes evolved by going down into maladaptive valleys by drift and founder effects, and back up again by selection. Then it will be possible to consider how general this conclusion is.

A number of workers—see, e.g., Schuster et al. (1994), Reidys et al. (1997), Gavrilets (1997), and Reidys et al. (2001), and references in all these papers—have modeled secondary structures of RNA molecules, and shown that populations can move between several adaptively equivalent structures or even from less fit to more fit folding of the RNA via what they term neutral networks. These are routes on the adaptive landscape that are adaptively neutral, and often appear as ridges around “holes”, which are valleys of lower fitness in three (or more) dimensions. Schultes and Bartel (2000) have taken this beyond modeling and shown empirical evidence for these neutral networks, artificially making a computer-designed intermediate form of an enzyme and linking it via adaptively neutral, artificial mutations to both a natural ligase and a natural cleavage enzyme. All these were RNA ribozymes. Every mutated form between the ligase and the artificial intermediate ribozyme had ligase function, and every mutated form between the intermediate ribozyme and the cleavage ribozyme had cleavage function. So they showed a neutral, functional pathway from a natural ligase ribozyme to a natural cleavage ribozyme—a real-world neutral network. This mechanism of travel along an adaptive landscape does not necessarily lead to crossing from one peak to another, although it could. Is there a way to do this with certainty? Is the only type of neutral path along adaptive landscapes found in secondary folding of RNA molecules, since no other is in known at this point? There are actually ways to cross over maladaptive valleys from one adaptive peak to another, and I will now present three novel ways of doing so, all quite distinct from moving between adaptively equivalent secondary RNA structures.

Osawa and Jukes (1988) and Osawa et al. (1992) proposed and argued for a mechanism by which mitochondria evolved novel genetic codes, called the “codon disappearance theory.” In this theory, the first step is the complete disappearance of a codon, which is necessary to avoid a great many deleterious to lethal amino acid substitutions after codon reassignment when the new code manifests. Thus, every codon in the genome must be replaced by a synonymous codon, or mutated to another codon. They posit that this occurs by either genetic drift, or mutation pressure, which either increases GC or AT content of the genome. Then the tRNA(s) that read this codon disappear. Next, another tRNA’s anticodon mutates to become complimentary to the lost codon. This could be, e.g., a duplicated and hence dispensable tRNA for another amino acid. The final step is the reappearance of the codon, now specifying the new amino acid. The authors believed that no codon could have two meanings simultaneously, so considered the disappearance of the codon a necessary intermediate step. This mechanism of changing the code via elimination of a codon can occur only in a very small genome, a genome sufficiently small to have few enough copies of a given codon that every one of them can be eliminated or cease to be used with a realistically high probability. Mitochondria and chloroplasts have sufficiently small genomes. The prokaryotes and unicellular eukaryotes in which changes in the code occurred may possibly have had small enough genomes at the times their codes changed, especially if they had a bias against the use of certain codons. When the codon reappears, it does so one triplet at a time, so that the phenotypic change is slow, and not lethal or unduly disruptive to the organism.

The key point is that the genetic code is changed with only a gradual set of changes in the amino acid sequence in the proteins, changes that do not tend to be lethal or disruptive to the organism, even though the changes in the DNA may be greater and faster. Hence, the change in the genetic code occurs with little to no phenotypic effect. Therefore, the code change is not likely to be lethal or even necessarily maladaptive to the organism. Another key point in this mechanism of code change is that such a change is possible because of the degeneracy of the code, which means the redundancy of the code can cover for lost codons. When a codon disappears, it is converted to a synonymous codon, so that no change in protein sequence or maladaptive disruption occurs, even though there is a change in DNA sequence. The key to the prevention of both disruption and change in the amino acid sequence in the proteins is redundancy. See Maynard Smith and Szathmary (1995) for another description of this process of how the genetic code can change without disrupting the organism through amino acid substitutions.

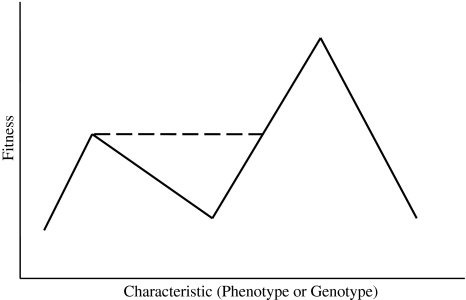
From the above discussion of the mechanism of genetic code alteration, one can conclude that a population does not cross a valley of lower fitness from a lower to a higher adaptive peak by relying on random factors or temporary lucky victories of less fit genetic sequences (or phenotypes) due to small population size. New codes do not evolve by founder effects. Rather, on a graph of the adaptive landscape, the population moves over the maladaptive valley in a line parallel to the x-axis, from the lower adaptive peak that it is originally on, to a point at the same height as this lower peak on the slope of the “mountain” leading to the higher peak, and from there up the slope to the higher peak, as shown in Fig. 1. I will now coin a new term: I will call this straight-line movement over the maladaptive valley an “adaptive bridge”. Bear in mind that Fig. 1 shows only a two-dimensional slice of a multi-dimensional surface. Another way to look at this mechanism is that the Wrightian adaptive landscape, being multidimensional, has many possible routes through these dimensions to new peaks. These possible routes change with changes in the genetic composition of the population, or with changes in the environment. A very small number of mutations in theory can change the adaptive landscape and the routes available to the new peak. In the case of mitochondrial codes, the fact that the process starts with the loss of a codon and its replacement with a synonymous codon means a route that does not require going downhill can be taken. The mechanism of changing a codon’s meaning by eliminating it for a period of time and using redundancy changes the adaptive landscape. This mechanism of temporarily eliminating a codon allows the building of an adaptive bridge, while a mechanism that suddenly requires a multitude of amino acid substitutions associated with the new codon would not, would require descent into the valley, and would likely be lethal. The idea of the use adaptive bridges to cross from one peak to another is further supported by the work of Gavrilets (2003), who argues that speciation can be understood as the divergence along nearly neutral networks, and what he calls holey adaptive landscapes, accompanied by the accumulation of reproductive isolation as a by-product. The nearly neutral networks are similar to adaptive bridges in that there is no descent into and ascent out of a maladaptive valley, for both have the population moving on a neutral path over maladaptive valleys.

Fig. 1.

How a population crosses from a lower to a higher adaptive peak, over a valley of lower fitness, changing the adaptive landscape with an adaptive bridge. The dashed line indicates that the adaptive bridge is a less direct route in that in it requires more genetic changes in order for the population to take it. Although this is a two-dimensional graph, the adaptive landscape may be visualized as multi-dimensional. This very general graph can represent any adaptive landscape, which could include genetic codes or any other phenotypic or genotypic traits (see text for further explanation)

Schultz and Yarus (1994) proposed an alternative mechanism for code change in which a translationally intermediate, equivocal tRNA appears that can translate the original codon and the novel one, which means there would also be an ambiguous mRNA that can be read by two tRNAs. This mechanism, called the “ambiguous intermediate theory,” does not involve the disappearance of a codon, or take advantage of redundancy as a result of the degeneracy of the code. The cognate tRNA loses function through mutation. Additionally, the near-cognate tRNA mutates to improve its reading of the codon to be reassigned. There is selection to make the novel, near-cognate tRNA more and more functional, and to gradually eliminate the original, cognate tRNA. The idea can involve wobble on the first base of the codon as well as the third.

The codon disappearance theory explains some mitochondrial genetic code changes, and unassignment of the CGG and AGA/AUA codons in Mycoplasma capricolum and Micrococcus luteus (Ohama et al. 1990; Oba et al. 1991). The ambiguous intermediate theory explains some code changes in mitochondria, bacteria, and eucaryotes, e.g., the decoding of leucine CUN (where N is any nucleotide) codons as threonine in yeast mitochondria, and of leucine CUG codons as serine in various Candida species (Schultz and Yarus 1994; Massey et al. 2003; Miranda et al. 2006).

Does the ambiguous intermediate theory use adaptive bridges, or does it require descending into a maladaptive valley and ascent back up to the next adaptive peak? It would appear that the latter is the case at first glance. However, it turns out the empirical evidence favors the adaptive bridge model.

First, the progressive transition from cognate to near-cognate tRNA allows time for the subset of sites on the proteins that are damaged by the novel amino acid to mutate. Also, simultaneous assignment of two amino acids to a single codon is less damaging to the cell than once thought, and cells tolerate a surprisingly large amount of amino acid substitutions. At least half of the total amino acid substitutions yield functional proteins (Zabin et al. 1991; Huang et al. 1992). Even substitutions involving different amino acid types that are especially unstable and that one would expect to be deleterious, such as charged amino acids in a hydrophobic core, are sometimes tolerated (Hellinga et al. 1992). Silva et al. (2004) showed that the accumulation of aberrant proteins during code transitions in yeast triggered expression of stress proteins—namely, the molecular chaperones Hsp40 and Hsp70—that protect ambiguous cells on exposure to severe stress, even giving them a selective advantage under conditions of extreme environmental stress. Next, amazingly, Silva et al. (2007) showed that up-regulation of proteasome activity, induction of stress proteins, cell wall remodeling, and accumulation of trehalose and glycogen contributed to the elimination or recovery of aberrant proteins, in the yeast genus Candida. Glycogen and trehalose are reserve carbohydrates that accumulate under stress as energy reserves, and trehalose stabilizes protein structure at high temperatures and decreases the aggregation of unfolded or heat-denatured proteins (Singer and Lundquist 1998; Ueda et al. 2001). Silva et al. (2007) also found 58 genes were up-regulated, 34% of which were stress response genes, and 21 genes were down-regulated. Also, a permanent diploid state was induced as a way to increase gene dosage to counter damaged proteins, implying increase in ploidy may be a response to mask the phenotypic effects of aberrant proteins. Thus, a multitude of responses to protect the cell from and decrease the effects of less functional proteins with the novel amino acid during transition to the new code via an ambiguous intermediate codon has evolved. In addition, concerning code changes in mitochondria and chloroplasts, there are many of these of each cell. Thus, during the code transition, there would be a mixture of these organelles, some of which have the original code, others the novel code. The ones with the original code would mask a great deal of the effects of the ones with the new code. Of course, this effect would decrease as the organelles with the novel code increased, as they inevitably would have to during a full transition to the new code. But this masking effect, again using redundancy, would allow time for adjustment during the transition largely before the deleterious effects of the code change could be manifest in the phenotype. Also, since the population of the organelles is high, the arguments of Mayr (1963) and then Eldredge and Gould (1972) referred to earlier concerning drift allowing a less fit code to descend to a low, maladaptive valley by luck, then ascend to the new adaptive peak, lacks the requirement of a low population. These arguments do not guarantee that, in the ambiguous intermediate theory, there could not be any descent at all into a maladaptive valley before ascent to the new adaptive peak, as the codon disappearance theory does, but it is clear that such a descent would be slight, and the valley would be very shallow, if such a descent occurred at all.

It does not matter whether the deviant mitochondrial codes are superior to the canonical code from which they evolved, as far as the genetic code being on an adaptive peak or mitochondrial codes originating by the crossing of adaptive bridges are concerned. And this would be hard to test, since codon usage in the mitochondrial codes often differs from that of the canonical code; thus, the code that is best for a given mitochondrial code differs from the one that is best for the canonical code. Nonetheless, I counted codon usage in some mitochondrial codes. Surprisingly, my counting of codon usage showed that some mitochondrial codes are less fit for the mitochondrion than the standard code would be for them had they stuck with the latter. And Freeland et al. (2000b) found all extant, naturally occurring, secondarily derived, nonstandard genetic codes to appear less adaptive than the canonical code. It is possible that some mitochondrial codes changed as a consequence of selection for genomic economization. The deletion of a tRNA gene could be selected for because it reduces total genome length, allowing more rapid replication (Andersson and Kurland 1991, 1995), and a code change could be indirectly selected for in this process. This could lead to a code less adapted for error minimization, but to mitochondria and their organism that are more fit overall, because of the mitochondrion’s smaller genome. This is an interesting case of conflicting evolutionary pressures. If one drew an adaptive landscape with fitness plotted against the various possible mitochondrial codes, the crossing in this case would be from a higher to a lower adaptive peak. If the adaptive landscape were plotted with fitness against the possible overall mitochondrial genotypes or phenotypes, the crossing would likely be from a lower to a higher peak. Another explanation for the lower fitness of some mitochondrial codes is that they were arrived at as an indirect consequence of mutation pressure. This would be most interesting, for it would show that natural selection can be out-done by directional mutation pressure, resulting in a less fit organism. This raises the question as to how general this phenomenon is, and suggests an interesting area of research. If some mitochondrial codes changed as an indirect consequence of selection for genomic economization or mutation pressure resulting in less fit codes, this would not affect my argument that they result from adaptive bridges, because they would still cross over a maladaptive valley via codon disappearance or an ambiguous intermediate codon. Of course, their genetic codes would end up on a lower adaptive peak than the one they came from. Also, note that Knight et al. (2001b) found evidence against the hypothesis that mitochondrial code changes are selected for due to genomic economization.

In my count of codon usage, I found some mitochondrial codes to be superior for the mitochondria to the standard code had the mitochondria in question kept the canonical code. I will demonstrate one case in which the deviant code is better for the mitochondrion than the standard code would be, to show that this can happen. I counted codon usage in the Echinoderm Paracentrotus lividus from the sequence of it provided by Cantatore et al. (1989). The codon AAA is Lys in the canonical code, and Asn in the mitochondria of Echinoderms. This means Lys is represented by 2 codons in the standard code, but only 1 codon in Echinoderms. The proteins of P. lividus use Lys 0.9 times per 61 residues. Thus, the ideal code for the mitochondria of P. lividus would have but 1 codon for Lys. Asn has 2 codons in the standard code, and 3 codons in Echinoderms. P. lividus uses Asn 2.9 times per 61 amino acids. Its ideal code would thus have 3 Asn codons. Thus, this change in the meaning of the AAA codon is adaptive in P. lividus, with respect to both Lys and Asn.

This mechanism of crossing from one adaptive peak to another is of tremendous importance to evolutionary theory. There are very few examples of adaptive peaks in nature, the genetic code is very basic, and novel codes are created by crossing over adaptive bridges. This opens up the possibility that the adaptive bridge may be the general mechanism by which a population moves from one adaptive peak to another.

Indeed, since the mechanism of how a population crosses from a lower adaptive peak to a higher one is an important question in evolutionary theory, it is of great interest to know: How general is this mechanism of building adaptive bridges, as opposed to crossing from one adaptive peak to another by descending into a maladaptive valley and climbing back out again? It is clear from this discussion that the mechanism is valid for all examples in which the novel codes evolved from the standard code. There is another area of empirical examples in nature in which adaptive bridges were built using redundancy to shield the phenotypic effects of deleterious mutations until the right set of mutations resulted in a new adaptive function: gene duplication. Ohno (1970) thoroughly discussed how evolution could occur by gene duplication. A second, redundant copy of a gene, called a pseudogene, is free to accumulate mutations at no cost to the organism, since the other copy will carry out the function of the gene. Eventually, through chance, the pseudogene could on rare occasions hit on the right set of mutations to take on a new, adaptive function. This apparently happened with the genes for trypsin and chymotrypsin, myoglobin and hemoglobin, the L- and H-chains of immunoglobulin, as well as other genes (see Ohno 1970, and references therein). Significantly, the only examples of crossing from one adaptive peak to another that we have in protein function involve gene duplication, and hence are of the adaptive bridge type, as opposed to traveling down a fitness slope into a maladaptive valley and back up again.

Another way of building and crossing an adaptive bridge, but not employing redundancy, is through the molecular chaperone heat shock protein, Hsp90, which assists in the regulation of many key proteins in the regulatory process. Sangster et al. (2004) showed that genetic variation accumulates and yet remains phenotypically silent until there is a challenge to Hsp90 function, which then can reveal the genetic variation in the phenotype. Small environmental changes can cause the variation to manifest itself. These so-called cryptic polymorphisms, diverse in distant lineages, and rooted in protein folding, have significant implications for evolution’s pace and nature. Rutherford and Lundquist (1998) similarly showed that when Drosophila Hsp90 is mutant or pharmacologically impaired, phenotypic variation can result that affects nearly any structure in the adult fly, in both laboratory and wild populations. The variants are produced by multiple, previously silent genetic factors. When enhanced by selection, they actually quickly became independent of the Hsp90 mutation. Once again, widespread variation affecting developmental and morphogenic pathways occurs naturally, though it is usually silent, buffered by Hsp90, which allows it to accumulate. When this buffering is interfered with, by mutation, temperature, or another mechanism, the expression of cryptic variants occurs in the population. These are illustrated by stunning photos in the article. Even when Hsp90 function is restored, selection can lead to the continued expression of these traits, allowing a plausible mechanism for evolutionary change, even in otherwise entrenched developmental processes. This is a variation on the use of the adaptive bridge to cross over a maladaptive valley, because the phenotype is neutral, allowing the genotype to move around the adaptive landscape. The population can change as the various genotypes of its individual organisms move over differing adaptive bridges. When an environmental change occurs, even a mild one, the changes can be expressed in various phenotypes, a few of which may be selected for and be on new adaptive peaks. How common cryptic variation of this type is, compared to redundancy as a mechanism of peak shifts, can only be determined by further research. Thus, there are three known types of adaptive bridges that can cross over valleys from peak to peak: code changes, evolution by gene duplication, and evolution masked and hence facilitated by suppression of deleterious phenotypes by heat shock protein. This indicates adaptive bridges may be common, general phenomena.

In order to clarify the originality of some of the ideas I am presenting here, it is worth discussing the differences between adaptive bridges and the neutral networks of Reidys, Gavrilets, and others that I discussed earlier. Though they both are routes around a Wrightian landscape that skirt maladaptive valleys, adaptive bridges are a route over a maladaptive valley that is neutral due to the suppression or masking of the expression of the genotype as a phenotype, sometimes, but not always, using redundancy. They are alternate routes along the landscape that are more fit, but longer in the number of genetic changes needed to reach their destination. They are best visualized as bridges over the shorter, less fit valley that the population would have to attempt, and likely fail, to cross in their absence. Neutral networks, on the other hand, do not rely on suppression of expression of the phenotype, or redundancy. Also, they move along neutral routes from one point on the landscape to another that are best visualized and drawn as going around a maladaptive valley in three or more dimensions. They do not generally cross over maladaptive valleys from one peak to another. Also, neutral networks have only been shown for RNA folding, and are from computer-generated models, with the exception of but one experimental example. I have shown adaptive bridges to be mechanisms for crossing from one adaptive peak to another in nature in changing genetic codes, gene duplication, and heat shock protein suppression of maladaptive phenotypes.

It is necessary to point out that some authors would argue that the mechanism of peak shifts over maladaptive valleys is not a problem that needs addressing, because a change in the phenotypic variance or the environment can change the adaptive landscape, resulting effectively in a peak shift. For example, Whitlock (1995) has shown that an increase in phenotypic variance that occurs in small populations due to bottlenecks and founder effects can cause the adaptive landscape to change from bimodal to unimodal. This allows the population’s mean phenotype to change deterministically by selection. When the amount of phenotypic variance later returns to an equilibrium state, multiple peaks re-appear; however, the population has undergone a peak shift in this process. Whitlock (1997) has also shown that changes in the environment can change the adaptive landscape, resulting in peak shifts, even when those environmental changes are small. However, these arguments are not mutually exclusive with and do not negate the existence of adaptive bridges and neutral networks.

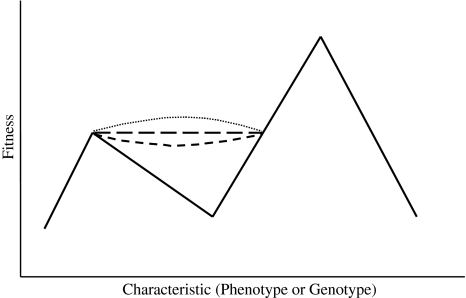
One can conclude from the ideas presented in this article that Sewell Wright’s idea of the adaptive landscape needs the following modification. The adaptive landscape actually has multiple routes between any given pair of fitness points on the graph. The multiple routes between the same two fitness points can vary in the number of mutations required to traverse the route, and in the positive or negative change in fitness conferred on the organism by each of these mutations. The former factor determines the length of the route taken between fitness points, while the latter factor determines the direction of the route. Both the factors affect the slope. A longer route requiring more mutations will tend to have less probability of being manifest than a shorter route requiring less mutations, all other factors being equal. And if there are deleterious mutations, the route will go down through a valley of lower fitness, and the more such mutations, the deeper the valley will tend to be. Routes through maladaptive valleys are much less probable than those following only adaptive bridges (and hence relying exclusively on adaptive or neutral mutations), and the deeper the maladaptive valley, the lower the probability that the route will be taken, all other factors being equal. The probability that a given route will be taken is determined by the distance (number of mutations) between the fitness points and the fitness value of each mutation along the route. This is illustrated in Fig. 2, a simplified graph in two dimensions, although in reality the various routes should be visualized as happening in multi-dimensional space. We can conclude from this that there are some cases, such as the standard genetic code in today’s organisms, in which all possible routes are so improbable as pathways to higher fitness points that the point that the population occupies is clearly a frozen, highly stable adaptive peak. Thus, the adaptive landscape seems to be more interesting than Sewell Wright suggested, with multiple routes to higher fitness points varying in the probability that they will be taken; his concept of adaptive landscapes is valid, but it is more rich and complex than he suggested. In the changing from the standard genetic code to one of the novel deviant codes, it may at first glance appear that there are two possible routes, the adaptive bridge and the descent down the fitness slope and back up again. But there are likely more routes than these, for, in the case of the changing of genetic codes, the building of an adaptive bridge can be accomplished by several different routes. If the code change is accomplished by codon disappearance, it requires the mutation of all copies of the lost codon to a codon synonymous to it, and there is more than one way this can occur, since the copies of this codon can mutate in several different chronological orders, with different copies of it mutating first, second, third, and so on. For example, if there are ten AAA codons that mutate to one synonymous codon, this can occur in 10! (ten factorial) different ways. In addition, if a codon has more than one synonymous codon, each copy of it can mutate to any of the other synonymous codons. If there is AT or GC mutation pressure, some synonymous codons will be favored over others and result in greater abundance than others when a codon is lost and mutates to synonymous codons. This is yet another way in which the various possible routes from one adaptive peak (or fitness popint) to another are not all equally probable. By the same token, the evolution of novel protein function by gene duplication can occur in several ways with unequal probabilities when the nonfunctional gene is undergoing several different silent mutations over a period of time.

Fig. 2.

Multiple possible routes a population can take in traveling from a lower to a higher adaptive peak. The V-shaped route that descends deep into a valley of lower fitness is solid to indicate it requires the least genetic changes of all the possible routes. Nevertheless, it is the least probable because it requires the population to descend through a valley of much lower fitness, requiring the less fit members of the population to survive better and produce more offspring than the more fit during the descent. The convex curve that descends as it leaves the lower peak is the least probable of the three routes represented by dashed lines for the same reason. How concave or convex the curve happens to be, and thus how far the convex curve descends into the valley of lower fitness before ascending, is not necessarily correlated with the number of genetic changes required to cross the maladaptive valley. There may be many more than four possible routes available to the population. Although this is a two-dimensional graph, the adaptive landscape is best visualized as multi-dimensional. This very general graph can represent any adaptive landscape, which could include genetic codes or any other phenotypic or genotypic traits (see text for further explanation)

This raises a problem. If a population can cross a maladaptive valley by the use of an adaptive bridge, one could argue there is no such thing as adaptive peaks, for the bridge changes the adaptive landscape, and eliminates the lower peak. However, the adaptive bridge requires more mutations, and is hence a longer route than the one down through the maladaptive valley. In building an adaptive bridge, the loss of a codon, or the duplication of a gene, for example, may be required, while traveling down to the bottom of the valley and up again could require a mere handful of mutations. For this reason, the concept of adaptive peaks remains a useful one, and eliminating it would cause more confusion and less understanding and clarity than keeping it. The adaptive landscape is best viewed as a complex structure with multiple routes from one peak or fitness point to another, including the maladaptive valleys between peaks and adaptive bridges. It is best drawn with all these routes shown, and an indication of the genetic distance and probability of each route. Thus, a modification of the depiction of Sewell Wright’s adaptive landscapes is necessary and desirable. Figure 2 is a crude start on this. No adaptive landscape has yet been drawn with so much information, but realizing the need for it shows the type of research and thinking we need to do.

The canonical genetic code is on an adaptive peak with respect to its evolution as an adaptation for error minimization, as are the deviant genetic codes. They represent rare empirical examples of adaptive peaks in nature. This is of great significance to evolutionary theory because the genetic code is basic to life and the concept of adaptive peaks and landscapes are of interest to evolutionary biology. The deviant genetic codes are empirical examples in nature of a mechanism by which populations can cross over maladaptive valleys from one adaptive peak to another via adaptive bridges, on a rich, complex adaptive landscape with multiple, but not equally probable, routes, a suggestion whose generality is supported by the observation that this also occurs by gene duplication and heat shock protein action. A modification of the depiction of Sewell Wright’s adaptive landscapes, showing genetic distances and probabilities of travel along their multiple possible routes, would throw light on this important concept. The fact that the canonical genetic code is on an adaptive peak and the mechanism of crossing from one such peak to another, profound in their implications for evolutionary theory, call for further research to achieve a better understanding of the generality of the occurrence of adaptive peaks in nature, the nature of adaptive landscapes, and the movement of populations on them across maladaptive valleys from one adaptive peak to another.