Fitting model of ABR age dependency in a clinical population of normal hearing children

Abstract

The purpose of this study was to present a simple and powerful fitting model that describes age-dependent changes of auditory brainstem responses (ABR) in a clinical population of normal hearing children. A total of 175 children (younger than 200 weeks postconceptional age) were referred for audiologic assessment with normal ABR results. ABR parameters of normal hearing children between 2003 and 2008 were included. The results of the right ears recorded at 90 dB nHL were analyzed. A simple and accurate fitting model was formulated based on these data. A very similar age-dependent effect was found for peaks III and V, and I–III and I–V intervals; latencies decrease as postconceptional age increases. It shows that the total age-dependent effect will be completed after 1.5–2 years. The age-dependent effect can be modeled by a relatively simple and accurate exponential function. This fitting model can be easily implemented to analyze ABR results of infants in daily clinical practice. We speculate about the underlying physiological processes.

Introduction

Auditory brainstem responses (ABR) were first reported by Jewett et al. [1] and also by Sohmer and Feinmesser [2]. ABR response waves reflect the conduction of a neural signal as a result of a sound stimulus along the auditory nerve and different levels of the brainstem. Several authors studied the location of the waves [3–6]. Most authors agree that wave I and II reflect the auditory nerve and cochlea (peripheral response) and that waves III, IV and V are generated more centrally, i.e., by brainstem structures. It is assumed that wave III reflects the ascending auditory pathway or the cochlear nuclei in the ventral acoustic striae. Wave V reflects activity toward the inferior colliculus, most likely the lateral lemniscus.

The ABR response in human development first appears around 25 weeks of gestational age [7, 8]. This response matures during the first few years of life, resulting in decreased latencies of most of the response peaks. In full-term infants, the peripheral response, reflected in wave I, is reported to show no signs of maturation or development as a function of age [6, 9–11]. The central conduction time, reflected by the I–V interval, is reported to mature from 11 to 18 months [6] up to 3–5 years of age [7]. This maturation effect differs for preterm and term infants [7, 11–13]. Preterm infants are reported to have increased absolute latencies compared to term infants up to 2 years of age [9].

ABR is the most important tool in diagnosing hearing impairment in infants. While ABR thresholds are important in establishing the degree of hearing loss, ABR latencies are important in differentiating between different types of hearing loss. In infants, ABR latencies are important to identify delayed auditory maturation and neural pathology, such as auditory neuropathy. In addition, differentiation between conductive and cochlear hearing loss can be based on latencies, which should be corrected for age to obtain adequate classification of hearing loss. While ABR response thresholds only show a little age-dependent effect, ABR latencies are age dependent especially in young infants. To adequately diagnose hearing loss, age adjusted normal values are required. Several authors have reported average ABR normal values for infants of specific ages [7, 10, 12–17]. There was no fitting model to analyze ABR results in daily clinical practice reported in these studies.

Teas et al. [10] first reported a fitting model to describe the time course in a quantitative way. This fitting was derived from a statistical model rather than from modeling on a physiological basis. Eggermont and Salamy [13] proposed a fitting model based on maturational mechanisms. They used either a single exponential or the sum of two exponentials in their model. However, it was not completely clear which of these two models was best suited to describe the data.

Issa and Ross [18] established another normative data set, including age-dependent correction values for ABR latencies up to 10 years of age. A fitting with a double exponential fitting model was used to compute these correction values. Gorga et al. [19] presented a fitting model for wave V latency as a function of postconceptional age and stimulus level.

There is no consensus about a general model that can be easily implemented in daily clinical practice to interpret ABR results in individual infants. Therefore, we would like to propose a simple and powerful fitting model that describes ABR age dependency and may serve as a reference for daily clinical practice.

Materials and methods

Subjects

We analyzed ABR parameters of children with normal ABR thresholds who were tested at the Sophia Children’s Hospital between 2003 and 2008. This clinical population of normal hearing children was measured from term age onwards. A total number of 175 children were included. Both ears were sequentially tested, and a strong correlation between the left and right ear can be expected. To prevent statistical overestimation, only the results of one ear, the right ear, were analyzed. Postconceptional age at the time of ABR measurement ranged from 38 to 194 weeks. Postconceptional age is defined as the period of time since conception. Postconceptional age is calculated as gestational age plus postnatal age. A total of 69 girls and 106 boys were included.

Inclusion criteria for the selection of these children were: presence of wave I, III and V at 90 dB measurement; infants measured in quiet or calm conditions and (sub)normal ABR thresholds (≤30 dB nHL). For children younger then 42 weeks, postconceptional age an ABR threshold of 40 dB nHL was considered normal. Exclusion criteria were: ABR measured under general anesthesia or known retrocochlear pathology.

To calculate the asymptote in our fitting model, normal ABR results from 194 subjects older than 200 weeks postconceptional age were analyzed.

Apparatus and procedures

All ABR measurements were recorded at our outpatient clinic in a soundproof room. All children were in natural sleep or in calm conditions throughout the assessment. Both ears were tested, but only the right ears were included for analysis. ABRs were recorded with a EUPHRA-1 system using a Toennies preamplifier. Responses were recorded using silver cup electrodes placed at both mastoids with a reference at the vertex and a ground electrode on the forehead and then band pass filtered (20–3,000 Hz). These filter settings are commonly used in clinical practice. The repetition frequency was 23 Hz. Click stimuli were presented starting at a level of 90 dB nHL. With step sizes of 10 dB, the level was decreased until no response was found.

Analysis of response

The response parameters studied were the absolute latencies of peaks I, III and V, the I–III and I–V intervals and the response thresholds. Experienced clinical specialists interpreted the ABR response waves. The response latencies in milliseconds were obtained by establishing the peak of the wave and reading out the digitally displayed time. The I–III and I–V intervals were obtained by subtracting the latency of peak I from peaks III and V, respectively. The threshold was estimated by the lowest level at which a response was found. The corresponding hearing loss was estimated as 10 dB below this level.

Fitting model

Our fitting model for the age dependency of the ABR latencies is based on a few assumptions. A nearly age independency of wave I is reported in the literature and is confirmed by our data [6, 9–11]. Stimulus level dependency is equally reflected in peak I and later peaks. Therefore, our model assumes that the stimulus level dependency is realized solely in the first stage and age dependency is realized in the later peaks. Thus, we can split the model into two parts: one for peak I and another for peaks III and V. The latency level model for peak I that can be used to generalize our fitting model for different stimulus levels is described in “Appendix”. Henceforth, we will only focus on the age-dependent part of the fitting model.

Secondly, for reasons of simplicity, we assumed equal age dependency for the I–III and III–V intervals. A function with two age-dependent fitting parameters resulted in a simple and sufficiently accurate fitting of ABR interval latencies:

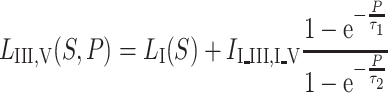1

Table 1 shows the explanations of the variables used in the different functions.

Table 1.

Explanation of variables in the fitting model

Variable	Explanation	Value
L	Latency (ms)
S	Stimulation level	90 dB
P	Postconceptional age (weeks)
L I (90)	I latency 90 dB (adults)	1.60 ms (SD 0.13 ms)
I I_III (∞)	I–III interval (90 dB adults)	2.17 ms (SD 0.15 ms)
I I_V (∞)	I–V interval (90 dB adults)	4.04 ms (SD 0.18 ms)
τ 1	Time constant “nerve growth”	21.7 weeks (SE 2.1 weeks)
τ 2	Time constant “nerve maturation”	35.4 weeks (SE 1.8 weeks)

Table 1 shows the explanation and the values of the variables used in our fitting model. The time constants of τ ₁ and τ ₂ can predict maturation from 38 weeks onwards. To use these time constants as a measure of postnatal maturation, 38 weeks should be added

For larger age values, the interval functions approach the adult values asymptotically. These values are calculated separately from the mean of an adult data set.

Considering the intended use as normative curve, the intervals were fitted directly (I–V and I–III together) instead of the reciprocal. Independent fitting was considered, but the results of combined fitting were equally reliable.

Results

Peak latencies are derived from the ABR recordings at 90 dB nHL of the 175 included normal hearing children as described in the “Materials and methods” section of this study. Since the earliest measurement in our data set was conducted at 38 weeks postconceptional age, results are shown for 35–200 weeks postconceptional age. Between 38 and 45 weeks postconceptional age, only limited data are available, as infants in our clinic are usually measured at later ages after they have completed the total neonatal screening pathway.

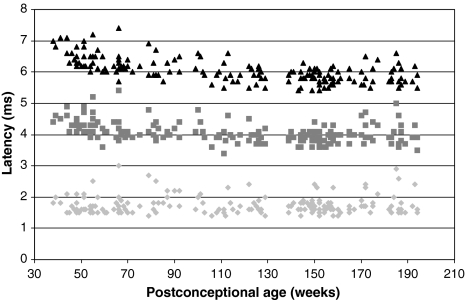
The individual data points for peaks I, III and V from our data set are shown in Fig. 1. The age-dependent changes are clear from these results. Peak I latency shows little or no age dependency. Peaks III and V latencies show a clear age-dependent decline, which is most evident up to 80 weeks.

Fig. 1.

Latencies of peaks I, III and V recorded at 90 dB nHL of 175 normal hearing right ears at different postconceptional ages. The light grey diamonds represent peak I, the grey squares represent peak III and the black triangles represent peak V

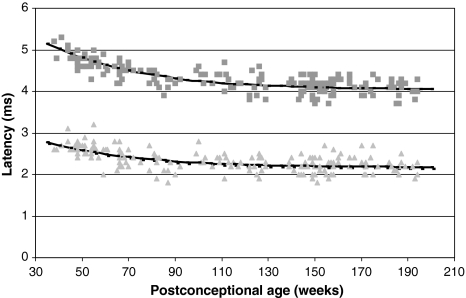
Figure 2 shows the absolute data for the I–III and I–V intervals and the corresponding fitting curves. A similar age-dependent effect as described for peaks III and V is observed for the I–III and I–V intervals.

Fig. 2.

The I–III and I–V intervals recorded at 90 dB nHL of 175 normal hearing right ears and corresponding fitting curves at different postconceptional ages. The light grey triangles represent the I–III interval, and the black line represents the corresponding fitting curve. The grey squares represents the I–V interval, and the black line represents the corresponding fitting curve

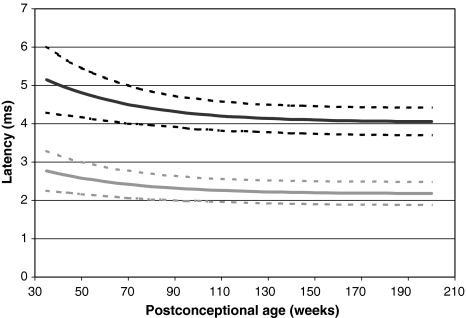
Table 2 shows the average values and standard deviations derived from our fitting model for peaks I, III and V, and I–III and I–V intervals for different postconceptional ages. The standard deviations decrease with increasing postconceptional age. The overall standard deviations are small, which imply that accurate measurement can be rightfully implemented in our fitting model. Figure 3 shows the fitting curves for I–III and I–V intervals including the standard deviations. As a reference for normal results, a cutoff of two standard deviations is used.

Table 2.

Values of peak latencies and intervals for different postconceptional ages

PCA (weeks)	Peak I		Peak III		Peak V		I–III interval		I–V interval
	Latency (ms)	SD	Latency (ms)	SD	Latency (ms)	SD	Latency (ms)	SD	Latency (ms)	SD
35	1.60	0.23	4.37	0.27	6.75	0.44	2.77	0.26	5.15	0.43
40	1.60	0.23	4.30	0.25	6.63	0.39	2.70	0.24	5.02	0.39
45	1.60	0.23	4.24	0.23	6.51	0.36	2.64	0.22	4.91	0.35
50	1.60	0.23	4.19	0.22	6.41	0.33	2.58	0.21	4.81	0.32
55	1.60	0.23	4.14	0.21	6.32	0.31	2.54	0.20	4.72	0.30
60	1.60	0.23	4.10	0.20	6.24	0.29	2.49	0.19	4.64	0.28
65	1.60	0.23	4.06	0.19	6.17	0.27	2.45	0.18	4.57	0.26
70	1.60	0.23	4.02	0.19	6.11	0.25	2.42	0.18	4.50	0.25
75	1.60	0.23	3.99	0.18	6.05	0.24	2.39	0.17	4.45	0.23
80	1.60	0.23	3.97	0.18	6.00	0.23	2.36	0.17	4.40	0.22
85	1.60	0.23	3.94	0.18	5.96	0.23	2.34	0.16	4.36	0.21
90	1.60	0.23	3.92	0.18	5.92	0.22	2.32	0.16	4.32	0.20
95	1.60	0.23	3.91	0.17	5.89	0.21	2.30	0.16	4.28	0.20
100	1.60	0.23	3.89	0.17	5.86	0.21	2.29	0.15	4.25	0.20
105	1.60	0.23	3.88	0.17	5.83	0.20	2.27	0.15	4.23	0.19
110	1.60	0.23	3.86	0.17	5.81	0.20	2.26	0.15	4.20	0.19
115	1.60	0.23	3.85	0.17	5.79	0.20	2.25	0.15	4.18	0.19
120	1.60	0.23	3.84	0.17	5.77	0.20	2.24	0.15	4.17	0.18
125	1.60	0.23	3.83	0.17	5.76	0.19	2.23	0.15	4.15	0.18
130	1.60	0.23	3.83	0.16	5.74	0.19	2.22	0.15	4.14	0.18
135	1.60	0.23	3.82	0.16	5.73	0.19	2.22	0.15	4.13	0.18
140	1.60	0.23	3.82	0.16	5.72	0.19	2.21	0.15	4.11	0.18
145	1.60	0.23	3.81	0.16	5.71	0.19	2.21	0.15	4.11	0.18
150	1.60	0.23	3.81	0.16	5.70	0.19	2.20	0.15	4.10	0.18
155	1.60	0.23	3.80	0.16	5.69	0.19	2.20	0.15	4.09	0.18
160	1.60	0.23	3.80	0.16	5.69	0.19	2.19	0.15	4.08	0.18
165	1.60	0.23	3.80	0.16	5.68	0.19	2.19	0.15	4.08	0.18
170	1.60	0.23	3.79	0.16	5.68	0.19	2.19	0.15	4.07	0.18
175	1.60	0.23	3.79	0.16	5.67	0.19	2.19	0.15	4.07	0.18
180	1.60	0.23	3.79	0.16	5.67	0.19	2.19	0.15	4.07	0.18
185	1.60	0.23	3.79	0.16	5.67	0.19	2.18	0.15	4.06	0.18
190	1.60	0.23	3.79	0.16	5.66	0.19	2.18	0.15	4.06	0.18
195	1.60	0.23	3.78	0.16	5.66	0.19	2.18	0.15	4.06	0.18
200	1.60	0.23	3.78	0.16	5.66	0.19	2.18	0.15	4.06	0.18

Table 2 shows the derivative values of peaks I, III and V and the average derivative values of the fitting of the I–III and I–V intervals at 90 dB nHL for different postconceptional ages. The standard deviations of the I–III and I–V fittings were also fitted

Fig. 3.

Fitting curves of the I–III and I–V intervals. The grey line represents the I–III interval, and the dotted grey lines indicate the I–III interval plus or minus two standard deviations (considered cutoff of normal). The black line represents the I–V interval, and the dotted black lines indicate the I–V interval plus or minus two standard deviations. Data were recorded at 90 dB nHL stimulation intensity

Discussion

We present a simple and accurate fitting model that describes the age-dependent effect found for ABR latencies and can be easily implemented to serve as a reference for daily clinical practice. Our model is based on a clinical population of normal hearing children. An age-dependent effect of ABR latencies for peaks III and V, and I–III and I–V intervals can be concluded from our results. The latencies of peaks III and V, and I–III and I–V intervals decrease as postconceptional age increases. For peak I, no clear age-dependent effect was found. The age-dependent effect we found for peaks III and V, and I–III and I–V intervals is concurrent with other studies [10, 13].

Only one variable (postconceptional age) is used in our fitting model. Our fitting model contains two fitting parameters with an opposite effect. The fitting parameters represent time constants in an exponential function. The time constant in the denominator (τ ₂) results in decreased ABR latency intervals with increasing age. A plausible explanation for this effect is nerve maturation caused by a combination of increased myelination and synaptic efficacy. The time constant in the numerator (τ ₁), which was introduced to improve the accuracy of the fit for the youngest infants, results in increased ABR latency intervals with increasing age. This effect could be explained by growth of the nerve: a longer pathway results in increased conduction time. Moore et al. [20] demonstrated that both of these theoretical principles were involved in ABR maturation. The effect of nerve maturation is reported to be stronger than the effect of nerve growth [20].

There are a few basic assumptions underlying our model. First of all, we assume the latency of peak I to be constant. This is based on the literature as well as on our own results [6, 9, 10]. However, it must be noted that before 55 weeks of postconceptional age, peak I latency may show a small decline with age, but no sufficient data are available.

Since we assume peak I to be constant, the age-dependent effect can be found in the I–III and III–V intervals. Secondly, we assume this effect to be uniform for both intervals. However, some authors suggest that this effect is not completely the same for the I–III and III–V intervals [13, 18, 21]. Eggermont and Salamy did find some degree of association between I–III and III–V intervals. For reasons of simplicity and because the extent of this effect is not well known, we argue an equal age-dependent effect for I–III and III–V intervals in our model. Also, separate fitting parameters for I–III and III–V did not produce a more accurate fitting model. The standard deviations originating from our fitting are at least as accurate as the values given by other authors [10, 13, 18].

For age dependency, we only analyzed latencies obtained at 90 dB nHL stimulation level. A stimulus intensity level-dependent effect cannot be obtained from these results. We assume age dependency to be independent of intensity level, as stimulus dependency takes place in the cochlea (i.e., peripherally) and therefore does not influence the maturation effect, which is located more centrally. This is supported by Teas et al. [10], who found that age-related latencies are similar for two intensities (50 and 30 dB).

Some authors suggest that this central maturation effect is caused by increased myelination of axons, thereby reducing axonal conduction time [6, 7, 12, 16, 18, 20]. This is in line with our assumption that age dependency is equally distributed along the total I–V interval. Other theories include a mild conductive hearing loss and tuning of the cochlea to lower frequencies located in the apical part of the cochlea, resulting in an elevated threshold and latency delay [9]. However, this does not explain the maturation of the I–V interval. Also increased synaptic efficacy is mentioned as a cause of the maturation effect [6, 10, 18].

As a general rule for exponential fitting functions, 95% of the total maturation effect can be expected to end after three times τ. From our data, a total age-dependent effect of 103.1 and 144.2 weeks for τ ₁ and τ ₂, respectively, can be computed. After 2–2.5 years this effect will be completed. This is in line with earlier reports of a maturation effect for the I–V interval of 4–5 months [6] up to 3–5 years of age [7].

Our data were obtained from a large number of infants and fitted to adult results (>200 weeks postconceptional age). Whether our model is suitable to fit data for preterm infants cannot be concluded from our results. It may be possible that the time constants that describe the age-dependent effect are different for preterm infants.

A separate function for each gender has been considered. This was abandoned for the sake of simplicity since the intersex differences in time constants were negligible (men, τ ₁ 20.2, τ ₂ 33.7; women, τ₁ 20.6, τ₂ 33.4). Sleifer et al. [11] also found no gender differences for ABR latencies.

We chose to analyze only the results obtained from the right ears. Since we expect a strong correlation between the left and right ears, inclusion of both ears could lead to statistical overinterpretation of the age-dependent effect. However, small left to right latency differences are found in ABR results of neonates [22–24]. Since the interaural differences are very small, we feel that our results can be extrapolated to the left ears.

We studied the results obtained at 90 dB nHL stimulation level to optimize quality and insure the presence of peak I responses (especially in the younger infants). We experienced no problems with the interpretation of the results due to acoustic reflexes. ABR results were analyzed by two experts in our clinic. However, we were unable to provide data on the interrater reliability.

A selection bias may have occurred in our study because all included children were referred for auditory assessment to our tertiary care clinic. Therefore, the chance that they had a condition altering ABR results was higher than in the normal population. We tried to minimize this effect by applying strict inclusion and exclusion criteria. On the other hand, by deriving our fitting model from a clinical population of normal hearing children it is a true reflection of the population it is intended for.

The strength of our fitting model compared to the current fitting models proposed by Eggermont, Issa and Teas is that it is a relatively simple model that leads to accurate fitting of the data. Furthermore, the model reflects physiological processes of myelination and nerve growth. Teas et al. [10] based their fitting model on statistical analysis of the ABR results, resulting in a non-linear equation with four parameters for latencies of peaks III and V. For peak I, a linear model was used. Peak I showed similar results compared to adults, except for 2 kHz, where peak I latencies decreased with age. Peak V showed a larger age-dependent decrease in latency, but did not reach adult values yet at 60 weeks of age. They also found a frequency-dependent immaturity at rostral sites for higher frequencies (8 kHz). Eggermont and Salamy [13] proposed two models, with either one or two exponential parameters. The I–V interval is always fitted with one exponential, but it is not completely clear how the other latencies should be fitted. Peak I latencies are nearly mature at term age. Issa and Ross [18] used an exponential function with two time constants to derive age-dependent correction values. They fitted the latencies and intervals of peaks I, III and V (measured at 70 dB nHL) individually. The two time constants resulting from their fitting are surprisingly diverse, which is difficult to explain. Children were not equally divided along different age groups and they did not use threshold criteria to exclude conductive hearing losses.

The present study introduces a simple and powerful fitting model that can be easily implemented in daily clinical practice to be used as a reference for ABR results in infants. We speculate on the underlying physiological processes.

Since our data are based on mostly full-term infants, it is uncertain whether our model would be suitable to fit data from preterm infants.

Appendix

The model is constructed for values measured at 90 dB nHL only as it is primarily meant to describe age-dependent changes. To be used generally by including stimulus intensity level dependency, the model had to be substituted to a latency level model for peak I using

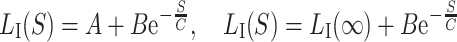2

The complete result latency as a function of stimulation level and postconceptional age reflects a “mathematical surface”:

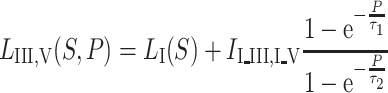3

where S is the stimulation level (dB) and P is the postconceptional age (weeks). We use the following variables derived from the fitting of our own data: A = 1.46, B = 1.10 ms, C = 43 dB.