Introduction
Identification and characterization of critical macromolecular interactions within the cell is one of the central research problems of the post-genomic era. High throughput mapping of protein-protein interactions is providing a global picture of the cellular interaction networks (1). However, quantitative methods capable of accurately defining the stoichiometry, affinity, cooperativity and thermodynamics are required for a fundamental mechanistic understanding and to effectively target molecular interactions for therapeutic intervention. Although many biologically significant interactions involve association of identical subunits (homogeneous interactions), a much larger class of binding events involves interactions of dissimilar partners (heterogeneous interactions or mixed interactions). Rigorous investigation of heterogeneous interactions presents particular challenges for experimental design, data analysis and interpretation. In this chapter, we present the mathematical formalism to describe heterogeneous equilibria, with particular attention to the relationship between the macroscopic and microscopic equilibrium constants. We then compare features of several biophysical methods that are commonly used to characterize heterogeneous interactions. Equilibrium and velocity analytical ultracentrifugation are particular useful as baseline methods to define assembly models and extract equilibrium parameters. Other chapters in this volume describe new methods for analysis of interacting systems by velocity sedimentation (2, 3); here, we focus on sedimentation equilibrium and illustrate this approach with an analysis of a nonspecific protein-nucleic acid interaction.
Formalism for the Analysis of Heterogeneous Interactions
Heterogeneous interactions involve at least two distinct macromolecular components. For simplicity, we consider systems composed of just two components, designated as A and B, that combine to form one or more species, designated AiBj. In some cases A or B self-associate as well, and either i or j can be zero. Note that each species AiBj may also exist in multiple conformational states with distinct hydrodynamic properties; here we only consider equilibria among species with differing composition.
The equilibria governing the association of A and B to form a family of complexes AiBj can be expressed as
| (1) |
where the equilibrium constants, Kij, are defined on the molar concentration scale according to the mass action law:
| (2) |
Note that macromolecular association constants are often expressed in a weight/volume concentration scale in the analytical ultracentrifugation literature. Conversion among these different scales is straightforward (4). It is important to realize that Kij represents the overall equilibrium constant between the monomeric forms of A, B and the complex AiBj. Often, assembly proceeds via sequential formation of a series of complexes of increasing stoichiometry. For example, if a monomer of A contains multiple binding sites for interaction with B the following equilibria will pertain:
| (3) |
where K1, K2,…Kj represent the stepwise equilibrium constants. Here, the overall equilibrium constant Kij is the product of each of the stepwise constants. As described below, analysis of these stepwise equilibrium constants can provide insight into the assembly mechanism.
Discrete Interactions
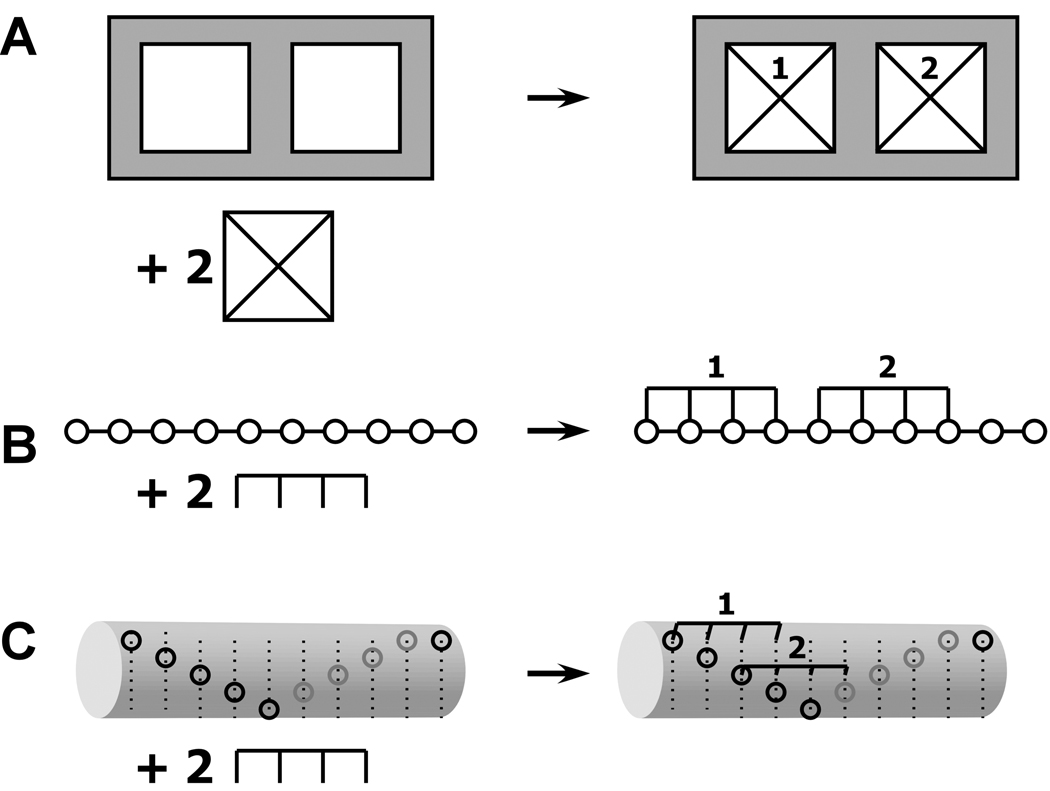
It has long been recognized in multisite ligand binding systems that the experimentally accessible, macroscopic equilibrium constants are related to the intrinsic binding constants governing the microscopic equilibria by statistical factors (5). These same considerations apply to more complex heterogeneous macromolecular interactions. The stepwise, macroscopic binding constant Kij represents the product of an intrinsic binding constant k and a statistical factor related to the number of microscopic configurations of A, B and the complex AiBj. For example, consider the A+2B ↔ AB2 system depicted in Figure 1A, where A contains two identical binding sites for B. This model is commonly used to analyze bivalent antibody-antigen interactions (6). There is only a single configuration for the free A and B species. However, in the AB complex there are two microscopic states with B bound to the left or right site, respectively. Thus, the AB state has a statistical weight of 2 and the stepwise, macroscopic binding constant K1 =2k. There is only a single configuration for the AB2 complex and K2=k/2. Thus, the statistical effects cause a sequential decrease in the macroscopic binding constants with increasing saturation. In the general case where A contains s identical binding sites capable of binding B, the statistical factor Cx for the complex ABx is given by (7):
| (4) |
Figure 1.
Schematic illustraiton of specific and nonspecific hetero-interactions. A) Discrete binding with A+2B → AB2 model. B) Nonspecific binding of a large ligand to a finite, one-dimensional lattice. One of the 6 possible configurations for binding of two ligands of length 4 to a linear lattice of length 10. The open circles represent lattice sites. C) Overlapping ligand model for the nonspecific binding of two ligands of length 4 to a helical lattice of length 10 with a minimal offset of 2. The leftmost binding site on the ligand must contact a lattice site indicated by an open circle. Only one of the 15 possible configurations is shown.
The overall, macroscopic binding constant defining the equilibrium is then given by
| (5) |
Or, in terms of in terms of the stepwise binding constants,
| (6) |
Procedures for enumerating the statistical weights for more complex association models have been presented (8).
When analyzing experimental data for multiple equilibria, it is useful to initially fit data in a model-independent fashion, where each of the equilibrium constants is treated as an independent parameter. The relative values of the equilibrium constants are then compared with those predicted by statistical considerations to test the association model. Deviations from these predictions are an indication that the model is incorrect. Possible causes are that the binding sites are not equivalent or interactions between sites (cooperativity). This approach may not be feasible for more complex models, where a large number of adjustable parameters gives rise to extensive cross-correlation among the equilibrium constants and unacceptably broad confidence intervals. In this case, it is more productive to directly fit for the intrinsic binding constants using the statistical factors to generate the macroscopic constants in the fitting function.
Nonspecific interactions
In contrast to the discrete binding phenomena described above, in some heterogeneous systems one component (A) consists of a polymeric lattice of identical or near-identical subunits and B interacts with one or more of these subunits without distinguishing among different positions in the lattice. For obvious reasons this type of binding is termed "nonspecific". Biologically significant examples include protein-nucleic acid interactions (9), drug-DNA binding (10) and protein binding to polysaccharide lattices (11). Often the binding site for B consists of two or contiguous subunits. This situation is illustrated in figure 1B, where the open circles represent the repeating subunits in a polymeric molecule A and B occupies four contiguous lattice sites. The overlapping character of these sites results in the exclusion of binding of adjacent ligands, giving rise to binding isotherms that appear anticooperative. McGhee and von-Hippel derived the binding isotherm for this model in the case of an infinite, one-dimensional lattice (12)
| (7) |
where νns is the number of nonspecifically bound ligands (B) per lattice site, Kns is the intrinsic binding constant for B interacting with an isolated region of A, [B] is concentration of free B and N is the number of lattice sites occluded by B.
Many binding experiments are performed using short lattices of defined length, such as oligonucleotides (e.g. see references (13–17). Here, a more relevant approach is to treat A as a finite one-dimensional lattice. An approximate isotherm for the finite lattice model been presented (18, 19)
| (8) |
where M is the size of the lattice. Equation 8 is a good approximation to the exact solution over the entire saturation range even for lattices only slightly larger than the site size N (19). A useful feature of this expression for fitting experimental data is that the site size does not have to be an integer and thus can be treated as an adjustable parameter in nonlinear least squares analysis. This finite lattice model has also been extended to accommodate the combination of a specific binding site and nonspecific interactions (19). One limitation of this approach is that equation 8 does not readily permit calculation of the statistical factors and populations of partially liganded species. In contrast, exact, combinatorial expressions have been derived to describe noncooperative and cooperative binding of large ligands to finite, one-dimensional lattice. The statistical weights for each ligation state are given by (11, 18, 20)
| (9) |
For example, in the case depicted in figure 1B with M=10, N=4, there are four ways to arrange two molecules of B on a lattice A and thus C2=4. The advantage of using this formalism is that it allows one to calculate the statistical weight for each species in solution rather than simply the saturation of the lattice with the component B. This approach is more appropriate for techniques, such as analytical ultracentrifugation, that are capable of resolving such partially liganded species. A restriction is that N cannot be treated as an adjustable parameter.
In recent studies of the nonspecific binding of protein kinase R (PKR) to double-stranded RNA sequences higher binding stoichiometries are found than can be explained within the one dimensional finite lattice model (17). Based on structural data, a new model was proposed in which the lattice supports overlapping ligand binding to different faces of the double helical RNA. Consecutive ligands initiate binding in fewer than N bases and thus the ligands overlap along the primary sequence of the lattice. This situation is depicted in figure 1C, which illustrates a configuration where a ligand that occupies 4 lattice sites binds to a helical lattice of length 10. The open circles represent the leftmost edge of a binding site, e.g., the minor groove of a double-stranded nucleic acid. In this model, we define a minimum offset, Δ, which refers to the minimum number of lattice sites at which consecutive ligands can initiate binding. (Δ=2 in figure 1C). The value of Δ is determined by the size of the ligand and the geometry of the lattice. In this model, the limiting stoichiometry (s) is given by the largest integer value of S that satisfies the following inequality
| (10) |
Finally, the statistical weights are given by
| (11) |
The examples in figure 1 illustrate that the presence of ligand overlap significantly increases both the stoichiometry and statistical factors for nonspecific interactions.
Our discussion has emphasized the role of statistical factors in the analysis of apparent binding constants for both discrete and nonspecific hetero-interactions. Obviously, these two classes of binding models differ substantially and interpretation of the relative values of the macroscopic constants should be done in the context of the appropriate model. Although PKR is known to bind to RNA nonspecifically, in some early studies binding constants were analyzed using statistical factors derived from the discrete model (equation 4); discrepancies between the observed data and the predicted ratios were interpreted evidence for positive cooperativity (13, 15). In contrast, when PKR binding data are analyzed in the context of a more appropriate, nonspecific binding model there is no evidence for cooperativity (17).
Experimental Methods
When beginning a project to characterize a molecular interaction one is faced with the problem of choosing an appropriate method. This can be a daunting task, since there are many experimental biophysical approaches available for quantifying heterogeneous macromolecular interactions. Here, we briefly consider the factors that govern the choice of methodology and consider some of the unique capabilities of each approach. At the outset, it should be acknowledged that no single approach is superior in all aspects, and as previously pointed out (21), the most fruitful research strategies generally involve the use of a combination of methods.
Outside of the obvious considerations of the availability of instrumentation and personal experience, one of the key factors that govern the choice among alternative techniques is the type of information that is required by the researcher. Generally, simple evidence of a macromolecular interaction can be obtained using qualitative biochemical methods and the biophysical approaches are employed to obtain quantitative information, such as binding stoichiometries. At the next level of complexity, one may require equilibrium constants; in some cases, only a rank-order of affinities is sufficient. Finally, it may be essential to obtain additional data such as the thermodynamic parameters (ΔH, ΔS, ΔCp) and association and dissociation rates for the interaction.
The second set of considerations relates to sample-specific issues. First, how much material is available and how many samples must be assayed? Second, what are the properties of the material? The chief considerations are solubility and stability. Other issues relate to modification of the sample for analysis. Can the reagent be readily labeled with extrinsic probes for fluorescence measurements or immobilized for surface plasmon resonance? Do these modifications alter the reactivity of the sample? Finally, if one wishes to measure affinities, what is the expected range of Kd? This will determine sample concentrations and the experimental sensitivity that are required.
Given these considerations, table I compares the information content, sensitivity, and unique features for several of the most popular biophysical methods. Admittedly, this comparison is somewhat superficial in that each of these approaches actually constitutes a diverse family of experimental configurations with differing detection methodologies, sensitivities and sample requirements. In particular, we have combined together static and dynamic light-scattering measurements as well the range of fluorescence-based methods (anisotropy, correlation spectroscopy, energy-transfer). However, some interesting categories that differentiate these approaches do emerge and are summarized below:
Component properties. Several methods (sedimentation, light scattering, fluorescence) provide potentially useful information about the separate components (A and B) as well as the complexes.
Complex properties. It may be important to determine the absolute stoichiometry of a complex rather than a molar ratio of components; for example, it may be necessary to distinguish AB from A2B2. Techniques that are based on the mass or hydrodynamic properties of the complex provide this information.
Species resolution. In some methods, the experimental observable is the fractional saturation of A with B; in others, the separate species are resolved. A particularly attractive feature of sedimentation velocity is the multiple species are resolved based on differences in sedimentation coefficients and diffusion constants. Note that sedimentation velocity analysis methods based on weight-average sedimentation coefficients (22), sedimentation coefficient distribution analysis (3) and direct boundary analysis (23) are expanding the power of this method to characterize complex heterogeneous interactions. In sedimentation equilibrium, the species are resolved based on mass and optical properties and in dynamic light scattering analysis of the autocorrelation function yields a diffusion constant distribution function. However, both of these methods involve analysis of data using model functions consisting of sums of exponential terms, which can be an ill-conditional fitting problem (24).
Table I.
Biophysical Methods to characterize macromolecular interactions
| Sedimentation Equilibriuma |
Sedimentation Velocityb |
Isothermal Titration Calorimetryc |
Surface Plasmon Resonanced |
Light Scatteringe |
Fluorescencef | |
|---|---|---|---|---|---|---|
| Component Properties |
Mass | Mass and Hydrodynamics |
- | - | Mass and Shape | Hydrodynamics |
| Complex Properties |
Stoichiometry | Stoichiometry | Molar Ratio | Molar Ratio | Stoichiometry | Molar Ratio |
| Species Resolution |
Resolved Complexes |
Resolved Complexes |
Fractional Saturation |
Fractional Saturation |
Resolved Complexesg |
Fractional Saturation |
| Kd Range (M) | 10−3 – 10−9 | 10−4 – 10−8 | 10−3 – 10−8 (10−2 – 10−12)h |
10−3 – 10−12 | - | 10−3 – 10−12 |
| Additional Information |
- | Kinetics and Hydrodynamics |
Thermodynamics | Kinetics | - | - |
| Material Requirements |
20–120µL | 400 µL | 1.5 mL | µL | - | µL- nL |
h In dynamic light scattering resolution is achieved by analysis of the autocorrelation function as a continuous distribution of diffusing species (59).
In summary, there are a variety of approaches to define heterogeneous interactions with complementary capabilities. In our opinion, analytical ultracentrifugation methods (equilibrium and velocity) fill a unique niche in the repertoire of techniques used to measure macromolecular interactions due to their rigor and ability to discriminate among alternative association models. Other methods are more sensitive and rapid. In particular, surface plasmon resonance and fluorescence approaches are easily configured for screening large numbers of samples. The more fundamental methods are most profitably used at the outset of a project to define the correct reaction scheme or model for the interaction and to accurately measure equilibrium constants. Subsequently, methods that are more rapid may be used to process large number of samples. This paradigm has been employed in studies of the activation of the 2',5'-oligoadenylate (2,5A)-dependent ribonuclease. Sedimentation equilibrium measurements defined an activation model in which one 2,5A activator (A) binds to a ribonuclease monomer (B) to produce the AB complex, which subsequently dimerizes to the active form, A2B2 (25, 26). Subsequently, fluorescence polarization (25) and enzymatic activity assays (27) were used to obtain structure-activity relationships for large numbers of enzymatic activators
Sedimentation Equilibrium
Sedimentation equilibrium is a rigorous and well established method to define the stoichiometry and affinity of macromolecular interactions, and the basic principles have been the subject of several recent reviews (28–31). Here, we consider the mathematical formalism for analysis of hetero-interacting systems by sedimentation equilibrium, describe some practical issues for experimental design and computer fitting of experimental data using global nonlinear least squares, and present an example of a protein RNA interaction. Other chapters in this volume describe new methods for analysis of interacting systems by velocity sedimentation (2, 3).
Analysis of heterogeneous interactions is considerably more difficult than self-association because the fitting models give rise to a larger number of adjustable parameters. The analyses are plagued by multiple minima and by unacceptably broad confidence intervals for the deduced parameters due to extensive cross-correlation. A variety of methods have been described to circumvent these problems (4, 32). In the case of protein-nucleic acid interactions, where the two reactants have markedly different absorption spectra, collection of radial absorption gradients at multiple wavelengths is particularly useful to accurately define the concentration of each of the components and to enhance sensitivity. Thus, there has been renewed interest in the use of sedimentation equilibrium in the quantitative analysis of protein nucleic acid interactions (14, 17, 25, 33–36).
Our preferred approach is to directly analyze sedimentation equilibrium concentration gradients by nonlinear least squares fitting methods. Alternatively, secondary parameters, such as weight-average molecular weights or the omega function, can be extracted from the raw data and these secondary parameters can be fit to various association models (4, 37, 38). Also, Lewis and coworkers have described a matrix method in which sedimentation equilibrium profiles at multiple wavelengths are used to construct molar concentration distributions of each reactant (35). These concentration distributions are then jointly fit to an association model to obtain equilibrium constants. We prefer the direct fitting approach because it requires less manipulation of the data and the experimental uncertainty is statistically well defined.
For a single ideal species (A), the radial absorption gradient at sedimentation equilibrium is given by:
| (12) |
where A(r,λ) is the radial-dependent absorbance at wavelength λ, δλ is a baseline offset, εA,λ is the molar extinction coefficient of A, C0,A is the molar concentration of A at the arbitrary reference distance r0 and M*A is the buoyant mass of A. M*A is defined by
| (13) |
where MA is the mass of A, v̄A is the partial specific volume of A and ρ is the solvent density. The factor Φ is given by
| (14) |
where ω is the angular velocity of the rotor in radians/sec, R is the molar gas constant and T is the absolute temperature. The baseline offset term arises from absorption mismatches between the sample and reference sectors due to the presence of nonsedimenting, absorbing contaminants or unequal oxidation of reductants such as DTT. The concentrations of each of the complexes AiBj at are defined in terms of equilibrium constants and the concentrations of A and B using equation 2. The total radial concentration gradient A(r,λ) is then written as the sum of the contributions from the free A, B and each of the complexes:
| (15) |
Here, the Kjj terms are written as overall equilibrium constants and are expressed in the form exp [ln Kj] to constrain them to be positive. It is worth noting a few of the implicit assumptions contained within equation 15:
Reversible equilibrium. It is assumed that all of the species present in the sample participate in a reversible mass-action equilibrium. If there are monomeric or oligomeric species that are not in equilibrium or significant impurities present, additional terms must be added to accommodate this additional heterogeneity.
Absence of absorption changes. We assume that the molar extinction coefficient of the species AiBj is the composition-weighted sum of the extinction of the individual components A and B. The extent of hypo- or hyper-chromism effects can easily be tested beforehand using absorption mixing experiments.
Absence of volume changes. In the absence of volume changes the buoyant molecular mass of the complex is the composition-weighted sum of the components: iMA* + jMB*.
Analysis of Sedimentation Equilibrium Data
When using equation 15 to fit experimental data it is critical to reduce the number of adjustable parameters to obtain reliable, unique and well-defined estimates of the equilibrium constants. Typically, we measure the buoyant masses of A and B in a series of independent experiments and fix these values for the analysis of the hetero-interaction. This also serves as a quality-control step to ensure that the individual reactants are homogeneous and well behaved in solution. Sedimentation velocity experiments are also useful to determine homogeneity. In addition, where possible the baseline offsets are measured by overspeeding following the experiment. This is accomplished by increasing the rotor speed to 45,000 RPM following the experiment, waiting 4–10 hours to allow the meniscus region to become depleted of macromolecular species, and then recording the absorption near the meniscus at each of the wavelengths of interest. It is not possible to completely deplete the meniscus of A or B when these components are lower molecular weight. In this case, estimates of the offsets can be obtained by fitting the radial absorption gradient near the meniscus using a single ideal species model (equation 12), but this approach is less reliable.
It is critical that the relative molar extinction coefficients are accurately determined at each wavelength when performing global analysis on data obtained at multiple wavelengths. The accuracy of wavelength selection for the monochromator in the XL-A centrifuge is on the order of ± 2 nm, which can result in substantial errors, particularly at 230 nm, which is on a steeply rising shoulder of the protein absorbance. In each experiment we include at least two sample channels containing pure components, A and B, respectively. Once equilibrium is achieved, data are collected at each wavelength of interest. It is critical to scan all the cells at one wavelength before collecting data at the next wavelength; otherwise, the wavelength setting will not be consistent between the different cells. We typically calculate the absolute extinction coefficients for protein at 280 nm and nucleic acid at 260 nm based on composition or other experimental measurements. Then, the relative extinction coefficients at other wavelengths is experimentally determined in the XL-A centrifuge by jointly fitting absorption gradients obtained from channels containing either pure protein or nucleic acid using a procedure described by Lewis et al. (35). In this manner, a self-consistent set of extinction coefficients are obtained for each experiment.
There are several software options available for global analysis of heterogeneous interactions by sedimentation equilibrium. First, it should be noted that the popular WinNonlin software ((39); www.ucc.uconn.edu/~wwwbiotc/UAF.html ) is limited to self-association models as are the ORIGIN-based software supplied with the Beckman-Coulter instrument and the ULTRASCAN package ( www.ultrascan.uthscsa.edu). Two freely-distributed packages for analysis of hetero-interactions are TWOCOMP ((4); www.bbri.org/rasmb/rasmb.html) and ULTRASPIN (www.mrc-cpe.cam.ac.uk/ultraspin_intro.php) Although these packages are very useful for certain applications they are somewhat limited in the models that can be analyzed and the quantity of the data that can be simultaneously fit. Therefore, many researchers, including us, employ commercial mathematical software packages such as IGOR Pro (Wavemetrics; www.wavemetrics.com), MLAB (Civilized software; www.civilized.com) and MATLAB (Mathworks, www.mathworks.com). For complex association models, it can be useful to perform experimental simulations to test whether the parameters of interest are experimentally accessible and to ensure that the experimental conditions (loading concentrations, rotor speeds, wavelengths) are devised to maximize the information content. In particular, if the user is interested in measuring equilibrium constants with accuracy it is important that the loading concentrations are chosen such that each of the species participating in the equilibria are significantly populated. A useful simulation package is available within the TWOCOMP software.
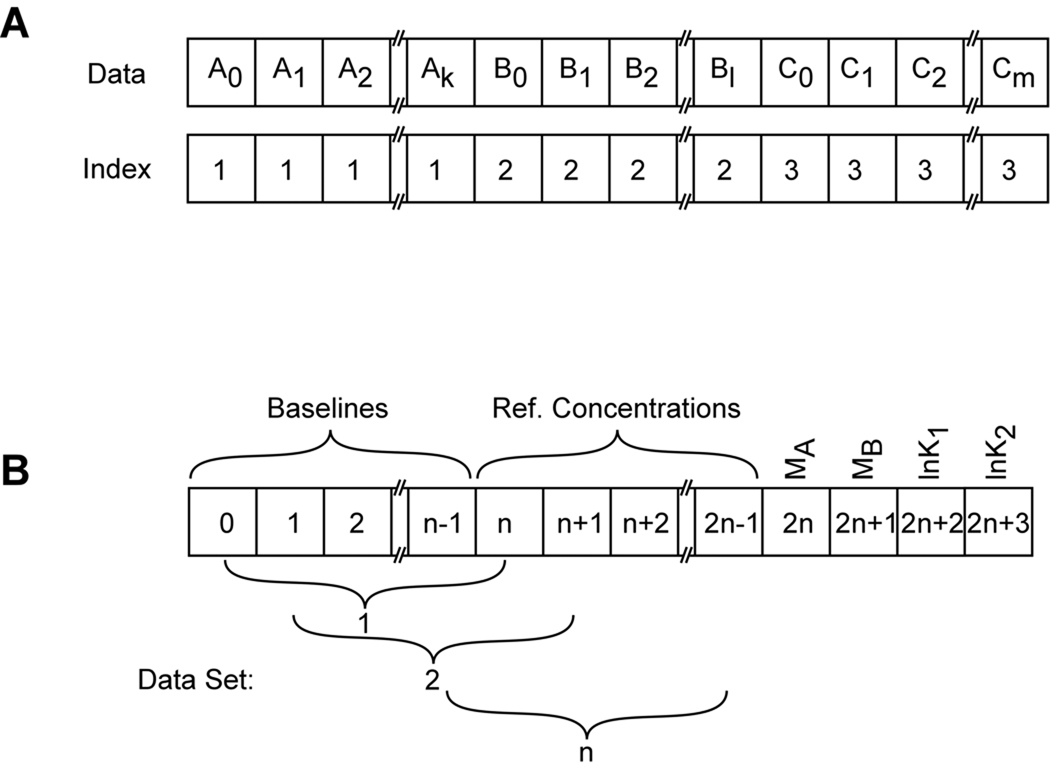
The general issues involved in global nonlinear least squares analysis have been described in this series (40). However, there are a few particular considerations for global analysis of heterogeneous interactions by sedimentation equilibrium: some parameters must be defined to be local to each centrifuge cell or radial absorbance scan and others must be global to the entire data set. Our implementation of global analysis (XLAnalysis) is a collection of functions and procedures within the IGOR Pro software. It uses a simple indexing scheme (41). Each data file contains two arrays: the independent variable x (radius) and the dependent variable y (absorbance or fringe displacement). For global analysis the data sets from each of the channels, A,B,C,…n, are concatenated to produce a single x and a single y array (Figure 2). An integer index array is also created which labels each point in the concatenated array with the source data file. Additionally, arrays are also created which contain ancillary data (reference distances, rotor speeds, extinction coefficient(s)). In the fitting procedure, certain parameters (baseline offsets, reference concentrations) are usually local to each channel and others (buoyant masses, equilibrium constants, stoichiometries) are global. In multiwavelength experiments, multiple radial absorption gradients may originate from the same physical sample cell and the reference concentrations for A and B that refer to the same sample should be constrained to be equal. The reference radii chosen for these data channels must be equal as well. The fitting parameters are passed to the fitting functions in an array that allow the function to discriminate between these local and global parameters using the index array and a global variable containing the number of fit files, n (see figure 2). The array is designed such that it is independent of the number of files being fit but it is dependent on the nature of the fitting model.
Figure 2.
Array designs used in global nonlinear least squares fitting of sedimentation equilibrium experiment. A) Design of the concatenated data arrays. Individual data sets are denoted A, B, C, with elements 0-k, 0-l, and 0-m, respectively. The index vector labels each point in the array with the source data file. B) Design of the parameter array for an A+2B → AB2 model with n data sets.
There are several numerical algorithms commonly in use for parameter estimation by nonlinear least squares analysis (42, 43). The original Nonlin program (39) utilizes a variation of the Gauss-Newton method that does not make the assumption of orthogonality at the initial stages of convergence (42). The Marquardt algorithm is the most commonly used method and combines the steepest descent and Gauss-Newton methods (43, 44). In our experience, the two methods work equally well for systems in which a well-defined minimum is present in the error surface. Finally, the Simplex directed search method is less efficient but is guaranteed to converge (45).
In many commercial software packages, the usual method to obtain parameter confidence intervals is based on the variance/covariance matrix, which can seriously underestimate the actual confidence intervals for nonlinear models. We use the F-statistic as a more rigorous measure of significance of the increase in the value of the least squares norm (42, 43). The confidence intervals for a parameter of interest are obtained by fixing it at some value slightly removed from the best fit and performing a fit where all of the other parameters are free to adjust to their best-fit values. The variance of this fit is calculated and the parameter is incremented or decremented until the ratio of the variance for this constrained fit to the variance for the best-fit value (s2/s2minimum) equals the target ratio, defined by
| (14) |
where M is the number of parameters, N is the number of data points, F is the F-statistic and P is the probability that two fits are equivalent. The search is conducted for each parameter in turn using a bisection algorithm. This method makes no assumptions regarding the shape of the error surface and accounts for the cross-correlation (nonorthogonality) of the fitting parameters and the nonlinearity of the fitting equation. It is also helpful to visualize the error surface by examining two or three-dimensional projection plots of the multidimensional error surface (42, 43). These plots can be used to verify whether a global minimum has been found and to probe parameter correlation (25, 46).
Example: Binding of protein kinase R to RNA
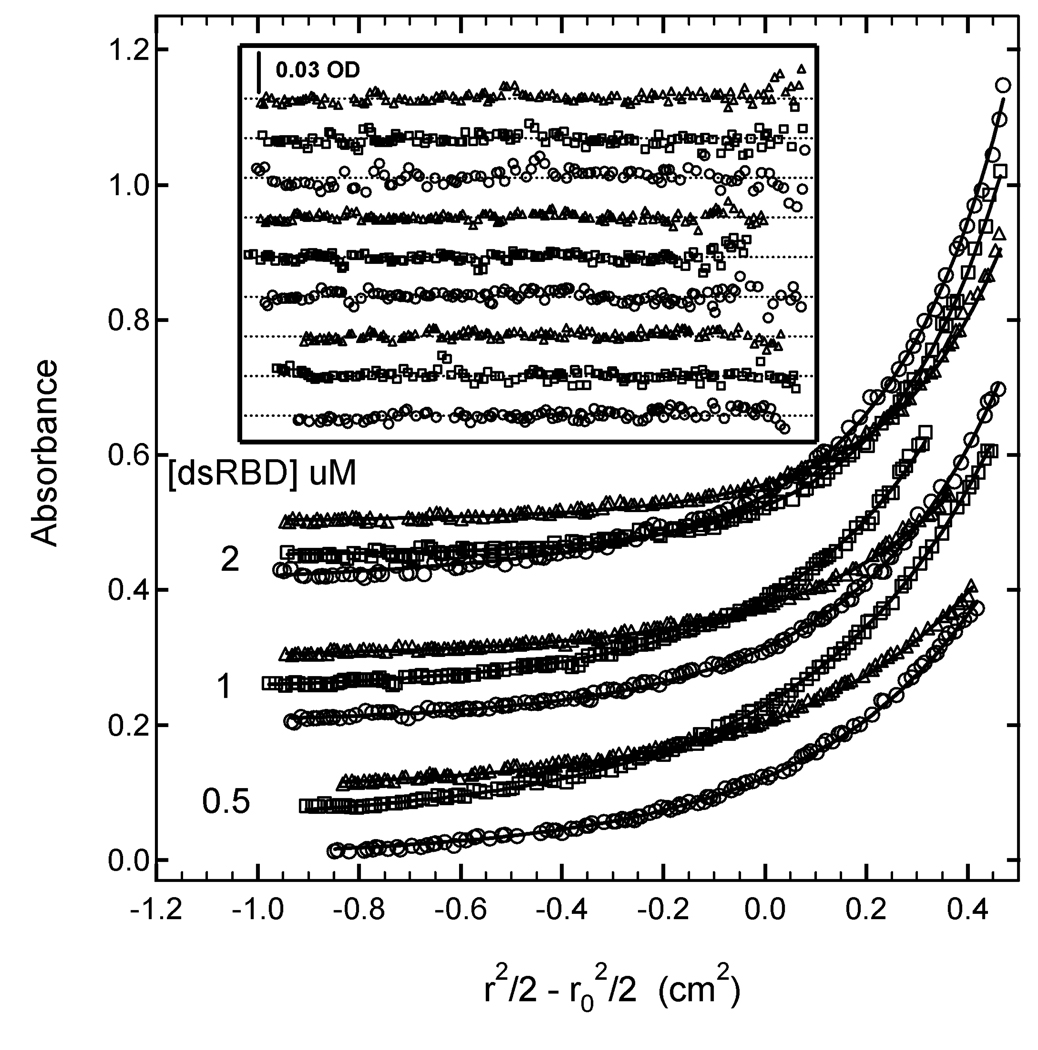
Protein kinase R (PKR) is contains an N-terminal double-stranded RNA binding domain (dsRBD) and a C-terminal kinase domain (47). PKR binds to RNA in a nonspecific manner. Here, we characterize binding of the N-terminal dsRBD domain (amino acids 1–184) with a 20 base pair RNA by sedimentation equilibrium. Previous experiments established a binding stoichiometry of three dsRBD/RNA (17). Based on this data, samples for sedimentation equilibrium were prepared at multiple concentrations of A (RNA) and B (protein) ([A] = 0.5 µM, [B] = 0.5, 1 and 2 µM). Data were collected at three detection wavelengths (230,260 and 280 nm) and were globally analyzed using several alternative models to a model that incorporated AB, AB2 and AB3 species (17). Figure 3 shows the data from all nine channels and a global fit to a model using three independent stepwise equilibrium constants. The best-fit parameters and statistics are summarized in table 2. The global fit is a good description of the experimental data, with no systematic deviations in the residuals and a low value of the RMS deviation of 0.00437 OD, which is consistent with the noise level in the optical system. The high value of LnK1 of 18.32 indicates that first dsRBD binds strongly to the dsRNA (Kd= 11 nM). Although the 95% joint confidence intervals are relatively broad, there is a clear trend of decreasing binding strength with successive ligands, such that the third dsRBD binds significantly weaker, with LnK3= 14.07 (Kd = 0.78 µM). The ratios of the equilibrium constants are: K1/K2 = 19 and K1/K3 = 70.
Figure 3.
Multiwavelength sedimentation equilibrium of PKR dsRBD binding to 20 mer dsRNA. The data were obtained under the following conditions: rotor speed, 23,000 RPM; temperature, 20°C; RNA concentration, 0.5 µM and protein concentrations of 0.5 µM, 1 µM and 2 µM in 75 mM NaCl, 20 mM HEPES, 5 mM MgCl2, 0.1 mM EDTA, pH 7.5. Detection wavelengths are: 230 nm (o), 260 nm ( ) and 280 nm (△). Solid lines are a global fit of the data to an unconstrained model of three ligands binding to the 20 mer RNA. The results of the fit are given in table I. Inset: residuals. Traces have been vertically offset for clarity.
) and 280 nm (△). Solid lines are a global fit of the data to an unconstrained model of three ligands binding to the 20 mer RNA. The results of the fit are given in table I. Inset: residuals. Traces have been vertically offset for clarity.
Table 2.
Equilibrium Constants for binding of PKR dsRBD to a 20-mer RNA as determined by sedimentation equilibrium.
| Model | ln K1a | ln K2a | ln K3a | ln kb | RMS X10−3c |
|---|---|---|---|---|---|
| Unconstrainedd | 18.32 [17.21,19.48] | 15.38 [14.43,16.94] | 14.07 [13.54,14.47] | - | 4.37 |
| N=14, Δ=3e | 17.96 | 16.37 | 13.71 | 16.01 [15.77,16.23] | 4.48 |
| N=12, Δ=4e | 18.51 | 16.82 | 13.60 | 16.31 [16.07, 16.58] | 4.48 |
Natural logarithm of the macroscopic binding constant. The values in brackets represent the 95% joint confidence intervals.
Natural logarithm of the intrinsic binding constant. The values in brackets represent the 95% joint confidence intervals.
Root mean square deviation of the fit in absorbance units (OD).
Independent binding of three ligands. The natural logarithms of the macroscopic binding constants are the fitted parameters.
Finite lattice models. The natural logarithms of the intrinsic binding constants are the fitted parameters. The macroscopic binding constants are calculated using coefficients determined by equation 11.
A decrease in equilibrium constants with successive ligand binding events is predicted from statistical effects in the context of both the simple finite lattice model as well the finite lattice model that includes ligand overlap. Table 2 summarizes fits to several of these models in which the intrinsic equilibrium constant lnk is the fitted parameter and the values of LnK1, LnK2 and Lnk3 are calculated using equations 6 and 11. In all cases, the stoichiometry s was fixed at 3. In the context of the model that includes ligand overlap, an equally good fit is found for N=14 with Δ=3 (Table 2); successively worse fits are found as N is reduced and Δ is held constant (data not shown). We have not considered larger site sizes, since for Δ=3 a value of N> 14 reduces S to 2. A good fit is also found for N=12 with Δ=4. Again, worse fits are found with smaller site sizes and larger site sizes reduce the stoichiometry to 2. Models with Δ=2 are not considered because this close overlap between adjacent bound ligands would likely be disallowed due to steric hindrance. In summary, the multiwavelength sedimentation data fit well to several models where three dsRBD interact with the 20 bp dsRNA and the relative values of the three equilibrium constants are constrained according to the finite lattice model including ligand overlap. The best fits consistent with available structural information include a minimum offset (Δ) of 3–4 and site size (N) of 12–14 bp. These fits also reveal a value of the intrinsic binding constant of ln k = 16.0–16.3, or kd= 83–110 nM.
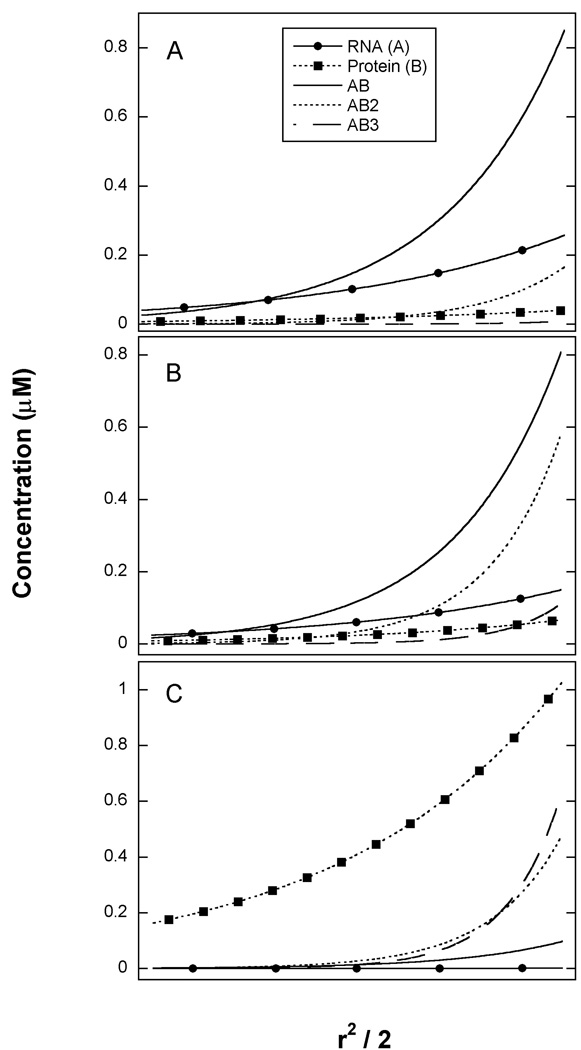
It is worthwhile to graphically analyze the fitting results by plotting the modeled radial distributions for each species in the three samples in order to appreciate why the sedimentation equilibrium experiment is capable of resolving the three equilibrium constants. At the lowest protein concentration (panel A) the most abundant species are the AB complex and free A, along with low concentrations of AB2 and free B. Thus, each of the species participating in the equilibrium governed by K1 are populated: A, B and AB. At intermediate protein concentration (Panel B), the AB and AB2 species are most prominent and at the highest protein concentration (panel C), the most abundant complexes are AB2 and AB3 along with high concentrations of free B. Thus at higher protein concentrations, the species governed by K2 and K3 become populated. In order to accurately define equilibrium constants it is necessary that all of the species participating in the equilibrium are populated. In the present case, it was necessary to span a range of A:B ratios to achieve significant population of each of the complexes. In the case of heterogeneous associations it has also been pointed out that much useful information can come from samples that are prepared far from the preferred stoichiometry (32).
Conclusion
A variety of biophysical techniques with a range of capabilities are available to probe heterogeneous macromolecular interactions. The choice of technique is governed chiefly by the type of information that is required and by the specific properties of the material under investigation. Analytical ultracentrifugation measurements are particularly useful at the beginning of a study to define an association model; subsequently, higher-throughput methods may be more convenient to analyze large numbers of samples.
Figure 4.
Species distribution from sedimentation equilibrium analysis of PKR dsRBD binding to 20 mer dsRNA. Best fit parameters from the unconstrained analysis in Table 2 were used to generate radial concentration gradients for all the species present in solution. Species are RNA ( ), protein (
), protein ( ), AB (
), AB ( ), AB2 (
), AB2 ( ), AB3 (
), AB3 ( ). A) [RNA] = 0.5 µM, [Protein] = 0.5 µM. B) [RNA] = 0.5 µM, [Protein] = 1 µM. C) [RNA] = 0.5 µM, [Protein] = 2 µM.
). A) [RNA] = 0.5 µM, [Protein] = 0.5 µM. B) [RNA] = 0.5 µM, [Protein] = 1 µM. C) [RNA] = 0.5 µM, [Protein] = 2 µM.
Acknowledgements
I thank Jason Ucci for his contributions to the studies of PKR and Jeff Lary for careful reading of this manuscript. This work was supported by the University of Connecticut's Research Advisory Council Programs.
References
- 1.von Mering C, Krause R, Snel B, Cornell M, Oliver SG, Fields S, Bork P. Nature. 2002;417:399–403. doi: 10.1038/nature750. [DOI] [PubMed] [Google Scholar]
- 2.Stafford WF. Methods Enzymol. 2003 This volume. [Google Scholar]
- 3.Dam J, Schuck P. Methods Enzymol. 2003 doi: 10.1016/S0076-6879(04)84012-6. This volume. [DOI] [PubMed] [Google Scholar]
- 4.Minton AP. Prog. Colloid Polym. Sci. 1997;107:11–19. [Google Scholar]
- 5.Edsall JT, Wyman J. Biophysical Chemistry. New York: Academic Press; 1958. [Google Scholar]
- 6.Doyle ML, Brigham-Burke M, Blackburn MN, Brooks IS, Smith TM, Newman R, Reff M, Stafford WF, Sweet RW, Truneh A, Hensley P, O'Shannessy DJ. Methods Enzymol. 2000;323:207–230. doi: 10.1016/s0076-6879(00)23368-5. [DOI] [PubMed] [Google Scholar]
- 7.Cantor CR, Schimmel PR. New York: W.H. Freeman and Co; 1980. pp. 849–886. [Google Scholar]
- 8.Johnson ML, Straume M. Methods Enzymol. 2000;323:155–167. doi: 10.1016/s0076-6879(00)23365-x. [DOI] [PubMed] [Google Scholar]
- 9.Revzin A. The biology of nonspecific DNA-protein interactions. Boca Raton: CRC Press; 1990. [Google Scholar]
- 10.Correia JJ, Chaires JB. Methods Enzymol. 1994;240:593–614. doi: 10.1016/s0076-6879(94)40065-2. [DOI] [PubMed] [Google Scholar]
- 11.Munro PD, Jackson CM, Winzor DJ. J. Theor. Biol. 2000;203:407–418. doi: 10.1006/jtbi.2000.1099. [DOI] [PubMed] [Google Scholar]
- 12.McGhee JD, von Hippel PH. J. Mol. Biol. 1974;86:469–489. doi: 10.1016/0022-2836(74)90031-x. [DOI] [PubMed] [Google Scholar]
- 13.Schmedt C, Green SR, Manche L, Taylor DR, Ma Y, Mathews MB. J. Mol. Biol. 1995;249:29–44. doi: 10.1006/jmbi.1995.0278. [DOI] [PubMed] [Google Scholar]
- 14.Wojtuszewski K, Hawkins ME, Cole JL, Mukerji IJ. Biochemistry. 2001;40:2588–2598. doi: 10.1021/bi002382r. [DOI] [PubMed] [Google Scholar]
- 15.Bevilacqua PC, Cech TR. Biochemistry. 1996;35:9983–9994. doi: 10.1021/bi9607259. [DOI] [PubMed] [Google Scholar]
- 16.Levin MK, Patel SS. J Biol Chem. 2002;277:29377–29385. doi: 10.1074/jbc.M112315200. [DOI] [PubMed] [Google Scholar]
- 17.Ucci JW, Cole JL. Biophys. Chem. 2003 doi: 10.1016/j.bpc.2003.10.033. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Epstein IR. Biophys. Chem. 1978;8:327–339. doi: 10.1016/0301-4622(78)80015-5. [DOI] [PubMed] [Google Scholar]
- 19.Tsodikov OV, Holbrook JA, Shkel IA, Record MT., Jr Biophys. J. 2001;81:1960–1969. doi: 10.1016/S0006-3495(01)75847-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Latt SA, Sober HA. Biochemistry. 1967;6:3293–3306. doi: 10.1021/bi00862a040. [DOI] [PubMed] [Google Scholar]
- 21.Hensley P. Structure. 1996;4:367–373. doi: 10.1016/s0969-2126(96)00042-1. [DOI] [PubMed] [Google Scholar]
- 22.Correia JJ. Methods Enzymol. 2000;321:81–100. doi: 10.1016/s0076-6879(00)21188-9. [DOI] [PubMed] [Google Scholar]
- 23.Stafford WF, Sherwood PJ. Biophys. Chem. 2003 doi: 10.1016/j.bpc.2003.10.028. In press. [DOI] [PubMed] [Google Scholar]
- 24.Holmstrom K, Petersson J. Appl. Math. Comput. 2002;126:31–61. [Google Scholar]
- 25.Cole JL, Carroll SS, Blue ES, Viscount T, Kuo LC. J. Biol. Chem. 1997;272:19187–19192. doi: 10.1074/jbc.272.31.19187. [DOI] [PubMed] [Google Scholar]
- 26.Cole JL, Carroll SS, Kuo LC. J. Biol. Chem. 1996;271:3979–3981. doi: 10.1074/jbc.271.8.3979. [DOI] [PubMed] [Google Scholar]
- 27.Carroll SS, Cole JL, Viscount T, Geib J, Gehman J, Kuo LC. J. Biol. Chem. 1997;272:19193–19198. doi: 10.1074/jbc.272.31.19193. [DOI] [PubMed] [Google Scholar]
- 28.Cole JL, Hansen JC. J. Biomolecular Techniques. 1999;10:163–174. [PMC free article] [PubMed] [Google Scholar]
- 29.Schuck P, Braswell E. Current Protocols in Immunology. 2002 doi: 10.1002/0471142735.im1808s79. Section 18.8.1–18.8.22. [DOI] [PubMed] [Google Scholar]
- 30.Lebowitz J, Lewis MS, Schuck P. Protein Sci. 2002;11:2067–2079. doi: 10.1110/ps.0207702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Laue TM, Stafford WF. Ann. Rev. Biophys. Biomol. Struct. 1999;28:75–100. doi: 10.1146/annurev.biophys.28.1.75. [DOI] [PubMed] [Google Scholar]
- 32.Philo JS. Methods Enzymol. 2000;321:100–120. doi: 10.1016/s0076-6879(00)21189-0. [DOI] [PubMed] [Google Scholar]
- 33.Bailey MF, Davidson BE, Minton AP, Sawyer WH, Howlett GJ. J. Mol. Biol. 1996;263:671–684. doi: 10.1006/jmbi.1996.0607. [DOI] [PubMed] [Google Scholar]
- 34.Kim SJ, Tsukiyama T, Lewis MS, Wu C. Protein Sci. 1994;3:1040–1051. doi: 10.1002/pro.5560030706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lewis MS, Shrager RI, Kim S-J. In: "Modern Analytical Ultracentrifugation". Shuster TM, Laue TM, editors. Boston: Birkhauser; 1994. pp. 94–115. [Google Scholar]
- 36.Laue TM, Senear DF, Eaton S, Ross JB. Biochemistry. 1993;32:2469–2472. doi: 10.1021/bi00061a003. [DOI] [PubMed] [Google Scholar]
- 37.Milthorpe BK, Jeffrey PD, Nichol LW. Biophys. Chem. 1975;3:169–176. doi: 10.1016/0301-4622(75)80007-x. [DOI] [PubMed] [Google Scholar]
- 38.Winzor DJ, Jacobsen MP, Wills PR. Biochemistry. 1998;37:2226–2233. doi: 10.1021/bi972211v. [DOI] [PubMed] [Google Scholar]
- 39.Johnson ML, Correia JJ, Yphantis DA, Halvorson HR. Biophys. J. 1981;36:575–588. doi: 10.1016/S0006-3495(81)84753-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Beecham JM. Methods Enzymol. 1992;210:37–54. doi: 10.1016/0076-6879(92)10004-w. [DOI] [PubMed] [Google Scholar]
- 41.Johnson ML, Straume M. In: "Modern Analytical Ultacentrifugation". Shuster TM, Laue TM, editors. Boston: Birkhauser; 1994. pp. 37–65. [Google Scholar]
- 42.Johnson ML, Faunt LM. Methods Enzymol. 1992;210:1–37. doi: 10.1016/0076-6879(92)10003-v. [DOI] [PubMed] [Google Scholar]
- 43.Bevington PR, Robinson DK. Data Reduction and Error Analysis for the Physical Sciences. New York: McGraw-Hill; 1992. [Google Scholar]
- 44.Marquardt DW. SIAM J. Appl. Math. 1963;14:1176. [Google Scholar]
- 45.Nelder JA, Mead R. Computer J. 1965;7:308–313. [Google Scholar]
- 46.Schuck P, Radu CG, Ward ES. Mol. Immunol. 1999;36:1117–1125. doi: 10.1016/s0161-5890(99)00093-0. [DOI] [PubMed] [Google Scholar]
- 47.Clemens MJ, Elia A. J. Interferon Cytokine Res. 1997;17:503–524. doi: 10.1089/jir.1997.17.503. [DOI] [PubMed] [Google Scholar]
- 48.Rivas G, Stafford W, Minton AP. Methods. 1999;19:194–212. doi: 10.1006/meth.1999.0851. [DOI] [PubMed] [Google Scholar]
- 49.Fisher HF, Singh N. Methods Enzymol. 1995;259:194–221. doi: 10.1016/0076-6879(95)59045-5. [DOI] [PubMed] [Google Scholar]
- 50.Weber PC, Salemme FR. Curr. Opin. Struct. Biol. 2003;13:115–121. doi: 10.1016/s0959-440x(03)00003-4. [DOI] [PubMed] [Google Scholar]
- 51.Myszka DG. Methods Enzymol. 2000;323:325–340. doi: 10.1016/s0076-6879(00)23372-7. [DOI] [PubMed] [Google Scholar]
- 52.Schuck P. Annu Rev Biophys Biomol Struct. 1997;26:541–566. doi: 10.1146/annurev.biophys.26.1.541. [DOI] [PubMed] [Google Scholar]
- 53.Harding SE, Sattelle DB, Bloomfield VA. Laser light scattering in biochemistry. Cambridge: Royal Society of Chemistry; 1992. [DOI] [PubMed] [Google Scholar]
- 54.Harding SE. Methods Mol. Biol. 1994;22:85–95. doi: 10.1385/0-89603-232-9:85. [DOI] [PubMed] [Google Scholar]
- 55.Wen J, Arakawa T, Philo JS. Anal. Biochem. 1996;240:155–166. doi: 10.1006/abio.1996.0345. [DOI] [PubMed] [Google Scholar]
- 56.Jameson DM, Sawyer WH. Methods Enzymol. 1995;246:283–300. doi: 10.1016/0076-6879(95)46014-4. [DOI] [PubMed] [Google Scholar]
- 57.Thompson NL, Lieto AM, Allen NW. Curr. Opin. Struct. Biol. 2002;12:634–641. doi: 10.1016/s0959-440x(02)00368-8. [DOI] [PubMed] [Google Scholar]
- 58.Lundblad JR, Laurance M, Goodman RH. Mol. Endocrinol. 1996;10:607–612. doi: 10.1210/mend.10.6.8776720. [DOI] [PubMed] [Google Scholar]
- 59.Provencher SW. Comp. Phys. Comm. 1982;27:229–242. [Google Scholar]
- 60.Zhang YL, Zhang ZY. Anal. Biochem. 1998;261:139–148. doi: 10.1006/abio.1998.2738. [DOI] [PubMed] [Google Scholar]
- 61.Doyle ML, Louie G, Dal Monte PR, Sokoloski TD. Methods Enzymol. 1995;259:183–194. doi: 10.1016/0076-6879(95)59044-7. [DOI] [PubMed] [Google Scholar]
- 62.Sigurskjold BW. Anal. Biochem. 2000;277:260–266. doi: 10.1006/abio.1999.4402. [DOI] [PubMed] [Google Scholar]