Global Analysis of Nonspecific Protein-Nucleic Interactions by Sedimentation Equilibrium

Abstract

Protein-nucleic acid interactions govern a variety of processes, including replication, transcription, recombination and repair. These interactions take place in both sequence-specific and nonspecific modes, and the latter occur in many biologically significant contexts. Analytical ultracentrifugation is a useful method for the detailed characterization of the stoichiometry and affinity of macromolecular interactions in free solution. There has been a resurgence of interest in the application of sedimentation equilibrium methods to protein-nucleic acid interactions. However, these studies have generally focused on sequence-specific interactions. Here we describe an approach to analyze nonspecific interactions using sedimentation equilibrium. We have adapted an existing model for nonspecific interaction of proteins with finite, one-dimensional nucleic acid lattices for global fitting of multiwavelength sedimentation equilibrium data. The model is extended to accommodate protein binding to multiple faces of the nucleic acid, resulting in overlap of consecutive ligands along the sequence of the RNA or DNA. The approach is illustrated in a sedimentation equilibrium analysis of the interaction of the double-stranded RNA binding motif of protein kinase R with a 20 basepair RNA construct.

1. Introduction

Reversible protein - nucleic acid interactions are a highly diverse family of binding phenomena that govern many significant biological processes, including replication, transcription, recombination and repair. Historically, sedimentation velocity measurements played an important role in quantitative analysis of protein-nucleic acid binding reactions [1-4] and one study pointed to the use of SE for protein-nucleic acid interactions [5]. However, the electrophoretic mobility shift assay [6,7] and the nitrocellulose filter binding assays [8] largely supplanted analytical ultracentrifugation as the prevalent methods to define protein-nucleic interactions. More recently, there has been a resurgence of interest in the use of SE in the quantitative analysis of protein nucleic acid interactions [9-14]. Most of these studies have focused on sequence specific protein-nucleic acid interactions, where high affinity binding requires a specific DNA or RNA sequence. In other systems, the interactions involve the sugar-phosphate backbone or do not discriminate among the nucleic acid bases and are not sequence specific. Although somewhat less glamorous, these nonspecific interactions are ubiquitous in molecular biology [15]. Replication, recombination and repair all involve proteins that exhibit nonspecific, cooperative binding to single-stranded DNA. Helicases and retroviral integrases interact nonspecifically with ds nucleic acids. A large class of enzymes and proteins contain one or more copies of the dsRBM that confers nonspecific binding to dsRNA [16]. Even proteins that interact at specific nucleic acid sites, such as repressors, RNA polymerases and restriction enzymes, show significant nonspecific binding to nucleic acids.

A variety of experimental approaches have been applied to study non-specific protein –nucleic acid binding reactions [17]. In some of the more popular methods, such as the electrophoretic mobility shift and nitrocellulose filter binding assays, the measurements are performed under non-equilibrium conditions. Re-equilibration of the bound and free protein ligand may occur on the timescale of the experiment and can result in inaccurate parameter estimation [18]. Under carefully controlled conditions, the gel shift [19] and filter binding [20] assays can accurately define solution equilibria. However, nonspecific interactions generally have lower affinity and higher dissociation rates than specific interactions and are thus particularly susceptible to artifacts associated with dissociation during the measurement. In addition, nonspecific interactions typically involve binding of multiple protein ligands, and in the case of the filter-binding assay, there is no defined relationship between the extent of saturation and the degree of filter retention [21]. Therefore, it is advantageous to employ alternative methods that directly probe solution equilibria, such as spectroscopic measurements, calorimetry and analytical ultracentrifugation. Most studies have employed fluorescence spectroscopy, using long homopolymeric DNA incorporating fluorescent-labeled bases. Here, we focus on the applications of SE for the analysis of nonspecific interactions. We adapt an existing model for the interaction of protein with finite nucleic acid lattices for SE analysis, and extend this model to accommodate the overlapping binding of ligands on different faces of a ds RNA or DNA. We then apply this approach to analyze the interaction of the RNA binding domain of PKR with a 20 bp dsRNA.

2. Materials and Methods

2.1 Protein Expression and Purification

The plasmid His-p20 was cut with NdeI /BamHI and the insert was ligated into pET 11a (Novagen) to produce the expression vector pET-p20. This plasmid encodes the dsRBD of PKR (amino acids 1-184) The vector was transformed into Rosetta DE3 (pLysS) E. coli expression cells (Novagen). Our expression and purification protocol is adapted from a previous method [22]. Cells were grown in LB medium containing 50 μg/ml ampicillin and 34 μg/ml chloramphenicol at 37°C until OD₆₀₀ = 0.6. Protein expression was induced with 1mM isopropyl-1-thio-β-D-galactopyranoside followed by an additional 3 hours incubation at 37°C. Cells were harvested by centrifugation at 3,000 X g for 15 min and resuspended in 15 ml of lysis buffer (20 mM HEPES, 100 mM NaCl, 1 mM EDTA, 5% Glycerol, 1 mM DTT, pH 7.5) containing protease inhibitor cocktail (Sigma). Cells were lysed by sonication (Fisher sonic dismembrator) for twenty 30 sec intervals on power level 6. The lysate was precipitated with the addition of 0.5% w/v polyethyleneimine, incubation on ice for 15 min. and centrifugation at 30,000 X g for 15 min. The supernatant was loaded onto an S-Sepharose FF (Amersham) column and the column was washed with buffer A (20 mM Bicine, 50 mM NaCl, 1 mM EDTA, 5% Glycerol, 10 mM BME, pH 8.65). The dsRBD was eluted using a 50 mM to 500 mM linear gradient of NaCl. Fractions containing dsRBD were pooled, diluted 3-fold with buffer A containing no NaCl, and loaded onto Heparin Sepharose FF column (Amersham). The dsRBD was eluted using a 50 mM to 500 mM linear gradient of NaCl. A final gel filtration purification step was performed on a Sephacryl S-100 column (Amersham) equilibrated in 20 mM HEPES, 75 mM NaCl, 1 mM EDTA 1 mM DTT, pH 7.5. Peak fractions were concentrated and stored at −80°C. Purity was assayed by SDS-PAGE and the protein identity was confirmed by MALDI mass spectroscopy. Protein concentration was determined by absorbance at 280 nm. A value of ε₂₈₀= 1.23 ×10⁴ M⁻¹ cm⁻¹ was determined using a modification of the Edelhoch method [23].

2.2 RNA Preparation

The following synthetic oligoribonucleotides were obtained from IDT: TS20, 5′- GGA GAA CUU CAU GCC CUU CG - 3′; BS20, 5′-CGA AGG GCA UGA AGU UCU CC - 3′. dsRNA was prepared by mixing equimolar amounts of each strand at 10 μM in 10 mM Tris, pH 7.5, heating to 60° C and slowly cooling to room temperature. The concentration of dsRNA was assayed by absorbance using ε₂₆₀= 3.26 ×10⁵ M⁻¹cm⁻¹.

2.3 Analytical Ultracentrifugation

SE was performed using 6-channel (1.2 cm path) charcoal-Epon cells with a Beckman XL-I centrifuge and an An-60Ti rotor at a temperature of 20 °C. Protein and dsRNA samples were prepared by buffer exchange into 20 mM HEPES, 75 mM NaCl, 0.1 mM EDTA, pH 7.5 using Biogel P6 spin columns (Biorad). Sample volumes were 108 μL with 10 μL of FC43 and reference channels contained 123 μL of buffer. Sedimentation was performed at the indicated rotor speed until equilibrium was achieved, as judged by the absence of systematic deviations in a plot of the difference between successive scans taken 4 h apart and using the WinMatch program. Scans were recorded using 0.001 cm point spacing and averaging 10 readings at each point.

3. Methodology

3.1 Multiwavelength SE Analysis of Protein – Nucleic Acid Interactions: Practical Issues

SE analysis of interactions between dissimilar partners (hetero-interactions) is considerably more complex than self-association because the fitting models give rise to a larger number of adjustable parameters. The analyses are plagued by multiple minima and by unacceptably broad confidence intervals for the deduced parameters due to extensive cross-correlation. A variety of methods have been described to circumvent these problems [24,25]. In the case of protein-nucleic acid interactions, where the two reactants have markedly different absorption spectra, collection of SE gradient profiles at multiple wavelengths is particularly useful to accurately define the concentration of each of the components and to enhance sensitivity. The bases in DNA or RNA have absorption maxima near 260, and for a typical oligonucleotide of 20 bp, ε260 ~ 3 × 10⁵ M⁻¹ cm⁻¹. This value is reduced by about a factor of two at 280 nm. In contrast, the protein side chains absorption maximum is near 280 nm; for a 30 kDa protein with a typical aromatic amino acid content, ε280 ~ 3×104 M⁻¹ cm⁻¹ and is reduced by about two-fold at 260 nm. Thus, the concentration of protein and DNA or RNA can be independently assayed by the absorbance at two wavelengths, 260 and 280 nm. However, the overall absorbance is dominated by the nucleic acid and the sensitivity for protein is ~10-fold lower. For this reason, we also collect data at shorter wavelengths where the protein extinction is greater than at 280 nm and the contribution of nucleic acid is reduced. It is convenient to work at 229-230 nm, where the flashlamp source in the XL-A centrifuge has a high output peak and the protein extinction is 7-8 –fold greater than at 280 nm. With typical noise levels in the XL-A centrifuge of about 0.004 OD, the lowest practical concentrations of protein and RNA for SE studies are about 0.1-0.5 μM and the lowest K_d values that can be reliably determined are in the low nM range [10]. Alternatively, several studies have exploited DNA labeled with fluorescein to collect data at 490 nm. [26-28]. Selectively monitoring of the protein can be accomplished by biosynthetic incorporation of 5-hydroxytryptophan, which allows detection at 310 nm [13]. Finally, a new fluorescence optics system should extend the sensitivity of SE significantly using protein and nucleic acids labeled with high quantum yield fluorophores.

3.2 Stoichiometry of Nonspecific Protein – Nucleic Acid Interactions

A useful first step in studies of nonspecific protein-nucleic acid binding is to define the stoichiometry of association prior to more detailed studies required to measure equilibrium constants. It is convenient to perform these studies at moderate rotor speeds or short column samples (column heights< 3 mm) such that relatively shallow concentration gradients are achieved. Under these conditions, the radial dependence of the solution composition is small, and we can treat the sample as being characterized by an average molecular weight [25]. When using absorption optics, a “signal average” molecular weight is obtained where the contribution of each species in solution is weighted according to its molar concentration and extinction coefficient. In order to measure the stoichiometry, it is useful to monitor the gradients at 260 nm where the absorbance of the nucleic acid predominates. The buoyant, signal-average molecular weight at 260 nm (M*₂₆₀) is given by

$$M_{260}^{\ast }=\frac{{\epsilon }_{P,260}\left[P\right]M_P^{\ast }+\sum _{i=0}^S({\epsilon }_{R,260}+i{\epsilon }_{P,260})\left[R{P}_i\right](M_R^{\ast }+i{M}_P^{\ast })}{{\epsilon }_{P,260}\left[P\right]+\sum _{i=0}^S({\epsilon }_{R,260}+i{\epsilon }_{P,260})\left[R{P}_i\right]}$$ (1)

where ε_P,260 is the extinction coefficient of the protein monomer P at 260 nm, [P] is the molar concentration of P, M*_P is the buoyant mass of P, S is the maximal number of protein monomers that bind to the nucleic acid R, and [RP_i] is the molar concentration of the complex contain one molecule of R and i molecules of P. The buoyant mass is defined by

$$M^{\ast }=M(1-\stackrel{‒}{v}\rho )$$ (2)

where M is the mass (P or R), $\stackrel{‒}{\nu }$ is the partial specific volume and ρ is the solvent density. In equation 1, we assume that the molar extinction coefficient of the species RP_i is the composition-weighted sum of the extinction of the individual components R and P. In some cases, protein binding to a nucleic acid results in hypo- or hyper-chromism. The extent of these effects can be experimentally tested using absorption mixing experiments. In the absence of volume changes, the buoyant molecular mass of the complex is the composition-weighted sum of the components: M_R* + iM_P*. Typically, we measure the properties of individual components R and P alone to obtain M_R* and M_P* and to detect possible self-association. Alternatively, the molecular mass of the protein, the partial specific volume of the protein and the solvent density can be used to calculate the value of M_P* [29]. In contrast, for RNA and DNA oligonucleotides there are no reliable data to calculate partial specific volumes based on composition or sequence, and average values must be used.

The value of M*₂₆₀ is obtained by directly fitting the experimental absorption gradients to the following expression

$$A(r,260)={\delta }_{260}+A_{0,260}\exp \left[M_{260}^{\ast }\varphi (r^2-r_0^2)\right]$$ (3)

where A(r, 260) is the radial-dependent absorbance at 260 nm, A_0,260 is the absorbance at the arbitrary reference distance r₀ and

$$\varphi =\frac{{\omega }^2}{2RT}$$ (4)

where ω is the angular velocity of the rotor in radians/sec, R is the molar gas constant and T is the absolute temperature.

Although equation 1 appears complex, it can be simplified for many situations where the interpretation of M*₂₆₀ is straightforward. Under conditions where the absorption contribution of the nucleic acid is much greater than the protein (ε_R,260 >> ε_P,260), the first terms in the numerator and denominator of equation 1 are negligible, and the saturating stoichiometry of binding can be assessed by simply measuring the increase in the buoyant mass of the oligonucleotide in the presence of a saturating concentration of protein ligand

$$S=\frac{M_{260}^{\ast }\left(\max \right)-M_{R,260}^{\ast }}{M_{P,260}^{\ast }}$$ (5)

where M*₂₆₀(max) is the value of M*₂₆₀ in the presence of saturating ligand concentrations: M*₂₆₀(max) = M*_R + sM*_P. Note that in SE the “y-axis” is calibrated to directly provide information about the number of bound ligands. In contrast, for most other methods used to assess binding, the signal amplitudes cannot be directly related to the binding stoichiometry. It is necessary to work under stoichiometric binding conditions, where [R] >> K, when using these methods, such that prior to saturation of the nucleic acid lattice the concentration of free P is negligible and the stoichiometry can be assessed as the ratio of P:R resulting in a maximal signal increase. This approach can also be applied to SE measurements where the protein contribution to the absorbance at 260 is not negligible. Again, if [R] >> K, the value of M*₂₆₀ will increase with increasing protein concentration until the equivalence point where [P] = S·[R] and M*₂₆₀ = M*₂₆₀(max). Because M*_P < M*_R+S·M*_P, further increase in protein concentration will actually cause M*₂₆₀ to decrease. This dependence of M*₂₆₀ on [P] can be modeled using equation 1. Finally, in the general case where the nucleic acid concentration cannot be increased well above K and the protein contributes significantly to the absorption at 260 nm, it is necessary to explicitly incorporate binding equilibria into the model. In fact, the dependence of the signal-average buoyant molecular mass on solution composition and detection wavelength can be analyzed to discriminate among alternative association models and to determine association constants [25]

3.3 Measurement of Equilibrium Constants for Nonspecific Protein – Nucleic Acid Interactions

Lewis and coworkers have described a matrix method in which SE profiles at multiple wavelengths are used to construct molar concentration distributions of each reactant [12]. These concentration distributions are then jointly fit to an association model to obtain equilibrium constants. Alternatively, the absorption data at multiple wavelengths can be directly fit to specific association models [9,10,14]. We prefer the latter approach because it requires less manipulation of the data and it is not clear how to generate weighting coefficients for the molar concentration distributions.

The reversible association of a protein component P with an oligonucleotide R to form a series of complexes with composition RP_j is governed by a set of stepwise equilibrium constants K_i

$$R{P}_{i-1}+P\stackrel{K_i}{\leftrightarrow }R{P}_i$$ (6)

where i ranges from 1 to the maximum number of bound protein monomers, S. The concentrations of each complex can then be expressed in terms of the products of the stepwise equilibrium constants K_i and the concentration of free R and P using mass-action:

$$\left[R{P}_i\right]=K_i\left[R{P}_{i-1}\right]\left[P\right]=\prod _{j=1}^i{K}_j\left[R\right]\left[P\right]$$ (7)

In SE studies of such a hetero-association, the absorption gradients will potentially contain contributions from the free R, P and each of the complexes RP_i participating in the equilibrium. Using equation 7, we define the concentrations of each of the complexes RP_i at the reference distance r₀ in terms of stepwise equilibrium constants and the concentrations of R and P. Assuming that all of the species sediment ideally, at sedimentation equilibrium the radially-dependent concentration gradients of each species is given by the usual exponential form (equation 3), where the buoyant molecular weights are determined by composition. Finally, the radially- and wavelength-dependent absorbance gradients, A(r,λ) are the sum of the contributions from the free nucleic acid, protein and each of the complexes:

$$A(r,\lambda )={\delta }_{\lambda }+{\epsilon }_{R,\lambda }{C}_{0,R}\exp \left[M_R^{\ast }\varphi (r^2-r_0^2)\right]+{\epsilon }_{P,\lambda }{C}_{0,P}\exp \left[M_P^{\ast }\varphi (r^2-r_0^2)\right]+\sum _{i=1}^S({\epsilon }_{R,\lambda }+i{\epsilon }_{P,\lambda })C_{0,R}{C_{0,P}}^i\exp [(M_R^{\ast }+i{M}_P^{\ast })\varphi (r^2-r_0^2)+\sum _{j=1}^i\ln K_j]$$ (8)

where δ_λ is a wavelength-dependent baseline offset and c_0,R is the molar concentration of R at reference distance r₀. The baseline offsets are caused by absorption mismatches between the sample and reference sectors. In order to derive the maximal benefit from global data analysis using equation 8 it is important to constrain as many parameters as is feasible. The stepwise equilibrium constants K_j are expressed in the form exp [ln Kj] in equation 8 to constrain them to be positive. Typically, the buoyant masses of R and P are obtained from independent experiments and the baseline offsets are obtained by overspeeding after the experiment. In addition, we have found that it is very helpful to constrain reference radii and reference concentrations to be equal for data channels obtained at multiple wavelengths that originate from the same physical sample. It is critical that the relative molar extinction coefficients are accurately determined at each wavelength in order to obtain good global fits when implementing these constraints. The accuracy of wavelength selection for the monochromator in the XL-A centrifuge is on the order of ± 2 nm, which can result in substantial errors, particularly at 230 nm, which is on a steeply rising shoulder of the protein absorbance. We typically calculate the absolute extinction coefficients for protein at 280 nm and nucleic acid at 260 nm based on composition. Then, the relative extinction coefficients at other wavelengths is experimentally determined in the XL-A centrifuge by jointly fitting absorption gradients obtained from channels containing either protein or nucleic acid using a procedure described by Lewis et al. [12].

3.4 Interpretation of Equilibrium Constants for Nonspecific Protein – Nucleic Acid Interactions

With one exception [14], previous studies of protein-nucleic acid interactions by SE involved sequence specific binding [9-13]. In the simplest case, where the nucleic acid contains a unique specific binding site, the experimentally observed macroscopic binding constant is equal to the intrinsic microscopic binding constant. For a system containing multiple identical and independent binding sites, the stepwise macroscopic constants are equal to the product of the intrinsic constant and a statistical factor determined by the number of microscopic states constituting each level of saturation of the nucleic acid with ligand [30]. Similarly, for nonspecific interactions, multiple protein ligands also bind to the nucleic acid and the macroscopic constants are determined by the product of the intrinsic interaction constant and statistical factors. However, each protein binding site is generally larger than a single nucleotide and generally interacts with more than one contiguous base (or bp). Furthermore, steric hindrance may render several of the neighboring bases inaccessible to binding of an adjacent protein ligand even if they are not directly contacted. This overlap of the binding sites gives rise to binding isotherms that differ from discrete models and the statistical factors relating the macroscopic and microscopic interaction constants are different.

An analytical isotherm for nonspecific protein-nucleic acid binding was developed by McGhee and Von Hippel, where the nucleic acid is modeled as an infinite, one dimension lattice [31]. In this model, the relevant parameters are the intrinsic binding constant, k, that characterizes binding of a protein ligand to an isolated binding region, the ligand site size, N, and a unitless cooperativity parameter ω. N represents the number of lattice sites that are occluded upon ligand binding. Note that N may be greater than the number of lattice sites directly involved in molecular interactions due to steric hindrance between adjacent ligands. This model has been extensively employed for the analysis of nonspecific binding of proteins to long homopolymeric DNA sequences. However, the McGhee-von Hippel isotherm is not relevant for studies of nonspecific protein binding to finite length oligonucleotides such as performed in SE measurements.

Epstein has derived exact, combinatorial expressions describing noncooperative and cooperative binding of large ligands to finite, one-dimensional lattices [32], and we have adapted this formalism for the interpretation of SE studies of nonspecific protein nucleic acid interactions. In addition to the parameters defined above for the infinite lattice model, we also need to consider the length of the nucleic acid lattice, M. The number of bound ligands at saturation (S) is the highest integer value less than or equal to M/N. The macroscopic, stepwise equilibrium constants Ki are related to the intrinsic binding constant k by statistical factors, C_x, describing the number of microscopic configurations that have x bound ligands on the lattice.

$$\prod _{i=1}^x{K}_i=C_x{k}^x$$ (9)

Several workers have derived combinatorial expressions for C_x [32-34]. The number of possible places to distribute x ligands on the lattice is given by M-Nx. The total number of items to be arranged on the lattice is the sum of the number of free positions available M-Nx, and x, the number of ligands, and the combinatorial expression is [34]

$$C_x=\frac{(M-Nx+x)!}{(M-Nx)!x!}$$ (10)

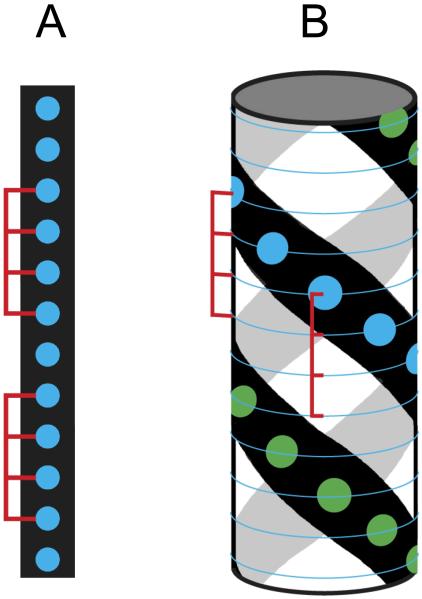
Figure 1A is a schematic illustration of one of the C_x=15 configurations available with M=12, N=4 and x=2. There are two methods to use this model for analysis of SE data. First, one may treat each of the stepwise binding constants in equation 8 as a separate adjustable parameter and compare the ratios of these experimentally determined binding constants with those predicted by equations 9-10. Alternatively, one can express each of the macroscopic constants in terms of the intrinsic equilibrium constant k and fit using a single adjustable binding constant.

Figure 1.

Schematic illustration of nonspecific binding of a large ligand to a finite nucleic acid lattice. A) Linear model. One of the 15 possible configurations for binding of two ligands of length 4 to a linear lattice of length 12. The blue circles represent lattice sites. B) Overlapping ligand model for binding of two ligands of length 4 to a double helical lattice of length 12 with a minimal offset of 2. The leftmost binding site on the ligand must contact a lattice site indicated by a blue circle. Only one of the 28 possible configurations is shown.

In our recent studies of the nonspecific binding of PKR to dsRNA sequences we have observed higher binding stoichiometries than can be explained within the one dimensional finite lattice model and we have found it necessary to consider that ds nucleic acids may support overlapping ligand binding to different faces of the double helical lattice. In the one-dimensional model illustrated in figure 1A, consecutive ligands can initiate every N bases. However, if the ligand is capable of binding to multiple faces of the nucleic acid, consecutive ligands initiate binding in fewer than N bases and the ligands overlap along the primary sequence of the RNA or DNA. We are led to propose such a binding mode based on the crystal structure of another dsRBM bound to a dsRNA [35]. In the crystal-packing diagram, each protein ligand interacts with about 16 bp of a central dsRNA helix that extends through the crystal. Each protein ligand binds to the dsRNA similarly across two adjacent minor groove regions and the intervening major groove. Binding of successive protein ligands occurs at 90° intervals around the helix, giving rise to substantial ligand overlap. In our revised model, we define a minimum offset, Δ, which refers to the minimum number of lattice sites at which consecutive ligands can initiate binding. The value of Δ is determined by the size of the ligand and the pitch of the ds lattice. This situation is depicted in figure 1B, which illustrate a configuration where a ligand that occupies 4 bases binds to a ds lattice of length 12 with Δ=2. For a system capable of binding a maximum of S ligands, the number of configurations available for binding the last ligand is M-N-(S-1)Δ+1. This value must be greater than unity, such that the limiting stoichiometry is given by the largest integer value of S that satisfies the following inequality

$$S\le \frac{M-N}{\Delta }+1$$ (11)

Finally, to calculate C_x we consider the total number of items to be arranged on the lattice as the sum of the number of free positions available, given by M-N-(x-1)Δ, and x, the number of ligands. Then, by analogy to equation 10,

$$C_x=\frac{(M-N-(x-1)\Delta +x)!}{(M-N-(x-1)\Delta )!x!}$$ (12)

In the example in figure 1B, a total of 28 configurations are available for the lattice with two ligands bound, which is significantly larger than the number of configurations available in the absence of ligand overlap.

4. Application: Binding of dsRBD to a 20 bp dsRNA

PKR is a dsRNA-activated protein kinase comprised of an N-terminal double-stranded RNA binding domain (dsRBD) and a C-terminal kinase domain [36]. The dsRBD contains two tandem copies of the ~70 amino-acid dsRBM. We are interested in defining the mechanism by which RNA binding activates PKR by detailed studies of the interaction thermodynamics of various PKR constructs with structurally-defined dsRNA sequences. Here, we characterize the binding of the N-terminal dsRBD domain (amino acids 1-184) with a 20 bp dsRNA.

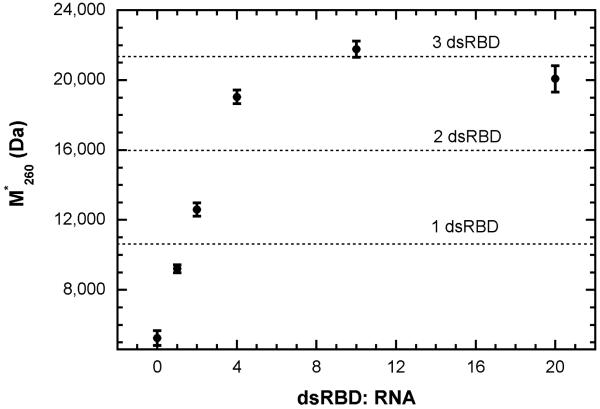
Figure 2 shows a titration of a 20 bp dsRNA with the dsRBD monitored by SE at 260 nm and 21,000 RPM. Under these conditions, the absorption contribution from the protein is negligible relative to the RNA (ε_R,260 >50 · ε_P,260). The signal-average buoyant mass in the absence of protein is 5250, which is consistent with value calculated from the sequence and an average partial specific volume for dsRNA of 0.55 ml/g. The calculated buoyant mass of the dsRBD is 5365. Over a protein concentration range of 0 to 10 μM, M*₂₆₀ increases and saturates at ~21,000. As shown in figure 2, this increase corresponds to a binding stoichiometry (S) of three dsRBD: RNA. We have confirmed this stoichiometry by CD spectroscopy at 260nm, which monitors the change in helical winding angle of the dsRNA induced by dsRBD binding (data not shown). In the context of the one dimensional lattice model, this stoichiometry implies a site size (N) of less than 20/3 or 6-7 bp. This value is considerably smaller than the 14-16 bp observed to directly contact the protein in crystallographic [35] and NMR [37] studies of related dsRBM complexed with dsRNA, suggesting that dsRBD may bind with substantial overlap. In the crystal structure, the protein ligands are bound at 90° intervals around the helix, giving rise to an offset of about 3 bp. In the present study, the stoichiometry of 3 dsRBD: RNA is consistent with a site size of 14 bp and minimum offset (Δ) of 3 bp.

Figure 2.

Stoichiometry of PKR dsRBD binding to 20-mer dsRNA. Samples containing 0.5 μM BS20/ TS20 dsRNA in 75 mM NaCl, 20 mM HEPES, 5 mM MgCl₂, 10 nM TCEP, pH 7.5 were prepared with the indicated molar ratio of dsRBD: RNA. Sedimentation equilibrium was performed in 6-channel cells at 21,000 RPM and 20 °C until equilibrium was achieved (28 hours). The signal-average buoyant molecular masses were determined by fitting the absorbance obtained at 260 nm to a single ideal species model. The error bars indicate the 95% joint confidence intervals and the dotted lines indicate the values of M*₂₆₀ expected for the binding of one, two or three dsRBD to the dsRNA.

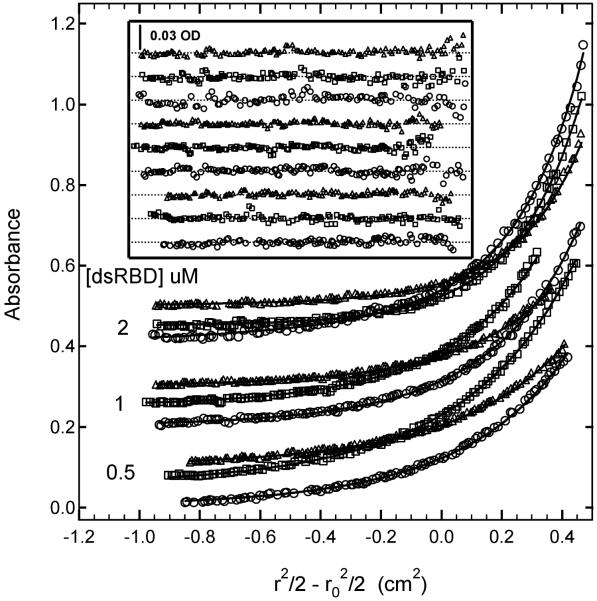
Having established a binding stoichiometry, we carried out multiwavalength SE studies to define the binding model in detail and determine equilibrium constants. SE data were obtained using three samples ([Protein] = 0.5, 1 and 2 μM; [dsRNA] = 0.5 μM) with three detection wavelengths (230,260 and 280 nm) and were globally analyzed using several alternative models. Figure 3 shows the data from all nine channels and a global fit to a model using three independent stepwise equilibrium constants. The best-fit parameters and statistics are summarized in table 1. The global fit is a good description of the experimental data, with no systematic deviations in the residuals and a low value of the RMS deviation of 0.00437 OD, which is consistent with the noise level in the optical system. The high value of LnK₁ of 18.32 indicates that first dsRBD binds strongly to the dsRNA (K_d= 11 nM). Although the 95% joint confidence intervals are relatively broad, there is a clear trend of decreasing binding strength with successive ligands, such that the third dsRBD binds significantly weaker, with LnK₃= 14.07 (Kd = 0.78 μM). The ratios of the equilibrium constants are: K₁/K₂ = 19 and K₁/K₃ = 70. As expected from the stoichiometry experiment in Figure 2, the data in Figure 3 do not fit well to a model of only two ligands binding, with significant systematic deviations and a high RMS =0.0073 OD (Table 1).

Figure 3.

Multiwavelength Sedimentation equilibrium of PKR dsRBD binding to 20 mer dsRNA. The data were obtained under the following conditions: rotor speed, 23,000 RPM; temperature, 20°C; RNA concentration, 0.5 μM and protein concentrations of 0.5 μM, 1 μM and 2 μM in 75 mM NaCl, 20 mM HEPES, 5 mM MgCl₂, 0.1 mM EDTA, pH 7.5. Detection wavelengths are: 230 nm (o), 260 nm (ڤ) and 280 nm (Δ). Solid lines are a global fit of the data to an unconstrained model of three ligands binding to the 20 mer RNA. The results of the fit are given in table I. Inset: residuals. Traces have been vertically offset for clarity.

Table 1.

Equilibrium Constants for binding of PKR dsRBD to 20-mer RNA determined by SE

Model	ln K1a	ln K2a	ln K3a	ln kb	RMS X10−3c
P=3d	18.32 [17.21,19.48]	15.38 [14.43,16.94]	14.07 [13.54,14.47]	-	4.37
P=2e	20.13	18.36	-	-	7.31
N=14, Δ=3 f	17.96	16.37	13.71	16.01 [15.77,16.23]	4.48
N=12, Δ=4 f	18.51	16.82	13.60	16.31 [16.07, 16.58]	4.48
N=6, no overlapf	17.93	16.32	13.72	15.22 [14.98, 15.46]	4.48

^aNatural logarithm of the macroscopic binding constant. The values in brackets represent the 95% joint confidence intervals.

^bNatural logarithm of the intrinsic binding constant. The values in brackets represent the 95% joint confidence intervals.

^cRoot mean square deviation of the fit in absorbance units (OD).

^dIndependent binding of three ligands. The natural logarithms of the macroscopic binding constants are the fitted parameters.

^eIndependent binding of two ligands. The natural logarithms of the macroscopic binding constants are the fitted parameters.

^fFinite lattice models. The natural logarithms of the intrinsic binding constants are the fitted parameters. The macroscopic binding constants are calculated using coefficients determined by equations 10 and 12.

A decrease in equilibrium constants with successive ligand binding events is predicted from statistical effects in the context of both the simple finite lattice model as well the finite lattice model that includes ligand overlap. In table 1, we have summarized fits to several of these models, in which the intrinsic equilibrium constant is the fitted parameter and the values of LnK₁, LnK₂ and Lnk₃ are calculated using equations 9-12. In all cases, S was fixed at three. The data fit reasonably well to the model without overlap and N=6 with an RMS value only slightly higher than in the fit where all three equilibrium constants are allowed to independently vary. However, as mentioned above, this site size is inconsistent with the structural data for other dsRBM complexes with dsRNA. In the context of the model that includes ligand overlap, an equally good fit is found for N=14 with Δ=3 (Table 1); successively worse fits are found as N is reduced and Δ is held constant (data not shown). We have not considered larger site sizes, since for Δ=3 a value of N> 14 reduces S to 2. A good fit is also found for N=12 with Δ=4. Again, worse fits are found with smaller site sizes and larger site sizes reduce the stoichiometry to 2. We have also not considered models with Δ=2, because this close overlap between adjacent bound ligands would likely be disallowed due to steric hindrance. In summary, the multiwavelength SE data fit well to several models where three dsRBD interact with the 20 bp dsRNA and the relative values of the three equilibrium constants are constrained according to the finite lattice model including ligand overlap. The best fits consistent with available structural information include a minimum offset (Δ) of 3-4 and site size (N) of 12-14 bp. These fits also reveal a value of the intrinsic binding constant of ln k = 16.0–16.3, or k_d= 83-110 nM.

5. Discussion and Future Prospects

Previous work has demonstrated that multiwavelength SE is a practical method to characterize the stoichiometry and affinity of sequence specific protein-nucleic acid interactions. Because of the strong chromophores present in protein and DNA or RNA, these studies do not require any labeling of the reagents and require modest amounts of material. In addition, collection of data at multiple wavelengths improves the accuracy of global analysis methods. Here, we have extended this approach to non-specific interactions by interpreting macroscopic equilibrium constants in terms of finite lattice models, and we have applied this method to a nonspecific protein-RNA interaction. In contrast to spectroscopic methods that only measure the fractional saturation of the nucleic acid with protein, SE measures the sequential binding of each protein ligand to the lattice. Thus, the analysis model can explicitly determine the relationship between sequential binding constants, and these data can then be used to determine molecular binding parameters using the simple finite lattice model or the model presented here incorporating ligand overlap. Gel mobility shift assays can also measure the stepwise binding events. However, nonspecific interactions generally have lower affinity and higher dissociation rates than specific interactions and are thus particularly susceptible to artifacts associated with dissociation during electrophoretic separation. Indeed, in previous studies of the binding of the PKR dsRBD to 20 bp RNA using the gel shift assay, a 1:1 stoichiometry was determined [38], in contrast to the 3:1 stoichiometry determined here. Presumably, weaker binding of the second and third dsRBD results in dissociation during the gel assay. In addition, in previous gel mobility studies of PKR binding to dsRNA, a site size of 11 bp was reported [22,38], in contrast to the 12-14 bp determined here. However, in these studies, a discrete binding site model was employed and ligand overlap was not considered.

There are several areas in which the method might be improved or extended. In the PKR analysis, the confidence intervals on the equilibrium constants are relatively broad in the fit where the relative values of the three macroscopic constants are not constrained. Presumably, this problem will be accentuated with higher stoichiometries. The confidence intervals are smaller in the analyses where we fit in terms of a single, intrinsic binding constant. However, several combinations of N and Δ fit the data equally well. It may be possible to differentiate among closely related models by jointly fitting experiments performed using a range of lattice lengths. Also, including multiple rotor speeds and more sample concentrations may reduce parameter uncertainty.

In our studies of PKR binding to dsRNA, the noncooperative binding models fit the data well and there is no evidence of cooperative binding interactions. However, there is high degree of cooperativity in other nonspecific protein-nucleic acid systems [15]. Pairwise cooperativity is easily accommodated with the simple finite lattice model using the expressions developed by Epstein [32], However, in the context of the overlapping ligand model presented here cooperative interactions may occur between adjacent ligands that are bound along different faces of the helix or between ligands on the same face of the helix.

Finally, the SE method may also be applicable to models that are more complex. In some systems [39,40], a protein binds to a nucleic acid lattice in two modes in which different numbers of lattice sites are occluded. In other cases, nonspecific binding competes with specific binding, [41] and oligonucleotides can be designed to contain a specific binding site flanked by nonspecific sequences. There is evidence that PKR binding to dsRNA and activation are strongly affected by secondary structure defects [36]; these effects can be probed by SE studies using oligoribonucleotide sequences engineered to contain mismatches, bulges and loop regions.

Abbreviations

Bicine

N,N-Bis(2-hydroxyl)glycine

bp

base pair

ds

double-stranded

dsRBD

double-stranded RNA binding domain

dsRBM

double-stranded RNA binding motif

EDTA

Ethylenediaminetetraacetic acid

HEPES

N-[hydroxyethyl]piperazine-N’-[2-ethanesulfonic acid]

PKR

Protein kinase R

SE

sedimentation equilibrium