Suppression of deep brain stimulation artifacts from the electroencephalogram by frequency-domain Hampel filtering

Abstract

Objective

Currently, electroencephalography (EEG) cannot be used to record cortical activity during clinically effective DBS due to the presence of large stimulation artifact with components that overlap the useful spectrum of the EEG. A filtering method is presented that removes these artifacts whilst preserving the spectral and temporal fidelity of the underlying EEG.

Methods

The filter is based on the Hampel identifier that treats artifacts as outliers in the frequency domain and replaces them with interpolated values. Performance of the filter was tested with a synthesized DBS signal and actual data recorded during bilateral monopolar DBS.

Results

Mean increases in signal-to-noise ratio of 7.8 dB for single-frequency stimulation and 13.8 dB for dual-frequency stimulation are reported. Correlation analysis between EEG with synthesized artifacts and artifact-free EEG reveals that distortion to the underlying EEG in the filtered signal is negligible (r² > 0.99).

Conclusions

Frequency-domain Hampel filtering has been shown to remove monopolar DBS artifacts under a number of common stimulation conditions used for the treatment of Parkinson’s disease.

Significance

Application of frequency-domain Hampel filtering will allow the measurement of EEG in patients during clinically effective DBS and thus may increase our understanding of the mechanisms of action of this important therapeutic intervention.

Introduction

Deep brain stimulation (DBS) of the subthalamic nucleus or internal segment of the globus pallidus has been shown to provide effective long-term treatment for patients with movement disorders such as Parkinson’s disease (PD) (Diamond and Jankovic, 2005; Rodriguez-Oroz et al., 2005) and dystonia (Hung et al., 2007). Yet, despite its proven clinical efficacy, the mechanisms of action of DBS remain poorly understood (McIntyre et al., 2004). Since the basal ganglia do not project directly to the spinal cord, DBS-induced improvements in motor function are considered to be mediated by alterations in basal ganglia output to thalamocortical pathways or the brain stem (Montgomery and Gale, 2008). Alternatively, DBS may act more directly on the cortex via antidromic activation of corticofugal fibers (Ashby et al., 2001; Baker et al., 2002; MacKinnon et al., 2005). To date, exploration of the effects of DBS on movement-related cortical activity has principally been limited to neuroimaging studies using radioactive tracers (Ceballos-Baumann et al., 1999; Hershey et al., 2003; Limousin et al., 1997; Payoux et al., 2004; Sestini et al., 2002). Yet, these imaging modalities do not possess the temporal resolution required to investigate movement-related modulations in cortical activity associated with the preparation, initiation and execution of movement in both the time and frequency domains. High resolution temporal information about movement-related activity can be obtained with electroencephalography (EEG), but the implementation of this technique is confounded by the DBS-induced electrical noise that obscures the relatively low magnitude of the EEG signal.

Previous studies have circumvented this issue by switching the stimulators off and observing the immediate after-effects of stimulation (Kuhn et al., 2008). However, the residual effects of stimulation are short-lasting and it is unknown if these effects mimic the actions of chronic DBS. The DBS artifact recorded with EEG can be greatly reduced if DBS is applied in bipolar mode (stimulation and reference electrodes are one or more of the four implanted macroelectrode contacts) (Devos et al., 2004; Frysinger et al., 2006). Yet, in the majority of cases, DBS is applied in monopolar mode (stimulation through one or more macroelectrode contacts, referenced to the implanted pulse generator in the chest). Under these conditions, the induced artifact can easily exceed the EEG signal by more than a factor of ten.

Several methods for the removal of DBS artifact from extracellular recordings in animals have been proposed, such as, template matching (Hashimoto et al., 2002) and temporal interpolation (Heffer and Fallon, 2008). However, signals recorded on the scalp surface record global activity and therefore have different properties to extracellular spike trains recorded with macroelectrodes. In addition, low-pass filtering due to volume conduction and the integrating effects of the scalp electrodes ensures that artifacts are smoothed periodic signals rather than spike-like signals seen in extracellular recordings. Hence, DBS artifacts in EEG can be represented by a Fourier series with a few discrete frequency components. Notch filtering of these artifact frequencies has been proposed as a method to obtain useful EEG signals (Jech et al., 2006). This is generally an unsatisfactory method of artifact removal, however, since notch filtering does not discriminate between signal and noise, and can be a source of error if notches occur within regions of interest, such as, the α- or β-bands. The requirements for an ideal artifact filter, therefore, would be: that it attenuates only the noise components at the interference frequencies and not the actual EEG; it does not attenuate frequencies where artifacts are not present; and that it causes minimal phase distortion, as this may adversely affect transient time-domain phenomena, such as, event-related potentials.

An example of a single channel of EEG (C3 on the International 10–20 System) with DBS artifact is shown in Figure 1. Initially, both stimulators were switched off. After a period of 30 s the stimulator on the patient’s right-hand side was turned on. It can be seen that the amplitude of the time series increases significantly at this point. The corresponding time-frequency map in Figure 1 reveals that the artifact is not broadband, but consists of a number of high-magnitude narrowband interference components spread throughout the spectrum. In particular, note the presence of interference components in the β (13–30 Hz) and γ (40–80 Hz) bands. Oscillations in these frequency bands are related to normal movement control and are altered by disease and therapeutic interventions (Brown, 2003). Thus, it is imperative that methods to remove DBS artifact retain the EEG signal content in these frequency bands.

Figure 1.

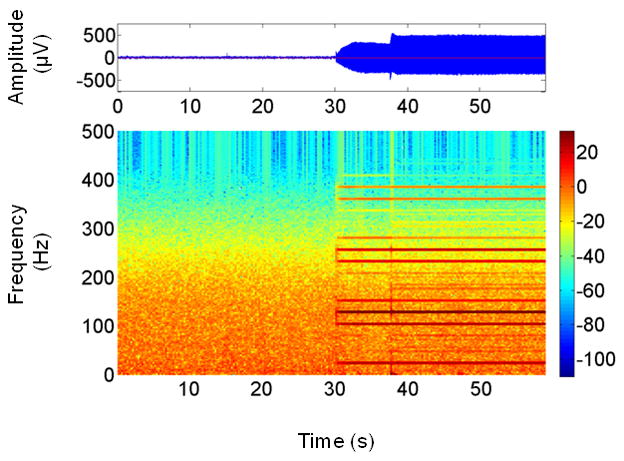
EEG time series (top) showing the increase in signal amplitude at 30 s when the pulse generator for DBS stimulator was turned on. The time-frequency map of this signal (bottom) reveals that the artifact comprises multiple narrowband signals spaced at regular intervals. Note the transient changes in both amplitude and frequency content of the artifact over the first ~10 s of unilateral stimulation, after which the artifact’s amplitude is constant and can be considered stationary.

The time-frequency map in Figure 1 reveals two characteristics of the interference components that are favorable for their removal, namely that they have high magnitude and are spaced apart in the spectrum. Consequently, they can be considered to be spectral outliers, and as such can be removed with an appropriate outlier detection and replacement method. Such a method would fulfill the requirement that only those frequencies at which artifacts are present are modified. A filtering method based on the Hampel identifier, a robust outlier detector, has previously been demonstrated for the removal of narrowband interference at multiple frequencies from electromyograms (Allen, 2009). An important feature of the Hampel filter is that it introduces minimal phase distortion to the signal, thus satisfying another of the requirements of an ideal filter outlined above. This paper reports on the use of the Hampel filter for the removal of DBS artifact from EEG. It is shown with the use of EEG contaminated with actual and synthesized DBS artifacts that the filter is capable of attenuating the artifacts without distorting the underlying EEG.

Methods

Hampel Filter

The Hampel filter described by Allen (2009) is an off-line frequency-domain filtering method for the removal of spectral outliers. In brief, the filter transforms a time-domain signal into the frequency domain with the fast Fourier transform (FFT), detects outliers in the real and imaginary spectra with the Hampel identifier, replaces those outliers with interpolated values, and transforms the cleaned spectra back to the time domain via the inverse FFT. Operating on the complex spectra in such a manner, as opposed to the power spectrum, ensures zero phase distortion at the non-interpolated frequencies, which results in minimum distortion to the reconstructed signal and hence preserves temporal information. The Hampel identifier is a robust statistic that defines data points in a sequence {x_j | j = 1: N} as outliers if their absolute difference from the median value x* is greater than a pre-determined threshold t, as given by (1), in which S is given by (2) (Pearson, 2002). S is a scale estimator that quantifies the statistical dispersion of the median absolute deviation of a data sequence from its median value, and is analogous to the spread about the mean value described by the standard deviation.

$$\left|x_j-x^{\ast }\right|>tSj=1\text{to}N$$ (1)

$$S=1.4286\mathit{median}\left\{\left|x_j-x^{\ast }\right|\right\}$$ (2)

The data sequence {x_j} is formed by a sliding window of length N applied to the spectra. There are thus two parameters, t and N, that control the sensitivity of the filter. In practice, though, for N > 10, t can typically be set to ~5 (Davies and Gather, 1993). The breakdown point of the median statistic, or ratio of the number of outliers to the total number of samples in the data sequence for which the median value becomes one of the outliers, is 50%. This suggests, therefore, that the value of N should be at least twice the width of the outlying spectral peak and any adjacent spectral leakage, the extent of which can be obtained from spectral analysis (Allen, 2009). For example, if the width of a spectral peak is 1 frequency bin and appreciable leakage extends over 9 frequency bins, then the minimum value of N would be 21. If two or more arbitrarily close outliers were present within the window, the filter will still detect their presence providing N is at least twice the width of the combined spectral peaks and leakage.

Subjects and experimental protocol

Four subjects participated in the study. Each was diagnosed with idiopathic PD and had quadripolar electrodes (Medtronic Model 3387) implanted bilaterally in the subthalamic nucleus and connected to subclavicular pulse generators. Subjects were tested after overnight withdrawal from their Parkinson’s medications. The stimulation parameters for each subject are listed in Table 1, which shows that left and right stimulation frequencies were different for subjects #1 and #2, and equal for subjects #3 and #4. These parameters are typical of those used for the treatment of PD (Volkmann et al., 2006).

Table 1.

Stimulation parameters for the 4 subjects. Electrode numbers indicate cathode (anode = IPG case).

	Left				Right				UPDRS Score
Subject	Voltage (V)	Pulse Width (μs)	Frequency (Hz)	Electrode	Voltage (V)	Pulse Width (μs)	Frequency (Hz)	Electrode	OFF Stim	ON Stim
1	3.2	60	130	1	3.3	60	185	1,2	58	43
2	3.6	90	185	1	3.2	60	130	1	44	16
3	3.7	60	130	2	3.2	60	130	2	48	39
4	3.2	60	185	2	3.6	60	185	2	51	31

Patients were seated in a comfortable chair and instructed to remain stationary and relaxed throughout the data collection. The stimulators were initially switched off and EEG signals were collected for approximately 140 s. Both stimulators were then sequentially switched on and the data collection was repeated. The experimental protocol was approved by the Institutional Review Board, and all subjects gave their written informed consent.

Data Acquisition

Subjects were fitted with an electrode cap (EasyCap) containing 72 Ag/AgCl sintered electrodes that encompassed the surface of the scalp using a 10–20 International System montage (Jasper, 1958). The scalp surface beneath the electrodes was gently abraded with gel and electrodes were filled with a conductive paste to ensure impedances of less than 5 kΩ. All EEG signals were referenced to an electrode placed over the right mastoid process. EEG was collected with a Neuroscan SynAmps system; band-pass filtered (DC to 250 Hz), amplified with a gain of 2500, sampled at 1000 Hz, and digitized with a 16-bit analogue-to-digital converter. Data were processed off-line with MATLAB^® Version 7.5 (The MathWorks, Inc., Natick, MA). The analysis methods described in this paper were applied to the recording obtained from the electrode over the left sensorimotor cortex (C3), but would apply equally to signals obtained at any site. Spatial filtering of the EEG using Laplacian or other such methods was not applied to the data.

Signal Processing

EEG were high-pass filtered to remove DC offset and drift (4^th-order Butterworth filter, cut-off frequency 1.0 Hz), and low-pass filtered with an 8^th-order Type II Chebychev filter (cut-off frequency 100 Hz, 40 dB attenuation in the stop band). The Chebychev filter has a superior roll-off to a Butterworth filter of equivalent order, and thus provides greater attenuation of the high magnitude artifacts that occur close to the cut-off frequency, such as those observed at the frequency of stimulation.

Since the magnitude of the artifacts is relatively constant, artifacts can be considered to be stationary. For this reason, plus the fact that the Hampel filter is relatively insensitive to epoch length (Allen, 2009), it is not necessary in this case to epoch the data into smaller segments. Rather, the FFT can be applied to the entire signal and can thus be processed in one operation. The amount of artifact removed from noisy signals was estimated by calculating the ratio of signal variance or power with stimulators turned off to the variance of the contaminated signal pre- and post-filtering. The closer the post-filter ratio is to 1, i.e., 0 dB, the more alike the two signal variances are and hence the better the performance of the filter.

Synthesized Artifacts

As stated in the introduction, a requirement of an artifact rejection filter is that it causes minimum distortion to the signal in the time domain. In theory, distortion can be determined from the mean squared error (MSE) and the cross-correlation between the filtered contaminated signal and a clean version of the same signal without any artifacts. Clearly, this is not practicable with experimental data, since a noise-free version of the same signal cannot be obtained. Furthermore, EEG recorded from another epoch cannot be used as a reference, since the two signals, although statistically similar, are independent realizations of a random process and hence are uncorrelated. One solution to this problem is to use synthesized artifacts of known frequency and amplitude added to an otherwise artifact-free signal that acts as the reference. Therefore, for each subject, the magnitude and frequency of artifacts were identified manually from spectra of EEG recorded with the stimulators turned on; synthesized artifacts consisting of sine waves with these same parameters were then added to EEG recorded with the stimulators turned off. Thus, synthesized noisy EEG were generated with artifacts having identical frequency-domain characteristics as actual artifacts. The phase of the synthesized artifacts was distributed randomly in the range ± π/2 rad.

An example of a synthesized signal is shown in Figure 2 together with the actual EEG from which the artifact parameters were determined. It can be seen that, while the fine detail of the two signals differ, their gross features are similar. It is important to note that the synthesized signals were not constructed to be identical to the real DBS waveform in the time domain. Rather, since we are applying the filter in the frequency domain, it is their spectral similarity that is of most importance here, and this has been satisfied by generating artifacts with a spectral profile identical to the real artifacts.

Figure 2.

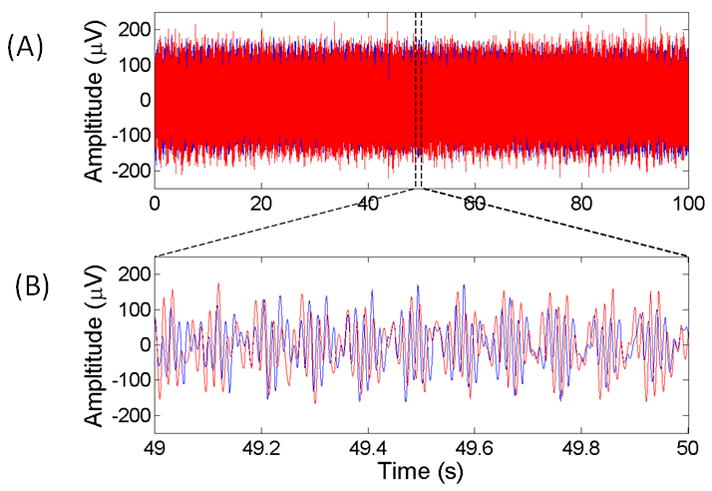
(A) 100 s and (B) 1 s segment of synthesized (red) and actual (blue) EEG contaminated with DBS artifact showing the similarity in the time-domain characteristics between the two signals.

Results

The ability of the Hampel filter to remove spectral outliers in EEG was tested with signals contaminated with actual and synthesized DBS artifact. Threshold values t were determined iteratively by minimizing the ratio of pre- and post-filtered signal variance for a given Hampel window length N. According to Allen (2009), the value of N should be at least twice the width of the interference spectral power and adjacent leakage power. It was found that N = 80 data points, i.e., a spectral band of N × 1/T = 0.57 Hz, and a threshold t = 6 were suitable parameters all subjects. A threshold value of t = 6 corresponds with the analytical value given by Davies and Gather (1993) for N > 10.

The ratios of signal variance pre- and post-filtering are presented in Table 2 for both synthesized and actual DBS artifacts. It can be seen that, for each subject, the Hampel filter removed most of the power from synthesized and actual artifacts, as the magnitude of post-filter ratios are < 0.4 dB in all cases.

Table 2.

Ratio of artifact-free signal variance to contaminated signal variance before and after application of the Hampel filter for both synthesized and actual DBS artifact data.

	Synthesized Artifact		Actual Artifact
Subject	Pre-filter (dB)	Post-filter (dB)	Pre-filter (dB)	Post-filter (dB)
1	−14.87	−0.00	−15.43	0.30
2	−10.48	−0.01	−11.47	0.35
3	−3.09	0.01	−4.33	0.39
4	−10.56	0.01	−10.91	−0.12

Figure 3A shows the time series and time-frequency map of an EEG signal contaminated with DBS artifact from subject #2. Figure 3B shows the results of applying the Hampel filter to the same data. It is apparent from the time-frequency map in Figure 3B that the magnitude of the artifact components is greatly reduced compared to the on-stimulation condition. In this particular example, the pre- and post filter variance ratios were −11.47 and 0.35 dB, respectively. The time series in Figure 3B also shows a considerable reduction in amplitude compared to Figure 3A. Similar plots for subjects #1, #3 and #4 are presented in Figure 4.

Figure 3.

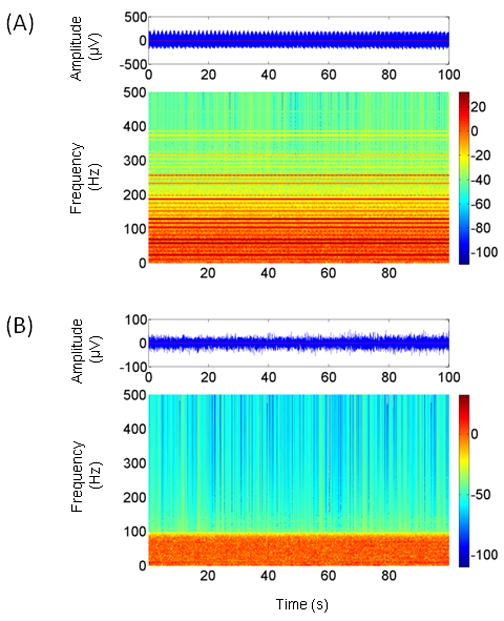
(A) A 100 s segment of EEG time series contaminated with DBS artifact (top). The spectral components of the artifact are visible in the corresponding time-frequency map. (B) Results of applying the Hampel filter to the EEG time series in Fig. 3A. The time-frequency map shows that the artifact components have been greatly attenuated. Prior to applying the Hampel filter, the data were low-pass filtered with a cut-off frequency of 100 Hz, hence the difference in background activity above this frequency compared to Fig. 3A. The time series in Fig. 3B shows a corresponding reduction in amplitude. Note the different amplitude scales for the EEG time series in (A) and (B).

Figure 4.

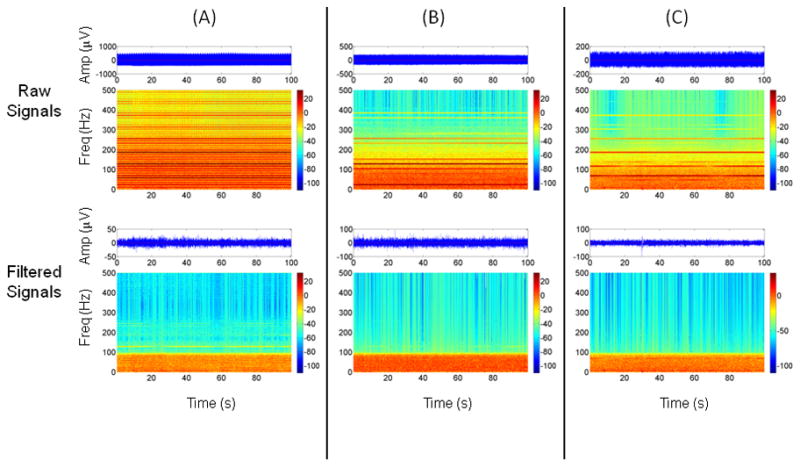
Spectrograms and time series plots showing the effects of applying the Hampel filter to artifacts from (A) subject #1, (B) subject #3, and (C) subject #4. See Figure 3 for details. Note the different amplitude scales for the EEG time series before and after filtering and between subjects.

Table 3 lists the correlation and MSE values obtained from Hampel filtering signals containing synthesized artifacts. The filter was first applied to artifact-free data, i.e., with stimulators off, and the correlation and MSE between the filtered and artifact-free signals were determined (condition OFF-OFF_HF in Table 3). The correlation between these pairs of signals is high (> 0.99) and MSE values are all relatively low for all subjects, thus suggesting that the filter did not distort the signal, which was to be expected with this condition. Conversely, when artifacts were added to the signal, the correlation between noisy and artifact-free signals decreased, while the corresponding MSE values increased (OFF-ON). The relatively high correlation value for subject #3 (0.6949) suggests that the amount of artifact present was less than that observed in the other subjects. When the Hampel filter was applied to the contaminated signals (OFF-ON_HF), correlation coefficients increased for all subjects (> 0.99) and MSE decreased accordingly, thus indicating that the filter had attenuated the artifacts without distorting the signal.

Table 3.

Cross-correlation r² and mean squared error between artifact-free and data with synthesized contamination.

	OFF-OFFHF		OFF-ON		OFF-ONHF
Subject	r2	MSE (×103)	r2	MSE (×103)	r2	MSE (×103)
1	0.9998	0.0001	0.1806	3.0232	0.9961	0.0010
2	0.9999	0.0001	0.3069	2.5350	0.9954	0.0024
3	0.9987	0.0008	0.6949	0.2997	0.9982	0.0007
4	0.9977	0.0005	0.2573	1.6412	0.9954	0.0010

Key: OFF-OFF_HF – stimulation off/Hampel-filtered stimulation off; OFF-ON – stimulation off/stimulation on; OFF-ON_HF – stimulation off/Hampel-filtered stimulation on.

An example of the correlation between filtered and artifact-free EEG is shown in graphical form in Figure 5, in which a 0.5 s segment of artifact-free EEG from subject #2 is plotted together with a noisy version of the same signal with artifacts. Also shown is the result of applying the Hampel filter to the noisy signal. The close similarity between filtered and artifact-free signals is exemplified by the overlap of the traces. The plots also indicate that the Hampel-filtered signal had zero phase lag.

Figure 5.

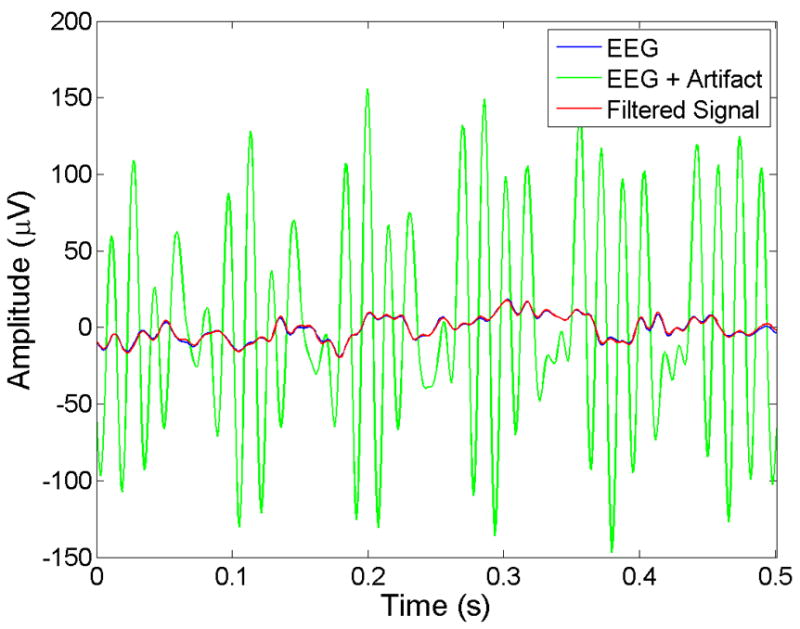
Plots showing a 0.5 s section of artifact-free EEG (Blue) from subject #2, together with the same signal with synthesized DBS artifacts (Green) and the filter response (Red). The plots show that the filtered signal closely resembles the artifact-free data with little distortion and zero phase lag.

Discussion

This paper presents a method for the removal of DBS artifacts from EEG signals in the frequency domain. The method is based on the Hampel filter, which treats artifacts as outliers in the complex spectra of the FFT. The filter was tested with actual and synthetic DBS artifacts, and was shown to be capable of removing these artifacts without attenuating signal power in the underlying EEG. Furthermore, correlation and MSE analysis revealed that the filter does not distort the signal excessively or introduce a phase delay. The significance of these results is that it is now possible to obtain useful EEG from subjects receiving monopolar DBS, which was not possible before.

One of the features of the Hampel filter is that it operates blind, i.e., it does not need a priori knowledge of which frequencies to process. This is a significant advantage when the number of artifacts is unknown, as is often the case with DBS. Two of the subjects tested received stimulation at different frequencies, while the remaining two were at the same frequency, and consequently both groups had different numbers of artifacts present in the EEG. The Hampel filter produced similar results for both sets of subjects, however, thus indicating its ability to process artifacts for a number of typical stimulation conditions.

The filter was tested with EEG recorded under resting conditions, but the results should hold equally for dynamic EEG. However, since in addition to attenuating power, the Hampel filter also modifies the phase of interference frequencies, a reduction in temporal fidelity at those frequencies inevitably follows. This may not be an issue for resting EEG as the signal is reasonably stationary, but may affect EEG recorded under dynamic conditions, in which the timing of changes in amplitude of oscillations in, for example, the α- β- and γ-bands is important (Brown, 2003). In such circumstances, the spectral resolution of the FFT is a critical factor, as this affects the width of spectral peaks and hence determines the band of frequencies at which the loss of temporal fidelity applies. The longer the epoch length, the higher the resolution of the FFT, hence the narrower the width of an artifact’s spectral peak and the narrower the band of frequencies affected. For these reasons, the length of the epoch should be chosen to be as long as possible for a given application determined by the stationarity of the artifacts. In the future, as demand-driven DBS becomes available in which the magnitude of the artifacts varies in time, the epoch length may need to be set adaptively. These same limitations regarding epoch length apply of course to EEG in the resting state or to DBS for low frequency events such as seizures. In the case of resting EEG, however, experiments are usually of relatively long duration, and since artifacts are relatively stationary, the issue of poor spectral resolution due to short epoch lengths is not an issue. Another potential pitfall with the Hampel filter occurs when a high number of closely separated spectral artifacts occur that cannot be readily identified as outliers. This does not appear to be a problem with DBS, however, since artifact frequencies are generally widely spaced and hence are easily distinguishable (Figure 1).

In conclusion, the Hampel filter has been shown to remove monopolar DBS artifacts under a number of common stimulation conditions used for the treatment of PD. The use of this filter will allow experimenters to collect EEG with the stimulators switched on instead of the current practice of observing the transient effects of residual carry-over stimulation. Application of the Hampel filter method will allow the measurement of both continuous and event-related EEG in patients during clinically effective DBS and thus may increase our understanding of the mechanisms of action of this important therapeutic intervention.