Abstract
Recently, it has been suggested that the concept of preloading is limited by using a standard amount of unlabeled antibody. To identify the potential of optimal preloading, a pharmacokinetic model that describes the biodistribution of anti-CD20 antibody was developed. Simulations were conducted for different tumor burdens, spleen sizes, and tumor permeabilities. The optimal amount of unlabeled antibody was determined for each scenario. These simulations show that the currently administered standard amount is not optimal. A preload of 150 mg or lower would result in equal or higher tumor uptake in all cases. For tumors with high permeability, the uptake of labeled antibody could be increased by a factor of 8.5 using the considerably reduced optimal preload. The most sensitive parameter for the choice of the optimal amount of unlabeled antibody is the tumor uptake index. The results indicate that a personalized approach for radioimmunotherapy (RIT) with anti-CD20 antibody is required to account for the interpatient variability. The optimal amount of unlabeled antibody, which has to be determined by using a pharmacokinetic model, could substantially improve tumor uptake and thus RIT with anti-CD20 antibody.
Key words: anti-CD20 antibody, pharmacokinetic modeling, preload, radioimmunotherapy
Introduction
Radioimmunotherapy (RIT) with anti-CD20 antibody is widely used in the treatment of non-Hodgkin lymphoma (NHL).1 The concept of preloading2–5 is applied to improve the biodistribution of the radiolabeled antibodies.1 Currently, a standard amount of unlabeled antibody, dependent on the body surface area, is administered.1 However, it has been suggested to reassess the cold preloading dose,6 as the unlabeled antibody represents a competitor of labeled antibody for free antigen sites in the tumor.7 Further, it has been proposed that for RIT with anti-CD20 antibody an optimal amount of antibody, leading to the most favorable biodistribution, does exist for each individual patient.7 As the unlabeled antibody has a treatment effect itself, larger amounts of unlabeled anti-CD20 antibody could be administered after the radioactivity dose as consolidation.8
In this study, the potential of optimal preloading with respect to a maximal absorbed dose in the tumor is investigated using a pharmacokinetic model. The model incorporates the distribution of antibody to antigen sites, the competitive binding of labeled and unlabeled antibody,9 and the degradation of bound and unbound antibody.5,10 Model simulations are conducted to estimate the antibody preload that leads to the most favorable biodistribution under varying conditions such as different tumor and spleen sizes or different uptake indexes of antibody in tumor, as variability for such parameters is known to be high.2,11 This quantitative biodistribution analysis is a pivotal step for personalizing the treatment toward a more effective RIT with anti-CD20 antibody.
Materials and Methods
Model
A pharmacokinetic model (Fig. 1 and Appendix 1) was developed to describe the biodistribution of 111In-labeled anti-CD20 antibody using the modeling software MATLAB Simulink.12 The basic features5,9,10 and parameters2,13 are derived from the literature and described below. Equal biodistribution of 111In- and 90Y-labeled anti-CD20 antibody is assumed.
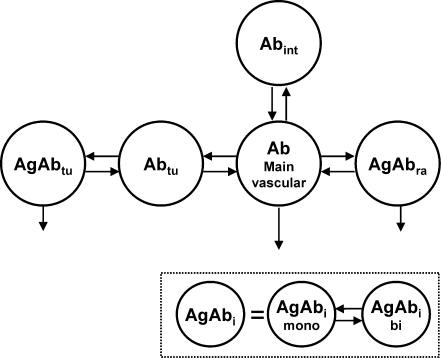
FIG. 1.
Compartmental model. The model consists of two equivalent systems (one for the labeled and one for the unlabeled antibody), which are connected by the same number of antigens and the physical decay λphys. The antibody is administered into the main plasma compartment. There is a certain capacity of readily accessible antigens (Agra), where the antibody can directly bind from the serum because of discontinuous capillary structures. To bind to most of the antigens in the tumor (Agtu), first the antibody has to pass the capillary walls. Degradation takes place wherever the antibody is bound. Degradation of unbound antibody is simplified by a linear degradation rate from the plasma compartment. AgAbi, bound antibody (i = tu or ra), Ab, free antibody; tu, tumor; ra, readily accessible; int, interstitial spaces; mono, monovalently bound; bi, bivalently bound.
For reasons of parsimony the numbers of compartments and parameters were reduced to a minimum. Thus, only two antigen sites—“readily accessible” and “tumor”—were implemented in the model and the uptake of antibody into the tumor (kin,tu) is simplified to the product of tumor mass Masstu and tumor uptake index (TUI).14 The “tumor” compartment includes all B cells of the lymph nodes and tumor, which are not readily accessible. The highly accessible antigen sites of the blood, red marrow, spleen, and liver10 are merged into one compartment named “readily accessible antigen sites” (Agra). The number of Agra was derived from the literature for normal adults.13 The increased number of such antigens due to NHL was taken into account by simulating different spleen sizes. Many antigen sites in the lymph nodes or lymphomas are less accessible,15,16 and thus the uptake of antibody in this tissue has been modeled in two steps: first, the transport of antibody through the capillary wall (kin,tu), and second, the binding to B cells. The antibody is also distributed to the interstitial spaces of normal tissue without antigens (kin,n and kout,n).
The monovalent and bivalent association (kon,mono and kon,bi) and dissociation (koff,mono and koff,bi) of antibody to antigen, as well as degradation of bound (λdb) and unbound antibody (λdu) has been incorporated in the model.5,9 Competitive binding of labeled and unlabeled antibody5 was modeled by using two circulation systems (composed of the described features), which are connected by the assumed stationary total number of antigens Ag0,i and the radioactive decay λphy5 (Fig. 1, Supplemental Data).
Model simulations
The simulations focus on the variation of tumor size, tumor uptake rate, and size of the spleen. The preload is “infused” at a constant rate over 255 minutes.17 The labeled antibody is “injected” in the 256th minute, as a bolus. The biodistribution was simulated for 1 week. The optimal biodistribution is defined as the maximal ratio of the residence times of tumor and total body τtu/τtotal.
Optimal preload depending on tumor burden
In a normal adult the mass of B cells found in all lymph nodes adds up to ∼38 g, assuming that 20% of the 1.9 × 1011 lymphocytes in the lymph nodes are B cells.13 An average expression of CD20 antigens of 149,000 per cell18 leads to 0.25 nmol of CD20 per 1 g of B cells. Knox et al.2 reported a variation of tumor size from <25 to >500 g. To account for such variability, a range of tumor antigen number (Agtu) of 3.6–328 nmol (increment 36 nmol) was investigated. The TUI and Agra were set constant to the base values of 4 mL/100 g/hour and 12 nmol,13 respectively.
Optimal preload depending on TUI
As the normal lymph node tissue and tumor are merged into one compartment, the TUI of antibody is valid for both tissues. The uptake of antibody into different lymphomas can vary considerably.11 For normal tissue (muscle, skin, etc.), an average uptake of 0.22 mL/100 g/hour was reported.19 As it is known that the permeability of tumor is higher and that lymphomas do not have elevated interstitial pressure (at least not as high as in other solid tumors20), values smaller than 0.22 mL/100 g/hour were not considered. The upper limit TUI = 40 mL/100 g/hour was chosen to test the influence of higher permeability. Agtu and Agra were set to 36 nmol2 and 12 nmol, respectively.
Optimal preload depending on spleen size
The spleen can be considerably enlarged in patients with NHL.2 It has also been observed that the spleen size is an important determinant for the biodistribution.7 The normal spleen contains a mass of B cells of ∼38 g. Therefore, the mass of B cells in the spleen was varied from 24 g (6 nmol CD20) to 240 g (60 nmol CD20). The TUI and Agtu were set constant to the base values of 4 mL/100 g/hour and 36 nmol, respectively.
Results
The optimal preload has been determined for different scenarios. The results are shown in Figures 2–4 and are described below.
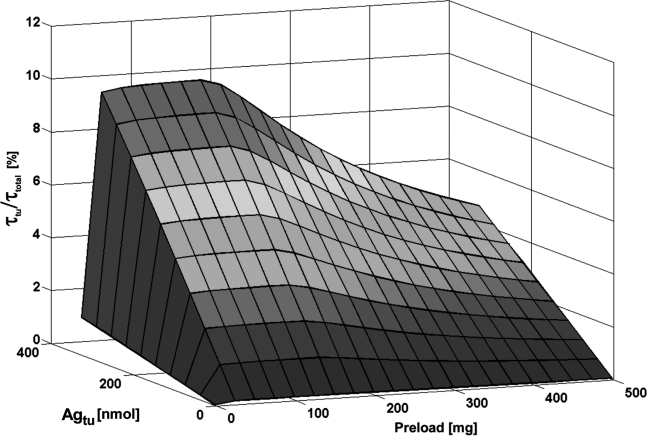
FIG. 2.
Relative residence time of tumor (τtu/τtotal) depending on the administered antibody preload and on the amount of tumor antigens (Agtu).
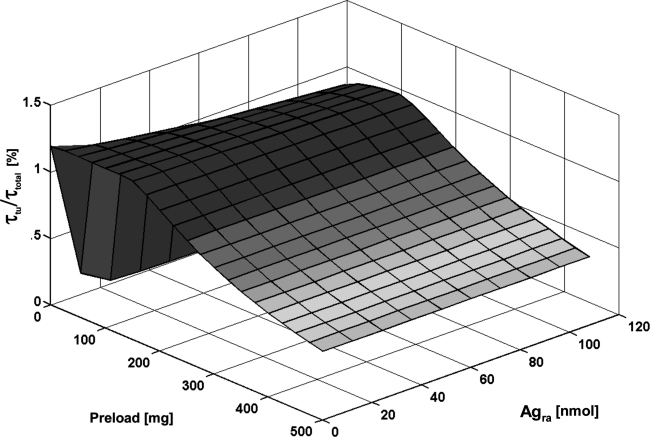
FIG. 4.
Relative residence time of tumor (τtu/τtotal) depending on the administered antibody preload and on the amount of readily accessible antigens (Agra).
Optimal preload depending on tumor burden
The simulations yielded that a preload of about 125 mg led to the most favorable biodistribution for Agtu = 3.6–220 nmol. For higher numbers of antigens (256–328 nmol), 150 mg resulted in an optimal biodistribution (Fig. 2). Such a reduced preload increased τtu/τtotal by a factor of 1.0 (Agtu = 3.6 nmol) or 2.1 (Agtu = 328 nmol), compared with the standard preload of about 500 mg.
Optimal preload depending on TUI
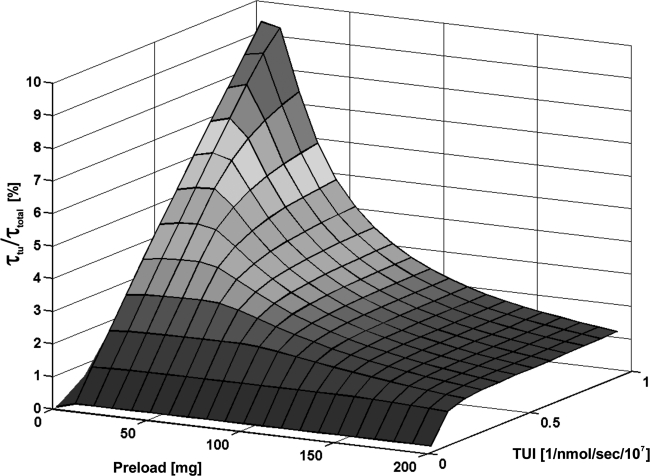
The TUI strongly influenced the value of the optimal preload (Fig. 3). Increasing TUI yielded lower optimal preloads and higher τtu/τtotal (for 0.22 mL/100 g/hour 1-fold to 40 mL/100 g/hour 16-fold compared with the biodistribution applying 500 mg). Lower TUIs required a higher concentration of antibodies for adequate tumor uptake. However, for a very low TUI (0.22 mL/100 g/hour), a preload higher than 150 mg did not improve the biodistribution.
FIG. 3.
Relative residence time of tumor (τtu/τtotal) depending on the administered antibody preload and on the tumor uptake index (TUI).
Optimal preload depending on spleen size
With an increasing B-cell mass of the spleen, more antibodies are required to saturate the antigen sink of readily accessible antigens (Fig. 4). The optimal preload (25–125 mg) improved the ratio τtu/τtotal by a factor of 2.4 compared with the standard preload of 500 mg.
Discussion
In this simulation study, a PBPK model was constructed to investigate the biodistribution of labeled anti-CD20 antibody depending on interpatient variability and preload. To identify the optimal preload, simulations with different tumor burdens, TUIs, and spleen sizes were conducted. The results suggest that when using the optimal preload a substantial improvement of tumor uptake is achievable.
In addition, the results of the present study show that there is an optimal cold dose for each patient, which is in agreement with recent findings.7 Moreover, an important result in the present study is that in no case the frequently administered amount of 250 mg/m2 leads to the most favorable biodistribution. This is especially true for tumors with higher TUI values: A fivefold increase of the TUI would lead to 8.5 times improved biodistribution when choosing the optimal amount. High accessibility for some lymphoma may be expected, as Knox et al.2 observed that for some patients even 0 mg of unlabeled antibody was sufficient to image a number of known sites of disease. For a small TUI (here 0.22 mL/100 g/hour), a high concentration of antibody in the serum is needed to transport the antibody over the capillary wall. However, a preload of >150 mg does not improve the biodistribution. To overcome the antigen sink even in case of 500 g readily accessible B cells, not >19 mg of unlabeled antibody is required. For a TUI of 4 mL/100 g/hour,14 the simulations yielded an optimal dose of 125 mg, which is comparable to 2.5 mg/kg, a dose where most of the known sites of disease (in 4 patients) were imaged in the study by Knox et al.2 The present work shows that for pretherapeutic measurement purposes the cold dose most probably can be reduced to 150 mg or less.
Comparing these results with the modeling of RIT using anti-CD45 antibody,5 it can be observed that, in general, more antibody is necessary to saturate the anti-CD45 antigen sites in liver and spleen, as all leucocytes express CD45. However, modeling RIT with anti-CD20 antibody is a greater challenge, as the lymphomas vary strongly in their permeability11 (accessibility of antigens) in contrast to the readily accessible target cells in the red marrow.10 Note that the red marrow is the target organ for myeloablative RIT with anti-CD45 or anti-CD66 antibody, whereas it is the critical organ for (nonmyeloablative) RIT using anti-CD20 antibody.
Certain assumptions were made to ensure a parsimonious model. The FcRn binding is not saturated until a total immunoglobulin G concentration of 7 mg/mL (which would correspond to 21 g antibody in this case21). Therefore, the Fc-specific uptake rate was linearized. The TUI is a semiquantitative value14 that includes all mechanisms of transport through the capillary wall. Larger lymph nodes (tumor) might be differently permeable. In addition, even in the same patient different tumors may have different TUIs. Although the main model elements and parameters are derived from published models, which were fitted to real data, the presented model needs to be further validated with experimental data. This study was primarily concerned in the overall dependence on the preload and thus the effect of different degradation rates between labeled and unlabeled antibody was not investigated. Nevertheless, different degradation rates of labeled and unlabeled antibody and other features can be simply integrated into the model.
The optimal preload was defined as the amount of antibody leading to the maximal ratio of τtu and τtotal because this study was basically concerned in how much of the administered labeled antibody actually decays in the target organ. The ratio of τtu to τ of a well-perfused or antigen-rich (critical) organ such as the red marrow could also be used as a maximization criterion. Clearly, other criteria for optimal preload might lead to a different optimal amount of antibody.
As the results show a strong dependence of the optimal preload on the individual parameters, especially the TUI, this study suggests conducting pretherapeutic biodistribution measurements for each patient to identify the individual optimal dose for therapy. The presented model (or a similar one) could then be used to identify the individual model parameters for the patient. With these model parameters, simulations using the model can be performed to identify the optimal preload.5 Higher amounts of antibody could be administered after RIT as consolidation.6
Conclusions
This study indicates that the uptake of radiolabeled antibody in RIT with anti-CD20 antibody might be considerably improved using the individually determined optimal amount of unlabeled antibody. In general, a reduction of antibody is advocated. An individual assessment of the optimal dose for therapy can probably be conducted using a pharmacokinetic model.
Supplementary Material
Appendix 1. Equations and Parameters
Model Equations (see Manuscript, Fig. 1)
The following equations describe the transport of labeled (indexed with *) and unlabeled antibody to the antigen sites, its mono- and bivalent binding,1–3 degradation, and radioactive decay. The injection of antibody is simulated as a bolus using the bolus function of SAAM2. The variables are defined in Table 1. The compartment “readily accessible” (denoted with index “ra”) is composed of all antigen sites in the liver, spleen, blood, and red marrow, which are readily accessible. The compartment “tumor” (denoted with “tu”) is composed of all antigen sites of normal lymph node tissue and tumor.
Table 1.
Parameter Definition
| Variable | Value | Unit | Source (Ref. no.) | |
|---|---|---|---|---|
| kon,mono | Association rate monovalent | 0.03 | L nmol−1 min−1 | 3 |
| kon,bi | Surface association rate bivalent | kon,bi = kon,mono × E | cm2 nmol−1 min−1 | 1 |
| koff | Dissociation rate | 0.3 | min−1 | 6 |
| E | Enhancement factor | 1.67 × 106 | cm−1 | 1 |
| Masstu | Tumor mass | 15–1330 g | g | 7 |
| VP | Total plasma volume | 3000 | mL | 3 |
| Vtu | Interstitial distribution volume | Masstu × 0.2 | mL | 8 |
| [Ag]s | Surface concentration of antigen | 7.9 × 10−5 | nmol cm−2 | 9 |
| Agi | Free antigens (ra or tu) | nmol | ||
| Ag0,i | Total antigens (ra or tu) | 0.25 nmol/g × Massi | nmol | |
| AgAbmono,i | Monovalently bound antibody (ra or tu) | nmol | ||
| AgAbbi,i | Bivalently bound antibody (ra or tu) | nmol | ||
| Abi | Unbound antibody of interstitial spaces in normal tissue or tumor or plasma | nmol | ||
| kin,n | Transport rate: VP to interstitial space | 0.0017 | min−1 | 10 |
| kout,n | Transport rate: interstitial space to VP | 0.005 | min−1 | 10 |
| kin,tu | Transport rate: VP to interstitial space tumor | TUI × Masstu | min−1 | 10 |
| kout,tu | Transport rate: interstitial space tumor to VP | kin,tu × VP/Vtu | min−1 | 10 |
| TUI | Tumor uptake index | 4 | mL (100 g)−1 h−1 | 4 |
| λdb | Degradation of bound antibody | 7.2 × 10−5 | min−1 | 2 |
| λdu | Degradation of unbound antibody | 3.9 × 10−4 | min−1 | 10 |
| λphy | Physical decay 111In | 1.72 × 10−4 | min−1 | 3 |
ra, readily accessible; tu, tumor.
Constraint for Antigen Sites (i = Readily Accessible or Tumor)
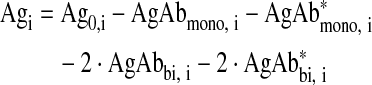 |
Eq. (1) |
Bound Antibody (i = Readily Accessible or Tumor)
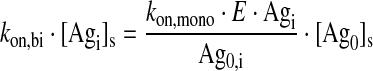 |
Eq. (2) |
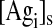 represents the surface concentration of unbound antigens on B cells.
represents the surface concentration of unbound antigens on B cells.
The ratio of kon,mono to kon,bi ( = E = 1.67 × 106 cm−1) used in the literature1 basically stems from the conversion of bulk to surface concentrations using average binding site concentrations.
Differential Equations
Monovalently bound antibody in tumor
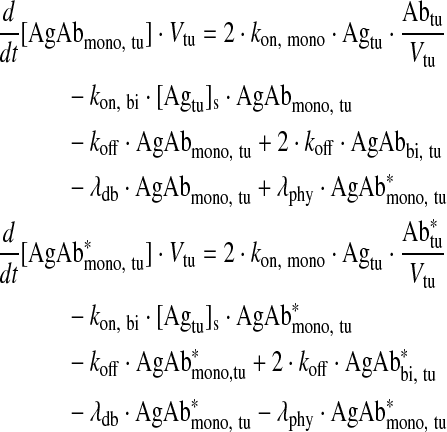 |
Eq. (3) |
Monovalently bound antibody in readily accessible antigen compartment
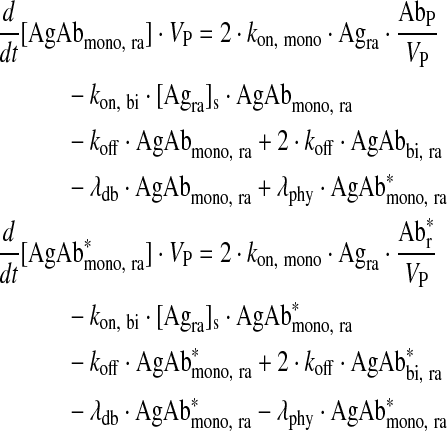 |
Eq. (4) |
Bivalently bound antibody in tumor
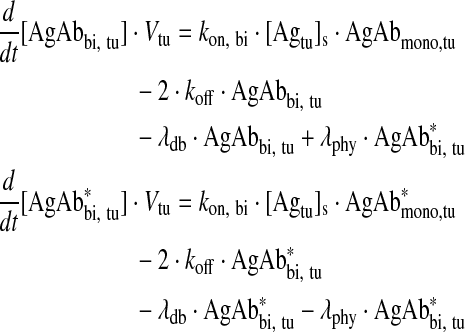 |
Eq. (5) |
Bivalently bound antibody in readily accessible antigen compartment
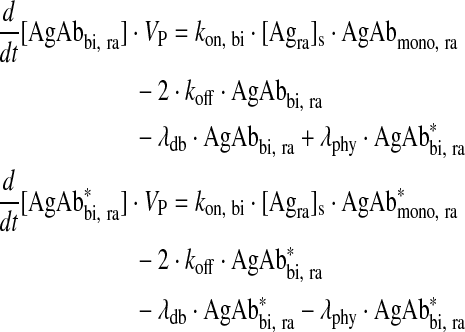 |
Eq. (6) |
Free antibody in interstitial spaces of tissues without B cells
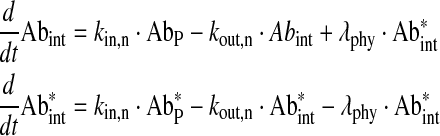 |
Eq. (7) |
Free antibody tumor
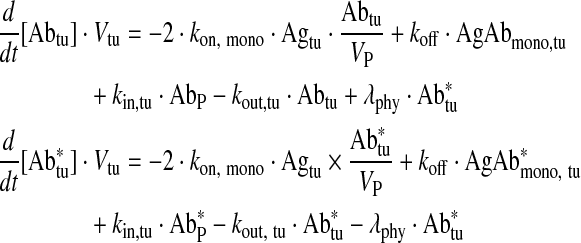 |
Eq. (8) |
Free main vascular compartment
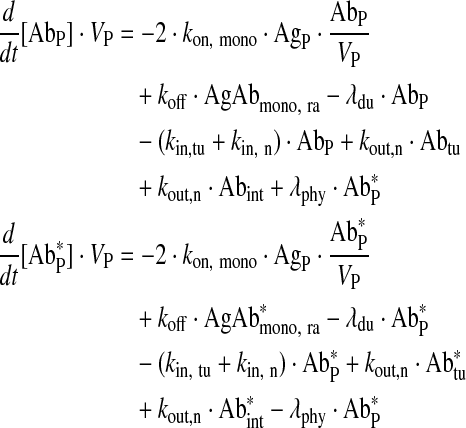 |
Eq. (9) |
Definition of Transport Rates: Tumor/Vascular4,5
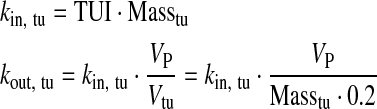 |
- 1.Kaufman EN. Jain RK. Effect of bivalent interaction upon apparent antibody affinity: Experimental confirmation of theory using fluorescence photobleaching and implications for antibody binding assays. Cancer Res. 1992;52:4157. [PubMed] [Google Scholar]
- 2.Kletting P. Kull T. Bunjes D, et al. Radioimmunotherapy with anti-CD66 antibody: Improving the biodistribution using a physiologically based pharmacokinetic model. J Nucl Med. 2010;51:484. doi: 10.2967/jnumed.109.067546. [DOI] [PubMed] [Google Scholar]
- 3.Kletting P. Bunjes D. Reske SN, et al. Improving anti-CD45 antibody radioimmunotherapy using a physiologically based pharmacokinetic model. J Nucl Med. 2009;50:296. doi: 10.2967/jnumed.108.054189. [DOI] [PubMed] [Google Scholar]
- 4.Jain RK. Transport of molecules across tumor vasculature. Cancer Metastasis Rev. 1987;6:559. doi: 10.1007/BF00047468. [DOI] [PubMed] [Google Scholar]
- 5.Baxter LT. Zhu H. Mackensen DG, et al. Physiologically based pharmacokinetic model for specific and nonspecific monoclonal antibodies and fragments in normal tissues and human tumor xenografts in nude mice. Cancer Res. 1994;54:1517. [PubMed] [Google Scholar]
- 6.Johnstone RW. Andrew SM. Hogarth MP, et al. The effect of temperature on the binding kinetics and equilibrium constants of monoclonal antibodies to cell surface antigens. Mol Immunol. 1990;27:327. doi: 10.1016/0161-5890(90)90045-2. [DOI] [PubMed] [Google Scholar]
- 7.Knox S. Goris M. Trisler K, et al. Yttrium-90-labeled anti-CD20 monoclonal antibody therapy of recurrent B-cell lymphoma. Clin Cancer Res. 1996;2:457. [PubMed] [Google Scholar]
- 8.Baxter LT. Zhu H. Mackensen DG, et al. Biodistribution of monoclonal antibodies: Scale-up mouse to human using a physiologically based pharmacokinetic model. Cancer Res. 1995;55:4611. [PubMed] [Google Scholar]
- 9.Bikoue A. George F. Poncelet P, et al. Quantitative analysis of leukocyte membrane antigen expression: Normal adult values. Cytometry. 1996;26:137. doi: 10.1002/(SICI)1097-0320(19960615)26:2<137::AID-CYTO7>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- 10.Eger RR. Covell DG. Carrasquillo JA, et al. Kinetic model for the biodistribution of an 111In-labeled monoclonal antibody in humans. Cancer Res. 1987;47:3328. [PubMed] [Google Scholar]
Acknowledgments
The authors gratefully acknowledge the grant from the Deutsche Forschungsgemeinschaft (German Research Foundation; grant no. GL 236/7-2).
Disclosure Statement
No competing financial interests exist.
References
- 1.Cheson BD. Leonard JP. Monoclonal antibody therapy for B-cell non-Hodgkin's lymphoma. N Engl J Med. 2008;359:613. doi: 10.1056/NEJMra0708875. [DOI] [PubMed] [Google Scholar]
- 2.Knox S. Goris M. Trisler K, et al. Yttrium-90-labeled anti-CD20 monoclonal antibody therapy of recurrent B-cell lymphoma. Clin Cancer Res. 1996;2:457. [PubMed] [Google Scholar]
- 3.Glatting G. Müller M. Koop B, et al. Anti-CD45 monoclonal antibody YAML568: A promising radioimmunoconjugate for targeted therapy of acute leukemia. J Nucl Med. 2006;47:1335. [PubMed] [Google Scholar]
- 4.Sgouros G. Update: Molecular radiotherapy: Survey and current status. Cancer Biother Radiopharm. 2008;23:531. doi: 10.1089/cbr.2008.0502. [DOI] [PubMed] [Google Scholar]
- 5.Kletting P. Bunjes D. Reske SN, et al. Improving anti-CD45 antibody radioimmunotherapy using a physiologically based pharmacokinetic model. J Nucl Med. 2009;50:296. doi: 10.2967/jnumed.108.054189. [DOI] [PubMed] [Google Scholar]
- 6.Sharkey RM. Press OW. Goldenberg DM. A re-examination of radioimmunotherapy in the treatment of non-Hodgkin lymphoma: Prospects for dual-targeted antibody/radioantibody therapy. Blood. 2009;113:3891. doi: 10.1182/blood-2008-11-188896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gopal AK. Press OW. Wilbur SM, et al. Rituximab blocks binding of radiolabeled anti-CD20 antibodies (Ab) but not radiolabeled anti-CD45 Ab. Blood. 2008;112:830. doi: 10.1182/blood-2008-01-132142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sharkey RM. Karacay H. Johnson CR, et al. Pretargeted versus directly targeted radioimmunotherapy combined with anti-CD20 antibody consolidation therapy of non-Hodgkin lymphoma. J Nucl Med. 2009;50:444. doi: 10.2967/jnumed.108.058602. [DOI] [PubMed] [Google Scholar]
- 9.Kletting P. Kull T. Bunjes D, et al. Radioimmunotherapy with anti-CD66 antibody: Improving the biodistribution using a physiologically based pharmacokinetic model. J Nucl Med. 2010;51:484. doi: 10.2967/jnumed.109.067546. [DOI] [PubMed] [Google Scholar]
- 10.Eger RR. Covell DG. Carrasquillo JA, et al. Kinetic model for the biodistribution of an 111In-labeled monoclonal antibody in humans. Cancer Res. 1987;47:3328. [PubMed] [Google Scholar]
- 11.Schmid J. Möller P. Moldenhauer G, et al. Monoclonal antibody uptake in B-cell lymphomas: Experimental studies in nude mouse xenografts. Cancer Immunol Immunother. 1993;36:274. doi: 10.1007/BF01740910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dhingra S. Freedenberg M. Quo CF, et al. Computational modeling of a metabolic pathway in ceramide de novo synthesis. Proceedings of the 29th Annual International Conference of the IEEE EMBS Cité Internationale; Lyon, France. Aug 23–26;2007 ; p. 1405. [DOI] [PubMed] [Google Scholar]
- 13.Westermann J. Pabst R. Distribution of lymphocyte subsets and natural killer cells in the human body. Clin Investig. 1992;70:539. doi: 10.1007/BF00184787. [DOI] [PubMed] [Google Scholar]
- 14.Jain RK. Transport of molecules across tumor vasculature. Cancer Metastasis Rev. 1987;6:559. doi: 10.1007/BF00047468. [DOI] [PubMed] [Google Scholar]
- 15.Matthews DC. Development of a marrow transplant regimen for acute leukemia using targeted hematopoietic irradiation delivered by 131I-labeled anti-CD45 antibody, combined with cyclophosphamide and total body irradiation. Blood. 1995;85:1122. [PubMed] [Google Scholar]
- 16.Matthews DC. Badger CC. Fisher DR, et al. Selective radiation of hematolymphoid tissue delivered by anti-CD45 antibody. Cancer Res. 1992;52:1228. [PubMed] [Google Scholar]
- 17.Ng CM. Bruno R. Combs D, et al. Population pharmacokinetics of rituximab (anti-CD20 monoclonal antibody) in rheumatoid arthritis patients during a phase II clinical trial. J Clin Pharmacol. 2005;45:792. doi: 10.1177/0091270005277075. [DOI] [PubMed] [Google Scholar]
- 18.Bikoue A. George F. Poncelet P, et al. Quantitative analysis of leukocyte membrane antigen expression: Normal adult values. Cytometry. 1996;26:137. doi: 10.1002/(SICI)1097-0320(19960615)26:2<137::AID-CYTO7>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- 19.Thomas GD. Chappell MJ. Dykes PW, et al. Effect of dose, molecular size, affinity, and protein binding on tumor uptake of antibody or ligand: A biomathematical model. Cancer Res. 1989;49:3290. [PubMed] [Google Scholar]
- 20.Curti BD. Urba WJ. Alvord WG, et al. Interstitial pressure of subcutaneous nodules in melanoma and lymphoma patients: Changes during treatment. Cancer Res. 1993;53:2204. [PubMed] [Google Scholar]
- 21.Ferl GZ. Wu AM. DiStefano JJ., 3rd A predictive model of therapeutic monoclonal antibody dynamics and regulation by the neonatal Fc receptor (FcRn) Ann Biomed Eng. 2005;33:1640. doi: 10.1007/s10439-005-7410-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.