Abstract
The purpose of this study was to test whether an empirical mathematical model (EMM) of dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) can distinguish between benign and malignant breast lesions. A modified clinical protocol was used to improve the sampling of contrast medium uptake and washout. T1-weighted DCE magnetic resonance images were acquired at 1.5 T for 22 patients before and after injection of Gd-DTPA. Contrast medium concentration as a function of time was calculated over a small region of interest containing the most rapidly enhancing pixels. Then the curves were fitted with the EMM, which accurately described contrast agent uptake and washout. Results demonstrate that benign lesions had uptake (P < 2.0 × 10−5) and washout (P <.01) rates of contrast agent significantly slower than those of malignant lesions. In addition, secondary diagnostic parameters, such as time to peak of enhancement, enhancement slope at the peak and curvature at the peak of enhancement, were derived mathematically from the EMM and expressed in terms of primary parameters. These diagnostic parameters also effectively differentiated benign from malignant lesions (P <.03). Conventional analysis of contrast medium dynamics, using a subjective classification of contrast medium kinetics in lesions as ‘washout,’ ‘plateau’ or ‘persistent’ (sensitivity=83%, specificity=50% and diagnostic accuracy=72%), was less effective than the EMM (sensitivity=100%, specificity=83% and diagnostic accuracy=94%) for the separation of benign and malignant lesions. In summary, the present research suggests that the EMM is a promising alternative method for evaluating DCE-MRI data with improved diagnostic accuracy.
Keywords: Breast lesion, DCE-MRI, Gd-DTPA, Pharmacokinetic modeling
1. Introduction
Magnetic resonance imaging (MRI) of the breast has demonstrated advantages over other imaging modalities. These include improved staging and treatment planning, enhanced evaluation of the augmented breast, better detection of recurrence and improved screening of high-risk patients [1,2]. Dynamic contrast-enhanced (DCE) MRI is a promising method for detecting and diagnosing breast cancer. This is because the rates of contrast medium uptake and washout are related to tumor blood flow — an important indicator of malignancy [3]. Extraction of hemodynamic parameters from DCE-MRI data requires the calculation of contrast medium concentration as a function of time (C(t)) either in each image voxel or in regions of interest (ROI). C(t) is analyzed based on various pharmacokinetic models from which hemodynamic parameters, such as perfusion rate, blood volume and capillary permeability, are extracted. However, the accuracy of such parameters depends on an appropriate theoretical model and related assumptions used to interpret data. With current approaches to data analysis and interpretation, DCE-MRI has high sensitivity for the detection of invasive breast cancer, but variable specificity is a major limitation [4,5]. Therefore, improvements in specificity are highly desirable. In addition, while sensitivity is high, further improvements would be helpful for reliable detection of early noninvasive cancers such as ductal carcinoma in situ (DCIS).
Generally, breast DCE-MRI data are analyzed using a two-compartment model approach [6-11] or a modified two-compartment model [12]. This allows determination of the transfer constant (Ktrans) and the extracellular extravascular space fraction (ve). However, the two-compartment model requires that the rates of contrast uptake and washout be closely related [10]. This is not the case for many tumors; as a result, this model sometimes does not provide a good fit to experimental data, thereby limiting its diagnostic utility. Models with three or more compartments are more realistic [13], but due to the complexity of these algorithms, meaningful fits to experimental data can only be obtained when raw images have a very high signal-to-noise ratio (SNR). In addition, physiological models require knowledge of contrast medium concentration in the blood as a function of time and, thus, the measurement of arterial input function (AIF). Measuring the AIF is often very difficult, and errors in the AIF translate into errors in measurements of tracer kinetics.
To overcome problems associated with limited SNR, semiquantitative analysis of DCE-MRI data can be performed. Most commonly in clinical practice, contrast medium uptake and washout are analyzed by simply classifying contrast medium kinetics without fitting C(t). Some common diagnostic parameters include the ‘initial area under the curve’ [14,15], ‘signal enhancement ratio’ [16], ‘maximum slope’ [15,17], ‘time to peak of enhancement’ [18], ‘washout ratio’ [19] and so on. The most widely used clinical approach is the system proposed by Kuhl et al. [20], which classifies C(t) curves as either ‘washout,’ ‘plateau’ or ‘persistent.’
As an alternative to these approaches, empirical functions can be used to fit C(t) accurately, without making assumptions about tumor physiology. Diagnostic parameters are derived from these functions, rather than from raw C(t), which reduces the effect of noise. Unfortunately, the mathematical functions with limited parameters employed so far — for instance, Gamma functions [21] — do not have the flexibility to accurately describe contrast uptake and washout for long periods of time in a number of different types of tissue. Some functions accurately fit the concentration-versus-time curve or the signal-intensity-versus-time curve, but only for short periods after contrast medium injection. Recently, we developed an empirical mathematical model (EMM) with five parameters to describe contrast uptake and washout behavior [22]. The EMM has been tested on transplanted rodent prostate tumors and accurately fits data for both low-molecular-weight and high-molecular-weight contrast agents, even at times long after contrast agent injection. Previous work [22,23] demonstrated that parameters derived from the EMM distinguish between metastatic and nonmetastatic rodent prostate tumors more reliably than the ‘two-compartment model’ approach. This is likely due to improved fits to experimental data obtained with the EMM.
In the present study, we employed the EMM to fit DCEMRI data from suspicious breast lesions acquired with a clinical 1.5-T scanner. Three useful secondary diagnostic parameters — time to peak of enhancement, enhancement slope at the peak and curvature at the peak of enhancement — were also derived from the EMM after fits to experimental data had been performed. The use of the EMM to distinguish between benign and malignant lesions was compared to the standard classification of C(t) performed by experienced radiologists using the aforementioned ‘Kuhl method’. Finally, the sensitivity of the EMM to various phases of contrast medium uptake and washout kinetics was evaluated.
2. Materials and methods
2.1. Patients and imaging protocol
Women with suspicious breast lesions detected by mammography or physical exams frequently undergo DCE-MRI scans before biopsy as part of normal clinical care at the University of Chicago Hospital. We analyzed MRI data from 22 female patients aged 34–79 years (mean age=59±11 years) using a protocol approved by the Institutional Review Board after the patients had given informed consent. Based on the pathologist's (W.R.) analysis of biopsy samples, six patients had benign lesions, nine had DCIS, two had infiltrative ductal carcinoma (IDC) and one had infiltrative lobular carcinoma (ILC). In addition, four patients had lesions missed by DCEMRI (because slices were not properly positioned) or had no lesions.
MRI exams were performed with a 1.5-T Signa scanner (General Electrical Medical System, Milwaukee, WI, USA). T1-weighted spoiled gradient-echo images of four slices (TR/TE=8.9/4.2 ms, field of view=24 cm, slice thickness=6 mm, acquisition matrix size=256×160, reconstruction matrix size=256×256, flip angle=30°, bandwidth=31.25 kHz, number of acquisitions=1) containing the suspicious lesion and surrounding tissues were acquired with high temporal resolution (7 s) before and for 1.5 min after contrast medium injection. Subsequently, the same pulse sequence was used to sample contrast medium washout at approximately 8.5, 20 and 30 min after injection during gaps in routine clinical imaging sequences. The same gain and shim settings were used for all of these scans. Omniscan was injected at a dose of 0.1 mM kg−1 and at a rate of 2 ml s−1. About 200 images were collected for each patient.
2.2. Contrast concentration calculations
Contrast agent concentration as a function of time C(t) after contrast medium injection was estimated by comparing the signal intensity S(t) from selected ROI to the control signal intensity S(0) (i.e., before contrast injection) in a reference tissue with known T1 [24]. A uniform fat region was selected as a reference tissue in this study. Since TR ⪡ T1, we can approximate signal intensity as a linear function of T1 and contrast medium concentration, obtaining:
| (1) |
where R1 (4.5 mM−1 s−1) is the longitudinal relaxivity of the contrast agent at 1.5 T and T1(fat)=260 ms [25]. Fat ROIs were selected near the suspicious lesions to minimize errors due to the B1 inhomogeneity of breast coil.
2.3. EMM
A typical plot of contrast medium concentration as a function of time C(t) can be approximated by three components: uptake, transition and washout. The EMM was designed to accurately describe these three phases. After tests of various equations, the final EMM was selected because it provided the best fit of C(t) with a relatively small number of parameters. The EMM uses a single equation to describe tissue contrast medium concentration during uptake and washout [22]:
| (2) |
where C(t) is the concentration curve as a function of time (t) calculated from the time series of MR images, A is the upper limit of tracer concentration, α is the rate of contrast uptake (min−1), β is the overall rate of contrast washout (min−1), γ is the initial rate of contrast washout (min−1) and q is related to the slope of early uptake and the curvature of the transition from uptake to washout. DCE-MRI data were acquired with very high temporal resolution (7 s) during the first 1.5 min after contrast medium injection and then at lower temporal resolution during washout. The number of independent time points was sufficient to allow the EMM to provide reliable, reproducible and unique solutions.
Appropriate choices of initial guesses of the parameters were important; poor initial guesses resulted in long computational times or, occasionally, failure to converge on a good fit. Based on our earlier experience [22,23], the best initial guesses were: A=maximum value of contrast concentration, α=1.0 (min−1), β =0.01 (min−1), q =1.0 and γ=0.01 (min−1). In a few cases, the EMM algorithm did not converge rapidly to a good fit, usually due to motion artifacts. In cases where a good fit was not obtained (goodness of fit parameter R2<.90) and the poor fit was not explained by noise level, the range of solutions was limited by testing a limited range of values for A. Parameter A was selected because a very accurate initial estimate could be obtained from the peak value of concentration. Specifically, values of A were allowed to vary between 0.5 and 2 times the peak value of contrast concentration in increments of 5% of peak value, and the best possible EMM fit for each value of A was found by optimizing the remaining parameters. The best EMM fit was selected from the resulting group of solutions. This approach resulted in an excellent fit (R2≥.90) in all cases.
2.4. Secondary parameters
Three secondary diagnostic parameters (time to peak of enhancement, enhancement slope at the peak and curvature at the peak of enhancement) are derived from Eq. (2). The concepts of time to peak of enhancement and enhancement slope at the peak have been used by other investigators [18], while curvature at the peak of enhancement is being utilized here for the first time in the analysis of DCE-MRI data. The calculation of these parameters from the EMM fit to experimental data, rather than directly from raw data, reduces the introduction of error due to noise. The following derivations establish the relationship between these diagnostic parameters and EMM parameters and illustrate how these diagnostic parameters vary as a function of EMM parameters.
2.4.1. Time to peak of enhancement (Tpeak)
The peak signal intensity of the curve occurs at the point at which the curve's first derivative is zero. By taking the derivative of Eq. (2) with respect to time, we obtain the following expression:
| (3) |
where
| (4) |
To find Tpeak, we require CD=0. Obviously, C≠0 for 0<t<∞, so we solve Tpeak for D=0. Eq. (4) cannot be solved analytically unless γ=0. However, if we recognize that γt⪡1 for t=Tpeak, we can simplify the last term of Eq. (4) to 0.5γ. We can justify this approximation because when peak concentration occurs very early after injection, Tpeak is very small, and when peak concentration occurs later, γ is very small. After some simple manipulations, we can solve the time to peak of enhancement as:
| (5) |
This formula is exactly true for γ=0.
2.4.2. Maximum value of contrast concentration (Cmax)
Cmax can be found by substituting Tpeak into Eq. (2). By the same argument used in Section 2.4.1, at the time of peak enhancement, either Tpeak or β (as well as γ) is very small. Therefore, βt⪡1 as is γt⪡1 at t=Tpeak. Using this approximation, we can find Cmax by simplifying Eq. (2) to obtain:
| (6) |
Thus, Cmax is approximately equal to A when both β and γ are small.
2.4.3. Enhancement slope at the peak (ESpeak)
There are different ways to define an enhancement slope. Here, we defined the Cmax/Tpeak ratio as the ESpeak of the curve, where Tpeak and Cmax are given by Eqs. (5) and (6), respectively.
2.4.4. Curvature at the peak of enhancement (κpeak)
The time to peak of enhancement does not distinguish between contrast concentration curves that peak at the same time but have completely different washout behaviors. In other words, the curve could bend more or less sharply at the peak, and this can be described mathematically with curvature. Therefore, we use curvature at the peak of enhancement to further characterize curves with the same Tpeak and Cmax. Since the plot of contrast uptake and washout C(t) is a two-dimensional curve, its curvature (κ) can be calculated by the following formula:
| (7) |
At D(Tpeak)=0, the absolute value of curvature at signal maximum can be expressed as:
| (8) |
where
| (9) |
When Tpeak obtained from Eq. (5) is substituted into Eq. (8), the expression for curvature κ(t) is complicated. However, noting that γTpeak ⪡ 1, the second term in Eq. (9) can be approximated as 0.25γ2. The first term with α in Eq. (9) is easily evaluated at Tpeak and C(Tpeak)=Cmax given by Eq. (6). It is then straightforward to obtain the following simplified curvature formula:
| (10) |
Eq. (10) is exactly true when γ=0.
2.5. Relative sensitivity of parameters used in EMM
To obtain accurate and efficient fitting of experimental data using a numerical algorithm, the initial guess of the parameters is important. The EMM may be more sensitive to some parameters than to others, and sensitivity to each parameter changes over the course of medium uptake and washout. Therefore, it is useful to analyze the sensitivity of each parameter as a function of time. For a given function y=f(x), the relative sensitivity (S) of the function to variations in the parameter x is . The relative sensitivity quantifies how the value of the EMM function changes as the values of various parameters change [26]. Applying this formula to the EMM (Eq. (2)), we obtain the following sensitivity functions for all five parameters:
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
2.6. Data analysis and statistical evaluation
Imaging data were processed with IDL (Research Systems, Inc., Boulder, CO). The average values of primary and secondary EMM parameters over all benign and malignant lesions were calculated, and Student's t-tests were performed to evaluate which parameters showed significant differences between benign and malignant (IDC, DCIS and ILC combined) breast lesions. The diagnosis of the pathologist was taken as the gold standard. A confidence interval of 95% or greater (P<.05) was considered statistically significant.
3. Results
3.1. Accuracy of fits obtained with the EMM
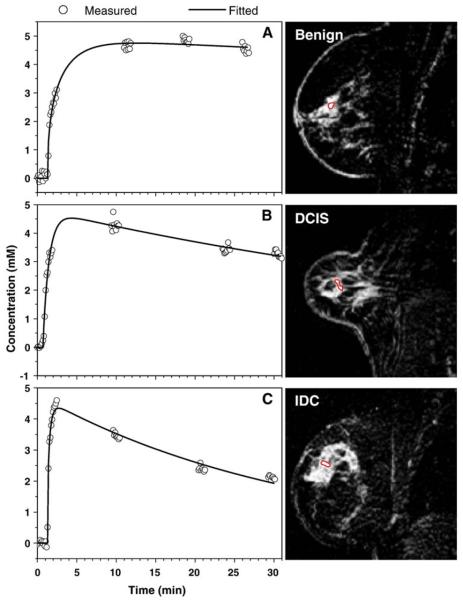
The average value of contrast agent concentration as a function of time was calculated in small ROIs that were manually selected to include the most rapidly enhanced voxels from suspicious lesions, using Eq. (1). Data were analyzed for six benign lesions, nine DCIS lesions, two IDC lesions and one ILC lesion, and C(t) for each case was fitted using the EMM. Typical results of fitting (solid line) the C(t) (open circles) obtained from MRI are shown in Fig. 1A, B and C for a benign lesion, a DCIS lesion and an IDC lesion, respectively. For benign and malignant lesions, the transition from uptake to washout was not adequately sampled. Therefore, we set γ=0.0 for these curves. It can be seen that the EMM provided excellent fits for all cases despite the fact that, in some cases, time courses were not adequately sampled and, in some other cases, data were quite noisy.
Fig. 1.
The contrast concentration curves (open circle) calculated from the average signal over the ROI using Eq. (1) are plotted as a function of time for (A) benign, (B) DCIS and (C) IDC lesions. The fitted curves (solid lines) obtained from the EMM demonstrate goodness of fit. The ROI are shown in images next to the plots.
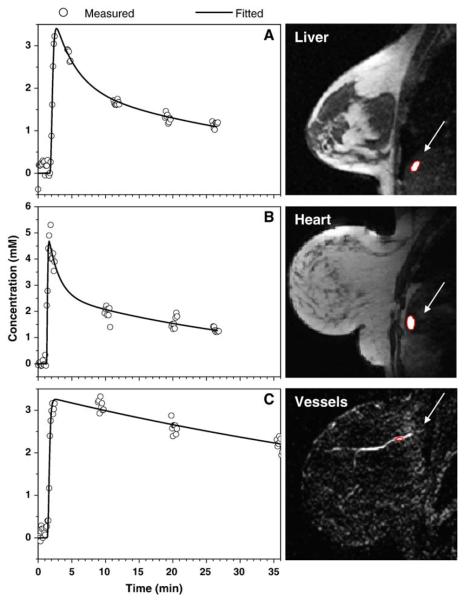
The liver and the heart often appeared in sagittal breast images. In addition, blood vessels (arteries or veins) far from the lesion appeared in most of these images. The EMM was used to fit their contrast uptake and washout curves for comparison with the lesions. Because the breast coil was not optimized for scans of the liver and the heart and because of significant motion artifacts, image quality in these regions was sometimes not acceptable. Data from manually selected ROI were analyzed only if the SNR was adequate and if there were no abrupt changes in image intensity due to motion artifacts. The contrast concentration curves (open circles) calculated for the small ROI over the most rapidly enhancing voxels and EMM fits (solid line) are shown in Fig. 2A–C for the liver, heart and vessels, respectively. Again, the EMM provided good fits in all cases despite coarse sampling after the first 90 s contrast medium injection. The heart had uptake and initial washout faster than those of the liver and vessels.
Fig. 2.
The contrast medium concentrations (open circle) calculated from the average signal over the ROI using Eq. (1) are plotted as a function of time for the (A) liver, (B) heart and (C) vessels. The fitted curves (solid lines) obtained from the EMM demonstrate goodness of fit. The ROI are shown in images next to the plots. The location of the liver, heart and vessels is indicated by arrows.
3.2. Averages of primary parameters of the EMM
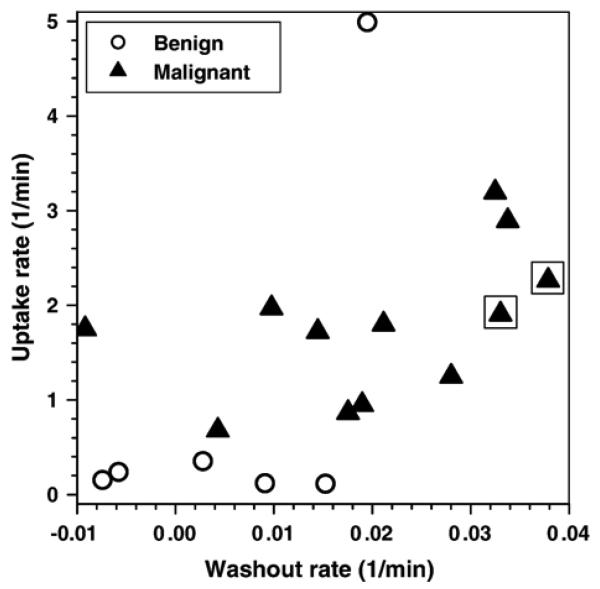
The average values of the five parameters obtained from the EMM for benign lesions, malignant lesions (combined DCIS, IDC and ILC), liver, heart and blood vessels are summarized in Table 1. The goodness of fit (R2) is also given. The EMM accurately fits all cases. Note that some R2 values that are slightly lower than .90 are likely due to noise in experimental data. Benign lesions have an average uptake rate α about two times slower (P<.4, not significantly different) and an average washout rate β about three times slower those of malignant lesions (a significant difference with P<.03). However, there is one very prominent outlier in the group of benign lesions. Without the outlier, benign lesions have an average uptake rate α about nine times slower (P<2.0×10−5) and an average washout rate β about seven times slower than malignant lesions (P<.01). In addition, benign lesions have A values smaller than those of malignant lesions, but the difference was not statistically significant (P<.2). A plot of contrast medium uptake rate versus washout rate for all lesions, as shown in Fig. 3, demonstrates good separation between benign and malignant breast lesions, except in the case of one benign lesion outlier, which was identified by the pathologist as sclerosing adenosis. The average uptake rate (2.1 min−1) and washout rate (0.035 min−1) for IDC were larger than those of DCIS (1.8 and 0.017 min−1, respectively). However, these differences were not statistically significant, possibly due to the small number of samples. If we pick an uptake rate a α>0.5 min−1 as a cutoff for malignant lesions, then calculated sensitivity=100% (12 of 12; 95% confidence interval=86–100%), specificity=83% (5 of 6; 95% confidence interval=55–83%) and diagnostic accuracy=94% (17 of 18; 95% confidence interval=76–94%).
Table 1.
A summary of the parameters obtained from the EMM to describe contrast medium uptake and washout in small ROI from benign lesions (n =6), malignant lesions (DCIS=9, IDC=2 and ILC=1), liver, heart and blood vessels
| A | α (1 min−1) | β (1 min−1) | γ (1 min−1) | q | R2 | |
|---|---|---|---|---|---|---|
| Benign | 4.0±2.1 | 1.00±1.96 | 0.006±0.011 | 0.0a | 0.8±0.7 | .96±.03 |
| Malignant | 5.7±3.0 | 1.77±0.77 | 0.020±0.014 | 0.0a | 0.8±0.5 | .93±.07 |
| Liver | 2.9±0.8 | 5.88±3.04 | 0.027±0.008 | 0.35±0.12 | 4.0±2.6 | .90±.06 |
| Heart | 5.1±2.8 | 13.4±2.01 | 0.026±0.007 | 0.46±0.15 | 4.5±1.7 | .86±.02 |
| Vessels | 4.9±2.4 | 10.1±7.71 | 0.028±0.015 | 0.03±0.11 | 4.5±3.5 | .86±.10 |
Values are reported as mean±S.D. for all slices.
Since the transition from contrast uptake to washout was undersampled for benign and malignant lesions, γ was set to zero for these curves.
Fig. 3.
Plot of uptake rate (α) versus washout rate (β) obtained by fitting the contrast concentration curves with the EMM for 6 benign lesions and 12 malignant lesions. Triangles inside squares indicate IDC. There is clear separation between benign and malignant lesions, although one of the benign lesions is an outlier.
The heart and major vessels had similar uptake rates but significantly different washout behaviors (see Table 1). The initial washout rate γ in the vessels was very small compared to that in the heart. Furthermore, the liver and the heart had similar washout behaviors but different uptake behaviors.
3.3. Averages of secondary parameters of the EMM
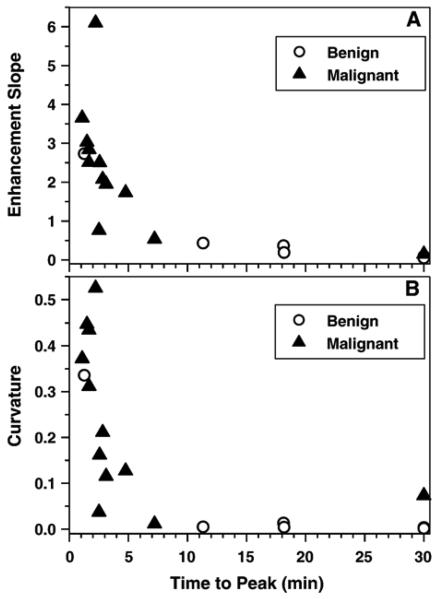
The average values of secondary parameters, as calculated from the formulas given in the Materials and Methods section for all ROI, are given in Table 2. Both figures and data show a Tpeak that is substantially longer in benign lesions than in malignant lesions, liver, heart and vessels. Although all curves for the liver, heart and vessels reached their peak within less than a minute of each other (i.e., they have closer time to peak of enhancement values), the heart had the largest curvature and the maximum enhancement slope at the peak. The curvatures and enhancement slopes at the peak were significantly smaller for benign lesions than for malignant lesions (P<.03). Curvature and enhancement slope versus time to peak of enhancement for all lesions is shown in Fig. 4A and B, respectively. Both plots display separation between benign and malignant lesions, but in this small sample, separation is less effective than that obtained using parameters directly from the model (Fig. 3). If we pick Tpeak<10 min as a cutoff for malignant lesions, then calculated sensitivity=92% (11 of 12; 95% confidence interval=76–98%), specificity=83% (5 of 6; 95% confidence interval =53–95%) and diagnostic accuracy=89% (16 of 18; 95% confidence interval =68–97%).
Table 2.
A summary of the secondary parameters time to peak of enhancement (Tpeak), maximum of contrast concentration (Cmax), enhancement slope at the peak (ESpeak) and curvature at the peak of enhancement (κpeak) derived from the EMM for the same small ROI as in Table 1
| Tpeak (min)a | Cmax (mM) | ES (mM min−1) | κ peak | |
|---|---|---|---|---|
| Benign | 18.1±11.1 | 3.8±1.8 | 0.64±1.03 | 0.06±0.13 |
| Malignant | 5.09±8.02 | 5.7±2.9 | 2.32±1.58 | 0.23±0.17 |
| Liver | 0.91±0.37 | 2.8±0.7 | 3.49±1.53 | 1.67±1.00 |
| Heart | 0.42±0.11 | 5.1±2.7 | 12.0±5.42 | 8.61±4.88 |
| Vessel | 1.38±1.25 | 4.9±2.3 | 7.54±7.79 | 2.32±3.52 |
Data are shown for benign lesions (n =6), malignant lesions (DCIS=9, IDC=2 and ILC=1), liver, heart and vessels.
Values are reported as mean±S.D. for all slices.
For those curves that did not reach a peak within the duration of the experiment, we assumed a time to peak of 30 min.
Fig. 4.
Plots of calculated secondary parameters (A) enhancement slope at the peak versus time to peak of enhancement and (B) curvature at the peak of enhancement versus time to peak of enhancement for 6 benign lesions and 12 malignant lesions. The plots show that most benign lesions have longer times to peak of enhancement, more gentle enhancement slopes and smaller curvatures at the peak of enhancement compared to malignant lesions.
3.4. Kuhl classifications
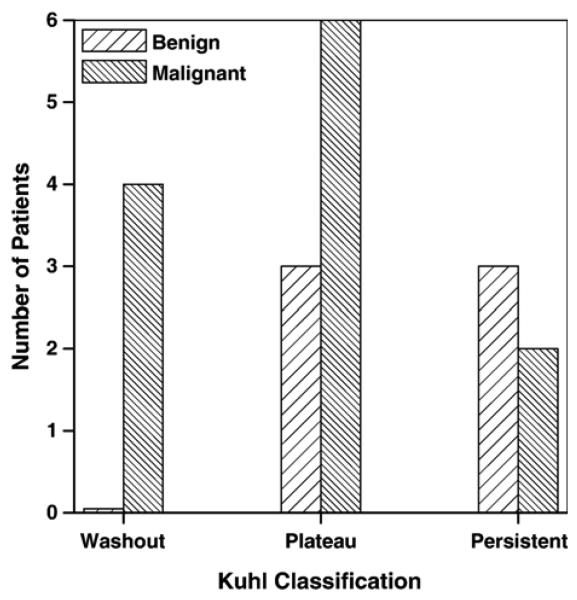
Signal-intensity-versus-time curves were evaluated using normal clinical procedures. Radiologists manually selected ROI to include the most enhancing portions of suspicious breast lesions and classified signal intensity as a function of time following contrast medium injection according to the three categories identified by Kuhl et al. The results are summarized in Fig. 5. In general, this standard clinical procedure was effective in identifying malignant lesions, which were all in either the ‘plateau’ or the ‘washout’ category. There were no benign lesions in the ‘washout’ category; however, 3 of 6 benign lesions were in the ‘plateau’ category and 2 of 12 malignant lesions were in the ‘persistent’ category. Using the criteria proposed by Kuhl et al., calculated sensitivity=83% (10 of 12; 95% confidence interval=69–94%), specificity=50% (3 of 6; 95% confidence interval=22–72%) and diagnostic accuracy=72% (13 of 18; 95% confidence interval=54–87%). All these values are slightly lower than those obtained by Kuhl et al. [20] in a study of 266 patients.
Fig. 5.
The number of lesions classified by radiologists as ‘washout,’ ‘plateau’ and ‘persistent’ based on the system proposed by Kuhl et al. for 6 benign lesions and 12 malignant lesions. There is a clear overlap between benign and malignant lesions in the ‘plateau’ and ‘persistent’ groups.
3.5. Sensitivity of parameters used in the EMM
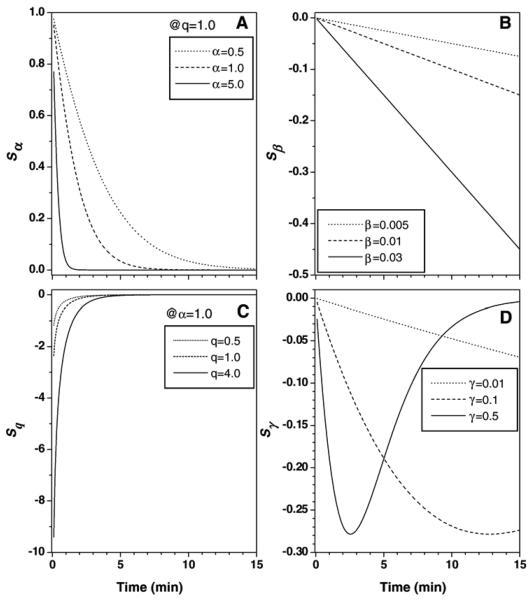
From Eqs. (11)-(15), it can be seen that the relative sensitivity of the function C(t) to variations in the parameter A does not change as a function of time. The other parameters' relative sensitivity functions are plotted as a function of time in Fig. 6. It can be seen that the relative sensitivity functions for the parameters α and q (Sα and Sq) decay exponentially as a function of time after injection. Therefore, they have their largest effect on the value of the EMM during the early uptake phase. Note that Sα is dependent on q and that Sq is dependent on α. On the other hand, the sensitivity function for β (Sβ) increases linearly as a function of time. The sensitivity function for γ (Sγ) is bounded and reaches a maximum at a characteristic time determined by the value of γ. These properties clearly reflect the role of each EMM parameter in fitting different phases of C(t) and show that the initial estimates for α and q are more important than for other parameters. If an initial estimate for the more sensitive parameter is too far from the true value, the curve-fitting algorithm may not converge.
Fig. 6.
(A–D) Plot of sensitivities of four parameters of the EMM based on Eqs. (12)-(15). The vertical axis is unitless and corresponds to changes in C(t) due to variations in each parameter. The a value used in simulations does not cover the range seen in the data because decay was too rapid at larger α values.
4. Discussion
The EMM provided excellent fits to data from all lesions and tissues despite large variations in their uptake and washout behavior. The quality of these fits likely contributed to the relatively high diagnostic accuracy of the EMM in this small group of patients. The EMM effectively separated benign and malignant lesions based on a combination of uptake and washout rate constants. Conventional clinical evaluation, based on the classification of contrast medium kinetics as ‘washout,’ ‘plateau’ or ‘persistent,’ showed differences between benign and malignant lesions, but the sensitivity and the specificity were lower than those of the EMM. Because of the relatively small number of patients studied, the 95% confidence intervals are large, and the differences in sensitivity, specificity and diagnostic accuracy between conventional clinical evaluation and the EMM are not highly statistically significant. However, there was a statistically significant difference at the 80% confidence interval. This suggests that the diagnostic accuracy for the EMM is higher than the simple classification of kinetic curves and that this approach warrants evaluation in a larger clinical trial.
The differences between benign and malignant lesions reported here are particularly promising because most of the malignant lesions studied here are DCIS and because DCIS is typically difficult to differentiate from benign lesions [27]. In addition, both uptake and washout rates for IDC tended to be larger than those for DCIS. In the present work, washout rate was accurately measured because the washout was sampled for at least 15 min after contrast medium injection, and this suggests that extended sampling of washout may result in increased diagnostic accuracy.
The secondary parameters derived from the primary parameters also distinguished between benign and malignant lesions. This is in agreement with previous studies [18]. Tpeak, ESpeak and κpeak were all significantly different between benign and malignant lesions. This is the first time that the ‘curvature at the peak of enhancement’ has been used as a diagnostic parameter. Curvature may be a useful parameter because two different plots of concentration versus time having the same time to peak of enhancement and maxima may have very different curvatures at the peak. Derivation of these secondary parameters — some of which are commonly used in clinical practice — from the primary parameters of the EMM provides some degree of noise suppression. Calculations made directly from raw experimental data are more susceptible to errors due to noise.
DCE breast MRI has high a sensitivity for the detection of breast cancer. However, a major limitation of DCE-MRI is its relatively low specificity [4,28]. Normally, malignant lesions have contrast agent uptake more rapid than that of benign lesions. Most benign lesions do not enhance or enhance slowly with delayed washout due to poor vascularization [29] and microvascular distribution [30]. However, some benign lesions have enhancement similar to that of malignant lesions. For example, in this study, the contrast-medium-concentration-versus-time plot for sclerosing adenosis was similar to that of malignant lesions, with fast uptake and washout of the contrast agent. This may be due to physiological similarities between some benign lesions and cancer. Rapid perfusion may be associated with proliferative activity of hyperlastic paraenchymal cells [31]. In addition, systematic errors in MRI measurements may decrease specificity. For example, Yankeelov et al. [32] recently showed that equilibrium transcytolemmal water exchange also significantly affects the time course of signal change after contrast medium injection and results in errors in the calculation of contrast medium concentration.
To increase specificity, morphologic markers for malignancy [33,34], including spiculated or irregular borders, peripheral enhancement and ductal enhancement [35], should be considered in combination with kinetic parameters. Improved sampling of early contrast uptake kinetics to cover the transition from uptake to washout and extended sampling of the ‘tail’ of the contrast medium washout may also increase specificity. The experience reported here suggests that the ‘tail’ should be sampled for at least 15 min. Previous work on the EMM applied to rodent tumor models demonstrated that the ‘tail’ of the washout is important for accurate diagnosis [22,23].
These preliminary results suggest that accurate fits to experimental data provided by an empirical function with a small number of parameters lead to accurate diagnoses based on contrast medium uptake and washout kinetics. Empirical function, to its advantage, does not make assumptions about tumor physiology or microanatomy, whereas the assumptions required by two-compartment or multiple compartment models lead to fitting errors and subsequent diagnostic errors. For example, tumor regions with a contrast medium washout rate that is small or zero frequently have rapid uptake rates [15]. This kinetic behavior is not accurately represented using the two-compartment model because of the necessary connection in the two-compartment model between uptake and washout rate; this limits diagnostic accuracy. The EMM does not suffer from this limitation.
The primary disadvantage of the EMM approach is that the parameters extracted do not correspond directly to identifiable physiological or anatomic features. However, this problem can be addressed by deriving equations that connect parameters of the EMM to physiological and anatomic parameters associated with various models (i.e., two or more compartment models). This can be illustrated as a first approximation by making relatively crude assumptions; if we set γ=0.0 and q=1.0, then the parameters A, α and β in the EMM can be directly compared with two-compartment models described in Eqs. (13)-(16) of Armitage et al. [36]. For example, to compare the EMM with the Tofts–Kermode model [6] described in Eq. (13) of Armitage et al., it can be seen that A=DveKtrans/Vp(Ktrans−koutve), β=kout and α+β=Ktrans/ve, where D is the dose of administered contrast agent, ve is the extravascular extracellular space volume fraction, Ktrans is the transfer constant, Vp is the volume of the plasma and kout is the rate constant for contrast medium elimination. Of course, initial assumptions (γ =0.0 and q =1.0) result in poor fits to the data and, therefore, the physiological parameters that result are probably not accurate. However, these assumptions can be refined with first-order and second-order corrections, and this may lead to more accurate descriptions of physiology combined with optimal fits to experimental data. Work on this approach is currently underway.
In the present experiments, the sparse temporal sampling beginning 90 s after contrast injection — a consequence of the requirements of the clinical protocol — may have resulted in fitting errors. In the future, we hope to obtain better sampling due to improvements in technology, such as ‘parallel imaging,’ which may increase diagnostic accuracy. Further improvements can be obtained by applying the EMM on a pixel-by-pixel basis rather than in small ROIs, as reported here. This requires careful handling of data with limited SNR, but we hope to demonstrate the feasibility of this approach in a future publication.
Nonlinear numerical curve fitting is sometimes sensitive to the initial estimate of the parameters. If this initial estimate is too far off from true values, fitting could fail. The present results show that the EMM is very sensitive to the parameters α and q. Thus, accurate fits to data are difficult to obtain when the initial estimate of these parameters is far from true values, particularly when the initial phase of rapid uptake is undersampled. On the other hand, the high level of sensitivity for α and q was needed to fit data accurately at early times after contrast injection, and improved fits resulted in increased diagnostic accuracy.
The EMM, in its present form, does not require an AIF but could be adapted to accommodate an AIF, which may reduce variability and systematic error. A number of reliable methods have been developed for the measurement of the AIF, including the reference tissues method [37-39]. The AIF obtained using one of these approaches could be deconvolved from raw data, and the result could be fitted with the EMM. Alternatively, to reduce the error of deconvolution due to noise, one could fit raw data using the EMM and then deconvolve the fitted curve from the measured AIF.
This is a pilot study with a limited number of patients, and the results do not conclusively demonstrate advantages of the EMM. However, the results are promising and justify further effort to develop and test this method with a larger number of patients.
Acknowledgments
This work was supported by grants from the Cancer Research Foundation, the National Institute of Biomedical Imaging and Bioengineering (RO1 EB003108-01), the National Cancer Institute (RO1CA78803) and the Army Breast Cancer Research Program (DAMD 17-02-1-0033).
References
- 1.Goscin CP, Berman CG, Clark RA. Magnetic resonance imaging of the breast. Cancer Control. 2001;8:399–406. doi: 10.1177/107327480100800502. [DOI] [PubMed] [Google Scholar]
- 2.Orel SG, Schnall MD. MR imaging of the breast for the detection, diagnosis, and staging of breast cancer. Radiology. 2001;220:13–30. doi: 10.1148/radiology.220.1.r01jl3113. [DOI] [PubMed] [Google Scholar]
- 3.Brix G, Kiessling F, Lucht R, Darai S, Wasser K, Delorme S, et al. Microcirculation and microvasculature in breast tumors: pharmacokinetic analysis of dynamic MR image series. Magn Reson Med. 2004;52:420–9. doi: 10.1002/mrm.20161. [DOI] [PubMed] [Google Scholar]
- 4.Orel SG. MR imaging of the breast. Radiol Clin North Am. 2000;38:899–913. doi: 10.1016/s0033-8389(05)70208-6. [DOI] [PubMed] [Google Scholar]
- 5.Rankin SC. MRI of the breast. Br J Radiol. 2000;73:806–18. doi: 10.1259/bjr.73.872.11026854. [DOI] [PubMed] [Google Scholar]
- 6.Tofts PS, Kermode AG. Measurement of the blood–brain barrier permeability and leakage space using dynamic MR imaging: 1. Fundamental concepts. Magn Reson Med. 1991;17:357–67. doi: 10.1002/mrm.1910170208. [DOI] [PubMed] [Google Scholar]
- 7.Brix G, Semmler W, Port R, Schad LR, Layer G, Lorenz WJ. Pharmacokinetic parameters in CNS Gd-DTPA enhanced MR imaging. J Comput Assist Tomogr. 1991;15:621–8. doi: 10.1097/00004728-199107000-00018. [DOI] [PubMed] [Google Scholar]
- 8.Buckley DL, Kerslake RW, Blackband SJ, Horsman A. Quantitative analysis of multi-slice Gd-DTPA enhanced dynamic MR images using an automated simplex minimization procedure. Magn Reson Med. 1994;32:646–51. doi: 10.1002/mrm.1910320514. [DOI] [PubMed] [Google Scholar]
- 9.Hayton P, Brady M, Tarassenko L, Moore N. Analysis of dynamic MR breast images using a model of contrast enhancement. Med Image Anal. 1997;1:207–24. doi: 10.1016/s1361-8415(97)85011-6. [DOI] [PubMed] [Google Scholar]
- 10.Tofts PS. Modeling tracer kinetics in dynamic Gd-DTPA MR imaging. J Magn Reson Imaging. 1997;7:91–101. doi: 10.1002/jmri.1880070113. [DOI] [PubMed] [Google Scholar]
- 11.Tofts PS, Brix G, Buckley DL, Evelhoch JL, Henderson E, Knopp MV, et al. Estimating kinetic parameters from dynamic contrast-enhanced T(1)-weighted MRI of a diffusable tracer: standardized quantities and symbols. J Magn Reson Imaging. 1999;10:223–32. doi: 10.1002/(sici)1522-2586(199909)10:3<223::aid-jmri2>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 12.Li X, Huang W, Yankeelov TE, Tudorica A, Rooney WD, Springer CSJ. Shutter-speed analysis of contrast reagent bolus-tracking data: preliminary observations in benign and malignant breast disease. Magn Reson Med. 2005;53:724–9. doi: 10.1002/mrm.20405. [DOI] [PubMed] [Google Scholar]
- 13.Port RE, Knopp MV, Hoffmann U, Milker-Zabel S, Brix G. Multicompartment analysis of gadolinium chelate kinetics: blood–tissue exchange in mammary tumors as monitored by dynamic MR imaging. J Magn Reson Imaging. 1999;10:233–41. doi: 10.1002/(sici)1522-2586(199909)10:3<233::aid-jmri3>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 14.Evelhoch JL. Key factors in the acquisition of contrast kinetic data for oncology. J Magn Reson Imaging. 1999;10:254–9. doi: 10.1002/(sici)1522-2586(199909)10:3<254::aid-jmri5>3.0.co;2-9. [DOI] [PubMed] [Google Scholar]
- 15.Moate PJ, Dougherty L, Schnall MD, Landis RJ, Boston RC. A modified logistic model to describe gadolinium kinetics in breast tumors. Magn Reson Imaging. 2004;22:467–73. doi: 10.1016/j.mri.2004.01.025. [DOI] [PubMed] [Google Scholar]
- 16.Kaiser WA, Zeitler E. MR imaging of the breast: fast imaging sequences with and without Gd-DTPA. Preliminary observations. Radiology. 1989;170:681–6. doi: 10.1148/radiology.170.3.2916021. [DOI] [PubMed] [Google Scholar]
- 17.Buadu LD, Murakami J, Murayama S, Hashiguchi N, Sakai S, Masuda K, et al. Breast lesions: correlation of contrast medium enhancement patterns on MR images with histopathologic findings and tumor angiogenesis. Radiology. 1996;200:639–49. doi: 10.1148/radiology.200.3.8756909. [DOI] [PubMed] [Google Scholar]
- 18.Szabo BK, Aspelin P, Wiberg MK, Bone B. Dynamic MR imaging of the breast. Analysis of kinetic and morphologic diagnostic criteria. Acta Radiol. 2003;44:379–86. doi: 10.1080/j.1600-0455.2003.00084.x. [DOI] [PubMed] [Google Scholar]
- 19.Ikeda O, Yamashita Y, Morishita S, Kido T, Kitajima M, Okamura K, et al. Characterization of breast masses by dynamic enhanced MR imaging. A logistic regression analysis. Acta Radiol. 1999;40:585–92. doi: 10.3109/02841859909175592. [DOI] [PubMed] [Google Scholar]
- 20.Kuhl CK, Mielcareck P, Klaschik S, Leutner C, Wardelmann E, Gieseke J, et al. Dynamic breast MR imaging: are signal intensity time course data useful for differential diagnosis of enhancing lesions? Radiology. 1999;211:101–10. doi: 10.1148/radiology.211.1.r99ap38101. [DOI] [PubMed] [Google Scholar]
- 21.Benner T, Heiland S, Erb G, Forsting M, Sartor K. Accuracy of gamma-variate fits to concentration–time curves from dynamic susceptibility-contrast enhanced MRI: influence of time resolution, maximal signal drop and signal-to-noise. Magn Reson Imaging. 1997;15:307–17. doi: 10.1016/s0730-725x(96)00392-x. [DOI] [PubMed] [Google Scholar]
- 22.Fan X, Medved M, River JN, Zamora M, Corot C, Robert P, et al. New model for analysis of dynamic contrast-enhanced MRI data distinguishes metastatic from nonmetastatic transplanted rodent prostate tumors. Magn Reson Med. 2004;51:487–94. doi: 10.1002/mrm.10737. [DOI] [PubMed] [Google Scholar]
- 23.Fan X, Medved M, Foxley S, River JN, Zamora M, Karczmar GS, et al. Multi-slice DCE-MRI data using P760 distinguishes between metastatic and non-metastatic rodent prostate tumors. MAGMA. 2006;17 doi: 10.1007/s10334-005-0022-y. [DOI] [PubMed] [Google Scholar]
- 24.Medved M, Karczmar G, Yang C, Dignam J, Gajewski TF, Kindler H, et al. Semiquantitative analysis of dynamic contrast enhanced MRI in cancer patients: variability and changes in tumor tissue over time. J Magn Reson Imaging. 2004;20:122–8. doi: 10.1002/jmri.20061. [DOI] [PubMed] [Google Scholar]
- 25.Bushberg JT, Seibert JA, Leidholdt EM, Jr, Boone JM. The essential physics of medical imaging. 2nd ed. Lippincott Williams and Wilkins; Philadelphia: 2001. [Google Scholar]
- 26.Karnavas WJ, Sanchez P, Bahill AT. Sensitivity analyses of continuous and discrete systems in the time and frequency domains. IEEE Trans Syst Man Cybern. 1993;SMC 23:488–501. [Google Scholar]
- 27.Kumar AS, Chen DF, Au A, Chen YY, Leung J, Garwood ER, et al. Biologic significance of false-positive magnetic resonance imaging enhancement in the setting of ductal carcinoma in situ. Am J Surg. 2006;192:520–4. doi: 10.1016/j.amjsurg.2006.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Heywang-Kobrunner SH, Bick U, Bradley WGJ, Bone B, Casselman J, Coulthard A, et al. International investigation of breast MRI: results of a multicentre study (11 sites) concerning diagnostic parameters for contrast-enhanced MRI based on 519 histopathologically correlated lesions. Eur Radiol. 2001;11:531–46. doi: 10.1007/s003300000745. [DOI] [PubMed] [Google Scholar]
- 29.Cosgrove DO, Bamber JC. Colour Doppler in breast diseases. Br J Radiol. 1989;62:659. [Google Scholar]
- 30.Weind KL, Maier CF, Rutt BK, Moussa M. Invasive carcinomas and fibroadenomas of the breast: comparison of microvessel distributions — implications for imaging modalities. Radiology. 1998;208:477–83. doi: 10.1148/radiology.208.2.9680579. [DOI] [PubMed] [Google Scholar]
- 31.Bone B, Wiberg MK, Parrado C, Falkmer U, Aspelin P, Gad A. Mechanism of contrast enhancement in breast lesions at MR imaging. Acta Radiol. 1998;39:494–500. doi: 10.1080/02841859809172214. [DOI] [PubMed] [Google Scholar]
- 32.Yankeelov TE, Rooney WD, Li X, Springer CSJ. Variation of the relaxographic “shutter-speed” for transcytolemmal water exchange affects the CR bolus-tracking curve shape. Magn Reson Med. 2003;50:1151–69. doi: 10.1002/mrm.10624. [DOI] [PubMed] [Google Scholar]
- 33.Tozaki M, Igarashi T, Matsushima S, Fukuda K. High-spatial-resolution MR imaging of focal breast masses: interpretation model based on kinetic and morphological parameters. Radiat Med. 2005;23:43–50. [PubMed] [Google Scholar]
- 34.Orel SG. Differentiating benign from malignant enhancing lesions identified at MR imaging of the breast: are time–signal intensity curves an accurate predictor? Radiology. 1999;211:5–7. doi: 10.1148/radiology.211.1.r99ap395. [DOI] [PubMed] [Google Scholar]
- 35.Liberman L, Morris EA, Dershaw DD, Abramson AF, Tan LK. Ductal enhancement on MR imaging of the breast. AJR Am J Roentgenol. 2003;181:519–25. doi: 10.2214/ajr.181.2.1810519. [DOI] [PubMed] [Google Scholar]
- 36.Armitage P, Behrenbruch C, Brady M, Moore N. Extracting and visualizing physiological parameters using dynamic contrast-enhanced magnetic resonance imaging of the breast. Med Image Anal. 2005;9:315–29. doi: 10.1016/j.media.2005.01.001. [DOI] [PubMed] [Google Scholar]
- 37.Kovar DA, Lewis M, Karczmar GS. A new method for imaging perfusion and contrast extraction fraction: input functions derived from reference tissues. J Magn Reson Imaging. 1998;8:1126–34. doi: 10.1002/jmri.1880080519. [DOI] [PubMed] [Google Scholar]
- 38.Yang C, Karczmar GS, Medved M, Stadler WM. Estimating the arterial input function using two reference tissues in dynamic contrast-enhanced MRI studies: fundamental concepts and simulations. Magn Reson Med. 2004;52:1110–7. doi: 10.1002/mrm.20243. [DOI] [PubMed] [Google Scholar]
- 39.Yankeelov TE, Luci JJ, Lepage M, Li R, Debusk L, Lin PC, et al. Quantitative pharmacokinetic analysis of DCE-MRI data without an arterial input function: a reference region model. Magn Reson Imaging. 2005;23:519–29. doi: 10.1016/j.mri.2005.02.013. [DOI] [PubMed] [Google Scholar]