Abstract
The energy efficiency of stimulation is an important consideration for battery-powered implantable stimulators. We used a genetic algorithm (GA) to determine the energy-optimal waveform shape for neural stimulation. The GA was coupled to a computational model of extracellular stimulation of a mammalian myelinated axon. As the GA progressed, waveforms became increasingly energy-efficient and converged upon an energy-optimal shape. The results of the GA were consistent across several trials, and resulting waveforms resembled truncated Gaussian curves. When constrained to monophasic cathodic waveforms, the GA produced waveforms that were symmetric about the peak, which occurred approximately during the middle of the pulse. However, when the cathodic waveforms were coupled to rectangular charge-balancing anodic pulses, the location and sharpness of the peak varied with the duration and timing (i.e., before or after cathodic phase) of the anodic phase. In a model of a population of mammalian axons and in vivo experiments on cat sciatic nerve, the GA-optimized waveforms were more energy-efficient and charge-efficient than several conventional waveform shapes used in neural stimulation. If used in implantable neural stimulators, GA-optimized waveforms could prolong battery life, thereby reducing the frequency of recharge intervals, the volume of implanted pulse generators, and the costs and risks of battery-replacement surgeries.
Introduction
Implantable neural stimulators, including deep brain stimulators and spinal cord stimulators, assist thousands of individuals with neurological disorders. These devices are powered by either primary cell or rechargeable batteries. When the energy of a primary cell battery is depleted, the entire stimulator must be replaced through an expensive and invasive surgical procedure. The energy capacity of a rechargeable battery determines the recharge interval, as well as the overall volume of the implant. The frequency of battery-replacement surgeries or recharge intervals, as well as the stimulator volume, could be decreased by improving the energy efficiency of stimulation. This can be achieved by optimizing the stimulation parameters, including the waveform shape. Previous studies using passive membrane models to analyze the effects of waveform shape on efficiency all concluded that the energy-optimal waveform shape is a rising exponential (Offner 1946; Fishler 2000; Kajimoto et al. 2004; Jezernik and Morari 2005). However, in more realistic models and in vivo experiments, the rising exponential waveform was no more energy-efficient than rectangular, ramp, or decaying exponential waveforms (Wongsarnpigoon et al. 2010). The objective of the present study was to use model-based optimization to design energy-optimal waveform shapes for neural stimulation.
In realistic membrane models, the energy-optimal waveform shape cannot be determined analytically because of the complexity and non-linearity of the equations that define the excitable membrane. Also, a “brute force” method of testing every possible waveform shape is not feasible since the number of possible waveform shapes is infinite. Instead, these types of problems are well suited for global optimization algorithms. We designed a genetic algorithm (GA) and applied it to a computational model of extracellular stimulation of a mammalian myelinated axon. The outcome of these simulations was a set of waveform shapes that were more energy-efficient than many conventional waveforms used in neural stimulation. As well, the resulting waveforms were more energy-efficient than the conventional waveforms for excitation of nerve fibers in vivo. The results suggest that this novel approach to designing efficient stimulus waveforms may have significant clinical relevance. In particular, the optimal waveforms could prolong battery life, thus reducing the frequency of recharge intervals, the volume of implanted pulse generators, and the costs and risks of battery-replacement surgeries. Preliminary results of this study were presented previously in a conference abstract (Wongsarnpigoon and Grill 2009).
Methods
Overview of genetic algorithms
Genetic algorithms seek optimal solutions through a process based on the principles of biological evolution. The first generation of a GA starts with a population of candidate solutions, which are analogous to organisms, and the parameters that characterize each solution are its “genes”. Next, the fitness of each solution is assessed using a cost function specific to the optimization problem. Then, the solutions “mate” with each other, resulting in offspring solutions that possess a combination of the parents’ genes, and the genes of the offspring are mutated. Both the mating process and mutations promote a thorough search of the solution space to improve the chances of discovering the global optimum rather than a local optimum. Following each generation, the population is partially or completely replaced by the offspring. As the GA progresses, beneficial genes remain in the gene pool of the population while unfavorable genes are discarded. This process—evaluating fitness, mating, and replacing solutions—is repeated either for a predetermined number of generations or until the solutions converge upon a fitness value. The solution with the overall greatest fitness is the resulting estimate of the optimal solution.
Specific implementation of the genetic algorithm
We designed a GA to seek the energy-optimal waveform shape in a computational model of extracellular stimulation of a single myelinated mammalian peripheral axon. Simulations were run in NEURON (Hines and Carnevale 1997) using the MRG model (fiber diameter = 11.5 μm), which represented a myelinated mammalian peripheral axon as a double cable model with a finite impedance myelin sheath and explicit representation of the nodes of Ranvier, paranodal sections, and internodal segments (McIntyre et al. 2002). Stimulation was delivered through a current-regulated point source situated within a conductive medium (300 Ω-cm) (McNeal 1976) located 1 mm directly above the center node of the fiber.
In each generation of the GA, the population consisted of 50 stimulation waveforms with fixed pulse width (PW). Waveforms were discretized in time using a time step equal to that of the computational model (dt = 0.002 ms), and the genes of each waveform represented the amplitudes at every time step. The values of the genes of the waveforms of the first generation were selected at random from a uniform distribution between 0 and two times the cathodic threshold of stimulation with a rectangular waveform at the equivalent PW (e.g., 807 μA for PW = 10 μs; 190 μA for PW = 100 μs; 79.8 μA for PW = 1 ms). The cost function (F) used to evaluate the fitness of each waveform equaled the sum of the energy consumed by the waveform (E) and a substantial penalty if the waveform failed to elicit an action potential:
| (1) |
| (2) |
where P is instantaneous power, t is time, I is current, and N is the number of discretizations (genes) of a stimulation waveform. If the waveform elicited an action potential, then Penalty equaled 0, but if the waveform did not elicit an action potential, then Penalty equaled 1 nJ/ohm (2 to 3 orders of magnitude larger than E).
At the end of each generation, the top 10 fittest waveforms (i.e., smallest F) remained in the population while the remaining 40 waveforms were replaced by offspring. Every waveform, regardless of its value of F, had an equal probability of being selected as a parent, and each offspring was generated by combining the genes of two parents using two crossover points. A crossover point was a randomly selected gene location, where during mating the genes prior to the crossover point from one parent were combined with the genes beyond the crossover point from the other parent. With two crossover points, the effect was a swap of a segment of one parent’s genes with the corresponding section of the other parent’s genes. Each gene of the offspring was mutated by scaling the value by a random factor chosen from a normal distribution (μ = 1, σ2 = 0.025). Because the initial waveforms were monophasic cathodic pulses, the genes were restricted to negative values.
The GA was run using a wide range of PWs (0.02, 0.05, 0.1, 0.2, 0.5, 1, and 2 ms) to determine whether the outcome of the GA varied with PW. For each PW, we ran the GA for 5 independent trials of 10,000 generations with different initial populations. For each trial, we recorded the energy consumed by the most energy-efficient waveform of each generation (generation energy), the most energy-efficient waveform of the final generation (GA waveform), and the charge delivered by the GA waveform:
| (3) |
For each PW, we calculated the means and standard errors of the energy and charge consumed by the GA waveforms across the 5 independent trials.
Population Model
The GA waveforms were evaluated in a population model of 100 parallel MRG axons (11.5-μm diameter) distributed uniformly within a cylinder with 3-mm diameter. Extracellular stimulation was delivered through a point current source located at the center of the cylinder. For each PW (0.02, 0.05, 0.1, 0.2, 0.5, 1, and 2 ms), 10 populations of randomly-positioned axons were selected. For each population, we constructed input/output (I/O) curves of the number of fibers activated vs. E, as well as the number of fibers activated vs. Q. To adjust the stimulation amplitude of a waveform, the entire waveform was scaled. For each I/O curve, the E and Q needed to activate 50% of the entire population were computed, and the means and standard errors of these values across the 10 axon populations were calculated. Using the same axon populations, we also calculated I/O curves for conventional waveforms used in neural stimulation: rectangular, rising/decreasing ramp, rising/decaying exponential, and sinusoid waveforms [See Appendix for equations].
In vivo experiments
Surgical preparation
All animal care and experimental procedures were approved by the Institutional Animal Care and Use Committees of Duke University and were followed according to The Guide to the Care and Use of Laboratory Animals, 1996 Edition, National Research Council. Experiments were performed on 3 adult male cats. Sedation was induced with acepromazine (Vedco Inc., 0.3 mg/kg; S.Q.), and anesthesia was induced with ketamine HCl (Ketaset 35 mg/kg; I.M.) and maintained during the experiment with α-chloralose (Sigma-Aldrich, Inc., initial 65 mg/kg supplemented at 15 mg/kg; I.V.). The cat was intubated, and respiration was controlled to maintain end tidal CO2 at 3–4%. Core temperature was monitored and maintained at 39°C. Fluid levels were maintained with saline solution and lactated ringers delivered through the cephalic vein (15 ml/kg/hr, I.V.). Blood pressure was monitored using a catheter inserted into the carotid artery.
The sciatic nerve was accessed via an incision on the medial surface of the upper hindlimb. A monopolar cuff electrode, composed of a platinum contact embedded in a silicone substrate, was placed around the nerve and secured with a suture around the outside of the electrode. The return electrode was a subcutaneous needle. Two stainless steel wire electrodes were inserted into the medial gastrocnemius muscle to measure the electromyogram (EMG) evoked by stimulation of the sciatic nerve. The EMG signal was amplified, filtered (1–3000 Hz), recorded at 500 kHz, rectified, and integrated to quantify the response (EMG integral).
Stimulation and recording were controlled with Labview (DAQ: PCI-MIO-16E-1) (National Instruments, Austin, TX). A voltage waveform was delivered at a rate of 500 ksamples/s to a linear voltage-to-current converter (bp isolator, FHC, Bowdoin, ME) and delivered through the cuff electrode. The voltage across (V) and current through (I) the cuff electrode and return electrode were amplified (SR560, Stanford Research Systems, Sunnyvale, CA) and recorded (fsample = 500 kHz). The energy delivered during stimulation was determined by integrating the product of V(t) and I(t):
| (4) |
The charge delivered during stimulation was determined by integrating I(t) (3).
Recruitment Curves
Recruitment curves of EMG integral as a function of E and Q were measured for rectangular, decaying exponential (time constant [τ] =132, 263, and 526 μs), and GA waveforms at various PWs (0.02, 0.05, 0.1, 0.2, 0.5, and 1 ms) in random order. At frequent intervals over the course of the experiment, we stimulated with the rectangular waveform at a fixed PW to monitor shifts in threshold. Threshold shifts occurred in only one animal, and the values of E and Q were scaled accordingly. Recruitment curves were generated using a similar procedure as in the computational models: stimulus amplitude was incremented, 3 stimulation pulses were delivered at ~1 Hz at each increment, and the average values of E, Q, and EMG integral were recorded. From each recruitment curve, the values of E and Q required to generate 50% of the maximal EMG was calculated, and the values at PW = 0.02 ms for the rectangular waveform were defined as baseline values. Subsequently, all values of E and Q were normalized to their respective baseline value, and the means and standard errors across experiments were calculated.
After log-transformation of the data, the effects of waveform shape on energy and charge efficiency were analyzed. A two-way repeated measures ANOVA was performed for each measure of efficiency; the dependent variable was E or Q, and the independent variables were waveform shape, PW (within-subjects factors), and cat (subject). Where interactions between waveform shape and PW were found to be significant (p < 0.05), the data were subdivided by PW for one-way repeated measures ANOVA. Again, the dependent variable was E or Q, and the independent variables were waveform shape (within-subjects factor) and cat (subject). For tests which revealed significant differences among waveforms (p < 0.05), post hoc comparisons were conducted using Fisher’s protected least significant difference (FPLSD). Although data were log-transformed for analysis, data were plotted as average percent difference with respect to the GA waveforms.
Results
We implemented a genetic algorithm in a computational model of peripheral nerve stimulation to determine the energy-optimal waveform shape for neural stimulation. The energy efficiencies of the GA waveforms were compared to those of conventional waveform shapes in a computational model of a population of axons and during in vivo stimulation of peripheral nerve fibers.
Genetic algorithm in single axon model
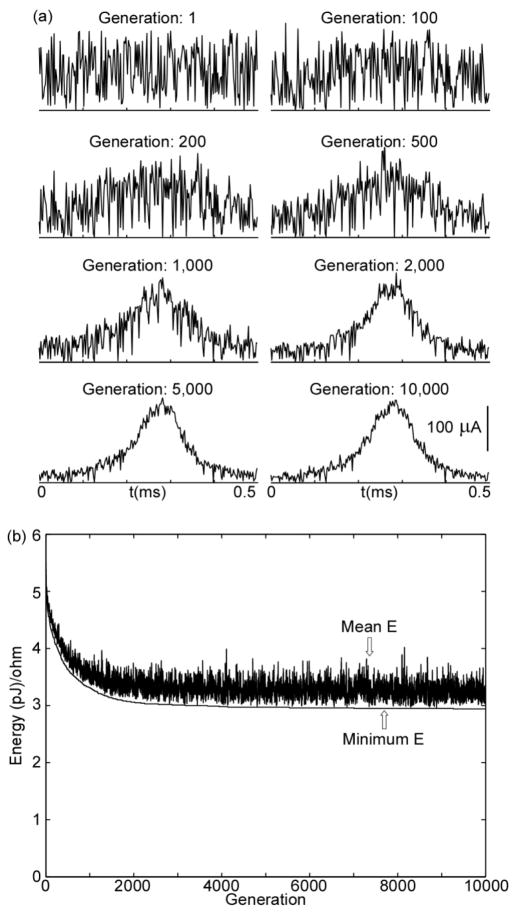
Each trial of the GA began with a different population of random waveforms, but by the end of each trial, the GA converged upon consistent and highly energy-efficient waveform shapes (figure 1). The generation energy converged to within 1% of the final generation energy by 5000 generations for PW ≤ 0.5 ms and by 9000 generations for PW = 1 and 2 ms. For each PW, the GA waveforms were very similar across trials, and across PWs the shapes of the GA waveforms were quite similar (figure 2). For PW ≤ 0.2 ms, the GA waveforms resembled truncated Gaussian curves, with the peak near the middle of the pulse. For PW ≥ 0.5 ms, the shapes of the GA waveforms also resembled Gaussian curves but with leading and/or trailing tails of negligible amplitude.
Figure 1.
Progression of genetic algorithm for a single trial (PW = 0.5 ms). a) Changes in waveform shapes across generations. The sequence of plots shows the most energy-efficient waveform at each indicated generation. b) Minimum and mean energy of population across 10,000 generations. Waveforms that failed to elicit an action potential were not included in the calculation of the mean energy.
Figure 2.
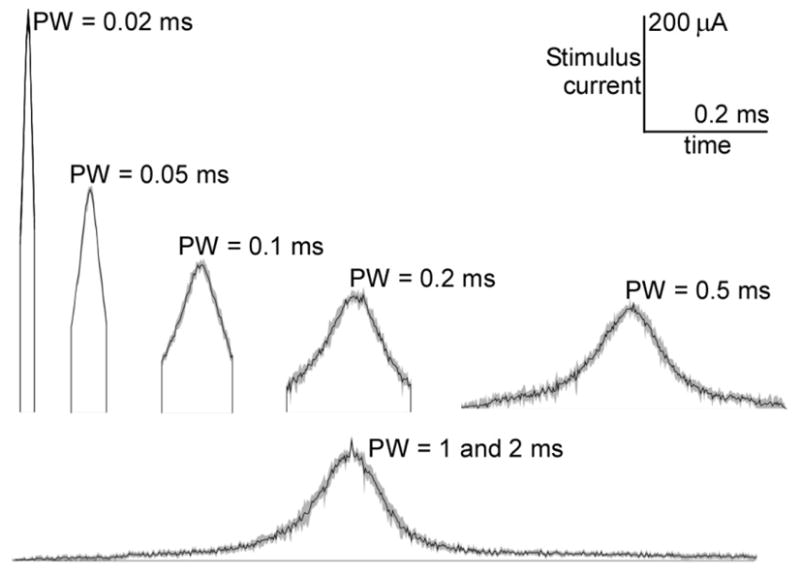
Energy-optimal stimulation waveforms resulting from the GA for different PWs. Curves represent the means of the resulting waveforms across 5 independent trials, and the gray regions define 95% confidence intervals. Waveforms for PW = 1 and 2 ms were combined, and the leading and trailing tails of low amplitude were truncated.
Efficiency of GA waveforms in the population model
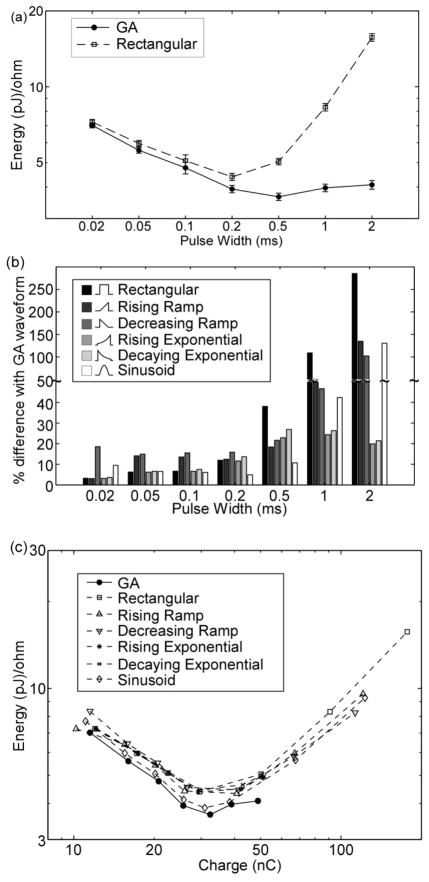
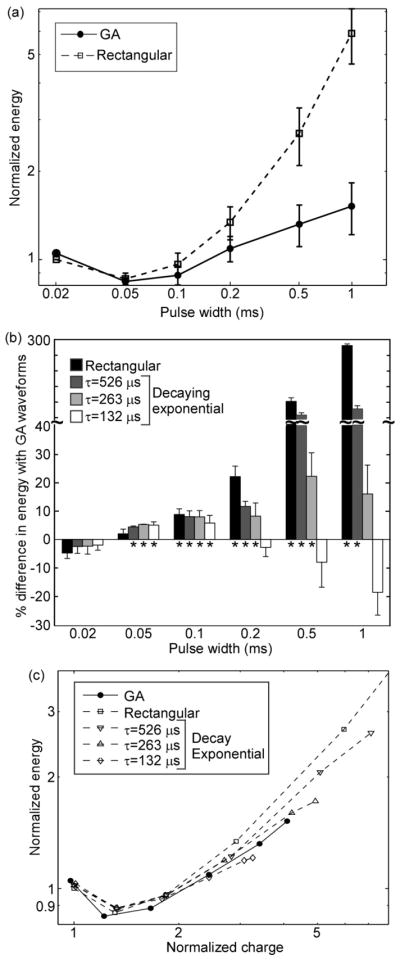
The GA waveforms were more energy-efficient than the conventional stimulation waveform shapes for all PWs in the population models. The energy-duration curve of the GA waveforms was concave up (figure 3(a)), and the minimum E for the GA waveforms across PWs was less than the minimum E for the conventional waveform shapes. Of these other shapes, the shape that most resembled the GA waveforms—the sinusoid—had the lowest minimum energy across PWs. For PW ≤ 0.2 ms, the GA waveforms were slightly more energy-efficient (< 20%) than the other waveform shapes (figure 3(b)). Between PW = 0.2 ms and 0.5 ms, the differences in energy efficiency between GA waveforms and the conventional shapes increased considerably, and these differences increased further with PW for all but the exponential waveforms. Because the positions of the axons were randomized in the population model, these results demonstrate that the superior energy efficiency of the GA waveforms was independent of the location of the electrode with respect to the axon.
Figure 3.
Energy efficiency of GA waveforms in a model of extracellular stimulation of a population of myelinated axons. a) Energy-duration curves for activation of 50% of the axons (mean +/− SE; n=10 different random populations of 100 axons). b) Energy efficiency of GA waveforms compared to conventional waveform shapes used in neural stimulation (mean, n=10; SE was negligible). Positive values of “% difference with GA waveform” indicate that GA waveforms were more energy-efficient. c) Energy efficiency plotted against charge efficiency.
The GA waveforms were also more energy-efficient than most of the waveform shapes when energy was plotted against charge. For all waveform shapes, the curves of E vs. Q were concave up and many of the curves overlapped substantially (figure 3(c)). However, the curves for the GA waveforms and sinusoid lay under the other curves, indicating that for a given amount of charge, the GA and sinusoid waveforms consumed less energy to reach threshold than the other waveform shapes.
Sensitivity analysis
The energy-optimal waveform shapes were largely insensitive to variations in the parameters of the GA. Doubling or halving the number of waveforms that survived to the next generation or the number of waveforms in each generation had no substantial effects on the shape of the GA waveforms or their energy efficiencies (< 0.1% difference). Also, the amplitudes of the waveforms in the initial generation were scaled between 0.4–1.6 times the original amplitudes, and scaling factors > 0.8 had little effect on the shape and energy efficiency (< 0.1% difference) of the GA waveform. Scaling factors below 0.6, however, resulted in initial waveforms that were all below threshold, and the GA did not converge to an energy-efficient waveform. In addition, the variance of the normal distribution used in mutations was scaled between 0–4 times the original variance. With variance = 0 (no mutations), the GA rapidly converged on an energy-inefficient waveform. However, for all other values of variance the GA produced nearly identical GA waveforms with approximately the same energy efficiencies (< 0.4% difference).
Although the shape of the GA waveforms remained consistent when dt was varied between 0.001–0.01 ms, the energy efficiency did change. Smaller values of dt produced finer resolution of the waveform shape, which created more energy-efficient GA waveforms for PW ≤ 0.1 ms (< 11%). However, the improved resolution also led to less energy-efficient GA waveforms for PW ≥ 1 ms, as a result of more noise in the waveform (< 10.5%).
In addition to using a fiber diameter of 11.5 μm, we ran the GA with fiber diameters of 5.7 μm and 16 μm. The GA waveforms produced for each fiber diameter remained the most energy-efficient waveforms in their respective models, and their overall shapes were consistent across diameters (figure 4(a)). Further, the GA waveforms optimized for diameter = 11.5 μm (figure 2) were still more energy-efficient than the conventional waveform shapes for excitation of the other two diameters.
Figure 4.
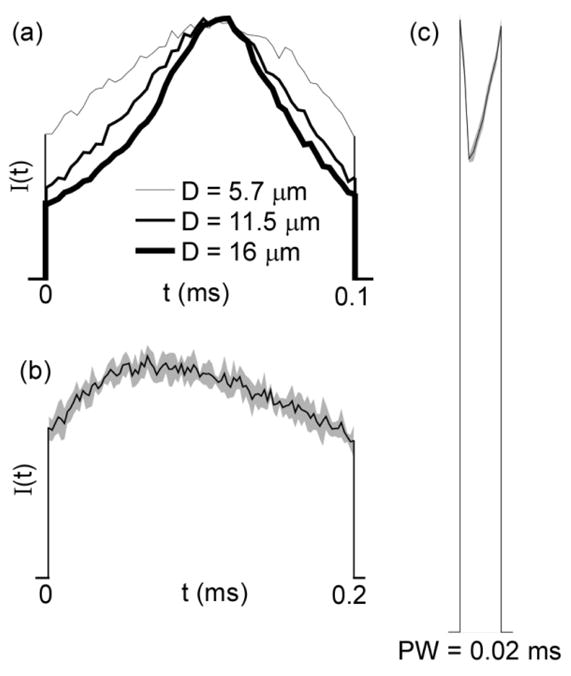
Sensitivity of GA waveforms to model parameters. a) Fiber diameter (D): curves represent mean of the GA waveforms across 5 trials for PW = 0.1 ms. b)–c) Hodgkin-Huxley model: Curves represent the means of the resulting waveforms across 5 independent trials, and the gray regions define 95% confidence intervals for PW = 0.2 ms (b) and PW = 0.02 ms (c). Amplitudes are not to scale.
The shape and efficiency of GA waveforms were dependent on the model of the neural membrane. We ran the GA in a model of a myelinated axon that consisted of nodes with Hodgkin-Huxley membrane parameters connected by electrically insulated myelinated internodes. This model differed from the MRG model both geometrically (e.g., no paranodal sections) and physiologically (e.g., lower temperature, no persistent sodium channels), but the fiber diameter and electrode-fiber distance were unchanged. In the Hodgkin-Huxley model, for PW ≥ 0.05 ms the GA waveforms generated in the Hodgkin-Huxley model were still unimodal as in the MRG model but were asymmetric (figure 4(b)). However, for PW = 0.02 ms the GA waveforms from the two models diverged (figure 4(c)). In addition, when tested in the Hodgkin-Huxley model, the original GA waveforms from the MRG model were not uniformly more energy-efficient than conventional waveform shapes.
GA waveforms fit with analytical equation
To gain a better understanding of the exact shapes of the energy-optimized waveforms, we fit the waveforms to a piece-wise generalized normal distribution:
| (5) |
where A is the amplitude at the peak, located at t = μ; α’s and β’s are scale and shape parameters, respectively, and must be greater than 0; and the subscripts correspond to the left (L) and to the right (R) of the peak. When αL = αR and βL = βR, the function is symmetric about μ, and the values of β dictate the kurtosis (i.e., peakedness) of the waveform. When αL ≠ αR and/or βL ≠ βR, varying degrees of kurtosis and skewness can be produced [see Appendix for equations].
The parameters of (5) were optimized to fit the mean GA waveforms (i.e., figure 2) using the lsqcurvefit function in Matlab (R2007b; The Mathworks, Natick, MA). The least-square optimized waveforms fit well with the energy-optimized waveforms (R2 > 0.96). Across PWs, the fitted waveforms were not very skewed (−0.5 < skewness < 0.5, where skewness = 0 is perfect symmetry), had sharper peaks (kurtosis > 0.55) than the normal distribution (kurtosis = 0), and the kurtosis of the fitted waveforms increased with PW.
Next, we ran a modified GA, where the stimulation waveforms were characterized by (5) instead of by the amplitudes at each time step. As a result, all waveforms were characterized by only six parameters—A, μ, αL, αR, βL, and βR—and initial values of these parameters were selected at random from uniform distributions (A: between 0 and four times the cathodic threshold of stimulation with a rectangular waveform at equivalent PW; μ: 0 – PW; α’s: 0.01–0.5; β’s: 0.01–3).
The waveforms that resulted from optimization with this modified GA were not substantially different from the waveforms generated by the initial GA. The shapes of the waveforms were quite similar to the initial GA waveforms across all PWs (R2 > 0.93), and the energy efficiencies improved very little (< 2%) for PW ≤ 0.5 ms. However, the modified GA waveforms were more energy-efficient than the initial GA waveforms for PW = 1 and 2 ms (5.6% and 10.4%, respectively), as a result of the smoothness of the modified GA waveforms and their ability to reach amplitudes near 0 at the tails. Consequently, the energy-duration curve with this GA was not concave up as with the original GA, but instead, E remained constant as PW increased.
In vivo measurements of stimulation efficiency
The in vivo measurements comparing the efficiency of GA waveforms to rectangular and decaying exponential waveforms largely corroborated the results of the population model. For PW ≥ 0.05 ms, the GA waveforms were significantly more energy-efficient than most of the rectangular and decaying exponential waveforms (p < 0.05, FPLSD) (figure 5(a), (b)). Although the decaying exponential with τ = 132 μs appeared to be more energy-efficient than the GA waveforms for PW ≥ 0.5 ms, this result was misleading; for long PWs, increasing the PW for exponential waveforms simply extends the low-amplitude tail, which has negligible effects on excitation. As a result, the energy-duration curve for the exponential waveforms leveled off at long PWs (Wongsarnpigoon et al. 2010), while the energy-duration curve for the GA waveforms increased with PW, as in the population model. When normalized E was plotted against normalized Q, the GA waveforms appeared to be more energy-efficient than the rectangular waveform for normalized Q > 2 (figure 5(c)). However, the GA waveforms were not substantially more energy-efficient than the decaying exponential waveforms.
Figure 5.
In vivo measurements of energy efficiency of neural stimulation with GA waveforms. a) Energy-duration curves for generation of 50% of maximal EMG (mean +/− SE; n=3). b) Energy efficiency of GA waveforms compared to rectangular and decaying exponential waveforms (mean +/− SE; n=3). Positive values of “% difference with GA waveform” indicate that GA waveforms were more energy-efficient. c) Energy efficiency plotted against charge efficiency.
Efficiency analysis of biphasic stimulation waveforms
Although the original GA revealed energy-optimal waveforms for monophasic stimulation, most waveforms used for nerve stimulation are biphasic. Because the charge recovery pulse can influence the threshold of the primary pulse (van den Honert and Mortimer 1979), it was unclear whether the monophasic GA waveforms would remain energy-optimal for biphasic stimulation. First, we recalculated thresholds in the single fiber model for all waveform shapes with the addition of rectangular charge-balancing anodic phases. We varied the duration (PWanodic/PWcathodic = 1, 5, or 10) as well as the timing (preceding or following the cathodic phase) of the charge-balancing phase. Amplitudes of the anodic phases were adjusted to produce zero net charge for the entire waveform, and E was calculated from both phases of the waveform.
The biphasic results showed that the GA waveforms optimized for monophasic stimulation were not the most energy-efficient waveforms across all PWs. Therefore, we modified the GA to seek energy-optimal biphasic waveform shapes. For each combination of duration and timing (i.e., before or after the cathodic phase) of the rectangular charge-balancing anodic phase, we ran 5 separate trials of the GA to optimize the shape of the cathodic pulse for PW = 0.02–1 ms, and E was calculated from both the anodic and cathodic phases of the waveform.
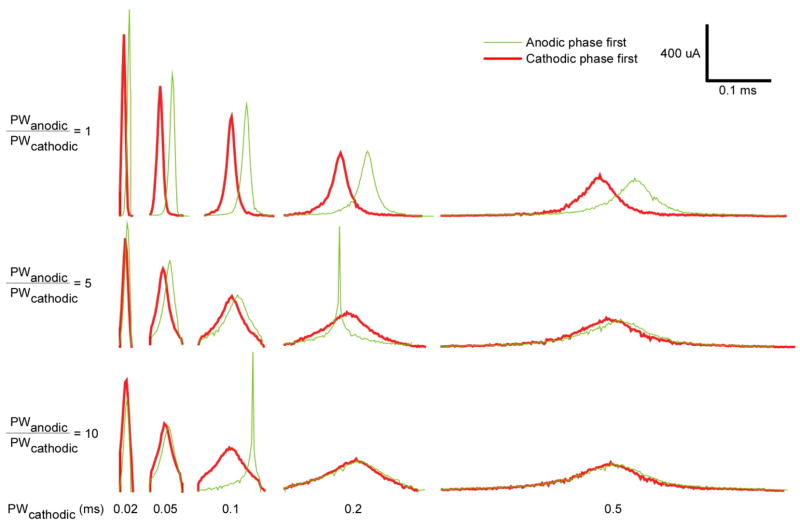
The shapes of biphasic GA waveforms varied with both the timing and duration of the anodic phase. Most waveforms still resembled truncated normal curves, but the peaks of the cathodic phases were shifted away from the anodic phase (figure 6). As with the monophasic GA waveforms, as PWcathodic increased the waveforms generally became flatter. The duration of the anodic phase relative to the cathodic phase influenced the peakedness of the resulting waveforms: the shorter the anodic phase, the sharper the peak of the cathodic phase. However, for waveforms with anodic phase first, PWanodic = 1 ms and PWcathodic = 0.2 or 0.1 ms, the peaks of the resulting waveforms were sharper than expected. Surprisingly, the peaks of both of these waveforms were located exactly 0.086 ms after the anodic pulse for every trial. Analysis of the gating parameters and membrane voltage during stimulation did not reveal any obvious explanations for this particular shape.
Figure 6.
Energy-optimal biphasic waveforms resulting from the biphasic GA for varying duration and timing of the anodic phase. The curves represent the mean of the cathodic phases of the waveforms across 5 trials of the GA, and waveforms were shifted to align the peaks.
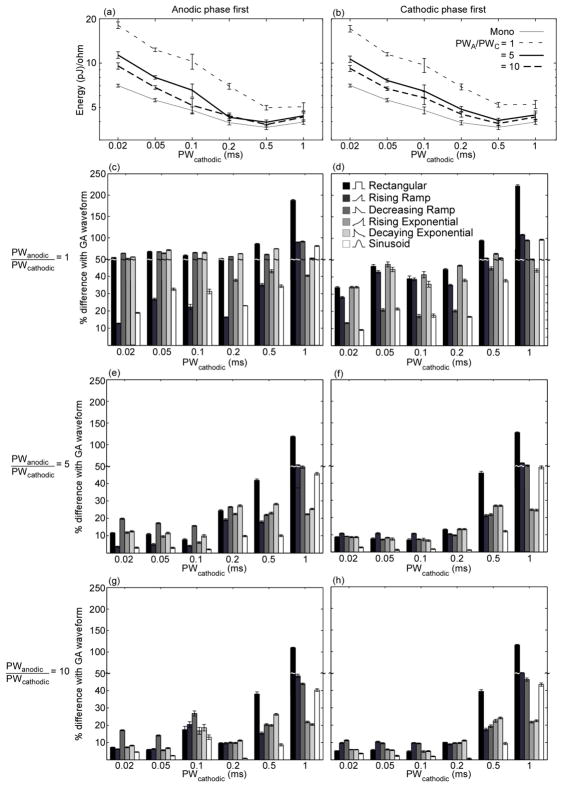
The biphasic GA waveforms were applied to 5 randomly selected populations from the population model, and energy-duration curves were calculated as in the monophasic case. Energy efficiencies of the biphasic GA waveforms as well as conventional waveforms were dependent on the timing and duration of the anodic phase (figure 7(a), (b)). Conventional waveform shapes were paired with rectangular charge-balancing anodic phases with the same duration and timing as the biphasic GA waveforms, and the energy efficiencies of these waveforms were calculated in the population model. The biphasic GA waveforms were always more energy-efficient than the conventional waveform shapes, and the differences in energy efficiency varied with the duration of the anodic phase. In general, as PWanodic/PWcathodic increased the difference in energy efficiency between the biphasic GA waveforms and the conventional waveform shapes decreased (figure 7(c)–(h)). As well, for PWanodic/PWcathodic = 1 the differences between the biphasic GA waveforms and the conventional waveforms were generally greater than in the monophasic case (figure 3), but for PWanodic/PWcathodic = 10 the differences were smaller than in the monophasic case.
Figure 7.
Energy efficiency of biphasic GA waveforms in a model of extracellular stimulation of a population of myelinated axons. a)–b) Energy-duration curves for activation of 50% of the axons (mean +/− SE; n=5 different random populations of 100 axons). c)–h) Energy efficiency of GA waveforms compared to conventional waveform shapes used in neural stimulation (mean +/−SE, n=5). Positive values of “% difference with GA waveform” indicate that GA waveforms were more energy-efficient. Waveforms with cathodic phase first were more energy-efficient than waveforms with anodic phase first for PWcathodic ≤ 0.2 ms, 0.05 ms, and 0.05 ms for PWanodic/PWcathodic = 1, 5, and 10, respectively (FPLSD: p < 0.0001). However, waveforms with anodic phase first were more efficient for PWcathodic ≥ 0.5 ms and 0.2 for PWanodic/PWcathodic = 1 and 5, respectively, and for 0.1 ms ≤ PWcathodic ≤ 0.5 ms for PWanodic/PWcathodic = 10 (FPLSD: p < 0.0001). Also, energy efficiency improved as PWanodic/PWcathodic increased (FPLSD: p < 0.0001). Compared to the monophasic GA waveforms, the biphasic GA waveforms were less energy-efficient, but the difference in energy efficiency decreased as PWcathodic increased.
Discussion
We used a genetic algorithm (GA), a computational optimization method that mimics biological evolution, to seek the energy-optimal waveform shape for neural stimulation. The GA succeeded in revealing highly energy-efficient waveforms that resembled truncated Gaussian curves. When tested in computational models and in vivo experiments of peripheral nerve stimulation, the GA waveforms were more energy-efficient than many conventional waveform shapes, and differences in energy-efficiency were more substantial for long PWs than for short PWs. More energy-efficient stimulation waveforms will extend the battery life of implantable stimulators, and thereby reduce the costs and risks associated with battery replacements, decrease the frequency of recharging, and reduce the volume of implanted stimulators.
Along with energy efficiency, the charge efficiency of stimulation is an important consideration with implanted devices. The charge delivered during a stimulus pulse contributes to the risk of tissue damage (Yuen et al. 1981; McCreery et al. 1990), and if the GA waveforms had delivered excessive amounts of charge, then the benefits of high energy efficiency would have been diminished. Charge efficiency could have been incorporated into the cost function, F (1), with weights associated with charge and energy efficiency that reflected the relative importance of each factor. Nevertheless, although charge efficiency was not considered in F, the GA waveforms ended up being simultaneously energy- and charge-efficient.
Although it is not always possible to prove that a solution is globally optimal, the results of this study provide strong evidence that in the computational models the GA waveforms were the most energy-efficient waveform shapes. All 5 independent trials of the GA converged to nearly the same shape for each PW and achieved similar levels of energy efficiency. In addition, all GA waveforms resembled truncated Gaussian curves, and none of the variations in the parameters of the GA had substantial effects on the outcome.
The GA waveforms bore a striking resemblance to Gaussian curves or sinusoids, the energy efficiencies of which have been investigated previously. Sahin and Tie (2007) found in a computational model of a mammalian myelinated axon (Sweeney et al. 1987) that Gaussian and sinusoid waveforms had the lowest threshold energies out of several conventional waveform shapes. However, unlike the GA waveforms, the Gaussian and sinusoid waveforms were not the most energy-efficient waveforms across all PWs. Qu et al. (2005) conducted in vitro experiments on rabbit hearts and found that defibrillation was achieved with significantly less energy for Gurvich (biphasic sinusoid) waveforms than with biphasic decaying exponential or rectangular waveforms. Dimitrova and Dimitrov (1992) found in a model of an unmyelinated Hodgkin-Huxley axon that waveforms that resembled postsynaptic potentials (skewed Gaussian) were more energy-efficient than rectangular waveforms. Although these previous studies showed that the sinusoid, Gaussian, or skewed Gaussian waveforms were more energy-efficient than other waveform shapes, these waveforms were not proven to be energy-optimal.
Although the GA with genes representing the parameters of the piece-wise generalized normal distribution (5) did not produce GA waveforms with noticeably different shapes, the waveforms were much smoother, and for long PWs the tails were much closer to 0. These differences improved the energy efficiency over the original GA waveforms, particularly for long PWs. As a result, the energy-duration curve was no long concave up, as in the original GA (figure 3(a)), but instead E never increased as PW increased. This result is more consistent with expectations; one would expect that at a given PW the GA could produce any waveform that was produced at a shorter PW bounded by tails of zero amplitude. Therefore, as PW increases E should either level off or decrease.
The different properties of the MRG axon and the Hodgkin-Huxley axon led to the dissimilarities in the genetically-optimized waveforms produced in the two models. Not only were the differences in ion channel dynamics between the two models substantial, but also the Hodgkin-Huxley axon lacked paranodal sections, and both factors likely contributed to the differences in GA waveforms. However, due to the non-linearity and complexity of the equations governing membrane voltage, it is difficult to pinpoint which characteristics of the axonal models were most responsible for the varying results. Additional trials of the GA in models where specific geometric and physiological parameters were varied systematically could determine how energy-optimal waveforms change with model parameters. Thus, the GA approach can determine energy-optimal waveform shapes for a given model or system, but the optimal shape may be different in each case.
The biphasic GA waveforms exhibited many similarities to the monophasic GA waveforms. Both sets of GA waveforms were more energy-efficient than several conventional waveform shapes and were unimodal in shape. However, the peakedness and locations of the peaks of the biphasic GA waveforms were different than the monophasic GA waveforms. The effects of the anodic phase on the sodium channels explain many of the differences among the shapes of the biphasic GA waveforms. The anodic phase hyperpolarizes the membrane, deactivating m-gates and de-inactivating the h-gates of the sodium channel. When the cathodic phase was delivered first, the peak likely shifted away from the anodic phase to open the sodium channels earlier than in the monophasic case, thus offsetting the deactivation generated by the anodic phase. When the anodic phase was delivered first, the peak shifted away from the anodic phase to allow the m-gate of the sodium channels to return to baseline. Differences between the monophasic and biphasic GA waveforms were not as great for long PWanodic. As PWanodic increased, the amplitude of the anodic phase decreased, reducing the effect of the anodic phase on membrane voltage and the sodium channels. Consequently, the biphasic GA waveforms began to resemble the monophasic GA waveforms in terms of shape and energy efficiency.
Although the current study examined energy and charge efficiency for excitation of peripheral nerve fibers, the results may also pertain to stimulation of other components of the nervous system. During spinal cord stimulation, the targets of stimulation are thought to be axons (Coburn 1985; Struijk et al. 1993; Struijk et al. 1993), and the current findings would likely be applicable. As well, our results would be valid for muscular stimulation, where the targets of stimulation are motor nerve axons (Crago et al. 1974). The current results may also be relevant for stimulation of the brain because in both cortical stimulation (Nowak and Bullier 1998; Manola et al. 2007) and deep brain stimulation (McIntyre and Grill 1999), the targets of stimulation are thought to be axons.
GA waveforms could substantially increase the battery life of implanted stimulators. For example, the stimulators used for deep brain stimulation last approximately 36–48 months with conventional waveforms (Ondo et al. 2007). Over 30 years, the device would have to be replaced about 8–10 times. Over a clinically relevant range of PWs (~0.05–0.2 ms) the GA waveforms were approximately 5–60% more energy-efficient than either the rectangular or decaying exponential waveforms, which are the most frequently used waveforms clinically (Butson and McIntyre 2007). The conservative estimate of 5% improvement would only lead to 1.8–2.4 months of additional battery life per device, while a 60% improvement in energy efficiency would extend battery life by over 21 months. As a result, over 30 years the device would only have to be replaced about 5–6 times. The energy efficiency as calculated in this study did not account for the energy consumed by the electronic circuitry of an implantable stimulator. A stimulation waveform that can be generated using a simple analog circuit may consume less energy than a waveform that requires several active components. If the energy consumption of the circuitry were incorporated into the GA, then the algorithm may produce different waveform shapes. This potential impact suggests that an investigation into the practical implementation of the GA waveforms is warranted.
Acknowledgments
The authors would like to thank Gilda Mills, Michael Wang, Xiaobai Sun, Merrill Birdno, Paul Yoo, Duke Statistical Consulting Center, and John Pormann and the staff of the Duke Scalable Computing Support Center. This work was supported by NIH R01 NS040894.
Appendix
Conventional waveform shapes
Thresholds were measured for conventional waveforms used in neural stimulation: rectangular, rising/decreasing ramp, rising/decaying exponential, and sine wave. For all shapes, stimulation was applied at t = 0 and turned off at t = PW. The equation for the stimulus current with the rectangular waveform was
| (6) |
where Ks is the current amplitude, t is time, and u(t) is the unit step function. The equations for the rising and decreasing ramp were
| (7) |
| (8) |
respectively, where Kr is the magnitude of the slope of the ramp. The equations for the rising and decaying exponential waveforms were
| (9) |
| (10) |
respectively, where Ke is the amplitude at t = 0 for (4) and at t = PW for (5). In the computational models, τ equaled 263 μs. The equation for the sine wave was
| (11) |
where Ksin is the amplitude of the sine wave. Note that only one period of the sine wave is delivered during the pulse.
Skewness and kurtosis of piece-wise generalized normal distribution
To quantify the shape of the GA waveforms, we fit the waveforms to a piece-wise generalized normal distribution, f(t) (5), and calculated the skewness and kurtosis. First, the peak was centered about t = 0:
| (12) |
Then, f(τ) was normalized so the time integral from −∞ to +∞ equaled 1:
| (13) |
| (14) |
Next, the mean and variance of the distribution were calculated:
| (15) |
| (16) |
Finally, from these equations, skewness and kurtosis were calculated:
| (17) |
| (18) |
References
- Butson CR, McIntyre CC. Differences among implanted pulse generator waveforms cause variations in the neural response to deep brain stimulation. Clin Neurophysiol. 2007;118(8):1889–94. doi: 10.1016/j.clinph.2007.05.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coburn B. A theoretical study of epidural electrical stimulation of the spinal cord--Part II: Effects on long myelinated fibers. IEEE Trans Biomed Eng. 1985;32(11):978–86. doi: 10.1109/TBME.1985.325649. [DOI] [PubMed] [Google Scholar]
- Crago PE, Peckham PH, Mortimer JT, Van der Meulen JP. The choice of pulse duration for chronic electrical stimulation via surface, nerve, and intramuscular electrodes. Ann Biomed Eng. 1974;2(3):252–64. doi: 10.1007/BF02368496. [DOI] [PubMed] [Google Scholar]
- Dimitrova NA, Dimitrov GV. Effect of stimulus (postsynaptic current) shape on fibre excitation. Gen Physiol Biophys. 1992;11(1):69–83. [PubMed] [Google Scholar]
- Fishler MG. Theoretical predictions of the optimal monophasic and biphasic defibrillation waveshapes. IEEE Trans Biomed Eng. 2000;47(1):59–67. doi: 10.1109/10.817620. [DOI] [PubMed] [Google Scholar]
- Hines ML, Carnevale NT. The NEURON simulation environment. Neural Comput. 1997;9(6):1179–209. doi: 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- Jezernik S, Morari M. Energy-optimal electrical excitation of nerve fibers. IEEE Trans Biomed Eng. 2005;52(4):740–3. doi: 10.1109/TBME.2005.844050. [DOI] [PubMed] [Google Scholar]
- Kajimoto H, Kawakami N, Tachi S. Optimal Design Method for Selective Nerve Stimulation. Electronics and Communications in Japan, Part 3. 2004;87(9):62–72. [Google Scholar]
- Manola L, Holsheimer J, Veltink P, Buitenweg JR. Anodal vs cathodal stimulation of motor cortex: a modeling study. Clin Neurophysiol. 2007;118(2):464–74. doi: 10.1016/j.clinph.2006.09.012. [DOI] [PubMed] [Google Scholar]
- McCreery DB, Agnew WF, Yuen TG, Bullara L. Charge density and charge per phase as cofactors in neural injury induced by electrical stimulation. IEEE Trans Biomed Eng. 1990;37(10):996–1001. doi: 10.1109/10.102812. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Grill WM. Excitation of central nervous system neurons by nonuniform electric fields. Biophys J. 1999;76(2):878–88. doi: 10.1016/S0006-3495(99)77251-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntyre CC, Richardson AG, Grill WM. Modeling the excitability of mammalian nerve fibers: influence of after potentials on the recovery cycle. J Neurophysiol. 2002;87(2):995–1006. doi: 10.1152/jn.00353.2001. [DOI] [PubMed] [Google Scholar]
- McNeal DR. Analysis of a model for excitation of myelinated nerve. IEEE Trans Biomed Eng. 1976;23(4):329–37. doi: 10.1109/tbme.1976.324593. [DOI] [PubMed] [Google Scholar]
- Nowak LG, Bullier J. Axons, but not cell bodies, are activated by electrical stimulation in cortical gray matter. I. Evidence from chronaxie measurements. Exp Brain Res. 1998;118(4):477–88. doi: 10.1007/s002210050304. [DOI] [PubMed] [Google Scholar]
- Offner F. Stimulation with Minimum Power. J Neurophysiol. 1946;9:387–390. doi: 10.1152/jn.1946.9.5.387. [DOI] [PubMed] [Google Scholar]
- Ondo WG, Meilak C, Vuong KD. Predictors of battery life for the Activa Soletra 7426 Neurostimulator. Parkinsonism Relat Disord. 2007;13(4):240–2. doi: 10.1016/j.parkreldis.2006.11.002. [DOI] [PubMed] [Google Scholar]
- Qu F, Zarubin F, Wollenzier B, Nikolski VP, Efimov IR. The Gurvich waveform has lower defibrillation threshold than the rectilinear waveform and the truncated exponential waveform in the rabbit heart. Can J Physiol Pharmacol. 2005;83(2):152–60. doi: 10.1139/y04-131. [DOI] [PubMed] [Google Scholar]
- Sahin M, Tie Y. Non-rectangular waveforms for neural stimulation with practical electrodes. 2007;4:227. doi: 10.1088/1741-2560/4/3/008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Struijk JJ, Holsheimer J, Barolat G, He J, Boom HBK. Paresthesia thresholds in spinal cord stimulation: a comparison of theoretical results with clinical data. IEEE Trans Rehabil Eng. 1993;1(2):101–108. [Google Scholar]
- Struijk JJ, Holsheimer J, Boom HB. Excitation of dorsal root fibers in spinal cord stimulation: a theoretical study. IEEE Trans Biomed Eng. 1993;40(7):632–9. doi: 10.1109/10.237693. [DOI] [PubMed] [Google Scholar]
- Sweeney JD, Mortimer JD, Durand D. Modeling of mammalian myelinated nerve for functional neuromuscular stimulation; IEEE/Ninth Annu Conf Eng Med Biol Sci; Boston, MA: 1987. [Google Scholar]
- van den Honert C, Mortimer JT. The response of the myelinated nerve fiber to short duration biphasic stimulating currents. Ann Biomed Eng. 1979;7(2):117–25. doi: 10.1007/BF02363130. [DOI] [PubMed] [Google Scholar]
- Wongsarnpigoon A, Grill WM. IEEE 31st Ann Intl Conf Eng Med Biol Soc. Minneapolis, MN, USA: 2009. Genetic algorithm reveals energy-efficient waveforms for neural stimulation. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wongsarnpigoon A, Woock JP, Grill WM. Efficiency Analysis of Waveform Shape for Electrical Excitation of Nerve Fibers. IEEE Trans Neural Syst Rehabil Eng. 2010 doi: 10.1109/TNSRE.2010.2047610. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuen TG, Agnew WF, Bullara LA, Jacques S, McCreery DB. Histological evaluation of neural damage from electrical stimulation: considerations for the selection of parameters for clinical application. Neurosurgery. 1981;9(3):292–9. [PubMed] [Google Scholar]