Potassium Model for Slow (2-3 Hz) In Vivo Neocortical Paroxysmal Oscillations

Abstract

In slow neocortical paroxysmal oscillations, the de- and hyperpolarizing envelopes in neocortical neurons are large compared with slow sleep oscillations. Increased local synchrony of membrane potential oscillations during seizure is reflected in larger electroencephalographic oscillations and the appearance of spike- or polyspike-wave complex recruitment at 2- to 3-Hz frequencies. The oscillatory mechanisms underlying this paroxysmal activity were investigated in computational models of cortical networks. The extracellular K⁺ concentration ([K⁺]_o) was continuously computed based on neuronal K⁺ currents and K⁺ pumps as well as glial buffering. An increase of [K⁺]_o triggered a transition from normal awake-like oscillations to 2- to 3-Hz seizure-like activity. In this mode, the cells fired periodic bursts and nearby neurons oscillated highly synchronously; in some cells depolarization led to spike inactivation lasting 50–100 ms. A [K⁺]_o increase, sufficient to produce oscillations could result from excessive firing (e.g., induced by external stimulation) or inability of K⁺ regulatory system (e.g., when glial buffering was blocked). A combination of currents including high-threshold Ca²⁺, persistent Na⁺ and hyperpolarization-activated depolarizing (I_h) currents was sufficient to maintain 2- to 3-Hz activity. In a network model that included lateral K⁺ diffusion between cells, increase of [K⁺]_o in a small region was generally sufficient to maintain paroxysmal oscillations in the whole network. Slow changes of [K⁺]_o modulated the frequency of bursting and, in some case, led to fast oscillations in the 10- to 15-Hz frequency range, similar to the fast runs observed during seizures in vivo. These results suggest that modifications of the intrinsic currents mediated by increase of [K⁺]_o can explain the range of neocortical paroxysmal oscillations in vivo.

INTRODUCTION

Although it is well established that the extracellular potassium concentration ([K⁺]_o) increases during epileptogenesis (Moody et al. 1974), whether this is the primary seizure-eliciting factor, or the increased firing causes the [K⁺]_o elevation, remains unknown. According to the Grafstein potassium hypothesis, K⁺ released during intense neuron firing can accumulate in the interstitial space, thus depolarizing neurons and leading to spike inactivation. Slow diffusion of K⁺ into surrounding areas could then depolarize neurons and create slowly propagating waves of spreading depression (SD) (Grafstein 1957). Delayed increase of [K⁺]_o compared with membrane potential depolarization measured during SD propagation (Herreras and Somjen 1993) suggests, however, that K⁺ diffusion may not be the primary mechanism maintaining SD waves, but it might still trigger SD phenomena (Kager et al. 2000).

Modulation of [K⁺]_o has a profound impact on the excitability of neurons and neuronal networks. Increase of [K⁺]_o depolarizes the K⁺ currents reversal potential and can affect the maximal conductances of some depolarizing currents such as the hyperpolarization-activated depolarizing current (I_h) (Spain et al. 1987) and the persistent sodium current (I_Na(p)) (Somjen and Muller 2000), increasing excitability. A recent study showed that K⁺-mediated increase of I_h may lead to periodic bursting in a cortical network model (Timofeev et al. 2002a). Periodic bursting was found in vitro after increasing [K⁺]_o (Jensen and Yaari 1997; Leschinger et al. 1993; Pan and Stringer 1997). Traumatic brain injury leading to loss of K⁺ conductance in hippocampal glia can result in the failure of glial K⁺ homeostasis and abnormal neuronal function including seizures (D'Ambrosio et al. 1999).

The Lennox-Gastaut syndrome is one of the most severe and difficult epileptic conditions (Niedermeyer 2002). The electroencephalographic (EEG) pattern for this type of seizure consists of slow spike-wave (SW) or polyspike-wave (PSW) complexes and runs of rapid EEG “spikes” (10–25/s). This pattern closely resembles paroxysmal oscillations observed in experiments with anesthetized and chronic animals, consisting of SW/PSW complexes recurring at 2–3 Hz, often interrupted by fast runs at 10–15 Hz (Steriade et al. 1998a). The thalamic or cortical origin of these seizures is still actively debated. The occurrence of SW complexes in the depths of monkey cortex without a reflection at the cortical surface (Steriade 1974) and observation of seizures with SW/PSW complexes in completely isolated cortical slabs in vivo (Timofeev et al. 1998) suggest that focal SW seizure are initiated within the cortex. Multi-site recordings show that SW/PSW seizures may be initiated in cortex and then spread to the thalamus after a few-second delay (Neckelmann et al. 1998). Dual recordings from cortex and thalamus indicate that thalamic reticular neurons faithfully follow each cortical EEG “spike,” whereas target thalamocortical (TC) neurons are relatively hyperpolarized during seizure episodes with SW/PSW complexes and thus cannot enhance paroxysmal bursting (Neckelmann et al. 1998; Steriade and Contreras 1995, 1998; Steriade et al. 1998a; Timofeev et al. 1998). Intracellular recordings from TC neurons during SW discharges in genetic models of absence epilepsy in rats also demonstrated that a majority of TC cells (>90%) were tonically hyperpolarized (Pinault et al. 1998).

This paper is a computational study of intracortical mechanisms for generating paroxysmal oscillations. We demonstrate an increased neuronal firing prior to seizure in vivo and we study with a computational network model whether local increases of [K⁺]_o, either after intensive neuronal firing or when K⁺ regulatory system fail to maintain [K⁺]_o level, can explain the observed transition to 2- to 3-Hz paroxysmal bursting in the cortical network.

METHODS

In vivo recordings

Intracellular recordings from neocortical neurons were performed in 16 cats anesthetized with ketamine-xylazine (10–15 and 2–3 mg/kg im). After ketamine-xylazine anesthesia, ~30% of cats (n = 6) displayed spontaneous electrographic seizures consisting of SW/PSW complexes at 1.5–3 Hz, often associated with fast runs at ~10–15 Hz. Details of surgery are described in the companion paper (Timofeev et al. 2004).

Focal field potentials and multiunit recordings were obtained by means of an array of six equally spaced tungsten electrodes inserted in the cortex with an angle 45° arranged in the way that tips of all electrodes were aligned perpendicular to cortical surface and that the most superficial electrode was at depth ~100 μm and the deepest electrode was at depth ~1.6 mm. Intracellular recordings from cortical neurons were obtained with sharp glass micropipettes having resistance of 30–80 MΩ. The intracellular pipette was lowered in the cortical depth at distances <500 μm from the tips of tungsten electrodes composing the array. All experimental procedures were performed according to national guidelines and were approved by the committee for animal care of Laval University.

Computational model

Models of cortical pyramidal (PY) cells and interneurons (INs) had two compartments with channels governed by Hodgkin-Huxley kinetics (Mainen and Sejnowski 1996):

$$C_{\mathrm{m}}\frac{\mathrm{d}{V}_{\mathrm{D}}}{\mathrm{d}t}=-g_{\mathrm{L}}(V_{\mathrm{D}}-E_{\mathrm{L}})-g(V_{\mathrm{D}}-V_{\mathrm{S}})-I_{\mathrm{D}}^{\text{int}}-I^{\text{syn}},g(V_{\mathrm{S}}-V_{\mathrm{D}})=-I_{\mathrm{S}}^{\text{int}}$$ (1)

where C_m, g_L are the membrane capacitance and the leakage conductance of the dendritic compartment, E_L is the reversal potential, V_D and V_S are the membrane potentials of dendritic and axo-somatic compartments, $I_{\mathrm{D}}^{\text{int}}$ and $I_{\mathrm{S}}^{\text{int}}$ are the sums of active intrinsic currents in axo-somatic and dendritic compartments, I^syn is a sum of synaptic currents, and g is the conductance between axo-somatic and dendritic compartments. In this model, the axo-somatic compartment had no capacitance, which sped up the simulations but had little effect on the spike firing patterns (Mainen and Sejnowski 1996).

The model included fast Na⁺ channels, I_Na, with a high density in the axo-somatic compartment and a low density in the dendritic compartment. A fast delayed rectifier potassium K⁺ current, I_K, was present in the axo-somatic compartment. A persistent sodium current, I_Na(p), was included in the axo-somatic and dendritic compartments (Alzheimer et al. 1993; Kay et al. 1998). A slow voltage-dependent noninactivating K⁺ current, I_Km, a slow Ca²⁺-dependent K⁺ current, I_K(Ca), a high-threshold Ca²⁺ current, I_Ca, hyperpolarization-activated depolarizing current I_h were included in the dendritic compartment. A potassium leak current, I_KL = g_KL(V – E_K), was included in the dendritic and axo-somatic compartments. For I_Na(P), I_Na(p) = g_Na(p) m(V – 50), dm/dt = (m_∞ – m)/0.2, m_∞ = 1/{1 + exp[–(V + 42)/5]} (Alzheimer et al. 1993). For I_h, I_h = g_h (0.8m₁ + 0.2m₂)(V + 40), dm_i/dt = –(m_∞ – m_i)/τ_i, m_∞ = 1/{1 + exp[(V + 82)/7]}, τ₁ = 38 ms, τ₂ = 319 ms (Spain et al. 1987). The slow I_h component (τ₂) was found to have little effect on the firing patterns and was omitted in these simulations. The expressions for the voltage- and Ca²⁺-dependent transition rates for all other currents are given in (Timofeev et al. 2000). In most of the simulations, the maximal conductances and passive properties were S_soma = 1.0·10^–6 cm² (Mainen and Sejnowski 1996), g_Na = 3,000 mS/cm² (Mainen and Sejnowski 1996), g_K = 200 mS/cm (Mainen and Sejnowski 1996), g_KL = 0.1 mS/cm², g_Na(p) = 0.07 mS/cm² (Kay et al. 1998) for axo-somatic compartment and C_m = 0.75 μF/cm² (Mainen and Sejnowski 1996), g_L = 0.033 mS/cm² (Mainen and Sejnowski 1996), g_KL = 0.01 mS/cm², S_dend = S_soma r, g_Ca = 0.022 mS/cm² (Reuveni et al. 1993), g_Na = 1 mS/cm² (Mainen and Sejnowski 1996), g_K(Ca) = 2.5 mS/cm², g_Km = 0.01 mS/cm² (Gutfreund et al. 1995), g_Na(p) = 0.07 mS/cm² (Kay et al. 1998), g_h = 0.01–0.02 mS/cm² (Alzheimer et al. 1993) for dendritic compartment. g_K(Ca) was chosen to prevent membrane potential “lock” in the depolarized state after [K⁺]_o increase. Many of these conductances were systematically varied to find the range for the observed phenomena. I_Na(p) was not included in IN cells. The resistance between compartments was R = 10 MΩ.

Reversal potentials for all K⁺-mediated currents were calculated using Nernst equation E_K = 26.64 ln ([K⁺]_o/[K⁺]_i), where [K⁺]_o is extra- and [K⁺]_i is intracellular K⁺ concentrations, E_K is reversal potential in millivolts. [K⁺]_i was held constant at 130 mM through most of the simulations. Reversal potentials for I_h and leak currents were calculated as

$$E_{\mathrm{h}}=26.64\ln ({\left[{\mathrm{K}}^{+}\right]}_{\mathrm{o}}+0.2{\left[{\mathrm{Na}}^{+}\right]}_{\mathrm{o}})∕({\left[{\mathrm{K}}^{+}\right]}_{\mathrm{i}}+0.2{\left[{\mathrm{Na}}^{+}\right]}_{\mathrm{i}})$$

$$E_{\mathrm{L}}=26.64\ln ({\left[{\mathrm{K}}^{+}\right]}_{\mathrm{o}}+0.085{\left[{\mathrm{Na}}^{+}\right]}_{\mathrm{o}}+0.1{\left[{\mathrm{Cl}}^{-}\right]}_{\mathrm{i}})∕({\left[{\mathrm{K}}^{+}\right]}_{\mathrm{i}}+0.085{\left[{\mathrm{Na}}^{+}\right]}_{\mathrm{i}}+0.1{\left[{\mathrm{Cl}}^{-}\right]}_{\mathrm{o}})$$

where [Na⁺]_o = 130 mM, [Na⁺]_i = 20 mM, [Cl^–]_i = 8 mM, [Cl^–]_o = 130 mM. In some simulations, [K⁺]_i, [Na⁺]_o, and [Na⁺]_i were continuously updated to examine whether they had any effect on the results.

The extracellular K⁺ concentration was continuously updated based on K⁺ currents, K⁺ pumps, K⁺ buffering simulating the glial K⁺ uptake system (Kager et al. 2000) and lateral K⁺ diffusion

$$\frac{\mathrm{d}{\left[{\mathrm{K}}^{+}\right]}_{\mathrm{o}}}{\mathrm{d}t}=k{I}_{\mathrm{K}}^{\Sigma }∕\mathrm{F}d+G+D∕\Delta x^2({\left[{\mathrm{K}}^{+}\right]}_{\mathrm{o}(+)}+{\left[{\mathrm{K}}^{+}\right]}_{\mathrm{o}(-)}-2{\left[{\mathrm{K}}^{+}\right]}_{\mathrm{o}})+D∕\Delta x^2({\left[K^{+}\right]}_{\mathrm{o}\left(\mathrm{sd}\right)}-{\left[{\mathrm{K}}^{+}\right]}_{\mathrm{o}})$$ (2)

where F = 96,489 C/mol is the Faraday constant, d = 0.15 μM is the ratio of extracellular volume (per cell compartment) to the surface area, k = 10 is the unit conversion constant for currents, $I_{\mathrm{K}}^{\Sigma }$ (in μA/cm²) in is a sum of all K⁺ currents including an inward K⁺ current produced by active K⁺ pumps (Kager et al. 2000)

$$I_{\text{pump}}=I_{\text{max}}∕{(1+{\left[{\mathrm{K}}^{+}\right]}_{\mathrm{o}\left(\mathrm{eq}\right)}∕{\left[{\mathrm{K}}^{+}\right]}_{\mathrm{o}})}^2$$

[K⁺]_o(eq) = 3.5 mM is an equilibrium [K⁺]_o concentration, I_max is the maximal flux generated by the pump (to compensate K⁺ leak at resting conditions we selected I_max = 5 μA/cm² for dendritic and I_max = 40 μA/cm² for somatic compartments), D = 4 10^–6 cm²/s is diffusion coefficient [D = 2.5–3.3 10^–6 cm²/s was estimated for cat neocortex (Fisher et al. 1976)]. In the model, we assumed that each cell compartment had an associated extracellular volume and [K⁺]_o indicates the average concentration within this volume, [K⁺]_o(+) and [K⁺]_o(–) are K⁺ concentrations in the adjacent volumes (corresponding to the neighboring cells), [K⁺]_o(sd) is K⁺ concentrations in the adjacent compartment (soma or dendrites), G is a variable describing the effect of the glial buffering system. In the one-dimensional approximation to diffusion along the x axis, the distance between volume centers was estimated as Δx = 100 μm based on the assumption that one synaptic footprint (10 cells in the model) corresponded to ~1 mm in the cortex. In most single cell simulations (except Figs. 3E and Fig. 4), the diffusion between somatic and dendritic compartments was set to zero to explore effects of difference in [K⁺]_o between compartments. In the network simulations (Figs. 8–11), the diffusion between compartments was always present and nearly identical levels of [K⁺]_o were maintained in all compartments.

FIG. 3.

Periodic activity induced by a current pulse. A: DC pulse (10 s in duration) was applied to the silent cell. After high-frequency firing, [K⁺]_o increased and maintained periodic 2- to 3-Hz oscillations in PY neuron lasted about 10 s after DC pulse was removed. B: time evolution of ionic conductances. C: when [K⁺]_o was increased around somatic (left) or dendritic (right) compartment only, low-frequency oscillations were absent. D: the same stimulus applied to interneuron (IN) was not followed by periodic bursting. E: including K⁺ diffusion between dendrites and soma eliminated difference in [K⁺]_o levels between compartments, but the neuron response patterns remained largely unchanged.

FIG. 4.

Effect of [K⁺]_o increase on neuron oscillations. A: bifurcation diagram (stable attractors) shows steady-state voltage for nonoscillatory regime ([K⁺]_o < 4.3 mM) and the maximum and minimal voltage for periodic solutions ([K⁺]_o > 4.3 mM). B: [Ca²⁺]_i on the secant V_m = 0 for different levels of [K⁺]_o. Appearance of the upper branch at [K⁺]_o > 4.95 mM indicates regimes with spike inactivation. Inset: interval 4.5 mM < [K⁺]_o < 5 mM. C: examples of oscillatory regimes corresponding to [K⁺]_o values marked by numbers 1 ([K⁺]_o = 3.5 mM), 2 ([K⁺]_o = 4.5 mM), 3 ([K⁺]_o = 4.9 mM), 4 ([K⁺]_o = 6 mM), 5 ([K⁺]_o = 10 mM), and 6 ([K⁺]_o = 14 mM) in A and B. D: phase portraits V_m([Ca²⁺]_i) for oscillatory regimes shown above.

FIG. 8.

Network oscillations following DC stimulation. A group of cells (numbers 30–50) was stimulated by DC pulse that induced high-frequency firing. A: after stimulus termination (at t = 38 s), the oscillations lasted continuously. B: when lateral (between cells) diffusion of K⁺ was introduced, oscillations were terminated ~15 s after stimulus termination. K⁺ diffusion between compartments maintained identical levels of [K⁺]_o around soma and around dendrites. Bottom: [K⁺]_o evolution for neurons 5 and 35 is shown. C: oscillation in a larger network with 300 PY and 75 IN neurons. Connections fan out was ±15 cells for AMPA and NMDA mediated PY-PY synapses; ±3 cell for AMPA- and N-methyl-d-aspartate (NMDA)-mediated PY-IN synapses; ±15 cells for GABA_A mediated IN-PY synapses.

FIG. 11.

Effect of glial buffering on network activity. Glial buffering system was blocked in a group of cells (numbers 30–50) at t = 5 s. A: low-frequency bursting was found in this group and was followed by permanent spike inactivation at about t = 20 s. B: when lateral (between cell) diffusion of K⁺ was introduced to the model, the cells outside the group also increased firing. After external random input to the network was removed at t = 50 s, the network displayed periodic oscillations at ~3 Hz.

The glial buffering was modeled by first-order kinetics

$$G=k_1({\left[\mathrm{B}\right]}_{\text{max}}-\left[\mathrm{B}\right])∕k_{1\mathrm{N}}-k_2{\left[{\mathrm{K}}^{+}\right]}_{\mathrm{o}}\left[\mathrm{B}\right]\frac{\mathrm{d}\left[\mathrm{B}\right]}{\mathrm{d}t}=k_1({\left[\mathrm{B}\right]}_{\text{max}}-\left[\mathrm{B}\right])-k_2{\left[{\mathrm{K}}^{+}\right]}_{\mathrm{o}}\left[\mathrm{B}\right]$$ (3)

where [B] is a free buffer concentration, [B]_max = 500 mM is total buffer, [KB] = [B]_max – [B] is K⁺ bound to the buffer, k₁ = 0.0008 and k₂ = k₁/{1+exp[([K⁺]_o – [K⁺]_o(th))/(–1.15)]} are rate constants, k_1N = 1.1, [K⁺]_o(th) = 15 mM for soma and [K⁺]_o(th) = 9 mM for dendritic compartment (Kager et al. 2000). The threshold [K⁺]_o concentrations, [K⁺]_o(th), were systematically varied and final values were chosen to achieve steady state levels of [K⁺]_o for two different modes of behavior: silent and tonic firing (see Fig. 2).

FIG. 2.

Silent and active states of a single neuron. A: Poisson distributed random input depolarized single pyramidal (PY) cell that fired randomly. Extracellular K⁺ concentration ([K⁺]_o) fluctuated ~2.5–3 mM and concentration of K⁺ bound to the buffer ([KB]) stabilized at ~25 mM. B: silent state with no external stimulation.

The firing properties of the two compartment model in Eq. 1 depend on the coupling conductance between compartments (g = 1/R, where R is resistance between compartments) and the ratio of dendritic area to axo-somatic area. The ratio, r, controls the firing patterns in the model (Mainen and Sejnowski 1996). We used a model of a regular-spiking neuron for PY cells (r = 165) and a model of a fast spiking neuron for IN cells (r = 50).

Synaptic currents

All synaptic currents were calculated according to

$$I_{\text{syn}}=g_{\text{syn}}\left[\mathrm{O}\right](V-E_{\text{syn}})$$ (4)

where g_syn is the maximal conductivity, [O](t) is the fraction of open channels, E_syn is the reversal potential. $E_{\mathrm{AMPA}}^{\text{syn}}=0\mathrm{mV}$ for AMPA and N-methyl-d-aspartate (NMDA) receptors, $E_{\mathrm{GABAA}}^{\text{syn}}=-80\mathrm{mV}$ for GABA_A receptors. A simple phenomenological model was used to describe short-term depression of intracortical excitatory connections (Abbott et al. 1997; Galarreta and Hestrin 1998; Timofeev et al. 2000; Tsodyks and Markram 1997). According to this a maximal synaptic conductance was multiplied to depression variable, D ≤ 1, representing the amount of available “synaptic resources”

$$D=1-(1-D_{\mathrm{i}}(1-U))\text{exp}(-(t-t_{\mathrm{i}})∕\tau )$$

where U = 0.07 is the fraction of resources used per action potential, τ = 700 ms the time constant of recovery of the synaptic resources, D_i the value of D immediately before the ith event, and (t – t_i) the time after ith event.

GABA_A, NMDA, and AMPA synaptic currents were modeled by first-order activation schemes (Destexhe et al. 1994). Dependence on postsynaptic voltage for NMDA receptors was 1/{1+exp[–(V_post – V_th)/σ]}, where V_th = –25 mV, σ = 12.5 mV (Destexhe et al. 1994; Golomb and Amitai 1997; Traub et al. 1991). The equations for all synaptic currents are given in (Timofeev et al. 2000). The maximal conductances (for each synapse) were g_AMPA(PY-PY) = 0.08–0.15 μS, g_NMDA(PY-PY) = 0.01 μS, g_AMPA(PY-IN) = 0.05 μS, g_NMDA(PY-IN) = 0.008 μS, g_GABAA(IN-PY) = 0.05 μS.

Network geometry and stimulation

The cortical model consisted of a one-dimensional two-layer array of 100 PY and 25 IN cells. This is the simplest possible network geometry capable of displaying a spatial expansion of the bursting activity initiated in a localized focus. Network models including 300 PY and 74 IN neurons were also tested. Varying the size of the inhibitory population versus excitatory one had minimal effect on the network dynamics: other PY to IN ratios (such as equal number of PY and IN neurons) produced similar network dynamics as long as the total inhibitory drive to a given PY cell was strong enough to compensate for excitatory inputs. In most of the simulations, the connection fan out was ±5 cells for AMPA and NMDA mediated PY-PY synapses; ±1 cell for AMPA and NMDA mediated PY-IN synapses; ±5 cells for GABA_A mediated IN-PY synapses. Other radii of synaptic interconnections were used to test the sensitivity of the results. The model geometry is based on assumption that the network size, N, is much larger than the number of neurons, M, within a synaptic footprint. Some of the intrinsic parameters of the neurons in the network were initialized with random variability (Gaussian distribution with σ = 5–10%) to ensure the robustness of the results (Bazhenov et al. 1998). In simulations with external input, all the cells in the network were stimulated by Poisson distributed spike trains with an average rate of 10 Hz.

RESULTS

Neuronal firing associated with seizures

In the six experiments in which an array of microelectrodes was inserted in the neocortex and in which simultaneous intracellular recordings were obtained, we recorded extra- and intracellular activities during >100 seizures. Of these, in three experiments (56 seizures), we observed an increased frequency of spontaneous neuronal firing prior to the seizure and a progressive decrease in the mean firing frequency toward the end of the seizure (Fig. 1). The progressive increase in the neuronal firing prior to seizure was often associated with progressive depolarization of the membrane potential of simultaneously recorded neuron that eventually led to a firing (Fig. 1). The decrease in firing rate during the seizure was related to the presence of prolonged hyperpolarizing, silent periods, which corresponded to the EEG “wave” components of seizures and to a strong depolarization to the level of spike inactivation, associated with paroxysmal depolarizing shifts (PDSs). In the focus of seizure, the high-frequency firing during the PDSs was recorded only in fast-spiking inhibitory interneurons (Timofeev et al. 2002b) and in some fast-rhythmic-bursting neurons (not shown). The increased firing in a large population of neurons recorded at different depths within one cortical column will likely lead to increased [K⁺]_o that should depolarize neighboring neurons due to depolarizing shift in the reversal potential for K⁺ conductances, thus further increasing their firing and leading to the generation of seizures.

FIG. 1.

Progressively increased neuronal firing at the onset of seizures and decreased firing toward the end of seizures. Top: simultaneous field potential and intracellular recordings as well as firing rates obtained from simultaneous multiunit recordings from different cortical depths and averaged firing rates. Seizures are indicated by gray rectangulars. The vertical distance between tips of recording tungsten electrodes was ~400 μm. The depth of intracellularly recorded neuron estimated from micromanipulator reading was 650 μm. Bottom left: 1 seizure from top expanded in which examples of multiunit recordings are shown. One spike-wave complex from this seizure is further expanded (right).

Extracellular K⁺ concentration in silent and active states

We further investigated seizure generation due to increased [K⁺]_o with computational models, starting with the periodic bursting in a single (isolated) PY cells. Based on these results we then study network dynamics.

In normal conditions, random Poisson-distributed input spike trains applied to an isolated PY cell induced asynchronous firing in the 30- to 40-Hz frequency range. K⁺ was released into the extracellular space with each spike and was largely taken up by the glial buffering system. The K⁺ pump also prevented [K⁺]_o from growing. It took ~50 s to reach steady state, where [K⁺]_o in the soma and dendrites were stabilized at ~3–3.5 mM and the concentration of somatic buffered K⁺, [KB], reached 20–25 mM (Fig. 2). When the external input was removed, the cell remained silent. The release of K⁺ to the extracellular space through K⁺ leak channels was reduced and the steady-state value of [KB], the potassium bound to the buffer, was much lower (~10 mM); [K⁺]_o in soma and dendrites were slightly lower than in the active state (see Fig. 2, right).

These results show that the glial buffering system implemented in the model can control [K⁺]_o in different neuron states. Because the total capacity of the K⁺ buffer was set to have a concentration of 500 mM, it would require a significantly higher frequency of firing before the buffer was saturated.

Effect of external stimulation on extracellular K⁺ concentration

When a long (10 s) DC pulse was applied to the cell, it fired at high frequency and led to a gradual increase in [K⁺]_o (Fig. 3). [KB] reached ~80 mM. After the DC stimulus was removed, the cell did not stop firing immediately but displayed 2.5- to 3.5-Hz oscillations lasting ~10 s, followed by a shorter (~5 s) period of 10- to 15-Hz activity and then by silence. Both [KB] and [K⁺]_o decayed during the oscillatory state. This decay was mainly due to the K⁺ pump: when the K⁺ pump was blocked just before removing the DC pulse, [K⁺]_o kept growing and the oscillations never stopped (not shown). Reducing the DC pulse amplitude reduced the frequency of firing, the [K⁺]_o was less elevated at the end of stimulation and the duration of the bursting phase was reduced. The minimal frequency of stimulus-induced firing to produce periodic bursting was ~65 Hz. For lower frequencies of firing (induced by stimulations of lower amplitude), the glial buffering and K⁺ pump were sufficient to restrict the [K⁺]_o increase and prevent oscillations. Note, however, that in this single-cell model [K⁺]_o increased faster during cell firing than it would normally in cortex because K⁺ was confined to the region surrounding a neuron and could not diffuse away.

During the initial phase of oscillations, each burst started with a few Na⁺ spikes followed by spike inactivation and a depolarizing plateau that lasted 50–100 ms (see Fig. 3A, left). Activation of the high-threshold Ca²⁺ channels increased the intracellular Ca²⁺ concentration and increased I_K(Ca), which eventually triggered a switch to the hyperpolarized state (Fig. 3B, top). During elevated [K⁺]_o, the reversal potentials for all K⁺ currents [including I_h (Spain et al. 1987)] were depolarized (Fig. 3A, bottom). The slow membrane potential depolarization after the burst termination eventually activated the persistent sodium current (Fig. 3B, bottom) and led to a new burst. The frequency of bursting was determined by I_h and I_K(Ca), which were the only two currents active during hyperpolarized state (Fig. 3B). Such bursting with spike inactivation is frequently observed during 2- to 3-Hz SW seizures (Neckelmann et al. 1998; Steriade and Contreras 1995, 1998; Steriade et al. 1998a; Timofeev et al. 1998). When [K⁺]_o was partially reduced 5–6 s later, the high-frequency bursts occurred without spike inactivation and the frequency of bursting was increased to 3–4 Hz (see Fig. 3A, right). During the last phase of oscillation, the bursting was replaced by single spikes or spike doublets occurred at 10–15 Hz. This later form of oscillation resembled “fast-runs” recorded during spike-wave seizures (Steriade et al. 1998a). The transition from low-frequency bursting with many spikes per burst to fast bursting with only few spikes was a result of progressive decrease of [K⁺]_o. In the next section, we will show that changing [K⁺]_o from 4 to 5 mM leads to a sequence of bifurcations when the spikes count per burst progressively changes (see Fig. 4).

To determine whether simultaneous depolarization of the K⁺ reversal potentials in the soma and dendrites was required for oscillations, [K⁺]_o was held constant during stimulation either around the dendritic compartment (Fig. 3B, left) or around the soma (Fig. 3B, right). In both cases the slow 2- to 3-Hz paroxysmal oscillations were not observed. Brief (~2 s duration) 10-Hz activity occurred in the latter case. This suggests that although elevation of [K⁺]_o in soma and dendrites can affect different conductances, both phenomena are required to initiate and maintain slow periodic oscillations (see following text). We also tested whether the difference in [K⁺]_o between soma and dendrites is critical for the results presented here. Figure 3E presents results of simulations identical to Fig. 3A except that K⁺ diffusion between dendrites and soma was included. It provided nearly identical levels of [K⁺]_o between compartments (see Fig. 3E, bottom) but results (neuron response patterns) stayed the same except that duration of post-stimulus oscillations was increased slightly.

When the same DC stimulus was applied to an isolated IN, periodic oscillation was not found after stimulus termination (Fig. 3D). This is explained by absence of I_Na(p) and reduced I_K(Ca) (g_K(Ca) = 0.3 mS/cm²), I_Ca (g_Ca = 10 μS/cm²), and I_h (g_h = 0.05 mS/cm²) conductances in the IN model. Direct increase of the [K⁺]_o led to IN tonic firing (not shown) but bursting was never observed in this model.

Effect of [K⁺]_o increase on neuron oscillations

To better explore the effect of [K⁺]_o on neuron oscillations, we blocked the subsystem updating [K⁺]_o in the model and then increased [K⁺]_o gradually from its baseline level [K⁺]_o = 3 mM, keeping [K⁺]_o identical around soma and dendrites. Figure 4A shows steady-state voltage for nonoscillatory regime ([K⁺]_o < 4.3 mM) and the maximum and minimal voltage for periodic solutions ([K⁺]_o > 4.3 mM). Figure 4B displays [Ca²⁺]_i versus [K⁺]_o on the secant V_m = 0. The first bifurcation occurs at [K⁺]_o ~4.3 mM where steady-state regime (Fig. 4C, top left) is replaced by periodic firing (Fig. 4C, top right). Near this point each burst was relatively short and included two to three spikes, which was not sufficient to activate I_K(Ca). The inset (Fig. 4B) shows a blow-up of the region where a few bifurcations were found that corresponded to changes in the spike count. In a narrow region 4.85 mM < [K⁺]_o < 4.95 mM long bursts with more than four spikes were observed (Fig. 4C, middle left). Starting from [K⁺]_o ~4.95 mM, periodic bursting was followed by spike inactivation (Fig. 4C, middle right). In Fig. 4B, the last oscillatory mode was characterized by the appearance of the upper branch corresponding to the burst termination after a depolarizing plateau. This regime was observed over a large range of [K⁺]_o; longer intervals of spike inactivation were observed for higher levels of [K⁺]_o (Fig. 4C, bottom left). Finally, when [K⁺]_o exceeded ~13.5 mM, the membrane potential became permanently locked in the depolarized state (Fig. 4C, bottom right). Projections of the phase space to the plane V_m([Ca²⁺]_i) for some of these regimes are shown in Fig. 4D.

Oscillations induced by K⁺ injection

To study the relative importance of the [K⁺]_o increase around the soma and dendrites, a fixed amount of K⁺ was directly injected into the extracellular space during the silent state of the neuron (Fig. 5). Increase of [K⁺]_o alone around the soma was not sufficient to induce oscillations (Fig. 5A). Note that [K⁺]_o at first increased significantly but then rapidly decayed to a lower steady-state level. This decay was due to the K⁺ glial buffering and occurred simultaneously with increase in [KB]. When [K⁺]_o was elevated both around the soma and dendrites (Fig. 5B), the previously described low-frequency bursting with spike inactivation occurred. Further increase of [K⁺]_o around dendrites led to bursting without spikes inactivation (Fig. 5C) and finally to fast 10- to 15-Hz oscillations (Fig. 5D). When [K⁺]_o was increased around dendrites to the same level as in Fig. 5B but with a less significant increase in soma, only fast 10- to 15-Hz oscillations were observed (Fig. 5E). These results are summarized at Fig. 5F where regions of different behavior are shown. Slow (<4 Hz) bursting with spike inactivation was observed over a wide range of [K⁺]_o including the line [K⁺]_o(soma = [K⁺]_o(dend). Note that the region of bursting without spike inactivation, which was relatively small in the model with identical levels of [K⁺]_o around soma and dendrites (4.3 mM < [K⁺]_o < 4.95 mM; see, Fig. 4), was now extended to much larger values of [K⁺]_o; however, [K⁺]_o(soma) had to be less than [K⁺]_o(dend) for this to occur.

FIG. 5.

Oscillations induced by [K⁺]_o injection. [K⁺]_o increase both around dendrites and soma was required to maintain 2- to 3-Hz activity. A–D: when [K⁺]_o around soma was set to ~5.5 mM, 5.5– 8 mM range of [K⁺]_o in the dendrites was required to initiate oscillations. E: insufficient increase of [K⁺]_o around soma prevented self-sustained oscillations. F: periodic 2- to 3-Hz bursting with spike inactivation (see, e.g., B) was observed in the large region including [K⁺]_o(soma) = [K⁺]_o(dend) line (- - -).

Effects of intrinsic conductances on K⁺-induced oscillations

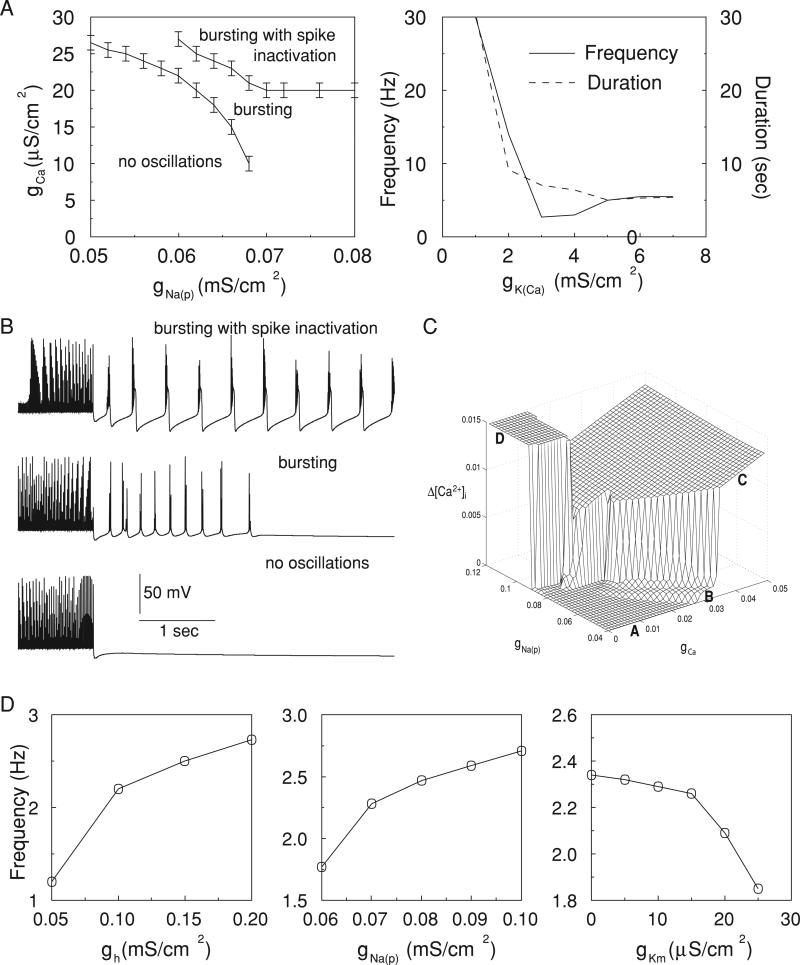
High-threshold Ca²⁺ and persistent Na⁺ currents were important in creating periodic bursting after a [K⁺]_o increase (Fig. 6). After oscillations were induced by long DC stimulation, as described in the preceding text, a sufficiently high maximal conductances for I_Na(p) and I_Ca were required to maintain periodic bursting. On the g_Ca(g_Na(p)) plane (see Fig. 6A, left), the region for bursting was bounded by two curves. Below the bottom curve no oscillations were observed. Above the top curve strong I_Ca and/or I_Na(p) induced a transient “lock” of the membrane potential in a depolarized state (spike inactivation). All these regimes are illustrated in Fig. 6C, where the maximal change of [Ca²⁺]_i during a burst duration is plotted for a cell held at a constant elevated level of [K⁺]_o = 5.5 mM (note that Fig. 4B shows [Ca²⁺]_i change as a function of [K⁺]_o). Increase of I_Na(p) and/or I_Ca led to bursts with more spikes producing higher [Ca²⁺]_i increase. A transient region B between lower plateau A and upper plateau C in Fig. 6C corresponds to the area between two curves in the Fig. 6A (left) where the number of spikes progressively increases as g_Ca and/or g_Na(p) changes; region C corresponds to long bursts with spike inactivation. Finally, in region D, the membrane potential was permanently “locked” in a depolarized state (see Fig. 4C, bottom right), which occurred for high g_Na(p) and relatively low g_Ca. The latter condition ensured weak I_K(Ca) activation. Examples of different firing patterns are shown in Fig. 6B.

FIG. 6.

Effect of intrinsic conductances on neuron oscillations. A: increase of [K⁺]_o during DC stimulation led to oscillations. Sufficiently high levels of persistent Na⁺ and high-threshold Ca²⁺ conductances were required to maintain periodic bursting (top left). Increase of Ca²⁺-dependent K⁺ current reduced both duration and frequency of oscillations (top right). B: examples of PY oscillations corresponding to different regimes indicated in A, left. C: [Ca²⁺]_i increase during a burst as a function of parameters g_Na(p) and g_Ca for a cell hold at a constant level of [K⁺]_o (5.5 mM). Longer bursts (more spikes or spike inactivation) produced higher [Ca²⁺]_i change. Four different regions can be selected: A, no oscillations; B, bursting; C, bursting with spike inactivation; D, membrane potential “lock” in depolarized state. D: effect of the intrinsic conductances on frequency of oscillations. The most significant frequency changes (1–3 Hz) occurred with variations of the I_h maximal conductance.

The conductance for I_K(Ca) significantly affected both the frequency and duration of poststimulus oscillations (Fig. 6A, right). When g_K(Ca) was below ~2 mS/cm² only fast long-lasting oscillations were observed. For higher conductances 2- to 3-Hz periodic bursting was found. The frequency increased slightly for g_K(Ca) >5 mS/cm², which was primary the result of a reduced burst duration. Stronger I_K(Ca) was more effective in terminating the depolarized plateau, so less Ca²⁺ entered during the depolarized state and repolarization from a hyperpolarized state was also faster.

Among all the currents, I_h was most effective in controlling the frequency of oscillations. Reduction of the g_h reduced the frequency to ~1 Hz and then eliminated bursting (Fig. 6D, left). This is consistent with the importance of I_h in maintaining paroxysmal oscillations as proposed previously (Timofeev et al. 2002a). Increase of the maximal conductances for I_Na(p) and I_Km had the opposite effect on frequency (Fig. 6D, middle and right). Changing maximal conductance for I_Ca had a relatively weak effect on the frequency, although it had to be above certain limit to maintain bursting. This limit depended on the maximal conductance for I_Na(p), as shown in the Fig. 6A, left.

Role of K⁺ pump and glial buffering

Results with single-cell simulations suggest that elevated [K⁺]_o might also be important for network oscillations. When [K⁺]_o was sufficiently elevated, periodic bursting was found, which resembled oscillations observed during SW seizure in vivo. Two different mechanisms—K⁺ pump and glial buffering—controlled [K⁺]_o in our model. We tested them by separately blocking each system. Figure 7A shows cell activity when glial buffering was blocked. Immediately following the block of the glial buffer (Fig. 7A), the asynchronous firing maintained by random input (see Fig. 2, left) was replaced by periodic ~2.5-Hz bursting with spike inactivation. [K⁺]_o continued to increase slowly during the oscillatory phase and after ~15 s the oscillations disappeared with the membrane potential permanently “locked” at a depolarized level. The K⁺ reversal potential increased to a point that I_K(Ca) became ineffective in terminating the depolarized state.

FIG. 7.

Effect of glial buffering and K⁺ pump on a neuron activity. A: blocking glial uptake system transformed “normal” random firing maintained by random external stimulation into periodic bursting and eventually led to permanent spike inactivation. B: after block of K⁺ pump, [K⁺]_o increased and led to fast bursting.

Blocking the K⁺ pump in a single cell had a less dramatic effect but eventually led to bursting (Fig. 7B). In the presence of random input, this bursting was irregular and occurred in a broad 4- to 20-Hz range. Periods of faster oscillations were interrupted by slower rhythms in the 4- to 7-Hz range. [K⁺]_o was increased both around the dendrites and in the soma; however, [K⁺]_o(soma) was saturated at a noticeably lower level. Based on the diagram shown in Fig. 5F, we expected that the [K⁺]_o(soma) increase was insufficient by itself to induce low-frequency oscillations with spike inactivation. When external input was removed at t = 30 s, the oscillation continued and become more regular (not shown). Later we will show that in a network of PY cells, blocking K⁺ pump can induce paroxysmal low-frequency bursting.

Stimulus-induced paroxysmal oscillations in the cortical network

To study the properties of [K⁺]_o-dependent oscillations in a population of cortical cells, a two-layer network model including 100 PY cells and 25 inhibitory interneurons (INs) was simulated without lateral diffusion of K⁺ (Fig. 8A). All cells were identical except that I_h was included only in a small (10%) randomly selected group of PY neurons (Timofeev et al. 2002a). Without random excitatory stimulation the background state was silent. A DC pulse applied to cells 30–50 induced high-frequency firing leading to the elevation of [K⁺]_o. When the DC stimulation was removed after 30 s, the network continued to oscillate at ~3 Hz. This low-frequency bursting had the same nature as oscillations previously described in an isolated PY cell. Starting ~10 s after the beginning of stimulation, the neurons outside the region of high [K⁺]_o also displayed periodic bursting. Their activity was mediated by synaptic input from the overexcited region.

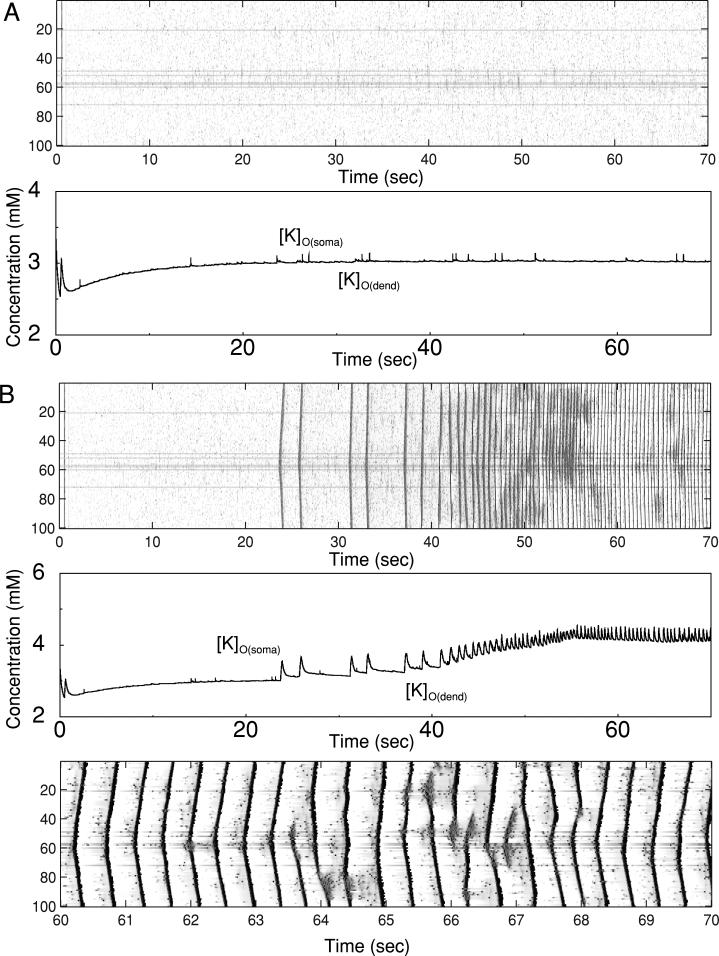
When the same simulation was repeated including lateral diffusion of K⁺ (between PY cells), the results were different (Fig. 8B). Increase of [K⁺]_o within the region of DC stimulation created diffusion of K⁺ to the neighboring regions, so almost all PY cells in the network oscillated starting from ~2 s after DC stimulation. One hundred percent of the cells displayed bursting after the stimulus was removed at t = 38 s; these oscillations were well synchronized across population. PY cells inside region of DC stimulation typically showed bursts with spike inactivation. The cells outside this region displayed high-frequency bursts without spike inactivation (see Fig, 8B, bottom). Each cycle of poststimulus oscillations was started in a small group of cells (numbers 50–60). These cells were located near the region of DC stimulation where [K⁺]_o was significantly increased; a few of these cells included I_h (these cells were slightly depolarized and could be identified at the graph by darker traces). In contrast to the model without diffusion, the oscillations lasted only ~15 s after removing DC stimulation. In the model with diffusion, a larger subpopulation of “glial cells” was effectively involved in accommodation of excessive [K⁺]_o; its level progressively reduced both in the soma and dendrites until the oscillations could no longer be sustained (see Fig. 8B, middle). Thus lateral K⁺ diffusion may reduce the duration of paroxysmal bursting. K⁺ diffusion between compartments maintained identical levels of [K⁺]_o around soma and dendrites.

Once started the oscillation propagated in both directions with a velocity of ~300 cells/s. We studied the effect of K⁺ diffusion on the velocity of burst propagation but could not find any significant velocity changes in a range of D = 0 to D = 1.2 10^–5 cm²/s. Lateral K⁺ diffusion promoted bursting by depolarizing neurons located outside the area of direct stimulation; however, this had only minimal effect of the burst velocity. Parameters controlling burst velocity in the model were maximal conductances for excitatory and inhibitory synapses. In agreement with previous works, an increase of lateral excitation between PY neurons increased velocity while increase of inhibitory feedback through IN slowed down propagation (see, e.g., Bazhenov et al. 2002; Compte et al. 2003; Golomb and Ermentrout 2001) .

To test effect of NMDA currents, we repeated simulations without NMDA conductances. In all cases, after blocking NMDA currents network bursting persisted with only minor changes in shape or duration as long as [K⁺]_o was elevated to the same level. Because the presence on NMDA receptors increased the frequency of firing during high-frequency stimulations, longer stimulation times were required to reach the same level of [K⁺]_o. Thus to obtain (after NMDA blocking), a response identical to the one shown in the Fig. 8, the duration of DC stimulation had to be increased from 20 to 40 s.

We compared responses found in the 100-PY-25-IN cell network with the larger networks and networks with different synaptic footprints. Our simulations show that doubling or halving the number of neurons in our model network while keeping the same number of synaptic neighbors did not change results. Effect of the footprint change in shown in the Fig. 8C presenting results of 300-PY-75-IN network simulations. In those cells (numbers 160–220) where external stimulation was applied, the oscillations were determined primarily by their intrinsic properties and by the level of [K⁺]_o and therefore were identical to activity in the equivalent group of cells in the smaller network (Fig. 8B). Neurons in the rest of the network were driven by synaptic inputs and K⁺ diffusion; all neurons in the network became involved in periodic bursting which continued for ~10 s after stimulus termination.

Effect of inhibition on network oscillations

In the simulations shown in Fig. 9, random network activity was induced by Poisson-distributed spike trains delivered to all PY cells as in the experiments with isolated PY neuron. To compensate for the external stimulation, the strength of synaptic coupling between PY neurons was reduced from 0.15 to 0.115 μS. In control conditions, the network displayed random firing with the level of [K⁺]_o oscillating around 3 mM, which was identical outside the soma and dendrites (see Fig. 9A). When all GABAergic synapses were blocked at t = 5 s, increase of firing in many PY neurons led to the gradual increase of [K⁺]_o (Fig. 9B). After ~20 s, the system started to display spontaneous bursting at progressively increasing frequency, which stabilized at 2–3 Hz after ~45 s. The periodic bursting was typically initiated in a group of cells with I_h (cells 55–60).

FIG. 9.

Effect of IN-mediated inhibition. Random network activity was maintained by Poisson distributed inputs to PY cells and INs. A: in control conditions, the network fired randomly with [K⁺]_o stabilized at relatively low level. B: when GABA_A conductance was blocked at t = 5 s, increased firing led to the grow of [K⁺]_o and bursting. [K⁺]_o evolution for neuron 35 is shown.

We also tested networks where inhibition was removed in only a small group of neurons (cells 30–50). In simulations with lateral PY-PY diffusion, localized disinhibition produced no noticeable effect (data not shown). Excessive firing in a small group of PY cells increased K⁺ concentration in adjacent extracellular space; however, most of K⁺ ions then diffused away so the total increase in [K⁺]_o was not sufficient to induce paroxysmal oscillations. This suggests that diffusion can control the “normal” level of network activity.

Effect of K⁺ pump on network oscillations

K⁺ pumps were blocked at t = 5 s in a group of cells (numbers 30–50) in the network (Fig. 10). Initially random firing that was maintained by random excitatory input as described in the previous section. Elevation of [K⁺]_o after pump blocking progressively depolarized PY neurons thus increasing their frequency of firing, which led to the release of additional K⁺ into the extracellular space. Starting at about t = 12 s, many cells in the network showed bursting, which continued even after random external input was removed at t = 50 s. Under these conditions, the neurons were locally synchronized similar to that observed after DC stimulation in the model with lateral diffusion (Fig. 8B). During first 15–20 s after K⁺ pumps were blocked in a group of cells, only neurons inside and near this group displayed oscillations. The size of bursting cluster of neurons increased progressively and a whole network started oscillating after ~25 s after K⁺ pumps blocking.

FIG. 10.

Effect of K⁺ pump on network activity. Blocking the K⁺ pump at t = 5 s led to increase of [K⁺]_o and bursting. Oscillations continued after removing random external input at t = 50 s. A group of cell with I_h led the network oscillations.

Effect of glial buffering on network oscillations

When glial buffering was blocked in a group of cells (numbers 30–50) from the same network as studies in the preceding text, slow 2-Hz bursting with spike inactivation immediately started (Fig. 11A). Without lateral K⁺ diffusion, this bursting in a group of cells did not have significant effect on the rest of the PY population (see Fig. 11A). As [K⁺]_o increased, the frequency of oscillations also increased, and ~15 s later the oscillations stopped with the PY cells’ membrane potential permanently “locked” into the depolarized state. When random external stimulation was removed at t = 50 s, all the cells became silent.

Including lateral PY-PY K⁺ diffusion to the model dramatically changed the firing patterns of all neurons (Fig. 11B). The flow of K⁺ out of the region where glial buffering was blocked prevented permanent depolarization, so the cells kept oscillating at ~3 Hz. It also increased [K⁺]_o in the surrounding region; the cells there fired at a higher frequency and eventually started to burst (see Fig. 11B). This bursting continued after removing external stimulation at t = 50 s. Similar to the results discussed in the previous sections, the bursts started in the middle of the network in the region where a few closely located PY neurons with I_h were found. Figure 11 also illustrates the [K⁺]_o dynamics near two different PY cells, one belonging to the region where glial buffering was blocked (cell 35) and another outside this region (cell 0). In the first cell, [K⁺]_o increased immediately after removal of the glial buffering. In the remote neuron, [K⁺]_o increase was much more gradual and the K⁺ concentration stabilized at lower level.

DISCUSSION

In vivo recordings from intact cat neocortex and cortical slab preparations suggest a cortical origin for SW and PSW electrographic seizures (Neckelmann et al. 1998; Steriade and Contreras 1995, 1998; Steriade et al. 1998a; Timofeev et al. 1998). These studies showed that although thalamic reticular GABAergic neurons faithfully display spike-burst after each synchronous firing of cortical neurons (EEG “spike”), target thalamocortical neurons are hyperpolarized during seizure episodes with SW/PSW complexes and cannot fire paroxysmal bursting. Sufficiency of intracortical mechanisms for generating paroxysmal activity is also supported by data from cortical slice preparations (Gutnick et al. 1982; Schwartzkroin and Prince 1978).

Different protocols are known to induce paroxysmal activity in vivo, including electrical stimulation and bicuculline infusion (Neckelmann et al. 1998; Steriade and Contreras 1998; Steriade et al. 1998b; Timofeev et al. 1998). These all lead to the excessive firing in large cell populations that can affect the extracellular K⁺ concentration. In vivo paroxysmal activity is frequently observed in acute (Topolnik et al. 2003) and chronic (Echlin and Battista 1963; Grafstein and Sastry 1957; Sharpless and Halpern 1962) cortical slab preparations. Although pathological development of paroxysmal activities in chronic slabs is likely to be due to homeostatic plasticity mechanisms (Turrigiano 1999), the increased likelihood of spontaneous seizures in acute preparations may be a partial result of [K⁺]_o increase after cells damage.

In this study, we tested the hypothesis that a combination of intrinsic conductances and elevated [K⁺]_o can be sufficient to initiate 2- to 3-Hz SW/PSW oscillations. Increased [K⁺]_o may occur due to spontaneous increase in local neuronal firing (see Fig. 1). In the model, the extracellular K⁺ concentration was continuously computed based on K⁺ currents and K⁺ pumps; extracellular K⁺ also depended on glial buffering. Increase in [K⁺]_o affected the reversal potentials for K⁺-mediated currents, such as I_Km, I_K(Ca), I_K(leak), and I_h. Previously we showed with a simplified model of the cortical network that K⁺-dependent enhancement of I_h, including I_h reversal potential depolarization and increase of the maximal conductance (Spain et al. 1987), is sufficient to produce 2- to 3-Hz bursting (Timofeev et al. 2002a). Here the elevation of [K⁺]_o was modeled with different protocols, including intensive stimulation leading to high-frequency firing, direct K⁺ injection to the extracellular space, blocking the K⁺ pump, and blocking the glial buffering system. In a single PY neuron when [K]_o increased sufficiently, slow 2- to 3-Hz bursting was often accompanied by spike inactivation. Typically, after one to two spikes the cell membrane potential became “locked” into the depolarized state maintained by the effects of I_Na and I_K. An increase of the intracellular Ca²⁺ mediated by a high-threshold Ca²⁺ current eventually increased I_K(Ca) to the level where the depolarized state became unstable and the membrane potential rapidly hyperpolarized. This hyperpolarization led to I_h activation and slow repolarization to the level where I_Na(p) became activated and initiated the next burst. The frequency of this bursting depended on many intrinsic conductances, especially g_K(Ca) and g_h. We also tested the model where both K⁺ and Na⁺ ionic concentrations were updated based on the currents flow and Na⁺/K⁺ pump and found that [K⁺]_o had a major effect on cell dynamics.

The role of elevated [K⁺]_o in producing synchronized neuronal bursts through the shift of the K⁺ reversal potential was previously studied in hippocampal slice models (Traub and Dingledine 1990). In Kager et al. (2000), periodic bursting after [K⁺]_o increase was described in a single cell; however, in this model, bursts occurred at very low frequency (1 every 10–15 s) that might be attributed to the lack of I_K(Ca). In recordings from granule cells of the dentate gyrus of the hippocampus at different levels of ionic concentrations in vitro, a simultaneous increase in [K⁺]_o and decrease in [Ca²⁺]_o caused cellular bursts to appear at K⁺/Ca²⁺ concentrations that were previously recorded in vivo before the onset of synchronized reverberatory seizure activity (Pan and Stringer 1997).

The firing patterns found in our model had close similarities with those observed in vivo. The progressive increase in the firing rate preceding periodic bursting in our model (see, e.g., Figs. 3 and 8–11) was similar to the increase in frequency of spontaneous neuronal firing prior to the seizure found in vivo (see Fig. 1). High-frequency bursting with or without spike inactivation in the different model neurons (see, e.g., Figs. 3 and 8) was also observed in vivo (see e.g., Figs. 1 and 2 in Timofeev et al. 2004). The “lock” of the membrane potential in the depolarized state found in the model for very high levels of [K⁺]_o (Fig. 4C) has also been observed in vivo (see Fig. 2 in Timofeev et al. 2004). Fast 10- to 15-Hz oscillations found in the model for particular region of [K⁺]_o values (see Figs. 3–5), were similar to fast runs in vivo (see e.g., Fig. 2, middle, in Timofeev et al. 2004).

In exploring the effects of different intrinsic currents, we found that a combination of a few conductances such as g_Ca, g_Na(p), g_h, and g_K(Ca) was sufficient to produce periodic bursting. When maximal conductances for I_Ca, I_Na(p), or I_h were reduced below a certain level no bursting occurred after [K⁺]_o elevation. Eliminating I_K(Ca) could produce a permanent “lock” of the membrane potential in the depolarized state. The importance of cooperative effects of several conductances for generating spreading depression has been previously shown in a computational study (Kager et al. 2000). In our model, paroxysmal oscillations were obtained without including a low-threshold Ca²⁺ (T-type) current, which was important in some other modeling studies (Destexhe et al. 2001). Synaptic conductances also were not required. These results are consistent with data from hippocampal slices where increasing neuronal excitability (by removing extracellular Mg²⁺ and increasing extracellular K⁺) in the presence of Cd²⁺, a nonselective Ca²⁺ channel antagonist, or veratridine, a persistent sodium conductance enhancer, induced spontaneous nonsynaptic epileptiform activity (Bikson et al. 2002). In recordings from rat hippocampal slices with high [K⁺]_o, the local generation of population bursts in CA1 was caused by intrinsically bursting pyramidal cells, which recruit and synchronize other neurons (Jensen and Yaari 1997).

In the network model that included layers of PY cells, IN cells, and lateral K⁺ diffusion between PY cells, an increase of [K⁺]_o in a small region was generally sufficient to maintain paroxysmal oscillations in the whole network. This local [K⁺]_o increase could be induced by intense stimulation or by disrupting homeostatic [K⁺]_o mechanisms; K⁺ diffusion increased the excitability of the neighboring cells so the whole network became oscillatory. The cells inside the region of high [K⁺]_o usually oscillated with spike inactivation while remote cells displayed high-frequency bursts. Paroxysmal discharges propagated from the single most active network focus. This focus typically included cells with the highest I_h. The threshold for initiating paroxysmal oscillations was lower in the network model compared with isolated PY cell. AMPA- and NMDA-mediated synaptic currents enhanced oscillations especially in the region surrounding paroxysmal foci where neurons fired high-frequency bursts without spike inactivation. However, NMDA currents were not necessary to maintain network bursting as long as [K⁺]_o was sufficiently elevated. This result is an agreement with data obtained in a companion paper where paroxysmal oscillations were found under ketamine anesthesia that blocks NMDA synaptic transmission (Timofeev et al. 2004). The role of long-range spatial buffering of K⁺ operated by glia in synchronizing and/or spreading of paroxysmal oscillations has been recently studied in vivo (Amzica et al. 2002).

The level of [K⁺]_o in the model was determined by K⁺-mediated currents, the K⁺ pump, and glial buffering. When either the K⁺ pump or glial buffering failed to perform normally, the [K⁺]_o increase led to paroxysmal bursting. Recent studies of physiological properties of glial cells from acute slices of biopsies from patients operated for intractable mesio-temporal lobe epilepsy indicate that glial K⁺ buffering could be impaired at the seizure focus, thus contributing to the pathophysiology of seizures (Bordey and Sontheimer 1998). In the model, excessive firing induced by external stimulation could produce K⁺ outward flow exceeding the capacity of the K⁺ pump and glial buffering system and could result in periodic bursting. Cell swelling during seizures (Jing et al. 1994; Perez-Pinzon et al. 1995) would restrict interstitial space and further amplify increase of [K⁺]_o. If all the cells in the model displayed bursts with spike inactivation, the lack of spiking reduced the outward flow of K⁺ and normal level of [K⁺]_o could be restored after a certain period of time, which eventually terminated the oscillations. The oscillations could last longer in a heterogeneous network when bursting with spike inactivation in a small group of cells maintained firing in the neighbor cortical population through synaptic coupling. In return, high-frequency bursts in this surrounding region helped to maintain a high level of [K⁺]_o inside the central focus.

Changes in [K⁺]_o could explain transitions between slow 2- to 3-Hz bursting and fast runs as observed in vivo (Timofeev et al. 1998). In the model, the oscillatory pattern (slow bursting or fast run) depended on the absolute level of [K⁺]_o and also on the relative levels of [K⁺]_o around soma and dendrites (Fig. 5). In particular, slow bursting could be replaced by fast ~10-Hz oscillations when the level of [K⁺]_o was reduced because of spike inactivation (see e.g., Fig. 3).

Our model suggests that increase of [K⁺]_o can transform random awake-like activity into paroxysmal oscillations reminiscent of electrographic SW/PSW seizures. This model predicts that paroxysmal bursting after [K⁺]_o increase depends on the balance of a few intrinsic conductances, can be generated in the isolated cortical network, and does not rely exclusively on any synaptic conductances. In acute conditions, brain lesions produce an immediate increase in [K⁺]_o from intracellular pools that may trigger paroxysmal activity (Topolnik et al. 2003). Data from patients with severe brain injury indicate that posttraumatic neuronal excitation by excitatory amino acids leads to an increase in [K⁺]_o, probably due to ion channel activation (Reinert et al. 2000). Thus increased risk for early epileptogenesis after brain trauma may be attributed to the increase of [K⁺]_o.