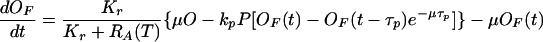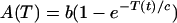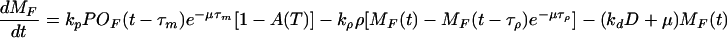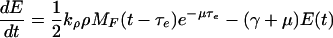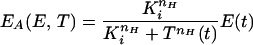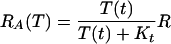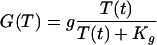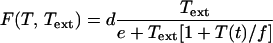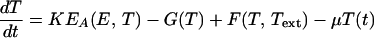Dynamic regulation of the tryptophan operon: A modeling study and comparison with experimental data

Abstract

A mathematical model for regulation of the tryptophan operon is presented. This model takes into account repression, feedback enzyme inhibition, and transcriptional attenuation. Special attention is given to model parameter estimation based on experimental data. The model's system of delay differential equations is numerically solved, and the results are compared with experimental data on the temporal evolution of enzyme activity in cultures of Escherichia coli after a nutritional shift (minimal + tryptophan medium to minimal medium). Good agreement is obtained between the numeric simulations and the experimental results for wild-type E. coli, as well as for two different mutant strains.

1. Introduction

In recent decades, we have witnessed spectacular advances in molecular biology, in particular the explosive growth in knowledge concerning gene control systems. However, the mathematical modeling of these molecular regulatory systems lags far behind the experimental work. In other areas of biology (neurobiology, for instance), the consideration of experimental data within the context of biologically accurate and realistic mathematical models has helped to sharpen experimental questions asked as well as interpretations of new data and to suggest new experiments. The present mathematical modeling study of the tryptophan operon is an attempt to help close the gap between experimental and theoretical studies of regulation at the molecular level. The choice of the tryptophan operon was made deliberately because this operon and the lactose operon are the molecular systems most extensively studied as prototypic gene control systems. Thus there is a large body of experimental data on which to draw.

The term “operon” was first proposed in a short paper in the proceedings of the French Academy of Sciences in 1960 (1). From this paper, the so-called general theory of the operon was developed. This theory suggested that all genes are controlled by means of operons through a single feedback regulatory mechanism: repression. Later, it was discovered that the regulation of genes is a much more complicated process. Indeed, it is not possible to talk of a general regulatory mechanism, as there are many, and they vary from operon to operon. Despite modifications (2), the development of the operon concept is considered one of the landmark events in the history of molecular biology.

Shortly after the operon concept was presented, a mathematical model for it was proposed (3). Bliss et al. (4) proposed a more detailed model for the tryptophan operon that considered repression and feedback inhibition. The system's inherent time delays, caused by transcription and translation, were also taken into account. More recent experimental results reveal that the dynamics of the interaction between repressor and tryptophan molecules are different than considered in Bliss' model. Furthermore, the Bliss model did not take into account another regulatory mechanism at the DNA level, which was discovered later and is called transcriptional attenuation. More recently, other models have been proposed (5–7). They take into account (with more detail) interactions among the repressor molecules, the operon, and the operon end product (tryptophan). Nevertheless, they consider neither feedback inhibition nor transcriptional attenuation and neglect inherent time delays.

We present a mathematical model of the tryptophan operon regulatory system. This model considers repression, enzyme feedback inhibition, and transcriptional attenuation, as well as the system's inherent time delays. In Section 2, an outline of the mathematical model is presented. A list of the model variables and symbols is given in Table 1. The model equations are shown in Table 2. A list of all the parameters and their estimated values is given in Table 3. The variables' steady-state values are presented in Table 4. In Section 3, the numerical method used to solve the model equations is described. The procedure to numerically simulate a given set of experiments and the comparison of the theory with the experiment are given. Some concluding remarks are given in Section 4, along with a discussion of the feasibility of the model and possible future directions.

Table 1.

Model variables and symbols

O	Total operon concentration
OF	Free operon concentration
MF	Free mRNA concentration
E	Total enzyme concentration
EA	Active enzyme concentration
T	Tryptophan concentration
R	Total repressor concentration
RA	Active repressor concentration
P	mRNA polymerase concentration
ρ	Ribosomal concentration
D	mRNA destroying enzyme concentration

Table 2.

Equations describing the evolution of the variables O_F, M_F, E, and T

1 2 3 4 5 6 7 8 9

See text for details of their derivation. 

Table 3.

The model parameters as estimated in supplemental section B

R ≃ 0.8 μM	O ≃ 3.32 × 10−3 μM
P ≃ 2.6 μM	k−r ≃ 1.2 min−1
ρ ≃ 2.9 μM	kr ≃ 460 μM−1·min−1
τp ≃ 0.1 min	k−i ≃ 720 min−1
τm ≃ 0.1 min	ki ≃ 176 μM−1·min−1
τρ ≃ 0.05 min	k−t ≃ 2.1 × 104 min−1
τe ≃ 0.66 min	kt ≃ 348 μM−1·min−1
γ ≃ 0 min−1	kp ≃ 3.9 μM−1·min−1
kdD ≃ 0.6 min−1	kρ ≃ 6.9 μM−1·min−1
nH ≃ 1.2	μ ≃ 1.0 × 10−2 min−1
b ≃ 0.85	c ≃ 4.0 × 10−2 μM
Kg ≃ 0.2 μM	g ≃ 25 μM min−1
e ≃ 0.9 μM	d ≃ 23.5 μM·min−1
f ≃ 380 μM	K ≃ 126.4 min−1

Table 4.

The steady-state values of the model variables corresponding to the parameter values shown in Table 3 and a medium without tryptophan

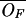≃ 1.54 × 10−4 μM

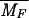≃ 3.78 × 10−4 μM

Ē ≃ 0.378 μM

T̄ ≃ 4.1 μM

Supplementary material (which is published on the PNAS web site, www.pnas.org) is given in two sections. The equation for the dynamics of repression is derived in supplemental section A. This is a partial result of the development of the model. The estimation of all the model parameters is described in supplemental section B.

2. The Model

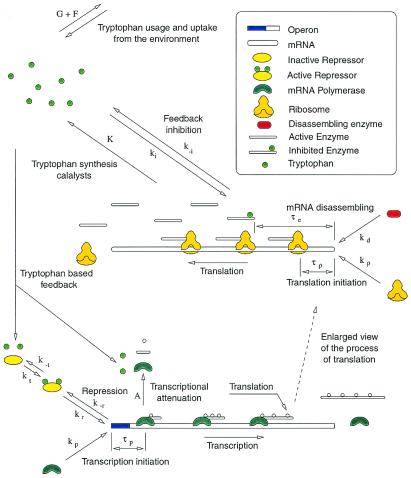
In this section, we introduce a mathematical model of the trp operon regulatory system. A schematic representation of this regulatory system is given in Fig. 1. As any other model, the present one is oversimplified in some sense. Many simplifying assumptions (discussed below) are made during its development. However, it is our premise that the model still considers enough of the system essential characteristics to reproduce some experimental dynamic observations. In Table 1, a list of the model independent variables is presented. The exact meaning of each one is discussed in the forthcoming paragraphs.

Figure 1.

Schematic representation of the tryptophan operon regulatory system. See text for details.

For the purpose of the present model, the tryptophan operon is considered to be constituted by the major structural genes, preceded by a controlling section, where both repression and transcription initiation take place. Consider all the trp operons in a bacterial (Escherichia coli) culture. The controlling sections can be in one of three states: free (O_F), repressed (O_R), or bound by a mRNA polymerase (O_P) (here the same symbols are used to represent the chemical species and their concentration, unless otherwise stated). We assume that there is a single type of repressor molecule, produced by the trpR operon, whose active form competes with mRNA polymerase (mRNAP) to bind free controlling sections. Let R_A denote the concentration of active repressor molecules. The repression process is assumed in this model to be a first-order reversible chemical reaction with forward and backward rate constants k_r and k_−r, respectively. These constants are estimated in supplemental section B and tabulated in Table 3.

When an mRNAP binds a free operon, the DNA-mRNAP complex has to undergo a series of isomerizations before it can assemble the first mRNA nucleotide. We assume that this whole process takes place with a rate proportional to the free operon and mRNA polymerase (P) concentrations, with a rate constant represented by k_p. After isomerization, the mRNAP starts moving along the operon, synthesizing the mRNA chain. A time τ_p after the mRNAP binds the controlling section, it has moved far enough to free the operon, which is then available to be bound by another mRNAP or a repressor molecule. The parameters k_p, P, and τ_p are estimated in supplemental section B and tabulated in Table 3.

These considerations, along with the assumption that the bacterial culture is exponentially growing at a rate μ, allow us to write down the equations governing the dynamics of O_F. In doing so, we point out that the estimated values of k_r, k_−r, and k_p reveal that the binding rate of repressor molecules to free operons is two orders of magnitude larger than the corresponding binding rate of mRNAPs. This fact justifies a quasisteady-state assumption for the repression process. From this assumption, the resulting equation for the dynamics of O_F is given by Eq. 1 of Table 2. The details of its derivation are given in supplemental section A.

The mRNA molecules synthesized by transcription encode five different polypeptides. These polypeptides are used to build up the enzymes that participate in the catalytic pathway that synthesizes tryptophan from chorismic acid.

The first enzyme in this pathway (anthranilate synthase) is a complex of two TrpE and two TrpD polypeptides, which are, respectively, the first and second proteins encoded by the trp mRNA. From the regulatory point of view, anthranilate synthase is the most important of the enzymes in the catalytic pathway. This is because it catalyzes the first reaction in the tryptophan synthesis pathway and because it is subject to feedback inhibition by tryptophan. Because there is evidence supporting the assumption that the production rates of all five polypeptides encoded by the trp mRNA are very similar under normal conditions (8), we focus on the production of TrpE polypeptide and assume that the anthranilate synthase production rate is just one-half that of TrpE.

Let M_F represent the concentration of free TrpE-related ribosome-binding sites. M_F increases because of transcription. Nevertheless, not all of the mRNAPs that initiate transcription produce functional mRNAs. Many of them terminate transcription prematurely depending on the availability of charged tRNA^Trp. The higher the concentration of charged tRNA^Trp, the more probable that a transcribing mRNAP aborts transcription at a premature stage. This regulatory mechanism is known as transcriptional attenuation. Because the amount of charged tRNA^Trp depends on the tryptophan concentration, we assume that the probability of premature transcription termination [A(T)] is just a function of tryptophan concentration. The functional form of A(T) is given by Eq. 2 of Table 2 and discussed in supplemental section B. From these considerations, if τ_m is the time it takes for an mRNAP to assemble a functional TrpE-related ribosome-binding site, the M_F production rate equals the rate of mRNAPs that bound free operons a time τ_m ago [k_pPO_F(t − τ_m)] times a factor e^−μτ_m, standing for the dilution because of exponential growth, times the probability of a just-bound mRNAP to produce a functional mRNA [1 − A(T)].

After a ribosome binds a free TrpE-related binding site, the mRNA-ribosome complex must suffer a series of isomerizations before it can assemble the first peptide bound. Here we assume that this whole process takes place with a rate proportional to M_F and to the ribosomal concentration ρ, with a rate constant denoted by k_ρ. After isomerization and assembly, the ribosome moves along the mRNA-performing translation. A time τ_ρ after binding, the ribosome has moved far enough to free the binding site. Thus, M_F is affected by translation initiation in the following way: in an infinitesimal period of time, it decreases in an amount equal to the rate of ribosome binding and initiating translation and increases by an amount equal to the rate that ribosomes bound and initiated translation a time τ_ρ ago, times the corresponding dilution factor. mRNA degradation is an active process carried out by different types of enzymes (9).

Following McAdams and Arkin (10), we consider in this model a single pool of mRNA-destroying enzymes (D) and assume they cause M_F to decrease with a rate proportional to M_F and D, being the rate constant denoted by k_d. The equation governing the dynamics of M_F, derived from all the above considerations and the exponential growth assumption, is given by Eq. 3 of Table 2.

Let E denote the anthranilate synthase concentration. As mentioned above, this enzyme is the most important from a regulatory point of view because it is the first one to catalyze a reaction in the Trp synthesis catalytic pathway, and because it is subject to feedback inhibition by tryptophan. Anthranilate synthase is a complex of two TrpE and two TrpD polypeptides. However, we focus on TrpE production only [on the basis of the fact that the production rate of all the trp polypeptides is similar under normal conditions (8)] and assume that the anthranilate synthase production rate is just one-half that of TrpE. If τ_e is the time it takes for a ribosome to synthesize a TrpE polypeptide, the TrpE production rate equals the ribosome-binding rate delayed a time τ_e, times the corresponding dilution factor. From this delayed production rate, the exponential growth assumption, and supposing that enzymes are degraded at a rate given by γE (γ is the enzymatic degradation rate constant), it is possible to derive the equation governing the dynamics of E given by Eq. 4 of Table 2.

Anthranilate synthase is feedback inhibited by tryptophan. This feedback inhibition is achieved by the binding of two Trp molecules to each of the TrpE subunits of anthranilate synthase. The binding of these two Trp molecules is not instantaneous but sequential and cooperative, with a Hill coefficient of n_H ≃ 1.2 (11). The forward (k_i) and backward (k_−i) reaction rate constants of the Trp feedback inhibition of anthranilate synthase reaction are estimated in supplemental section B and tabulated in Table 3. A comparison of k_i and k_−i with k_ρρ, μ, and γ (also tabulated in Table 3) reveals that the feedback inhibition of anthranilate synthase is at least two orders of magnitude larger than the enzymatic production, degradation, and dilution processes. This in turn justifies a quasisteady-state assumption for the feedback inhibition process. From this assumption, the concentration of active (noninhibited) anthranilate synthase can be calculated as given by Eq. 5 of Table 2 (4), where K_i = k_−i/k_i.

The tryptophan operon repressor TrpR is produced by an independent operon that is negatively feedback regulated by active TrpR. When produced, TrpR molecules are inactive (aporepressor) and unable to repress the trp and trpR operons. TrpR becomes active when bound by two tryptophan molecules at two independent sites with identical affinities and no cooperativity (12–15). The value of the forward (k_t) and backward (k_−t) rate constants of the repressor activation reaction are estimated in supplemental section B and given in Table 3. From these values, we observe that the repressor activation rate is about two orders of magnitude larger than the rate of active repressor molecules binding free operons and initiating transcription. Repression activation can then be assumed to take place in a quasisteady state. All these facts determine the relation between the active repressor concentration, the tryptophan concentration, and the total repressor concentration (R) given by Eq. 6 of Table 2, where K_t = k_−t/k_t. The synthesis of the trp aporepressor increases when tryptophan is growth limiting, because the repressor autoregulates its own synthesis. However, we assume that the total repressor concentration is constant. We do this for the sake of simplicity and because of the lack of experimental data in that respect.

Tryptophan is synthesized from chorismic acid by a series of reactions catalyzed by enzymes built up with the trp polypeptides. As argued above, of all the enzymes, the most important from a regulatory point of view is anthranilate synthase. From this, we assume that Trp production depends mostly on active anthranilate synthase concentration (E_A). Indeed, the Trp production rate is taken as KE_A, with K a constant to be estimated. Tryptophan is involved in the activation of the trp repressor and in the feedback inhibition of anthranilate synthase. However, here we assume both reactions take place under quasisteady-state conditions. This quasisteady-state condition means that the rate of tryptophan usage by the forward reactions equals the rate of tryptophan dissociation by the backward reactions, and therefore that Trp concentration is not affected by the repressor activation and feedback inhibition of anthranilate synthase processes.

Tryptophan is used in the production of the proteins the bacteria need to grow. The rate of tryptophan usage in protein production is modeled by the function G(T) given by Eq. 7 of Table 2. The functional form of G(T) is discussed in supplemental section B. E. coli are capable of synthesizing three different permeases responsible for the active uptake of tryptophan from the environment (16). The function F(T, T_ext) that stands for the rate of tryptophan uptake (T_ext represents the external tryptophan concentration) is studied in supplemental section B and given by Eq. 8 of Table 2. The equation for the dynamics of T derived from all these considerations is given by Eq. 9 of Table 2.

Eqs. 1–9 constitute the complete system of time-delay differential equations that model the trp operon regulatory system. They contain 28 parameters that must be estimated for the model to be completely specified. We emphasize the importance of having proper estimations for all of these parameters. Otherwise it is impossible to expect the model to reproduce the behavior of the real system. The complete procedure followed to estimate the model's parameters is described in supplemental section B. These parameters are tabulated in Table 3. The steady-state values of the model variables are shown in Table 4, and these steady-state values correspond to bacteria growing in a medium without external tryptophan.

3. Numerical Results and Comparison with Experiments

Having the estimated parameters of Table 3, the system of differential delay equations was solved numerically by using a fourth-order Runge–Kutta method. The program was implemented in fortran. The convergence of the program was tested empirically. A time step of 0.01 min was found to represent a good compromise between accuracy and speed.

Yanofsky and Horn (17) report experiments with wild and mutant strains of E. coli CY15000 strain. These experiments consisted of growing bacteria in the minimal medium of Vogel and Bonner (18) plus tryptophan during a time long enough for the culture to reach the steady state. Then the bacteria were washed and put into minimal media only. The response of the anthranilate synthase enzyme activity was measured as a function of time.

To simulate these experiments, we begin by setting all the variables at their normal steady-state values (Table 4). These steady-state values correspond to the parameters in Table 3 and a medium with no external tryptophan. For the wild strain of E. coli, all the parameters have their normal values (Table 3). The internal tryptophan concentration (T̄) estimated in supplemental section B for a medium without tryptophan is about 4.1 μM. The minimal plus Trp media Yanofsky and Horn (17) used in their experiments had a tryptophan concentration of 100 μg per milliliter of minimal media, which corresponds to about 400 times the value of T̄. On the basis of this experimental protocol, we set the external trp concentration T_ext = 400 × T̄ to simulate the growth of the bacteria culture in the minimal plus tryptophan medium. Then the system of differential delay equations is solved numerically until the solution reaches a steady state.

To simulate the shift of the bacteria to the minimal medium, we ran another numerical experiment where the initial conditions are the steady-state values of the variables in the minimal plus tryptophan medium solution, and the external Trp concentration is null. During this second numerical experiment, the enzyme activity [the number of tryptophan molecules produced per unit time, KE_A(t)] is plotted as a function of time.

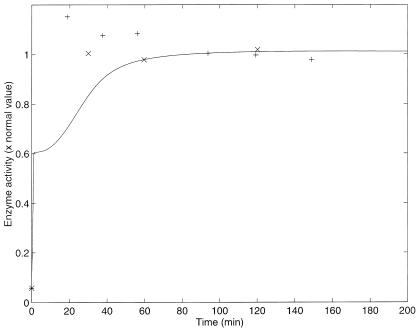
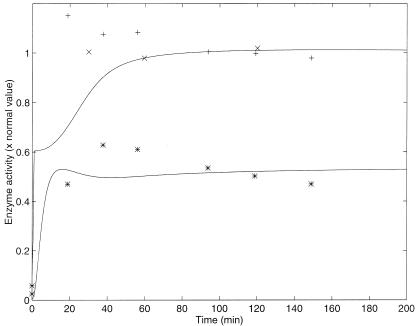
The results of two different experiments from ref. 17 with a normal strain of E. coli are plotted (with crosses and pluses) in Fig. 2. The results of the numerical simulation are plotted with a solid line in the same figure. Because Yanofsky and Horn (17) report values of enzyme activity in arbitrary units, to compare with our simulation the experimental values were scaled so the steady-state values of the experiment and the model were equal.

Figure 2.

Enzyme activity vs. time after a nutritional shift (minimal + tryptophan medium to minimal medium), with wild-strain cultures of E. coli. Two different sets of experimental results (crosses and pluses) as well as the model simulation (solid line), with the parameters of Table 3, are presented. The simulation was calculated by numerically solving the differential equations. The selection of initial conditions is described in the text. The normal enzyme activity is that of the steady state in a medium without tryptophan.

The simulation shows a very steep change a few minutes after the nutritional shift. This change can be explained as follows. In the first region of rapid growth of enzymatic activity, the release of transcriptional attenuation is the predominant regulatory mechanism. The probability of transcriptional attenuation saturates quickly as the intracellular Trp concentration decreases. In the second region of slower growth, the predominant regulatory mechanisms are repression and feedback inhibition. The recovery of enzymatic activity in this second region is much slower in the model than in the real system and fails to capture the overshoot evident in the data. This discrepancy may be because of an error in the estimation of some parameter(s). However, in all cases, we chose to use the reported experimental parameter values rather than to modify them arbitrarily to achieve the best fit to the experimental dynamic behavior. Further, on the basis of experimental evidence, we have no reason to pick one or another parameter to modify.

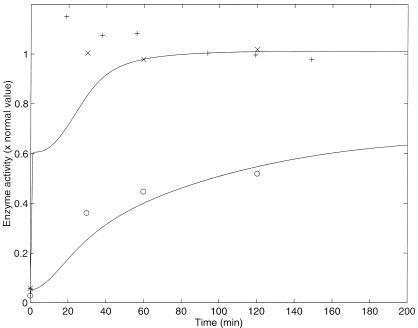
Yanofsky and Horn (17) also report similar experiments with trpL29 and trpL75 mutant strains of E. coli. The trpL29 mutant strain has a mutation A to G at base pair 29 in the leader region of the trp operon. This change replaces the leader peptide start codon by GUG and decreases operon expression in cells growing in the presence or absence of tryptophan. This mutation can be interpreted as decreasing the rate constant k_p, which determines the rate of polymerase-binding free operons and initiating transcription. We found by trial and error that with a k_p equal to 0.04 times the normal value, the numerical results fit the experimental data. To compare the experimental results and the model predictions, the experimental results were again scaled by the same factor as those of the normal strain. The results are shown in Fig. 3 and fit the experimental data (plotted with circles) of this trpL29 strain rather well. The wild-strain data and simulation are also shown for comparison.

Figure 3.

Enzyme activity vs. time after a nutritional shift (minimal + tryptophan medium to minimal medium), with wild-strain (crosses and pluses) and trpL29-mutated (circles) cultures of E. coli. The numerical simulations for each strain (solid lines), are also shown. The simulation for the trpL29-mutated strain was calculated by solving numerically the differential equations with the parameters estimated in Table 3 except for the parameter k_p, which was decreased to 0.04 times the normal value to simulate mutation. The selection of initial conditions is described in the text. The normal enzyme activity is that of the wild-strain steady state in a medium with no tryptophan.

The strain trpL75 of E. coli has a mutation of G to A at base pair 75 in the leader region of the trp operon. This change decreases the stability of the transcription antiterminator structure and increases transcription termination at the attenuator. Consequently, it decreases operon expression of cells growing in the presence or absence of tryptophan. The probability that transcription is terminated at the attenuator is given in the model by the function A(T) = b[1 − exp(−T/c)]. Therefore, an increase in parameter b implies that the probability of transcription termination increases for every tryptophan concentration. The mutation of the trpL75 strain was then simulated by increasing the value of b by trial and error up to 0.9996. With this value, the simulation captures the qualitative nature of experimental data reasonably well, although the simulation predicts an overshoot that is lower and earlier than found experimentally. The experimental results (asterisks) and the simulation results for this strain are shown in Fig. 4, along with those corresponding to the normal strain. In this case, the experimental results are also scaled by the same factor as those of the normal strain.

Figure 4.

Enzyme activity vs. time after a nutritional shift (minimal + tryptophan medium to minimal medium), with wild-strain (crosses and pluses) and trpL75-mutated (asterisks) cultures of E. coli. The numerical simulations for each strain (solid line) are also shown. The simulation for the trpL75-mutated strain was calculated by solving numerically the differential equations with the parameters of Table 3, except parameter b, which was increased to 0.9996 to simulate the mutation. The selection of initial conditions is described in the text. The normal enzyme activity is that of the wild-strain steady state, in a medium with no tryptophan.

4. Concluding Remarks

We have developed a mathematical model of the trp operon regulatory system. In this model, the following regulatory mechanisms are considered: repression, feedback inhibition of anthranilate synthase by tryptophan, and transcriptional attenuation. However, some other features are ignored or simplified. The most important to our consideration are: Only one of the enzymes participating in the tryptophan synthesis catalytic pathway is considered (anthranilate synthase). A single type of repressor molecule (the end product of the trpR operon) is taken into account. The total (active + inactive) repressor concentration is assumed constant, despite the fact that the trpR operon is feedback regulated negatively by active TrpR, and thus the synthesis of the trp aporepressor increases when tryptophan is growth limiting. The production rate of anthranilate synthase is assumed to be one-half that of TrpE. These simplifying assumptions are particularly delicate under conditions of low tryptophan concentration, because the synthesis of aporepressor molecules is increased and the production of the trp polypeptides is affected because some of them have Trp residues. Although there are more simplifying assumptions (explained in Section 2), we consider they do not affect model behavior as do those above. Special attention was given to the estimation of the model parameters.

Comparison of the model simulations with experimental results reveals that despite the simplifying assumptions, the model qualitatively reproduces the enzyme activity dynamic response of wild, trpL29, and trpL75 mutant cultures of E. coli when they are shifted from a minimal plus tryptophan to a minimal medium. As seen in Figs. 2–4, steady-state values are recovered for all strains. Relaxation times are also qualitatively reproduced by the model. Nevertheless, the relaxation time predicted by the model is larger than the real one in the case of the wild strain. Better agreement is observed for the trpL29 mutant strain. In the trpL75 mutant strain experimental results, a bump is observed before the steady state is reached. The model also predicts a bump, but it is smaller and shorter in duration. All these differences between the experiments and the model results may be caused by the simplifying assumptions or a deficient estimation of some parameters.

The mutations of the trpL29 and trpL75 strains were simulated by modifying the parameters k_p and b, respectively. These altered parameter values can be checked by comparing the experimental steady-state conditions with those of the model. The model predicts for the trpL75 mutant that in a high tryptophan medium, the transcriptional attenuation in the steady state is 4.9 times larger than for the wild strain. This result is in agreement with the experimental data of Zurawski et al. (19), who observed a 5-fold increment. The same authors also report the rate of synthesis of TrpE enzyme under high tryptophan conditions. This rate is 0.5 and 0.33 times that of the wild strain for the trpL29 and trpL75 mutant strains, respectively. The model predicts rates equal to 0.12 and 0.023 times that of the wild strain for the trpL29 and trpL75 strains. Although these model values do not agree quantitatively with the experimental ones, they are in the same qualitative direction.

In conclusion, although the comparisons reported here are not sufficient to assert that the present model is accurate in all details, the results are sufficiently encouraging to prompt us to seek further sources of data for comparison. Future work would mean an interactive cooperation between experiment and theory to obtain better parameter estimations, to test the dynamic response of the model under different circumstances, and to improve the model formulation.