Computational Biomechanics of the Distal Tibia from High-Resolution MR and Micro-CT Images

Abstract

The mechanical properties of bone estimated by micro-finite element (µFE) analysis on the basis of in-vivo micro-MR images (µMRI) of the distal extremities provide a new tool for direct assessment of the mechanical consequences of intervention. However, the accuracy of the method has not previously been investigated. Here, we compared µFE-derived mechanical parameters obtained from µMR images at 160 µm isotropic voxel size now achievable in vivo with those derived from 25 µm isotropic (reference) µCT images of thirty cadaveric tibiae from fifteen donors (4 females, 11 males, 55–84 yrs.). Elastic and shear moduli estimated from (5 mm)³ sub-volumes of trabecular bone (TB) derived from µMR images were significantly correlated with those derived from volume-matched reference µCT images (R² = 0.60–0.67). Axial stiffness of whole-bone sections (including both cortical and trabecular compartments) derived from µMR-based models were highly correlated (R² = 0.85) with those from high-resolution reference images. Further, µFE models generated from µCT images after downsampling to lower resolutions relevant to in-vivo µMRI (100–160 µm), showed mechanical parameters to be strongly correlated (R² > 0.93) with those derived at reference resolution (25 µm). Incorporation of grayscale image information into the µMR-based µFE model yielded slopes closer to unity than binarized models (1.07±0.15 vs. 0.71±0.11) when correlated with reference sub-regional elastic and shear moduli. The work suggests that elastic properties of distal tibia can be reliably estimated by µFE analysis from µMR images obtainable at in-vivo resolution.

Introduction

The success of osteoporosis management strategies hinges on both the predictability of bone’s fracture risk and detectability of treatment efficacy. Currently, such assessments are based on bone-mineral density (BMD), typically quantified with dual-energy X-ray absorptiometry (DXA), at the spine or proximal femur. However, BMD measurements often fail to predict fractures[1, 2] and a significant number of people classified as osteoporotic (BMD T-score <-2.5)[3] do not actually sustain fractures.[4] Furthermore, short-term BMD tests are not very useful in tracking treatment efficacy, because of the inability of BMD to detect structural changes that do not significantly alter overall bone mass.

The less-than-satisfactory performance of DXA-based BMD measurements in predicting fracture susceptibility and monitoring response to treatment have spurred the search for other markers of bone quality. Micro-magnetic resonance imaging (µMRI) and high-resolution peripheral quantitative computed tomography (HR-pQCT) are two emerging technologies with potential for assessment of bone quality. Both modalities are able to produce in-vivo images adequate to at least partially resolve trabecular bone (TB) micro-structure at the distal extremities (radius,[5, 6] tibia,[5, 6] and calcaneus [7, 8]). Images produced by these two modalities have also been shown to be suitable for the generation of micro-finite element (µFE) models that allow estimation of mechanical properties of bone such as stiffness and failure strength.[9, 10] Furthermore, the ability of µFE modeling to track short-term changes in mechanical properties in response to treatment has also been demonstrated, even in the absence of any detectable changes in either BMD or bone-volume fraction (BV/TV).[11, 12]

The validity of mechanical parameters estimated on the basis of high-resolution image-derived µFE analysis has been well established in comparison to actual mechanical testing of TB specimens.[13, 14] Furthermore, high-resolution (~10 µm) micro-computed tomography (µCT) has been widely considered as the gold standard for generating µFE models of TB due to its ability to faithfully resolve the micro-structure.[15] On the other hand, the resolutions achievable by in-vivo bone imaging modalities are considerably lower due to limitations imposed by signal-to-noise ratio (SNR) in µMRI and radiation dose in HR-pQCT. Typical in-vivo voxel sizes are on the order of (80 µm)³ and (160 µm)³ for HR-pQCT and µMRI, respectively. However, the actual resolutions of the two in-vivo modalities have been argued to be comparable on the basis of point-spread function characteristics.[10] While the implications of limited resolution (and SNR) on mechanical parameters derived from µMRI-based µFE analysis have been demonstrated,[10] the accuracy of such estimates has not previously been investigated on the basis of isotropic µMR images (160 µm) acquired using pulse-sequence parameters (TE/TR, scan time, etc.) now possible for in-vivo imaging of the extremities.[16]

Even though the feasibility of analyzing µFE models generated from high-resolution images of whole cross-sections has been demonstrated using highly parallel supercomputer systems,[17] the computational and memory demands imposed by µFE solvers have limited the analysis, thus far, on typical desktop computer systems, to TB sub-regions on the order of 1 cm³.[10, 12] Furthermore, the practicality of quantifying the relative contributions of cortical bone (CB) and TB compartments to overall bone stiffness at the distal extremities using µMRI-based µFE has not previously been addressed.

The main goal of the present work is to demonstrate the feasibility and practicality of µMR-based µFE estimates of bone mechanical competence at resolutions achievable in vivo. Towards this objective, we have conceived and implemented a µFE-analysis framework that can take grayscale images as input and generate mechanical parameters –stiffness, elastic moduli, and shear moduli-- of bone in the distal extremities. The accuracy of the µMR-derived mechanical parameters was established by comparison with those derived from high-resolution µCT images of cadaveric distal tibia specimens serving as a reference. Lastly, to support the notion that TB and CB compartments act synergistically to confer strength, we estimated bone stiffness with and without the cortex.

Materials and Methods

Image Acquisition

Thirty human distal tibia specimens of 25 mm length in axial direction, encompassing the distal metaphysis, were obtained from cadavers of fifteen donors (four females and eleven males; 55–85 years). Micro-CT images from the center 10 mm region were subsequently obtained (µCT 80, Scanco Medical, Switzerland) at 25 µm isotropic voxel size with marrow in situ (Figure 1). Subsequently, bone marrow was removed using a water jet and the specimens were immersed in 10% aqueous formalin doped with 1 mM Gd-DTPA to shorten the longitudinal relaxation time (T₁) to ~300 ms commensurate with fatty marrow (ex-vivo specimen imaging demands removal of marrow since air inclusions cause magnetic susceptibility and signal drop-out artifacts).[18] The specimens were then centrifuged at 2000 rpm for 5 minutes to remove remaining air trapped in the inter-trabecular spaces. Finally, 3D µMR images from the center 20 mm region in axial direction of the specimens were acquired (imaging time ~40 min) on a clinical 1.5 Tesla scanner (MAGNETOM Sonata, Siemens Medical Solutions, Germany) with a custom-built receive-only phased-array radiofrequency surface coil at 160µm isotropic voxel size using a variant of the 3D FLASE (fast large angle spin echo pulse) sequence.[19]

Figure 1.

Illustration of image acquisition and processing flow for validation of µMRI-based parameters against reference values derived on the basis of high-resolution µCT images.

Image Processing

Figure 1 schematically describes the preprocessing steps needed to extract common 3D volumes from µMR and µCT (reference) images for validation purposes. Bone regions of high-resolution µCT images were first segmented by setting a threshold at the midpoint between the peaks of bone and marrow in the voxel intensity histogram. For µMR images, the signal variations across the volume produced by inhomogeneous sensitivity of the receive coil were first corrected using a local thresholding algorithm.[20] Subsequently, µMR images were co-registered to µCT images using a rigid-body registration algorithm by maximizing the cross correlation between images.[21] Finally, common 5 mm × 5 mm × 5 mm subvolumes were extracted from the center of the TB region for analysis.

Micro-Finite-Element Modeling of TB Sub-Regions

The macroscopic mechanical properties (of the selected region), were computed by µFE analysis using custom-designed software.[22, 23] The µFE model largely follows that proposed by van Rietbergen et al.[24] for µCT-based analysis and was extended to allow for input of grayscale µMR and µCT images. The grayscale pixel values of the selected image volume were linearly scaled to cover the range from 0 to 100 with pure ‘marrow’ and pure bone having minimum and maximum values, respectively. We refer to the resulting 3D array as the bone-volume-fraction (BVF) map with entries representing the percentage of the voxel occupied by bone. Each voxel in the BVF map was directly converted to a hexahedral (brick) finite element with dimensions corresponding to image voxel size. The bone tissue material properties were chosen as isotropic and linearly elastic with each element’s Young’s modulus (YM) set to be linearly proportional to the BVF value (BVF-scaled) such that YM = (15 GPa) × (BVF) while the Poisson’s ratio was kept constant at 0.3 for all elements. Each finite-element vertex (node) was assumed to have three degrees of freedom corresponding to displacements along x, y, and z axes in the image coordinate. Hence, the number of free variables in the model is 3(N₁ + 1)(N₂ + 1)(N₃ + 1), where N₁ = N₂ = N₃ = 63 (array size) for the 1 cm³ sub-volume. The nodes surrounded by 8 elements with zero BVF values were excluded from the model. An empirically found partial threshold was applied by setting elements with BVF<20% to zero in order to remove the contributions from image noise.

Simulated Compression and Shear Testing of Cubic Sub-Volumes

To estimate the mechanical properties from the generated µFE model, the macroscopic relationship between stress and strain had to be determined. The macroscopic elastic and shear moduli were calculated by simulating compression and shear testing on the µFE model by imposing different boundary conditions on the eight surfaces of the modeled bone region. The elastic moduli (E₁₁, E₂₂, and E₃₃) along each of the three principal axes of the image coordinate system (x, y, and z) were found by performing three ‘compressive’ tests along each of the axes. The value of E₁₁, for example, was obtained by simulating a small displacement (compressive strain ~1%) along the × direction to all nodes on one of the boundary surfaces perpendicular to the x axis (x=0) in such a manner that the nodes on the opposite surface (x=N₁) are restrained along the x direction while lateral displacements remain unrestrained. Such a boundary condition yields 3(N₁ − 1)(N₂ + 1)(N₃ + 1) + 2(N₂ + 1)(N₃ + 1) free variables corresponding to the displacements of unrestrained nodes and displacements along y and z directions for the restrained nodes. The unknown displacements at each node can then be found by minimizing the total strain energy of the system. Subsequently, the resulting stress along the x direction was calculated by summing the x components for the reaction force on the x=0 surface and dividing by the surface area. Finally, E₁₁ was estimated as the ratio of calculated stress to the applied strain. Analogously, E₂₂ and E₃₃ were also obtained. Using a similar approach, shear moduli (G₂₃, G₃₁, and G₁₂) of the modeled region were estimated by simulating shear displacements applied to nodes on opposite surfaces along anti-parallel directions.

Evaluation of the Effect of Resolution

To evaluate the dependence of mechanical properties on image resolution, µFE simulations were performed on the basis of segmented µCT images, serving as an approximation to the ground truth. High-resolution µCT images (25-µm isotropic voxel size) were first binarized at the midpoint between the peaks of bone and marrow intensities of the histogram and subsequently resampled to 100, 120, 140, and 160 µm isotropic voxel sizes while retaining the grayscale information resulting from partial-volume mixing. Subsequently, BVF maps were generated for each of the datasets and common (5 mm)³ cubic TB regions were subjected to µFE analysis by directly converting each voxel into a finite element as described above. Mechanical parameters resulting from 25 µm images were taken as the ground truth. FE computations were carried out on a laboratory computer system (dual quad core Xeon 3.16 GHz CPUs equipped with 28 GB of RAM). Further, to evaluate whether 25-µm µCT images can sufficiently resolve the trabeculae, intensity histograms were examined for bimodality (minimal partial-volume mixing). In addition, trabecular thickness (Tb.Th) was computed within the same sub-volumes used for µFE analysis as input. Tb.Th was computed with a 3D fuzzy distance transform technique previously shown to provide accurate results even in the presence of significant partial volume effects.[25]

Evaluating the Effect of Retaining Grayscale Information

To evaluate the importance of retaining grayscale image information once the voxel size approaches Tb.Th, µFE analysis was performed on the basis of both BVF-scaled and binarized µMR images. First, BVF maps (with each voxel being assigned a value ranging from 0–100) of 5 mm × 5 mm × 5 mm TB sub-volumes were binarized by using an empirically determined constant threshold. Next, two sets of computations were performed as detailed above by taking µFE models generated from BVF-scaled and binarized images as input resulting in elastic and shear moduli.

Estimation of Whole-Bone Sectional Axial Stiffness

The µFE technique described above, which so far has been limited to a small sub-region of TB, was extended to estimate the stiffness of the entire cross-section of the distal tibia in the infero-superior (principal loading) direction. First, µFE models were generated, as detailed above, for common whole-bone sections selected from 160-µm µMR and reference µCT (25-µm) images. Simulated compression was applied along the principal loading direction (i.e. the bone’s longitudinal axis) by applying a constant displacement (~1% strain) to all FE nodes in the proximal face of the finite element mesh while keeping those in the distal face constrained. The µFE system was solved as described above yielding a 3D strain map for the whole-bone section. Finally, the µMR-based axial stiffness obtained as the ratio of the applied strain on the proximal face to the resulting stress was compared to those derived from reference µCT images.

Estimation of Cortical and Trabecular Bone Stiffness

The synergy between CB and TB in providing the overall structural competence can be understood by analyzing the axial whole-bone-sectional axial stiffness of the two compartments both individually and together. First, the CB and TB compartments of the µMR-based BVF maps (generated as described above) were first segmented by delineating the periosteal and endosteal boundaries by an operator-guided region selection program developed in the authors’ laboratory.[23] The segmentation resulted in three datasets for each specimen corresponding to CB, TB, and combined regions. Eight-millimeter sections along bone’s principal loading direction were then extracted for µFE analysis. Finally, axial stiffness of each compartment along the principal loading direction was computed as detailed above.

Statistical Analysis

After testing for normality using Chi-square test, all correlations of mechanical and structural parameters were evaluated by least-squares regression in terms of the Pearson correlation coefficient using JMP Discovery Software (Version 7.02, SAS Institute, Inc.).

Results

Registration of µMR and µCT Images

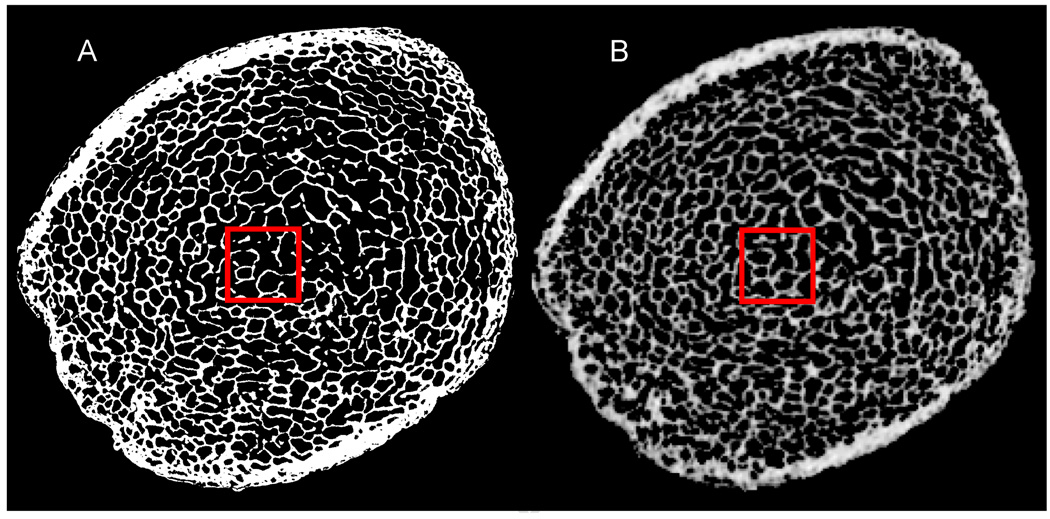
The 3D rigid-body registration between µMR (160 µm) and µCT (25 µm) images produced closely matched ROIs. As visually evident from Figure 2, the BVF maps derived from registered µMR images bear close similarity with those obtained by µCT in both CB and TB regions.

Figure 2.

Axial view of (A) reference µCT image at 25 µm and (B) 3D registered µMR BVF map at 160 µm isotropic voxel size, clearly showing close similarity in micro-structure with the (5 mm)³ ROI used for µFE analysis indicated.

Sub-Regional Elastic and Shear Moduli

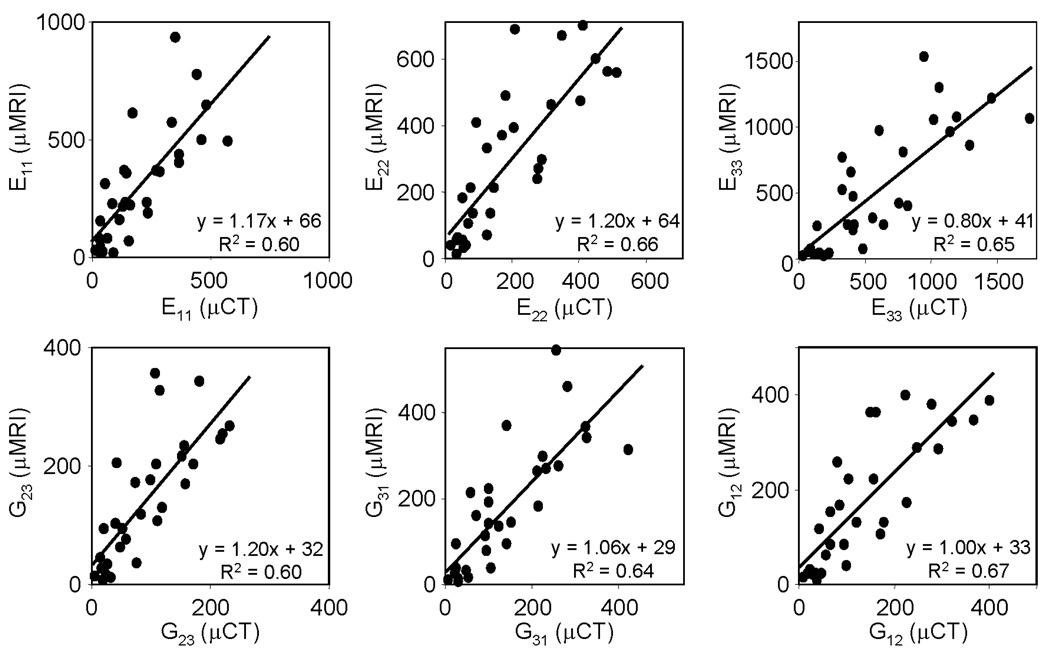
Figure 3 displays elastic and shear moduli of cubic sub-volumes of TB computed from µMR images at voxel sizes achievable in vivo (160 µm isotropic), showing these to be significantly correlated (R² 0.60–0.67) with those derived from volume-matched µCT (25 µm isotropic) images. The models generated from µCT and µMR images averaged 0.74±0.37 million and 2900±2000 finite elements, respectively. The convergence time for µCT and µMR-based models were 100±31 minutes and 6.0±0.30 seconds, respectively.

Figure 3.

Comparison of mechanical parameters (MPa) computed from (5 mm)³ TB sub-regions on the basis of µMR images (160 µm isotropic voxel size) with those derived from volume-matched reference µCT images (25µm).

Effect of Resolution on µFE-Derived Mechanical Parameters

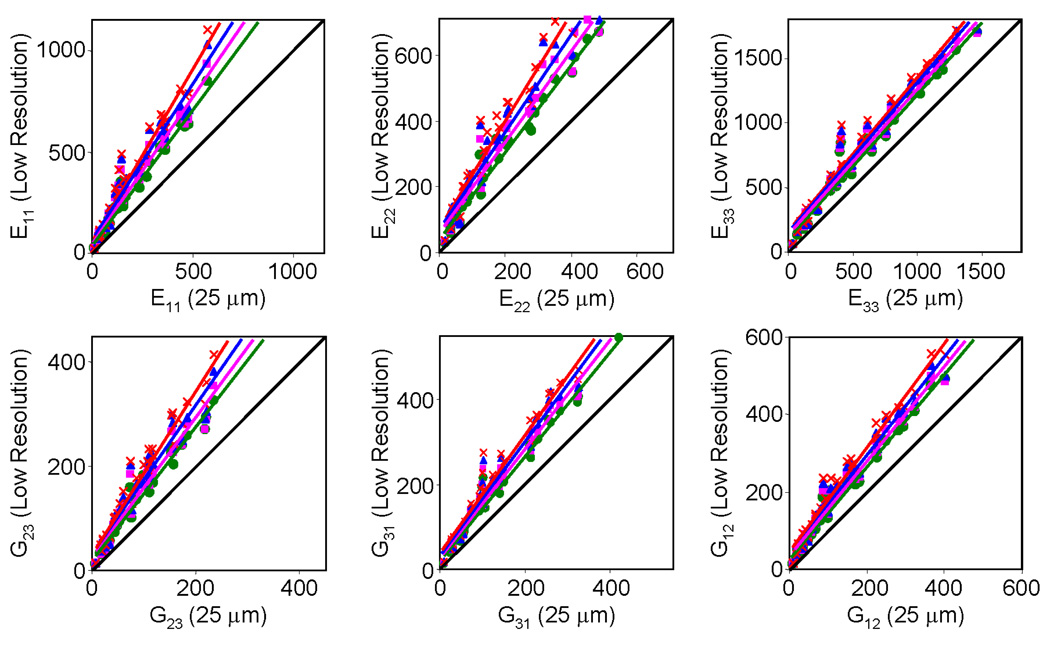
As can be seen from Table 1 and Figure 4, increased voxel size (100–160 µm) causes deviations of mechanical parameters compared to those obtained using reference µCT images at 25 µm. However, the deviations from ground truth values are highly predictable (R²>0.93) for all six mechanical parameters even at the largest simulated voxel size (160 µm isotropic), which equals the voxel size now achievable by in-vivo µMRI.[26] Furthermore, the deviations are less for the elastic modulus along the longitudinal loading (E₃₃) than for transverse directions (E₂₂ and E₃₃). Finally, we note that Tb.Th computed on the basis of highest resolution µCT images shows the image voxel size (25 µm) to be considerably below the trabecular bone thickness (40–105 µm), thereby justifying the use of these images and the derived mechanical parameters as representative of ground truth. The structural properties (BV/TV and Tb.Th) of the TB sub-regions used for the FE computation are listed in Table 2.

Table 1.

Correlations between mechanical parameters derived from µCT images at 25 µm isotropic voxel size and corresponding values obtained after resampling to lower resolution. For all correlations, p<0.0001.

		100µm	120µm	140µm	160µm
E11	R2 Slope/Intercept	0.97 1.35/37.90	0.95 1.44/51.18	0.94 1.55/61.46	0.95 1.69/63.34
E22	R2 Slope/Intercept	0.98 1.33/39.97	0.96 1.39/58.08	0.95 1.48/70.42	0.96 1.64/71.54
E33	R2 Slope/Intercept	0.98 1.12/10.93	0.97 1.14/131.37	0.97 1.17/145.63	0.97 1.19/160.10
G23	R2 Slope/Intercept	0.97 1.29/18.35	0.94 1.35/25.88	0.93 1.43/31.31	0.95 1.57/30.93
G31	R2 Slope/Intercept	0.98 1.22/24.31	0.97 1.27/29.74	0.97 1.33/34.01	0.97 1.39/38.45
G12	R2 Slope/Intercept	0.98 1.20/25.79	0.97 1.23/34.12	0.97 1.28/40.19	0.97 1.36/42.75

Figure 4.

Comparison of elastic moduli (MPa) computed from µCT images at 25 µm isotropic voxel size (abscissa) and corresponding values obtained after resampling the images to lower resolution: (100 µm)³, (120 µm)³, (140 µm)³, and (160 µm)³. Diagonal line represents line of identity.

Table 2.

Structural properties (Tb.Th and BV/TV) of the 30 specimens, computed on the basis of 25µm µCT images from the same 5 mm × 5 mm × 5 mm trabecular bone sub-regions used for µFE analysis.

Structural Parameter	Mean	Minimum	Maximum
Tb.Th (µm)	71.45	39.89	105.32
BV/TV (%)	9.07	1.12	18.17

Effect of Retaining Grayscale Information

The sub-regional elastic and shear moduli derived from µMR images at 160 µm using BVF-scaled and binary models showed significant correlations with those obtained from high-resolution µCT images at 25 µm (R² 0.60–0.67 and 0.50–0.68, respectively). However, the BVF-scaled models yielded slopes closer to unity (1.07±0.15 vs. 0.71±0.11 for those derived from the binary models), suggesting that the incorporation of grayscale image information into the µFE model increases the accuracy of derived mechanical parameters at resolutions typical of in-vivo µMRI.

Whole-Bone Sectional Axial Stiffness

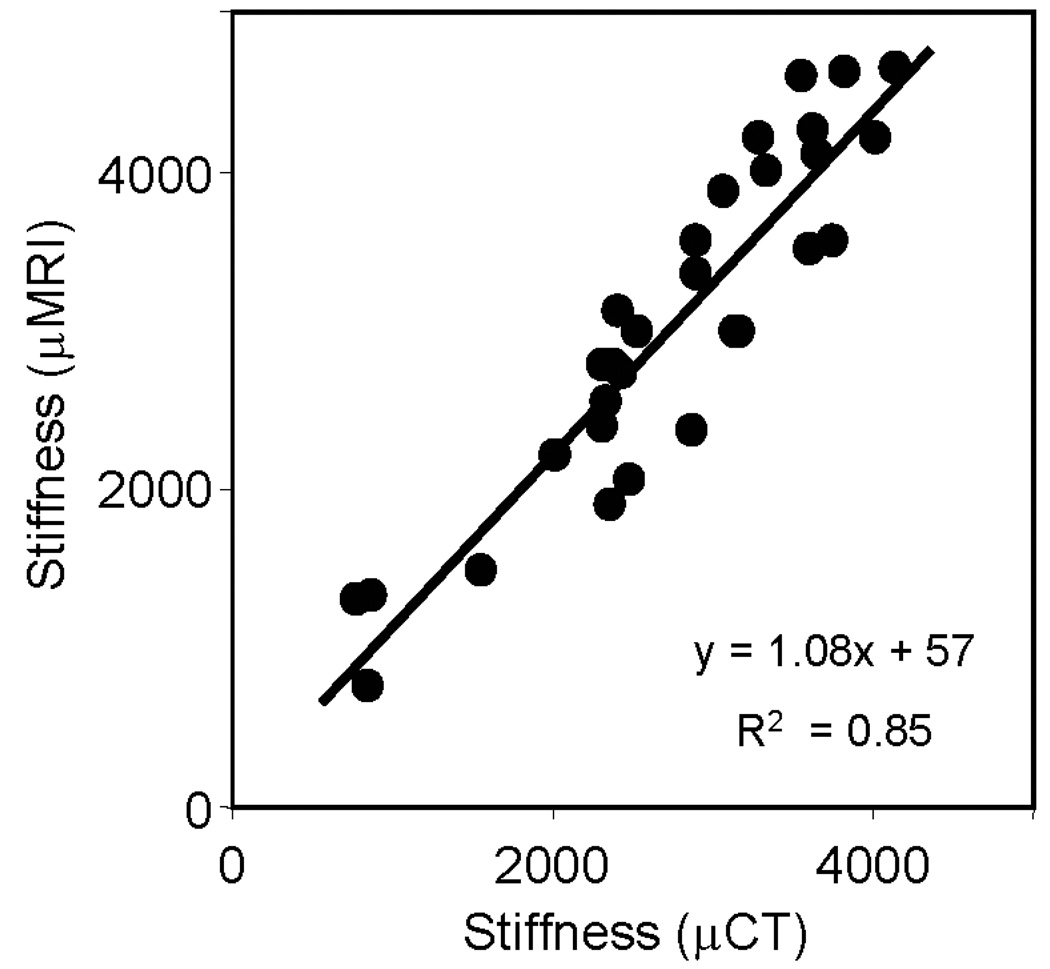
Figure 5 displays the axial stiffness of whole-bone sections computed from µMR images at voxel sizes achievable in vivo (160 µm isotropic), showing high correlation with those derived from volume-matched µCT (25 µm isotropic) images (R² = 0.85). The µCT and µMR based intact (composite) models averaged 8.7±2.7 million and 39,000±12,000 finite elements, respectively. The convergence time for µCT and µMR-based models were 8.9±2.6 hours and 86±53 seconds, respectively.

Figure 5.

Comparison of whole-bone sectional axial stiffness (MPa) computed from µMR images (160 µm isotropic voxel size) with those derived from volume-matched reference µCT images (25µm).

Cortical and Trabecular Bone Stiffness

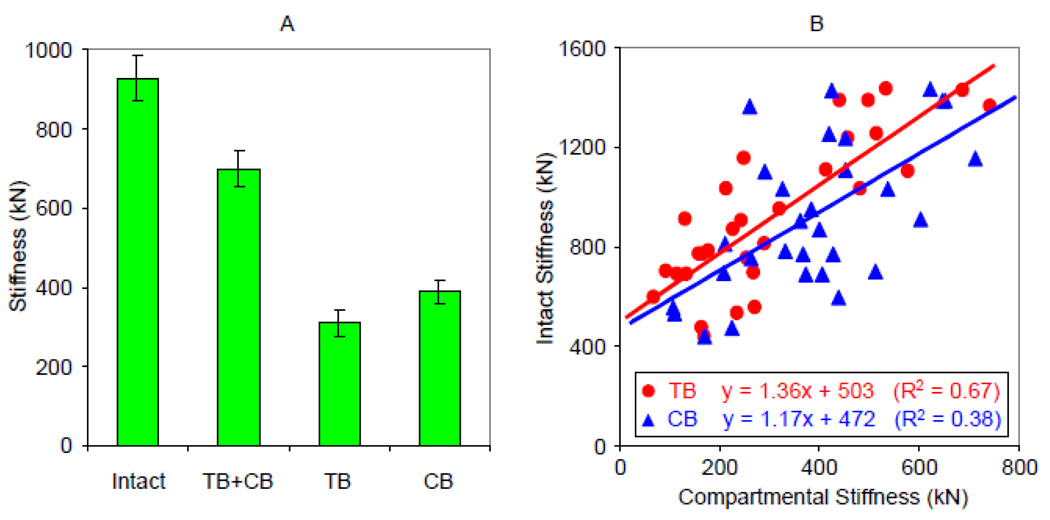
Based on the µMR images of the thirty tibia specimens, the mean stiffness of the CB was larger than that of the TB compartments (389±157 kN versus 310±178 kN). Mean stiffness of the isolated CB and TB compartments was 43±15% and 32±12%, respectively, of the values predicted for the intact model (927±397 kN). Whole-bone sectional stiffness of the intact bone comprising both compartments was 25±6% greater than the sum of stiffness values of the individual compartments (Figure 6a). Interestingly, the additional gain in stiffness of intact bone was highly correlated with the stiffness of the TB compartment (R² = 0.50, p = 0.0001) but there was no correlation with the stiffness of the cortical shell. Furthermore, when joined, stiffness correlated more strongly with TB than CB compartment (R² 0.67 versus 0.38) as illustrated in Figure 6b.

Figure 6.

(A) Average axial stiffness of tibia specimens computed from µMR images at 160 µm isotropic voxel size: individual compartment (TB and CB), both compartments intact, and sum of TB and CB compartments (TB+CB). (B) Relationship between intact whole-bone sectional stiffness and stiffness of individual compartments.

Discussion

We investigated the accuracy of mechanical parameters obtained from BVF-scaled µMRI-based µFE analysis of bone at resolutions achievable in vivo by comparison to those derived from high-resolution reference µCT images of human distal tibia specimens. Additionally, the predictability of whole-bone sectional axial stiffness from individual contributions representing CB and TB compartments as well as the effect of resolution and grayscale information on parameters computed at typical in vivo resolutions were studied.

In vivo µMR images of bone are characterized by considerably lower resolution and SNR than those obtainable by high-resolution µCT of cadavers due to practical limitations in scan time. Nevertheless, within the range of SNR levels achievable in vivo, the derived mechanical parameters have previously been shown to be remarkably immune to noise.[21] In this work, we investigated the effect of limited resolution on µFE parameters derived from µMR images acquired with pulse-sequence parameters and at voxel volumes that have recently been shown to be feasible with in vivo bone micro-imaging[19] and compared the data with those obtained from reference µCT images. Elastic and shear moduli of TB estimated from the µMR images were significantly correlated (R² 0.60 – 0.67) with those derived from µCT images (Figure 3), thus suggesting the feasibility of in-vivo assessment of mechanical properties of bone. We note that the R² values were somewhat lower for inter-modality correlations based on actual images compared to those derived from simulated images at 160 µm, possibly due to relatively small volume of trabecular bone (5 mm)³ analyzed and as a result of errors in selecting identical TB sub-regions from the dual-modality images. Additionally, interpolation of µMR images (160 µm) for the purpose of 3D registration may also have contributed to reduced strength of the inter-modality correlations. Overall, however, simulations show that increased voxel size causes systematic overestimation of mechanical parameters compared to the reference values (Figure 4), resulting from artificial connections being introduced into the TB network once voxel dimensions approach and exceed those of trabecular thickness and spacing. Nevertheless, the correlation between mechanical parameters derived on the basis of simulated low-resolution images remains strong (R²>0.93) compared to the reference high-resolution (25 µm) values even at the voxel sizes (160 µm) achievable by in-vivo µMRI. The data therefore suggest that the relative mechanical competence of bone in patients[12] can reliably be evaluated over a large range of bone-volume fraction and structural characteristics. Finally, we note that the degree of parameter overestimation at lower resolutions has a directional dependence, being least for the major loading direction. This observation can be explained by E₃₃ being largely determined by the trabeculae oriented along the principal loading direction of the distal tibia, thus, within limits, lowering resolution along this direction, will not substantially affect recovery of these trabeculae.

The work also highlights the potential benefits of using grayscale information rather than generating the µMR-based µFE models from binarized images as segmentation of images acquired in the limited spatial resolution regime of in-vivo imaging always entails significant errors. All 3D reconstructions of µMR images of bone contain a range of grayscale values resulting from partial volume effects. We incorporated the grayscale information into the µFE models by linearly scaling the tissue moduli assigned to each finite element by the voxel BVF. Most notably, the BVF-scaled µFE models yielded elastic moduli much closer to the reference values than those obtained by setting a threshold in the images. Homminga et al. previously demonstrated the importance of using grayscale image information for generating µFE models of TB at different voxel sizes using µCT images,[27] showing that grayscale µFE models produce mechanical parameters superior to those derived from binary images, especially when the voxel dimensions are on the order of trabecular thickness. MacNeil et al. used attenuation values extracted from HR-pQCT images of cadaver forearms to scale local tissue modulus when generating µFE models of bone, showing a slight improvement in the accuracy of estimated stiffness and strength values.[28] Our data show that the incorporation of grayscale information of µMR images of bone into µFE models can also improve the accuracy of the estimated mechanical parameters at resolutions achievable in vivo.

Even though most osteoporotic fractures occur at skeletal locations rich in TB the overall strength of bone depends on the integrity of both cortex and TB. Here, we showed the feasibility of estimating whole-bone-sectional axial stiffness of the distal tibia via µMRI-based µFE analysis in reasonable computation times on a laboratory computer system. Even though the cortex is known to contribute 45–75% of the bone strength,[29] the ability to quantify the relative contributions of the two compartments from µMR-based µFE analysis of extremities has not previously been investigated. After segmentation of the cortical shell from TB and quantification of the stiffness of individual compartments, we found overall axial stiffness to exceed the sum of stiffness values of the individual compartments by 25±6%, emphasizing the synergistic role of CB and TB in load bearing. The data also showed that the interaction stiffness (additional stiffness resulting from the interaction between the two compartments) increases with the elevated stiffness in the TB compartment (R² = 0.50, r<0.0001). On the other hand, the CB stiffness was not correlated to the interaction stiffness. This observation can be understood by analyzing the way TB is connected to the cortex at the endosteal boundary. While greater trabecular number and thickness enhance the stiffness of the TB compartment, one could argue that such a trend would be paralleled by a greater number of (stronger) connections to the endosteal cortical wall, and thus result in increased interaction stiffness relative to TB of lower trabecular number and thickness. The main contributor to the CB stiffness, on the other hand, is the thickness of the cortical shell, which has no direct influence on the number of connections to the TB compartment; therefore variations in CB stiffness not necessarily contribute to the variations in interaction stiffness.

Imaging capabilities are now available to obtain highly resolved isotropic µMR images of entire cross-section of distal extremities [16] which make the in-vivo assessment of individual compartmental stiffness and interaction stiffness feasible via µFE analysis. Trabeculae that connect to the endosteal cortical wall play an important role in re-routing load from cortex to trabecular bone compartment and vise versa, especially when the temporal changes in the two compartments are disproportionate. One such example is rapid cortical thinning prevalent in subjects with chronic kidney disease.[30] Therefore, the ability to measure strength of the interaction between the trabecular and cortical bone compartment (as indicated by interaction stiffness) in vivo could provide additional information about possible reduction in overall fracture risk of bone.

The estimation of the cross-sectional area of CB in the distal tibia (required for the computation of the macroscopic compressive modulus) is challenging, especially when the cortex is very thin -- on the order of voxel size. Therefore, stiffness (instead of modulus) was used as the primary mechanical parameter for the comparison of whole-bone sectional mechanical properties of the thirty tibia specimens.

Osteoporosis treatments – alendronate, parathyroid hormone, etc. -- are known to affect the CB and TB compartments differently.[31] Recently, Keaveny et al. showed that the femoral strength improvement following treatment, quantified using QCT-based FE analysis, is dominated by changes in the TB rather than the CB compartment.[32] Our data suggest that µMRI-based µFE analysis may be useful for noninvasive quantification of axial stiffness of the CB and TB compartments at extremities, thereby providing insight into the poorly understood relative biomechanical significance of the two compartments.

Some limitations of the study are noted. Currently, in-vivo µMRI (as well as HR-pQCT) is able of producing images with sufficiently resolved micro-structure of TB only at peripheral anatomic sites. Therefore, the validation study was performed on the basis of specimens extracted from distal tibia, which is a load-bearing surrogate site with a highly anisotropic trabecular network not dissimilar to vertebral bone. Even though the usefulness of nonlinear-µFE analysis in predicting bone strength has been demonstrated,[33] we confined our work to the linear-elastic regime due to current computational limitations on desktop computer systems. Furthermore, µFE analysis of trabecular bone and whole cross-section was limited to relatively small sub-regions in order to keep scan time tolerable in vivo and also to allow the computations to be performed on a high-end desktop computer system. Nevertheless, a previous translational patient study with a similar scan protocol (albeit with highly anisotropic voxels) has shown µMRI-based µFE analysis to detect alterations in mechanical properties in response to treatment from a comparably sized sub-region.[12] Even though the tibia specimens included more male than female donors, we note that both BV/TV and elastic moduli covered a wide range of bone quality expected in healthy and osteoporotic men and women. BV/TV ranged from 1% – 18% and elastic modulus varied by more than two orders of magnitude (13 MPa – 1500 MPa).

A fundamental difference in the nature of µMR compared to µCT images has to be emphasized. Because the signal producing entity is bone marrow, µMR images do not provide bone-mineral density values. Therefore, currently, variations in tissue mineralization cannot be taken into account when generating the µFE model. Nevertheless, recent advances in ultrashort echo-time radial MR imaging have shown potential for quantifying bone mineral and matrix properties in situ.[34, 35]

Finally, E₁₁, E₂₂, E₃₃, G₂₃, G₃₁, and G₁₂ represent the elastic and shear moduli of TB sub-regions relative to the image coordinate axes (rather than along the axes with best orthotropic symmetry[24]). However, because the z-axis of the image coordinate system was aligned to a high degree with the infero-superior direction (which coincides with the direction of principal trabecular orientation in the distal metaphysis) during imaging the estimated mechanical parameters should not deviate significantly from those computed relative to orthotropic axes.[10, 12] Lastly, the focus of this study was to evaluate intermodality agreement of mechanical parameters; therefore, as long as the images are cross-registered, the comparison is valid.

In summary, the present work indicates the feasibility of estimating mechanical properties of distal tibia on the basis of µMR images obtained at in-vivo resolution in good agreement with results from µFE modeling at much higher resolution. Application of the method for assessing the structural implications of drug intervention in patients undergoing high-resolution MRI in conjunction with computational biomechanics has recently been demonstrated in the authors’ laboratory.[36] Lastly, the key question to be addressed in the future is, of course, whether image-based assessment of parameters of bone strength represents valid surrogate estimates of fracture susceptibility and whether the technology is transferable to typical fracture sites.