Visualization of a water-selective pore by electron crystallography in vitreous ice

Abstract

The water-selective pathway through the aquaporin-1 membrane channel has been visualized by fitting an atomic model to a 3.7-Å resolution three-dimensional density map. This map was determined by analyzing images and electron diffraction patterns of lipid-reconstituted two-dimensional crystals of aquaporin-1 preserved in vitrified buffer in the absence of any additive. The aqueous pathway is characterized by a size-selective pore that is ≈4.0 ± 0.5Å in diameter, spans a length of ≈18Å, and bends by ≈25° as it traverses the bilayer. This narrow pore is connected by wide, funnel-shaped openings at the extracellular and cytoplasmic faces. The size-selective pore is outlined mostly by hydrophobic residues, resulting in a relatively inert pathway conducive to diffusion-limited water flow. The apex of the curved pore is close to the locations of the in-plane pseudo-2-fold symmetry axis that relates the N- and C-terminal halves and the conserved, functionally important N76 and N192 residues.

Aquaporins are a family of integral membrane proteins that serve as channels for rapid dissipation of osmotic gradients across the lipid bilayer (1–2). The N- and C-terminal halves of aquaporins are tandem repeats, each containing an absolutely conserved Asn-Pro-Ala (NPA) tripeptide sequence. The polypeptide chain is comprised of six transmembrane segments (3). Aquaporin-1 (AQP1), the archetype in the aquaporin family, is a constitutively open, osmo-regulated, bidirectional water-selective channel (4–5). It was discovered first in the erythrocyte membranes (6) and is widely expressed in the plasma membranes of several water-permeable epithelial and endothelial cells.

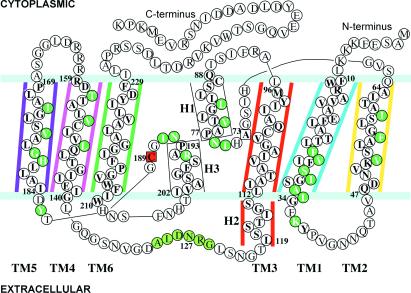
The polypeptide chain of AQP1 threads the bilayer six times (7), so that both the N and C termini are in the cytoplasm (8–10). Although AQP1 organizes as tetramers in vivo (11), several lines of evidence (12–15) indicate that each monomer is a functional channel. Although studies have implicated permeability to CO₂ (16–17) or to cAMP-dependent water permeability and cation conductance (18), there is a general consensus that AQP1 selectively transports water [at the rate of ≈2 × 10⁹ water molecules/second/monomer (4, 19)] and excludes small chemical species such as H⁺ and NH₃ (10, 20). Residues in the two NPA loops which connect the transmembrane helices 2,3 and 5,6 (Fig. 1) have been linked to functions based on site-directed mutagenesis experiments (21). In particular, the extracellular Cys-189 in the second NPA loop is the site of binding of mercurial reagents that leads to reversible blockage of water transport (12).

Figure 1.

Schematic demarcation of the polypeptide sequence of AQP1 into the six transmembrane α-helices TM1 to TM6, the cytoplasmic (H1) and extracellular (H3) α-helices in the two NPA loops, the short α-helix (H2) at the extracellular edge of TM3, and the intervening connecting loops. Amino acids belonging to the transmembrane helices (whose side chains either line the channel or point into the channel) are colored green. The mercurial-sensitive C189 (colored red) and the analogous A73 are indicated. Residues in the TM3-TM4 linker that line the entrance of the aqueous pathway on the extracellular side are colored light green. The color scheme indicated for TM1–TM6, H2, and the color white for H1, H3, and the connecting segments, follow in Fig. 2 a and b, Fig. 3, and Fig. 5b.

Highly ordered two-dimensional crystals of AQP1 were used to generate projected-density maps (22–24) and later, three dimensional (3-D) density maps at ≈6- to 7-Å resolution (25–27). The 3-D density maps revealed the organization of AQP1 in the form of a barrel composed of highly tilted α-helices that encloses a central density attributed to the interhelix NPA loops and packed with a right-handed twist (26–27). Our study (27) showed the presence of an in-plane pseudo-2-fold axis-of-symmetry located near the middle of the bilayer and ≈3Å toward the cytoplasmic side. The coupling of the tandem repeats in sequence and the observed pseudosymmetry provided an elegant solution to the problem of bidirectional transport across the bilayer. In addition, the observed in-plane symmetry ruled out sequential threading of the polypeptide chain. A 3-D density map determined at 4.5-Å resolution by Mitsuoka et al. (28) indicated that the densities attributed to the NPA loops harbor short α-helices (also suggested earlier by Li et al., ref. 25). Recently, we established the nature of the polypeptide folding (29) on the basis of a near-atomic, 4-Å resolution 3-D density map, which revealed the locations of most of the interhelix loops. By including additional high-resolution data, we have now generated a 3.7-Å resolution 3-D density map. This map was used to fit an atomic model, which was then refined against the electron diffraction amplitudes (30) to 3.7-Å resolution under strict geometry constraints. The aqueous pathway within the bilayer is characterized by a narrow curvilinear pore that is ≈4.0 ± 0.5Å in diameter and spans a length of ≈18Å. This pore, which acts as the size-selective filter, is outlined mostly by hydrophobic residues; the apex of the curvilinear pathway is close to the center of the bilayer where the N76 and N192 residues of the NPA motifs and the in-plane pseudo-2-fold axis are located. The atomic model provides clues to water selectivity and reveals interactions that stabilize the tertiary and quaternary organization of AQP1.

Materials and Methods

Highly ordered 2-D crystals of deglycosylated, purified AQP1 (24) embedded in vitrified buffer (20 mM NaH₂PO₄/Na₂HPO₄ (pH 7.1)/100 mM NaCl/0.1 mM EDTA/0.025% NaN₃) without any additives were examined in Philips CM12 and CM200FEG microscopes at −180°C. The pool of images and the diffraction patterns for tilted (up to 60°) views were the same as in our earlier analysis (29). However, the final set of sampled image phases was enhanced at the stage of merging by the inclusion of higher-resolution data not accessed earlier. For a given image, we had previously (29) truncated the data to a cut-off resolution as soon as the phase residual reached a value of 50° when compared with the full data set. Careful examination of the merging statistics indicated that for ≈90% of the chosen images the phase residual dropped again below the chosen cutoff value in higher resolution zones. Thus, by using a cutoff resolution as that beyond which phase residual increased monotonically, a larger volume of usable data could be accessed. Amplitude data from the electron diffraction patterns that were beyond 4-Å resolution were also included. Such an augmentation of the phase and amplitude data pool (≈23% increase in observed phases in 10- to 3.7-Å resolution range and ≈33% increase in observed amplitudes beyond 4-Å resolution) led to a more reliable fitting of the lattice lines (31), especially at the highest resolution. The overall (100- to 3.7-Å) phase residual was 25.7°, and the completeness was 63%, corresponding to structure factors with figure of merit ≥ 0.27 (Table 1).

Table 1.

Electron crystallographic data

Two-side plane group	p4212
Unit cell dimension	a = b = 99.58 ± 0.50 Å, c = 100 Å
IQ cut-off* of data	≤ 7
Number of observed amplitudes	48,037
Number of observed phases	19,839
Number of structure factors	2,947
Overall completeness† (100–3.7 Å)	63%
In-plane resolution	3.7 Å
Estimated resolution normal to the bilayer‡	6 Å
Overall phase residual	25.7°
Electron diffraction
Resolution limit	3.3 Å
Maximum tilt	57.5°
Number of patterns	44
RFriedel§	6.7–28.9% (15.8%)
Rmerge¶	15.4–47.3% (27.5%)
Image
Resolution limit	3.7 Å
Maximum tilt	60.2°
Number of images	72
Phase residual‖ in  resolution zones	(100–7.0 Å) 20.0°
	(7–4.0 Å) 39.7°
	(4.0–3.7 Å) 55.7°
Overall	(100–3.7 Å) 25.7°
Refinement statistics
Rfactor**	35.0%
Rfree**	45.1%
φfree‡‡	62.4°

^*Nomenclature of Henderson et al. (43). 

^† With figure of merit ≥ 0.27. Maximum completeness for data up to 60° tilt is 83%. 

^‡ Based on calculation of point-spread function (44) for the experimental map. 

^§ R_Friedel = ∑_hk|I_hk − I_h̄k̄|/∑_hk(I_hk + I_h̄k̄), average in parentheses. 

^¶ R_merge = ∑_hk|I_obs − I_fit|/∑_hkI_fit, average in parentheses. 

^‖ Weighting based on amplitudes. 

^**Using electron diffraction amplitudes (≥ 2σ) between 24 and 3.7 Å. 

^‡‡ Averaged difference between phases calculated from the model and the observed phases with figure of merit ≥ 0.50. 

On the basis of the topology reported in Ren et al. (29) and de Groot et al. (32), an initial model was fitted to the experimentally determined 3-D density map by using the program o (33). Bulky side chains—for example, H209, W210 and W213 in helix 6, and Y37, F26, F18, and W11 in helix 1—served as guide points to thread segments of the initial atomic model into the densities for the 6 transmembrane α-helices. Typically, the extremities of the helices were clearly identified from the narrowing of that density corresponding to an extended conformation in the interhelix loops. Clear densities for the long extracellular linker connecting helices 3 and 4 and for the cytoplasmic and extracellular NPA loops imposed constraints on the assignment of residues in the densities of adjacent helices. The positioning of residues, especially in channel-facing helices 2 and 5 that mostly contain small-sized amino acids, was guided by (i) an examination of a sharpened map calculated by using a negative Wilson B-factor of −38Ų (truncate; ref. 34) and by (ii) results from predictive analyses (29, 35) that suggest the identities of residues that line the inside of the monomer. The two NPA loops were modeled in such a manner that for each NPA motif, the Pro residues (φ restricted to ≈ −60°; ref. 36) are at the start of the respective short α-helices in the loop. The atomic model was refined against the 3-D diffraction amplitudes by using the positional refinement protocol in xplor (37) and using the neutral-atom electron scattering factors given by Peng (38). In this analysis, because of a low data-to-parameter ratio, a proper equilibrium between the lowering of the crystallographic R factor and the maintenance of good geometry and stereochemistry (30) was achieved by applying alternate cycles of 20- and 5-fold reduced values of recommended weight for scaling the diffraction data to the conformational energy. The diffraction amplitudes used in the refinement were those that were generated by an application of syncfit (39) by using weights of the diffraction spots calculated according to Grigorieff and Henderson (40), followed by the use of truncate (34). The R_free (37) and the free-phase residual (φ_free) (30), calculated as the difference between observed phases (not used in refinement) and the phases calculated from the fitted atomic model, were used to monitor the course of the refinement. To improve the map and side-chain fitting, the following analysis was carried out. Phases calculated from a polyalanine version of the best-fitted atomic model were combined with observed phases (sigmaa; ref. 41) and used to generate a weighted Fourier-difference map. Peaks ≥ 3.5σ in this difference map, which correspond to additional scattering centers, were considered as carbon atoms with which the polyalanine coordinate file was augmented after skeletonization by using mama (42). This file served as the input for the next cycle, and the process was repeated until there was no drop in the R factor between observed amplitudes and calculated amplitudes from the polyalanine + carbon-atom-skeleton ensemble. Finally, a sigmaa-weighted 2F_O−F_C map was calculated. This map is expected to be devoid of the model bias in the side-chain positions of the original best-fitted model.

Results and Discussion

Our 3.7-Å resolution electron–crystallographic analysis is an investigation in which specimens preserved in near-physiological condition (that is, in the absence of any additives while embedded in vitrified buffer) were used to arrive at an atomic-resolution model. This is noteworthy because, hitherto, all investigations deriving atomic or near-atomic resolution structures by using electron crystallography have exclusively used specimens preserved in sugars such as tannin, trehalose, or glucose. The coherent domains in the AQP1 crystals used in data collection typically measured better than 1 μm in diameter. Electron diffraction patterns from nominally untilted specimens regularly showed spots beyond 3-Å resolution. Diffraction patterns from highly tilted crystals indicated an effective 3-D resolution of ≈3.7Å in a direction perpendicular to the tilt axis (29). Selection of such large crystals, preserved in ice of optimum thickness, partially compensated for the exacerbation of the specimen-charging problem in ice-embedded vs. sugar-embedded specimens, and allowed us to record electron–crystallographic data that yielded good statistics (Table 1) when compared with values reported in the literature. This result, and the low overall phase residual, gave us the confidence that the quality of the 3.7-Å resolution density map is sufficiently reliable to allow the delineation of an atomic model. On the basis of the processed image areas, the phases used for calculating the density map were determined from an averaged view of ≈7 × 10⁵ tetramers (≈3 million AQP1 monomers).

Refinement of the Model.

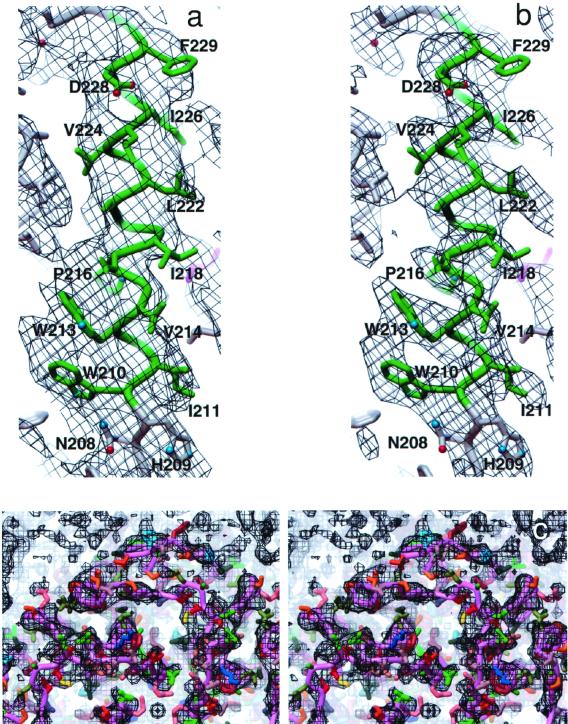
The atomic model presented includes residues L9 to A232; no clear densities for the rest of the residues were visible in the map. The starting R factor of the atomic model was 47%. Temperature factors were kept fixed after one round of grouped B factor refinement by using xplor. The 2F_o−F_c map calculated at the final stage (see Materials and Methods) helped to improve some of the side-chain locations. Thus, those that were in strong density in the experimental map generally appeared with cleaner density in the refined (2F_o−F_C) map and, in some cases, there were also improvements in the density for those that were less clear (Fig. 2 a and b). The higher (3.7-Å) in-plane resolution is apparent from the fitting of the model into the density when viewed normal to the bilayer (Fig. 2c). Further, elaborate refinements of smoothed B factor along the helices and along individual residue (30) or lipid positions seen in projection (45) were not attempted in the present study. The final φ_free value (62.4°) compares favorably with the value of 58.1° for the highly refined bacteriorhodopsin structure, the only other such reported result (30). In a Ramachandran plot, generated by using procheck, 93% of the nonglycyl residues were in most-favored and additional allowed regions, with none in the disallowed regions. On the basis of the 2F_o−F_c map, real-space crosscorrelation coefficients calculated by using the program o indicated that 89% of the residues in the model have correlations > 0.5, 35% > 0.7, and 2% < 0.4.

Figure 2.

A representative section defining the density for TM6 in the (a) experimental and (the corresponding) (b) calculated 2F_o−F_c map (Materials and Methods). (c) A stereo pair of the experimental 3-D density maps viewed normal to the bilayer from the extracellular side, and overlaid with the polypeptide model. The polypeptide backbone is shown in purple with the hydrophobic groups, groups with formal positive and negative charge, and aromatic side chains indicated with the colors green, blue, red, and brown, respectively. The depth cueing is such that the densities for the extracellular interhelix loops are primarily accentuated. Densities for one monomer and parts of adjacent monomers around the 4-fold axis are shown. The maps in this and in the other figures were rendered at 1.0σ of the mean density. Figures were generated by using the avs software (46).

Tertiary Folding and Stabilizing Interactions.

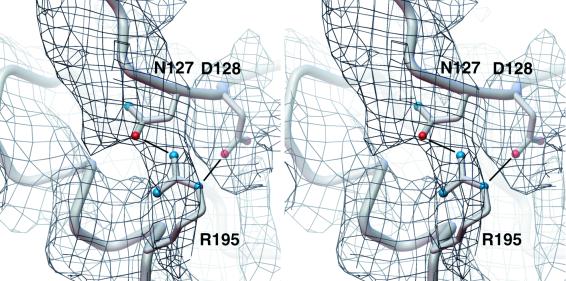
The tandemly repeating N- and C-terminal halves of AQP1 are each comprised of three tilted transmembrane α-helices and a short α-helix adjacent to the NPA motif (TM1, TM2, TM3, H1 and TM4, TM5, TM6, H3; Fig. 1). The long 3–4 interhelix linker containing a short α-helix (H2) at the extracellular edge of TM3 connects the two halves. The spatial dispositions of the two halves of the monomer are according to an approximate, in-plane 2-fold symmetry axis (27, 29) that places the transmembrane α-helices TM2 and TM5 proximal, and the two NPA loops vertically apposed and on the two sides of the symmetry axis. TM1, TM2, TM4, and TM5 define the interior of the monomer. TM6 (which displays a distinct kink near the highly conserved P216) and TM3 define the lipid-exposed exterior face (Fig. 3). The organization of the density attributed to the NPA loops is such that the planes containing the two NPA loops are in orthogonal orientation. The interfaces of adjacent helices elaborate hydrophobic interactions. For example, F18 of TM1 interacts with V107 of TM3; V50 of TM2 interacts with L181 of TM5; L139, I143, and L147 of TM4 interact with I211, G215, G219 and A223 of TM6, respectively. The refined model suggests several possible hydrogen-bonding interactions mediated by side chains, for instance, between E17 (highly conserved) and H69, between Q101 and T80 (stabilizing the cytoplasmic NPA loop), between S53 and H180, and between E142 (conserved) and T146 in TM4. The model suggests hydrogen-bonding interactions between the two neighboring NPA motifs that could stabilize these loops. A significant portion of the density for the 3–4 loop dips in from the extracellular side toward the extracellular NPA loop and, at this location, the atomic model elaborates a pocket displaying stabilizing interactions. Thus, the side-chain of the highly conserved R195 is stabilized by a hydrogen bond with that of the conserved N127 and a salt bridge with D128 (Fig. 4). Such an arrangement of the 3–4 linker not only helps stabilize the extracellular NPA loop but also positions some of the residues in the 3–4 loop (Fig. 1) at the entrance to the aqueous pathway. Indeed, a functional role for this linker in water transport in AQP2 has been suggested from mutagenesis experiments by Bai et al. (47); residues in this loop may be involved in influencing solute selectivity in glycerol transporters where this linker is significantly longer (48).

Figure 3.

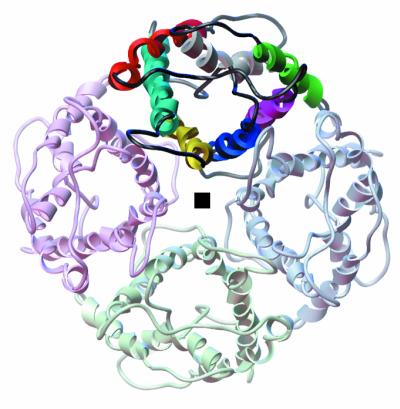
A ribbon diagram for the quaternary organization of the AQP1 monomer viewed from the extracellular side. The gray square indicates the location of the 4-fold axis; one monomer is highlighted. Color coding of individual helices in one of the monomers is the same as in Fig. 1.

Figure 4.

The density around the highly conserved R195 in helix H3 indicating stabilizing interactions with residues in the TM3-TM4 linker (hydrogen bonding with the conserved N127 and salt bridge with D128). The figure was generated by using the avs software (46).

Quaternary Structure and Stabilizing Interactions.

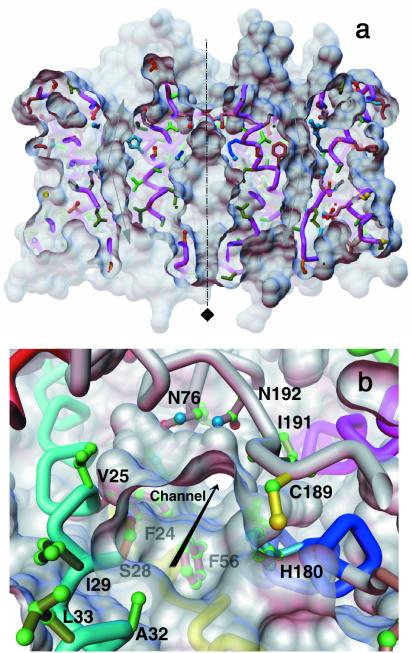
In the 2-D crystal, the AQP1 monomers organize as tetramers (Fig. 3), which is consistent with the p42₁2 two-sided plane-group symmetry. Within the lipid bilayer, the buried surface at the monomer interfaces (≈3,200Ų per monomer) is mostly hydrophobic. This surface is outlined by residues from TM1, TM2 and TM4, TM5 belonging to adjacent monomers that form a tightly packed, traditional, left-handed helix bundle (29). Between the adjacent monomers, the side chain of R159 (in the TM4-TM5 linker) hydrogen bonds with side chains of Q65 and S66 at the cytoplasmic surface, whereas on the extracellular face, the side chain of Y186 hydrogen bonds with Q43 (in the TM1-TM2 linker). Thus, the stability of the tetramer is derived both from hydrophobic interactions within and polar interactions outside the bilayer. The region around the 4-fold axis, which is bounded by helices 2 and 5, has an irregular shape and, because of different inclinations of these two helices, has the largest diameter near the center of the bilayer (Fig. 5a). It is wider on the cytoplasmic side than on the extracellular side, where the four symmetry-related Q47 residues of TM2 are in close apposition and serve to constrict the diameter of the region around the 4-fold axis to <≈3Å.

Figure 5.

Orthogonal views for the AQP1 channel. (a) The AQP1 tetramer sliced through the middle revealing the curved water-selective pathway in the two adjacent monomers and the region around the 4-fold axis as viewed parallel to the bilayer. The top is the extracellular side. The ≈25° bend of the pore as it traverses the bilayer is indicated by arrows. The color scheme of the residues is the same as in Fig. 2c. (b) A perspective view along the monomeric channel seen from the extracellular side; some of the residues lining the channel (including C189) are marked. The surface rendering of the atomic model was carried out by using the software msms (49) and a probe of radius 1.4Å.

Curvilinear Water Pathway.

As indicated schematically in Fig. 1, a majority of the side chains facing the channel in an AQP1 monomer are hydrophobic. This result is similar to that reported recently by Murata et al. (50) on the basis of a 3.8-Å density map determined by the examination of 2-D crystals preserved in the sugar trehalose. The results of our investigation provide further details of the channel architecture discussed below. As shown in Fig. 5a, the aqueous pathway is wide on both the extracellular and cytoplasmic sides and tapers down like a funnel to define a narrow curved pore that is ≈4.0 ± 0.5Å in diameter and that spans a distance of ≈18Å. This narrow pore (which acts as the size-selective filter to exclude small solutes) bends by ≈25° as it traverses the bilayer (Fig. 5a). It extends from the center of the bilayer ≈9Å to either side and is outlined mostly by hydrophobic residues (Fig. 1, Fig. 5b). The apex of the curvilinear pathway is close to the middle of the bilayer where the N76 and N192 residues of the NPA motifs and the in-plane pseudo-2-fold axis are located. Thus, the ≈18-Å long narrow part of the channel includes a region of the molecule where the approximate 2-fold symmetry is the strongest (27, 29), leading to a symmetrical environment that is consistent with observed bidirectional water flow (51). A curved pathway can promote an increase in the strain and/or the disruption of a hydrogen-bonded network of permeating water molecules, which, in effect, enhances the possibility that neighboring residues in the surrounding protein (for example, N76 and N192, located at the apex of the curved pathway) could compete for hydrogen bonds (52) with adjacent water molecules in the pore, thereby aborting H⁺ (50) or OH⁻ conduction.

Overall, the channel-lining residues in AQP1 correspond well to the analogous residues (53) in the aquaglyceroporin GlpF, a bacterial glycerol facilitator, whose structure (determined at 2.2-Å resolution by x-ray crystallography; ref. 54) shows that the glycerol molecules move through an amphipathic channel that has a constriction of ≈3.8Å on the extracellular side, ≈8Å away from the in-plane pseudo-2-fold axis. Interestingly, the selectivity filter in GlpF includes the highly conserved arginine R206 (analogous to R195 in AQP1). Our model suggests that R195, while interacting with N127 and D128 of the TM3-TM4 linker, also overlays the entrance to the narrow selectivity pore in AQP1. It is also of interest to compare the environment of the narrow pore in AQP1 to the hydrophobic cavity in the retro-GCN4 leucine-zipper structure (55). A wall of leucine and valine residues defines the hydrophobic interior of the retro-GCN4 structure, which is comprised of a parallel, left-handed, 4-helix bundle of a peptide with a palindromic sequence. Analogous to the environment in the middle of the narrow pore in AQP1, two symmetry-related Asn residues are the only polar side chains that point into the core; these residues coordinate and sequester a pair of water molecules.

Whereas the entrances to the AQP1 channel are mostly lined by polar or charged residues, the predominantly hydrophobic lining of the interior, narrow part of the channel presents a relatively noninteracting pathway for water diffusion without the presence of attractive energy minima that accompany a polar environment. It is formally similar to the pathway for K⁺ ions in the potassium channel from Streptomyces lividans (56). In that channel, the two pore helices are oriented so that the helix dipole moments act to attract K⁺ ions near the center of the bilayer. In AQP1, the orientation of the short helices in the NPA loops is opposite to that in the K⁺ channel and will repel a cation near the bilayer center. Also, the absence of an extensive polar lining in the channel means that it will be energetically expensive to locate a desolvated ion at the channel entrance, whereas a hydrated ion (including H₃O⁺) is too big to pass through. Because the channel is designed to be conducive to the passage of uncharged small solutes restricted by the diameter of the narrow part of the channel, the high physiological concentration of water (55 M) compared with any other water-soluble species in the milieu also effectively augments the selective passage of water.

Abbreviations

AQP1

Aquaporin-1

3-D

three-dimensional