Abstract
The description of frailty, a syndrome of the elderly due to the decline of homeostatic capacities, has opened new opportunities in the study of the biological basis of human aging. However, the noticeable heterogeneity for this trait in different geographic areas makes it difficult to use standardized methods for measuring the quality of aging in different populations. Consequently, the necessity to carry out population-specific surveys to define tools which are able to highlight groups of subjects with homogeneous aging phenotype within each population has emerged. We carried out an extensive monitoring of the status of the elderly population in Calabria, southern Italy, performing a geriatric multidimensional evaluation of 680 subjects (age range 65–108 years). Then, in order to classify the subjects, we applied a cluster analysis which considered physical, cognitive, and psychological parameters such as classification variables. We identified groups of subjects homogeneous for the aging phenotypes. The diagnostic and predictive soundness of our classification was confirmed by a 3-year longitudinal study. In fact, both Kaplan–Meier estimates of the survival functions and Cox proportional hazard models indicate higher survival chance for subjects characterized by lower frailty. The availability of operative frailty phenotypes allows a reappraisal of the biological basis of healthy aging as it regards both biomarkers correlated with the frail phenotype and the genetic variability associated with the phenotypes identified. Indeed, we found that the frailty phenotype is strongly correlated with clinical parameters associated with the nutritional status.
Electronic supplementary material
The online version of this article (doi:10.1007/s11357-010-9136-x) contains supplementary material, which is available to authorized users.
Keywords: Aging, Frailty, Physical decline, Homeostatic capacities
Introduction
In the last decades, there has been an increasing interest with respect to the research of the biological and environmental factors affecting the quality of human aging. This is primarily due to the social burden connected to the extraordinary increase of the elder population, which implies an increase of the subjects which are not autonomous and are affected by invalidating pathologies (Christensen et al. 2008 and references therein). Although aging is a general phenomenon, it is clear that a great interindividual variability on the rate and the quality of aging can be observed. The American Medical Association, in its white book on the health of the elderly, highlighted as the identification of the “frail” subjects would significantly improve the possibility to program and implement the assistance to the subjects who are in need, and then it has to be a priority for the health system (Walston et al. 2006). However, if a geriatrician is certainly able to distinguish the old subjects with a good quality of aging, it has turned out to be very difficult to find an objective index allowing us to define discrete phenotypes for the trait “quality of aging” (Gillick 2001; Pel Littel et al. 2009). For this reason, the definition of a discrete phenotype would certainly further our understanding of the biological basis of the aging-related decline. The emerging concept of “frailty” as a syndrome related to the decline of the homeostatic capacity is strongly favoring the research in this field (Walston et al. 2006; Levers et al. 2006). In particular, the definition of frailty given by Fried and coworkers, where frailty is defined as a wasting syndrome correlated to the lost of homeostasis which leads to a significant increase of the age-related decline of different physiological systems and then to disability, comorbidity, and death risk (Fried et al. 2001), seems particularly promising . Fried et al. highlighted that muscle strength, psychological resources, nutritional status, and physical activity are good indicators to measure the frailty in the elderly. Then, based on the distribution of the results at the different tests, they identified three different groups of old subjects: frail, nonfrail, and prefrail. In longitudinal follow-up, the subjects identified as “frail,” that is with a high degree of frailty, turned out to have a higher chance to be hospitalized or to die in the years next to the visit. However, the difficulty to obtain an operative definition of frailty is further increased by the observation that a noticeable heterogeneity for the quality of aging in different geographic areas exist. In particular, within Europe, a dramatic difference for the quality of aging between northern and southern Europe (Jeune et al. 2006) was shown. This makes it quite difficult to adopt the tests and their relevant thresholds set up to study the quality of aging in certain population, for monitoring aging in a different population. Consequently, the necessity to carry out population-specific surveys to define the tools which are able to highlight within each population the group of subjects with homogeneous aging phenotype (Passarino et al. 2007) has emerged. In this frame, the cluster analysis (CA) proved to be very useful. In fact, it is a very efficient statistical tool for analyzing data in order to obtain homogeneous groups of subjects with respect to some variables and so to classify homogenous subgroups within each population (Anderberg 1973; Dilts et al. 1995; Marengoni et al. 2008).
Our research group carried out different campaigns to monitor the quality of aging in Calabria, southern Italy. This has allowed us to set up an original protocol aimed at providing a multidimensional evaluation of the quality of aging of Calabrian old subjects. Recently, in order to obtain an operative definition of frailty, we proposed a cluster analysis approach (Passarino et al. 2007). The diagnostic and predictive soundness of our classification has been subsequently confirmed by a longitudinal study, which showed a differential incidence of comorbidity, disability, and mortality within 18 months from the visit among the different groups defined. In the present paper, we propose a reappraisal of our analysis, by using a larger sample and a longer follow-up period. In addition, we reconsidered the items used for the cluster analysis as well as the statistical details of the analysis. This has allowed us to find out population-specific frailty phenotypes that may be very useful for studying the aging process and for better taking care of most frail subjects. In addition, in order to describe the variability observed within each frailty group identified by cluster analysis, a frailty index (FI) was estimated.
Materials and methods
Samples
Two samples were analyzed. The first (S1) included 65–89-year-old subjects (376 subjects, 181 males and 195 females; median ages 72 and 73 years, respectively); the second (S2) included 308 subjects older than 90 years of age (136 males and 172 females; median ages 93 and 92 years, respectively). All the subjects were born in Calabria (southern Italy) and their ancestry in the region had been ascertained up to the grandparents’ generation. The samples have been recruited in the frame of different recruitment campaigns carried out by our research group between 2002 and 2007. Subjects older than 90 years (S2) were identified through the population registers and then contacted by specialized personnel and invited to join the study. Younger subjects were contacted either through general physicians or by means of the INRCA Hospital, which is a reference point for the care of the aging people in the Calabria region. Finally, each subject was met by a geriatrician and a person (usually a biologist) trained to conduct a structured interview. All the subjects were recruited after a complete multidimensional geriatric assessment with detailed clinical history, including anthropometric measures and a set of the most common tests to assess cognitive functioning, functional activity, physical performance, and depression. In addition, common clinical hematological tests were performed. Subjects with dementia and/or neurologic disorders were not included. Phenotypic information was collected by using the questionnaires available at the following web site: http://biologia.unical.it/echa/results.htm. Vital status at 36 months for S1 sample and at 18 months for S2 sample after the visit was traced for 273 subjects (72.6%) in S1 and for all the 308 subjects (100%) in S2 through the population registers of the municipalities where the respondents lived.
All the subjects had given informed consent for studies on aging carried out by our research group.
Geriatric assessment
Cognitive functioning The Mini Mental State Examination (MMSE) test (Folstein et al. 1975) is a 30-point cognitive scale which evaluates several different areas of thinking including memory, judgment, calculation, abstraction, language, and visual–spatial ability. MMSE scores range from 0 (lowest cognitive function) to 30 (highest cognitive function). Since the test is affected by age and educational status, the MMSE scores were normalized for these variables.
Functional activity The management of activities of daily living (bathing, dressing, eating, independence in and out of bed) was assessed by using a modification of an international and widely used scale, the Katz’ Index of activities of daily living (ADL; Katz et al. 1970). The assessment was based on what the subject was able to do at the time of the visit. Each activity was scored as 0 for people unable to perform the activity analyzed and 1 for people able to perform such activity. Then, ADL scores ranged between 0 (unable to perform any activity) and 5 (able to perform all the activities).
Physical performance Hand grip strength was measured by using a handheld dynamometer (SMEDLEY’s dynamometer TTM) while the subject was sitting with the arm close to his/her body. The test was repeated three times with the stronger hand; the maximum of these values was used in the analyses. When a test was not carried out, it was specified if it was due to physical disabilities or because the subject refused to participate.
Depression Depression was assessed by the short form (15 items) of the Geriatric Depression Scale (GDS; Sheikh and Yesavage 1986). The GDS uses a yes/no format, giving a score of 1 for each answer indicating depression. GDS scores ranged between 0 (best state) and 15 (worst state).
Self-reported health status Self-reported health status (SRHS) was assessed by asking the following question: “How is your health in general?” The possible answers were: “Very good” (coded as 5), “good” (coded as 4), “fair” (coded as 3), “poor” (coded as 2), or “very poor” (coded as 1).
Statistical analyses
Ward’s (1963) method was used to realize two distinct hierarchical CA, respectively, on S1 and S2 samples. For each sample, we performed the CA twice, by using two different sets of classification variables. The first set corresponds to those originally proposed by Passarino et al. (2007) and includes MMSE, hand grip strength, and GDS. The second one represents a new set of classification variables, composed by MMSE, hand grip strength (included also in the first classification), ADL, and SRHS. In correspondence to these two different sets of variables, two different classifications were obtained. We will refer to the classifications obtained by using the first set of variables as cluster analysis 1 (CA1), while those obtained by using the second set of variables as cluster analysis 2 (CA2). In order to choose the optimal number of groups, we plotted the increase in the total within-cluster sum of squares against the number of groups. We chose the optimal number of clusters where we saw the largest drop in the total within-cluster sum of squares.
Kaplan–Meier estimates were used to obtain the survival curves for each group identified by the two classifications in S1 and S2 samples. In order to evaluate the prediction of both classifications with respect to mortality risk, the obtained survival curves were then compared by log-rank test.
Since the prediction of our CA models could be biased by confounding factors, Cox proportional hazard models (Cox 1972) were used to assess the independent contribution of our CA classifications. Sex, age, and medical conditions were used as adjunctive covariates, since they showed to be predictive of mortality in different studies (McGue and Bouchard 1984). Before applying Cox models, indicators for frail and prefrail status were created in S1 sample, with the nonfrail serving as the reference group; indicator for very frail was created in S2 sample, with the frail group serving as reference. Moreover, Schoenfeld (1982) residuals were used to assess the proportional hazard assumption.
Finally, the regression equations resulting from the obtained Cox proportional hazard models have been used to formulate a Frailty Index (FI) (logit scores of the Cox models).
ANOVA test, t Student, and the correspondent nonparametric Mann–Whitney and Kruskal–Wallis tests were used (as appropriate) to compare the values of quantitative variables among the frailty groups defined by the CA approach. Statistical analyses were performed by using SPSS 15.0 (SPSS Inc., Chicago, IL, USA). A significance level of α = 0.05 was chosen in all the tests.
Results
Table 1 reports anthropometric characteristics in the two samples, together with information on some of the most important geriatric parameters (MMSE, hand grip strength, ADL, GDS, SRHS). The values of MMSE and hand grip strength were used after normalization with respect to the nonindependent variables. In particular, MMSE scores were normalized for education level (p < 0.001 in both S1 and S2) and age (p = 0.004 in S1 and p < 0.001 in S2); hand grip strength values were normalized for age (p < 0.001 in both S1 and S2), sex (p < 0.001 in both S1 and S2), and height (p < 0.001 in S1 and p = 0.002 in S2).
Table 1.
Mean values (standard deviation in parenthesis) of MMSE, hand grip strength, GDS, ADL, SRHS, and anthropometric characteristics of the surveyed subjects
| Sample 1 (N = 376) | Sample 2 (N = 308) | |||
|---|---|---|---|---|
| Men (N = 181) | Women (N = 195) | Men (N = 136) | Women (N = 172) | |
| Median age (years) | 72 | 73 | 93 | 92 |
| MMSE | 24.4 (4.42) | 22.2 (4.59) | 16.7 (5.98) | 14.1 (6.54) |
| Hand grip strength | 30.3 (7.98) | 17.6 (5.92) | 18.3 (7.16) | 11.5 (4.73) |
| GDS | 2.84 (3.04) | 6.02 (3.90) | 4.04 (2.97) | 5.31 (3.27) |
| ADL | 4.8 (0.70) | 4.6 (0.98) | 3.5 (1.80) | 2.9 (1.98) |
| SRHS | 3.3 (0.98) | 2.9 (1.06) | 3.1 (1.08) | 3.3 (0.94) |
| Height (cm) | 166.6 (6.97) | 153.7 (6.12) | 159.1 (7.07) | 147.2 (6.51) |
| Weight (kg) | 72.2 (12.88) | 64.9 (12.79) | 62.0 (11.29) | 51.4 (10.43) |
| BMI (kg/m2) | 26.3 (4.03) | 27.6 (4.96) | 24.4 (3.72) | 23.6 (4.24) |
| Knee height (cm) | 49.7 (2.77) | 44.9 (2.46) | 48.4 (2.69) | 44.4 (2.27) |
Data are reported by age group and by gender
BMI body mass index
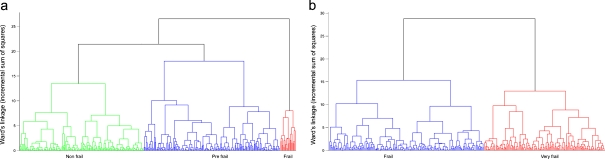
CA was then carried out according to the procedure previously described (Passarino et al. 2007). As in that case, the cluster dendrogram plots and the analysis of the increase in total within-cluster sum of squares suggested the stopping of the clustering process when three clusters were obtained in S1 and two clusters in S2 (Fig. 1 a, b). In Table 2, we report for each sample the mean values of the classification variables.
Fig. 1.
Schematic representation of the clusters obtained in S1 (a) and S2 (b) by applying hierarchical cluster analysis which used MMSE, GDS, and hand grip strength data as classification variables (CA1)
Table 2.
Mean values (standard deviation in parenthesis) of MMSE, hand grip strength, and GDS within the categories obtained by CA1 in the two samples
| Classification variables | |||
|---|---|---|---|
| Hand grip strength | MMSE | GDS | |
| Sample 1 | |||
| Non frail (N = = 105) | 0.13 (0.75) | 0.99 (0.50) | 0.14 (1.00) |
| Pre frail (N = 182) | 0.10 (1.06) | −0.27 (0.72) | −0.50 (0.53) |
| Frail (N = 53) | −0.61 (0.99) | −1.04 (0.94) | 1.46 (0.68) |
| Sample 2 | |||
| Frail (N = 221) | 0.15 (0.96) | 0.19 (0.93) | −0.42 (0.62) |
| Very frail (N = 64) | −0.50 (0.94) | -0.66 (0.92) | 1.45 (0.62) |
For MMSE and hand grip strength, standardized residuals were used after appropriate adjustment. Negative or positive numbers correspond to values lower or higher than the sample means, respectively
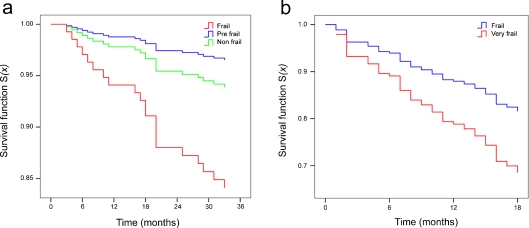
The analysis of the classification variables within the different clusters allowed us to define the three clusters in S1 as nonfrail (the cluster with subjects showing the best scores for the classification variables), frail (the clusters with subjects showing the worst scores for the classification variables), and prefrail (the cluster with subjects showing intermediate scores for the classification variables). Similarly, in S2, the two clusters obtained were defined as frail (the cluster with subjects showing the best scores for the classification variables) and very frail (the cluster with subjects showing the worst scores for the same variables). Kaplan–Meier estimates of the survival functions have been then obtained for each of the groups defined according to the CA1 classification obtained in S1 and in S2 samples. After 36 months, 21.4% of those who were frail had died, compared to 4.3% of those who were prefrail and 8.4% of those who were nonfrail at baseline in S1 sample. In S2 sample, after 18 months, 31.2% of those who were very frail had died, compared to 19.1% of those who were frail at baseline (Table 3).
Table 3.
Mortality with respect to CA1 classification: Kaplan–Meier estimates at 18 and 36 months after study entry for S1 sample and at 18 months for S2 sample
| Dead after 18 months | Dead after 36 months | p value | |
|---|---|---|---|
| Sample 1 | |||
| Nonfrail (N = 83) | 4.8% | 8.4% | 0.003 |
| Prefrail (N = 116) | 2.6% | 4.3% | |
| Frail (N = 42) | 11.9% | 21.4% | |
| Sample 2 | |||
| Frail (N = 220) | 19.1% | – | 0.036 |
| Very frail (N = 64) | 31.2% | – | |
p values refer to log-rank tests
To assess the independent predictive validity of these frailty phenotypes, we evaluated its association with prospective mortality risk by Cox proportional hazard models. In Table 4, the hazard ratio (HR) for mortality risk over the period of follow-up in S1 is displayed for those who were in the frail or prefrail status at baseline relative to those who were nonfrail. Unadjusted estimates resulted to be borderline significant for the predictive association of the frail status with mortality (p = 0.048) but not of the prefrail status. By contrast, no significance was observed when adjusted estimates were used. For the S2 sample, HR estimate for the mortality risk over the follow-up period was estimated for those who were in the very frail group at baseline relative to those who were frail. Unadjusted estimates resulted to be significant for the predictive association of the frail status with mortality (p = 0.039), while adjusted estimates turned out to show no significant association. The covariates included in the Cox models as confounding factors were sex, age, and medical conditions.
Table 4.
HR estimated by the fitted Cox proportional hazards models in S1 and S2 samples in the CA1 classification
| Sample 1 | Sample 2 | ||||
|---|---|---|---|---|---|
| Nonfrail (reference) | Prefrail | Frail | Frail (reference) | Very frail | |
| Unadjusted | HR = 1.0 | HR = 0.503 | HR = 2.708 | HR = 1.0 | HR = 1.750 |
| CI = (0.160–1.585) | CI = (1.008–7.273) | CI = (1.027–2.981) | |||
| p = 0.241 | p = 0.048 | p = 0.039 | |||
| Covariate-adjusted | HR = 1.0 | HR = 0.426 | HR = 2.591 | HR = 1.0 | HR = 1.318 |
| CI = (0.121–1.501) | CI = (0.748–8.981) | CI = (0.503–3.452) | |||
| p = 0.184 | p = 0.133 | p = 0.575 | |||
Covariate adjustment includes age, sex, and presence of the following pathologies: diabetes, hypertension, angina pectoris, heart failure, arrhythmias, asthma, arthritis, migraine, osteoporosis, stroke, heart attack, cancer, pneumonia. p values refer to the Wald tests
Figure 2 reports the age- and sex-adjusted estimated proportional hazard survival functions for the frailty groups defined by CA1 in S1 and S2 samples (Fig. 2 a, b).
Fig. 2.
Age- and sex-adjusted estimated proportional hazard survival functions for the frailty groups defined by CA1 in S1 (a) and S2 (b) samples
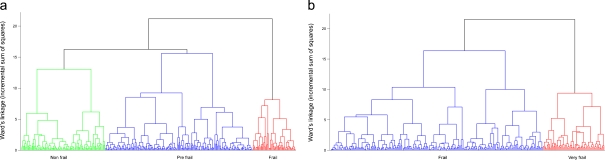
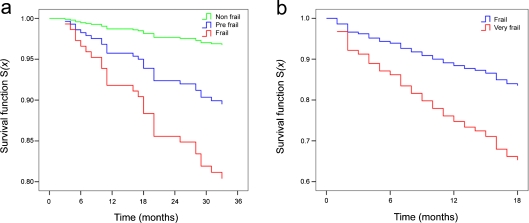
As mentioned before, CA2 has been performed by using the same clustering procedure of CA1, but with a different set of classification variables (MMSE, hand grip strength, ADL, and SRHS). Also, in this case, the cluster dendrogram plots and the analysis of the increase in total within-cluster sum of squares suggested the stopping of the clustering process when three clusters were obtained in S1 and two clusters in S2 (Fig. 3 a, b). Thus, as in the previous case, according to the average values of the classification variables, we identified the three clusters in S1 as nonfrail, prefrail, and frail phenotypes and the two clusters in S2 as frail and very frail phenotypes. Table 5 reports for each of the groups obtained by CA2 the mean values of the classification variables. Then, for each of the resulting groups, the Kaplan–Meier estimates of the survival functions in S1 and in S2 samples were obtained. After 36 months, 40.0% of those who were frail had died, compared to 12.7% of those who were prefrail and 3.2% of those who were nonfrail at baseline in S1 sample. After 18 months, 36.0% of those who were very frail had died, compared to 16.4% of those who were frail at baseline in S2 sample (Table 6).
Fig. 3.
Schematic representation of the clusters obtained in S1 (a) and S2 (b) by applying hierarchical cluster analysis which used SRHS, MMSE, ADL, and hand grip strength data as classification variables (CA2)
Table 5.
Mean values (standard deviation in parenthesis) of MMSE, hand grip strength, ADL, and SRHS within the categories obtained by CA2 in the two samples
| Classification variables | ||||
|---|---|---|---|---|
| SRHS | ADL | Hand grip strength | MMSE | |
| Sample 1 | ||||
| Nonfrail (N = 169) | 0.71 (0.69) | 0.31 (0.18) | 0.50 (0.89) | 0.34 (0.63) |
| Prefrail (N = 186) | −0.49 (0.79) | 0.13 (0.48) | −0.40 (0.86) | −0.22 (1.13) |
| Frail (N = 21) | −1.32 (0.80) | −3.64 (1.25) | −0.45 (1.23) | −0.81 (1.22) |
| Sample 2 | ||||
| Frail (N = 173) | −0.17 (1.03) | 0.78 (0.31) | 0.45 (0.85) | 0.46 (0.77) |
| Very frail (N = 135) | 0.22 (0.91) | −0.99 (0.63) | −0.58 (0.87) | −0.59 (0.95) |
For MMSE and hand grip strength, standardized residuals were used after appropriate adjustment. Negative or positive numbers correspond to values lower or higher than the sample means, respectively
Table 6.
Mortality with respect to CA2 classification: Kaplan–Meier estimates at 18 and 36 months after study entry for S1 sample and at 18 months for S2 sample
| Dead after 18 months | Dead after 36 months | p value | |
|---|---|---|---|
| Sample 1 | |||
| Nonfrail (N = 126) | 2.4% | 3.2% | <0.001 |
| Prefrail (N = 127) | 8.7% | 12.7% | |
| Frail (N = 20) | 15.0% | 40.0% | |
| Sample 2 | |||
| Frail (N = 173) | 16.3% | – | <0.001 |
| Very frail (N = 135) | 37.3% | – | |
p values refer to log-rank tests
Also, in this case, to assess the independent predictive validity of these frailty phenotypes, we evaluated its association, prospectively, with mortality risk ascertained in a prospective follow-up by using Cox proportional hazard models. Table 7 shows the HR for mortality risk over the period of follow-up. The predictive association of the prefrail and frail status with mortality turned out to be significant in the unadjusted model (p = 0.012 and p < 0.001 for prefrail and frail status, respectively). After adjustment with relevant covariates, mortality turned out to be significant in the frail group only (p = 0.029). In S2, both unadjusted and adjusted estimates resulted to be significant for the predictive association of the frail status with mortality (p < 0.001 and p = 0.009, respectively). Also, in this case, the covariates of interest were sex, age, and medical conditions.
Table 7.
HR estimated by the fitted Cox proportional hazards models in S1 and S2 samples in the CA2 classification
| Sample 1 | Sample 2 | ||||
|---|---|---|---|---|---|
| Nonfrail (reference) | Prefrail | Frail | Frail (reference) | Very frail | |
| Unadjusted | HR = 1.0 | HR = 4.084 | HR = 13.763 | HR = 1.0 | HR = 2.533 |
| CI = (1.365–12.216) | CI = (4.141–45.744) | CI = (1.589–4.038) | |||
| p = 0.012 | p < 0.001 | p < 0.001 | |||
| Covariate-adjusted | HR = 1.0 | HR = 2.515 | HR = 6.544 | HR = 1.0 | HR = 2.320 |
| CI = (0.744–8.507) | CI = (1.215–35.258) | CI = (1.239–3.344) | |||
| p = 0.138 | p = 0.029 | p = 0.009 | |||
Covariate adjustment includes age, sex, and presence of the following pathologies: diabetes, hypertension, angina pectoris, heart failure, arrhythmias, asthma, arthritis, migraine, osteoporosis, stroke, heart attack, cancer, and pneumonia. p values refer to the Wald tests
The data reported in Table 7 indicate that, after adjusting for relevant covariates in the model obtained in S1 sample, belonging to the most vulnerable groups (frail phenotype) is a significant predictor for mortality risk. In fact, the risk of death per unit of time for a frail subject is 6.54 times that for a nonfrail subject. Also, in the model obtained in S2 sample, after adjusting for relevant covariates, belonging to the very frail group is a significant predictor for mortality risk with a risk of death per unit of time equals to 2.32 times that for a frail subject.
In both models, proportional hazard assumptions were satisfied as shown by graphical (log–log survival plots involving the relevant covariates) and analytical (goodness-of-fit test involving the Schoenfeld residuals) approaches (data not shown).
Figure 4 reports the age- and sex-adjusted estimated proportional hazard survival functions for the frailty groups defined by CA2 in S1 and S2 samples (Fig. 4 a, b).
Fig. 4.
Age- and sex-adjusted estimated proportional hazard survival functions for the frailty groups defined by CA2 in S1 (a) and S2 (b) samples
On the basis of the regression equations obtained from the two fitted Cox proportional hazard models in S1 and S2 samples (CA2 classification), an FI has been formulated. This index corresponds to the logit scores from each Cox proportional hazard model previously obtained, that is
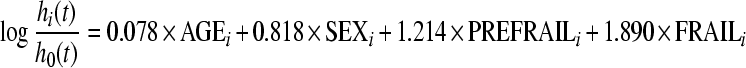 |
in S1 sample and
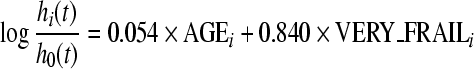 |
in S2 sample, where AGEi is the age of the subject i, SEXi assumes a value of 1 if the subject is male and 0 otherwise, and PREFRAILi, FRAILi, VERY_FRAILi, are dichotomous variables that assume a value of 1 whether the subject i belongs to the respective group.
In the S1 sample, the mean values of FI after standardization were −0.82, 0.53, and 1.81 in nonfrail, prefrail, and frail groups, respectively (p < 0.001). In the S2 sample, the FI-standardized values were −0.41 and 0.52 in very frail and frail groups, respectively (p < 0.001).
In addition, we explored the association between the frailty phenotypes and different hematological parameters (a complete list of the screened hematological parameters is given in the Supplementary Material). Tables 1SM and 2SM in Supplementary Material report that the hematological parameters are significantly associated with the frailty phenotype in S1 (Table 1SM) and S2 samples (Table 2SM) according to CA2 classification.
Discussion
The recent description of frailty has opened new opportunities in the research of the biological basis of aging. However, frailty is still a slippery concept, and it is debated how to measure frailty phenotypes, also considering its possible population specificity. We have been monitoring for a number of years the condition of the aging population in Calabria. In a previous study, by applying a cluster analysis to identify groups of subjects homogeneous with respect to chosen variables, we showed that monitoring the conservation of cognitive (MMSE), neuromuscular (hand grip), and psychological resources (Geriatric Depression Scale) may give good indications about the frailty phenotype (Passarino et al. 2007). In fact, these resources are the main component of the frailty circle and gauge some of the most important aspects of the age-related biological decline (Fried et al. 2001). In the present study, by using the same variables considered in the previous study on a larger sample and following the enrolled subjects for a longer time period, we could confirm that these items are good indicators of frailty. Indeed, the subjects identified as frail by means of cluster analysis had a higher risk of death in both S1 and S2 samples. However, better results were obtained by redefining the classification variables and using SRHS (which showed to be an effective indicator of the psychological status of the elderly, see Nybo et al. 2003) instead of GDS and by adding also ADL. In fact, the analysis of the data suggested that GDS scores may be too heavy on determining the outcome of the cluster analysis (possibly because the test ranges from 1 to 15, but most subjects are either close to zero or to 15); in addition, ADL scores were shown to be very tightly correlated to the evolution of the aging phenotype and to the energy expenditure (Pel Littel et al. 2009 and references therein). The new set of variables has allowed us to redefine frail, prefrail, and nonfrail subjects in S1 as well as very frail and frail subjects in S2. The analysis of perspective survival clearly showed a very significant difference in death risk among different groups. In fact, both Kaplan–Meier estimates of the survival functions and Cox proportional hazards model clearly indicate the higher survival chance for nonfrail and prefrail with respect to frail in S1 and of very frail with respect to frail in S2. It is important to notice that the difference in mortality between groups with different frailty increases as time goes, suggesting that the baseline inclusion in each group was able to reveal a difference in long-lasting resources more than diseases already present. This is further highlighted by the estimation of HR, which showed that being frail increases the risk of death by a factor of 6.54 after adjustment for age, sex, and a number of age-related pathologies. Similarly, in S2, very frail subjects have a more than double death risk with respect to frail subjects. The results are confirmed by the frailty index, where we also have the opportunity to better weigh the importance of different covariates. We observed that in S1 each year of age increases the hazard of death by a factor of exp(1.890), while to be male increases such a risk by a factor of exp(0.818). To be in the frail or in the prefrail group increases such a risk by a factor of exp(1.890) and exp(1.214), respectively. In other words, to be in the frail group is more “hazardous” than being 20 years older. Similar results were observed in S2, where, however, the sex is not discriminating. This last result may be related to the peculiar demographic situation of Calabria, where the survival of old males is higher than elsewhere and the male/female ratio among centenarians is about 1:2 instead of 1:4 or 1:5 as observed in northern Italy and northern Europe (Passarino et al. 2002; Montesanto et al. 2008).
It is of a particular interest also to see that selected laboratory parameters are strongly correlated to frailty phenotypes. It is important to underline that these parameters are often easy to obtain and then may give an immediate hint on the status of the elderly. They indicate the importance of lipids, thyroid hormones, iron and hemoglobin, inflammation, nutritional status, and immunological response on the aging phenotype. Besides confirming the relevant role of these parameters in defining the clinical phenotype of frailty, these results add to the present knowledge by demonstrating that serum albumin (i.e., a proxy of nutritional status) is the strongest correlate of the very frail phenotype in our sample 2 analysis. The latter finding suggests that nutritional status may help to distinguish very frail from frail subjects, and this hypothesis warrants further investigations. It is also interesting to notice that parameters related to the frailty status are different in the two groups, highlighting the importance of age-specific approaches for the evaluation of the frailty status in the elderly. On the other hand, this is in line with the findings of age-specific genetic determinants for longevity (Passarino et al. 2006).
These results may have important implications. The main implication of the novel approach to define frailty is that it represents a support to the view that frailty is not a synonymous of comorbidity and disability (Fried et al. 2001). Our findings may be important also from the clinical point of view. In fact, the identification of frail subjects may be very important to address specific medical care to support these subjects and to prevent the effects of frailty. Appropriate prescribing in old patients is known to represent an always-challenging issue. In such a complex scenario, the development of a predictive model identifying prefrail and frail subjects and, as a further research step, the development of its application in clinical practice might help us to tailor treatments on the basis of the real needs of each single patient, especially of prefrail and frail older patients with multiple chronic conditions and reduced life expectancy.
The population specificity of our approach allows the method to be used in different populations by highlighting the variables playing a major role in the determination of the frailty status in that population. However, it requires a preliminary close monitoring of the relevant aging population in order to build the appropriate model. Then, in order to find out to which group a new subject belongs to, a discriminant function (such as logistic regression models, Fisher discriminant analysis, Kernel discriminant analysis) can be used. This function should use the classification variables (MMSE, hand grip, ADL, and SRHS) as independent variables and the group membership as dependent variable. Alternatively, “classification trees” (Breiman et al. 1984) can be used in order to obtain easily understandable decision tree models that can allow us to classify new cases not included in the initial sample. For instance, we applied this approach to our dataset, and we obtained the decision trees reported in Figs. 1SM and 2SM of the Supplementary Material.
On the whole, our study confirms that cluster analysis may be very useful in the definition of frailty phenotype. In fact, it is a very efficient statistical tool for analyzing the data in order to obtain homogeneous groups of subjects with respect to some variables. On the other hand, we have been able to define groups of variables, all influenced by different aspects of the frailty circle described by Fried et al. 2001, that are quite efficient in defining frailty phenotype in our population. The combination of the statistical method and variables proposed in this paper, as they do not imply a priori threshold, may be valuable also for most populations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Supplementary Material Mean values of the hematological parameters within the groups obtained by CA2 in S1 sample. Only the parameters shown to be significantly different among “frailty phenotype” groups and the subjects for whom the relevant parameters were available are reported (DOC 80 kb)
Classification tree for S1 sample according to CA2 (JPEG 319 kb)
High Resolution Image (TIFF 160 kb)
Classification tree for S2 sample according to CA2 (JPEG 373 kb)
High Resolution Image (TIFF 173 kb)
Acknowledgments
The study was supported by Fondi di Ateneo from the University of Calabria and by the Italian Ministry of Health (Italian National Research Center on Aging, Fondi Ricerca Corrente).
Footnotes
Alberto Montesanto and Vincenzo Lagani equally contributed to the study.
References
- Anderberg M. Cluster analysis for application. New York: Academic; 1973. [Google Scholar]
- Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification regression trees. Belmont, California: Wadsworth International Group; 1984. [Google Scholar]
- Christensen K, McGue M, Petersen I, Jeune B, Vaupel JW. Exceptional longevity does not result in excessive levels of disability. Proc Natl Acad Sci U S A. 2008;105:13274–13279. doi: 10.1073/pnas.0804931105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox DR. Regression models and life tables. J Roy Stat Soc. 1972;34:187–220. [Google Scholar]
- Dilts D, Khamalah J, Plotkin A. Using cluster analysis for medical resource decision making. Med Decis Making. 1995;15:333–347. doi: 10.1177/0272989X9501500404. [DOI] [PubMed] [Google Scholar]
- Folstein MF, Folstein SE, McHugh PR. Mini-mental state. A practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res. 1975;12:189–198. doi: 10.1016/0022-3956(75)90026-6. [DOI] [PubMed] [Google Scholar]
- Fried LP, Tangen CM, Walston J, Newman AB, Hirsch C, Gottdiener J, Seeman T, Tracy R, Kop WJ, Burke G, McBurnie MA. Cardiovascular Health Study Collaborative Research Group. Frailty in older adults: evidence for a phenotype. J Gerontol A Biol Sci Med Sci. 2001;56:M146–M156. doi: 10.1093/gerona/56.3.m146. [DOI] [PubMed] [Google Scholar]
- Gillick M. Guest editorial: pinning down frailty. J Gerontol A Biol Sci Med Sci. 2001;56:M134–M135. doi: 10.1093/gerona/56.3.m134. [DOI] [PubMed] [Google Scholar]
- Jeune B, Skytthe A, Cournil A, Greco V, Gampe J, Berardelli M, Andersen-Ranberg K, Passarino G, Benedictis G, Robine JM. Handgrip strength among nonagenarians and centenarians in three European regions. J Gerontol A Biol Sci Med Sci. 2006;61:707–712. doi: 10.1093/gerona/61.7.707. [DOI] [PubMed] [Google Scholar]
- Katz S, Downs ID, Cash HR, Grotz RC. Progress in development of the index of ADL. Gerontologis. 1970;10:20–30. doi: 10.1093/geront/10.1_part_1.20. [DOI] [PubMed] [Google Scholar]
- Levers MJ, Estabrooks CA, Ross Kerr JC. Factors contributing to frailty: literature review. J Adv Nurs. 2006;56:282–291. doi: 10.1111/j.1365-2648.2006.04021.x. [DOI] [PubMed] [Google Scholar]
- Marengoni A, Winblad B, Karp A, Fratiglioni L. Prevalence of chronic diseases and multimorbidity among the elderly population in Sweden. Am J Public Health. 2008;98:1198–1200. doi: 10.2105/AJPH.2007.121137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGue M, Bouchard TJ., Jr Adjustment of twin data for the effects of age and sex. Behav Genet. 1984;14:325–343. doi: 10.1007/BF01080045. [DOI] [PubMed] [Google Scholar]
- Montesanto A, Passarino G, Senatore A, Carotenuto L, Benedictis G. Spatial analysis and surname analysis: complementary tools for shedding light on human longevity patterns. Ann Hum Genet. 2008;72:253–260. doi: 10.1111/j.1469-1809.2007.00405.x. [DOI] [PubMed] [Google Scholar]
- Nybo H, Petersen HC, Gaist D, Jeune B, Andersen K, McGue M, Vaupel JW, Christensen K. Predictors of mortality in 2,249 nonagenarians—the Danish 1905-Cohort Survey. J Am Geriatr Soc. 2003;51:1365–1373. doi: 10.1046/j.1532-5415.2003.51453.x. [DOI] [PubMed] [Google Scholar]
- Passarino G, Calignano C, Vallone A, Franceschi C, Jeune B, Robine JM, Yashin AI, Cavalli Sforza LL, Benedictis G. Male/female ratio in centenarians: a possible role played by population genetic structure. Exp Gerontol. 2002;37:1283–1289. doi: 10.1016/S0531-5565(02)00140-7. [DOI] [PubMed] [Google Scholar]
- Passarino G, Montesanto A, Dato S, Giordano S, Domma F, Mari V, Feraco E, Benedictis G. Sex and age specificity of susceptibility genes modulating survival at old age. Hum Hered. 2006;62:213–220. doi: 10.1159/000097305. [DOI] [PubMed] [Google Scholar]
- Passarino G, Montesanto A, Rango F, Garasto S, Berardelli M, Domma F, Mari V, Feraco E, Franceschi C, Benedictis G. A cluster analysis to define human aging phenotypes. Biogerontology. 2007;8:283–290. doi: 10.1007/s10522-006-9071-5. [DOI] [PubMed] [Google Scholar]
- Pel Littel RE, Schuurmans MJ, Emmelot Vonk MH, Verhaar HJ. Frailty: defining and measuring of a concept. J Nutr Health Aging. 2009;13:390–394. doi: 10.1007/s12603-009-0051-8. [DOI] [PubMed] [Google Scholar]
- Schoenfeld D. Residuals for the proportional hazard regression model. Biometrika. 1982;69:239–241. doi: 10.1093/biomet/69.1.239. [DOI] [Google Scholar]
- Sheikh JI, Yesavage JA. Geriatric Depression Scale (GDS): recent evidence and development of a shorter version. clinical gerontology: a guide to assessment and intervention. New York: Haworth; 1986. pp. 165–173. [Google Scholar]
- Walston J, Hadley EC, Ferrucci L, Guralnik JM, Newman AB, Studenski SA, Ershler WB, Harris T, Fried LP. Research agenda for frailty in older adults: toward a better understanding of physiology and etiology: summary from the American Geriatrics Society/National Institute on Aging Research Conference on Frailty in Older Adults. J Am Geriatr Soc. 2006;54:991–1001. doi: 10.1111/j.1532-5415.2006.00745.x. [DOI] [PubMed] [Google Scholar]
- Ward JH. Hierarchical grouping to optimize an objective function. J Am Stat Assoc. 1963;58:236–244. doi: 10.2307/2282967. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Below is the link to the electronic supplementary material.
Supplementary Material Mean values of the hematological parameters within the groups obtained by CA2 in S1 sample. Only the parameters shown to be significantly different among “frailty phenotype” groups and the subjects for whom the relevant parameters were available are reported (DOC 80 kb)
Classification tree for S1 sample according to CA2 (JPEG 319 kb)
High Resolution Image (TIFF 160 kb)
Classification tree for S2 sample according to CA2 (JPEG 373 kb)
High Resolution Image (TIFF 173 kb)