A new correlation-based measure of spike timing reliability

Abstract

We introduce a new correlation-based measure of spike timing reliability. Unlike other measures, it does not require the definition of a posteriori “events”. It relies on only one parameter, which relates to the timescale of spike timing precision. We test the measure on surrogate data sets with varying amounts of spike time jitter, and missing or additional spikes, and compare it with a widely used histogram-based measure. The measure is efficient and faithful in characterizing spike timing reliability and produces smaller errors in the reliability estimate than the histogram-based measure based on the same number of trials.

1. Introduction

Spike timing unreliability limits the amount of information a neuron can potentially transmit about a stimulus. Intrinsic noise and extrinsic influences, such as synaptic noise, cause a neuron to respond with variable spike timing to the same stimulus. This variability is expressed as jitter in the timing of individual spikes, missing spikes, and additional (noisy) spikes. Our goal is a reliability measure that captures all three phenomena.

Many measures have been used to characterize reliability of spike timing on the basis of the spike trains a neuron produces in response to repeated presentation of the same stimulus, see for instance [1–6]. Most measures are based on the post-stimulus time histogram (PSTH), which is insensitive to the structure of individual spike trains [5]. Here, we introduce a new measure of spike timing reliability, based on a measure of the similarity between pairs of individual spike trains. We test this measure with surrogate data sets designed to assess the performance of the measure with respect to additional spikes, missing spikes, and spike jitter.

2. Reliability measures

2.1. The histogram-based measure

Many measures of spike timing reliability rely on the construction of a PSTH, constructed from multiple trials. The PSTH depends on a particular choice of bin width, bin_h. “Events” are then defined as peaks in the PSTH. In order to reliably extract peaks, the PSTH is typically smoothed with a time window, τ_h. In practice, care must be taken to set the threshold, θ_h, to detect peaks, and exclude noise, which depends on bin_h. Once the events are detected, spikes are labeled as belonging to an event. This labeling depends on the choice of an allowable time window, w_h, around the time of peak outside of which spikes cannot be considered as part of the event. This parameter sets a time scale that depends on the phenomena of interest. Reliability, R_hist, is defined as the average number of spikes within events, divided by the total number of spikes, n_total, present in the histogram: R_hist = (Σ_e∈events n_e)/n_total. This procedure depends on four parameters (bin_h, τ_h, θ_h, and w_h), and a fair amount of discretion from the part of the experimenter. Hence, it is difficult to compare reliability measures between studies, unless exactly the same procedure has been used.

For comparison with the correlation-based measure, we smooth the PSTH with a Gaussian filter (standard deviation τ_h), the threshold, θ_h, is fixed, and only bins with values exceeding θ_h are considered event bins. The allowable window is defined as twice the width of the peak, at mid-height.

2.2. The correlation-based measure

In contrast to histogram measures, which ignore information about the structure of individual spike trains by summing over all trials, the correlation measure presented here relies on the structure of individual trials and does not depend on identifying events a posteriori. It is based on a similarity measure between individual pairs of spike trains. The spike trains obtained from N repeated presentations of the same stimulus are convolved with a Gaussian filter of a given width, σ_c. After convolving all trials, the inner product is taken between all pairs of trials and each inner product is then divided by the norms of the two trials of the respective pair. Reliability, R_corr, is the average of all similarity values. Therefore, if the filtered spike trains s⃗_i(i=1 ,…, N) are represented as individual vectors, the correlation measure is

$$R_{\text{corr}}=\frac{2}{N(N-1)}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=i+1}^N\frac{\overrightarrow{S_i}·\overrightarrow{S_j}}{|\overrightarrow{S_i}||\overrightarrow{S_j}|}.}}$$

It takes values between zero and one.

The measure depends only on the width of the Gaussian filter, σ_c, which is based on the phenomenological time scale of interest and directly tunes the measure with respect to the influence of spike jitter versus missing and additional spikes [6]. For a narrow filter, spike timing can yield high reliability values only if the spike jitter is less than or equal to the filter width. For a broad filter width, the influence of individual spike jitter (on a timescale below the filter width) is decreased and the value of reliability is dominated by the occurrence of additional and missing spikes. Therefore, the filter width is directly related to the precision of spike timing.

3. The surrogate test data sets

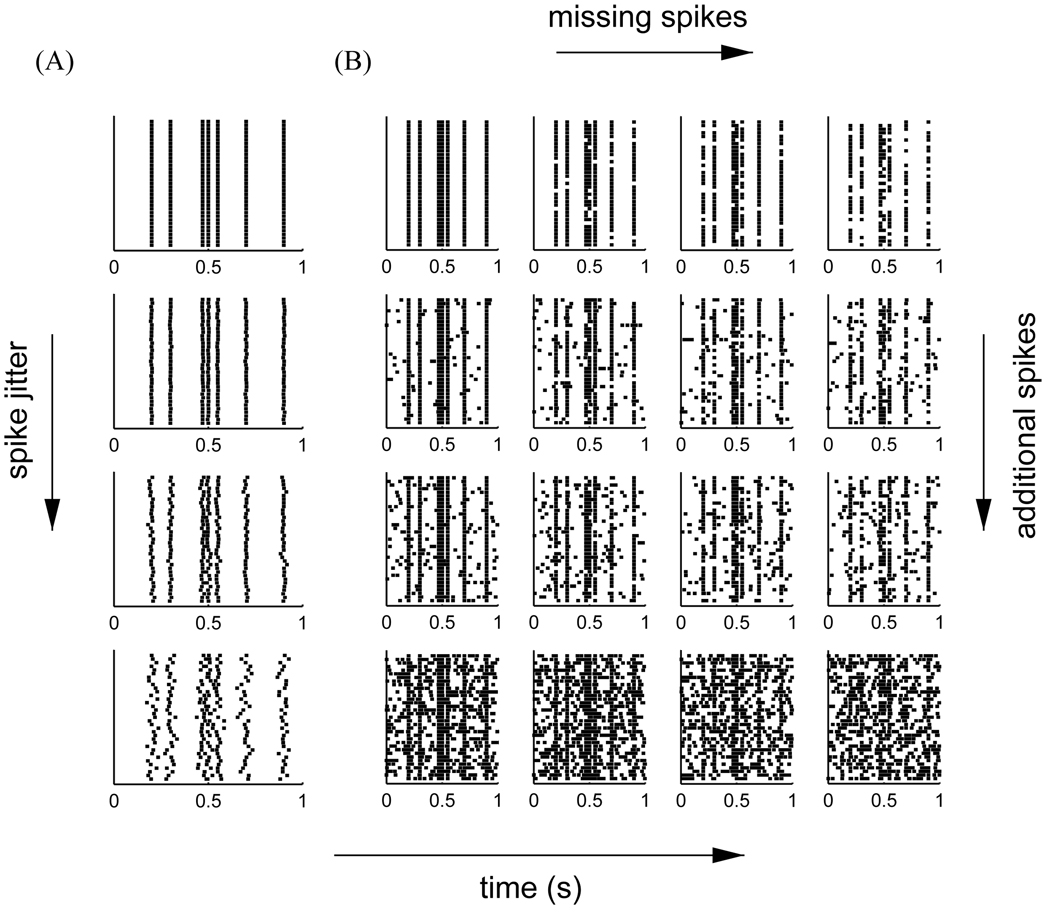
To test the new correlation measure we used a surrogate data set, consisting of seven firing events within one second, see Fig. 1. Each rastergram was comprised of N = 35 spike trains. Without jitter, extra spikes, and missing spikes all trials are identical, so that reliability should always be 1 (upper rastergram in Fig. 1A and upper left most rastergram in Fig. 1B). We used this rastergram to derive additional surrogate sets of spike trains, by systematically varying the amount of jitter and the amount of missing and additional spikes. For the sets with variation in jitter, each spike of every trial in the reliable set was independently shifted in time, according to a Gaussian distribution with a standard deviation of σ_j, which corresponded to the amount of jitter introduced. For the sets with missing and additional spikes, additional spikes were introduced at random times and randomly selected spikes of the reliable set were removed.

Fig. 1.

(A) The basis surrogate data set (events at 200, 300, 470, 500, 550, 700, and 900 ms) and three examples of data sets with different jitter, σ_j (2, 6, and 16 ms); (B) Examples of data sets of different amounts of missing and extra spikes (0%, 2%, 4%, and 16% extra spikes, and 0%, 10%, 20%, 30% missing event-spikes).

4. Results

4.1. Reliability with jitter

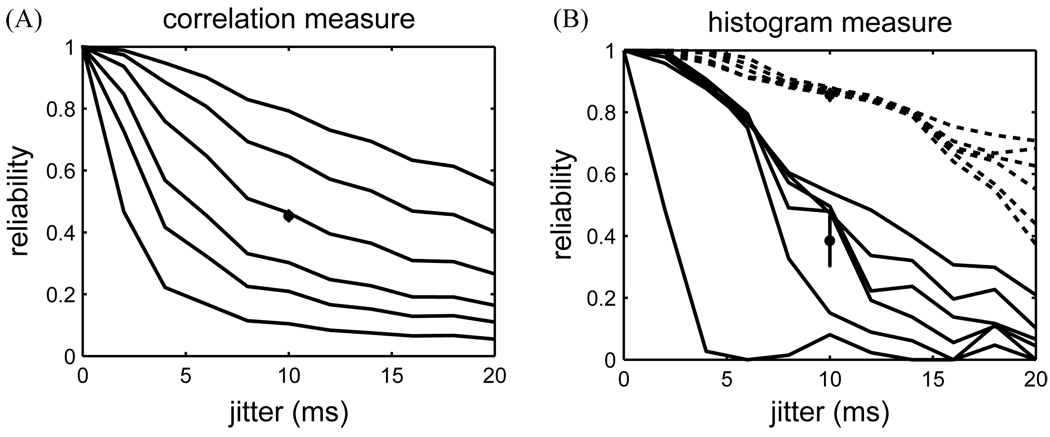
First, the reliability of the test data sets was characterized as a function of the amount of jitter in the data (Fig. 2). For the correlation measure, reliability degraded smoothly with jitter. For higher values of the filter width, σ_c, the reliability tended to be higher (Fig. 2A).

Fig. 2.

(A) Correlation-based reliability as a function of spike jitter. Different curves correspond to different filter width, σ_c (1, 2, 3, 5, 8, and 12 ms, bottom to top). In a control calculation, 25 different rastergrams with 10 ms jitter were generated and the reliability was computed for a filter width of 5 ms (circle, and standard deviation). (B) Histogram-based reliability as a function of jitter (bin_h = 2 ms). Different curves correspond to different smoothing filter widths, τ_h (1, 2, 3, 5, 8, and 12 ms, bottom to top). The solid curves were calculated with a threshold of θ_h = 1200 Hz. For the dashed curves the threshold was 600 Hz. Error bar based on 25 control data sets (σ_j = 10 ms, τ_h = 5 ms).

For the histogram measure, the degradation of reliability with jitter was less smooth (Fig. 2B). The solid set of curves was obtained for a histogram measure with high threshold. The dashed curves were obtained with the same parameters of the histogram measure, but a threshold value lowered by 50%. Measured with a higher threshold, reliability as a function of jitter depended on the smoothing filter width of the histogram measure, τ_h. The jaggedness of the curves of the histogram-based measure arose because, from one jitter value to the next, some events fell below threshold and hence changed the reliability estimate discontinuously. For a lower threshold (dashed curves), the reliability curves were highly similar and all reliability values were high. Although this measure was stable over a broad range of filter width parameters, the reliability values did not reflect the true jitter. Similar observations could be made for reliability as a function of jitter when varying the bin size of the histogram measure (data not shown). Altogether, the histogram-based measure proved sensitive to the choice of threshold.

4.2. Reliability with extra and missing spikes

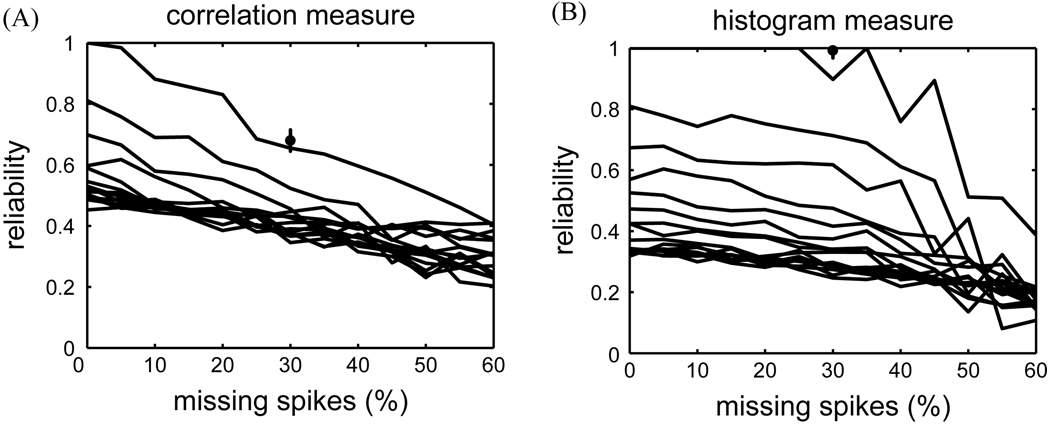
In Fig. 3 we compared how the reliability measures performed on the data sets that included extra and missing spikes. Fig. 3A shows the correlation-based reliability as a function of the percentage of missing event-spikes. Each curve was based on data sets with a fixed number of extra spikes per trial. Reliability values degraded smoothly as the number of missing spikes increased. The performance of the histogram-based measure on these data, shown in Fig. 3B, was similar. However, the degradation was less smooth and suffered from the same threshold choice sensitivity mentioned above.

Fig. 3.

(A) Correlation-based reliability as a function of missing spikes (σ_c = 5 ms). Different curves correspond to different levels of extra spikes (increasing from 0% to 30% from top to bottom). Error bar based on 25 different rastergrams (30% missing event-spikes, no extra spikes). (B) Histogram-based reliability as a function of missing spikes (τ_h = 5 ms, bin_h = 2 ms, θ_h = 1500 Hz). Different curves correspond to different levels of extra spikes (0% to 30% from top to bottom).

4.3. Dependence on the number of trials

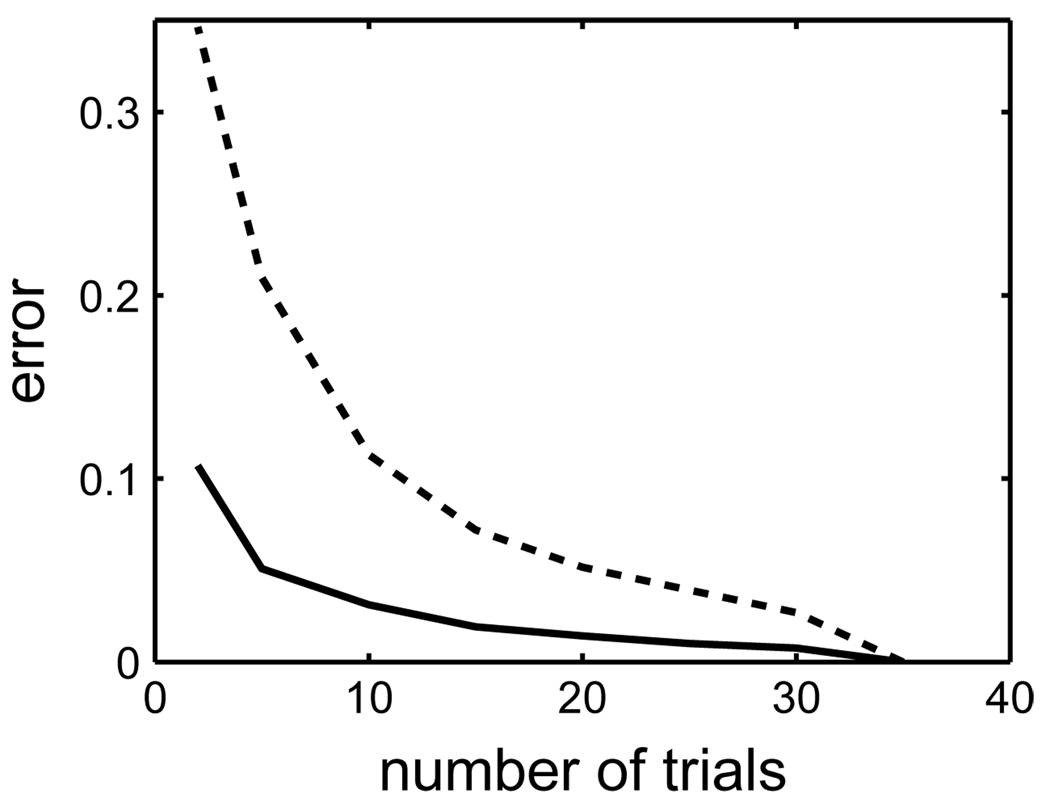
The estimate of spike timing reliability depended on the number of trials, N. The higher the number of trials, the smaller the (average) error in the estimate of reliability. Based on 208 surrogate data sets with extra and missing spikes (0–30% extra spikes, 0–60% missing spikes), we compared the errors in the reliability estimate between the histogram measure and the correlation measure as a function of the number of trials per data set, N. An error free reliability estimate would be based on an infinite number of trials; however, for practical reasons, we assume the estimate based on 35 trials to be the reference value for a given data set. The error for estimates based on fewer than 35 trials (N < 35) was the standard deviation of the reliability values based on N trials chosen randomly out of the full 35 trials. Fig. 4 depicts the average error as a function of the number of trials.

Fig. 4.

The average error in reliability for the correlation-based measure (solid line, σ_c = 5 ms) and the histogram-based measure (dashed line, θ_h = 1500/35 × N) as a function of the number of trials, N. The error in the correlation-based estimate was always more than a factor of two lower than the error in the histogram-based estimate.

The error rapidly decreased with increasing N for both reliability measures. However, the error in the correlation-based reliability estimate was less than half of the error in the histogram-based estimate. Hence, fewer trials need to be recorded in an experiment in order to obtain a good reliability estimate.

5. Conclusions

We introduced a new measure of spike timing reliability based on the correlation between pairs of individual responses of a neuron to repeated presentation of a stimulus. We showed that the new measure was robust in quantifying the reliability of data sets where the trial-to-trial variability was due to jitter in the timing of spikes or to the occurrence of additional or missing spikes. The correlation-based measure performed as well as traditional histogram-based measures [3] but needed 50% or fewer trials than the histogram-based measure for the same level of significance.

In contrast to traditional histogram-based measures it relies on only one parameter, σ_c, which is related to the precision of timing. σ_c can be varied to explore the data at different timescales. For a given data set, correlation-based reliability can be analyzed as a function of the filter width, σ_c. Regions of high and low slope indicate intrinsic times scales.

Histogram-based measures are not sensitive to slow variations in firing rate across cell trials, which might be characteristic of certain cells (e.g. stochastic switches between bursts and single spikes). A correlation measure, because it relies on individual trials rather than their average, is sensitive to such variations.