Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2010 Aug 24.
Published in final edited form as: Biol Theory. 2008 Apr;3(2):114–122. doi: 10.1162/biot.2008.3.2.114

Public goods with punishment and abstaining in finite and infinite populations

Christoph Hauert 1,2,*, Arne Traulsen 1,3, Hannelore Brandt 4, Martin A Nowak 1, Karl Sigmund 5,6
PMCID: PMC2927148  NIHMSID: NIHMS191308  PMID: 20740068

Abstract

The evolution and maintenance of cooperation in human and animal societies challenges various disciplines ranging from evolutionary biology, to anthropology, social sciences and economics. In social interactions, cooperators increase the welfare of the group at some cost to themselves whereas defectors attempt to free-ride and neither provide benefits nor incur costs. The problem of cooperation becomes even more pronounced when increasing the number of interacting individuals. Punishment and voluntary participation have been identified as possible factors to support cooperation and prevent cheating. Typically, punishment behavior is unable to gain a foothold in a population, while volunteering alone can efficiently prevent deadlocks in states of mutual defection but is unable to stabilize cooperation. The combined effects of the two mechanisms have surprisingly different consequences in finite and infinite populations. Here we provide a detailed comparison of the two scenarios and demonstrate that driven by the inherent stochasticity of finite populations, the possibility to abstain from social interactions plays a pivotal role, which paves the way for the establishment of cooperation and punishment.

Keywords: evolutionary game theory, cooperation, social dilemmas, public goods games, voluntary participation, punishment

1 Introduction

Cooperation is a recurrent theme in nature ranging from microbial colonies to human societies (Axelrod & Hamilton, 1981, Colman, 1995, Dugatkin, 1997, Nowak, 2006b, Trivers, 1971). Yet, the evolution of cooperative behavior that produces benefits to others at some cost to self is far from obvious under Darwinian selection. In fact, defectors that avoid the costs and produce no benefits are better off, while cooperators are doomed and bound to disappear. In evolutionary game theory such scenarios are captured by public goods games (Hardin, 1968, Kagel & Roth, 1995) where cooperators invest into a common good while defectors attempt to exploit the resource without contributing to it. However, if everybody defects they forego the public good: everybody would be better off had they cooperated. This describes a classical conflict of interest between the individual and the community arising in social dilemmas (Dawes, 1980, Hauert et al., 2006). The evolution and maintenance of cooperation in large groups of interacting individuals poses a challenging problem in evolutionary biology as well as in studies of human interactions (Boyd & Richerson, 1988, Hauert & Schuster, 1997).

It is well known that cooperation in public good situations requires positive or negative incentives discriminatingly directed at individual players (Olson, 1965). In particular, so called punishment directed by some of the players against cheaters in their group has proved to stabilise cooperation (Fehr & Fischbacher, 2004, Yamagishi, 1986). Such retaliatory peer-punishment can be viewed as a form of (direct or indirect) reciprocation. Clearly, defectors cannot invade a population of punishers (Boyd et al., 2003, Boyd & Richerson, 1992, Sigmund et al., 2001). But how can punishers establish themselves in a population of defectors? The emergence of punishing behaviour is viewed as a challenging problem. Interestingly, it can be resolved if participation in the public good interaction is optional rather than compulsory.

Voluntary participation means the game is extended from cooperators and defectors to include a third strategic type, the loners (Hauert et al., 2002b). Participating in public enterprises bears considerable risks because whether and how many participants turn out to be defectors is not known in advance. Loners are risk averse individuals that refuse to participate and, instead, rely on fixed autarkic resources. Recently, the combination of costly punishment and volunteering has led to some controversial results in infinite populations (Brandt et al., 2006, Fowler, 2005) but the issue has largely been resolved for the dynamics in finite populations and has revealed new insights relevant for real populations (Boyd & Mathew, 2007, Hauert et al., 2007). Here we provide a detailed analysis and comparison of the two different approaches.

2 Model & Methods

In order to model punishing and abstaining in public goods games we follow Fowler (2005) and Brandt et al. (2006) and consider the dynamics of four strategic types: the cooperators x, the defectors y, the loners z and the punishers w. In infinite populations (see section 2.1) x, y, z, w refer to the fraction of the population adopting the respective strategy (x + y + z + w = 1), whereas in finite populations (see section 2.2) of size M the capital letters X, Y, Z, W refer to the number of individuals adopting the respective strategy (X + Y + Z + W = M). A group of N individuals is randomly sampled from the population: cooperators, defectors and punishers participate in the public goods interaction, whereas the loners rely on a small but fixed payoff σ. Loners are not secluded but, for example, collect mushrooms instead of joining a hunting party. Cooperators and punishers invest a fixed amount c into the common good. The total investments into the common pool are then multiplied by a factor r and equally divided among all participants, irrespective of their contributions but excluding the loners. Thus, the common resource yields a net benefit of BS = rc(nx + nw)/S to defectors as well as BS − c to cooperators and punishers, where ni indicates the number of participants of type i in the sample and S = nx + ny + nw ≤ N denotes the effective number of participants, which varies based on the number of loners in the sample. If S = 1, the sole participant is forced to act as a loner and receives σ. Furthermore, punishers impose a fine β onto defectors at a cost γ with β > γ and, in addition, they also may punish cooperators because of their negligence and failure to punish defectors (if there were any) but the fines and costs of punishment are reduced to αβ and αγ with 0 ≤ α ≤ 1. In this context, cooperators are often termed second order free-riders because they avoid the costs of punishment. The loners payoff is assumed to satisfy (r − 1)c > σ > 0 such that loners are better off than groups of defectors (which score zero) but worse off than groups of contributors (mixtures of cooperators and punishers) obtaining (r − 1)c.

2.1 The Replicator Equation

The evolutionary process in infinite populations is traditionally studied using replicator dynamics (Hofbauer & Sigmund, 1998, Nowak & Sigmund, 2004, Taylor & Jonker, 1978). The state of the population is determined by the frequencies of the different types with x+y +z +w = 1, which confines the state space to the simplex S4. Individuals interact in groups of size N that are randomly formed according to multinomial sampling. Under replicator dynamics, every strategy that performs better than the population on average increases in abundance: ẋ = x(Px − P̄) etc. where Pi denotes the average payoff of strategy i and P̄ = xPx + yPy + zPz + wPw represents the average population payoff.

According to Brandt et al. (2006), which follows the approach in Hauert et al. (2002a), the average payoffs for each strategy are given by

Px=zN−1σ+B−F(z)c−w(N−1)G(y)αβPy=zN−1σ+B−w(N−1)βPz=σPw=zN−1σ︸+B−F(z)c︸−y(N−1)γ−x(N−1)G(y)αγ︸loner payoffpublic goods interactionpunishment (1a-1d)

with

B=rcx+w1−z(1−1−zNN(1−z))F(z)=1+zN−1(r−1)−rN1−zN1−zG(y)=1−(1−y)N−2.

Here B denotes the average benefit returned by the public good, F(z) indicates the effective costs of contributing to the public good and G(y) specifies the probability that the failure of cooperators to punish defectors is recognized by punishers. This occurs whenever a group consists of at least one cooperator, one defector and one punisher. Note that F(z) depends on the abundance of loners because they determine the number of participants in the public goods interaction and thus the effective group size S. The resulting effective costs of cooperation are given by (1 − r/S)c because the fraction r/S of the investment is returned to the investor. Thus, if loners abound the typical group size is small and cooperation becomes dominant whenever r > S, i.e. if cooperative investments have a positive net return (Hauert et al., 2002a, 2006). However, if S = 1, which happens with probability zN−1, no interaction partners are found and the single participant gets the loner’s payoff σ. We assume that r < N such that defection is the dominant solution in the absence of loners and punishers.

The dynamics of this system is bi-stable and the evolutionary outcome depends on the initial configuration of the population: either punishers disappear, which gives rise to endless oscillations of cooperators, defectors and loners (Hauert et al., 2002b), or a neutral mixture of cooperators and punishers establishes. In addition, the dynamics is structurally unstable, and hence cannot be relied upon to yield robust predictions. Thus, the analysis of the replicator dynamics is insufficient to draw final conclusions about the relative merits of volunteering and punishment. For a full analysis, we refer to Brandt et al. (2006) and use this scenario as a reference point for the following discussion of the dynamics in finite populations.

2.2 The Moran Process

In finite populations, the Moran process (Moran, 1962) captures the evolutionary dynamics in three elementary steps: birth, death and replacement. An individual is randomly selected for reproduction with a probability proportional to its payoff or fitness and produces a clonal offspring. Then, a randomly chosen individual (independent of fitness) is eliminated and replaced by the offspring. Thus, individuals with a higher fitness have better chances to reproduce but they can still be eliminated due to random drift. The overall population size is kept constant. Based on this process, the fixation probability of a single mutant in a homogeneous resident population can be determined, i.e. the probability that eventually the entire population adopts the mutant strategy. Traditionally, the Moran process is considered for constant fitness values assigned to residents and mutants. Only recently this approach was extended to include frequency dependent fitness (Nowak, 2006a, Nowak et al., 2004). In this framework, the fitness of an individual consists of two components 1 − s + sP: a static baseline fitness, which is normalized to one, and a dynamic component P, which depends on interactions with other members of the population. The selection strength s determines the relative contribution of the frequency dependent component to the overall fitness, i.e. s measures the importance of the game for overall success.

In the present context, the Moran process can be equivalently interpreted as an imitation process where a randomly selected individual adopts the strategy of a random member of the population, which is chosen with a probability proportional its fitness. In this case mutations do not refer to genetic changes but rather to random experimenting with different behavioral patterns.

Previous studies (Imhof et al., 2005, Nowak et al., 2004, Taylor et al., 2004, Traulsen et al., 2005) considered pairwise interactions among two or three strategic types. In the present case, new challenges arise because of the arbitrary interaction group size N: when sampling the interaction group, drawing one member affects the probabilities to select each strategic type in subsequent draws of the remaining members. In a population of size M = X+Y +Z+W where X, Y, Z and W refer to the number of cooperators, defectors, loners and punishers, respectively, the group formation process is given by a multivariate hypergeometric distribution such that the probability to interact in a group of nx cooperators, ny defectors, nz loners and nw punishers with nx + ny + nz + nw = N (nx + ny + nw = S) becomes

H(X,nx,Y,ny,Z,nz,W,nw)=(xnx)(yny)(znz)(wnw)(MN). (2)

Using Eq. (2) the average effective interaction group size S and its composition can be derived, to obtain the following average payoffs in finite populations:

PX=(ZN−1)(M−1N−1)σ+B−F(Z)c−WM−1(N−1)G(Y)αβPY=(ZN−1)(M−1N−1)σ+B−WM−1(N−1)βPZ=σPW=(ZN−1)(M−1N−1)σ︸+B−F(Z)c︸−YM−1(N−1)γ−XM−1(N−1)G(y)αγ︸loner payoffpublic goods interactionpunishment (3a-3d)

with

B=rcX+WM−Z−1(1−1N(M−Z)(M−(Z−N+1)(ZN−1)(M−1N−1)))F(Z)=1−rNM−NM−Z−1+(ZN−1)(M−1N−1)(rNZ+1M−Z−1+rM−Z−2M−Z−1−1)G(Y)=1−M−1M−Y−1(M−Y−1N−1)(M−1N−1)

In analogy to Eq. (1), B denotes the average return from the public good to defectors and F(Z) indicates the payoff difference between contributors (cooperators and punishers) and defectors before punishment. As before, G(Y) is the probability that the second order free-riders (cooperators) are found out and punished for their negligence. If S = 1, which happens with probability (ZN−1)/(M−1N−1), the single participant gets the loner payoff σ. In the limit M → ∞, Eq. (3) recovers Eq. (1) when converting strategy numbers into fractions using X → xM, etc.

In order to study finite populations analytically, we consider the limit of rare mutations, μ ≪ 1/M2 (Fudenberg et al., 2006, Imhof et al., 2005). In this limit, the population generally consists of a single type (in each generation μM mutants are produced and, typically, it takes less than M generations for a successful mutant to reach fixation). Occasionally a mutant appears and either disappears again or takes over the entire population before the next mutant appears. This restricts the evolutionary process to the edges of the simplex S4 where at most two strategic types are present at any one point in time. For this setting we derive the probabilities to find the system in either one of the four homogenous states with all cooperators, defectors, loners or punishers. This determines the relative time the system spends in each of the four corners of S4.

2.3 Dynamics along edges

In order to analyze the dynamics along the edges of S4, using Eq. (2) or Eq. (3) yields the payoffs in a population that consists of only two strategic types. For example, if the population consists of X cooperators and Y = M − X defectors, then the average payoffs to cooperators PXY and defectors PYX are given by:

PXY=∑k=0N−1H(X−1,k,M−X,N−1−k,0,0,0,0)(k+1Nr−1)c=rcN(1+X−1M−1(N−1))−cPYX=∑k=0N−1H(X,k,M−1−X,N−1−k,0,0,0,0)(kNrc)=rcNXM−1(N−1).

Note that for the calculation of the payoff to cooperators, there are only X − 1 cooperators left in the reservoir when sampling its N − 1 co-players and the reservoir size is M − 1. Similarly, the payoffs Pij of strategic type i competing against type j can be derived for all other possible pairings:

PXW=PWX=(r−1)cPZX=PZX=PZW=σPXZ=PWZ=(r−1)c−(ZN−1)(M−1N−1)((r−1)c−σ)PYZ=(ZN−1)(M−1N−1)σPYW=WM−1(N−1)(rcN−β)PWY=rcN(1+W−1M−1(N−1))−c−M−WM−1(N−1)γ

The above payoffs together with the selection strength s determine the transition probability that the number of individuals mi of type i increases by one, Tij+, or decreases by one, Tij−, (and the corresponding change in the count mj = M − mi of type j individuals):

Tij+=mi(1−s+sPij)M(1−s)+s(miPij+(M−mi)Pji)M−miM (4a)
Tij−=(M−mi)(1−s+sPji)M(1−s)+s(miPij+(M−mi)Pji)miM (4b)

Note that this requires that the overall fitness of all types is always positive (1 − s + sPij ≥ 0), which can be ensured by adding a suitable constant to all payoff values or by putting an upper limit on the selection strength s. The maximal selection strength is given by smax = 1/(1 − min Pij) for all strategic types i, j under consideration.

The transition probabilities Tij+,Tij− define a Master equation which describes the time evolution of the state of the system. From the Master equation, the fixation probability ρij of a single mutant strategy of type i in a resident population of type j can be derived (Karlin & Taylor, 1975, Nowak et al., 2004):

ρij=11+∑k=1M−1∏mi=1kTij−Tij+=11+∑k=1M−1∏mi=1k1−s+sPji1−s+sPij (5)

Finally, the fixation probabilities ρij define the transition probabilities of a Markov process between the four different homogeneous states of the population. The transition matrix A is given by:

A=(1−ρyx−ρzx−ρwxρxyρxzρxwρyx1−ρxy−ρzy−ρwyρyzρywρzxρzy1−ρxz−ρyz−ρwzρzwρwxρwyρwz1−ρxw−ρyw−ρzw) (6)

The stationary distribution is given by the normalized right eigenvector of A to the largest eigenvalue (which is one because AT is a stochastic matrix). This returns the probability to find the system in one of the four homogeneous states and concludes the analysis of the dynamics along the edges of S4.

3 Results

The analysis of the dynamics is restricted to the limiting cases of infinite populations (M → ∞) or rare mutations (μ → 0) but the general dynamics can be explored with simulations such as provided by the VirtualLabs (Hauert, 2007) or Brandt (2007). Before discussing the effects of finite population sizes on cooperation in voluntary public goods games with punishment, we analyze the effects and efficiency of the two mechanisms of volunteering and punishment separately.

3.1 Volunteering in public goods games

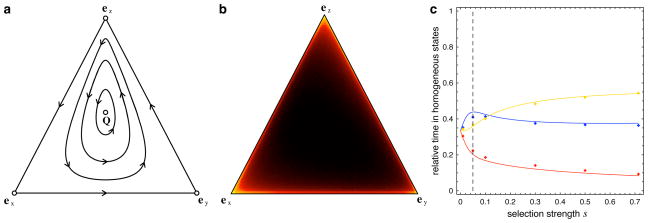
In infinite populations, the dynamics in voluntary public goods interactions without punishment is characterized by a rock-scissors-paper-type dominance of the three strategic types to cooperate, to defect and to abstain (loners). This cyclic dominance is reflected in the heteroclinic cycle along the boundaries of the simplex S3. For N > 2 the interior of S3 contains a unique fixed point Q, which is surrounded by closed periodic orbits (see Fig. 1a and Hauert et al. (2002a) for a detailed analysis). For our purposes it is important to note that only the homogeneous states with all cooperators and all defectors are hyperbolic saddle points but the loner’s corner ez is not and is neutrally stable to first order. The intuitive reason is that a single cooperator does not affect the payoffs in the population (nor does a single defector) because this cooperator will never find an interaction partner. It takes at least two cooperators to invade the loner population. As a consequence, the motion along the trajectory slows down in the vicinity of ez, which can be easily verified (Brandt, 2007, Hauert, 2007).

Figure 1.

Figure 1

Open in a new tab

Voluntary participation in public goods games as a mechanisms to promote cooperation in infinite and finite populations. a Evolutionary dynamics in infinite populations. The cyclic dominance of the strategies cooperate, defect and loner leads to a heteroclynic cycle along the boundaries of S3 and an interior fixed point Q that is surrounded by closed periodic orbits (N > 2). b In finite populations the population spends most of the time in the cooperator (28.3%), defector (12.7%) and loner (22.9%) corners, as compared to < 10−3% in states in the center of S3. The densities are color coded on a logarithmic scale with black indicating low, red intermediate and yellow high densities. c In the limit of rare mutations the dynamics is restricted to the boundary of S3. The probabilities to find the system in homogeneous states with all cooperators (blue), defectors (red) or loners (yellow) are shown as a function of the selection strength s. The dashed vertical line indicates the selection strength used in panel b. In the limit of neutral evolution (s → 0) the strategic differences disappear and all three states are equally likely. For s > 0 the system spends the least time in the defector state and significantly more time in the cooperator or loner states. Under weak selection the system even spends most of its time in the cooperative state. Simulation results of the average fraction of each strategic type confirm the analysis (colored dots). Parameters: N = 5, r = 3, c = 1, σ = 1; b M = 100, mutation rate μ = 10−3, s = 0.05; c M = 100, μ = 10−3, smax = 0.714.

In finite populations it seems natural to assume that the system is most likely found in a state with all loners. Interestingly, however, this is not the case (see Fig. 1b, c). Instead, in the limit of rare mutations, the system spends significantly less time in the defector corner and similar times in the cooperator and loner corners. Intuitively this can be understood by noting that the average population payoff is at its maximum if everybody cooperates and at its minimum if everybody defects. The fitness difference between a mutant defector and a resident cooperator tends to be much smaller than the fitness difference between a mutant loner and a resident defector. Hence, the mutant defector is more likely to be eliminated by random drift than the mutant loner and consequentially the system spends more time in the cooperator state than in the defector state. Under weak selection, the population may even cooperate most of the time. Simulations confirm this result even for higher mutation rates.

3.2 Punishment in public goods games

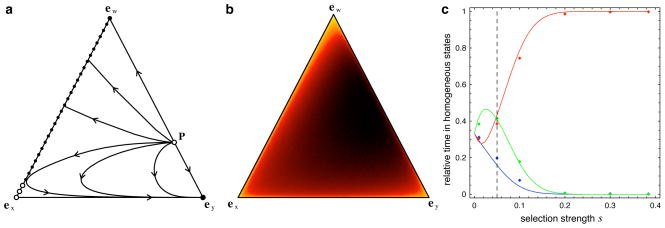
In infinite populations, punishment in compulsory public goods interactions (in the absence of loners) produces a bi-stable situation: depending on the initial configuration, the system either evolves to an asocial state where everybody defects or into a state where cooperation is enforced by punishment (see Fig. 2a). Along the boundary of the simplex S3 the bi-stability is reflected by an unstable fixed point P on the edge between punishers and defectors. The edge between cooperators and punishers consists of fixed points and those with w > wc = (N − r)/(βN(N − 1)) are stable Nash equilibria.

Figure 2.

Figure 2

Open in a new tab

Punishment opportunities in public goods games as a mechanism to promote cooperation in infinite and finite populations. a In infinite populations the dynamics is bi-stable and, depending on the initial configuration, the evolutionary end state is either a homogeneous population with all defectors or a neutral mixture of cooperators and punishers. The size of the basins of attraction are essentially determined by the location of the fixed point P along the punisher-defector-edge. b In finite populations the population spends slightly more time in the punisher corner (29.7%) than in the defector corner (28.4%) and significantly less in the cooperator corner (11.9%), as compared to < 10−4% in states in the center of S3. The densities are color coded on a logarithmic scale with black indicating low, red intermediate and yellow high densities. c In the limit of rare mutations the dynamics is restricted to the boundary of S3. The probability to find the system in homogeneous states with all cooperators (blue), defectors (red) or punishers (green) is shown as a function of the selection strength s. The analysis is confirmed by simulation results of the average fraction of each strategic type (colored dots) and the dashed vertical line indicates the selection strength used in panel b. The population is usually found in a state with all defectors except for weak selection where punishers manage to get the upper hand (c.f. panel b). Increasing the efficacy of punishment, i.e. increasing β, supports punishment directly by increasing the time spent in the punisher state as well as indirectly by reducing the maximal selection strength. Parameters: N = 5, r = 3, c = 1, γ= 0.3, β = 1, α = 0.1; b M = 100, mutation rate μ = 10−3, s = 0.05; c M = 100, μ = 10−3, smax = 0.385.

In this case, changes that arise due to stochasticity in finite populations are equally surprising (see Fig. 2b, c). In the limit of rare mutations (Fig. 2c), the system spends most of the time in states where everybody defects. Only for very weak selection or efficient punishment (γ ≪ β), punishers manage to enforce cooperation. This outcome changes when increasing the mutation rate (Fig. 2b). For mutation rates of the order of 1/M, punishers prevail. The intuitive reason for these differences is the slow drift dynamics along the neutral cooperator-punisher-edge. This leaves ample time for defectors to appear through mutation. As long as w > wc, mutant defectors actually promote punishment and push the system closer towards the punisher state. Thus, punishment can be stable provided that the punishers are challenged sufficiently often.

3.3 Volunteering and punishment in public goods games

In infinite populations, the combined effects of voluntary participation and punishment opportunities in public goods interactions lead to different conclusions based on different modeling techniques. Fowler (2005) reports that loners pave the way for punishers to establish cooperation, whereas Brandt et al. (2006) demonstrate that bi-stable situations arise, in which the initial configuration determines whether the evolutionary end state corresponds to endless cycles of cooperators, defectors and loners or whether a neutral mixture of cooperators and punishers evolves (everybody cooperates, no punishment). Moreover, the dynamics is structurally unstable, because neither the periodic orbits nor the fixed points are isolated. These differences arise because the former approach favors punishers in a twofold way. First, a single punisher (or cooperator), being the only participant in the public goods game, can profit from the public good instead of being reduced to the loner’s payoff and second, punishers punish cooperators even if there were no defectors in the interaction group. It seems that the latter approach presents a more convincing analysis.

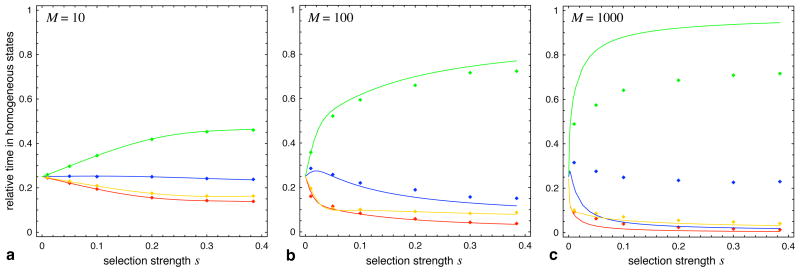
Interestingly, however, finite population sizes change the odds in favor of punishers. In the limit of rare mutations, the system spends most of the time in the homogeneous state with all punishers (see Fig. 3). This effect becomes more pronounced for larger population sizes such that for M = 1000 the system typically spends > 80% of the time in the punisher state. These results are supported by simulation data for small mutation rates. Thus, the original intuition of Fowler (2005) is vindicated in finite populations. However, in contrast to Fowler (2005), punishing second order free-riders (α > 0) turns out to have only marginal effects (Hauert et al., 2007).

Figure 3.

Figure 3

Open in a new tab

Punishment and abstaining in public goods games in finite populations. In the limit of rare mutations, the dynamics is restricted to the boundary of S4. The average fractions of cooperators (blue), defectors (red), loners (yellow) or punishers (green) are shown as a function of the selection strength for different population sizes M. Simulations where the fitness is determined through a single random interaction confirm the results (colored dots). The mutation rate μ is the same for all M and thus effects of mutations increases and deviations become larger when increasing the population size. The analytical approximations are expected to hold for μ < 1/M2 but the qualitative predictions remain valid for larger mutation rates (μ = 1/M in c). Parameters: N = 5, r = 3, c = 1, σ = 1, γ = 0.3, β = 1, α = 0.1, smax = 0.385; Simulations: μ = 10−3, a sampling times, T > 108, b, c T > 106.

In larger populations, the effects of random fluctuations become weaker and deterministic drift becomes increasingly important (Traulsen et al., 2005). Therefore, strong selection has much stronger effects in large populations. In tiny populations with M = 10 individuals, strong selection leads to approximately the same result as ten times weaker selection for M = 100 and a hundred times weaker selection for M = 1000 (see Fig. 3), which suggests that the relevant quantity characterizing the evolutionary process is given by sM. This is in agreement with other results for frequency dependent selection (Traulsen et al., 2006). Similarly, the product of population size and difference in fitness of two genotypes denotes the relevant evolutionary parameter in population genetics (Crow & Kimura, 1970).

4 Conclusions

In Nowak (2006b), five mechanisms have been proposed for the evolution of cooperation: direct reciprocity (Axelrod, 1984, Lindgren, 1991, Nowak & Sigmund, 1993, Trivers, 1971), indirect reciprocity (Nowak & Sigmund, 1998, 2005), kin selection (Grafen, 1985, Hamilton, 1964, Queller, 1985), group selection (Fletcher & Zwick, 2004, Maynard Smith, 1964, Traulsen & Nowak, 2006) and graph selection (Hauert, 2001, Nowak & May, 1992, Ohtsuki et al., 2006). Costly punishment (Clutton-Brock & Parker, 1995, Fehr & Gächter, 2002, Fehr & Rockenbach, 2003, Rockenbach & Milinski, 2006, Yamagishi, 1986) can be viewed as a special form of direct or indirect reciprocity. If you punish a person who has defected against you, then direct reciprocity is at work. If you punish a person who has defected against others (Fehr & Fischbacher, 2004) then indirect reciprocity is used.

Voluntary participation and the opportunity to punish defectors have been identified as potent mechanisms to promote and stabilize cooperation in public goods interactions in sizeable groups. The dynamics of model systems that combine both mechanisms have recently been analyzed for infinite populations (Brandt et al., 2006, Fowler, 2005) as well as in finite populations (Hauert et al., 2007). This approach does not require group selection (Boyd et al., 2003) or spatial structure (Brandt et al., 2003, Nakamaru & Iwasa, 2006) to establish cooperation and punishment. In agreement with earlier results (Imhof et al., 2005, Nowak et al., 2004, Traulsen et al., 2005), the stochastic components of the dynamics in finite populations produces qualitatively different results and requires to modify intuitions, which are based on infinite dynamics.

In voluntary public goods interactions, i.e. in the absence of punishers, mutation and selection in finite populations supports cooperation such that the system spends most of the time either in the state with all cooperators or all loners. This contrasts with expectations from infinite populations where loners should dominate because the dynamics slows down near the loner’s corner. Instead, in the limit of rare mutations, the systems spends roughly 40% of the time in the cooperator state as compared to 50% in the loner state and only 10% in states with all defectors. Conversely, in compulsory public goods games with punishment, i.e. in the absence of loners, finite populations tend to reduce cooperation such that the system spends little time in the cooperator or punisher states but most of the time in the state with all defectors (typically more than 80%). Only if fines are very high or punishment very cheap, punishers can rule the world. In that case, individuals will do whatever it takes to avoid punishment and just as Boyd & Richerson (1992) have put it: punishment can stabilize cooperation - or anything else. However, this does not explain the evolution of punishment behavior itself.

The dynamics changes considerably when considering the joint effects of voluntary participation and punishment opportunities. In infinite populations this leads to bi-stable dynamics where the evolutionary outcome depends on the initial configuration. However, in finite populations, volunteering creates an evolutionary pathway for establishing punishment behavior. The state with all loners acts as a junction where the system switches to the cooperative state or the punishing state with equal probabilities (Boyd & Mathew, 2007, Hauert et al., 2007). In both cases, cooperative behavior emerges because whenever the groups of participants are small, there is some probability that they consist, through sheer chance, mostly of cooperators or punishers. In each case, the group is highly successful, and will find many imitators. The difference is that in a population consisting of mostly cooperators, defectors will thrive, and the rock-scissors-paper-cycle will repeat itself. If the population consists mostly of punishers, it is much more stable, and can only get undermined by the slow process of non-punishing cooperators invading through random drift. Thus, finite populations promote the establishment of punishment. This emphasizes the pivotal role of loners in the evolutionary process. The possibility to abstain from public enterprises not only prevents economic stalemate by providing an escape hatch out of states of mutual defection but it also paves the way for establishing punishment mechanisms that are capable of largely stabilizing cooperation in sizeable groups. Cooperation (and punishment) is more likely to occur and persist if interactions are voluntary rather than compulsory.

Acknowledgments

Support from the John Templeton Foundation and the NSF/NIH joint program in mathematical biology (NIH grant R01GM078986) is gratefully acknowledged. A.T. is supported by the “Deutsche Akademie der Naturforscher Leopoldina” (Grant No. BMBF-LPD 9901/8134). K.S. and H.B. are supported by I-104-G15 (EUROCORES TECT). The Program for Evolutionary Dynamics (PED) at Harvard University is sponsored by Jeffrey Epstein.

References

  1. Axelrod R. The Evolution of Cooperation. Basic Books; New York: 1984. [Google Scholar]
  2. Axelrod R, Hamilton WD. The evolution of cooperation. Science. 1981;211:1390–1396. doi: 10.1126/science.7466396. [DOI] [PubMed] [Google Scholar]
  3. Boyd R, Gintis H, Bowles S, Richerson P. The evolution of altruistic punishment. Proc Natl Acad Sci USA. 2003;100:3531–3535. doi: 10.1073/pnas.0630443100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Boyd R, Mathew S. A narrow road to cooperation. Science. 2007;316:1858–1859. doi: 10.1126/science.1144339. [DOI] [PubMed] [Google Scholar]
  5. Boyd R, Richerson PJ. The evolution of reciprocity in sizeable groups. J theor Biol. 1988;132:337–356. doi: 10.1016/s0022-5193(88)80219-4. [DOI] [PubMed] [Google Scholar]
  6. Boyd R, Richerson PJ. Punishment allows the evolution of cooperation (or anything else) in sizable groups. Ethology and Sociobiology. 1992;13:171–195. [Google Scholar]
  7. Brandt H. Interactive simulations. 2007 http://homepage.univie.ac.at/hannelore.brandt/publicgoods/
  8. Brandt H, Hauert C, Sigmund K. Cooperation, punishment and reputation in spatial games. Proc R Soc Lond B. 2003;270:1099–1104. doi: 10.1098/rspb.2003.2336. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Brandt H, Hauert C, Sigmund K. Punishing and abstaining for public goods. Proc Natl Acad Sci USA. 2006;103 (2):495–497. doi: 10.1073/pnas.0507229103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Clutton-Brock TH, Parker GA. Punishment in animal societies. Nature. 1995;373:209–216. doi: 10.1038/373209a0. [DOI] [PubMed] [Google Scholar]
  11. Colman AM. Game Theory and its Applications in the Social and Biological Sciences. Butterworth-Heinemann; Oxford: 1995. [Google Scholar]
  12. Crow JF, Kimura M. An Introduction to Population Genetics Theory. Harper and Row; New York: 1970. [Google Scholar]
  13. Dawes RM. Social dilemmas. Ann Rev Psychol. 1980;31:169–193. [Google Scholar]
  14. Dugatkin LA. Cooperation among animals: an evolutionary perspective. Oxford University Press; Oxford: 1997. [Google Scholar]
  15. Fehr E, Fischbacher U. Third-party punishment and social norms. Evol Hum Behav. 2004;25:63–87. [Google Scholar]
  16. Fehr E, Gächter S. Altruistic punishment in humans. Nature. 2002;415:137–140. doi: 10.1038/415137a. [DOI] [PubMed] [Google Scholar]
  17. Fehr E, Rockenbach B. Detrimental effects of sanctions on human altruism. Nature. 2003;422:137–140. doi: 10.1038/nature01474. [DOI] [PubMed] [Google Scholar]
  18. Fletcher J, Zwick M. Strong altruism can evolve in randomly formed groups. J theor Biol. 2004;228:303–313. doi: 10.1016/j.jtbi.2004.01.004. [DOI] [PubMed] [Google Scholar]
  19. Fowler JH. Altruistic punishment and the origin of cooperation. Proc Nat Acad Sci USA. 2005;102 (19):7047–7049. doi: 10.1073/pnas.0500938102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Fudenberg D, Nowak MA, Taylor C, Imhof LA. Evolutionary game dynamics in finite populations with strong selection and weak mutation. Theor Pop Biol. 2006;70:352–363. doi: 10.1016/j.tpb.2006.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Grafen A. Oxford Surveys in Evolutionary Biology. Vol. 2. Oxford University Press; Oxford: 1985. A geometric view of relatedness; pp. 28–89. [Google Scholar]
  22. Hamilton WD. The genetical evolution of social behaviour I. J theor Biol. 1964;7:1–16. doi: 10.1016/0022-5193(64)90038-4. [DOI] [PubMed] [Google Scholar]
  23. Hardin G. The tragedy of the commons. Science. 1968;162:1243–1248. [PubMed] [Google Scholar]
  24. Hauert C. Fundamental clusters in spatial 2 × 2 games. Proc R Soc Lond B. 2001;268:761–769. doi: 10.1098/rspb.2000.1424. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hauert C. Virtuallabs: interactive tutorials on evolutionary game theory. 2007 http://www.univie.ac.at/virtuallabs.
  26. Hauert C, De Monte S, Hofbauer J, Sigmund K. Replicator dynamics in optional public goods games. J theor Biol. 2002a;218:187–194. doi: 10.1006/jtbi.2002.3067. [DOI] [PubMed] [Google Scholar]
  27. Hauert C, De Monte S, Hofbauer J, Sigmund K. Volunteering as red queen mechanism for cooperation in public goods games. Science. 2002b;296:1129–1132. doi: 10.1126/science.1070582. [DOI] [PubMed] [Google Scholar]
  28. Hauert C, Michor F, Nowak M, Doebeli M. Synergy and discounting of cooperation in social dilemmas. J theor Biol. 2006;239:195–202. doi: 10.1016/j.jtbi.2005.08.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Hauert C, Schuster HG. Effects of increasing the number of players and memory size in the iterated prisoner’s dilemma: a numerical approach. Proc R Soc Lond B. 1997;264:513–519. [Google Scholar]
  30. Hauert C, Traulsen A, Brandt H, Nowak MA, Sigmund K. Via freedom to coercion: the emergence of costly punishment. Science. 2007;316:1905–1907. doi: 10.1126/science.1141588. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Hofbauer J, Sigmund K. Evolutionary Games and Population Dynamics. Cambridge University Press; Cambridge: 1998. [Google Scholar]
  32. Imhof LA, Fudenberg D, Nowak MA. Evolutionary cycles of cooperation and defection. Proc Natl Acad Sci USA. 2005;102 (31):10797–10800. doi: 10.1073/pnas.0502589102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Kagel JH, Roth AE, editors. The handbook of experimental economics. Princeton University Press; Princeton: 1995. [Google Scholar]
  34. Karlin S, Taylor HM. First Course in Stochastic Processes. 2. Academic Press; London: 1975. [Google Scholar]
  35. Lindgren K. Evolutionary phenomena in simple dynamics. In: Langton CG, Farmer JD, Rasmussen S, Taylor C, editors. Artificial Life II; Proc. of the Santa Fe Institue Studies in the Sciences of Complexity; Redwood City, CA: Addison-Wesley; 1991. pp. 295–312. [Google Scholar]
  36. Maynard Smith J. Group selection and kin selection. Nature. 1964;201 (4942):1145–1147. [Google Scholar]
  37. Moran PAP. The Statistical Processes of Evolutionary Theory. Clarendon; Oxford, UK: 1962. [Google Scholar]
  38. Nakamaru M, Iwasa Y. The coevolution of altruism and punishment: role of the selfish punisher. J theor Biol. 2006;240 (3):475–488. doi: 10.1016/j.jtbi.2005.10.011. [DOI] [PubMed] [Google Scholar]
  39. Nowak MA. Evolutionary Dynamics. Harvard University Press; Cambridge MA: 2006a. [Google Scholar]
  40. Nowak MA. Five rules for the evolution of cooperation. Science. 2006b;314:1560–1563. doi: 10.1126/science.1133755. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Nowak MA, May RM. Evolutionary games and spatial chaos. Nature. 1992;359:826–829. [Google Scholar]
  42. Nowak MA, Sasaki A, Taylor C, Fudenberg D. Emergence of cooperation and evolutionary stability in finite populations. Nature. 2004;428:646–650. doi: 10.1038/nature02414. [DOI] [PubMed] [Google Scholar]
  43. Nowak MA, Sigmund K. A strategy of win-stay, lose-shift that outperforms tit-for-tat in the prisoner’s dilemma game. Nature. 1993;364:56–58. doi: 10.1038/364056a0. [DOI] [PubMed] [Google Scholar]
  44. Nowak MA, Sigmund K. Evolution of indirect reciprocity by image scoring. Nature. 1998;393:573–577. doi: 10.1038/31225. [DOI] [PubMed] [Google Scholar]
  45. Nowak MA, Sigmund K. Evolutionary dynamics of biological games. Science. 2004;303:793–799. doi: 10.1126/science.1093411. [DOI] [PubMed] [Google Scholar]
  46. Nowak MA, Sigmund K. Evolution of indirect reciprocity. Nature. 2005;437:1291–1298. doi: 10.1038/nature04131. [DOI] [PubMed] [Google Scholar]
  47. Ohtsuki H, Hauert C, Lieberman E, Nowak MA. A simple rule for the evolution of cooperation on graphs and social networks. Nature. 2006;441:502–505. doi: 10.1038/nature04605. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Olson M. The Logic of Collective Action. Harvard University Press; Cambridge MA: 1965. [Google Scholar]
  49. Queller DC. Kinship, reciprocity and synergism in the evolution of social behavior. Nature. 1985;318:366–367. [Google Scholar]
  50. Rockenbach B, Milinski M. Indirect reciprocity resolves the efficiency dilemma of costly punishment. Nature. 2006;444:718–723. doi: 10.1038/nature05229. [DOI] [PubMed] [Google Scholar]
  51. Sigmund K, Hauert C, Nowak MA. Reward and punishment. Proc Natl Acad Sci. 2001;98:10757–10762. doi: 10.1073/pnas.161155698. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Taylor C, Fudenberg D, Sasaki A, Nowak MA. Evolutionary game dynamics in finite populations. Bull Math Biol. 2004;66:1621–1644. doi: 10.1016/j.bulm.2004.03.004. [DOI] [PubMed] [Google Scholar]
  53. Taylor P, Jonker L. Game dynamics and evolutionarily stable strategies. Math Bio Sci. 1978;40:145–156. [Google Scholar]
  54. Traulsen A, Claussen JC, Hauert C. Coevolutionary dynamics: from finite to infinite populations. Phys Rev Lett. 2005;95:238701. doi: 10.1103/PhysRevLett.95.238701. [DOI] [PubMed] [Google Scholar]
  55. Traulsen A, Nowak MA. Evolution of cooperation by multilevel selection. Proc Natl Acad Sci USA. 2006;103 (29):10952–10955. doi: 10.1073/pnas.0602530103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Traulsen A, Nowak MA, Pacheco JM. Stochastic dynamics of invasion and fixation. Phys Rev E. 2006;74:011909. doi: 10.1103/PhysRevE.74.011909. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Trivers RL. The evolution of reciprocal altruism. Q Rev Biol. 1971;46:35–57. [Google Scholar]
  58. Yamagishi T. The provision of a sanctioning system as a public good. J Personal Soc Psychol. 1986;51:110–116. [Google Scholar]

RESOURCES