Discovery Through the Computational Microscope

Summary

All-atom molecular dynamics simulations have become increasingly popular as a tool to investigate protein function and dynamics. However, researchers are concerned about the short time scales covered by simulations, the apparent impossibility to model large and integral biomolecular systems, and the actual predictive power of the molecular dynamics methodology. Here we review simulations that were in the past both hotly disputed and considered key successes, namely of proteins with mainly mechanical functions (titin, fibrinogen, ankyrin, and cadherin). The simulation work covered shows how state-of-the-art modeling alleviates some of the prior concerns, and how unrefuted discoveries are made through the “computational microscope".

Introduction

The power of molecular dynamics (MD) simulations to make relevant discoveries on their own, i.e., without corroborating experimental evidence, is a hotly debated topic today and an issue for readers and editors of this journal. This topic is of pressing significance as many important research problems in modern cell biology require a combined experimental-computational approach and computing has to be a reliable partner. Indeed in many cases, experimental researchers must team up with MD experts who complement and resolve ambiguity in experimental data, as in the case of atomic force microscopy studies (Rief and Grubmüller, 2002; Zlatanova and van Holde, 2006; Sotomayor and Schulten, 2007; Prevost et al., 2009) or the analysis of macromolecular structures using electron microscopy (Saibil, 2000; Frank, 2006; Trabuco et al., 2008). Furthermore, it is often the case that only MD simulations can extend static structural data into the dynamic domain (Karplus and Petsko, 1990; Daggett and Levitt, 1993; Adcock and McCammon, 2006; Sotomayor and Schulten, 2007). Time-evolved snapshots of atomic coordinates, combined sequentially into sets called trajectories, result in astonishingly detailed “movies" of how a biomolecule behaves over time under a variety of tunable conditions. However, creation of such movies through MD simulations is computationally very demanding, the limited size of biomolecules simulated and the limited time-scale covered becoming an issue, e.g., when size and time scale of a simulation do not overlap with those of the corresponding experimental system. This limitation in the scope of MD simulations together with the well-known inaccuracies of force fields employed in simulations (see for example Freddolino et al. (2009) and Mackerell (2004)) begs then the question of whether computational studies are accurate enough to make genuine discoveries on their own.

Large system sizes and long timescales are two hurdles that MD simulations are constantly making gains to overcome. Recently, MD simulations have been performed on large macromolecular systems such as the ribosome (Sanbonmatsu and Tung, 2007; Villa et al., 2009) or entire viral capsids (Freddolino et al., 2006; Zink and Grubmüller, 2009). Moreover, smaller systems have been simulated for 10–100 µs (Freddolino et al., 2008, 2009; Freddolino and Schulten, 2009; Maragakis et al., 2008; Klepeis et al., 2009). On the one hand, we are still far from realistically simulating most integral cellular components, which often involve many million atoms, or from reaching simulation-wise the millisecond timescale relevant for the fastest cellular processes. Nevertheless, MD simulations are already often providing insights that guide basic and applied science, e.g., in the case of single molecule studies (Sotomayor and Schulten, 2007) or nanosensor development (Aksimentiev et al., 2008). To overcome the size and time scale limitation, MD descriptions have been simplified through so-called coarse-graining (Shih et al., 2006; Arkhipov et al., 2006; Klein and Shinoda, 2008; Yin et al., 2009) and biomolecular processes have been accelerated by applying external forces in so-called steered molecular dynamics (SMD) simulations (Izrailev et al., 1999; Isralewitz et al., 2001b, 2001a; Grubmüller, 2005), bridging the time-scale gap between experiment and simulation through a theoretical framework (Izrailev et al., 1997; Evans and Ritchie, 1997; Park and Schulten, 2004; Evans and Calderwood, 2007). Fortunately, there exist also cases where MD simulation and experimental observation of biomolecular processes truly overlap in regard to size and timescale, permitting direct comparison. Examples are mechanotransduction (Christensen and Corey, 2007) and protein mechanics (Sotomayor and Schulten, 2007), where typical time-scales are on the order of tens of microseconds (Sukharev and Corey, 2004; Shapovalov and Lester, 2004) and systems involving large biomolecules are now becoming accessible to large-scale MD simulations (Schulten et al., 2008). In these cases, SMD simulations are used to mimic forces that naturally arise in the context of the cell, or that are applied in atomic force microscopy (AFM) and optical tweezer experiments (Florin et al., 1994; Svoboda et al., 1993; Smith et al., 1996; Cluzel et al., 1996; Rief et al., 1997; Kellermayer et al., 1997).

Indeed, theorists and experimentalists have joined together to combine SMD simulations and AFM experiments with remarkable success (Rief and Grubmüller, 2002; Gao et al., 2006; Sotomayor and Schulten, 2007), relating structure, function, and observation to physical mechanisms that permit biopolymers to bear forces arising from natural cellular processes. Notable examples that have benefited from this combined approach include studies on the elastic behavior of the muscle protein titin (Marszalek et al., 1999), the extracellular matrix protein fibronectin (Gao et al., 2003; Craig et al., 2004), and the cytoskeletal proteins spectrin (Ortiz et al., 2005; Rief et al., 1999; Paramore and Voth, 2006) and ankyrin (Bennett and Chen, 2001; Sotomayor et al., 2005; Lee et al., 2006b; Li et al., 2006). In complementing observation into the structure and dynamics realm, modeling has become a veritable computational microscope.

In a previous review we described how simulations of titin, fibronectin, spectrin, and ankyrin repeats gave unique insights into the function of these proteins at the single molecule level (Sotomayor and Schulten, 2007). In this review we address the limitations of MD simulations by presenting new data and showcasing through examples the value of the computational microscope in the field of cellular mechanics. While there are multiple excellent examples of molecular dynamics simulations uniquely complementing experimental work (Carrion-Vazquez et al., 2003; Brockwell et al., 2003; Gräter et al., 2005; Arkin et al., 2007; Puchner et al., 2008), we focus here on three protein systems that have been extensively studied in our group. First we revisit SMD simulations of the muscle protein titin where technological advances extended the timescale accessible through molecular modeling by three orders of magnitude to microseconds. Next we turn to fibrinogen, the building block of blood clots, where SMD simulations of over 1 million atoms were reproducibly performed and used to interpret AFM experiments investigating the molecular basis for blood clot elasticity. Finally, we illustrate the predictive power of the MD methodology in case of ankyrin and cadherin protein mechanics and also briefly highlight examples in which simulations are used hand-in-hand with experiments to interpret data and further develop the MD methodology.

Simulated and Experimental Unfolding of Titin Ig-domains

SMD simulations have proven to be valuable in complementing force spectroscopy experiments, uncovering the molecular mechanisms governing protein elasticity. Due to the timescale limitation of MD simulations alluded above, the stretching velocities in computational modeling studies for a long time were many orders of magnitude higher than those employed in experiments. As a result, SMD simulations (stretching biomolecules faster than done in experiment) needed to apply forces that were larger than those experimentally recorded, raising the question whether unfolding events witnessed in simulation correspond mechanism-wise to the mechanical unfolding events measured. Here we consider this question for the protein titin.

Titin is the largest known protein in nature (Bang et al., 2001) and is believed to confer the passive elasticity that protects muscle fibers from mechanical injury (Tskhovrebova and Trinick, 2003; Granzier and Labeit, 2004). In humans, titin is composed of 300 modular domains, 90% of which share immunoglobulin (Ig) or fibronectin-type-3 (FN3) folds (Labeit and Kolmerer, 1995; Bang et al., 2001) with the remaining domains being composed of flexible insertion sequences such as proximal N2B and distal PEVK regions (rich in proline, glutamate, valine, and lysine) (Linke et al., 1998; Li et al., 2001; Ma et al., 2001). An initial understanding of titin’s mechanical properties arose from extensive single molecule force spectroscopy studies of isolated titin (Rief et al., 1997; Kellermayer et al., 1997; Carrion-Vazquez et al., 1999; Marszalek et al., 1999; Li et al., 2002; Fowler et al., 2002; Li and Fernandez, 2003; Williams et al., 2003; Garcia et al., 2008; Grutzner et al., 2009). From these studies a picture began to form of how titin reacts to mechanical stretching. Upon stretching, titin first elongates by reorienting, but not unfolding, its domains (an example of so-called tertiary structure elasticity as discussed in (Sotomayor et al., 2005; Lee et al., 2007; Sotomayor and Schulten, 2008), followed by extension of its natively disordered N2B or PEVK segments, and finally followed by sequential rupture of secondary structure elements in its Ig and FN3 domains (an example of secondary structure elasticity, e.g. (Lee et al., 2006a; Sotomayor and Schulten, 2007; Linke and Grutzner, 2008)). Yet, while these experimental studies conveyed how far titin can be stretched and how much force it can bear, there was insufficient data to ascertain what specific molecular mechanisms were responsible for granting titin its mechanical resilience. MD simulations offered an opportunity to shed light on the missing detail.

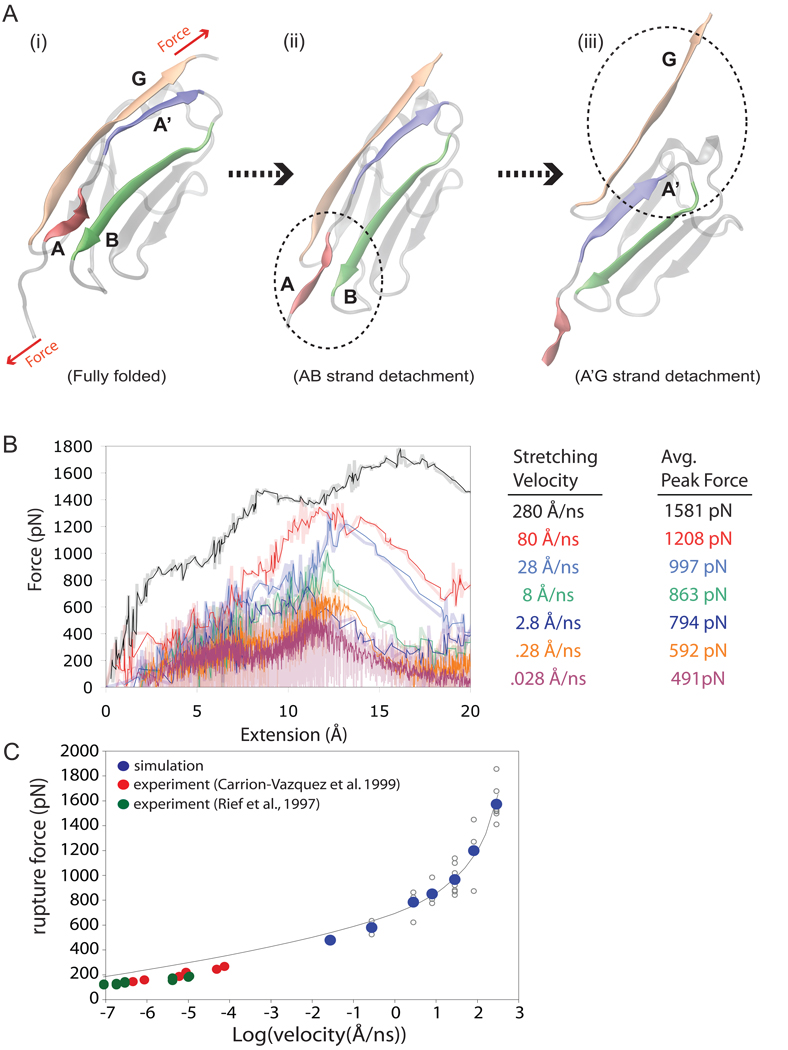
SMD simulations on titin’s I91 domain (formerly I27) revealed that the source of titin’s secondary structure elasticity lay in the architecture of I91’s terminal β-strands (Lu et al., 1998; Lu and Schulten, 1999, 2000; Gao et al., 2001, 2002; Best et al., 2003). Specifically, simulations showed that I91’s unfolding comes about through nearly synchronous breaking of a network of hydrogen bonds that stabilize the domain’s terminal β-strands. I91 is depicted in Figure 1A-i in its fully folded state. When I91 is stretched at a certain force, the β-strand pair called AB, shown in Figure 1A-ii, ruptures first. At this stage of unfolding, further rupture is prevented by the stabilization of a β-strand called A'G. Once A'G is disrupted at a very slightly higher force (see Figure 1A-iii), though, I91 quickly unravels completely. Simulations shed light on how the β-strand pairing involved in AB and A'G guard the titin domain against forced unfolding like two pieces of “molecular velcro".

Figure 1.

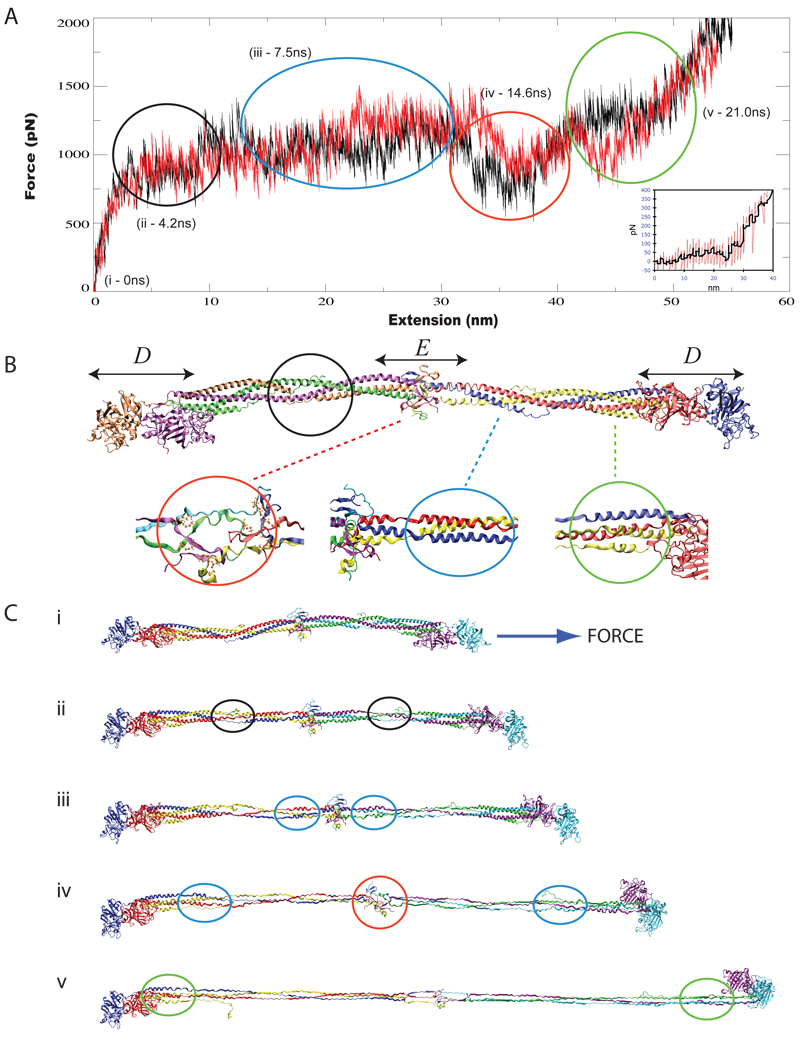
Steered molecular dynamics simulations for stretching fibrinogen. The force-extension curves derived from SMD simulations stretching a whole fibrinogen molecule (1,000,000 atom system) are shown in (A). The black trace is from the SMD simulation reported in (Lim et al., 2008) and the red trace is from a new simulation reported here. An AFM force-extension trace for a single fibrinogen molecule is shown in the inset (from Lim et al. (2008)). Shown in (B) is a cartoon representation of the most complete atomic structure of fibrinogen resolved to date (pdb code 1m1j), showing the distinct terminal D β-sheet globular domains encapsulating mirror-symmetric coiled-coil domains and a central domain, labelled E. SMD simulations stretching the coiled-coil domain of fibrinogen reveal a stepwise unraveling according to helical density. The regions of distinct helical density are also shown in (B), comprised of a two helix region (black circle), a three helix region (blue circle), and a four helix region (green circle). The central domain is denoted by a red circle. Snapshots of the fibrinogen molecule during simulation at time intervals (denoted (i) through (v), also shown in (B)) corresponding to the unraveling of specific regions are shown in (C).

How can one be certain, though, that overly fast simulations are capturing the same events, presumably governing biological function, as in the experiment? Many mechanisms first observed in simulations of titin have subsequently been confirmed with experiments, specifically in regard to the unfolding properties of its Ig- and kinase domains. Based on predictions from simulations that the segments of parallel β-strands AB and A'G are the force bearing components of I91, experimentalists engineered a mutant in which the A'G β-strand interaction was weakened; when this mutant was stretched using AFM (Marszalek et al., 1999), the characteristic two-stage (due to AB and A'G, but only AB contributing for the mutant) unfolding “hump" seen in the native state was abolished, corroborating the scenario predicted by MD. MD simulations of I91 also suggested a previously unknown role for water participating in the domain unfolding; specifically, it was observed that water molecules competed for interstrand hydrogen bonds on the surface of the protein, thereby lowering the unfolding barrier for protein unfolding (Lu and Schulten, 2000). This key discovery, made possible only through simulation, was previously considered to be an unimportant background event, but turned out to play a central role in mechanical unfolding. Subsequent force spectroscopy experiments have validated this prediction by demonstrating that water molecules and other osmolytes (both actively regulated in vivo) control the mechanical transition state structure of proteins (Dougan et al., 2008). Simulations also found that the catalytic site of titin’s C-terminal kinase domain could be opened without significantly unraveling the protein (Gräter et al., 2005). These predictions were later confirmed in AFM experiments (Puchner et al., 2008) which showed that mechanical strain to titin kinase activated ATP binding before the domain unfolded. In the same study, mutations to residues on titin kinase, identified in MD simulations to be involved with critical interactions with the phosphates on ATP, were verified in experiments to significantly reduce the ATP affinity of titin kinase, further illustrating the predictive power of molecular modeling.

A historic limitation of MD, however, was that computational capacity has restricted simulations so far to the nanosecond timescale, requiring the use of stretching velocities about six orders of magnitude above those employed in experiments. Since unfolding force depends on stretching speed, the protein rupture forces arising in simulation are significantly higher than those seen in AFM on the same protein (Evans and Ritchie, 1997). In an effort to bridge the gap between MD and experiment, we extended the time scale of SMD simulations of I91 by a thousand-fold, employing the most recent version of our group’s molecular dynamics program NAMD (Phillips et al., 2005). This permitted us to close the gap between computational and experimental stretching rates to nearly two orders of magnitude. Numerical details of these new simulations are described in Supplementary Materials.

Titin I91 was chosen for this study as it offers an abundance of experimental AFM (Linke and Grutzner, 2008) and molecular dynamics (Lu and Schulten, 2000; Best et al., 2003) data, and as the rupture barrier for I91 is easy to sample over multiple trajectories since it occurs within the first 10 percent of the extension needed to fully unfold the protein. Furthermore, a theoretical model, albeit a rather schematic one, for the rupture event is available that can account for a wide range of stretching velocities (Hummer and Szabo, 2003) connecting experimental and computational regimes (Carrion-Vazquez et al., 1999; Hummer and Szabo, 2003). The constant velocity SMD method utilized in our simulations mimics the force application in AFM experiments. The stretching velocities employed spanned a wide range; the fastest rate (280 Å/ns, or 28 m/s) is comparable to one previously employed in simulations (Lu and Schulten, 2000) on I91; the slowest rate applied in the new simulations is four orders of magnitude slower (0.028 Å/ns, or 0.0028 m/s). At a stretching velocity of 0.0028 m/s, it takes 1 µs to stretch I91 to the rupture point of the AB and A'G β-strands. Overall, I91 rupture was sampled using seven different stretching velocities ranging from 280 Å/ns (28 m/s) to 0.028 Å/ns (0.0028 m/s) (see Figure 1B). The simulations employing velocities of 28, 2.8, 0.28, and 0.028 m/s stretched I91 to a fully extended polypeptide, whereas in simulations employing velocities of 8, 0.8, and 0.0028 m/s only the first 25 Å of extension were sampled, which is just enough to capture the rupture of the AB and A'G β-strand pairs.

The force-extension curves of the first 20 Å extension are shown in Figure 1B for representative simulations at each of the seven different stretching velocities, reflecting the rupture of hydrogen bonding between β-strand pairs AB and A'G. The magnitude of the peak rupture forces, for each simulation and stretching velocity, are listed in Supplementary Materials. Across all runs, the average peak rupture forces varied from 1581 pN at v=280 Å/ns to 491 pN at v=0.028 Å/ns (Figure 1B). In each case, the rupture of I91, as seen in the force peak, occurs between 11 and 14 Å extension, consistent with previously reported I91 unfolding simulations. Furthermore, the forces reported here agree with those in simulations previously reported (Lu and Schulten, 2000) that produced peak rupture forces of 2100 pN (v = 500 Å/ns) and 1350 pN (v = 100 Å/ns).

The relationship between stretching velocity v and average rupture force F obtained in the SMD simulations was analyzed using an approximate model suggested by Hummer and Szabo, 2003 (illustrated in Figure S3). Although this model does not characterize well the force dependency of reaction rates (Schlierf et al., 2004; Garcia-Manyes et al., 2009a, 2009b) and had indeed been refined later (Dudko et al., 2003, 2006, 2008; Best et al., 2008; Guo et al., 2008; Dudko, 2009), it has been employed successfully to interpret AFM force vs. velocity measurements of I91 reported in (Carrion-Vazquez et al., 1999). The Hummer and Szabo, 2003 model is characterized by four parameters, κ_s (effective force constant, where k_BTκ_s = k_s is the spring constant of the pulling apparatus; k_B is the Boltzmann constant), k₀ (intrinsic, i.e., zero force, rupture rate), κ_m (stability parameter), and x_b (rupture extension). The positive result of our analysis is shown in Figure 1C where the force-extension curve resulting from the model is plotted over the wide range of velocities (10⁻⁷–10³ Å/ns) spanning simulation and experiment [results from Rief et al., 1997 and Carrion-Vazquez et al. 1999]. For the model we employed the same κ_s as in the SMD simulations, namely, k_BTκ_s = 208.4 pN/Å (T = 300 K); given that the effective spring constant in AFM experiments is smaller, namely, k_BTκ_s ~ 1 pN/Å (Carrion-Vazquez et al., 1999; Hummer and Szabo, 2003), the computed curve, as expected, lies slightly above the experimental force values. Figure 1C demonstrates that the microscopic model employed covers both simulation data and experimental data, i.e., all data fall on basically the same curve, implying that simulations describe the same mechanical mechanism as seen in AFM traces, and do so for all pulling velocities. The theoretical analysis underlying Figure 1C is described in detail in Supplementary Materials.

The high forces reported in earlier MD studies casted doubt on whether the unfolding phenomenon captured by experiments is the same as that being captured in the simulations. The results from our simulations show now that across a wide range of stretching velocities, the mechanism of I91 rupture remained unchanged. The results of MD simulations reported a decade ago have stood the test of time. The conclusions from this success, however, is not to trust fast simulations in general, as I91 is clearly a fortunate case with a rupture event induced through small extension. In case of rupture events requiring larger extension, fast stretching may direct a system into an alternative rupture pathway with then misleading conclusions. On the other hand, the naive opinion often voiced that higher (than experimentally observed) rupture forces in simulations imply an incorrect mechanism is proven wrong by the I91 example. This example, indeed, shows the computational microscope at its best: it extends and explains AFM observation, revealing the structural features actually involved in protein mechanics.

Reproducible Simulations of a Very Large System, Fibrinogen

Some mechanical proteins contain intricately interwoven components exhibiting separately very different elasticity. To learn how such proteins respond to stretching forces requires one to simulate the entire protein and its overall stretching, exacting a heavy toll on computational resources. Such simulations can push the atom count to well over a million, which prevents extended sampling. Is it worth the computational effort then, to perform an extremely large simulation and rely on results from just one trajectory? Here we review the case of fibrinogen, which required calculations on a system size of over one million atoms and serves as an example of how simulations of large systems have led to key discoveries concerning the mechanical behavior of proteins with complex architectures. This case also illustrates the outcome of a strenuous effort in sampling when each simulation is very costly.

Fibrinogen is a protein that comprises a main building block of blood clots. Blood clots are necessary to stem bleeding in the event of mechanical injury, but can also obstruct blood flow if they form or become lodged in a vessel, leading to life-threatening pathologies such as heart attack and stroke. Understanding the mechanical properties of a fibrin blood clot, therefore, is of tremendous importance for developing treatments to either disrupt clots which have blocked major vessels, or prevent them from forming in the first place (Weisel, 2004, 2005). Fibrinogen, schematically shown in Figure 2B, is converted to fibrin through peptide cleavage, forming then a mesh-like network that in concert with platelets, traps red blood cells to stem the flow of blood. During clot formation, fibrinogen molecules can bind both along the longitudinal and latitudinal axes (Doolittle, 1984; Weisel, 2005). Crystallography, spectroscopy, and biochemical studies have revealed that a fibrinogen molecule consists of several distinct domains arranged linearly (Yang et al., 2001), the central region of fibrinogen (called the E region, Figure 2B) being flanked on each side by long helical domains which themselves are capped at the ends with β-strand domains. AFM (Liu et al., 2006) and optical tweezer (Collet et al., 2005) studies have attributed remarkable elasticity to fibrin fibers, which are able to stretch two to six times their resting length before rupture. While such experiments reveal macroscopic information about the relative stiffness or elasticity of the linear fibril being stretched, they do not explain where stiffness or elasticity originate from in the protein and how the two properties can be chemically modified.

Figure 2.

Steered molecular dynamics simulations for stretching fibrinogen. The force-extension curves derived from SMD simulations stretching a whole fibrinogen molecule (1,000,000 atom system) are shown in (A). The black trace is from the SMD simulation reported in (Lim et al., 2008) and the red trace is from a new simulation reported here. An AFM force-extension trace for a single fibrinogen molecule is shown in the inset (from Lim et al. (2008)). Shown in (B) is a cartoon representation of the most complete atomic structure of fibrinogen resolved to date (pdb code 1m1j (Yang et al., 2001)), showing the distinct terminal D β-sheet globular domains encapsulating mirror-symmetric coiled-coil domains and a central domain, labelled E. SMD simulations stretching the coiled-coil domain of fibrinogen reveal a stepwise unraveling according to helical density. The regions of distinct helical density are also shown in (B), comprised of a two helix region (black circle), a three helix region (blue circle), and a four helix region (green circle). The central domain is denoted by a red circle. Snapshots of the fibrinogen molecule during simulation at time intervals (denoted (i) through (v), also shown in (A)), corresponding to the unraveling of specific fibrinogen regions, are shown in (C).

In order to understand the mechanisms behind fibrin elasticity, scanning electron microscopy (Brown et al., 2009), AFM experiments (Brown et al., 2007), and SMD simulations combined with AFM experiments (Lim et al., 2008) were used to yield a molecular-level picture of how blood clots respond to mechanical stretching. While initial efforts at characterizing the mechanical response of whole-molecule fibrinogen using MD simulations and AFM appear to have been successful, the conclusions generated relied on a single MD trajectory. In order to verify that simulations capture consistently the same mechanical unfolding events, we performed an additional SMD simulation to stretch fibrinogen, beginning from an equilibration point different from the one used in (Lim et al., 2008). The force-extension curve from the new simulation (shown in Figure 2A, red trace) agrees with and corroborates the observations from the earlier simulation and agrees with the AFM trace (shown in Figure 2A, black trace and inset, respectively). In principle the accuracy of simulation results benefits from increased sampling. The results reported here demonstrate, however, the utility and reproducibility of single simulation trajectories of very large systems where sampling multiple trajectories is extremely expensive computationally.

SMD simulations aid in the interpretation of AFM force-extension data. Force-extension curves from AFM experiments on single-molecule fibrinogen (Lim et al., 2008), shown in Figure 2A inset, exhibit a force plateau during which the majority of stretching takes place, interrupted by a dip in force (Figure 2A-iv). While one could speculate about the features observed in relationship to structural transformations without a means to visualize the actual sequence of events, one can go no further. Only the computational microscope, through simulations, revealed that the plateau phase in Figure 2A corresponds to coiled-coil extension, assigning each step in the force plateau to the specific part of fibrinogen being extended (see timepoints in Figure 2A). Fibrinogen’s coiled-coil helical domain is not uniform, but rather, has regions where the coils intertwine as a series of double-, triple-, and quadruple helices which are shown and circled in Figure 2B. The simulations showed that when fibrinogen is stretched from a relaxed state (Figure 2C-i), fibrinogen’s double helical region (Figure 2C-ii) unravels before its triple helical region (Figure 2C-iii), with the last region to unravel consisting of four bundled α-helices near the terminal D regions (Figure 2C-v). Furthermore, simulations were able to interpret a pronounced dip in the force extension curve following the plateau phase, correlating it to the partial unraveling of the central E domain. It is fair to say that the computational microscope played a crucial role, as important as experiment, in the elucidation of fibrinogen mechanics.

A Priori Prediction of Ankyrin and Cadherin Elasticity

The ultimate challenge for MD simulations is arguably the prediction of unknown properties of a biomolecular system, and the subsequent experimental corroboration of these predictions. The elasticity of ankyrin and cadherin repeats studied through all-atom MD simulations provide two examples in which modeling has been able to provide predictions, some of which are already confirmed through experiments (Sotomayor and Schulten, 2007).

Ankyrin repeats are 33-amino-acid motifs found in sets of four or more in the sequence of hundreds of proteins in all domains of life (Bork, 1993; Bennett and Baines, 2001). The architecture of a single ankyrin repeat is characterized by two antiparallel α-helices joined by a short loop. A longer, finger-like loop, links adjacent ankyrin repeats that stack in parallel to form an elongated and curved super-helical structure (Michaely et al., 2002; Mosavi et al., 2002) as shown in Figure 3A. Interestingly, large stacks of ankyrin repeats are found in proteins that have been hypothesized to play a mechanical role in the living cell. Ankyrin proteins, which contain 24 ankyrin repeats, provide a connection between the cytoskeleton of red blood cells and its membrane through a varied set of membrane proteins, potentially acting as molecular shock absorbers (Lee et al., 2006b). In addition, ion channels of the transient receptor potential (TRP) family, likely involved in mechanotransduction, feature large stacks of ankyrin repeats with up to 29 units at the cytoplasmic end (Christensen and Corey, 2007; Bechstedt and Howard, 2008; Gaudet, 2008). These ankyrin repeats were suggested to act as molecular springs (Howard and Bechstedt, 2004; Corey and Sotomayor, 2004), but the molecular elasticity of ankyrin repeats was unknown until SMD simulations were performed to probe the general mechanical properties of ankyrin domains.

Figure 3.

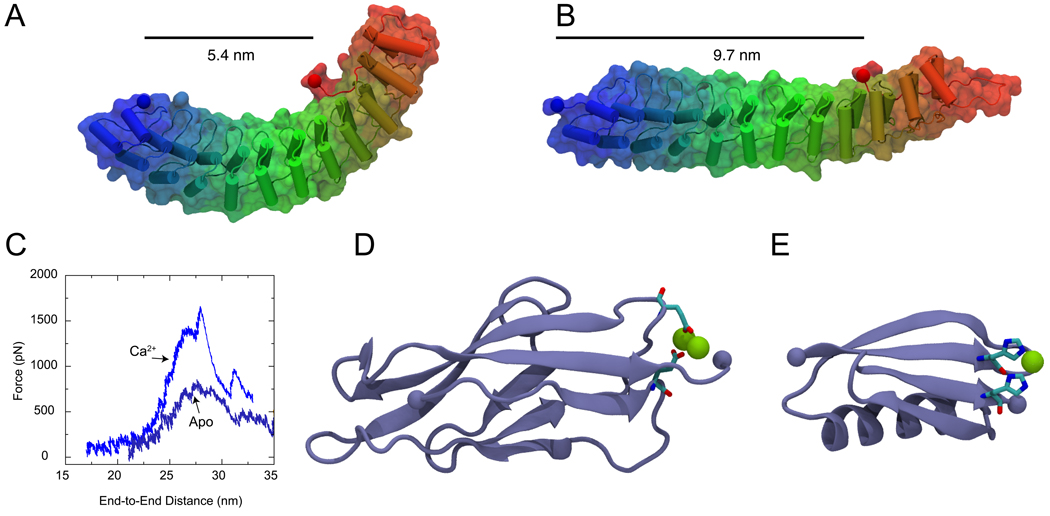
Tertiary structure elasticity of Ankyrin-R and divalent-controlled secondary structure elasticity of cadherin and GB1 proteins. (A) Snapshot of an Ankyrin-R domain in its crystallographic conformation (Michaely et al., 2002). The elongated and curved shape results from parallel stacking of 12 ankyrin repeats. The protein is shown in cartoon and surface representation. (B) Stretched conformation of Ankyrin-R obtained through SMD simulations (Sotomayor et al., 2005). The protein reversibly changes its shape without modifying its secondary structure elements. The end-to-end distance measured from terminal C_α atoms (taking into account the spectrin binding domain) is shown before and after stretching. (C) The unfolding force as a function of distance is shown for C-cadherin simulations performed in the presence (Ca²⁺) and absence (Apo) of calcium. A significant reduction in the force required to unfold cadherin repeats is observed in the absence of calcium. (D) Snapshot of the first C-cadherin repeat structure (Boggon et al., 2002) shown in cartoon representation. Calcium ions (shown in green) link β-strands A and F through highly conserved and charged amino-acids (shown in licorice representation). (E) Structure of GB1 protein illustrating the position of an engineered histidine-metal chelation site at position G8-55, based on (Cao et al., 2008). (F) Topology of cadherin repeats. A link between β-strands A and F is formed in the presence of Ca²⁺. (G) Similarly, a link between GB1 β-strands A and D is formed upon addition of Ni²⁺. The links enhance the mechanical stability of these proteins.

SMD simulations of proteins containing 4, 12, 17, and 24 ankyrin repeats revealed a novel, two-phase, elastic response (Sotomayor et al., 2005). Upon application of low force, large stacks of ankyrin repeats reversibly rearranged tertiary structure elements to straighten their overall shape (Figure 3A&B). This so-called tertiary structure elasticity provides a spring-like response that might be functionally relevant in mechanotransduction and the mechanics of red blood cells. The second phase of the ankyrin elastic response follows the predicted straightening of the protein shape and is characterized by sequential unfolding of individual repeats at large force. The unfolding of ankyrin repeats was characterized through constant-velocity SMD simulations reporting a saw-tooth pattern with force-peaks separated ~10 nm from each other, as well as constant-force SMD simulations featuring ~10 nm end-to-end distance steps. Controlled unfolding of individual repeats may provide a protection mechanism against large mechanical stimuli. The outcome of these simulations and the discovery of ankyrin’s mechanical properties was reported ahead of subsequent and independent AFM experiments (Lee et al., 2006b; Li et al., 2006). The experiments confirmed the linear elasticity of large stacks of ankyrin repeats, as well as the stepwise unfolding of individual repeats observed in simulations. The role played by ankyrin repeats in direct, in vivo, mechanotransduction remains to be established (Christensen and Corey, 2007; Bechstedt and Howard, 2008; Gaudet, 2008). However, ankyrin now serves as an archetypical example of the elastic properties featured by other repeat proteins (Zachariae and Grubmüller, 2006, 2008).

The original ankyrin simulations were performed using an aggressive, but rather standard, multiple-time stepping protocol that allowed one to achieve the multi-nanosecond time-scale required to observe ankyrin’s conformational changes. In this protocol, interactions involving covalent bonds are computed every time step (1 femtosecond), while van der Waals interactions are computed every other time step, and the more slowly varying electrostatic interactions are computed every fourth time step. Employing efficiency enhancing measures, such as multiple-time stepping, may lead to numerical inaccuracies which result in a slow temperature drift over the course of a simulation (Bishop et al., 1997; Izaguirre et al., 2001; Ma et al., 2003). Because SMD simulations are best performed in the microcanonical (NVE) ensemble to avoid artificial viscosity in the system, this temperature drift cannot be easily controlled using standard thermostats. This leads to numerical errors, e.g., to an energy increase and, hence a temperature increase, as reported and briefly discussed in (Sotomayor et al., 2005). Thus, criticism about the accuracy and validity of the ankyrin simulations was raised. To address this temperature increase, additional simulations were carried out for the present study that decreased the integration time steps resulting in rather impractical, i.e., very long, computing times (Sotomayor, 2007). These control simulations yielded the same ankyrin elastic properties as reported in (Sotomayor et al., 2005), while the increase in temperature was drastically reduced (less than one degree Celsius during six nanoseconds) and energy was well conserved (to better than 0.5%). The results of these calculations reveal that employing short and uniform discrete timesteps (such as 1 fs) for covalent bonds, short-range nonbonded interactions, and long-range electrostatic forces minimize energy drift for simulations performed in the NVE ensemble. Moreover, such calculations permit one to match the amount of work done during constant force SMD simulations to the increase of total energy in the system (Sotomayor, 2007), confirming the accuracy and validity of the reported simulations of ankyrin. Details are described in Supplementary Materials.

While ankyrin simulations provide a clear cut case in which predictions from simulations were successfully tested a posteriori through experiments, the study of cadherin elasticity provides a more subtle, but equally impressive, example of a priori prediction. Cadherin repeats are made of about 100 amino-acids forming a greek-key motif with seven β-strands organized in two β-sheets (Shapiro et al., 1995b, 1995a) (Figure 3D). These cadherin repeats are arranged in series and form large and elongated extracellular domains with 5 to 30 units featuring highly conserved calcium binding motifs at the linker regions between repeats (Boggon et al., 2002). Cadherin proteins are known to mediate calcium-dependent cell-cell adhesion (Takeichi, 1990; Gumbiner, 2005; Leckband and Prakasam, 2006) and have been implicated recently in inner-ear mechanotransduction (Corey, 2007; Kazmierczak et al., 2007). In both cases the elasticity of cadherin domains is likely to be functionally relevant, but the molecular details and the role played by calcium in cadherin elasticity was only discovered through simulations (Sotomayor et al., 2005; Sotomayor and Schulten, 2008).

Equilibrium and SMD simulations performed on the largest crystal structure of a cadherin molecule containing five repeats (Boggon et al., 2002) revealed several known and unknown properties that are likely to hold for all cadherin repeats (Sotomayor and Schulten, 2008). First, equilibrium simulations showed how a set of five cadherin repeats conserves its shape and behaves as a stiff rod when calcium binding motifs are completely loaded with this divalent ion. On the other hand, the set of repeats quickly loses its shape and behaves as a flexible chain with repeats moving independently from each other in the absence of calcium. These findings are in agreement with experiments showing that calcium rigidifies cadherin domains (Pokutta et al., 1994) and give confidence that simulations can accurately describe cadherin dynamics (see also (Cailliez and Lavery, 2005, 2006)). In addition, the simulations revealed that the availability of certain residues essential for cell-cell adhesion depends on the presence of calcium, a prediction that remains to be tested. SMD simulations also showed how calcium ions protect cadherin repeats from mechanical unfolding, predicting furthermore an increase in the unfolding force of cadherin repeats in the presence of calcium (Figure 3C).

Although there is no direct experimental test for the role of calcium in the forced unfolding of cadherin repeats, recent AFM experiments (Cao et al., 2008) have confirmed that divalent ions can enhance protein mechanical stability through a mechanism that closely resembles the one observed in cadherin simulations. SMD simulations (Sotomayor et al., 2005) showed how calcium ions bridging different β-strands through interactions with charged residues protect cadherin repeats from mechanical unfolding (Figure 3C,D&F). In a similar fashion, engineered bi-histidine metal chelation sites linking β-strands of GB1 (Figure 3E&G) were shown to increase mechanical unfolding forces by as much as 100 pN in the presence of divalent ions (Cao et al., 2008). This elegant experimental study indirectly and independently proves the underlying molecular mechanism discovered through cadherin simulations, namely, divalent ions can act as “staples” between different regions of a protein and enhance its mechanical properties. The discovery of such mechanisms through simulations may guide engineering of proteins with desired mechanical properties (Li, 2008).

In the case of ankyrin and cadherin the computational microscope did not only provide atomic resolution images of structural transformations resulting from mechanical forces, but it also measured quantitative properties before experiments could: the extremely soft elasticity for ankyrin and the calcium-induced stiffening of cadherin.

Discoveries Through Simulation

The work reviewed here not only demonstrates how MD simulations can bring about genuine discoveries that shed light on important cellular processes, but also that computational methods and capabilities continuously evolve to bridge the gap between experiment and theory. Nano- to microsecond SMD simulations of titin I91 reveal how hydrogen bonds control its secondary structure elasticity, and at the same time provide a strong argument against concerns that SMD simulations stretch proteins “too fast.” Simulations of fibrinogen, a large and complex protein with various architectural motifs arranged in series, demonstrate the feasibility of employing large and costly simulations for interpreting ambiguous experimental data by revealing how the number of helices forming a coiled-coil determines a hierarchy of mechanical strengths and the overall elastic response of the protein. In addition, ankyrin and cadherin simulations revealed how the rearrangement of structural motifs within a protein, without modification of the protein secondary structure, results in tertiary structure elasticity. Cadherin simulations also show how divalent ions can control secondary and tertiary structure elasticity of proteins, a behavior observed through AFM experiments on engineered GB1 proteins as well. Overall, simulations can cast light on the basic architectural principles of molecules which explain fundamental cellular mechanics and might eventually direct the design of proteins with desired mechanical properties. Most importantly, beyond the understanding gained regarding the molecular mechanisms of force bearing proteins, these examples serve to demonstrate that incessant advancements of MD methodology bring about discoveries stemming from simulation rather than from experiment. Molecular modeling, while useful as a means to complement many experimental methodologies, is rapidly becoming a tool for making accurate predictions and, thereby, discoveries that stand on their own. In other words, it is becoming a computational microscope.