Abstract
Detection and classification of ventricular complexes from the electrocardiogram (ECG) is of considerable importance in Holter and critical care patient monitoring, being essential for the timely diagnosis of dangerous heart conditions. Accurate detection of premature ventricular contractions (PVCs) is particularly important in relation to life-threatening arrhythmias. In this paper, we introduce a model-based dynamic algorithm for tracking the ECG characteristic waveforms using an extended Kalman filter. The algorithm can work on single or multiple leads. A ‘polargram’ - a polar representation of the signal - is introduced, which is constructed using the Bayesian estimations of the state variables. The polargram allows the specification of a polar envelope for normal rhythms. Moreover, we propose a novel measure of signal fidelity by monitoring the covariance matrix of the innovation signals throughout the filtering procedure. PVCs are detected by simultaneous tracking the signal fidelity and the polar envelope. Five databases, including 40 records from MIT-BIH arrhythmia database, are used for differentiating normal, PVC, and other beats. Performance evaluation results show that the proposed method has an average detection accuracy of 99.10%, aggregate sensitivity of 98.77%, and aggregate positive predictivity of 97.47%. Furthermore, the method is capable of 100% accuracy for records that contain only PVCs and normal sinus beats. The results illustrate that the method can contribute to, and enhance the performance of clinical PVC detection.
Index Terms: Characteristic waves, Electrocardiogram (ECG), Extended Kalman filter (EKF), Premature ventricular contraction (PVC), Signal quality, Signal fidelity, Wave-based dynamical model
I. Introduction
Cardiovascular diseases (CVDs) are the leading single cause of death in the developed world and are responsible for more than 30% of all deaths in most countries. For instance, the American Heart Association (AHA) recently reported that nearly 80 million people in the U.S.A. were burdened by some form of CVD, of which eight million experienced myocardial infarction, or a ‘heart attack’. Additionally, CVDs were the underlying cause of one in every 2.8 deaths in 2008 [1]. The detection of CVD and the determination of the underlying etiology of the disease for prevention and treatment is therefore a crucial task. Identifying premature ventricular contractions (PVCs) in Holter recordings or during monitoring is of particular interest. PVCs result from irritated ectopic foci in the heart’s ventricles, and are independent of the pace set by the sinoatrial node. Recent studies have shown that the occurrence of PVCs is indicative of increased risk of sudden cardiac death, and is linked to mortality when associated with myocardial infarction [2]. The presence of PVCs has also been shown to be associated with an increased total mortality in some patient subgroups, suggesting that a high frequency of PVCs is a marker of a more severe disease process, rather than the provocateur of a terminal electrical event. Events that occur after a PVC are alos of interest, and in particular, the rate of acceleration and deceleration of the heart rate immediate after a PVC has shown to be more effective than ejection fraction in stratifying patients post-myocardial infarction [3]. Therefore, accurate detection of PVCs is of great significance for stratifying patients at high risk and predicting life-threatening ventricular arrhythmias.
Accurate, noninvasive diagnosis of and screening for CVD has been a challenge. Electrocardiogram (ECG) analysis is routinely used as the first tool for initial screening and diagnosis in clinical practice. The ECG as a noninvasive and low-cost method provides valuable clinical information regarding the rate, timing and regularity of the heart [4]. Analysis of the ECG remains the benchmark method for cardiac arrhythmia detection. Several methods have been proposed in the literature for automatic detection and classification of various arrhythmias. The vast majority of the developed techniques includes algorithms based on time domain features [5], ECG morphology and heartbeat interval features [6], principal component analysis (PCA) [7], hidden Markov models [8]–[10], self organizing maps [11], wavelets and filter banks [12], [13], statistical classifiers [14] and neural networks (NN) [15], [16]. On the other hand, efforts have been aimed at coping with the specific problem of PVC detection. Most works in this field employ NNs to classify the PVCs after performing a suitable processing for the extraction of discriminant features [17]–[22], and some authors underline the advantages of the competitive classifiers [18], [23]. Although these methods have shown promising results, they have several disadvantages. First, the methods suffer from the problem of finding efficient feature sets [19]–[22]. Second, since there are various choices for selecting the network structure to achieve an acceptable performance, finding the optimum architecture has not a unique solution [20]–[22]. The use of symbolic dynamics analysis [24] and Gaussian processes [25] for PVC detection has also been reported.
Recently, Bayesian filters were proposed for ECG denoising [26] and filtering cardiac contaminants [27]. The state-space model used in this approach was inspired from the model proposed by McSharry et al [28], who suggested the use of Gaussian mixture models to generate synthetic ECGs. It was later found that by some modifications, the filtering framework developed by Clifford et al [29] and Sameni et al [26] could be used as a parameter-based framework for model-based ECG filtering [29], [30], simultaneous denoising and compression [29], [31], and beat segmentation [29], [32].
In this paper, we propose the tracking of the parameters of an updated Gaussian wave-based representation of the ECG by employing a Bayesian estimation procedure through an extended Kalman filter (EKF). A new polar representation is then introduced together with a procedure to track rhythm changes using the innovation sequence provided by the EKF. The paper is organized as follows. In section II, the wave-based dynamical model is presented. Section III provides relevant background on the theory of the EKF. In section IV, our proposed algorithm for PVC detection is explained in detail. Section V is devoted to simulation results. Finally, a discussion and conclusions are provided in section VI.
II. Wave-Based ECG Dynamical Model
A simple interpretation for modeling an ECG record is to model every heart beat as a combination of finite characteristic waveforms (CWs), each of which represented by the sum of Gaussian kernels. In other words, we assume that every cycle of a heart beat recorded on an ECG can comprise a finite number of CWs, (typically the P wave, QRS complex and T wave). However, every CW reflects the electro-physiologic functioning of a specific part of the heart, which in turn facilitates the analysis of the ECG events. This idea originates from the synthetic nonlinear dynamic model that was proposed for generating artificial ECGs by McSharry et al [28]. The model generates a three-dimensional trajectory which consists of a circular limit cycle that is pushed up and down as it approaches each of the turning points in the ECG (P, Q, R, S and T) whose centers are the center of each Gaussian. The simplified discrete version of the model in the polar plane is given by [26]:
| (1) |
where δ is the sampling period, ω = 2πf, f is the beat-to-beat heart rate and Δθik = (ϕk − θik)mod(2π). The phase, ϕ, is a saw-tooth shape signal that is expected to be zero at R-peaks, and is linearly assigned a value between −π and π for each sample between two successive R-peaks. αi, bi and θi are the amplitude, angular spread and location of the Gaussian functions, respectively, and η represents random additive white noise which accounts for baseline wander effects and other additive sources of process noise. It can be seen that the ECG signal s is represented by a sum of Gaussian functions, whose locations are controlled by the phase signal ϕ. In order to model the separate events of an ECG signal, the second dynamical equation in (1) can be divided into separate state variables, each of which has a similar behavior to the original equation. However, the separation and the corresponding increase in the dimensionality facilitate the analysis of different events in the ECG signal.
Assuming the presence of three distinct CWs, corresponding to the P wave, QRS complex and T wave, the ECG signal is divided into three components. In addition, to have a more accurate representation of the CWs, the number of Gaussian functions can be varied. Clifford et al proposed an extension of the model which used an arbitrary number of Gaussians, with 2 Gaussians for each asymmetric turning point (P and T) [29]. Since Gaussians are symmetric, asymmetric turning points require more than one Gaussian and that two is the minimum number in this case and therefore the best choice, as we want to minimize the number of parameters for computational simplicity. Accordingly, P and T waves are characterize by two Gaussian kernels to account for bi-phasic P waves and the asymmetric nature of the T wave at low to medium heart rates. In contrast, the inclusion of more than one kernel for Q, R, and S is of negligible importance. Specifically, Sayadi and Shamsollahi showed that minimum five kernels are essential for preserving the morphological features in the EKF filtered signal [31]. However, increasing the number of Gaussians has a negligible effect on the filtering performance, yet provides a slightly improved compression ratio [30], [31]. Consequently, we adopted 7 Gaussian kernels to model an ECG beat. The modified model is given by:
| (2) |
where ηP, ηC and ηT represent the baseline perturbations of the P wave, QRS complex and T wave, respectively.
III. Bayesian State Estimation Through Extended Kalman Filter
Having derived the state space representation for the ECG signal, the process equations of a Bayesian framework are formed. Relating the ECG signal as an observation to the state variables in the left side of state-space model (2) is now straightforward, since the CWs are summed up to form the ECG. The observed noisy phase φk and noisy amplitude zk of the ECG are given by:
| (3) |
where u1k and u2k are the observation noises of the ECG in the phase and spatial domains, respectively. Using the wave-based dynamical model (2) as the process equations and the observation relations (3), the state variables vector, xk and the observation vector, yk, the process noise vector, wk, and the observation noise vector, vk, are defined, respectively, as:
| (4) |
The wave-based dynamic model, equation (2), is a nonlinear function of the state and process noise vectors. Therefore, nonlinear extensions of the Kalman filter (KF) are required for estimating the state vector. Our proposed framework is built upon an extended Kalman filter structure for its simplicity and improved numerical stability over other Bayesian filters [33]. In order to use the KF formalism for this system, it is necessary to derive a linear approximation of (2) near a desired reference point (x̂k, ŵk, v̂k), to obtain the following linear approximate model:
| (5) |
where f is the state evolution function, equation (2), and g represents the relationship between the state vector and the observations, equation (3). The linear approximate coefficients in (5) are given by [34]:
| (6) |
In order to implement the EKF, the time propagation and the measurement propagation equations are summarized as follows [34]:
| (7) |
where is the a prior estimate of the state vector, xk, at the kth stage using the observations y1 to yk−1, and is the a posteriori estimate of this state vector after using the kth observation yk. and are defined in the same manner to be the estimations of the covariance matrices, in the kth stage, before and after using the kth observation, respectively. In addition, Qk=E{wkwkT} and Rk=E{vkvkT} are the covariance matrices of the process noises and measurement noises, respectively, and w̄k = E{wk}, v̄k = E{vk} [35]. As it can be seen in (7), the key idea of the EKF is to linearize the nonlinear system model in the vicinity of the previous estimated point, and to recursively calculate the filter gain Kk, the innovation signal rk and the state covariance matrices and from the linearized equations, while the KF time propagation is performed via the original nonlinear equations [36].
IV. Bayesian Detection of PVC
A PVC is a morphological abnormality that generally only appears in a small number of the ECG cycles and imposes a rhythm change in the normal ECG pattern, so that the P wave vanishes by the occurrence of a dominant wide QRS followed by a dominant T wave. This morphological change can lead to large errors in the Gaussians functions’ locations. In this case the EKF estimations are not expected to be satisfactory. However, the benefit of the Gaussian mixture representation is that the effect of each Gaussian term vanishes very quickly (in less than the ECG period), meaning that the errors are not propagated to the following ECG beats [26]. Moreover, by monitoring the state estimates’ covariance matrices and the variations of the innovation signals, it is possible to detect such unexpected abnormalities. Therefore, in this section we define some signal fidelities by tracking the covariance matrix of the innovation signal throughout the filtering procedure to detect unexpected morphological changes, such as a PVC. We also introduce a new polar representation to distinguish PVCs from other rhythm changes.
A. Monitoring the signal fidelity
In practice, due to the Gaussian assumption on the noise sources and the initial state vector values, the state estimate entries of should lie within the envelope of the square roots of their corresponding diagonal entries in for the majority of the time. Therefore, by monitoring the variance of the state estimations, it is possible to detect these morphological changes [33].
Another approach to provide a means of monitoring the fidelity of the filter is to update the values of Qk and Rk, which is practically convenient to monitor the covariance matrix of the innovation signal throughout the filtering procedure and to compare it to the innovation covariance matrices estimated by the KF [37]. Specifically, with a diagonal (or diagonalized) noise covariance matrix of Rk, the following term can be formed for the ith ECG measurement, which we call the signal fidelity:
| (8) |
where is the second entry of the zero-mean innovation vector of rk defined in (6), corresponding to the kth ECG measurement, N is the length of the averaging window, and is the KF estimated variance of for CWs, given by:
| (9) |
where is the 2nd row of the Mk matrix defined in (7), and are the 2nd, 3rd and 4th entry of , respectively. Similarly, and are the 2nd, 3rd and 4th column of the matrix, respectively, and is the second diagonal entry of Rk. In fact, γCW is an average of the variances of the N recent ECG innovations, normalized by their KF estimated variances of the corresponding CWs. This formulation originates from the proposal of Sameni et al [26] to use the KF estimated variance for improving the filtering performance. However, since we are intended to investigate the fidelity for every characteristic component, in the current approach, the original formulation is modified to provide three signal fidelities corresponding to three CWs. It is worth noting that as long as the ECG morphology remains normal, γi ≈ 1. Values much greater than unity indicate that the innovation signal variance is being underestimated by the KF, while values close to zero indicate that the innovation signal variance is being overestimated. Sameni et al benefited from this property of γi to adaptively modify the KF noise parameters to ensure the filter stability and to achieve better filtering performances in low SNR scenarios [26]. However, in the current approach, we monitor the γCW’s to detect any significant rhythm change in the ECG signal, which will affect the P-QRS-T morphology. In addition, unlike the original model (1), the wave-based model (2) enables us to define three γCW corresponding to each CW. Hence, the morphological changes may be simply identified and localized by monitoring the γCW signals. Three adaptive thresholds, thrCW, corresponding to three γCW signals are used to detect the fidelity peaks. The value of thrCW is defined to preserve 95% of the γCW energy, and is at least 3 times the mean value of γCW. In other words, with L be the length of the signal fidelity, the thresholds should satisfy the following conditions:
| (10) |
The best values of the energy and multiplier of the mean value of γCW were found by changing all possible values over the used database.
As a disadvantage, the innovation sequences are affected not only by morphological changes of the observation signals, but also by local noise artifacts and filter divergences [37]. Hence, in order to identify the PVCs using γCW, we need a symptom of rhythm change for discrimination between artifacts and real rhythm changes. In the next section we introduce a polar representation using the estimations provided by the EKF and address how to use this representation for PVC rhythm identification.
B. Polargram formation and envelope extraction
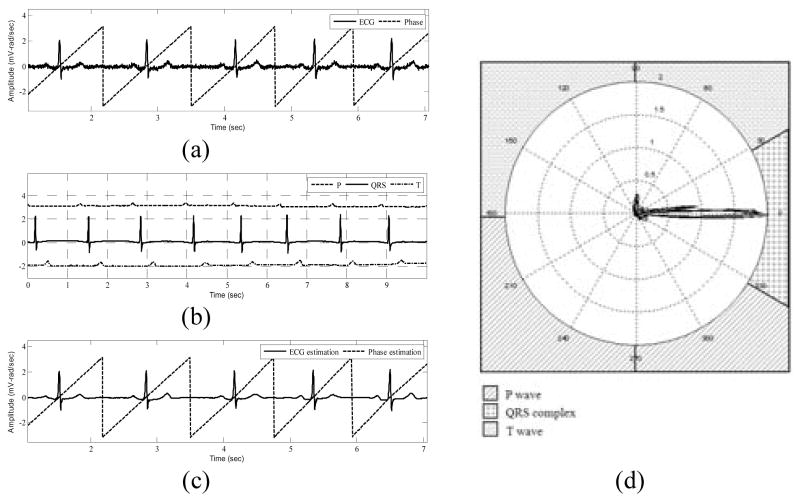
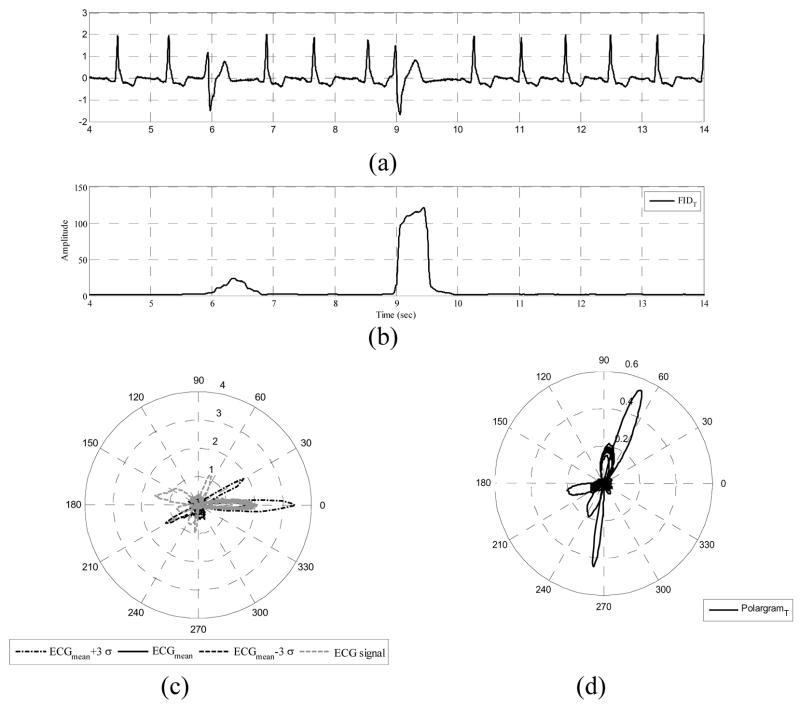
The wave-based ECG dynamical model (2) suggests that the ECG signal is considered as a combination of three characteristic waveforms. Using a Bayesian filter structure, each of these CWs, as well as the phase signal, can be tracked in time. A polar representation for the ECG signal, which we call polargram, can be obtained using the 2D vector [ϕk (P +C +T)k]′ at each time instance, k. By simply plotting the samples of the summed CWs, as the amplitude, and their corresponding phase values, a polargram for the whole ECG signal is obtained. The polargram clearly shows the beat to beat variations during different ECG cycles. In addition, by analyzing a specific portion of the polar plane, it is possible to investigate the inter-beat variations for every CW. This is because in the phase signal construction, the R-peak is always assumed to be located at θR = 0 and the ECG contents lying between two consecutive R-peaks are assumed to have a phase between − π and π [26]. Visual inspection of various ECG signals shows that the QRS complex lies in the range of [−π/6, π/6]. Hence, the preceding P wave and the proceeding T wave will occur in the range of [−π, −π/6] and [π/6,π], respectively. Fig. 1 shows a typical normal ECG signal and the corresponding phase signal, the estimations provided by the EKF and the polargram with the corresponding partitioning. In fact, the polargram is simply the polar plot of (P +C +T)k vs. ϕk, and the idea of partitioning the polargram is the key to identifying PVCs from normal sinus beats.
Fig. 1.
EKF estimations and polargram formation for a typical normal ECG signal. (a) ECG noisy record and the corresponding phase signal, (b) CW estimation provided by EKF4, (c) The estimated phase and filtered ECG signals using EKF4, (d) Polargram with the CW partitioning included.
As stated before, the morphological changes imposed by PVC occurrence lead to large errors in the Gaussian kernels’ locations, which result in unsatisfactory filtering performance. In other words, the PVC morphology has minimum amount of phase overlap with the underlying morphology of the normal ECG signal. Hence, if we specify a specific span in the polargram, any undesired change in the morphology of the signal would lie out of this span. Using the mean ( ) and the standard deviation (σECG(θ)) of this new representation, we define a polar envelope which spans between the upper and lower ranges of in the polar plane. Hence, any morphological changes are expected to happen outside this envelope.
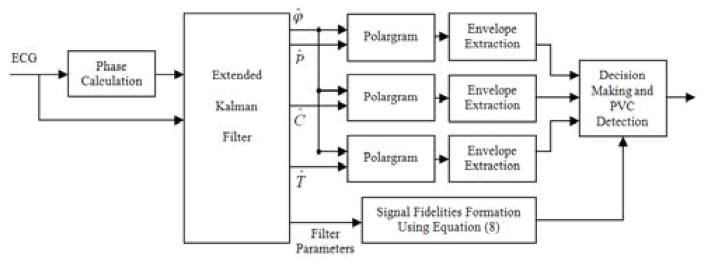
In order to classify PVCs and other abnormal beats, we can take advantage of the CW parameter estimations provided by the EKF. Since we have the estimations of the CWs, as well as the phase signal, it is possible to have 3 different polargrams corresponding to P, QRS and T. In other words, the 2D vectors [ϕk Pk]′, [ϕk Ck]′ and [ϕk Tk]′ provide three separate polar paths for all time instances, k. Any morphological changes are detected by monitoring γCW, and their corresponding envelope . However, to verify the PVCs, one should search the CW polargrams for the absence of a P wave together with the increase in the width of QRS complex and T wave polar paths. The overall PVC detection algorithm is illustrated in figure 2, in which the phase calculation block is simply an R-peak location detector, followed by linear assigning of a phase value between −π and π to the intermediate samples [26]. The decision making block uses the polargrams and the signal fidelities to detect PVC occurrence. In fact, we use equation (10) to compute the values of thrCW using the γCW signals. Afterwards, the thresholding is performed to locate γCW peaks. Finally, the polargram is examined for the occurrence of cycles outside the polar envelope in different partitions. If this occurrence holds for all polargrams and the corresponding γCW passes the threshold, then the beat is determined to be a PVC.
Fig. 2.
General block diagram of the proposed PVC detection algorithm.
V. Results
The proposed algorithm was implemented in MATLAB®. The MIT-BIH Arrhythmia Database [38], [39] was used to study the performance of the proposed method. The performance of the KF is influenced by the initial value for the state vector, as well as the covariance matrices of the process and the measurement noise. Hence, we employ the initialization procedure described in [26] and [31]. Accordingly, the angular frequency ω, is set to ; where is the average RR-interval of the whole signal. In order to estimate the initial values for the Gaussian kernels, a typical nonlinear optimization scheme such as the Levenberg-Marquardt procedure [40],[41] is performed on the mean ECG ( ) and the standard deviation (σECG(θ)) [29]. Similarly, the covariance values of Qk are found by calculating the magnitude of the deviation of the parameters of the Gaussian functions around the estimated mean, that best model the acceptable deviations of the mean ECG within the upper and lower ranges of . In a similar manner to [26], we set , and to the mean variance of baseline perturbations. The values of and are found from the deviations of the inactive segments of the ECG, around the corresponding CW portion.
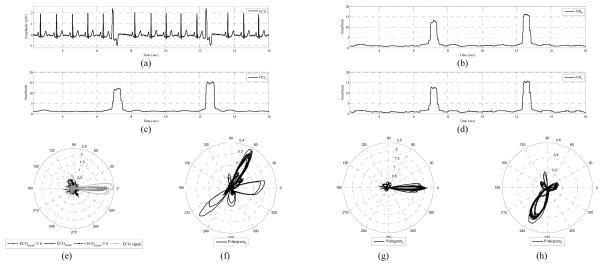
Fig. 3 shows a typical ECG signal with PVCs included, the γCW’s and the polargrams. The envelopes of normal rhythms are also provided, which excludes the PVCs. Visual inspection reveals that these exclusions correspond to the peaks of γCW, as was expected. Moreover, two PVCs are obvious in all CW polargrams, as well as in all γCW’s, see Fig. 3(f)–(h).
Fig. 3.
Elements of PVC monitoring provided by the Bayesian framework. (a) ECG record 119, (b) γP, (c) γC, (d) γT, (e) signal polargram and the polar envelope, (f) P wave polargram, (g) QRS complex polargram, and (h) T wave polargram.
As discussed in the previous section, γCW is sensitive to any morphological changes. However, the benefit of the proposed wave-based model is that it provides 3 different γCW s, each of which monitors the fidelity of the corresponding CW estimation, and is dependant on the corresponding CW rhythm change. Hence, unlike a PVC which imposes a dominant peak in all the γCW s, other morphological changes are expected to be tracked in a specific γCW. Fig. 4 shows the γCW s, ECG polargram and the T-polargram for a 17 beats segment of an ECG signal. The segment has two PVCs (3rd and 11th beats), three aberrated atrial premature beat (5th, 7th and 14th beats) and two non-conducted P wave abnormalities, i.e. blocked atrial premature beats (the last 2 beats). It can be seen that all the γCW s locate the PVC beat, as well as the aberrated atrial premature beat, which have different morphologies compared to the normal cycles. However, these two abnormalities are classified correctly in the polargram, since only the PVC spans outside the envelope. In contrast, the blocked atrial premature beats are identified only in γT, and have no effect on the outside of the polargram.
Fig. 4.
Effects of PVC, aberrated atrial premature beat and blocked atrial premature beat on signal fidelities and polargram. (a) ECG record 201, (b) γCW signals, (c) signal polargram, (d) T wave polargram.
For performance evaluation we chose 40 ECG records with the same lead configuration, i.e. modified lead II, which contains 5 types of signals; records with only normal beats (type A), records that contain only normal beats and PVCs (type B), records with no PVCs (type C), records with no normal beats (D) and records consisting normal beats and multiple arrhythmias (type E). We quantified our classifier performance using the most common metrics found in literature: accuracy, sensitivity, and positive predictivity. Accuracy (Ac) is perhaps the most crucial metric for determining overall system performance, and is defined as follows:
| (11) |
where Ne and Nt represent the total number of classification errors and beats in the file, respectively. To express how successfully a classifier recognizes beats of a certain class without missing them, sensitivity (Sn) is used. Likewise, to measure how exclusively it classifies beats of a certain type, positive predictivity (+P) is used. These two metrics are given by:
| (12a,b) |
In these equations, TP, FP, and FN denote true positives, false positives and false negatives, respectively. Similar to [19], to evaluate the overall performance, the averages are weighted according to the number of beats of each class that were present in a file. The weighted measure is written as:
| (13) |
where nbi is the number of beats for the ith record, nf is the total number of records, and is the value of a specific measure for the ith record in the class “CL”. The file-by-file comprehensive results are provided in Table I. The results show the capability of the proposed wave-based Bayesian framework for PVC identification among other beat types. Performance evaluation results of type A signals shows that normal beats are accurately detected. It can be seen that for type B records, where no other abnormality than PVC is presented, the detection algorithm achieves an accuracy, sensitivity and positive predictivity of 100%. In other words, the algorithm is fully capable of discriminating PVCs and normal beats. Likewise, the results for type C records show that the method is capable of classifying normal beats and other abnormalities in the absence of PVC. In a similar manner, the analysis of type D records illustrates that the algorithm is still reliable for PVC detection, in absence of normal beats. Finally, for type E signals, where a mixture of abnormalities is often presented in the ECG, the PVC detection results are very promising. It can be seen that in most cases, the sensitivity of PVC detection, as well as the positive predictivity of other beat types, is equal to 100% which demonstrates that the PVCs are identified with minimum error and the algorithm misses no PVCs. The overall performance evaluation results show a weighted average Sn and +P of 98.77% and 97.47%, respectively. Evaluation results for the identification of other beat types is also well in the acceptable range, however, the polar-envelope-based decision making should be modified to incorporate a wide range of abnormalities, which is beyond the scope of the current study.
Table I.
Comprehensive Results for PVC Detection Using the Proposed Algorithm.
| Type | Record | Nt | Ac (%) | Normal |
PVC |
Other |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nb | Sn (%) | +P (%) | Nb | Sn (%) | +P (%) | Nb | Sn (%) | +P (%) | ||||
| A | 115 | 1952 | 100.00 | 1952 | 100.00 | 100.00 | 0 | --- | --- | 0 | --- | --- |
| 122 | 2474 | 100.00 | 2474 | 100.00 | 100.00 | 0 | --- | --- | 0 | --- | --- | |
| B | 106 | 2027 | 100.00 | 1507 | 100.00 | 100.00 | 520 | 100.00 | 100.00 | 0 | --- | --- |
| 119 | 1987 | 100.00 | 1543 | 100.00 | 100.00 | 444 | 100.00 | 100.00 | 0 | --- | --- | |
| 123 | 1517 | 100.00 | 1514 | 100.00 | 100.00 | 3 | 100.00 | 100.00 | 0 | --- | --- | |
| 221 | 2427 | 100.00 | 2031 | 100.00 | 100.00 | 396 | 100.00 | 100.00 | 0 | --- | --- | |
| 230 | 2255 | 100.00 | 2254 | 100.00 | 100.00 | 1 | 100.00 | 100.00 | 0 | --- | --- | |
| C | 101 | 1864 | 100.00 | 1859 | 100.00 | 100.00 | 0 | --- | --- | 5 | 100.00 | 100.00 |
| 103 | 2083 | 100.00 | 2081 | 100.00 | 100.00 | 0 | --- | --- | 2 | 100.00 | 100.00 | |
| 112 | 2537 | 99.96 | 2535 | 100.00 | 99.96 | 0 | --- | --- | 2 | 50.00 | 100.00 | |
| 113 | 1794 | 100.00 | 1788 | 100.00 | 100.00 | 0 | --- | --- | 6 | 100.00 | 100.00 | |
| 117 | 1534 | 99.93 | 1533 | 100.00 | 99.93 | 0 | --- | --- | 1 | 0.00 | 100.00 | |
| 212 | 2747 | 99.82 | 922 | 99.46 | 100.00 | 0 | --- | --- | 1825 | 100.00 | 99.73 | |
| 220 | 2046 | 98.10 | 1952 | 99.39 | 98.63 | 0 | --- | --- | 94 | 87.23 | 75.23 | |
| D | 107 | 2136 | 99.91 | 0 | --- | --- | 59 | 96.61 | 100.00 | 2077 | 100.00 | 99.90 |
| 109 | 2530 | 99.96 | 0 | --- | --- | 38 | 100.00 | 97.44 | 2492 | 99.96 | 100.00 | |
| 118 | 2277 | 100.00 | 0 | --- | --- | 16 | 100.00 | 100.00 | 2261 | 100.00 | 100.00 | |
| 214 | 2260 | 100.00 | 0 | --- | --- | 256 | 100.00 | 100.00 | 2004 | 100.00 | 100.00 | |
| E | 100 | 2271 | 99.43 | 2237 | 100.00 | 99.42 | 1 | 100.00 | 100.00 | 33 | 60.61 | 100.00 |
| 102 | 2185 | 98.81 | 99 | 100.00 | 79.20 | 4 | 100.00 | 100.00 | 2082 | 98.75 | 100.00 | |
| 105 | 2572 | 99.30 | 2501 | 100.00 | 100.00 | 41 | 100.00 | 69.50 | 30 | 40.00 | 100.00 | |
| 114 | 1879 | 99.79 | 1820 | 100.00 | 99.89 | 43 | 100.00 | 100.00 | 16 | 75.00 | 100.00 | |
| 116 | 2411 | 99.50 | 2301 | 99.87 | 100.00 | 109 | 91.74 | 97.09 | 1 | 100.00 | 100.00 | |
| 121 | 1862 | 99.95 | 1860 | 100.00 | 99.95 | 1 | 100.00 | 100.00 | 1 | 0.00 | 100.00 | |
| 200 | 2600 | 98.88 | 1742 | 100.00 | 98.36 | 826 | 100.00 | 100.00 | 32 | 9.37 | 100.00 | |
| 201 | 1963 | 98.11 | 1625 | 100.00 | 98.60 | 198 | 95.96 | 93.60 | 140 | 79.28 | 93.27 | |
| 202 | 2135 | 98.59 | 2060 | 100.00 | 98.89 | 19 | 89.47 | 77.27 | 56 | 50.00 | 93.33 | |
| 203 | 2979 | 98.19 | 2528 | 98.10 | 99.68 | 444 | 97.35 | 91.49 | 7 | 57.14 | 22.22 | |
| 205 | 2655 | 99.81 | 2570 | 100.00 | 99.80 | 71 | 100.00 | 100.00 | 14 | 64.28 | 100.00 | |
| 208 | 2953 | 92.92 | 1585 | 98.93 | 89.14 | 992 | 99.90 | 100.00 | 376 | 49.20 | 91.13 | |
| 210 | 2648 | 98.86 | 2421 | 99.83 | 99.26 | 194 | 98.97 | 96.97 | 33 | 27.27 | 60.00 | |
| 213 | 3249 | 96.74 | 2639 | 100.00 | 100.00 | 220 | 95.90 | 68.50 | 390 | 75.13 | 97.02 | |
| 215 | 3361 | 98.93 | 3194 | 99.47 | 100.00 | 164 | 88.41 | 100.00 | 3 | 100.00 | 8.33 | |
| 217 | 2208 | 96.47 | 244 | 83.20 | 100.00 | 162 | 98.76 | 82.05 | 1802 | 98.06 | 97.62 | |
| 219 | 2154 | 99.40 | 2082 | 100.00 | 99.38 | 64 | 89.06 | 100.00 | 8 | 25.00 | 100.00 | |
| 223 | 2604 | 95.77 | 2028 | 96.74 | 98.34 | 473 | 97.67 | 100.00 | 103 | 67.96 | 51.47 | |
| 228 | 2053 | 98.88 | 1688 | 98.87 | 99.88 | 362 | 99.45 | 100.00 | 3 | 33.33 | 4.55 | |
| 231 | 1570 | 98.92 | 314 | 100.00 | 94.59 | 2 | 100.00 | 100.00 | 1254 | 98.64 | 100.00 | |
| 233 | 3077 | 99.90 | 2229 | 100.00 | 100.00 | 830 | 100.00 | 100.00 | 18 | 83.33 | 100.00 | |
| 234 | 2752 | 99.38 | 2699 | 100.00 | 99.37 | 3 | 100.00 | 100.00 | 50 | 66.00 | 100.00 | |
| Total | 92588 | --- | 68411 | --- | --- | 6956 | --- | --- | 17221 | --- | --- | |
| Mean | 2314.7 | 99.10 | 1710.27 | 89.35 | 88.81 | 1739.0 | 75.98 | 74.35 | 4305.2 | 57.39 | 72.34 | |
| Standard Deviation | --- | 1.44 | --- | 30.28 | 30.20 | --- | 41.58 | 41.32 | --- | 39.58 | 41.67 | |
| Weighted Average | --- | 99.01 | --- | 99.66 | 99.38 | --- | 98.77 | 97.47 | --- | 96.54 | 98.81 | |
Furthermore, one should note the impressive results for records 105, 118, 213, 214, 215, and 223, compared to the results reported in [19]. These six records are the most difficult for PVC detection (sensitivity for records 105 and 215 is less than 5%, while others result in Sn ≈ 40% [19]). Hence, they are usually excluded from the database [21], [25]. To show the PVC detection capability of our proposed method, we have compared its performance to the file-by-file results of the NN-based approach in [19]. Statistical improvement results are shown in Fig. 5(a). It can be seen that for all cases, the proposed method enhances the mean improvement, while shifting the upper improvement quartile to the positive values. In addition, there are cases whose related improvements are very impressive, and can be followed by the upper side of the error-bars, indicating the maximum achieved improvement. Using the numerical evaluation results reported in the reference paper [19], it is also possible to compute the correlation coefficient (CC) as:
| (14) |
where TN represents the number of elements predicted as false that are false (true negatives). The ratio in (14) scores positively correct predictions and negatively incorrect ones, and takes a value between −1 and 1. Accordingly, the CC measure falls into the interval of [0,1]. The more correct the method is, the closer CC would be to unity. Another metric for measuring the correctly predicted elements is specificity(Sp), given by:
| (15) |
Fig. 5.
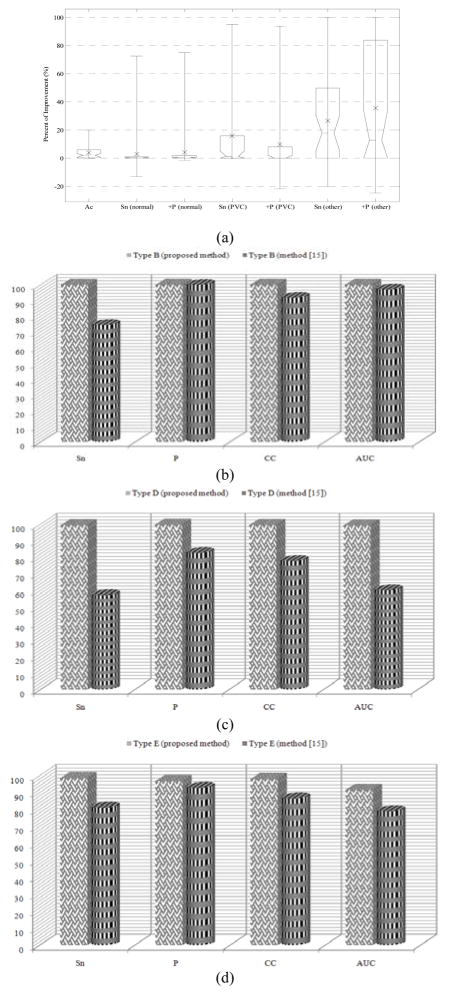
Performance comparison of the proposed method to the wavelet-based NN algorithm [17], evaluated on the same 40 records from MIT-BIH Arrhythmia Database. (a) Improvement statistics for the whole database shown with box plots. The box lines show the lower quartile, median (dotted) and upper quartile improvement values, and the error-bars indicate the min and max improvement values. The mean improvement is shown with a cross symbol, (b)–(d) comparative results for PVC detection using type B, type D, and type E signals, respectively. The results of our proposed method are shown by box bars while those of [19] are shown with cylindrical bars.
Having computed the values of Sn and Sp, a plot of Sn vs. Sp, namely the receiver operating characteristic (ROC) curve, is built for the same classification method using a series of detection results. However, since we do not vary the filter parameters and we have no thresholds to obtain stepwise Sn and Sp values, the best classification method is the one that describes the largest area under the curve (AUC).
In order to investigate the true positive PVC detection performance, we have chosen type B, D and E signals for analysis. Fig 5(b–d) show the mean values of different metrics for these types of records, evaluated using the proposed method (box bars) and the NN-based technique [19] (cylindrical bars). The figure illustrates that in contrast to the NN-based method, all metrics’ values for the proposed algorithm are over 90%, and are often very close to 100%.
Furthermore, the improvement in PVC detection is obvious by visual comparison of the height of cylindrical bars to that of box bars. Specifically, we note the improvement in sensitivity, which demonstrates that the Bayesian method has much fewer FN detections. Hence, the minimum number of PVCs is misclassified by the proposed approach. In other words, unlike the method in [19] which is based on feature extraction and neural network classification with no temporal memory, our proposed technique benefits from the tracking potential of the Bayesian framework to obtain much better detection accuracies for PVCs.
To appreciate the merits of the proposed method over conventional PVC classification algorithms and to ensure its ability to locate PVCs, we have compared our results to those of some benchmark techniques in the literature. The results are reported in table II. Since the results of methods are reported for different databases, we have also provided the number of ECG records (Nrec) and number of PVCs (NPVC) used in each method. It can be seen from table II that our proposed method provides a higher Ac and Sn, while preserving the +P in the acceptable range. Additionally, taking the number of analyzed PVCs into consideration, the +P results of our algorithm is comparable to and usually superior to the other methods, which shows the ability of the proposed framework to distinguish the PVCs from other beat types more accurately.
Table II.
Performance Comparison of Benchmark Methods for PVC Detection to the Proposed Model-Based Method.
| Detection Strategy | Method | Database | Performance measures | |||
|---|---|---|---|---|---|---|
| Nrec | NPVC | Ac (%) | Sn (%) | +P (%) | ||
| Time-domain statistics | Moody et al [5] | 20 | 5677 | --- | 91.90 | 89.46 |
| 44 | 6731 | --- | 74.51 | 97.36 | ||
| PCA | Moody et al [6] | 20 | 5677 | --- | 93.12 | 94.76 |
| 44 | 6731 | --- | 92.73 | 96.92 | ||
| Neural networks | Inan et al [19] | 40 | 6958 | 95.20 | 85.20 | 92.40 |
| Ince et al [20] | 40 | 6958 | 97.00 | 93.40 | 93.30 | |
| Shyu et al [21] | 7 | 953 | 97.04 | 96.67 | 97.04 | |
| KNN classifier | Christov et al [23] | 20 | 5677 | --- | 97.30 | 97.70 |
| 44 | 6731 | --- | 81.60 | 78.03 | ||
| Gaussian process | Melgani and Bazi [25] | 18 | 2720 | 97.10 | 97.60 | 97.00 |
| 27 | 4080 | 96.90 | 84.70 | 97.50 | ||
| Bayesian filtering | Proposed | 40 | 6956 | 99.10 | 98.77 | 97.47 |
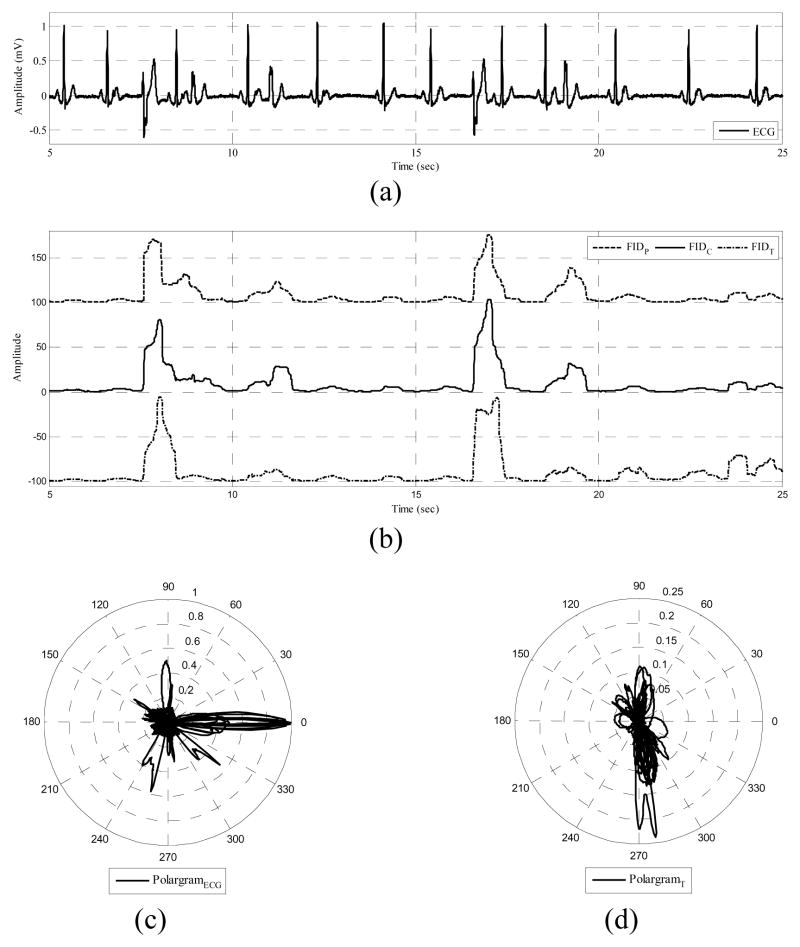
Another interesting feature of the proposed method is that the PVC detection depends upon both the γCW and the polar envelope, which together enables the algorithm to distinguish between PVCs and rhythms with similar morphologies, which is a significant problem in feature-based methods. As an example, previous studies could not distinguish between PVCs and left bundle branch blocks (LBBB) beats [19], [21]. LBBB is a cardiac conduction abnormality seen on ECG, in which activation of the left ventricle is delayed, which results in the left ventricle contracting later than the right ventricle. The criteria to diagnose a LBBB are QRS widening and T wave discordance, in which the T wave should be deflected opposite the terminal deflection of the QRS complex. This is similar to PVC, however, in the case of a PVC, the P wave is fused in the QRS complex and the dominant T wave is not essentially deflected opposite the terminal deflection of the QRS complex. Hence, using the time interval features and a NN [17] or wavelet features and fuzzy NN [21], it is very difficult to distinguish between a PVC and a LBBB beat. For instance, Shyu et al [21] reported 405 LBBB as FN detections while characterizing PVCs. The potential of the Bayesian framework enables it to correctly identify LBBB as non-PVCs. This is due to the polar envelope formation based on the LBBB, which spans a different partition from the PVCs. Specifically, γCW identifies the LBBB as a monotone rhythm in ECG, whereas the PVC is characterized as a rhythm change. This is obvious by comparing the results of our algorithm for record 214 (Sn= 100%, +P=100%) to the reported results of [19] for the same record (Sn=47.66%, +P=92.42%), which includes 256 PVCs and 1996 LBBB beats. Fig. 6 illustrates a segment of record 214, the signal and T wave polargrams and the signal fidelity γT corresponding to the T wave.
Fig. 6.
Distinguishing LBBB and PVCs for a typical ECG signal. (a) ECG record 214, (b) γT, (c) signal polargram and the polar envelope, (d) T wave polargram.
I. Discussion and Conclusion
In this paper, a wave-based Bayesian framework was presented and validated for PVC beat detection which is capable of running on a single ECG lead. The method is based on an EKF algorithm that incorporates the characteristic waves of the ECG into a dynamical model. By separating the Gaussian functions, and using 2 kernels for each asymmetric wave, a state space model was constructed. The proposed set of equations aims at integrating into the ECG model a mechanism that estimates an ECG signal as a combination of finite characteristic waveforms, each of which represents a particular physiological state of the heart. According to this specific model, the EKF structure provides a means of tracking the behavior of the CWs, throughout the filtering procedure.
From a filtering point of view, KFs can be thought of as adaptive filters that continuously move the location of the poles and zeros of their transfer functions, according to the signal or noise content of the input observations and the prior model of the signal dynamics. The filter structure is based upon a unique dynamical model, which is adapted to the observations according to the propagation equations. In this way, we can track the reliability of the estimations, as well as the fidelity of the filter. Moreover, this feature allows the filter to adapt with different spectral shapes and temporal non-stationarities, since the variance of the observation noise in (4) represents the degree of reliability of a single observation, as well as the degree of adaptively tracking the input noisy measurement. Based on this concept, we introduced the signal fidelity, γCW, corresponding to each CW, and monitored these parameters to detect PVC occurrence. Furthermore, a polar representation was introduced to distinguish between the rhythm changes that occur inside the polar envelope and PVCs, which span a different portion of the polargram. The designed filter was applied to standard ECG databases, and compared to other published methods. The results demonstrate the filter’s capability in tracking the PVCs. It was also shown that the γCW’s are capable of discrimination between PVCs and other abnormalities that exhibit a defect in a specific CW. However, for those abnormalities that affect the γCW’s the same manner as would a PVC, the polargram is used to verify the occurrence outside the polar envelope.
Performance evaluation results showed that the developed method provides a reliable and accurate PVC detection, providing an accuracy of 98.83%, weighted average specificity of 99.29% for normal and 98.43% for PVC, and a mean positive predictivity of 99.75% for normal and 96.68% for PVC, which is well within the acceptable range, and is superior to the previously reported results. Moreover, in comparison to other published methods for PVC detection, our proposed approach provides a superior performance, and there is no need to employ decision rules based on comparison against thresholds, feature extraction, training, and selection of the classifiers’ structure. Another point of interest is the capability of the algorithm to fully determine the PVCs, with Ac, Sn and +P equal to 100%, for the records that contain only two specific beat types: normal sinus beats and PVCs. It was also shown that the proposed method is applicable to reliable PVC detection in presence of other abnormalities, and in particular left bundle branch block.
It should be noted that the initial value for the state vector as well as the selection of the covariance matrices of the process and the measurement noise will influence the trajectory of the estimated vectors. The dependence of the results on these initial estimations is the major drawback of the proposed method. Hence, an automated procedure for reliable initialization was proposed. Although the Bayesian method we present depends on the initial values, the method is still more efficient compared to NN-based approaches since the initialization and training of the EKF parameters can be performed using just a few early cycles.
Due to the recursive structure of the KF, the proposed method is also computationally tractable and of special interest for real-time applications. Generally, the computation time of this method is linearly proportional to the signal length in samples. For the currently developed MATLAB® code, the computation time is already close to real time using a Core Duo 1.86 GHz CPU. Compilation and optimization of this code, or conversion into a low-level language for use in pre-processing units of clinical monitoring systems would result in a significant increase in performance speed. This would allow the algorithm to run on multiple ECG leads in real time on most embedded systems which are increasingly available with on-board DSP chipsets.
Biographies

Omid Sayadi (S’06) received the B.Sc. degree in Biomedical Engineering from Shahed University, Tehran, Iran, in 2005, and the M.Sc. degree in Electrical Engineering, Biomedical Engineering, from Sharif University of Technology, Tehran, Iran, in 2007. He is currently a Ph.D. student of Biomedical Engineering at the Electrical Engineering Department of Sharif University of Technology, Tehran, Iran, and a member of Biomedical Signal and Image Processing Lab (BiSIPL). His PhD research deals with dynamical models for cardiovascular signal generation, model-based ECG signal processing, and heart abnormality verification in Bayesian and Markovian frameworks.

Mohammad B. Shamsollahi (M’02) received the B.Sc. degree in Electrical Engineering from Tehran University, Tehran, Iran, in 1988, and the M.Sc. degree in Electrical Engineering, Telecommunications, from the Sharif University of Technology, Tehran, Iran, in 1991. He received the Ph.D. degree in Electrical Engineering, Biomedical Signal Processing, from the University of Rennes 1, Rennes, France, in 1997. Currently, he is an Associate Professor with the Department of Electrical Engineering, Sharif University of Technology, Tehran, Iran. His research interests include biomedical signal processing, brain computer interface, time-scale and time-frequency signal processing.

Gari D. Clifford (S’01–M’03–SM’06) received a B.Sc. in Physics with Electronics, an M.Sc. in Applied Mathematics and Theoretical Physics and a Ph.D. (oxon) in Biomedical Engineering. He is currently a Principal Research Scientist in the Laboratory for Computational Physiology at the Harvard-MIT Division of Health Sciences where, for the last 6 years, he has managed a R01 NIH-funded research program, “Integrating Data, Models, and Reasoning in Critical Care”. Dr Clifford also contributes to the NIH Physionet Research Resource. His research is focused on open-source tools and public-access data for the evaluation of predictive patient monitoring algorithms and has published widely on this topic. Dr Clifford is currently a Lecturer in Medicine at Harvard Medical School, an Instructor in Biomedical Engineering at MIT and an Editor for Biomedical Engineering OnLine. Dr Clifford is also a Senior Member of the IEEE and has worked in industry on the patenting, design and production of several CE- and FDA-approved medical devices.
Contributor Information
Omid Sayadi, Email: osayadi@ee.sharif.edu, Biomedical Signal and Image Processing Laboratory (BiSIPL), School of Electrical Engineering, Sharif University of Technology, Tehran 11365-9363, Iran.
Mohammad B. Shamsollahi, Email: mbshams@sharif.edu, Biomedical Signal and Image Processing Laboratory (BiSIPL), School of Electrical Engineering, Sharif University of Technology, Tehran 11365-9363, Iran.
Gari D. Clifford, Email: gari@mit.edu, Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA 02142 USA.
References
- 1.Jones DL, et al. Heart disease and stroke statistics—2009 update. A report from the American heart association statistics committee and stroke statistics subcommittee. Circulation. 2008 Dec 15; doi: 10.1161/CIRCULATIONAHA.108.191261. [DOI] [PubMed] [Google Scholar]
- 2.Atsushi I, Hwa M, Hassankhani A, Liu T, Narayan SM. Abnormal heart rate turbulence predicts the initiation of ventricular arrhythmias. Pacing Clin Electrophysiol. 2005;11:1189–97. doi: 10.1111/j.1540-8159.2005.50186.x. [DOI] [PubMed] [Google Scholar]
- 3.Schneider R, Barthel P, Watanabe M. Heart rate turbulence on Holter. In: Malik M, Camm AJ, editors. Dynamic Electrocardiography. ch 20. New York: Futura; 2004. pp. 190–193. [Google Scholar]
- 4.Dubin D. Rapid Interpretation of EKG’s. 5. Tampa, FL: Cover; 2000. [Google Scholar]
- 5.Moody GB, Mark RG. Development and evaluation of a 2-lead ECG analysis program. Computers in Cardiology. 1982:39–44. [Google Scholar]
- 6.Chazal PD, O’Dwyer M, Reilly RB. Classification of Heartbeats Using ECG Morphology and Heartbeat Interval Features. IEEE Trans Biomed Eng. 2004 July;51:1196–1206. doi: 10.1109/TBME.2004.827359. [DOI] [PubMed] [Google Scholar]
- 7.Moody GB, Mark RG. QRS Morphology Representation and Noise Estimation using the Karhunen-Loève Transform. Computers in Cardiology. 1989:269–272. [Google Scholar]
- 8.Cheng WT, Chan KL. Classification of electrocardiogram using hidden markov models. Proc. 20th Annu. Int. Conf. IEEE EMBS; 1998. pp. 143–146. [Google Scholar]
- 9.Coast DA, Stern RM, Cano GG, Briller SA. An Approach to Cardiac Arrhythmia Analysis Using Hidden Markov Models. IEEE Trans Biomed Eng. 1990;37:826–835. doi: 10.1109/10.58593. [DOI] [PubMed] [Google Scholar]
- 10.Andreão RV, Dorizzi B, Boudy J. ECG Signal Analysis Through Hidden Markov Models. IEEE Trans Biomed Eng. 2006;53:1541–1549. doi: 10.1109/TBME.2006.877103. [DOI] [PubMed] [Google Scholar]
- 11.Risk MR, Sobh JF, Saul JP. Beat detection and classification of ECG using self organizing maps. Proc. 19th Int. Conf. IEEE EMBS; 1997. pp. 89–91. [Google Scholar]
- 12.Senhadji L, Carrault G, Bellanger JJ, Passariello G. Comparing wavelet transforms for recognizing cardiac patterns. IEEE Eng Med Biol Mag. 1995 Mar-Apr;14(2):167–173. [Google Scholar]
- 13.Alfonso X, Nguyen TQ. ECG beat detection using filter banks. IEEE Trans Biomed Eng. 1999 Feb;46(2):192–202. doi: 10.1109/10.740882. [DOI] [PubMed] [Google Scholar]
- 14.Chazal PD, O’Dwyer M, Reilly RB. Automatic classification of heartbeats using ECG morphology and heartbeat interval features. IEEE Trans Biomed Eng. 2004 Jul;51(7):1196–1206. doi: 10.1109/TBME.2004.827359. [DOI] [PubMed] [Google Scholar]
- 15.Hosseini HG, Luo D, Reynolds KJ. The comparison of different feed forward neural network architectures for ECG signal diagnosis. Med Eng Phys. 2006;28:372–378. doi: 10.1016/j.medengphy.2005.06.006. [DOI] [PubMed] [Google Scholar]
- 16.Ham FM, Han S. Classification of cardiac arrhythmias using fuzzy ARTMAP. IEEE Trans Biomed Eng. 1996 Apr;43:425–430. doi: 10.1109/10.486263. [DOI] [PubMed] [Google Scholar]
- 17.Christov I, Bortolan G. Ranking of pattern recognition parameters for premature ventricular contractions classification by neural networks. Physiol Meas. 2004;25:1281–1290. doi: 10.1088/0967-3334/25/5/017. [DOI] [PubMed] [Google Scholar]
- 18.Bortolan G, Jekova I, Christov I. Comparison of four methods for premature ventricular contraction and normal beat clustering. Proc. Comp. Cardiol.; 2005. pp. 921–924. [Google Scholar]
- 19.Inan OT, Giovangrandi L, Kovacs GTA. Robust neural-network-based classification of premature ventricular contractions using wavelet transform and timing interval features. IEEE Trans Biomed Eng. 2006 Dec;53(12):2507–2515. doi: 10.1109/TBME.2006.880879. [DOI] [PubMed] [Google Scholar]
- 20.Ince T, Kiranyaz S, Gabbouj M. Automated patient-specific classification of premature ventricular contractions. Proc. 30th Int. Conf. IEEE EMBS; 2008. pp. 5474–5477. [DOI] [PubMed] [Google Scholar]
- 21.Shyu LY, Wu YH, Hu W. Using wavelet transform and fuzzy neural network for VPC detection from the Holter ECG. IEEE Trans Biomed Eng. 2004 Jul;51(7):1269–1273. doi: 10.1109/TBME.2004.824131. [DOI] [PubMed] [Google Scholar]
- 22.Zhou J. Automatic detection of premature ventricular contraction using quantum neural networks. Proc. BIBE; 2003. pp. 1–5. [Google Scholar]
- 23.Christov I, Jekova I, Bortolan G. Premature ventricular contraction classification by the Kth nearest-neighbours rule. Physiol Meas. 2005;26:123–130. doi: 10.1088/0967-3334/26/1/011. [DOI] [PubMed] [Google Scholar]
- 24.Zhao L, Wiggins M, Vachtsevanos G. Premature ventricular contraction beat detection based on symbolic dynamics analysis. Proc. IASTED; 2003. pp. 48–50. [Google Scholar]
- 25.Melgani F, Bazi Y. Detecting premature ventricular contractions in ECG Signals with Gaussian processes. Proc. Comp. Cardiol.; 2008. pp. 237–240. [Google Scholar]
- 26.Sameni R, Shamsollahi MB, Jutten C, Clifford GD. A nonlinear Bayesian filtering framework for ECG denoising. IEEE Trans Biomed Eng. 2007 Dec;54(12):2172–2185. doi: 10.1109/tbme.2007.897817. [DOI] [PubMed] [Google Scholar]
- 27.Sameni R, Shamsollahi MB, Jutten C. Model-based Bayesian filtering of cardiac contaminants from biomedical recordings. Physiol Meas. 2008;29:595–613. doi: 10.1088/0967-3334/29/5/006. [DOI] [PubMed] [Google Scholar]
- 28.McSharry PE, Clifford GD, Tarassenko L, Smith LA. A dynamic model for generating synthetic electrocardiogram signals. IEEE Trans Biomed Eng. 2003 Mar;50(3):289–294. doi: 10.1109/TBME.2003.808805. [DOI] [PubMed] [Google Scholar]
- 29.Clifford GD, Shoeb A, McSharry PE, Janz BA. Model-based filtering, compression and classification of the ECG. International Journal of Bioelectromagnetism. 2005;7(1):158–161. [Google Scholar]
- 30.Sayadi O, Sameni R, Shamsollahi MB. ECG denoising using parameters of ECG dynamical model as the states of an extended Kalman filter. Proc. 29th Int. Conf. IEEE EMBS; 2007. pp. 2548–2551. [DOI] [PubMed] [Google Scholar]
- 31.Sayadi O, Shamsollahi MB. ECG denoising and compression using a modified extended Kalman filter structure. IEEE Trans Biomed Eng. 2008 Sep;55(9):2240–2248. doi: 10.1109/TBME.2008.921150. [DOI] [PubMed] [Google Scholar]
- 32.Sayadi O, Shamsollahi MB. A model-based Bayesian framework for ECG beat segmentation. Physiol Meas. 2009;30:335–352. doi: 10.1088/0967-3334/30/3/008. [DOI] [PubMed] [Google Scholar]
- 33.Gelb A, editor. Applied Optimal Estimation. Cambridge, MA: MIT Press; 1974. [Google Scholar]
- 34.Kay SM, editor. Fundamentals of Statistical Signal Processing: Estimation Theory. Englewood Cliffs, NJ: Prentice Hall PTR; 1993. [Google Scholar]
- 35.Simon D, editor. Optimal State Estimation. New York: Wiley; 2006. [Google Scholar]
- 36.Haykin S, editor. Kalman Filtering and Neural Networks. New York: Wiley; 2001. [Google Scholar]
- 37.Grewal MS, Weill LR, Andrews AP, editors. Global Positioning Systems, Inertial Navigation, and Integration. New York: Wiley; 2001. [Google Scholar]
- 38.The MIT-BIH Arrhythmia Database. [Online]. Available: http://physionet.org/physiobank/database/mitdb/
- 39.Goldberger AL, Amaral LAN, Glass L, Hausdorff JM, Ivanov PCh, Mark RG, Mietus JE, Moody GB, Peng CK, Stanley HE. PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals. Circulation. 2000 June 13;101(23):e215–e220. doi: 10.1161/01.cir.101.23.e215. Circulation Electronic Pages; http://circ.ahajournals.org/cgi/content/full/101/23/e215. [DOI] [PubMed]
- 40.Levenberg K. A Method for the Solution of Certain Problems in Least Squares. Quarterly Applied Math. 1944;2:164–168. [Google Scholar]
- 41.Marquardt D. An Algorithm for Least Squares Estimation of Nonlinear Parameters. SIAM Journal Applied Math. 1963;11:431–441. [Google Scholar]