Abstract
Directional epistasis describes a situation in which epistasis consistently increases or decreases the effect of allele substitutions, thereby affecting the amount of additive genetic variance available for selection in a given direction. This study applies a recent parameterization of directionality of epistasis to empirical data. Data stems from a QTL mapping study on an intercross between inbred mouse (Mus musculus) strains LG/J and SM/J, originally selected for large and small body mass, respectively. Results show a negative average directionality of epistasis for body-composition traits, predicting a reduction in additive allelic effects and in the response to selection for increased size. Focusing on average modification of additive effect of single loci, we find a more complex picture, whereby the effects of some loci are enhanced consistently across backgrounds, while effects of other loci are decreased, potentially contributing to either enhancement or reduction of allelic effects when selection acts at single loci. We demonstrate and discuss how the interpretation of the overall measurement of directionality depends on the complexity of the genotype–phenotype map. The measure of directionality changes with the power of scale in a predictable way; however, its expected effect with respect to the modification of additive genetic effects remains constant.
EPISTASIS is present when the effect of a genetic substitution depends on the genotypes at other loci. At the population level, this means that average allelic effects change as allele frequencies at other loci change, and thus that gene effects can evolve. The evolutionary significance of epistasis has been recognized mainly in relation to the allele-frequency changes that are caused by genetic drift (e.g., Goodnight 1987, 1988, 1995; Cheverud and Routman 1996; Barton and Turelli 2004; De Brito et al. 2005; Turelli and Barton 2006), whereas the epistatic effects under directional selection have been treated only recently (e.g., Carter et al. 2005; Weinreich et al. 2005; Carlborg et al. 2006; Hansen et al. 2006; Yukilevich et al. 2008). Technically, the effects of epistatic interaction can be considered as having two aspects: the architecture itself (i.e., the existence of a nonadditive component, the so-called functional aspect, see below), and the effect of allele frequency on genetic variance (i.e., the statistical aspect). An additional consideration is crucial for the response to selection of a given trait, namely that the response is generated by the joint action of many epistatic interactions. Each of the interactions can either enhance or diminish the additive genetic effect in any specific phenotypic dimension. Their composite effect depends on the pattern, i.e., whether the effects accumulate or cancel each other out (Hansen and Wagner 2001a,b; Carter et al. 2005; Hansen et al. 2006). In the following we provide a brief general account of epistasis and then focus on the effect of its composite pattern, the empirical assessment of which is the goal of this study.
The traditional population-genetic approach to selection response initially emphasized additive genetic variance and treated any variance unexplained by the additive effects, including variance due to interactions within or between loci, as residual variance (Fisher 1918). Later this model was extended to account for epistasis (Cockerham 1954, Kempthorne 1954). The interaction component of this residual variance is dependent on population allele frequencies at the interacting loci. Starting with nonadditive effects within a single locus (dominance), Falconer (1960) described the effect of allele frequencies on the statistical measure of average allelic effect. Cheverud and Routman (1995) explored the analogous effect at the two-locus level, leading to distinction between allele-frequency-dependent statistical epistasis (contributing to epistatic variance) on population level, and allele-frequency-independent physiological (or functional) epistasis on the individual level, which contributes to all the genetic variance components, i.e.,, additive, dominance, and epistatic. Thus while physiological epistasis describes the genetic architecture of a given phenotype defining the potential for epistatic effects, statistical epistasis describes the realization of individual-level epistatic effects in terms of allele-frequency-dependent genetic variance components. Several authors have worked out tools to estimate gene interaction effects at the individual level independently of the allele frequencies to distinguish between the physiological and statistical epistasis (Cheverud and Routman 1995; Wagner et al. 1998; Hansen and Wagner 2001a; Barton and Turelli 2004; Yang 2004; Zeng et al. 2005; Wang and Zeng 2006). These methods have been recently generalized in a common framework for measuring epistasis and translating between the population and individual levels (NOIA: Alvarez-Castro and Carlborg 2007; Alvarez-Castro et al. 2008; see Le Rouzic 2008 for R software package). An understanding of the pattern of epistatic architecture enables prediction of its effects at any given set of allele frequencies.
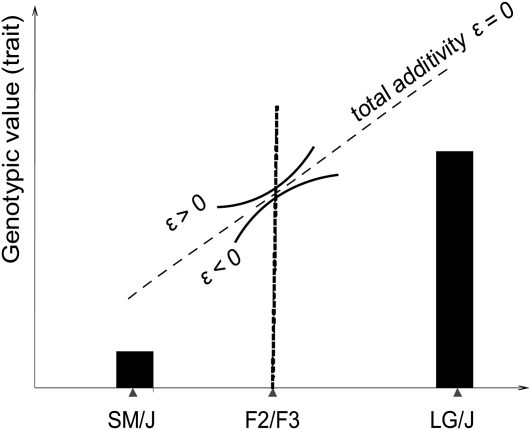
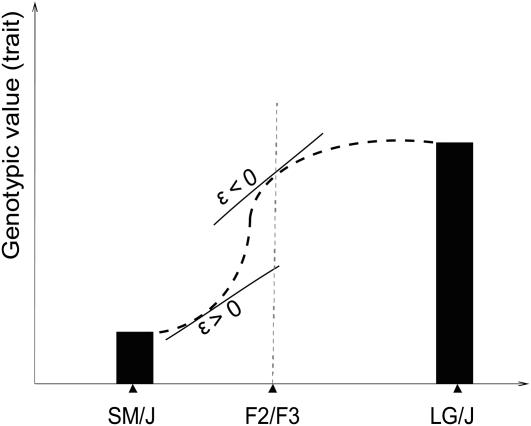
The original physiological epistasis has often referred to isolated pairwise interactions. The genetic basis of a complex trait is affected by more than two interacting loci; thus the trait's genetic variance is affected by the combination of these interaction effects. Effects at the individual loci can add up, or cancel out. For example, when the alleles at background loci become fixed (e.g., due to a bottleneck), previously background-dependent genetic effects at loci A and B can become additive effects of the same or of the opposite sign. Depending on the sign and size of their effects, the two allele substitutions at loci A and B therefore add up to increase, decrease, or have no overall effect on additive genetic variance. Hansen and Wagner (2001a) introduced the notion of directionality of epistasis to emphasize the importance of the pattern of epistatic architecture for the system's evolvability. Directionality measures the consistency of epistatic effects on additive variance for a specific locus and trait across the genome, given a defined reference genotype. It describes whether epistasis tends to enhance or diminish the additive effects of interacting loci on a trait in a specified phenotypic direction. The population-dynamic studies analyzing effects of the epistatic pattern show that the directionality of epistasis can be a major determinant of evolution on time scales beyond a few generations (Hermisson et al. 2003; Carter et al. 2005; Hansen et al. 2006; Yukilevich et al. 2008; Alvarez-Castro et al. 2009; Fierst and Hansen 2010). Averaged across interactions, positive directional epistasis increases additive variance and the response to positive selection relative to that predicted by the additive genetic effects alone, while negative directional epistasis tends to decrease the response to selection in that same phenotypic direction. An absence of epistatic directionality occurs when positive and negative directional epistatic effects cancel out on average or, trivially, from the absence of epistasis. Thus directionality describes the local, population-specific curvature of the genotype–phenotype map (Figure 1).
Figure 1.—
Directionality of epistasis describes the local curvature of the genotype–phenotype map. The genotypic values of the trait of interest in the two parental inbred populations and in an intercross are plotted on y-axis. Given a defined direction on a trait axis and a reference point for measurement of genetic effects, the directionality ( ) describes whether the epistasis increases or decreases the effect of allelic substitutions relative to the value predicted by additive effects alone. The extrapolation of the curvature beyond the local effects requires the knowledge of higher-order epistatic effects; however, the local effects can be calculated for different reference points and different phenotypic directions (see Hansen and Wagner 2001a,b).
) describes whether the epistasis increases or decreases the effect of allelic substitutions relative to the value predicted by additive effects alone. The extrapolation of the curvature beyond the local effects requires the knowledge of higher-order epistatic effects; however, the local effects can be calculated for different reference points and different phenotypic directions (see Hansen and Wagner 2001a,b).
Aspects of epistatic directionality have been addressed previously with respect to the effect on fitness (reviewed in Phillips et al. 2000), with focus on the synergistic epistasis for deleterious effect enhancement (e.g., Kondrashov 1988; Charlesworth 1990; Hansen and Wagner 2001b). However, the empirical study of overall directionality of epistasis, and its measurement in morphological or physiological traits, is still lacking (Hansen 2006). Implicit indications from empirical studies are ambiguous (see examples in Carter et al. 2005). Here, we present an assessment of directionality of two-way epistasis between QTL in an intercross population of laboratory mice, paying special attention to scale effects.
THEORETICAL BACKGROUND
Directionality of epistasis and the multilinear model:
The concept of epistatic directionality was developed in the framework of the multilinear model by Hansen and Wagner (2001a). Here, we briefly explain the parameters of the multilinear model used to measure the directionality of two-way epistasis in this article, above all the epistatic coefficient ɛ (for detail and higher-order epistasis, see Hansen and Wagner 2001a; Hansen et al. 2006).
The multilinear model first defines an arbitrary multilocus reference genotype and the effects of substitutions at single loci into this reference genotype as the reference genetic effects:
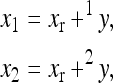 |
(1) |
where 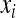 is an observed phenotype,
is an observed phenotype,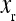 is the phenotype of individuals with the reference genotype,
is the phenotype of individuals with the reference genotype, 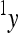 is a reference effect of a substitution at locus 1 in the reference genotype, and
is a reference effect of a substitution at locus 1 in the reference genotype, and 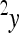 is the reference effect of a substitution at a second locus (2) in the reference genotype. Epistasis is then modeled as the change in the effect of locus 2 due to a prior change at locus 1, which provides locus 2 with an altered genetic background:
is the reference effect of a substitution at a second locus (2) in the reference genotype. Epistasis is then modeled as the change in the effect of locus 2 due to a prior change at locus 1, which provides locus 2 with an altered genetic background:
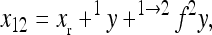 |
(2) |
where the reference effect 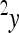 is adjusted for the epistatic effect due to the change in background at the first locus, by multiplying the second reference effect (
is adjusted for the epistatic effect due to the change in background at the first locus, by multiplying the second reference effect (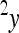 ) by the epistatic factor
) by the epistatic factor 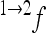 (Wagner et al. 1998). The epistatic factor is a dimensionless number and describes the rescaling of the locus' reference effect due to the change in genetic background. Note that
(Wagner et al. 1998). The epistatic factor is a dimensionless number and describes the rescaling of the locus' reference effect due to the change in genetic background. Note that 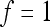 means no epistasis,
means no epistasis, 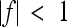 indicates a decrease in the effect of a substitution with respect to the reference effect, and
indicates a decrease in the effect of a substitution with respect to the reference effect, and 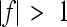 reflects an increase in the substitution effect relative to the reference effect. The case
reflects an increase in the substitution effect relative to the reference effect. The case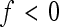 is a special case where both the magnitude and the sign of the effect changes. The
is a special case where both the magnitude and the sign of the effect changes. The 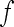 value is a function of the change in the background, in this case,
value is a function of the change in the background, in this case,
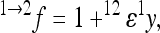 |
(3) |
where 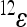 is an epistatic coefficient describing the epistatic relationship between loci 1 and 2. Note that positive values of
is an epistatic coefficient describing the epistatic relationship between loci 1 and 2. Note that positive values of 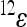 mean that positive changes at locus 1 enhance the positive effects at locus 2 with respect to the reference effect, because they increase the positive and decrease the negative effects, while negative values of
mean that positive changes at locus 1 enhance the positive effects at locus 2 with respect to the reference effect, because they increase the positive and decrease the negative effects, while negative values of 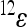 have the opposite effects. The coefficient
have the opposite effects. The coefficient 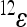 therefore describes the directionality of epistasis in this interaction. It follows that any phenotype can be expressed (with respect to the two loci) as
therefore describes the directionality of epistasis in this interaction. It follows that any phenotype can be expressed (with respect to the two loci) as
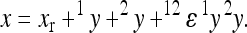 |
(4) |
The model makes two assumptions: (i) that the effects of a substitution after the change in the background can be described as a linear transformation of the effect this substitution has in the reference background, and (ii) that the end phenotype is invariant with respect to the order of substitutions (i.e., the symmetry of epistasis, Wagner et al. 1998). Applying this model, each genotype can be described as a sum of linearly transformed reference effects at the loci deviating from the reference genotype, respectively, as a sum of the reference effects and the epistatic terms describing the effect of change in the reference. Hence, considering two-way epistasis,
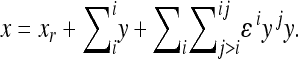 |
(5) |
For the extension of the original model to explicitly model dominance see Le Rouzic and Alvarez-Castro (2008).
In summary, epistatic contributions are modeled as functions of the multilinear model's reference effects, rather than by introducing new independent epistatic values. The phenotypic effect of the epistatic term depends on the factor modifying the reference effects (f and ɛ) as well as of the reference effects themselves. The choice of the reference depends on the question asked. In empirical studies, the population mean is a convenient reference choice from which to measure the effects of substitutions. Thus the reference effects in this study are measured at every locus from the phenotypic mean of the studied mice intercross population.
Here we focus on the combined effect of multiple pairwise interactions in a mouse intercross population at two levels: (i) across interactions of a focal locus with different other loci, and (ii) across all pairwise interactions between loci of the selected subset. The analysis is conducted for each trait separately.
Scale effects:
Phenotypic traits are often measured on different scales (lengths, surfaces, volumes, or masses). The scale is known to affect the interaction effects to some extent. To understand whether the patterns of directionality are trait specific or also scale specific, we assessed the directionality of epistasis for all traits on both linear (one-dimensional traits, lengths) and cubic scale (three-dimensional traits, mass). In this study, both these scales are the original scale for some of the measurements considered (lengths vs. weights).
The expected effect of power transformation of scale on directionality of epistasis can be approximated analytically. Considering a simple model for two allele substitutions without dominance effects, the predicted relationship between coefficient of directionality on the linear scale and coefficient of directionality on the scale with k-th exponent (e.g., k = 3 for cubic scale) is approximately 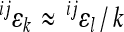 , where
, where 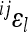 is the coefficient of directionality for the loci i, j on the linear scale, and
is the coefficient of directionality for the loci i, j on the linear scale, and 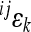 on the scale with k-th exponent (for derivation see appendix: effects of scale transformations). This relationship is a valid approximation for the mean-standardized phenotypic measurements as used in this study (see below). The epistatic coefficient of directionality on the linear scale is thus expected to be roughly threefold greater than the epistatic coefficient of directionality on the cubic scale. The accuracy of this estimation, especially when extrapolated to the average directionality across many interactions, depends on the details of dominance, distribution of reference effect sizes and the presence of sign epistasis.
on the scale with k-th exponent (for derivation see appendix: effects of scale transformations). This relationship is a valid approximation for the mean-standardized phenotypic measurements as used in this study (see below). The epistatic coefficient of directionality on the linear scale is thus expected to be roughly threefold greater than the epistatic coefficient of directionality on the cubic scale. The accuracy of this estimation, especially when extrapolated to the average directionality across many interactions, depends on the details of dominance, distribution of reference effect sizes and the presence of sign epistasis.
Scale transformation also affects the fit of the multilinear model to data. The multilinear model is a polynomial function separately linear for each of its variables. When fitted to data transformed to a different scale, the accuracy of the approximation differs between scales. For example, when the reference effects are positive, increasing the exponent of scale relative to the scale of maximal fit of multilinear model results in the genotypic values being described by the increasingly convex function of gene effects. The multilinear model therefore tends to underestimate this curvature (true absolute value of coefficient of epistasis is greater than the fitted one). Decreasing the exponent of scale relative to the scale with best fit results in an increasingly concave mapping from gene effects and interactions to the genotypic value, and the multilinear model may overestimate the general curvature, i.e., the measured absolute epsilon is greater than the real value.
METHODS
Data:
The study population consists of 2060 F2 and F3 generation individuals from an intercross between the large LG/J and small SM/J inbred mouse (house mouse, Mus musculus) strains (Jackson Labs, Maine). The parental strains were selected for large or small body weight at 60 days of age over many generations (Goodale 1938; Macarthur 1949). The two lines were generated in separate experiments, applying up- and downselection on weight to two different stock populations. Nonetheless, previous mapping studies have shown that the alleles from the LG/J line generally cause increased size relative to SM/J alleles in the intercross of these two lines (Cheverud et al. 1996, 2001, 2004). For details on the population, husbandry, experimental design, and mapping see Cheverud et al. (1996), Vaughn et al. (1999), Fawcett et al. (2008), and Norgard et al. (2008).
We focused on the genetic effects on a series of morphological traits: the lengths of the tail and long bones (femur, tibia, humerus, and ulna), the weights of internal organs (heart, liver, spleen, and kidney), and the total body weight at necropsy (10 weeks of age). Body weight at necropsy is strongly correlated with the target of selection in original lines, the body weight at 60 days (Falconer et al. 1978; Vaughn et al. 1999). All phenotypic measurements were taken at necropsy and were corrected for the effect of sex, age at necropsy, and litter size (<10 vs. >10) by partialing out the effect of these factors using the general linear model prior to further analysis. The residuals were then added to the mean of the respective trait, producing the corrected individual trait scores. As the traits are on different scales (length and volume), the analyses were conducted for all traits on linear and on cubic scales to be able to distinguish the effect of scale. To this end, the corrected weight measurements (body, heart, kidney, spleen, and liver weight) were transformed by taking the cube root of the individual values for the analyses on linear scale, whereas the corrected linear traits (bone and tail lengths) were cubed for the analyses on cubic scale. The raw trait means and standard errors of the parental and experimental populations are listed in Table 1. Preceding the analyses, the scores of all traits (on linear and cubic scales) were mean standardized by dividing the individual scores by the respective arithmetic trait means. An alternative common standardization method is to divide individual scores by the standard deviation of the particular trait. Both methods aim at comparability across traits, expressing the results either as a proportion of the trait mean or of the trait standard deviation (dispersion of trait scores). Both transformations affect the distribution of marginal effects; however, they are both equivalent to a multiplication by a constant (1/mean, or 1/standard deviation), resulting in a proportional increase or decrease of the marginal effects, and thus do not affect the directionality of epistasis. All scores are on a ratio scale (i.e., differences as well as ratios between measurements are meaningful). Note that mean standardization produces very similar results to those of logarithmic transformation (Wright 1952).
TABLE 1.
The phenotypic description of parental inbred lines and the experimental intercross population
| Experimental population |
Parental lines |
||||
|---|---|---|---|---|---|
| Trait | Mean ± SE | VA | IA (%) | Mean ± SE LG/J | Mean ± SE SM/J |
| Femur length | 15.75 ± 0.012 mm | 0.445 mm2 | 0.179 | 17.60 ± 0.068 mm | 14.78 ± 0.049 mm |
| Humerus length | 12.36 ± 0.008 mm | 0.214 mm2 | 0.140 | 13.76 ± 0.017 mm | 11.60 ± 0.012 mm |
| Tibia length | 17.36 ± 0.012 mm | 0.411 mm2 | 0.137 | 18.87 ± 0.056 mm | 16.64 ± 0.063 mm |
| Ulna length | 14.14 ± 0.009 mm | 0.225 mm2 | 0.113 | 15.41 ± 0.001 mm | 13.20 ± 0.035 mm |
| Tail length | 92.43 ± 0.121 mm | 32.645 mm2 | 0.382 | 97.08 ± 0.506 mm | 73.28 ± 0.435 mm |
| Body weight | 35.042 ± 0.112 g | 40.338 g2 | 3.242 | 47.925 ± 3.039 g | 29.35 ± 0.521 g |
| Heart weight | 0.170 ± 0.001 g | 0.0004 g2 | 1.376 | 0.190 ± 0.035 g | 0.170 ± 0.014 g |
| Kidney weight | 0.300 ± 0.001 g | 0.0023 g2 | 2.580 | 0.341 ± 0.084 g | 0.292 ± 0.048 g |
| Spleen weight | 0.106 ± 0.001 g | 0.0004 g2 | 4.048 | 0.147 ± 0.026 g | 0.105 ± 0.006 g |
| Liver weight | 2.106 ± 0.008 g | 0.1163 g2 | 2.604 | 2.614 ± 0.420 g | 1.527 ± 0.006 g |
Phenotypic description of the experimental population and both parental lines. The values are reported on the untransformed scale (unstandardized and on original scale of measurements). The scores of experimental population have been previously corrected by multiple regression for sex, litter size, and age at necropsy (see text). VA, the additive variance for the experimental population; IA, the mean-scaled additive variance.
Given the large number of loci across the genome, and to make the study of directionality feasible, we preselected the loci to be included in the current study from the results of previous mapping studies of epistatic QTLs in the same population (Fawcett et al. 2008; Norgard et al. 2008). The population (N = 2060) was genotyped at 351 approximately evenly distributed single-nucleotide polymorphisms (SNPs), located on 19 chromosomes (excluding the sex chromosome). Both studies applied Haley–Knott regression (Haley and Knott 1992) and interval mapping (Lander and Botstein 1989; Haley and Knott 1992) to map QTLs. The criterion for QTL detection was based on significance thresholds controlling for multiple comparisons and the family structure (for detailed description of threshold-generating technique see Pavlicev et al. 2008) to avoid false positives (type I error). Here we used a subset of loci reported in Fawcett et al. (2008) and Norgard et al. (2008) as having significant marginal and/or epistatic effects for each trait (see supporting information, Table S1, for data and for the list of QTL; see File S1 and File S2 for genotypic and phenotypic data). We calculated the interaction directionality separately for each trait. We included a single locus per chromosome for every trait to avoid problems due to linkage disequilibrium in this population. This restriction resulted in the loss of only a few loci per trait. The final number of loci per trait ranges from 12 to16 loci. In a preliminary analysis we examined the effect of adding nonsignificant loci to the list for each trait and estimating the overall directionality of epistasis including these loci of small, subsignificant effect. The results were very similar to those presented here. The inclusion of additional loci thus had no systematic effect on the overall pattern of epistatic interactions (not shown).
Having preselected the sets of loci for each trait, all subsequent analyses were conducted on all pairwise interactions among the loci within each trait-specific set, and directionality of epistasis is assessed across all these interactions. Thus, whereas in the gene-mapping studies it is useful to focus the efforts on the single loci, in this study, we consider the collective effects of the chosen subset of loci. Even small individual epistatic effects can accumulate substantial effect, if their pattern is directional.
Genetic effects:
We estimated the interaction and marginal genetic effects at the selected set of loci anew for this study, using the multilinear model. The epistatic effects considered here are thus different from the classical epistasis components reported in the original studies (Fawcett et al. 2008; Norgard et al. 2008). All models were fitted using the NOIA framework (Alvarez-Castro et al. 2008), as operationalized in the R package noia (Le Rouzic 2008, Le Rouzic and Alvarez-Castro 2008). This software enables an estimate of statistical as well as physiological genetic effects by regression methods and allows manipulations of the parameters in the model, such as the presence of interaction effects (dominance and epistasis), introducing the third order of epistasis (not used here), etc.
All two-locus interactions were fitted with and without dominance terms included, and model fits were compared using the AIC criterion. The model with better fit was chosen and the corresponding estimate of the epistatic coefficient (i.e., two-locus coefficient of directionality, 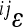 ; see below) was included in the analyses of overall directionality. The genetic effects reported refer to the allele-frequency-independent physiological effects (a, d), rather than the statistical average effects of the allele substitution (α, δ).
; see below) was included in the analyses of overall directionality. The genetic effects reported refer to the allele-frequency-independent physiological effects (a, d), rather than the statistical average effects of the allele substitution (α, δ).
The locus-specific additive variances 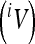 were calculated as
were calculated as
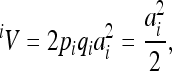 |
(6) |
where ai is the additive genetic effect at the locus i, and pi, qi are the allele frequencies of the diallelic model (∼0.5 in the present case).
We also report the total additive genetic variance of the mean-standardized trait scores, estimated as twice the among-litter variance in the F3-generation animals (Table 1), as is common for a full-sib design (Ehrich et al. 2005). Table 1 furthermore lists the univariate measure of evolvability of the traits IA (Houle 1992; Hansen et al. 2003; Hansen and Houle 2008), calculated as the additive variance, scaled by the square of the trait mean:
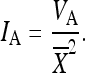 |
(7) |
Note that, while we use the term epistatic “modification” for the change in additive effects that is due to substitution at background loci, we do not imply that the epistatically interacting loci would not themselves affect the mean values.
Overall directionality:
Carter et al. (2005) identified a composite directional epistatic effect measure, which captures the main dynamical consequences of epistasis under directional selection. This measure is a variance-weighted average of the pairwise epistasis coefficients, 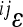 ,
,
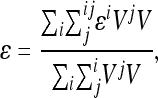 |
(8) |
where the pairwise epistatic coefficients 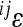 are estimated for all (N(N − 1)/2) interactions among the loci i, j within the chosen set N. The estimate for overall directionality is calculated from the pairwise epistasis coefficients, separately for each trait. The overall estimate of epistatic directionality in the current population thus includes weighing by the variances and therefore considers not only the sign of the interactions and genetic effect sizes, but also population-specific allele frequencies.
are estimated for all (N(N − 1)/2) interactions among the loci i, j within the chosen set N. The estimate for overall directionality is calculated from the pairwise epistasis coefficients, separately for each trait. The overall estimate of epistatic directionality in the current population thus includes weighing by the variances and therefore considers not only the sign of the interactions and genetic effect sizes, but also population-specific allele frequencies.
An alternative overall measure of directionality is the average absolute epistatic factor. The epistatic factor can be positive or negative; hence we use a geometric mean of absolute values of f. This value is informative about the magnitude of effect modification, but it neglects sign changes (sign epistasis).
Locus-specific directionality:
Apart from overall consistency of epistasis, an effect of the substitution at the specific locus may be modified in a consistent way. This aspect of directionality thus focuses on the pattern of epistatic interactions involving a particular locus interacting with the remaining (N − 1) loci, where N is the number of loci considered. This aspect of genetic architecture is interesting because the presence of directionality on a per-locus basis plays a role in evolution of individual gene effects by selection (e.g., loci with small effects vs. major-effect loci).
To estimate directionality at the locus level we consider only the subset of interactions (N − 1) involving the locus of interest. The equation for locus-specific average coefficient of directionality at locus j simplifies to
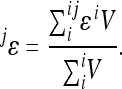 |
(9) |
Proportion of directional epistasis:
It is also of interest to determine what proportion of the epistatic effects is directional. First we calculate the total epistasis as the weighted average of absolute pairwise epsilons:
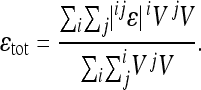 |
(10) |
For the locus-specific subset of interactions at locus j this again simplifies to
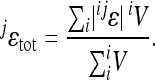 |
(11) |
An index of directional epistasis is then given as
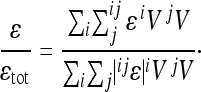 |
(12) |
across all interactions, and
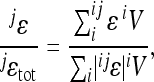 |
(13) |
for locus-specific interactions with locus j.
We also considered the effect of measurement error on the parameters in this study by generating additional random variance (20% of the phenotypic variance) around the mean. Not surprisingly, the heritabilities of the traits decrease as a consequence of increased residual variance, but neither the estimates of the additive genetic variance nor the average directionality of epistatic interactions changed substantially. In the current data, the relative measurement error is expected to be higher for internal organ weights than for skeletal traits, due to the nature of the measurement itself (organ extraction by dissection and taking wet weight at necropsy vs. measurement by calipers) as well as due to the small size of some organs. Furthermore, the estimation of measurement error is difficult for the internal organs, as their dissection and removal from the carcass cannot be repeated on the same animal.
RESULTS
We present the results of analyses of the traits on the linear scale. In most accompanying tables and figures, however, the results are presented in parallel for data on the linear scale (original scale for the lengths, cube-root transformed for the weights) and on the cubic scale (original scale for the weights, cubed for the lengths), to facilitate the discussion of scale effects in the last section. The results have three parts: (i) a brief characterization of marginal effects, (ii) the directionality of epistasis, and (iii) the effect of scale transformation.
Marginal effects:
Marginal effects refer to the additive and dominance effects of the single loci in the reference background, in this case the population mean phenotype. They are allele-frequency-independent values. The distributions of absolute values are described in Table 2 by the mean values, standard errors (SE) and the coefficients of variation (CV = 100% × standard deviation/mean). Marginal effects in this population have been discussed in detail in previous articles (Fawcett et al. 2008; Norgard et al. 2008). Note that the traits in this study are mean standardized; hence the effects are measured as dimensionless ratios to the mean and are comparable across traits.
TABLE 2.
The average marginal effects, standard errors (SE) and coefficients of variance (CV) across studied loci, on all traits and both scales
| Linear scale |
Cubic scale |
||||
|---|---|---|---|---|---|
| Trait | Average ± SE (% of the mean) | CV (%) | Trait | Average ± SE (% of the mean) | CV (%) |
| Additive effects | |||||
| Femur length | 0.73 ± 0.12 | 57.8 | (Femur length)3 | 2.19 ± 0.36 | 57.5 |
| Humerus length | 0.72 ± 0.08 | 38.1 | (Humerus length)3 | 2.15 ± 0.23 | 38.3 |
| Tibia length | 0.76 ± 0.09 | 44.8 | (Tibia length)3 | 2.27 ± 0.27 | 44.3 |
| Ulna length | 0.71 ± 0.08 | 40.9 | (Ulna length)3 | 2.10 ± 0.24 | 41.1 |
| Tail length | 1.12 ± 0.19 | 67.1 | (Tail length)3 | 3.35 ± 0.58 | 67.2 |
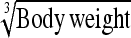 |
0.70 ± 0.11 | 64.6 | Body weight | 2.11 ± 0.32 | 63.3 |
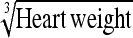 |
0.38 ± 0.06 | 56.9 | Heart weight | 1.13 ± 0.18 | 57.0 |
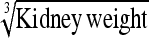 |
0.59 ± 0.10 | 72.3 | Kidney weight | 1.74 ± 0.31 | 72.6 |
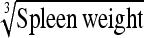 |
0.79 ± 0.15 | 69.8 | Spleen weight | 2.31 ± 0.42 | 68.9 |
 |
0.84 ± 0.14 | 58.2 | Liver weight | 2.48 ± 0.42 | 59.1 |
| Dominance effects | |||||
| Femur length | 0.23 ± 0.04 | 56.0 | (Femur length)3 | 0.65 ± 0.11 | 59.6 |
| Humerus length | 0.23 ± 0.05 | 78.0 | (Humerus length)3 | 0.68 ± 0.15 | 79.2 |
| Tibia length | 0.28 ± 0.05 | 65.0 | (Tibia length)3 | 0.80 ± 0.14 | 67.4 |
| Ulna length | 0.25 ± 0.04 | 57.6 | (Ulna length)3 | 0.73 ± 0.12 | 59.5 |
| Tail length | 0.42 ± 0.09 | 88.3 | (Tail length)3 | 1.08 ± 0.12 | 96.4 |
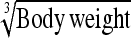 |
0.20 ± 0.04 | 81.5 | Body weight | 0.58 ± 0.11 | 82.2 |
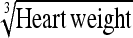 |
0.22 ± 0.06 | 104.4 | Heart weight | 0.63 ± 0.19 | 108.7 |
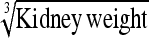 |
0.37 ± 0.06 | 68.0 | Kidney weight | 1.06 ± 0.17 | 67.5 |
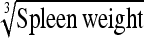 |
0.38 ± 0.09 | 88.5 | Spleen weight | 1.21 ± 0.27 | 82.6 |
 |
0.21 ± 0.05 | 81.1 | Liver weight | 0.62 ± 0.14 | 75.8 |
Directionality of epistatic effects:
Overall directionality:
The pairwise epistatic coefficients (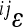 ) were combined to produce a composite directional epistasis coefficient
) were combined to produce a composite directional epistasis coefficient 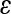 for each trait. By definition, the unit of
for each trait. By definition, the unit of 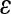 is the inverse of the trait unit. In the current work, the use of the mean-standardized data results in a unit-less coefficient of epistasis, expressing the change in genetic effects as a percentage change relative to the additive effects of the loci involved (
is the inverse of the trait unit. In the current work, the use of the mean-standardized data results in a unit-less coefficient of epistasis, expressing the change in genetic effects as a percentage change relative to the additive effects of the loci involved (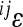 corresponds to the
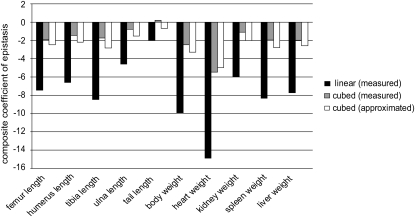
corresponds to the 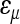 in Carter et al. 2005). The mean standardization allows direct comparison of coefficients of directionality among the traits. For example, the composite epsilon of +1 means that an allele substitution at the locus 1, increasing the phenotypic mean by 1% (1y = 0.01), increases the effects of the substitution at other loci on average by ɛ × 1y = 1%. We detected negative overall directionality in epistatic coefficients for all traits on the linear scale (Figure 2, solid bars). The strength of directionality is interpreted as the influence that the composite epsilon would have on the trait in the case of selection along the specified phenotypic direction (Carter et al. 2005); in this case the direction of selection considered is toward increased size. With the composite epsilon equal to −10, as in body weight, a substitution of a SM/J allele with a LG/J allele (henceforth SM ← LG) that has an effect of a 1% increase in trait mean at one locus decreases the effect of the substitution SM ← LG at the second locus by 10%. A negative composite epsilon thus indicates that epistasis, on average, has a canalizing effect in the phenotypic direction considered, in this case, increased size. The analysis yielded negative directionality with magnitudes in the range of
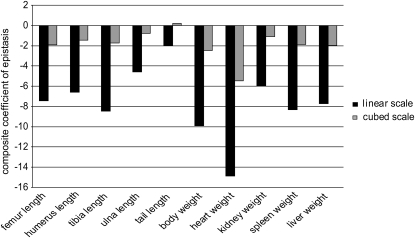
in Carter et al. 2005). The mean standardization allows direct comparison of coefficients of directionality among the traits. For example, the composite epsilon of +1 means that an allele substitution at the locus 1, increasing the phenotypic mean by 1% (1y = 0.01), increases the effects of the substitution at other loci on average by ɛ × 1y = 1%. We detected negative overall directionality in epistatic coefficients for all traits on the linear scale (Figure 2, solid bars). The strength of directionality is interpreted as the influence that the composite epsilon would have on the trait in the case of selection along the specified phenotypic direction (Carter et al. 2005); in this case the direction of selection considered is toward increased size. With the composite epsilon equal to −10, as in body weight, a substitution of a SM/J allele with a LG/J allele (henceforth SM ← LG) that has an effect of a 1% increase in trait mean at one locus decreases the effect of the substitution SM ← LG at the second locus by 10%. A negative composite epsilon thus indicates that epistasis, on average, has a canalizing effect in the phenotypic direction considered, in this case, increased size. The analysis yielded negative directionality with magnitudes in the range of 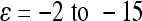 (Figure 2 and Table 3). To illustrate the effect of composite epsilon at the phenotypic level we present in Table 4 the estimated sum of additive (column 3) and total genetic effects (i.e., including the directional epistatic term; column 5). The differences in phenotypic means between the SM/J and LG/J strains are listed in column 2. Columns 4 and 6 list the proportion of this difference that is accounted for by additive (4) and additive plus directional epistatic effects (6). The overall additive effect equals the sum of additive effects at all included loci (column 3), while the overall total effect equals the sum of additive and directional epistatic contributions in all pairwise interactions (column 5). Note that in spite of negative directionality, epistasis sometimes increases the phenotypic effect relative to the prediction based on additivity. This happens when the genotype-to-phenotype mapping is complex, above all when there is sign reversal of genetic effects. This issue is discussed in more detail below. We note that the effects are similar on both scales. The ratio of the total effect, including epistasis, to the additive effect alone (rightmost column in Table 4) reveals that in most traits, the epistasis reduces the effect (up to 47% in spleen). In some traits there is no net phenotypic effect of epistasis, or the effect is even positive in spite of the negative coefficient of directionality. This effect is generated predominantly by sign epistasis.
(Figure 2 and Table 3). To illustrate the effect of composite epsilon at the phenotypic level we present in Table 4 the estimated sum of additive (column 3) and total genetic effects (i.e., including the directional epistatic term; column 5). The differences in phenotypic means between the SM/J and LG/J strains are listed in column 2. Columns 4 and 6 list the proportion of this difference that is accounted for by additive (4) and additive plus directional epistatic effects (6). The overall additive effect equals the sum of additive effects at all included loci (column 3), while the overall total effect equals the sum of additive and directional epistatic contributions in all pairwise interactions (column 5). Note that in spite of negative directionality, epistasis sometimes increases the phenotypic effect relative to the prediction based on additivity. This happens when the genotype-to-phenotype mapping is complex, above all when there is sign reversal of genetic effects. This issue is discussed in more detail below. We note that the effects are similar on both scales. The ratio of the total effect, including epistasis, to the additive effect alone (rightmost column in Table 4) reveals that in most traits, the epistasis reduces the effect (up to 47% in spleen). In some traits there is no net phenotypic effect of epistasis, or the effect is even positive in spite of the negative coefficient of directionality. This effect is generated predominantly by sign epistasis.
Figure 2.—
Directionality of epistasis on both scales. The plot shows overall directionality on linear and on cubic scales. Overall directionality is expressed as variance-weighed composite epsilon across the pairwise interactions among selected sets of loci. The sets of loci included differ between traits.
TABLE 3.
Coefficient of directionality, the proportion of directional epistasis in total epistasis and the epistatic factor
| Linear scale |
Cubic scale |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Trait | ɛ |
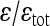 (%) (%) |
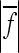 |
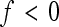 (%) (%) |
Trait | ɛ |
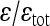 (%) (%) |
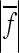 |
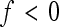 (%) (%) |
| Femur lt | −7.46 | 40.5 | 0.937 | 2.4 | (Femur lt)3 | −1.92 | 32.2 | 0.958 | 3.1 |
| Humerus lt | −6.59 | 26.9 | 0.954 | 0.7 | (Humerus lt)3 | −1.46 | 18.3 | 0.968 | 0.6 |
| Tibia lt | −8.45 | 41.5 | 0.902 | 0.0 | (Tibia lt)3 | −1.73 | 26.4 | 0.927 | 0.0 |
| Ulna lt | −4.58 | 18.3 | 0.924 | 0.7 | (Ulna lt)3 | −0.78 | 9.7 | 0.940 | 0.6 |
| Tail lt | −2.02 | 22.6 | 0.881 | 1.0 | (Tail lt)3 | 0.19 | 6.1 | 0.920 | 2.0 |
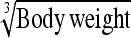 |
−9.90 | 40.9 | 0.892 | 10.1 | Body wt | −2.49 | 31.9 | 0.904 | 10.8 |
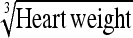 |
−14.88 | 16.3 | 0.896 | 15.5 | Heart wt | −5.47 | 17.1 | 0.823 | 16.2 |
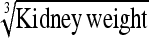 |
−6.01 | 18.8 | 0.923 | 6.9 | Kidney wt | −1.12 | 11.2 | 0.929 | 7.6 |
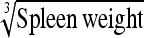 |
−8.33 | 30.9 | 0.960 | 13.5 | Spleen wt | −1.88 | 18.3 | 0.874 | 15.5 |
 |
−7.72 | 33.7 | 0.870 | 6.4 | Liver wt | −1.96 | 25.7 | 0.931 | 7.1 |
The values of the composite coefficient of directionality (ɛ), ratio between directional and total epistasis 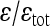 , the geometric mean of the absolute epistasis factor (
, the geometric mean of the absolute epistasis factor (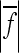 ), and the percentage of interactions with negative f (sign epistasis). Results are shown for all traits, on linear and cubic scale. wt, weight; lt, length.
), and the percentage of interactions with negative f (sign epistasis). Results are shown for all traits, on linear and cubic scale. wt, weight; lt, length.
TABLE 4.
Predicted additive effects and their changed corresponding values due to directional epistasis on linear and cubic scales
| Predicted additive effects |
Predicted additive effects + epistasis |
Total effect/additive effect | ||||
|---|---|---|---|---|---|---|
| Trait | LG/J – SM/J (mean ± SE) | Absolute value | Proportion of LG/J-SM/J (%) | Absolute value | Proportion of LG/J-SM/J (%) | |
| Linear scale | ||||||
| Femur lt | 2.820 ± 0.08 mm | 2.277 mm | 80.76 | 1.922 mm | 68.15 | 0.84 |
| Humerus lt | 2.160 ± 0.02 mm | 2.100 mm | 97.24 | 2.189 mm | 101.34 | 1.04 |
| Tibia lt | 2.230 ± 0.08 mm | 3.096 mm | 138.85 | 2.738 mm | 122.80 | 0.88 |
| Ulna lt | 2.210 ± 0.04 mm | 2.593 mm | 117.33 | 2.598 mm | 117.57 | 1.00 |
| Tail lt | 23.800 ± 0.66 mm | 20.258 mm | 85.12 | 20.622 mm | 86.65 | 1.02 |
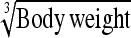 |
0.548 ± 0.08 g⅓ | 0.599 g⅓ | 109.31 | 0.467 g⅓ | 85.18 | 0.78 |
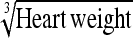 |
0.021 ± 0.04 g⅓ | 0.011 g⅓ | 53.54 | 0.023 g⅓ | 111.32 | 2.08 |
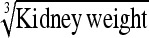 |
0.035 ± 0.07 g⅓ | 0.067 g⅓ | 190.33 | 0.055 g⅓ | 155.09 | 0.81 |
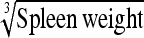 |
0.056 ± 0.03 g⅓ | 0.022 g⅓ | 39.55 | 0.012 g⅓ | 21.13 | 0.53 |
 |
0.226 ± 0.07 g⅓ | 0.232 g⅓ | 102.57 | 0.228 g⅓ | 100.77 | 0.98 |
| Cubic scale | ||||||
| (Femur lt)3 | 2223.11 ± 219.55 mm3 | 1686.970 mm3 | 75.88 | 1525.192 mm3 | 68.61 | 0.90 |
| (Humerus lt)3 | 1044.39 ± 49.01 mm3 | 963.084 mm3 | 92.21 | 1032.592 mm3 | 98.87 | 1.07 |
| (Tibia lt)3 | 2111.73 ± 257.11 mm3 | 2804.255 mm3 | 132.79 | 2725.599 mm3 | 129.07 | 0.97 |
| (Ulna lt)3 | 1359.42 ± 64.12 mm3 | 1546.468 mm3 | 113.76 | 1597.118 mm3 | 117.49 | 1.03 |
| (Tail lt)3 | 521422.47 ± 43815.27 mm3 | 523270.645 mm3 | 100.35 | 556992.890 mm3 | 106.82 | 1.06 |
| Body wt | 18.575 ± 3.08 g | 18.995 g | 102.26 | 15.970 g | 85.97 | 0.84 |
| Heart wt | 0.020 ± 0.04 g | 0.010 g | 48.16 | 0.018 g | 89.31 | 1.85 |
| Kidney wt | 0.049 ± 0.09 g | 0.089 g | 181.61 | 0.074 g | 150.10 | 0.83 |
| Spleen wt | 0.042 ± 0.02 g | 0.015 g | 36.15 | 0.010 g | 24.60 | 0.68 |
| Liver wt | 1.087 ± 0.42 g | 1.126 g | 103.55 | 1.141 g | 104.92 | 1.01 |
The absolute phenotypic difference between the parental strains LG/J and the SM/J (column 1), the predicted absolute phenotypic effect of substitution of both alleles based on sum of estimated additive genetic effects (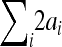 , column 2), and expressed as the percentage of the phenotypic difference between mean LG/J and SM/J (
, column 2), and expressed as the percentage of the phenotypic difference between mean LG/J and SM/J (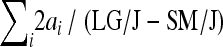 , column 3) . Column 4 is analogous to the column 2, predicting the phenotypic effect but including epistasis:
, column 3) . Column 4 is analogous to the column 2, predicting the phenotypic effect but including epistasis: 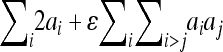 , column 5 expresses the predicted phenotypic effect including epistasis as the percentage of phenotypic difference between the parental strains (
, column 5 expresses the predicted phenotypic effect including epistasis as the percentage of phenotypic difference between the parental strains (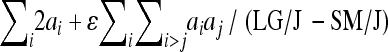 ). Column 6 shows the proportion between total (additive + epistatic) and the additive effect. Negative directionality is manifested as this ratio being <1. wt, weight; lt, length.
). Column 6 shows the proportion between total (additive + epistatic) and the additive effect. Negative directionality is manifested as this ratio being <1. wt, weight; lt, length.
Note that sign epistasis (f < 0) is associated with a negative coefficient of directionality, regardless of the absolute value of f. This follows from Equation 3, from which we can see that 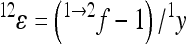 ; hence epsilon has the opposite sign compared to the reference effect, for all f < 1. When calculating a composite epsilon in the presence of sign epistasis at many loci, both the epistatic interactions reducing reference effects of an allele without sign change, as well as epistatic interactions reversing the sign (reducing or increasing the absolute reference effect) contribute to the negative overall directionality. This causes deviations from the straightforward interpretation that a negative composite epistatic coefficient translates into reduced positive gene effects on the phenotypic value.
; hence epsilon has the opposite sign compared to the reference effect, for all f < 1. When calculating a composite epsilon in the presence of sign epistasis at many loci, both the epistatic interactions reducing reference effects of an allele without sign change, as well as epistatic interactions reversing the sign (reducing or increasing the absolute reference effect) contribute to the negative overall directionality. This causes deviations from the straightforward interpretation that a negative composite epistatic coefficient translates into reduced positive gene effects on the phenotypic value.
Examination of epistatic factors (Table 3) reveals sign epistasis (f < 0) in up to 16% of the interactions, the highest proportion being in spleen and heart (14 and 16%, respectively), and the lowest in humerus, tibia, and ulna (< 1%).
In general, the comparison between the predicted phenotype based on the local estimate of directionality and the total phenotypic difference between the parental strains in Table 4 assumes that the local curvature estimated in our experimental population is stable over all generations between the two parental strains. We do not have the information on directionality from other generations; therefore, Table 4 is presented here for purpose of illustration of the meaning, rather than as extrapolation of the actual effects across populations.
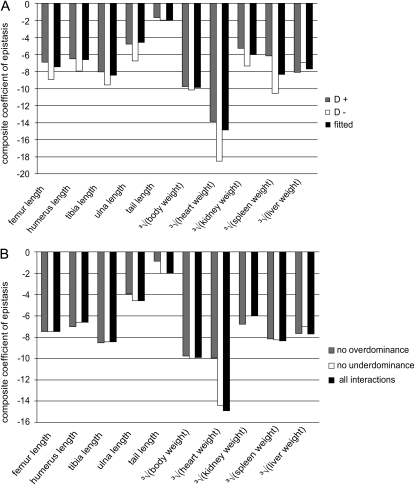
We further tested how dominance in general and over- and underdominance specifically affects our results. We included and then excluded dominance from all pairwise interactions and calculated composite coefficient of epistasis each time to explore the overall effect of dominance on the directionality of epistasis. The two resulting composite epsilons differed somewhat in magnitude, but the pattern of directionality was maintained (Figure 3A). This indicates a weak effect of dominance on the overall pattern of directionality. Even so, rather than settling for the general model with or without dominance, we included or excluded dominance in individual interactions on the basis of whether the inclusion of dominance resulted in a better fit (using the Akaike criterion, AIC). On average, 54% of models including dominance produced a better fit (with a range from 24 to 78% for different traits). Another concern associated with the parameterization of epistasis in the multilinear model is the existence of over- or underdominance. In the empirical data, apart from the true over- and underdominance in genetic effects, some stochastic over- and underdominance due to random errors in estimates can be expected at loci with very small additive genetic effects. While the multilinear model itself can include overdominance, the interpretation of epsilon in terms of evolutionary dynamics becomes more complex when overdominance is present. To test to what extent our estimate of directionality is affected by over- and underdominance we have excluded the interactions involving both phenomena from the data set and repeated the analysis. The effects on the magnitude of ɛ due to over- or underdominance are minimal, and the pattern of directionality in all traits was maintained (Figure 3B).
Figure 3.—
Effect of dominance on epistatic directionality. (A) The resulting composite epistatic coefficients if all interactions are modeled with (shaded) and without (open) dominance. The solid columns show the results based on the applied method of selecting interaction with or without dominance based on the better fit to data. (B) The effect of under- and overdominance on directionality of epistasis. The overall directionality of epistasis resulting from data excluding the interactions with overdominance (shaded) or underdominance (open) is compared to the case where all interactions are included (solid). Note that in spite of some difference in absolute values of epsilon, the pattern is unchanged. The coefficients are unitless and the traits are on the linear scale in both plots.
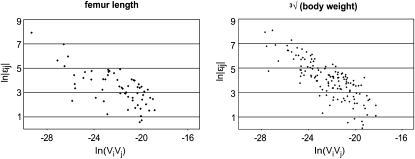
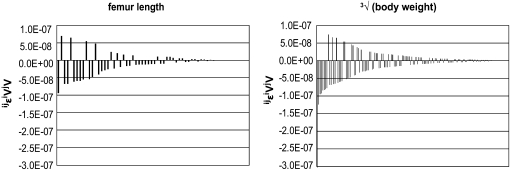
To understand the contributions of the individual interactions to the overall pattern of directionality, we explored the distribution of pairwise epistasis, between loci i and j (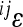 ). When plotted against additive variances at the interacting loci, we see that large values of
). When plotted against additive variances at the interacting loci, we see that large values of 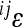 tend to coincide with small marginal effects of the involved loci and vice versa. Figure 4 shows examples of this for 2 of the 10 traits: femur length and the cube root of body weight. The plots show the relationship between
tend to coincide with small marginal effects of the involved loci and vice versa. Figure 4 shows examples of this for 2 of the 10 traits: femur length and the cube root of body weight. The plots show the relationship between 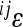 and the product of additive variances at the locus (
and the product of additive variances at the locus (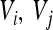 ), on the log–log scale. For this plot, the absolute values of the directional epistasis coefficients,
), on the log–log scale. For this plot, the absolute values of the directional epistasis coefficients, 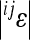 , were used to represent the magnitude. We can see from this plot that the effect of even very large
, were used to represent the magnitude. We can see from this plot that the effect of even very large 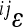 on the mean phenotype is small, as mostly the additive variance (i.e., reference effects
on the mean phenotype is small, as mostly the additive variance (i.e., reference effects 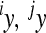 ) of the substitution at the respective loci was small. The relationship for the remaining traits was similar (not shown).
) of the substitution at the respective loci was small. The relationship for the remaining traits was similar (not shown).
Figure 4.—
The relation between the epistatic coefficient and additive variance across interactions. The two exemplary scatter plots show the decrease of the pairwise epistatic coefficient with increased additive variance at the loci involved in interaction. The plots are on log–log scale and use absolute size of epsilon, as the sign is irrelevant in this context. Note that when additive effects are small, even small epistatic effect on phenotype results in large estimated epsilon, and vice versa.
Having established the relationship between the magnitude of 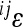 and the additive effects at the interacting loci, we considered the distribution of contributions to average directionality as the phenotypic effect of
and the additive effects at the interacting loci, we considered the distribution of contributions to average directionality as the phenotypic effect of 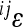 , expressed as
, expressed as 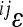 weighted by the genetic variance at the two loci involved:
weighted by the genetic variance at the two loci involved: 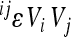 . All variables refer to the mean-standardized data on a linear scale. The examples of distributions are shown in the two profiles in Figure 5 for the two traits used above; the remaining traits follow the same pattern. The profiles show few interactions with large effect, slight predominance of interactions with negative directionality, and a long tail of interactions with small effects, for most traits.
. All variables refer to the mean-standardized data on a linear scale. The examples of distributions are shown in the two profiles in Figure 5 for the two traits used above; the remaining traits follow the same pattern. The profiles show few interactions with large effect, slight predominance of interactions with negative directionality, and a long tail of interactions with small effects, for most traits.
Figure 5.—
Distributions of weighed epistatic effects on phenotype. The weighed effects (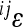 iVjV) of single epistatic interactions are ordered from largest to smallest according to their absolute magnitude. The asymmetry of the distribution is an indication of directionality of epistasis. Two exemplary traits corresponding to those in Figure 4 are represented on the same scale, and the remaining traits follow a similar pattern, with varying absolute effect sizes. The single bars represent single interactions, ordered from left to right according to their decreasing absolute size. They can be positive or negative on the y-axis, while the x-axis has no quantitative meaning. The traits are on a linear scale.
iVjV) of single epistatic interactions are ordered from largest to smallest according to their absolute magnitude. The asymmetry of the distribution is an indication of directionality of epistasis. Two exemplary traits corresponding to those in Figure 4 are represented on the same scale, and the remaining traits follow a similar pattern, with varying absolute effect sizes. The single bars represent single interactions, ordered from left to right according to their decreasing absolute size. They can be positive or negative on the y-axis, while the x-axis has no quantitative meaning. The traits are on a linear scale.
Locus-specific directionality of epistasis:
Directionality of epistatic interactions for single focal loci exhibits a large amount of variation in locus-specific directionality among the focal loci, in all traits (presented in Table S2). Some of this variation may be due to a higher level of error, as the sample size of interactions is smaller compared to the overall analysis (N − 1 vs. N(N − 1)/2). The locus-specific epistatic factors are similarly variable (not shown separately). Here, between 0 and 39% of interactions involve sign reversal (f < 0), meaning that the substitution of SM/J allele by a LG/J allele (SM/J ← LG/J) at a particular locus increases the size in most backgrounds. The sign reversal is more frequent in internal organ measurements (up to 33% of locus-specific interactions) than in the long bone and tail lengths (up to 13% locus-specific interactions). It is apparent that sign epistasis tends to be associated with single loci rather than distributed across interactions.
Proportion of directional epistasis relative to the total epistasis:
Across all interactions, ɛ/ɛtot:
The estimated total and directional average epistasis coefficients are shown in Table 3 for all traits. The total epistatic effects are on average 2.5- to 6-fold as large as the directional effects.
Across locus-specific interactions, jɛ/jɛtot:
The median ratios of directional to total average epistasis for the subsets of interactions with single focal loci are listed in Table 5. The complete list of values of directionality and ratios of directional to total epistasis for each focal locus is presented in Table S2. The ratio of directional epistasis to total epistasis varied strongly among single focal loci: from 1:100 to 1:1.
TABLE 5.
The median ratio of directional epistasis to total epistasis for locus-specific interaction subsets
| Linear scale |
Cubic scale |
||
|---|---|---|---|
| Trait | Median jɛ/jɛtot (min–max) | Trait | Median jɛ/jɛtot (min–max) |
| Femur lt | 36.6% (1.7–78.5) | (Femur lt)3 | 30.7% (3.0–64.8) |
| Humerus lt | 26.0% (2.8–73.5) | (Humerus lt)3 | 23.5% (1.7–68.9) |
| Tibia lt | 42.7% (2.0–86.2) | (Tibia lt)3 | 32.8% (4.4–75.3) |
| Ulna lt | 23.9% (0.2–90.1) | (Ulna lt)3 | 27.5% (2.0–88.3) |
| Tail lt | 40.1% (1.0–96.1) | (Tail lt)3 | 31.1% (2.6–88.0) |
 |
38.0% (2.2–72.6) | Body wt | 29.3% (3.5–63.9) |
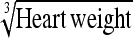 |
40.5% (15.1–86.2) | Heart wt | 41.1% (11.1–89.8) |
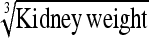 |
30.7% (2.5–89.3) | Kidney wt | 30.1% (4.0–90.0) |
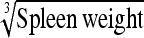 |
30.0% (1.5–91.7) | Spleen wt | 22.0% (1.0–87.7) |
 |
35.7% (1.9–80.7) | Liver wt | 37.6% (0.4–79.7) |
Medians across all sets (corresponding to 12–16 focal loci, depending on a trait) are given and supplemented by the ranges below the median. The values summarized here are listed in full for each focal locus in Table S2. wt, weight; lt, length.
Scale effects:
The effect of scale is observable in the marginal effects (Table 2). The effects of an allele substitution measured in percentage of the mean on a cubic scale are roughly threefold higher than on the linear scale for all traits, as expected. When traits were analyzed to assess directional epistasis on a cubic scale, the weights, as well as cubed linear measurements, manifest lesser values of composite directional epistatic coefficients (Figure 2), as predicted from the effects of scale transformation.
To compare the scale-related change in directionality with the change predicted due to scale transformation alone, we have used the estimate of directionality on the linear scale and predicted its change when transforming the scale to cubic. Figure 6 shows the comparison of the observed values of the composite coefficient of directionality on the cubic scale and the ones predicted on the basis of the composite epsilon on the linear scale. In spite of simplifications, the prediction matches the observation rather well. The sources of discrepancy can be diverse, including the fit of the multilinear model on both scales and the distribution of allelic effects, as discussed in detail in the next section.
Figure 6.—
Change in directionality due to scale transformation. Plot shows the composite measure of directionality measured on linear and cubic scales in comparison with the approximation of directionality for the cubic scale.
DISCUSSION
We have applied a novel theoretical concept, epistatic directionality, to empirical data in order to describe how epistasis affects the response to directional selection in a population. We found predominantly negative overall directional epistasis for increased trait size. However, we also found that composite measures of directionality across loci may be difficult to interpret as predictive of response to selection, when the mapping of genotype to phenotype is less well behaved, for example, when there is sign epistasis. We furthermore explored the effect of measurement scale and demonstrated how the genetic effects are expected to change with the power transformation of scale and how this manifests itself in the estimate of overall directionality. In the following, we first discuss particularities of applying the multilinear model to QTL data in general, and specifically the application of the composite measures of directionality. Next, we address the detected directionality and finally the effects of power transformation of scale in more detail.
The multilinear model and overall directionality of epistatic interactions:
We have demonstrated the implementation of the multilinear model (Hansen and Wagner 2001a) to QTL data and the application of measures of overall epistatic directionality (Carter et al. 2005). Here we focus on the details of data that may impose limitations to the use of multilinear model or difficulties to the interpretation of the measure of overall directionality.
The first limitation applies to the scale of measurements. The scale of trait measurements affects the directionality of epistatic interaction in two ways: by the model limitations and by the scale-dependent change in genotype–phenotype map. Here we briefly address the effect of scale on the model fit, whereas the effect of scale on the genotype–phenotype map is discussed in a separate section below (see Scale in genetic architecture). The multilinear model cannot fit equally well to data on multiple scales. Therefore the comparison of fit (by, e.g., the Akaike criterion) among scales may be useful when deciding on which scale the model will give the most accurate assessment of directionality of epistasis. In the data used here, the approximation is better on the linear scale than on the cubic scale for all traits. The estimate of epistatic directionality on the cubic scale may thus show some bias due to a worse fit of the model.
The second limitation of the model concerns the interpretation of the composite coefficient of directionality (ɛ) with respect to the phenotypic change. The presence of opposite effects of allele substitution in reference effects (iy < 0, jy > 0), as well as in form of sign epistasis, may obscure the interpretation of the composite epsilon in terms of directional phenotypic change if such opposite effects are frequent and/or large. The interpretation of the pairwise coefficients of directionality is opposite in this case: a negative coefficient increases the phenotypic value and enhances response to selection, while a positive coefficient decreases the phenotypic value. For example, given the interaction between loci with opposite reference effects, the term 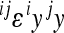 is positive and increases the phenotype if
is positive and increases the phenotype if 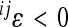 . This is analogous to what we have shown previously for the sign epistasis, in which the sign reversal occurs in a different background genotype. In the presence of sign reversal, either in reference effect or due to sign epistasis, the sign of the overall coefficient of epistasis may be composed of the opposite effects on the phenotype and may lead to a misinterpretation of the overall effect of epistasis on the phenotypic response to directional selection. A strongly negative epsilon does not necessarily mean less (relative to additive effects) potential response to selection toward increased values if some of the canalized loci have in fact negative effects. Note that this is an interpretational complication of composite epsilon in terms of the phenotypic effect rather than a problem of the model itself.
. This is analogous to what we have shown previously for the sign epistasis, in which the sign reversal occurs in a different background genotype. In the presence of sign reversal, either in reference effect or due to sign epistasis, the sign of the overall coefficient of epistasis may be composed of the opposite effects on the phenotype and may lead to a misinterpretation of the overall effect of epistasis on the phenotypic response to directional selection. A strongly negative epsilon does not necessarily mean less (relative to additive effects) potential response to selection toward increased values if some of the canalized loci have in fact negative effects. Note that this is an interpretational complication of composite epsilon in terms of the phenotypic effect rather than a problem of the model itself.
The opposite reference effects can occur due to the choice of reference, or due to estimation error. In the first case, the allelic reference effects may be measured in a particular direction, because they are classified by their source population rather than by their effects. For example, in this study we distinguish the LG/J alleles from SM/J alleles and are interested in keeping track of the origin of the alleles. In general, LG/J alleles are associated with larger phenotypic values than SM/J alleles. In some cases, however, LG/J alleles are associated with smaller phenotypic values. This causes negative reference effects. The effect of the sign of reference effects can be avoided by different coding of the alleles. The alleles need not be thought to have classification due to the source population (SM/J and LG/J); instead the low vs. high allele can be evaluated locus by locus with respect to allelic effect on the phenotype within the study, as would be the case in a natural population. In this way, the above effect may be minimized.
The negative reference effects can also occur due to model fitting. Reference genotypic values and reference effects are estimated anew for every pairwise interaction. The reference effects of a substitution at the same locus vary somewhat across interactions, depending on the locus it is interacting with. Very small positive reference effects may sometimes become negative due to estimation error. This effect is reduced when calculating the composite epsilon by weighing by the (correspondingly small) variances; however, it can accumulate weight if the same locus with large effects is involved in interaction with change of sign in reference effects of many other loci. We demonstrate the consequences of this effect in two traits: tail and spleen. In both cases, we detected a single locus (Bod19.1) with large positive reference effects that is involved in many interactions with negative reference effects. When other loci interact with Bod19.1, their reference effects are slightly negative. Thus the substitutions of a small with a large allele (SM ← LG) at several loci lead to smaller phenotype in the presence of SM/J at the locus Bod19.1. As the effect (and thus the variance) due to locus Bod19.1 is larger than average, these multiple interactions contribute a considerable portion to the variance-weighed composite coefficient of directionality. The particular interactions are often associated with the negative pairwise coefficient of directionality (as explained above); however, they increase the phenotypic value relative to the expectation from the additive effects only. Including this locus into the study inflates the negative directionality of tail from −2 to −21 and of spleen −8.3 to −18. We found in locus-specific analysis that sign changes are often associated with single loci. This shows that some caution with respect to sign reversal either in reference effects or in epistatic effects is needed when interpreting the composite coefficient of directionality, especially with loci of large effects. With some attention to the detail of data, these limitations can be identified and considered prior to interpreting composite coefficient of directionality. Also, the average absolute epistatic factor offers an alternative measure of modification of genetic effects that is not susceptible to the sign change.
Selection and directionality of epistasis:
Our analysis of epistatic interactions in the mouse population revealed negative overall directionality of epistatic coefficients on the linear scale for all 10 traits considered. In other words, if the allele substitutions at loci i and j individually increase a length measurement by 1% each when measured separately, their simultaneous substitution increases the measurement by less than 2%. Negative overall directionality expresses this kind of effect as being the average overall effect in the interactions included in the analysis. These results predict that epistasis on average reduces the percentage response to directional selection for size increase relative to the expectation based on the additive genetic effects alone. The strength of the directional effect for traits on the linear scale is between ɛ = −2 and ɛ = −15, which in this population mostly decreases the summed additive genetic effects across loci (by up to 47%; see column 7 in Table 4). In some traits, however, the coefficient of epistasis has no straightforward interpretation due to presence of sign reversals. The mean absolute epistatic factor (Table 3), which describes the modification of the absolute allelic effect by epistasis, indicates reduction in the size of allelic effects in all traits. When considered as the absolute value, the mean epistatic factor may be a more informative measure of overall effects, especially in more complex genotype–phenotype map as described above.
Locus-specific analysis of the average epistatic directionality revealed wide variation in how the effects of single loci are modified by epistasis. Thus, the effect of single loci can be increased as well as reduced relative to the additive genetic variance due to epistasis. The difference between locus-specific and overall directionality demonstrates that directionality tends to be cancelled out when averaged across interactions. This directionality nevertheless has an effect when selection acts on genetic effects at single loci.
Several assumptions are involved in using these results to predict the outcome of directional selection. The main assumption is that the subset of loci included and their interactions are an unbiased representation of genetic effects in the population. The choice of loci in this study was influenced by the size of their effects and their location on separate chromosomes. Undoubtedly, many loci were excluded that could potentially affect the pattern of directionality detected here if their effects differed from the ones found. Nevertheless, the relative consistency of the pattern across traits, as well as the finding that the same pattern is supported when larger sets of loci were used (not shown), is remarkable and suggests that these results are robust. We further assumed that the independent estimation of the pairwise epistatic coefficients (two loci at the time as opposed to simultaneously including all loci) is a fair approximation of interaction effects. Studying pairwise interactions including only two loci at a time can introduce error due to confounding effects, i.e., the variation contributed by the correlated loci. The theoretical solution to these problems, namely including all loci as covariates in the single model, remains problematic both due to linkage disequilibrium and due to computational unfeasibility, particularly if we assume that the variation of traits is underlain by a high number of loci with small effects. Both of the above assumptions are common in studies of epistasis, but are nevertheless noteworthy.
We might also ask whether the pattern itself may be a consequence of past selection in the parental strains during their origination. There is evidence of reduced selection response in spite of existing additive genetic variance after the 35th generation of selection in the LG/J line (Chai 1966, Wilson et al. 1971). However, this effect has been attributed to pleiotropic effects (Wilson et al. 1971) and could also have been caused by opposing natural selection on the same traits. The negative directional epistasis could be an alternative explanation. In general, the inference from the effects of allele substitution present in the generation of the LG/J line to the effects in the present intercross population would require that the epistatic effects are just as similar between the two populations as are the additive effects of allele substitutions (LG/J alleles mostly causing larger phenotypes, SM/J mostly causing smaller phenotypes). It is clear, however, that the LG/J alleles in the LG/J × SM/J intercross are, at least in part, exposed to a different genetic background than was experienced during the production of the LG/J strain.
The context dependency of allelic effects also means that changes in the genetic background may change the directionality of epistasis. The potential to infer the long-term effect on selection on the basis of the directionality of epistatic effects detected in the current population depends on the smoothness of the genotype–phenotype map (Hermisson et al. 2003; Carter et al. 2005). A map with well-behaved genetic effects (e.g., little under- or overdominance, little sign reversal) has a relatively constant curvature and allows such inference. In contrast, a complex genotype–phenotype map with variable sign and value of coefficient of directionality (see example in Figure 7) allows only short-term prediction of the effects of epistasis. Higher-order epistasis needs to be assessed to predict the change in directionality (Hansen et al. 2006). So far we know little about the curve connecting different populations between parental strains in Figure 7. One indication of a complex map may be high variance of pairwise epistatic coefficients contributing to composite epsilon and strong effects of single alleles. As shown in the examples of tail and spleen, single loci with large effects, as are often present in selected populations, may strongly influence the coefficient of directionality. This study also shows that the traits differ in the complexity of their epistatic architectures. The estimation of directionality intended in this study refers to the current population and is a local estimate of the curvature of the genotype–phenotype map. Whether the detected pattern of epistatic directionality is population specific or is a common pattern remains to be addressed by exploring further populations, for example different line crosses.
Figure 7.—
local curvature of genotype–phenotype (GP) map changes in different populations. The plot shows a hypothetical example of a variable GP map, where the curvature changes. In such situations, prediction of the long-term effects of epistasis by a composite parameter becomes complex (see Hansen et al. 2006).
Scale in genetic architecture:
Scale affects the measurement of genetic effects in general (e.g., Lynch and Walsh 1998); thus considering and understanding such effect is important, as it may affect the inference of the measured parameters. The invariance to scale change is a desirable property characterizing a generally applicable measurement.
We have shown that numerical difference between the directionality of epistasis on linear and on cubic scales can be explained by the predictable effect of power transformation on genetic effects. However, the effect of directionality is invariable across scales even though the numerical values of coefficient of directionality change. The modification (in percentage) of the effect of substitution at the locus i is a product of the coefficient of directionality with the effect of substitution at locus j. For example, if the effects of substitution increase threefold due to scale transformation, and the value of epsilon decreases threefold, the modification of the effects, expressed in percentage of the reference effect at the locus i, is maintained. This means that genetic architecture of the trait does not change with respect to directionality of epistasis, if the data are transferred to a different scale. This is valid, because the coefficient of directionality only has a meaning in the context of the reference effects. Thus fitting the multilinear model on linear scale, we can approximate the numerical value of epsilon on the cubic scale.
Is there an inherent scale on which to measure the particular traits? We find no evidence that either of the two scales was more or less appropriate for any particular trait type; the numerical difference between the values of epsilon on two scales is consistent with the prediction based on scale transformation in all trait types. Rather, the effects of scale transformation present here are influenced by the particular size and distribution of genetic effects, specific to single traits.
Acknowledgments
The authors thank members of Cheverud Lab for data collection and L. S. Pletscher for help with the database. We thank Arne Gjuvsland for improving the code. Also thanks go to Jason Wolf for data access. Work was supported by the grant no. 177857 from the Norwegian Research Council to T.F.H. and National Science Foundation grant BCS-0725068 to J.M.C. M.P. was supported in part by Erwin Schrödinger Postdoctoral Fellowship (J2631-B12) of the Austrian Science Fund (FWF), and A.P.S.L. was supported by a Marie Curie fellowship (EIF-220558).
APPENDIX: EFFECTS OF SCALE TRANSFORMATIONS
Epistasis is a consequence of nonlinearities in the genotype–phenotype map. Any description of epistasis therefore changes with nonlinear transformation of the data. In this article we consider epistasis on two different scales, “cubic” and “linear.” In this appendix we consider the consequences of power transformations on the multilinear model. We note that these are of two sorts. On one hand, there is the necessary inherent change in the genotype–phenotype map when the phenotype is transformed, and on the other, there is the change in fit of the multilinear model, which should be viewed as an approximation to a more complex genotype–phenotype map. Here we focus on the former effect.
Since we are considering only pairwise epistasis, we focus on the two-locus case. We consider four genotypes:
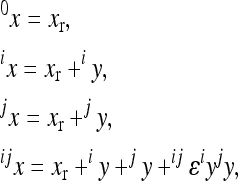 |
where 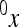 is the genotypic value of the reference genotype where no substitutions have been made,
is the genotypic value of the reference genotype where no substitutions have been made, 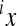 is the genotypic value after a substitution with effect
is the genotypic value after a substitution with effect 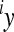 on locus i,
on locus i, 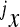 is the genotypic value after a substitution with effect
is the genotypic value after a substitution with effect 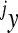 at locus j, and
at locus j, and 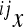 is the genotypic value after both substitutions have been made.
is the genotypic value after both substitutions have been made.
Note that in this study the phenotypic values are mean standardized. We can therefore rewrite these equations for the mean-standardized scale as
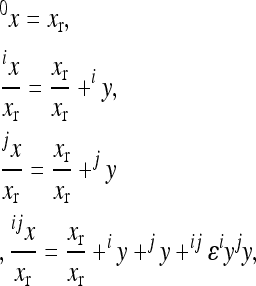 |
or
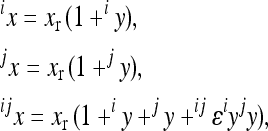 |
Now consider the same genotypes after a power transformation  . Then we get
. Then we get
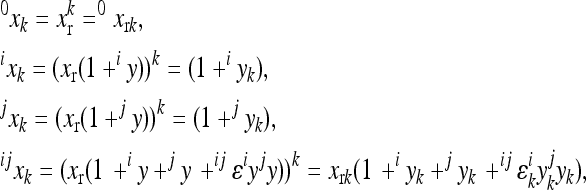 |
where a subscribed k means parameters pertaining to the scale resulting from the k-power transformation. We can solve these equations to derive an approximate relationship between the parameters at different scales.
The above equations are equivalent to
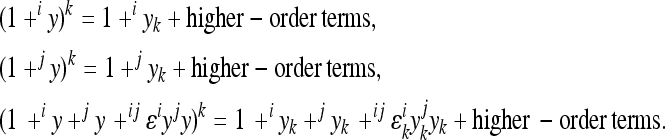 |
Assuming that the reference effects of individual allele substitutions are small, we can approximate by neglecting higher-order terms. Thus we obtain
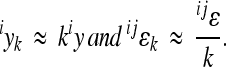 |
Hence the reference effects on the cubic scale are expected to be three times larger than those on the linear scale, while the epistasis coefficients are expected to be three times smaller. These results can serve as a baseline for comparing the strength of epistasis on different power scales. Deviations from the assumption of small x cause overestimation of the effect of the power transformation from linear to cubic scale on reference effects. This leads to coefficient of directionality on cubic scale that is greater than one-third of the coefficient of directionality on the linear scale ( ).
).
Supporting information is available online at http://www.genetics.org/cgi/content/full/genetics.110.118356/DC1.
References
- Alvarez-Castro, J. M., and O. Carlborg, 2007. A unified model for functional and statistical epistasis and its application in quantitative trait loci analysis. Genetics 176 1151–1167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarez-Castro, J. M., A. Le Rouzic and O. Carlborg, 2008. How to perform meaningful estimates of genetic effects. PLoS Genet. 4 e1000062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarez-Castro, J. M., M. Kopp and J. Hermisson, 2009. Effects of epistasis and the evolution of genetic architecture: exact results for a 2-locus model. Theor. Popul. Biol. 75 109–122. [DOI] [PubMed] [Google Scholar]
- Barton, N. H., and M. Turelli, 2004. Effects of genetic drift on variance components under a general model of epistasis. Evolution 58 2111–2132. [DOI] [PubMed] [Google Scholar]
- Carlborg, O., L. Jacobsson, P. Ahgren, P. Siegel and L. Andersson, 2006. Epistasis and the release of genetic variation during long-term selection. Nat. Genet. 38 418–420. [DOI] [PubMed] [Google Scholar]
- Carter, A. J. R., J. Hermisson and T. F. Hansen, 2005. The role of epistatic gene interactions in the response to selection and the evolution of evolvability. Theor. Popul. Biol. 68 179–196. [DOI] [PubMed] [Google Scholar]
- Chai, C. K., 1966. Characteristics in inbred mouse populations plateaued by directional selection. Genetics 54 743–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth, B., 1990. Mutation-selection balance and the evolutionary advantage of sex and recombination. Genet. Res. 71 85–89. [DOI] [PubMed] [Google Scholar]
- Cheverud, J. M., and E. J. Routman, 1995. Epistasis and its contribution to genetic variance components. Genetics 139 1455–1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheverud, J. M., and E. J. Routman, 1996. Epistasis as a source of increased additive genetic variance at population bottlenecks. Evolution 50 1042–1051. [DOI] [PubMed] [Google Scholar]
- Cheverud, J. M., E. J. Routman, F. A. Duarte, B. van Swinderen, K. Cothran et al., 1996. Quantitative trait loci for murine growth. Genetics 142 1305–1319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheverud, J. M., T. T. Vaughn, L. S. Pletscher, A. C. Peripato, E. S. Adams et al., 2001. Genetic architecture of adiposity in the cross of LG/J and SM/J inbred mice. Mamm. Genome 12 3–12. [DOI] [PubMed] [Google Scholar]
- Cheverud, J. M., T. H. Ehrich, T. T. Vaughn, S. F. Koreishi, R. B. Linsey et al., 2004. Pleiotropic effects on mandibular morphology II: differential epistasis and genetic variation in morphological integration. J. Exp. Zoolog. B Mol. Dev. Evol. 302 424–435. [DOI] [PubMed] [Google Scholar]
- Cockerham, C. C., 1954. An extension of a concept of partitioning hereditary variance for analysis of covariance among relatives when epistasis is present. Genetics 39 859–882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Brito, R. A., L. S. Pletscher and J. M. Cheverud, 2005. The evolution of genetic architecture. I. Diversification of genetic backgrounds by genetic drift. Evolution 59 2333–2342. [DOI] [PubMed] [Google Scholar]
- Ehrich, T. H., J. P. Kenney-Hunt, L. S. Pletscher and J. M. Cheverud, 2005. Genetic variation and correlation of dietary response in an advanced intercross mouse line produced from two divergent growth lines. Genet. Res. 85 211–222. [DOI] [PubMed] [Google Scholar]
- Falconer, D. S., 1960. Introduction to Quantitative Genetics. Ronald Press Co., New York.
- Falconer, D. S., I. K. Gauld and R. C. Roberts, 1978. Cell numbers and cell sizes in organs of mice selected for large and small body size. Genet. Res. 31 287–301. [DOI] [PubMed] [Google Scholar]
- Fawcett, G. L., C. C. Roseman, J. P. Jarvis, B. Wang, J. B. Wolf et al., 2008. Genetic architecture of adiposity and organ weight using combined generation QTL analysis. Obesity 16 1861–1868. [DOI] [PubMed] [Google Scholar]
- Fierst, J. L., and T. F. Hansen, 2010. Genetic architecture and postzygotic reproductive isolation: evolution of Bateson–Dobzhansky–Muller incompatibilities in a polygenic model. Evolution 64 675–693. [DOI] [PubMed] [Google Scholar]
- Fisher, R. A., 1918. The correlation between relatives on the supposition of Mendelian inheritance. Trans. R. Soc. Edinburgh 52 399–433. [Google Scholar]
- Goodale, H., 1938. A study of the inheritance of body weight in the albino mouse by selection. J. Hered. 29 101–112. [Google Scholar]
- Goodnight, C. J., 1987. On the effect of founder events on the epistatic genetic variance. Evolution 41 80–91. [DOI] [PubMed] [Google Scholar]
- Goodnight, C. J., 1988. Epistasis and the effect of founder events on the additive genetic variance. Evolution 42 441–454. [DOI] [PubMed] [Google Scholar]
- Goodnight, C. J., 1995. Epistasis and the increase in additive genetic variance: implications for phase 1 of Wright's shifting balance process. Evolution 49 502–511. [DOI] [PubMed] [Google Scholar]
- Haley, C. S., and S. A. Knott, 1992. A simple regression method for mapping quantitative trait loci in line crosses using flanking markers. Heredity 69 315–324. [DOI] [PubMed] [Google Scholar]
- Hansen, T. F., 2006. The evolution of genetic architecture. Ann. Rev. Ecol. Evol. Syst. 37 123–157. [Google Scholar]
- Hansen, T. F., and G. P. Wagner, 2001. a Modeling genetic architecture: a multilinear theory of gene interaction. Theor. Popul. Biol. 59 61–86. [DOI] [PubMed] [Google Scholar]
- Hansen, T. F., and G. P. Wagner, 2001. b Epistasis and the mutation load: a measurement-theoretical approach. Genetics 158 477–485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen, T. F., and D. Houle, 2008. Measuring and comparing evolvability and constraint in multivariate characters. J. Evol. Biol. 21 1201–1219. [DOI] [PubMed] [Google Scholar]
- Hansen, T. F., C. Pelabon, W. S. Armbruster and M. L. Carlson, 2003. Evolvability and genetic constraint in Dalechampia blossoms: components of variance and measures of evolvability. J. Evol. Biol. 16 754–766. [DOI] [PubMed] [Google Scholar]
- Hansen, T. F., J. M. Alvarez-Castro, A. J. R. Carter, J. Hermisson and G. P. Wagner, 2006. Evolution of genetic architecture under directional selection. Evolution 60 1523–1536. [PubMed] [Google Scholar]
- Hermisson, J., T. F. Hansen and G. P. Wagner, 2003. Epistasis in polygenic traits and the evolution of genetic architecture under stabilizing selection. Am. Nat. 161 708–734. [DOI] [PubMed] [Google Scholar]
- Houle, D., 1992. Comparing evolvability and variability of quantitative traits. Genetics 130 195–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kempthorne, O., 1954. The correlation between relatives in a random mating population. Proc. R. Soc. Lond. B 143 103–113. [PubMed] [Google Scholar]
- Kondrashov, A. S., 1988. Deleterious mutations and the evolution of sexual reproduction. Nature 336 435–440. [DOI] [PubMed] [Google Scholar]
- Lander, E. S., and D. Botstein, 1989. Mapping mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121 185–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Rouzic, A., 2008. noia: implementation of the Natural and Orthogonal InterAction (NOIA) model. R package version 0.92. http://cran.r-project.org
- Le Rouzic, A., and J. M. Alvarez-Castro, 2008. Estimation of genetic effects and genotype-phenotype maps. Evol. Bioinform. Online 4 225–235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch, M., and B. Walsh, 1998. Genetics and Analysis of Quantitative Traits. Sinauer, Sunderland, MA.
- Macarthur, J. W., 1949. Selection for small and large body size in the house mouse. Genetics 34 194–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Norgard, E. A., C. C. Roseman, G. L. Fawcett, M. Pavlicev, C. D. Morgan et al., 2008. Identification of quantitative trait loci affecting murine long bone length in a two-generation intercross of LG/J and SM/J Mice. J. Bone Miner. Res. 23 887–895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlicev, M., J. P. Kenney-Hunt, E. A. Norgard, C. C. Roseman, J. B. Wolf et al., 2008. Genetic variation in pleiotropy: differential epistasis as a source of variation in the allometric relationship between long bone lengths and body weight. Evolution 62 199–213. [DOI] [PubMed] [Google Scholar]
- Phillips, P. C., S. P. Otto and M. C. Whitlock, 2000. Beyond the average: the evolutionary importance of gene interactions and variability of epistatic effects, pp. 20–38 in Epistasis and the Evolutionary Process, edited by J. D. Wolf, E. D. Brodie III, and M. J. Wade. Oxford University Press, Oxford.
- Turelli, M., and N. H. Barton, 2006. Will population bottlenecks and multilocus epistasis increase additive genetic variance? Evolution 60 1763–1776. [PubMed] [Google Scholar]
- Vaughn, T. T., L. S. Pletscher, A. Peripato, K. King-Ellison, E. Adams et al., 1999. Mapping quantitative trait loci for murine growth: a closer look at genetic architecture. Genet. Res. 74 313–322. [DOI] [PubMed] [Google Scholar]
- Wagner, G. P., M.D. Laubichler and H. Bagheri-Chaichian, 1998. Genetic measurement theory of epistatic effects. Genetica 102–103 569–580. [PubMed] [Google Scholar]
- Wang, T., and Z. B. Zeng, 2006. Models and partition of variance for quantitative trait loci with epistasis and linkage disequilibrium. BMC Genet. 7 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinreich, D. M., R. A. Watson and L. Chao, 2005. Perspective: sign epistasis and genetic constraint on evolutionary trajectories. Evolution 59 1165–1174. [PubMed] [Google Scholar]
- Wilson, S. P., H. D. Goodale, W. H. Kyle and E. F. Godfrey, 1971. Long term selection for body weight in mice. J Hered. 62 228–234. [DOI] [PubMed] [Google Scholar]
- Wright, S., 1952. The genetics of quantitative variability, pp. 5–41 in Quantitative Inheritance, edited by E. C. R. Reeve and C. H. Waddington. Her Majesty's Stationery Office, London.
- Yang, R.C., 2004. Epistasis of quantitative trait loci under different gene action models. Genetics 167 1493–1505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yukilevich, R., J. Lachance, F. Aoki, J. True and M. Travisano, 2008. Long-term adaptation of epistatic genetic networks. Evolution 62 2215–2235. [DOI] [PubMed] [Google Scholar]
- Zeng, Z. B., T. Wang and W. Zou, 2005. Modeling quantitative trait loci and interpretation of models. Genetics 169 1711–1725. [DOI] [PMC free article] [PubMed] [Google Scholar]