Coalescence and Fragmentation of Cortical Networks during Focal Seizures

Abstract

Epileptic seizures reflect a pathological brain state characterized by specific clinical and electrical manifestations. The proposed mechanisms are heterogeneous but united by the supposition that epileptic activity is hypersynchronous across multiple scales, yet principled and quantitative analyses of seizure dynamics across space and throughout the entire ictal period are rare. To more completely explore spatiotemporal interactions during seizures, we examined electrocorticogram data from a population of male and female human patients with epilepsy and from these data constructed dynamic network representations using statistically robust measures. We found that these networks evolved through a distinct topological progression during the seizure. Surprisingly, the overall synchronization changed only weakly, whereas the topology changed dramatically in organization. A large subnetwork dominated the network architecture at seizure onset and preceding termination but, between, fractured into smaller groups. Common network characteristics appeared consistently for a population of subjects, and, for each subject, similar networks appeared from seizure to seizure. These results suggest that, at the macroscopic spatial scale, epilepsy is not so much a manifestation of hypersynchrony but instead of network reorganization.

Introduction

Epilepsy is a devastating disease affecting ∼50 million people worldwide. Although manifesting as specific clinical symptoms, epilepsy is perhaps best characterized as a disease of brain rhythms: a paroxysmal cerebral dysrhythmia (Gibbs et al., 2002). Understanding how this dysrhythmia propagates and is maintained is a key problem in the treatment of epilepsy. From a simplistic perspective, focal seizures can be understood as local events beginning in a circumscribed region with the potential to recruit connected areas in a cascade of spreading activity from the central focus outward through both pathological and normal brain tissue.

Presumably, changes in synchronization between brain regions underlie the mechanisms of seizure spread. Classically, seizures are thought to represent a hypersynchronous state (Penfield and Jasper, 1954). To be detected as voltage fluctuations at the scalp surface, there must be a sufficient number of simultaneously active neurons and synapses so at some spatial scale increased synchrony must occur, yet recent observations challenge the formal assertion of hypersynchrony at larger spatial scales (Jerger et al., 2005; Schindler et al., 2007), in in vitro recordings of experimental seizures (Netoff and Schiff, 2002), and in human temporal lobe seizures (Bartolomei et al., 1999, 2004; Guye et al., 2006; Ponten et al., 2007).

To understand seizure spread, synchronization measures are applied to the voltage activity of the brain (Brazier, 1973; Gotman, 1983; Bartolomei et al., 1999, 2004; Towle et al., 1999; Wendling et al., 2003; Ferri et al., 2004; Guye et al., 2006). For a few electrode pairs, these synchronization metrics are easily constructed and readily interpreted. However, for high-density electrode grids, complex functional topologies result whose quantitative understanding requires graph theory and network analysis techniques (Reijneveld et al., 2007; Bullmore and Sporns, 2009). Using these tools, specific network structures are revealed during the seizure, including such architecture patterns as small-world networks (Netoff et al., 2004; Ponten et al., 2007) and hubs (Kramer et al., 2008; Morgan and Soltesz, 2008).

In this paper, we analyze the dynamics of functional networks through the entire seizure in intracranial electrocorticogram (ECoG) recordings from a population of patients with intractable focal epilepsy. We show that some network properties are preserved whereas others change dramatically and predictably during initiation, propagation, and termination of the seizure. Analysis of the evolving networks suggests that, no matter what the cause of the particular focal epilepsy, stereotyped network patterns emerge. We propose that the changing synchronization structure of the seizure activity provides new insights into the mechanisms of seizures and novel intervention strategies. The analysis also suggests that seizures represent a paroxysmal cerebral dysrhythmia whose synchronization evolves through characteristic functional topologies without necessarily representing large-scale hypersynchrony.

Materials and Methods

Patients.

Electrocorticography from 48 seizures (from two to eight seizures per patient; mean of 4.4) in 11 patients (six women, mean age at surgery of 37.4 years with a minimum age of 19 years and maximum of 65 years) with long-standing pharmaco-resistant complex partial seizures (mean age at onset of 20.2 years and mean duration of epilepsy of 17.3 years) were analyzed (Table 1). Patients were selected who were known to have seizures with focal onset and typical complex partial events often with secondary generalization. All recordings were performed using a standard clinical recording system (Xltek, a subsidiary of Natus Medical) with a 500 Hz sampling rate. Analysis of the data from these patients was performed retrospectively under protocols monitored by the local Institutional Review Boards according to National Institutes of Health guidelines. Two-dimensional subdural electrode arrays as well as linear arrays of electrodes penetrating the brain (grid/strips and depth electrodes, respectively; Ad-Tech Medical) were placed to confirm the hypothesized seizure focus and locate epileptogenic tissue in relation to essential cortex, thus directing surgical treatment. Of the 11 patients, five were investigated with a combination of surface electrodes placed on the pia (grids and strips) as well as depth electrodes placed through the cortex to sample mesial structures (e.g., hippocampus, amygdala, cingulated gyrus, etc.). Six patients had just depth electrodes placed. All patients had some sampling of both neocortical structures and the mesial temporal lobe. As a result, all of the recordings possessed three-dimensional coverage of brain structures. Although extensive, these recordings do not permit observation of the entire brain; unobserved structures may play a role in the seizure process. The reference electrode was an electrode either placed on the neck (at the spinous process of the second cervical vertebrate) or a strip of electrodes placed outside the dura and facing the skull at a region remote from the other grid and strip electrodes. The decision to implant, the electrode targets, and the duration of implantation were made entirely on clinical grounds without reference to this research study.

Table 1.

Patient characteristics

Patient	Sex	Age at onset/surgery (years)	n	Duration of seizures (s)	Electrodes	Electrodes total/onset	Seizure type (n)	Onset activity	Etiology	Etiology (based on pathology)	Lobe of involvement
A	M	3/37	4	76, 63, 61, 134	Grids, strips, and depths	100/5	CPS + 2nd (4)	Beta, alpha, delta	Unknown	No significant abnormalities	Temporal (lateral)
B	F	20/45	4	114, 102, 121, 142	Depths	65/5	CPS + 2nd (4)	Delta	Temporal lobe–MTS	No pathology obtaineda	Temporal (mesial)
C	F	15/46	5	87, 93, 102, 100, 112	Grids, strips, and depths	122/5	CPS + 2nd (5)	Beta, alpha, delta	Cortical dysplasia	Cortical dysplasia	Temporo-parieto-occipital
D	F	17/45	3	80, 82, 42	Depths	40/2	CPS + 2nd, CPS (2, 1)	Beta, delta	Possible post-infectious	No pathology obtainedb	Parieto-occipital
E	M	7/22	2	87, 92	Grids, strips, and depths	124/4	CPS + 2nd (2)	Delta	Cortical dysplasia	Cortical dysplasia	Frontal (cingulate)
F	F	14/28	4	331, 111, 84, 128	Grids, strips, and depths	94/22	CPS + 2nd, CPS, SPS (1, 1, 2)	Delta	Encephalitis	Reactive gliosis	Temporal (mesial)
G	M	17/29	7	93, 137, 104, 134, 156, 179, 101	Depths	70/2	CPS, SPS (5, 2)	Delta	Traumatic brain injury	Reactive gliosis	Temporal (mesial)
H	F	13/31	2	65, 90	Depths	34/4	CPS (2)	Delta	Temporal lobe–MTS	No significant abnormalities	Temporal (mesial)
I	M	43/45	8	55, 57, 63, 49, 58, 199, 54, 90	Depths	64/4	CPS + 2nd, CPS, SPS (1, 1, 6)	Alpha, delta	Unknown	No pathology obtaineda	Temporal (mesial and lateral)
J	M	14/19	4	82, 138, 123, 40	Grids, strips, and depths	80/3	SPS (4)	Alpha, delta	Temporal lobe–MTS	Hippocampal sclerosis	Temporo-parieto-occipital
K	F	59/65	5	171, 121, 105, 224, 133	Depths	68/2	CPS, SPS (4, 1)	Beta, alpha	Unknown	No pathology obtainedc	Frontal (orbito-frontal)

Age at onset indicates the age at which seizures are first described by the patient. For each subject, n seizures were analyzed with durations listed in the fifth column. “Grids” and “strips” refer to surface (pial) electrode arrays that were also always accompanied by depth electrodes. “Depths” refer to patients who only received orthogonal placement of intraparenchymal arrays of electrodes. The total number of intracranial electrodes and the number of electrodes involved at seizure onset are listed for the dominant seizure type. All seizure types were complex partial seizures which had secondary generalization (CPS + 2nd), complex partial seizures without secondary generalization (CPS), or simple partial seizures (SPS); the number of each type of seizure for each patient is indicated. The frequency bands of maximum power at seizure onset were estimated using standard power spectrum analysis. Power spectra (Hann taper) were computed for 1 s of ECoG data immediately after clinical determination of seizure initiation and averaged over the onset electrodes. Beta, 15–30 Hz; alpha, 8–12 Hz; theta, 4–8 Hz; delta, 1–4 Hz. The etiology based on history, imaging, and seizure semiology refers to a diagnosis made by the clinical team with all available data before implantation of electrodes, surgical resection, and pathological examination of resected tissue. The etiology based on pathology comes directly from the clinical determination made by neuropathologists. The lobe of involvement was determined by examination of the seizure onsets on the intracranial recording electrodes. F, Female; M, male; MTS, mesial temporal sclerosis.

^aBilateral onsets, no resection performed.

^bEloquent cortex, no resection performed.

^cPatient decided not to go forward with resection.

Multiple etiologies were represented: mesial temporal sclerosis as diagnosed by history, seizure semiology, and imaging (n = 3); cortical dysplastic lesions confirmed with pathology (n = 2); posttraumatic epilepsy (n = 1); and sequelae from a presumed viral encephalitis or related injury (n = 2). In four of the patients, no resection and no pathological tissue were obtained. In two of these cases, this was because of bilateral disease. In one case, no resection was performed because of fear of injury to eloquent cortex. In the final situation, the patient declined to continue forward with surgery. Seizure onset regions were most common in neocortical temporal structures, mesial temporal structures, or a mix of the two (n = 6). In two patients, seizures arose from frontal lobe structures (the cingulated gyrus or orbitofrontal regions). In three patients, the seizures arose from the junction of the temporal, parietal, and occipital lobes.

Seizure onset zones and seizure characteristics were determined independently from this research by a team of clinical electroencephalographers. Seizure type was determined by examination of the patient's ECoG recording, simultaneously recorded closed circuit video recordings of the patient's behavior, and clinical history of the patient. Seizures in which consciousness was impaired in any way were considered complex partial (CPS). Seizures that culminated in bilateral tonic, clonic, or tonic–clonic movements and in which all or nearly all electrodes showed ictal activity were considered to have had secondary generalization. If awareness was maintained and the patient was able to interact appropriately, the seizure was considered a simple partial seizure (SPS). Seizures that were ambiguous (e.g., brief events in which no interactions occurred with the patient before the seizure ended) were classified based on other events that had similar behavioral and electrographic features. Delineation of the seizure onset zone was made by observing which of the intracranial electrodes first showed ictal electrographic activity, including low-voltage fast activity or repetitive spike-wave discharges. The initiation of the seizure as determined by this clinical team was used as the start of the seizure for purposes of the analysis discussed below. A count of the electrodes definitively involved in the onset of the typical seizure for a given patient is included in Table 1 as a reflection of focality. In all cases, there was significant spread of ictal activity. The semiology and ECoG recordings of all patients involved focal features at onset. In 28 of 33 CPS, the ictal activity spread to include all or nearly all of the intracranial electrodes, whereas the ictal activity of SPS did not achieve complete electrographic generalization. In 7 of the 11 patients, there was progression of at least one seizure to generalized tonic–clonic activity. In three of the patients, the complex partial seizures did not progress to such behavior, and in one patient only simple partial seizures occurred. Purely subclinical seizures were not included in this analysis.

We note that a potential concern in these data is the spatial spreading of electrical activity propagating through conductive tissue from a brain source to an electrode. To reach the scalp surface, electrical activity from a cortical source propagates through the cortex, CSF, skull, and scalp. The result is significant spatial spreading (or blurring) of the original source voltage. For the ECoG data of interest here, this spreading is much less severe (Zaveri et al., 2009). As a result, we do not expect that passive voltage spread will have significant effect on our results. If anything, the effect would be to increase overall levels of apparent synchronization. As described below, the results are the opposite of this.

Anatomical figures.

To create Figure 1A and the supplemental movie (available at www.jneurosci.org as supplemental material), we used FreeSurfer (Dale et al., 1999) to reconstruct a three-dimensional (3D) model of the cortical surface of the patient using preoperative high-resolution magnetic resonance imaging (MRI) data. We then coregistered these MRI data with a postoperative computed tomography (CT) scan showing the location of the intracranial electrodes. We obtained each electrode coordinate manually from the postoperative CT scan and subsequently projected them onto the reconstructed 3D model of the cortex.

Figure 1.

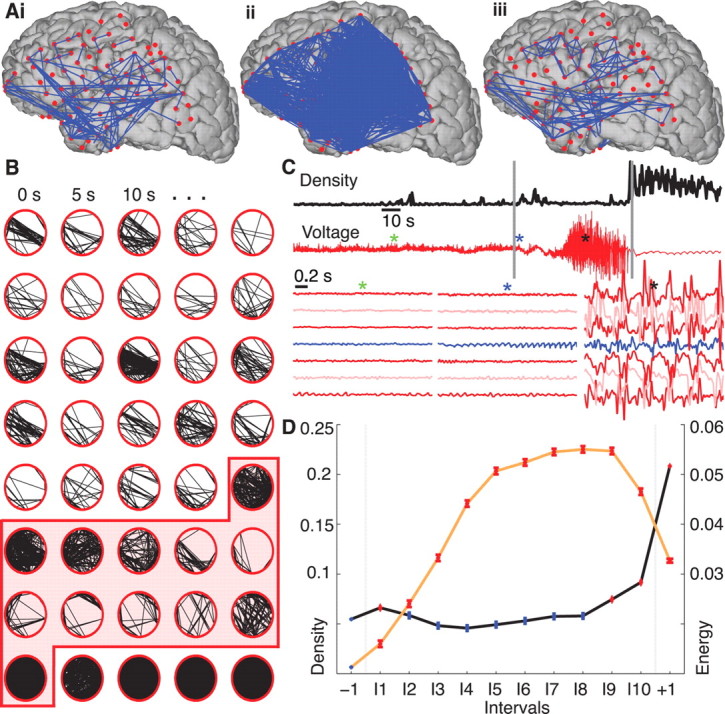
Network synchronization increases at ictal onset and offset but falls to preictal values during the seizure. A, Representative networks just before the seizure starts (i), at seizure initiation (ii), and in the middle of the seizure (iii) from a single seizure in a single patient. In this example, the electrode locations have been projected onto a reconstruction of this patient's cortical surface. Because some of the electrodes cannot be easily visualized in this two-dimensional representation, the data are displayed as circular networks containing all electrodes as individual nodes. B, The networks progress from left to right, top to bottom, with a 5 s interval between networks. We arrange the electrodes in a circle (without reference to their physical locations) and indicate sufficiently strong coupling between electrode pairs with black lines. The shaded region denotes the ictal interval. Visual inspection of the evolving network topologies suggests increased network density (i.e., more edges) near ictal onset and termination. C, The network density (black) and ECoG data from a single electrode (red, top) for the representative example. At ictal onset and termination, indicated with the vertical gray lines, the network density increases dramatically, whereas during the middle portion of the seizure, the ECoG data exhibits large-amplitude fluctuations. The colored asterisks indicate the location of three 2 s intervals plotted for representative grid and strip electrodes below, including the activity of the presumptive onset electrode as identified by the clinical team (blue trace). D, The density (black curve), averaged across all subjects and seizures and adjusted for differences in subjects, for 12 time intervals: one preictal (−1), 10 ictal (I1, I2, …, I10), and one postictal (+1). In each interval, the circle indicates the mean density (n = 9049 networks preictal, n = 939 networks per ictal interval, and n = 2817 networks postictal) and the vertical lines the SE. Statistically significant increases in density compared with preictal values (see Materials and Methods) are indicated in red and occur at ictal onset (interval I1) and near ictal offset (intervals I9, I10, +1). We also plot the normalized signal energy (orange curve) for each interval averaged across all subjects and seizures (n = 45609 preictal, n = 3614 per ictal interval, and n = 10842 postictal). Unlike the density, the signal energy increases significantly above preictal values for all ictal and postictal intervals.

Calculation of functional topologies.

Many different approaches exist to determine functional connectivity from time series data (Pereda et al., 2005). Different methods use distinct coupling measures (e.g., linear or nonlinear measures) and different strategies for assigning network edges. In this work, we focus on a simple measure of linear coupling: the cross-correlation. We outline here our particular data analysis approach; a detailed discussion of the measure, including its statistical properties and simulation results, may be found in the study by Kramer et al. (2009). Before applying the coupling analysis, we process the ECoG data from each seizure and subject in the following way. First, we low-pass filter the data (third-order Butterworth, zero-phase digital filtering) below 125 Hz and notch filter (third-order Butterworth, zero-phase digital filtering) the data at 60 and 120 Hz. Then, to reduce the contribution to coupling of the reference electrode, we compute the average reference of the filtered data and subtract it from each electrode (Towle et al., 1999). Next, we divide the ECoG data into 1.024 s windows with 0.512 s overlap beginning 120 s before seizure onset and ending 30 s after seizure termination. Finally, we normalize the data from each electrode within the 1.024 s window to have zero mean and unit variance.

With the data processed in this way, we construct a functional network for each (overlapping) ∼1 s window. Our procedure for constructing functional networks from the data involves three steps. We briefly describe these steps here; again, a complete discussion may be found in the study by Kramer et al. (2009). In the first step, we choose two electrodes, apply the cross-correlation to the ECoG data, and select the maximum correlation within time delays of ±200 ms. Second, we determine the statistical significance of this correlation value through an analytic procedure that accounts for our choice of an extremum (Kramer et al., 2009). Third, we correct for multiple significance tests using a linear step-up procedure controlling the false detection rate with q = 0.05. For this choice of q, 5% of the network connections are expected to be falsely declared. The result is a network for each ∼1 s window with an associated measure of uncertainty, namely the expected number of edges incorrectly declared present. Propagation of the network uncertainty to uncertainty in the network measures is nontrivial and the subject of future work.

We note that the rhythms dominating the ECoG data will also dominate the cross-correlation measure we use. Typically, these dominant rhythms occur in the low-frequency bands, and we expect that the cross-correlation measure will be most sensitive to this large-amplitude, low-frequency activity. To examine the networks that result in different frequency bands, we apply a separate coupling measure (the coherence) in the supplemental material (available at www.jneurosci.org). We find similar results for the networks produced by the cross-correlation measure and the coherence measure in the low-frequency bands, as expected (supplemental material, available at www.jneurosci.org).

Analysis of topologies: graph theory and network measures.

We illustrate the connectivity of the ECoG data as a network. In doing so, we represent each electrode as a node and a sufficiently strong connection (defined as a statistically significant cross-correlation) as an edge. The association measure we use does not distinguish the direction of coupling, and the resulting networks are therefore undirected. We choose to ignore the direction of coupling (determined by the lag of the maximum correlation) for two reasons. First, the cross-correlation is a poor indicator of coupling direction for periodic time series. Second, we developed the statistical methods only to detect nonzero correlations (Kramer et al., 2009). To make inferences about more subtle aspects of the cross-correlation, such as the sign, would require the development of a new measure and appropriate statistical tests. We show examples of the functional networks in Figure 1, A and B. Our analysis focuses on how the network topologies evolve in time, in particular how these topologies change at seizure onset and during the course of a seizure.

To analyze the functional networks derived from the ECoG data, we apply five network measures: the density, the components, the similarity coefficient, and, for the largest component, the characteristic path length and clustering coefficient. We briefly define these measures here; more detailed descriptions may be found elsewhere (Wasserman and Faust, 1994; Newman, 2003; Kolaczyk, 2009). The density is the number of edges in the network divided by the total possible number of edges; for n nodes, the total possible number of edges is n(n − 1)/2. A density of 1 indicates an edge between each pair of nodes in the network. A component is a subset of nodes in which each node is reachable from every other node (i.e., following edges one can travel from each node in the component to any other node). A single node is a trivial component of size one. We monitor the largest component, number of components, and number of trivial components in the networks. The Jaccard similarity coefficient compares the edge sets of two networks and divides the size of their intersection by the size of their union. The similarity coefficient approaches 1 if two networks (with the same number of nodes) share a similar pattern of edges between their nodes. For the largest connected component, we compute the characteristic path length (the number of edges traversed on average in traveling between pairs of nodes in the component) and the clustering coefficient [a measure of the cliquishness of a typical neighborhood (Watts and Strogatz, 1998)]. Both measures only apply to the largest component in which paths between nodes are well defined. We note that each measure summarizes a topological characteristic of the entire network as a single scalar; we do not study the characteristics of individual nodes (e.g., their degree or betweenness centrality) here. Instead, our goal is to summarize how the overall network topology evolves in time. In addition to the network measures, we also compute the signal energy of the ECoG data for each subject and seizure and within each interval. To define the signal energy, we first low-pass filter the data (third-order Butterworth, zero-phase digital filtering) below 125 Hz and notch filter (third-order Butterworth, zero-phase digital filtering) the data at 60 and 120 Hz. Then we choose an interval (e.g., the first ictal interval, defined in the next paragraph) and divide the data into ∼1 s windows (with ∼0.5 s overlap) that cover the interval. Next, for each ∼1 s window within the interval, we compute the squared value of the (filtered) ECoG data at each electrode and average the results over the window (Litt et al., 2001). We then repeat this procedure for all intervals. Because we bandpass filter the ECoG data, the signal energy only captures activity within this frequency range.

Population summary measures.

We applied the network topology measures to 48 seizures observed in 11 patients. Because seizure duration varies between seizures and subjects, we cannot summarize the population results by simply averaging in time. Instead, we normalize time for each subject and seizure by dividing the seizure duration into 10 intervals of equal length. We label these intervals I1, I2, …, I10. By normalizing time in this way, we assume that the seizures evolve in stereotypical ways that might occur more quickly or more slowly from subject to subject or even seizure to seizure. We have repeated the analysis using fixed time intervals of 10 s and find similar network topologies (supplemental Fig. 2, available at www.jneurosci.org as supplemental material). In addition to the 10 ictal intervals, we also analyze the network properties in a preictal interval (labeled −1) that begins 120 s before seizure onset and ends 30 s before seizure onset. Similarly, we define a postictal interval (labeled +1) that begins immediately at seizure termination and ends after $\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$10$}\right.$ of the seizure duration (∼30 s).

To determine significant changes in the network measures and signal energy across the intervals for the entire collection of seizures, we apply a one-way ANOVA blocked by patient (11 levels) and with intervals (12 levels) as the factor. We test the null hypothesis that samples at all interval levels are drawn from the same distribution. To determine which pairs of intervals exhibit significant differences in their means, we perform a multiple comparison procedure. We set α = 0.05 and use a critical value determined by Tukey's honestly significant difference criterion. In the figures, we plot the network results for each interval averaged over the population of subjects and adjusted for differences in subjects. We identify a significant change in a network measure during the seizure only if the ictal values differ significantly from the preictal value.

Results

Unlike the static structural networks based on anatomical connections between brain areas (Hilgetag and Kaiser, 2004; Sporns and Kötter, 2004; Bullmore and Sporns, 2009), we examine here dynamic, functional networks deduced from ECoG data. We determine these networks using a simple association measure: the cross-correlation. We choose this measure for two main reasons: simple linear and sophisticated nonlinear measures appear to perform equally well when applied to ECoG data (Mormann et al., 2005; Ansari-Asl et al., 2006; Kreuz et al., 2007; Osterhage et al., 2007), and, for the cross-correlation, we can derive an analytic and computationally efficient significance test (Kramer et al., 2009). Applying a frequency domain measure, the coherence, to the data produces similar results (supplemental material, available at www.jneurosci.org).

To construct functional networks from the ECoG data, we implement the following procedure. First, we divide the ECoG data into ∼1 s windows (with ∼0.5 s overlap) beginning 120 s before seizure onset and ending after seizure termination. We choose this window size to preserve weak stationary in the data but did find similar results with different window sizes and overlaps (supplemental material, available at www.jneurosci.org). We then compute the cross-correlation, and test the significance, between all electrode pairs for the ECoG data within each window. Finally, we threshold the results of the significance tests to construct a functional network with an associated measure of uncertainty. A detailed discussion of the correlation measure and appropriate statistical tests may be found in the study by Kramer et al. (2009). We analyze these networks to show that, although some properties (such as the overall level of network synchronization) are preserved during the seizure, others change dramatically.

Network synchronization decreases, whereas signal energy increases, during seizure progression

In Figure 1, we show example networks constructed from the ECoG data. Although the data can be displayed on a three-dimensional reconstruction of the cortical surface (Fig. 1A), it is more useful to show these data as a circular network; each subject had electrodes that entered the cortical surface and therefore remain hidden in the cortical surface reconstructions. Accordingly, to observe the connectivity of the entire network, we arrange the electrodes in a ring and connect electrodes exhibiting significant coupling with an edge (i.e., a directionless link between nodes). Figure 1, A and B, suggests an obvious way in which the network topologies change in time; there is a dramatic variation in the number of edges (an illustration of this variation in another subject is provided in the supplemental movie, available at www.jneurosci.org as supplemental material). In this example, at seizure onset and termination, the networks possess many more edges (i.e., become more synchronized) than during the middle portion of the seizure. To quantify the changing number of edges observed, we compute the density of each network. This measure ranges from 0 (a desynchronized network containing no edges) to 1 (a hypersynchronized network with edges connecting all possible pairs of nodes). In this example, the density increases briefly just after ictal onset, decreases to preictal values during the ictus itself, and again increases before seizure termination (Fig. 1C). For comparison, we also show the simultaneous ECoG activity recorded at a single electrode and for three 2 s intervals from multiple electrodes for this seizure (Fig. 1C). Surprisingly, the large-amplitude voltage oscillations characteristic of a seizure occur after the density returns to preictal levels.

To quantify the changing voltage dynamics and network synchronization during the seizure, we analyze an ensemble of 48 seizures collected from 11 patients. We first normalize time for each seizure by dividing the ictal period into 10 intervals of equal length. In doing so, we assume that seizures undergo characteristic progressions that can be stretched or compressed in time; repeating the analysis with time intervals of fixed duration and different seizure lengths produces similar results (supplemental Fig. 2, available at www.jneurosci.org as supplemental material). We then compute the density for all subjects and seizures within preictal, ictal, and postictal intervals and plot the average density per interval adjusted for differences in subjects with a blocked one-way ANOVA (Fig. 1D). Only after ictal onset (interval label I1) and before termination (I9, I10) do we observe a significant increase in density above preictal levels during the seizure (see Materials and Methods). During the middle portion of the seizure (intervals I2–I8), the density returns to preictal levels. We find similar changes in density for a subset of 10 patients with focal seizure onsets (i.e., all patients except patient F in Table 1) and for subsets of patients and seizures grouped by seizure type (supplemental Fig. 1, available at www.jneurosci.org as supplemental material). We also show in Figure 1D the signal energy (see Materials and Methods) within each interval adjusted for patient differences. In contrast to the density, we find a significant increase in overall signal energy for all ictal and postictal intervals compared with the preictal level. The increase in signal energy is not surprising; seizure activity typically manifests as large-amplitude voltage oscillations at the macroscopic spatial scale recorded in the ECoG or electroencephalogram (EEG). To support these large-amplitude oscillations, we expect increased synchrony at the microscopic spatial scale of individual neurons. Although increased synchrony at the microscopic spatial scale supports the large-amplitude ECoG rhythms, we find that synchrony decreases (i.e., density decreases) between macroscopic brain areas during seizure.

The network topology and signal energy also change dramatically at seizure termination. The density increases substantially in the postictal interval compared with preictal or ictal values, whereas the voltage fluctuations decrease. A low-amplitude, slow-wave rhythm (visible in Fig. 1C) that appears broadly throughout the brain dominates the postictal activity and contributes to the increased network density. Low-frequency rhythms often appear in the postical period (Kaibara and Blume, 1988), although the exact mechanisms that support this activity are unknown (Fisher and Schachter, 2000). We note that the density increase begins before seizure termination (Fig. 1D, I9 and I10), consistent with previous observations of increased synchrony in the late seizure stage (Topolnik et al., 2003; Schindler et al., 2007).

Dominant networks fracture, then reform, during seizure propagation

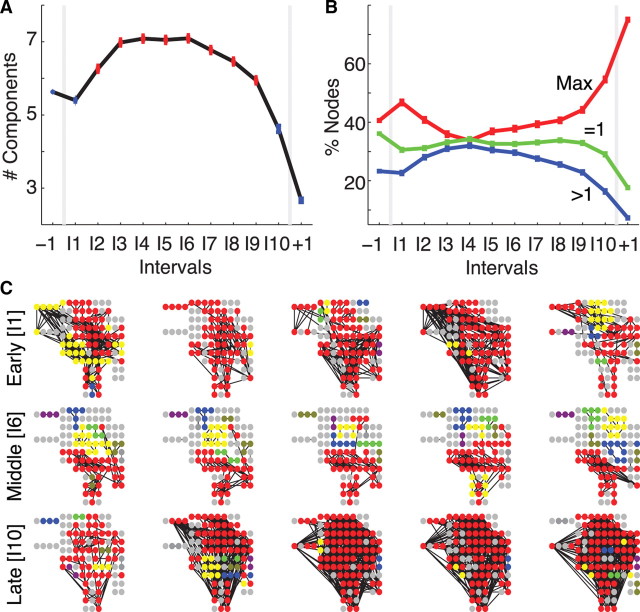
Although the voltage dynamics change dramatically during the seizure, our first measure of the network topology, the density, does not. Perhaps the ictal networks change in more subtle ways, reorganizing, rather than trimming or growing, their edges? To address this possibility, we examine the network components within each interval. Briefly, a component is a connected subnetwork of mutually reachable nodes (i.e., any node in the component can reach any other node in the same component by following a sequence of edges). The average number of nontrivial components, components that consist of two or more nodes, adjusted for differences in subjects increases significantly (see Materials and Methods) during the middle portion of the seizures (Fig. 2A).

Figure 2.

The largest network components fracture during the seizure. A, The average number of connected components (adjusted for differences in subjects) increases during the course of a seizure; points plotted in red indicate a statistically significant increase from the preictal value (number of networks per interval same as in Fig. 1; see Materials and Methods). B, The average percentage of nodes in the largest connected component (red, Max), in trivial components (green, =1), and in other connected components (blue, >1) for the population of subjects and adjusted for differences in subjects. After ictal onset, nodes leave the largest component and become isolated or join other connected components. C, Examples of connected components during early ictal (top row), middle ictal (middle row), and late ictal (bottom row) intervals for a single subject and seizure. Each circle indicates an electrode (including both those on the cortical surface or subcortical) oriented to match surgical placement, and each black line indicates an edge. The electrode colors signify components: all electrodes of the same color belong to the same component, red denotes the largest component, and gray denotes single (isolated) electrodes. During the middle seizure interval, the largest component shrinks as more nontrivial components appear compared with the early and late ictal intervals.

Thus, as the density returns to preictal levels during the seizure (Fig. 1C, intervals I2–I8), more nontrivial components emerge. Does one connected subnetwork dominate and contain most of the nodes? Or, are the nodes more evenly distributed between smaller subnetworks? To investigate this, we determine the percentage of nodes within each of the components for the ensemble of seizures (Fig. 2B). At ictal onset, nearly half of all nodes reside in the largest component, which therefore dominates the network. As the seizure progresses, the largest component fractures; nodes “leave” this component and become isolated or form other, smaller subnetworks. Finally, just before seizure termination, a majority of nodes rejoin to establish a single dominant component.

We illustrate the fracturing and reforming of the largest subnetwork for a single subject and seizure in Figure 2C. At ictal onset (I1), a majority of nodes join the largest component, which here covers portions of the frontal, parietal, and temporal lobes, almost the entire extent of the lateral neocortex as well as subcortical brain regions. During the seizure (I6, middle row), the largest component shrinks and collections of nontrivial components emerge. Finally, at ictal termination (I10, bottom row) nodes rejoin the largest component, which again dominates the network. In this example, and for the population of subjects, the ictal subnetworks merge at onset, fracture during seizure, and rejoin just before termination.

Small-world topologies of the largest subnetwork emerge during preictal and ictal intervals

The largest subnetworks, which incorporate 30–60% of the nodes during the seizure, play a prominent role in the network topology. To examine the properties of these dominant subnetworks, we determine the characteristic path length and clustering coefficient for the largest component of each network. Because the size of the largest subnetwork changes in time (as nodes break off and rejoin the dominant component), we scale the observed values by those expected for a one-dimensional lattice with the same number of nodes and average degree (Watts and Strogatz, 1998). We find that the (scaled) characteristic path lengths in the observed networks remain less than one for all intervals, whereas the (scaled) clustering coefficients tend to exceed one during seizure (Fig. 3). Combined, these results suggest that, for most of the seizure, the largest preictal and ictal subnetworks exhibit small-world topologies (greater clustering coefficients yet smaller path lengths than the associated one-dimensional lattices) for all examined intervals (Netoff et al., 2004; Ponten et al., 2007). Although the ictal subnetworks exhibit small-world topologies, the properties of these topologies evolve in time. Just after seizure onset (I3), both the path length and clustering coefficient tend to increase (the former increases significantly), and the networks move in the direction of becoming a more regular lattice with mesh-like connections between nodes, in agreement with previously reported observations near seizure onset (Ponten et al., 2007; Schindler et al., 2008). Just before seizure termination (I10), the (scaled) path lengths and clustering coefficients decrease dramatically, suggesting the networks evolve toward a more random configuration, as observed previously (Schindler et al., 2008).

Figure 3.

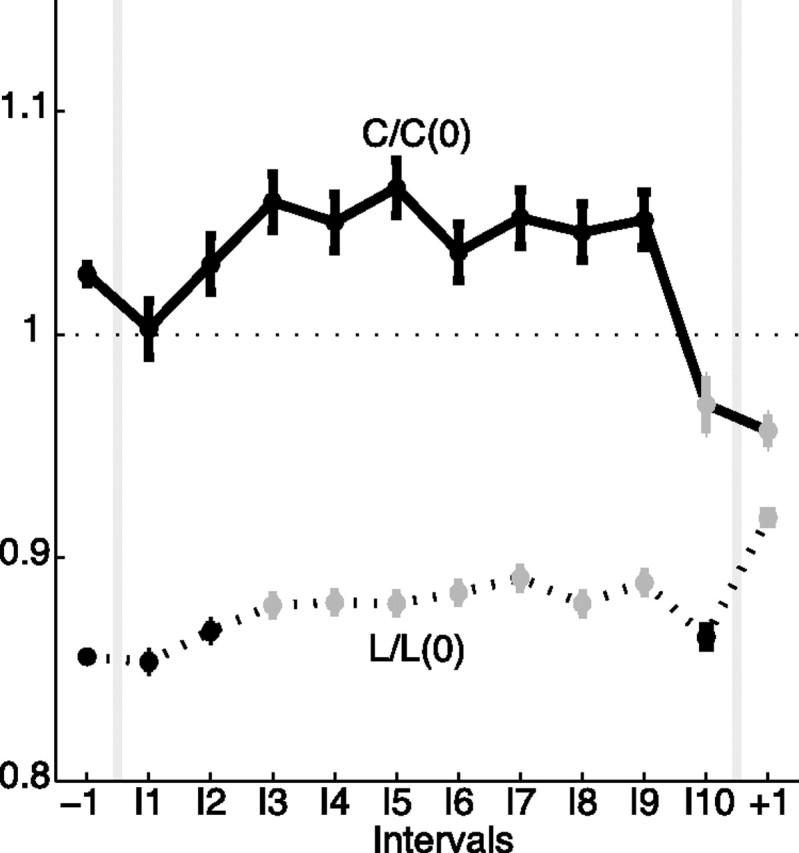
The topological properties of the dominant subnetwork evolve during the seizure. We plot the scaled characteristic path length [L/L(0), dashed curve] and scaled clustering coefficient [C/C(0), solid curve] for each interval (adjusted for differences in subjects and with the same number of networks per interval as in Fig. 1). Values that increase or decrease significantly from the preictal level are indicated in gray. For all intervals considered, the networks are approximately small-world. During the seizure, both measures tend to increase and the networks therefore become more regular. Just before seizure termination (interval I10), both measures decrease and the networks acquire a more random configuration.

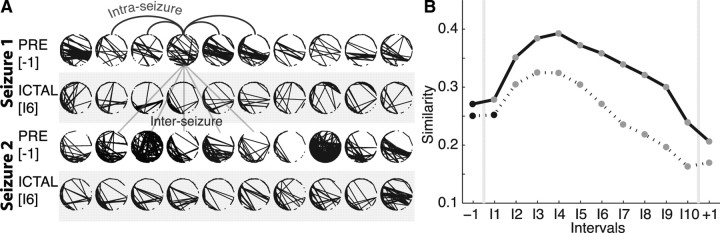
Network topologies become more similar during, and between, seizures

Most patients with epilepsy experience seizures with clinical manifestations (e.g., stereotyped motions) that are similar across seizures within an individual. The voltage activity observed during seizures also appears stereotyped. To determine whether the networks that appear during the seizure do so in stereotyped ways, we apply two measures focused on different aspects of the topological similarities (Fig. 4A). The top two rows show example networks extracted from the preictal interval (label −1) and a middle ictal interval (label I6) from a single seizure and subject. The bottom two rows show another set of networks extracted from the same subject and intervals but from a different seizure. Visual inspection suggests more variability in the preictal networks over time. In addition, the ictal networks appear generally consistent in the two seizures; notice, for example, the concentration of edges in the bottom left regions of the networks.

Figure 4.

Networks become more similar during, and between, seizures. A, Two examples of networks from a preictal interval (unshaded) and ictal interval (shaded) from two different seizures of a single subject. Visual inspection suggests that the ictal networks are more similar both within each seizure (i.e., within each shaded region) and between the two seizures (i.e., between the 2 shaded regions) compared with the preictal networks. The arched (straight) lines indicate example intra-seizure (inter-seizure) comparisons. B, The similarity between networks within each interval of the same seizure (i.e., intra-seizure similarity, solid curve) and between intervals of different seizures from the same subject (i.e., the inter-seizure similarity, dashed curve). The intra-seizure similarity increases during seizure; networks become more similar within ictal intervals compared with preictal intervals. The inter-seizure similarity, which compares networks from the same interval but different seizures of a subject, also increases during seizure. For both curves, circles denote the mean value (n = {82059, 10222, 30666}) of intra-seizure comparisons for the preictal, ictal, and postictal intervals, respectively, and n = {277537, 40169, and 120507} inter-seizure comparisons for the preictal, ictal, and postictal intervals, respectively, adjusted for differences in subjects; the vertical lines denoting the SE are no larger than the black or gray circles. Statistically significant changes from the preictal value are indicated in gray (see Materials and Methods).

We quantify these observations with two measures. The first, the intra-seizure similarity, examines the variability of networks within a fixed interval of a chosen seizure. To compute this measure, we compare each network within an interval (i.e., within interval −1 of the first seizure of a chosen subject) to all other networks within the same interval and seizure. The intra-seizure similarity is large when the variability in the networks within the interval is small. We apply the intra-seizure similarity measure to each interval for all subjects and seizures and plot the average results for each interval (adjusting for differences in subjects) in Figure 4B. During seizure (intervals I1–I9), the intra-seizure similarity increases significantly (see Materials and Methods) compared with preictal values; ictal topologies within each interval become more similar (or exhibit less variability) than the preictal networks. We note the dramatic decrease in similarity during the postictal interval. Although large subnetworks dominate this period (Fig. 2B), the topologies of these networks exhibit high variability.

To determine the consistency of networks between seizures, we apply a second measure: the inter-seizure similarity (see Materials and Methods). In this measure, we choose an interval (e.g., −1) and compare networks from the same interval and subject across different seizures. For example, we compare each network in the first and third rows (or second and fourth rows) of Figure 4A. We repeat this procedure for each patient and note that all patients studied here had at least two seizures. Compared with the intra-seizure similarity, the inter-seizure measure is smaller (Fig. 4B); we expect more variability (and less topological consistency) between different seizures of a subject, yet we observe that ictal networks in early and middle intervals become significantly more similar than preictal networks from seizure to seizure. We conclude that similar ictal networks appear from seizure to seizure for a patient, and, in that sense, the network topologies that emerge, such as the voltage rhythms, are consistent.

Discussion

Consistent topological changes during the seizures and implications for hypersynchrony

We have explored the dynamic topologies of cortical and subcortical functional networks during human epileptic seizures. Although these seizures resulted from multiple different etiologies, were recorded from different cortical and subcortical locations, and included both complex and simple partial seizures, we found remarkable consistency in the evolution of network structure during the seizure. Convention would suggest that the dramatic voltage oscillations characteristic of seizures correlate with hypersynchronous functional networks (i.e., networks with many edges or high density). Surprisingly, the onset of large-amplitude voltage oscillations does not affect the network density. Instead, networks were no more synchronous in the middle of the seizure than preictally (i.e., acquired no more edges). This suggests that seizures are not uniformly hypersynchronous states, at least not at the level of large neuronal populations. Instead, synchrony is largest at ictal onset and termination and evolves in time. These results are consistent with previous reports of an increase in coupling near seizure onset (after a rapid discharge) (Wendling et al., 2001, 2003; Bartolomei et al., 2004; Ponten et al., 2007; Arthuis et al., 2009) and subsequent desynchronization during large-amplitude, low-frequency oscillations characteristic of seizure progression (Schindler et al., 2007, 2008). We note that the spatial scale of measurement is critical here. At the microscopic scale of individual neurons, we expect increased synchrony in small regions to generate the large-amplitude voltage oscillations observed at an individual electrode (Fig. 1C), yet at the macroscopic spatial scale, we observe decreased synchrony between electrodes (i.e., between macroscopic brain regions). Relating dynamics and synchrony between these spatial scales remains a crucial question.

Overall network synchronization provides a crude characterization of network topology. To explore the detailed network structure, we applied a variety of analysis techniques that revealed stereotyped patterns of network evolution from seizure onset to termination. At seizure onset, a large subnetwork of connected nodes emerged. This dominant component then fractured into smaller subnetworks. Approaching seizure termination, these subnetworks rejoined to again establish a dominant network component. Throughout the seizure, the largest component always exhibited a small-world topology, yet this structure varied, becoming more regular (i.e., more like a structure with mesh-like connections between neighboring nodes) during the seizure and more random just before seizure termination.

Consistent topologies emerged between seizures in an individual. Specifically, each individual subject produced similar networks consistent from seizure to seizure. This result coincides with the clinical observation that an individual's seizures are stereotypical events with reproducible patterns of initiation and spread (Litt et al., 2001; Gibbs et al., 2002). In addition, we observed that seizures from heterogeneous etiologies (Table 1) resulted in similar topological progressions from seizure onset to termination, consistent with seizure progression through specific clinical stages (from aura to focal event to generalized event to postictal period), rhythmic stages (from very fast oscillations to large-amplitude, slowing rhythms to bursting to silence) and the more general stages of initiation, propagation, and termination (Pinto et al., 2005).

The similarity of topological evolution across heterogeneous etiologies bolsters the idea that the seizure is a unifying event, a final common pathway from a number of insults, and suggests that the biophysical mechanisms for seizure initiation and propagation are relatively conserved. Many different seizure types seem to share common cellular and network mechanisms (McCormick and Contreras, 2001), and we would like to understand the rhythmic and topological evolution of seizures in terms of specific biological mechanisms [e.g., in terms of neural discharges (Traub et al., 1996), evolving afterdischarges (Trevelyan et al., 2007), depolarization block of interneurons (Ziburkus et al., 2006), depression of excitatory postsynaptic potentials (Nita et al., 2008), or homeostatic synaptic plasticity (Houweling et al., 2005)]. Simulation studies (Netoff et al., 2004; Dyhrfjeld-Johnsen et al., 2007; Lytton, 2008; Bogaard et al., 2009) and multiscalar observations combining single-neuron recordings (microscale), local field potentials (mesoscale), and macroscopic ECoG may help uncover this relationship between dynamic network activity and its underlying mechanisms.

To summarize the network evolution, we emphasized measures that condensed important network features to single scalar values (e.g., the network density or number of components). These reductions of the complex network data facilitated a straightforward comparison of network attributes across the patient population. Although useful, the reductions prohibit a detailed analysis of the focal network features of individual nodes. Concentrating on these focal characteristics may serve an important role in examining the patterns of activity that emerge during seizure propagation [e.g., spiral waves (Huang et al., 2004)]. In addition, such focal measures may assist in seizure localization and treatment, for example, in identifying brain regions that act as “hubs” of seizure activity (Kramer et al., 2008; Morgan and Soltesz, 2008).

Topological and dynamical changes affecting seizure termination

Increasing density and growth of the largest component suggest more synchronization near seizure termination, consistent with recent observations (Topolnik et al., 2003; Schiff et al., 2005; Schindler et al., 2007, 2008). In addition, we observe that the topology of the largest network component evolves toward a more random configuration just before seizure termination, in agreement with previous studies (Schindler et al., 2008). These topological changes occur as the ECoG dynamics develop bursts (brief intervals of large-amplitude voltage activity interspersed with longer intervals of low-amplitude fluctuations) near seizure termination. Modeling studies show that random network topologies support bursting dynamics (Netoff et al., 2004) and better synchronize their dynamics than more regular network organizations (Chavez et al., 2006). In addition, in vitro observations reveal that bursting dynamics are more synchronous than ictal dynamics (Netoff and Schiff, 2002). We might therefore envision a positive feedback loop between the network topology and bursting dynamics that ends the seizure. As the seizure approaches termination, the networks acquire more random configurations and therefore might better synchronize their bursting dynamics. This increased synchronization results in more network edges that act to synchronize the dynamics even more. Eventually, enough edges unite the fractured subnetworks and the bursting dynamics cease. Unraveling the relationship between network topology and dynamics will provide insights into not only epilepsy but perhaps into the dynamics of complex networks in general (Gross and Blasius, 2008).

Ideally, we seek a complete spatiotemporal understanding of the entire ictal event. Such a characterization would incorporate the rhythmic patterns that emerge in the voltage activity during the seizure [e.g., high-frequency oscillations (Allen et al., 1992; Alarcon et al., 1995; Roopun et al., 2009), ictal chirps (Schiff et al., 2000), and spike-wave complexes (Gibbs et al., 2002)] with the spatial network characteristics. How to unify these rhythmic patterns (observed in ECoG or scalp EEG data recorded at individual electrodes) with the network topologies (observed across multiple electrodes) and pathological brain functioning remains an open challenge.

Implications for epilepsy therapies

The current mainstay of epilepsy treatment continues to be medications, with surgical treatments a last resort reserved for patients with pharmaco-resistant epilepsy. Unfortunately, surgical treatment of epilepsy has only limited effectiveness. It is estimated that, overall, surgery only helps 60–70% of patients with intractable seizures. Newer approaches include stimulation of cortex in response to seizure activity (Morrell, 2006). The results reported here suggest a variety of alternatives for surgical manipulation and electrical stimulation treatments responsive to the network topologies. Because the ictal networks evolve in time, the treatment strategies used may depend on the time of intervention. For example, it may be maximally efficient to prevent the formation of the largest component at onset through desynchronization (i.e., to prevent the increases in density observed at ictal onset). A more innovative technique would be a stimulation designed to assist in reformation of the large component after its fracturing; we note that the largest-amplitude pathological voltage oscillations characteristic of a seizure occur during this fracturing period. Perhaps appropriate electrical stimulation could prevent the march through network fracturing and lead to a rapid cessation of the seizure without clinical manifestations. A disadvantage of this proposed intervention is that it follows seizure initiation; to serve as an effective therapeutic target, the network fracturing must still precede the clinical manifestation of the seizure (e.g., loss of awareness). An advantage of this temporally focused approach is that no requirement for seizure prediction or anticipation would be necessary.

More fundamentally, the results presented here bolster a growing literature that is forcing us to reconsider the textbook description of seizures as hypersynchronous events. This realization and accompanying detailed, quantitative description of seizure dynamics may permit entirely new methods of seizure control.