Abstract
Background
The evaluation of the complexity of an observed object is an old but outstanding problem. In this paper we are tying on this problem introducing a measure called statistic complexity.
Methodology/Principal Findings
This complexity measure is different to all other measures in the following senses. First, it is a bivariate measure that compares two objects, corresponding to pattern generating processes, on the basis of the normalized compression distance with each other. Second, it provides the quantification of an error that could have been encountered by comparing samples of finite size from the underlying processes. Hence, the statistic complexity provides a statistical quantification of the statement ‘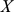 is similarly complex as
is similarly complex as 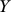 ’.
’.
Conclusions
The presented approach, ultimately, transforms the classic problem of assessing the complexity of an object into the realm of statistics. This may open a wider applicability of this complexity measure to diverse application areas.
Introduction
Complex systems is the study of interactions of simple building blocks that result in a collective behavior or properties absent in the elementary components of the system itself. Due to the fact that this problem does not fit into one of the traditional research fields, it is connected to various of these, for instance physics, biology, chemistry or econometrics [1]–[5]. Many measures, properties or characteristics of a multitude of different complex systems from these fields has been studied to date [6]–[8], however, the complexity of an object may have received the most attention. This property of complex systems has fascinated generations of scientists [9]–[11] trying to quantify such a notation. Very coarsely speaking, an object is said to be ‘complex’ when it does not match patterns regarded as simple, as López-Ruiz et al. [12] describe it in their article. Over the last decades, many approaches have been suggested to define the complexity of an object quantitatively [9], [11], [13]–[19]. An intrinsic problem with such a measure is that there are various ways to perceive and, hence, characterize complexity leading to complementing complexity measures [20]. For example, Kolmogorov complexity [9], [11], [21] is based on algorithmic information theory considering objects as individual symbol strings, whereas the measures effective measure complexity (EMC) [17], excess entropy
[22], predictive information
[23] or thermodynamic depth
[18] relate objects to random variables and are ensemble based. Interestingly, despite considerable differences among all these complexity measures 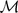 they all have in common that they assign a complexity value to each individual object
they all have in common that they assign a complexity value to each individual object 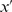 under consideration,
under consideration, 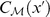 . In this paper we will assume that
. In this paper we will assume that 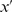 corresponds to a string sequence of a certain length and its components assume values from a certain domain, e.g.,
corresponds to a string sequence of a certain length and its components assume values from a certain domain, e.g., 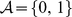 or
or 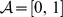 . It is of importance to note that there is a conceptually different measure recently introduced by Vitányi et al. that evaluates the complexity distance among two objects
. It is of importance to note that there is a conceptually different measure recently introduced by Vitányi et al. that evaluates the complexity distance among two objects 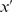 and
and 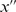 instead of their absolute values. This measure is called the normalized compression distance (NCD) [24],
instead of their absolute values. This measure is called the normalized compression distance (NCD) [24], 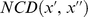 , and is based on Kolmogorov complexity [10].
, and is based on Kolmogorov complexity [10].
The purpose of this paper is to introduce a new measure of complexity we call statistic complexity that is not only different to all other complexity measures introduced so far, but also connects directly to statistics, specifically, to statistical inference [25], [26]. More precisely, we introduce a complexity measure with the following properties. First, the measure is bivariate comparing two objects, corresponding to pattern generating processes, on the basis of the normalized compression distance with each other. Second, this measure provides the quantification of an error that could have encountered by comparing samples of finite size from the underlying processes. Hence, the statistic complexity provides a statistical quantification of the statement ‘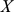 is similarly complex as
is similarly complex as 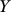 ’.
’.
This paper is organized as follows. In the next section we describe the general problem in more detail and introduce our complexity measure. Then we present numerical results and provide a discussion. We finish with conclusions and an outlook.
Methods
Currently, a commonly acknowledged, rigorous mathematical definition of the complexity of an object is not available. Instead, when complexity measures are suggested they are normally assessed by their behavior with respect to three qualitative patterns, namely simple, random (chaotic) and complex patterns. Qualitatively, a complexity measure is considered good if: (1) the complexity of simple and random objects is less than the complexity value of complex objects [17], (2) the complexity of an object does not change if the system size changes. For example, Kolmogorov complexity has the desireable property to remain unchanged if the system size doubles, i.e., 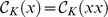 , however, it cannot distinguish random from complex pattern because in both cases the compressibility of an object is low resulting in high values of
, however, it cannot distinguish random from complex pattern because in both cases the compressibility of an object is low resulting in high values of 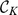 . We want to add a third property to the above criteria: (3) A complexity measure should quantify the uncertainty of the complexity value. As motivation for this property we just want to mention that there is a crucial difference between an observed object
. We want to add a third property to the above criteria: (3) A complexity measure should quantify the uncertainty of the complexity value. As motivation for this property we just want to mention that there is a crucial difference between an observed object 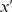 and its generating process
and its generating process 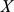 [23]. If the complexity of
[23]. If the complexity of 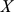 should be assessed, based on the observation
should be assessed, based on the observation 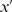 only, this assessment may be erroneous. This error may stem from the limited (finite) size of observations. Also, the possibility of measurement errors would be another source derogating the ability of an error-free assessment. For this reason, the major objective of this article is to introduce a complexity measure possessing all three properties listed above that assesses the complexity classes of the underlying processes instead of individual objects.
only, this assessment may be erroneous. This error may stem from the limited (finite) size of observations. Also, the possibility of measurement errors would be another source derogating the ability of an error-free assessment. For this reason, the major objective of this article is to introduce a complexity measure possessing all three properties listed above that assesses the complexity classes of the underlying processes instead of individual objects.
We start by pointing out that criteria (1) provides a relative statement connecting different objects. That means the complexity of an object is always related to the complexity of another object [20] leading to relative statements like ‘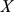 is similarly complex as
is similarly complex as 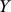 ’. Hence, a numerical value
’. Hence, a numerical value 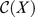 without knowledge of any other complexity value for other objects has no meaning at all. For reasons of mathematical rigor, we propose to include this implicit reference point into a proper definition of complexity. This implies that a fundamental complexity measure needs to be bivariate,
without knowledge of any other complexity value for other objects has no meaning at all. For reasons of mathematical rigor, we propose to include this implicit reference point into a proper definition of complexity. This implies that a fundamental complexity measure needs to be bivariate, 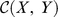 , instead of univariate comparing two processes
, instead of univariate comparing two processes 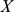 and
and 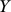 . As a side note, we remark that all complexity measures suggested so far we are aware of are univariate measures [13], [14], [16]–[18], [22], [23] with respect to the context set above, except for the normalized compression distance (NCD) [24], [27]. However, a practical problem of the NCD is that Kolmogorov complexity, on which it is based, is not computable but only upper semi-computable [27]. Li et al. introduced in [27] a normalized and universal metric called normalized
information
distance (NID) which can be approximated by,
. As a side note, we remark that all complexity measures suggested so far we are aware of are univariate measures [13], [14], [16]–[18], [22], [23] with respect to the context set above, except for the normalized compression distance (NCD) [24], [27]. However, a practical problem of the NCD is that Kolmogorov complexity, on which it is based, is not computable but only upper semi-computable [27]. Li et al. introduced in [27] a normalized and universal metric called normalized
information
distance (NID) which can be approximated by,
| (1) |
the normalized
compression
distance
[27]. Here, 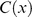 denotes the compression size of string
denotes the compression size of string  and
and 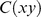 the compression size of the concatenated stings
the compression size of the concatenated stings  and
and 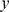 . Practically, the quantities
. Practically, the quantities 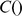 are obtained by compressors like gzip or bzip2, see [28], [29] for details.
are obtained by compressors like gzip or bzip2, see [28], [29] for details.
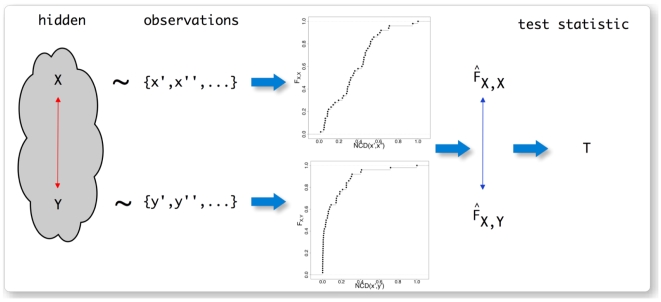
Criteria (3) of a complexity measure stated above acknowledges the fact that an assessment of an object's complexity cannot be without uncertainty or error in case only finite information about this object is available. That means, for a complexity measure to be applicable to real objects (rather than pure mathematical ones) it has to be statistic in order to deal appropriately with incomplete information. Based on these considerations, the statistic complexity measure we suggest is defined by the following procedure visualized in Fig. 1:
Figure 1. Visualization of the problem and the construction of the test statistic from observations.
The double headed arrows represent comparisons of entities. Red indicates that this comparison cannot be performed because the two entities are hidden (unobservable) whereas blue indicates a feasible comparison.
Estimate the empirical distribution function
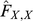 (We indicate estimated entities by
(We indicate estimated entities by 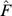 and refer to the ensemble by
and refer to the ensemble by 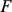 .) of the normalized compression distance from
.) of the normalized compression distance from 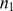 samples,
samples, 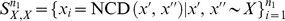 , from objects
, from objects 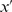 and
and 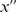 of size
of size  generated by process
generated by process 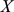 (Here
(Here 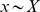 means that
means that  is generated (or drawn) from process (distribution)
is generated (or drawn) from process (distribution) 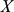 .).
.).Estimate the empirical distribution function
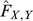 of the normalized compression distance from
of the normalized compression distance from 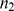 samples,
samples, 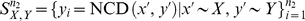 , from objects
, from objects 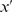 and
and 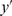 of size
of size  from two different processes,
from two different processes, 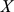 and
and 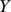 .
.Determine
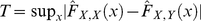 and
and 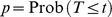 .
.Define,
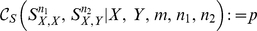 , as statistic complexity
, as statistic complexity
This procedure corresponds to a two-sided, two-sample Kolmogorov-Smirnov (KS) test [30], [31] based on the normalized compression distance [24], [27] obtaining distances among observed objects. The statistic complexity corresponds to the p-value of the underlying null hypotheses, 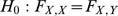 , and, hence, assumes values in
, and, hence, assumes values in 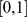 . The null hypothesis is a statement about the null distribution of the test statistic
. The null hypothesis is a statement about the null distribution of the test statistic 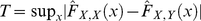 , and because the distribution functions are based on the normalized compression distances among objects
, and because the distribution functions are based on the normalized compression distances among objects 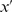 and
and 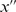 , drawn from the processes
, drawn from the processes 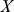 and
and 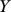 , this leads to a statement about the distribution of normalized compression distances. Hence, verbally,
, this leads to a statement about the distribution of normalized compression distances. Hence, verbally, 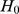 can be phrased as ‘in average, the compression distance of objects from
can be phrased as ‘in average, the compression distance of objects from 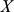 to objects from
to objects from 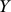 equals the compression distance of objects only taken from
equals the compression distance of objects only taken from 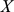 ’. It is important to emphasize that this equality holds in average and, thus needs to be connected to two ensembles
’. It is important to emphasize that this equality holds in average and, thus needs to be connected to two ensembles 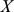 and
and 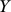 . If the alternative hypothesis,
. If the alternative hypothesis, 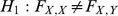 , is true this equality does no longer hold implying differences in the underlying processes
, is true this equality does no longer hold implying differences in the underlying processes 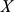 and
and 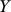 , leading to differences in the NCDs. From the formulation of the hypotheses, tested by the statistic complexity, it is apparent that we are following closely the guiding principle expressed by López-Ruiz et al. [12] as cited at the beginning of this paper, because
, leading to differences in the NCDs. From the formulation of the hypotheses, tested by the statistic complexity, it is apparent that we are following closely the guiding principle expressed by López-Ruiz et al. [12] as cited at the beginning of this paper, because 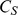 is intrinsically a comparative measure. As a side note regarding the choice of the null hypothesis we want to remark that substituting
is intrinsically a comparative measure. As a side note regarding the choice of the null hypothesis we want to remark that substituting 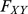 with
with 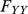 may encounter problems in cases where the complexity value of objects in
may encounter problems in cases where the complexity value of objects in 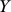 is systematically shifted compared to the complexity value of objects in
is systematically shifted compared to the complexity value of objects in 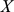 . In this case, the distributions
. In this case, the distributions 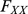 and
and 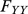 could be similar, although, the complexity of elements in
could be similar, although, the complexity of elements in 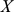 and
and 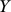 are different. Practically, this may correspond to a pathological case rarely encountered in practice, however, conceptually, such a null hypothesis is apparently less stringent.
are different. Practically, this may correspond to a pathological case rarely encountered in practice, however, conceptually, such a null hypothesis is apparently less stringent.
Regarding the notation and interpretation of the above procedure it is important to note the following. First, the entities  and
and 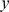 refer to values of the NCD. For example,
refer to values of the NCD. For example, 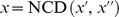 whereas
whereas 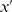 and
and 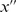 are observable objects that are identically and independently (iid) generated from a process
are observable objects that are identically and independently (iid) generated from a process 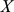 ,
, 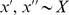 . Because
. Because 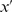 and
and 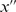 are generated from the same process
are generated from the same process 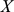 , the resulting distribution function
, the resulting distribution function 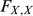 is only indexed by this process. The
is only indexed by this process. The 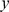 entities are obtained similarly, however, in this case
entities are obtained similarly, however, in this case 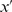 and
and 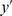 are objects generated from two different processes, namely
are objects generated from two different processes, namely 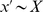 and
and 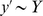 . For this reason the distribution function is indexed by these two processes,
. For this reason the distribution function is indexed by these two processes, 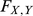 . Second, we use the notation,
. Second, we use the notation, 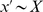 , to indicate that
, to indicate that 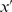 is generated from a process
is generated from a process 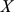 , but also that
, but also that 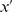 is drawn from
is drawn from 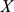 . The first meaning is clear if thinking of
. The first meaning is clear if thinking of 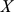 as a model for a complex system, e.g., a cellular automata or a stochastic process. The latter emphasizes the fact that such a process, even if deterministic, becomes random with respect to, e.g., random initial conditions and, hence, effectively is a stochastic process. Third, for reasons of conceptual simplicity we require all objects to have the same size
as a model for a complex system, e.g., a cellular automata or a stochastic process. The latter emphasizes the fact that such a process, even if deterministic, becomes random with respect to, e.g., random initial conditions and, hence, effectively is a stochastic process. Third, for reasons of conceptual simplicity we require all objects to have the same size  . This condition may be relaxed to allow objects of varying sizes but it may require additional technical consideration. On a technical note, the above defined statistic complexity has the very desirable property that the power reaches asymptotically
. This condition may be relaxed to allow objects of varying sizes but it may require additional technical consideration. On a technical note, the above defined statistic complexity has the very desirable property that the power reaches asymptotically 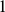 for
for  and
and  [32]. This means, for infinite many observations the error of the test to falsely accept the null hypotheses when in fact the alternative is true becomes zero. This limiting property is important to hold, because in this case all information about the system is available and, hence, it would be implausible if for such circumstances no error-free decision could be achieved. Formally, this property can be stated as
[32]. This means, for infinite many observations the error of the test to falsely accept the null hypotheses when in fact the alternative is true becomes zero. This limiting property is important to hold, because in this case all information about the system is available and, hence, it would be implausible if for such circumstances no error-free decision could be achieved. Formally, this property can be stated as 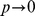 for
for  and
and  . Finally, we would like to note that despite the fact that statistic complexity is a statistical test, it borrows part of its strength from the NCD respectively Kolmogorov complexity on which this is based on. Hence, it unites various properties from very different concepts.
. Finally, we would like to note that despite the fact that statistic complexity is a statistical test, it borrows part of its strength from the NCD respectively Kolmogorov complexity on which this is based on. Hence, it unites various properties from very different concepts.
Results
In the following we provide different numerical examples for data frequently used when studying complexity measures. This allows a direct comparison of ours with different measures.
The first characteristic of the statistic complexity we study is the influence of the size  of objects on
of objects on 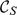 . Table 1 shows the results for comparing patterns generated by different rules of one-dimensional cellular automata. Column one represents the reference process,
. Table 1 shows the results for comparing patterns generated by different rules of one-dimensional cellular automata. Column one represents the reference process, 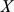 , and column two corresponds to
, and column two corresponds to 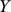 . The third and fifty column shows the averaged p-values obtained for cellular automata of length
. The third and fifty column shows the averaged p-values obtained for cellular automata of length 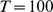 respectively
respectively 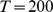 - column four and six provide the variances for the corresponding p-values. For the simulation results shown in Table 1 we generated spatiotemporal patterns for one-dimensional CA for
- column four and six provide the variances for the corresponding p-values. For the simulation results shown in Table 1 we generated spatiotemporal patterns for one-dimensional CA for 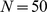 (space) and
(space) and 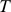 (time), an alphabet of size
(time), an alphabet of size 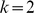 and a
and a 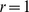 neighborhood with periodic boundary conditions. As burn-in time we used
neighborhood with periodic boundary conditions. As burn-in time we used 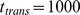 time steps. Each of these spatiotemporal pattern
time steps. Each of these spatiotemporal pattern 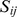 , with
, with  and
and 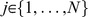 , is transformed to its difference pattern
, is transformed to its difference pattern 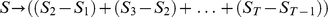 (Here
(Here 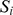 with
with  corresponds to a row vector of length
corresponds to a row vector of length 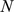 .) resulting in a string (object) of length
.) resulting in a string (object) of length 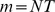 to be applicable for the NCD. Here, the operator
to be applicable for the NCD. Here, the operator  means concatenation of strings. See [29] for numerical details for the application of NCD. The results in Table 1 show that the p-values remain in the same order of magnitude if the size of an object
means concatenation of strings. See [29] for numerical details for the application of NCD. The results in Table 1 show that the p-values remain in the same order of magnitude if the size of an object  is doubled meaning that the overall quantitative assessment of two processes
is doubled meaning that the overall quantitative assessment of two processes 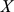 and
and 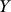 - based on sampled objects thereof - by the measure
- based on sampled objects thereof - by the measure 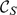 is invariant to extensions of the size
is invariant to extensions of the size  . Next we demonstrate that the statistic complexity is capable to differentiate between random and complex objects. For this reason we compare rule
. Next we demonstrate that the statistic complexity is capable to differentiate between random and complex objects. For this reason we compare rule 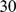 , producing random patterns, with rule
, producing random patterns, with rule 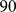 ,
, 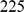 , both random, and rule
, both random, and rule 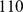 , which is complex because it is capable of universal computation. From Table 1 one can see that the p-values correspond with our expectations giving high values for
, which is complex because it is capable of universal computation. From Table 1 one can see that the p-values correspond with our expectations giving high values for 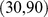 and
and 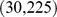 and low values for
and low values for 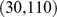 . In addition we compare rule
. In addition we compare rule 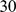 with rules
with rules 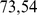 and
and 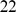 , classified according to Wolfram as random, and obtain very low p-values, suggesting significant differences among those patterns. The crucial point here is that not all CA rules that produce chaotic patterns are indistinguishable from each other. In [33] the growth exponent of the roughness along other measures have been used to obtain several subclasses for CA rules leading to chaotic behavior. Comparing our results with their classification reveals that actually rule
, classified according to Wolfram as random, and obtain very low p-values, suggesting significant differences among those patterns. The crucial point here is that not all CA rules that produce chaotic patterns are indistinguishable from each other. In [33] the growth exponent of the roughness along other measures have been used to obtain several subclasses for CA rules leading to chaotic behavior. Comparing our results with their classification reveals that actually rule 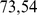 and
and 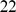 are in different subclasses whereas rule
are in different subclasses whereas rule 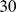 is classified together with rule
is classified together with rule 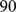 and
and 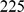 . Last, we compare rule
. Last, we compare rule 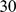 with a periodic pattern, rule
with a periodic pattern, rule 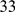 , and obtain also in this case a clear distinction. In summary,
, and obtain also in this case a clear distinction. In summary, 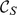 can not only distinguish between simple and complex patterns but finds also meaningful substructures among chaotic patterns if rule
can not only distinguish between simple and complex patterns but finds also meaningful substructures among chaotic patterns if rule 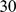 is used as reference process.
is used as reference process.
Table 1. Results for one-dimensional CA (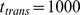 ,
, 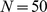 ,
, 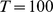 (third and fourth column) and
(third and fourth column) and 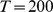 (fifth and sixth column)) averaged over
(fifth and sixth column)) averaged over 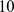 runs.
runs.
| X | Y | T = 100 | T = 200 | ||
| CA rule | CA rule |
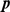
|
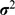
|
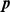
|
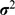
|
| 30 | 30 | 0.593 | 0.075 | 0.684 | 0.102 |
| 30 | 90 | 0.617 | 0.102 | 0.575 | 0.139 |
| 30 | 225 | 0.388 | 0.131 | 0.632 | 0.086 |
| 30 | 73 | 0.002 | 0.001 | 0.002 | 0.001 |
| 30 | 54 | 0.002 | 0.000 | 0.001 | 0.001 |
| 30 | 22 | 0.002 | 0.000 | 0.001 | 0.001 |
| 30 | 33 | 0.001 | 0.001 | 0.002 | 0.000 |
| 30 | 110 | 0.002 | 0.001 | 0.002 | 0.001 |
First column: process 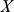 . Second column: process
. Second column: process 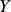 . Sample size is
. Sample size is 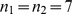 .
.
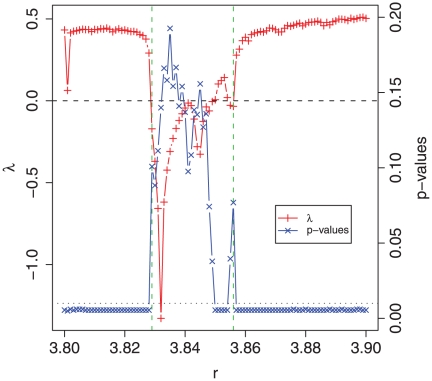
Next, we apply our measure to the logistic map and compare the results with the Lyapunov exponent (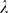 ). The results are summarized in Fig. 2. We calculate the time series for various values of
). The results are summarized in Fig. 2. We calculate the time series for various values of  (x-axis) in the intervall
(x-axis) in the intervall 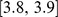 (
( was varied in step sizes of
was varied in step sizes of 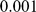 and sample size was
and sample size was 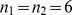 .).
.). 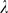 assumes negative values in
assumes negative values in 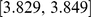 and
and 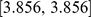 indicating a nonchaotic behavior of the logistic map for these values of
indicating a nonchaotic behavior of the logistic map for these values of  . The vertical dashed line separates positive from negative values. The p-values of the statistic complexity (blue line, cross symbols) are obtained for each value of
. The vertical dashed line separates positive from negative values. The p-values of the statistic complexity (blue line, cross symbols) are obtained for each value of  by averaging over
by averaging over 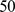 time series each of length
time series each of length 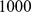 (After waiting a transient period of
(After waiting a transient period of 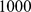 steps.). As reference process,
steps.). As reference process, 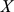 , we use a logistic map with
, we use a logistic map with 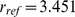 , which corresponds to a periodic behavior. From Fig. 2 one can see that there are essentially two types of p-values, ones that are not zero and ones that are close to zero. For example, using a significance level of
, which corresponds to a periodic behavior. From Fig. 2 one can see that there are essentially two types of p-values, ones that are not zero and ones that are close to zero. For example, using a significance level of 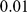 (dotted horizontal line) one obtains that significant values correspond to positive Lyapunov exponents and non-significant values to negative Lyapunov exponents. Again, we want to emphasize that the p-values do not provide a yes or no answer if the logistic map, for a given
(dotted horizontal line) one obtains that significant values correspond to positive Lyapunov exponents and non-significant values to negative Lyapunov exponents. Again, we want to emphasize that the p-values do not provide a yes or no answer if the logistic map, for a given  value, is chaotic or nonchaotic but the correct interpretation is that low p-values provide strong evidence against the null hypotheses whereas high p-values do not allow to reject the null hypotheses. Because we use
value, is chaotic or nonchaotic but the correct interpretation is that low p-values provide strong evidence against the null hypotheses whereas high p-values do not allow to reject the null hypotheses. Because we use 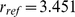 as reference - for which the logistic map shows periodic (nonchaotic) behavior - this is a similar though not identical question. The results for the logistic map allow a comparison with a well studied system. As demonstrated by our results shown in Fig. 2, for an appropriately chosen reference process,
as reference - for which the logistic map shows periodic (nonchaotic) behavior - this is a similar though not identical question. The results for the logistic map allow a comparison with a well studied system. As demonstrated by our results shown in Fig. 2, for an appropriately chosen reference process, 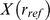 , there is a clear correspondence between the statistic complexity and the Lyapunov exponent. This property is certainly desirable to hold because it may allows to connect to traditional contributions in the field beyond the logistic map. The possibility of such a connection, despite the seemingly different methods underlying the statistic complexity respectively the Lyapunov exponent, can be attributed to the parametric form of our complexity measure allowing a flexibility that is entirely missing in other measures. More importantly, this flexibility is not imposed into the measure but follows naturally from a consequent interpretation of complexity as a referential measure [12] implying imperatively the existence of a reference process
, there is a clear correspondence between the statistic complexity and the Lyapunov exponent. This property is certainly desirable to hold because it may allows to connect to traditional contributions in the field beyond the logistic map. The possibility of such a connection, despite the seemingly different methods underlying the statistic complexity respectively the Lyapunov exponent, can be attributed to the parametric form of our complexity measure allowing a flexibility that is entirely missing in other measures. More importantly, this flexibility is not imposed into the measure but follows naturally from a consequent interpretation of complexity as a referential measure [12] implying imperatively the existence of a reference process 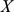 against which another process
against which another process 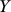 is quantitatively compared.
is quantitatively compared.
Figure 2. Lyapunov exponent (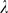 - red line, plus symbol) and p-values (blue line, cross symbol) of the logistic map in dependence on
- red line, plus symbol) and p-values (blue line, cross symbol) of the logistic map in dependence on  .
.
The dotted horizontal line corresponds to a significance level of 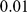 and the dashed line to
and the dashed line to 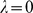 .
.
Discussion
The complexity measure introduced in this paper has several properties that are different to all other measures proposed so far. First, 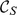 is a bivariate measure allowing to make comparative statements, instead of absolute ones. This may appear as a disadvantage first, however, as López-Ruiz et al. [12] point out, we inevitably compare patterns with each other to make a decision about their complexity (See also the comparative discussion on page 909 in [17] about the three patterns shown in Fig. 1.) [20]. Second, we do not make assumptions with respect to the size of patterns to which our measure can be applied, instead, principally, we allow patterns of any finite or infinite size
is a bivariate measure allowing to make comparative statements, instead of absolute ones. This may appear as a disadvantage first, however, as López-Ruiz et al. [12] point out, we inevitably compare patterns with each other to make a decision about their complexity (See also the comparative discussion on page 909 in [17] about the three patterns shown in Fig. 1.) [20]. Second, we do not make assumptions with respect to the size of patterns to which our measure can be applied, instead, principally, we allow patterns of any finite or infinite size  . For example, measures like EMC or excess entropy are based on block entropies of varying order
. For example, measures like EMC or excess entropy are based on block entropies of varying order  and the final measure is obtained in the limit for
and the final measure is obtained in the limit for  against infinity. Strictly, such measures require an infinite amount of data. Third, due to the fact that statistic complexity allows the comparison of patterns of any size
against infinity. Strictly, such measures require an infinite amount of data. Third, due to the fact that statistic complexity allows the comparison of patterns of any size  with finite sample sizes
with finite sample sizes 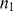 and
and 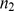 the result of the comparison may be erroneous. The KS test, underlying
the result of the comparison may be erroneous. The KS test, underlying 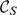 , allows a quantification of such an error statistically. Because this error can be quantified in dependence on
, allows a quantification of such an error statistically. Because this error can be quantified in dependence on  ,
, 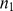 and
and 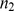 , there is no need to assume limiting properties. At this point we would like to re-emphasize that the term statistic complexity has been chosen to underline the involvement of a test statistic in our measure on which the complexity value is based. For this reason other complexity measures that have been named statistical complexity
[12], [34], [35] are not similar to our measure at all due to the fact that none of these measures uses a test statistic or a statistical test. Hence, they are actually not related to statistics (the field). An alternative name for these measures would be probabilistic complexity, which would make this difference more obvious. The fourth point relates to the empirical distribution functions. The reason for their introduction is, besides the fact that they allow a connection to the KS test, they allow the introduction of two ensembles, one for the process
, there is no need to assume limiting properties. At this point we would like to re-emphasize that the term statistic complexity has been chosen to underline the involvement of a test statistic in our measure on which the complexity value is based. For this reason other complexity measures that have been named statistical complexity
[12], [34], [35] are not similar to our measure at all due to the fact that none of these measures uses a test statistic or a statistical test. Hence, they are actually not related to statistics (the field). An alternative name for these measures would be probabilistic complexity, which would make this difference more obvious. The fourth point relates to the empirical distribution functions. The reason for their introduction is, besides the fact that they allow a connection to the KS test, they allow the introduction of two ensembles, one for the process 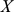 and one for processes
and one for processes 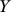 . These ensembles compensate that the classic Kolmogorov complexity is not related to any ensemble but only to one string. Further, the ensembles induce a probabilistic interpretation of the deterministic NCD with respect to the underlying processes that generate the patterns. This is in accordance with [17] emphasizing the importance of complexity measures being probabilistic. Taken together, this allows a quantifiable approximation, in dependence on
. These ensembles compensate that the classic Kolmogorov complexity is not related to any ensemble but only to one string. Further, the ensembles induce a probabilistic interpretation of the deterministic NCD with respect to the underlying processes that generate the patterns. This is in accordance with [17] emphasizing the importance of complexity measures being probabilistic. Taken together, this allows a quantifiable approximation, in dependence on  ,
, 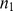 and
and 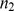 , of the underlying processes
, of the underlying processes 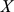 and
and 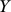 with respect to the information they provide about their complexity, in form of the real observable patterns.
with respect to the information they provide about their complexity, in form of the real observable patterns.
From an applied point of view, the direct connection of statistic complexity with statistical inference allows a confirmatory analysis of the complexity of objects. Due to the fact that the uncertainty of a complexity comparison is inherently provided by our measure, it is applicable to (real) objects from a multitude of different application domains. In the future we are planing to investigate the complexity of biological pathways in the context of cancer and other complex diseases [37]. A further potential direction would be an analysis of different goodness-of-fit tests. For example, it would be interesting to study a Cramér-von Mises or an Anderson-Darling test, instead of a Kolmogorov-Smirnov test [36]. Other tests may have advantages in different application areas or specific experimental conditions, although, a Kolmogorov-Smirnov test was sufficient with respect to the applications studied in this paper.
Acknowledgments
For the statistical simulations R [38] has been used.
Footnotes
Competing Interests: The author has declared that no competing interests exist.
Funding: The author has no support or funding to report.
References
- 1.Bar-Yam Y. Dynamics of Complex Systems. Perseus Books; 1997. [Google Scholar]
- 2.Nicolis G, Prigogine I. Exploring Complexity. Freeman; 1989. [Google Scholar]
- 3.Prokopenko M, Boschetti F, Ryan A. An information-theoretic primer on complexity, self-organization, and emergence. Complexity. 2009;15:11–28. [Google Scholar]
- 4.Schuster H. Complex Adaptive Systems. Scator Verlag; 2002. [Google Scholar]
- 5.Wolfram S. Statistical mechanics of cellular automata. Phys Rev E. 1983;55:601–644. [Google Scholar]
- 6.Dehmer M. A novel method for measuring the structural information content of networks. Cybernetics and Systems. 2008;39:825–842. [Google Scholar]
- 7.Dehmer M, Barbarini N, Varmuza K, Graber A. A large scale analysis of information-theoretic network complexity measures using chemical structures. PLoS ONE. 2009;4:e8057. doi: 10.1371/journal.pone.0008057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Watts D, Strogatz S. Collective dynamics of ‘small-world’ networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 9.Kolmogorov AN. Three approaches to the quantitative definition of ‘information’. Problems of Information Transmission. 1965;1:1–7. [Google Scholar]
- 10.Li M, Vitányi P. An Introduction to Kolmogorov Complexity and Its Applications. Springer; 1997. [Google Scholar]
- 11.Solomonoff R. A preliminary report on a general theory of inductive inference. 1960. Technical Report V-131, Zator Co., Cambridge, Ma.
- 12.López-Ruiza R, Mancinib H, Calbet X. A statistical measure of complexity. Physics Letters A. 1995;209:321–326. [Google Scholar]
- 13.Badii R, Politi A. Complexity: Hierarchical Structures and Scaling in Physics. 1997. Cambridge University Press, Cambridge.
- 14.Bennett C. Logical depth and physical complexity. In: Herken R, editor. The Universal Turing Machine– a Half-Century Survey. Oxford University Press; 1988. pp. 227–257. [Google Scholar]
- 15.Crutchfield JP, Young K. Inferring statistical complexity. Phys Rev Lett. 1989;63:105–108. doi: 10.1103/PhysRevLett.63.105. [DOI] [PubMed] [Google Scholar]
- 16.Gell-Mann M, Lloyd S. Information measures, effective complexity, and total information. Complexity. 1998;2:44–52. [Google Scholar]
- 17.Grassberger P. Toward a quantitative theory of self-generated complexity. Int J Theor Phys. 1986;25:907–938. [Google Scholar]
- 18.Lloyd S, Pagels H. Complexity as thermodynamic depth. Annals of Physics. 1988;188:186–213. [Google Scholar]
- 19.Zurek W, editor. Complexity, Entropy and the Physics of Information. 1990. Addison-Wesley, Redwood City.
- 20.Grassberger P. Problems in quantifying self-generated complexity. Helvetica Physica Acta. 1989;62:489–511. [Google Scholar]
- 21.Chaitin G. On the length of programs for computing finite binary sequences. Journal of the ACM. 1966:547–569. [Google Scholar]
- 22.Crutchfield J, Packard N. Symbolic dynamics of noisy chaos. Physica D. 1983;7:201–223. [Google Scholar]
- 23.Bialek W, Nemenman I, Tishby N. Predictability, complexity, and learning. Neural Computation. 2001;13:2409–2463. doi: 10.1162/089976601753195969. [DOI] [PubMed] [Google Scholar]
- 24.Cilibrasi R, Vitányi P. Clustering by compression. IEEE Transactions Information Theory. 2005;51:1523–1545. [Google Scholar]
- 25.Casella G, Berger R. Statistical Inference. Duxbury Press; 2002. [Google Scholar]
- 26.Mood A, Graybill F, Boes D. Introduction to the Theory of Statistics. McGrw-Hill; 1974. [Google Scholar]
- 27.Li M, Chen X, Li X, Ma B, Vitányi P. The similarity metric. IEEE Transactions on Information Theory. 2004;50:3250–3264. [Google Scholar]
- 28.Cebrian M, Alfonseca M, Ortega A. Common pitfalls using the normalized compression distance: What to watch out for in a compressor. Communications in Information and Systems. 2005;5:367–384. [Google Scholar]
- 29.Emmert-Streib F. Exploratory analysis of spatiotemporal patterns of cellular automata by clustering compressibility. Physical Review E. 2010;81:026103. doi: 10.1103/PhysRevE.81.026103. [DOI] [PubMed] [Google Scholar]
- 30.Conover W. Practical Nonparametric Statistics. 1999. John Wiley & Sons, New York.
- 31.Smirnov N. Estimate of deviation between empirical distribution functions in two independent samples. Bulletin Moscow University. 1939;2:3–16. [Google Scholar]
- 32.Milbrodt H, Strasser H. On the asymptotic power of the two-sided kolmogorov-smirnov test. Journal of Statistical Planning and Inference. 1990;26:1–23. [Google Scholar]
- 33.Mattos T, Moreira J. Universality Classes of Chaotic Cellular Automata. Brazilian Journal of Physics. 2004;34:448–451. [Google Scholar]
- 34.Crutchfield J, Feldman D. Statistical complexity of simple one-dimensional spin systems. Phys Rev E. 1997;55:R1239. [Google Scholar]
- 35.Feldman D, Crutchfield J. Measures of statistical complexity: Why? Physics Letters A. 1998;238:244–252. [Google Scholar]
- 36.Lehman E. Testing Statistical Hypotheses. Springer; 2005. [Google Scholar]
- 37.Emmert-Streib F. The chronic fatigue syndrome: A comparative pathway analysis. Journal of Computational Biology. 2007;14:961–972. doi: 10.1089/cmb.2007.0041. [DOI] [PubMed] [Google Scholar]
- 38.R Development Core Team. R: A Language and Environment for Statistical Computing. 2008. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0.