Interpretation of the prostate-specific antigen history in assessing life-threatening prostate cancer

Abstract

Objective

To present an effective approach to the early detection of lethal prostate cancer using longitudinal data on prostate-specific antigen (PSA) and its rate of change, i.e. PSA velocity (PSAV). This longitudinal approach might also be extendible to other biomarkers.

Subjects and methods

PSAV was calculated using five techniques for 634 subjects with at least three PSA measurements in a longitudinal ageing study, censoring PSA levels of > 10 ng/mL. The efficacy for predicting death from prostate cancer was assessed with concordance indices and by using net reclassification improvement (NRI), which indicated the net increase in sensitivity and specificity when adding a biomarker to a base Cox proportional hazards model. The PSAV techniques were compared for the 5–10 years before the clinical diagnosis of prostate cancer. The most effective technique was then applied at the transition point when each man's PSA history curve transformed from linear to exponentially increasing, and its predictive value was compared to that of concurrent PSA level.

Results

A PSA transition point was found in 522 (82%) of the 634 men, including all 11 who died from prostate cancer. At the transition point, the mean PSA level was 1.4 ng/mL, and PSAV but not PSA level was significantly higher among men who died from prostate cancer than among men who did not (P = 0.021 vs P = 0.112; Wilcoxon two-sample test). At the transition point, adding PSAV to a base model consisting of age and date of diagnosis improved the concordance index by 0.05, and significantly improved the overall sensitivity and specificity (NRI, P = 0.028), while adding PSA level to the same base model resulted in little improvement (concordance index increase < 0.01 and NRI P = 0.275).

Conclusion

When the shape of a man's PSA history curve changes from linear to exponential, PSAV might help in the early identification of life-threatening prostate cancer at a time when PSA values are still low in most men.

Introduction

PSA kinetics have been evaluated to improve the specificity of PSA testing for prostate cancer [1], and to identify lethal disease before diagnosis and treatment [2,3]. While PSA kinetics (PSA doubling time) is a surrogate endpoint for prostate cancer mortality among men with recurrent disease after treatment [4], the role of pretreatment PSA velocity (PSAV) is controversial [5] Although PSAV was associated with the presence of lethal prostate cancer before treatment [2,3,6] there are conflicting data on whether or not it adds to the predictive value of PSA alone [7,8]. The disparity between studies evaluating PSAV could be explained by the manner in which a PSA history is evaluated. For example, different methods of calculation and the use of different time points in a PSA history at which the PSAV is determined could influence the findings [9–13]. Also, the choice of statistical methods for evaluating two highly correlated variables (PSA and PSAV) could influence results [14].

To clarify the role of PSAV and the interpretation of a PSA history in the early identification of aggressive prostate cancer, we analysed data from the Baltimore Longitudinal Study of Aging (BLSA).

Subjects and methods

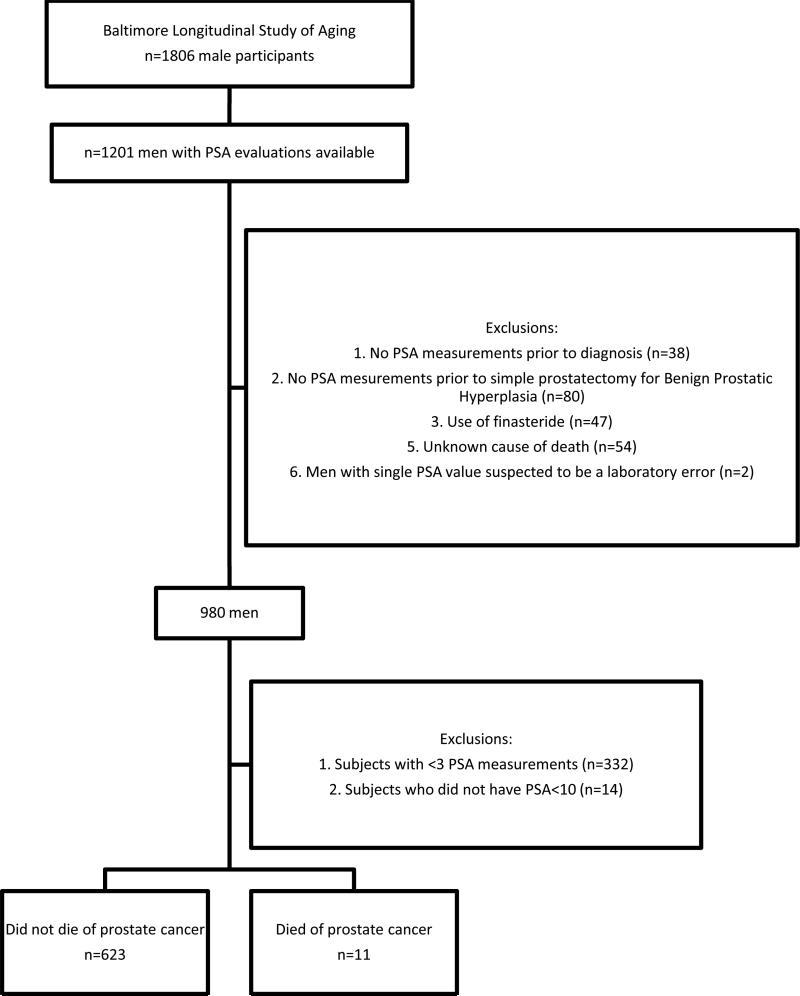
Subjects in the present study were participants in the BLSA [15], a prospective cohort study of the National Institute on Aging (Bethesda, MD), as previously described [2]. In the present study we excluded men with two or fewer PSA measurements or whose PSA levels were > 10 ng/mL (Fig. 1). After these exclusions, there were 634 men, of whom 11 died from prostate cancer. The racial distribution of these men was white (79%), African-American (17%), and other (4%). Table 1 shows the demographic characteristics of the subjects.

Fig. 1.

Selection of the study cohort from the BLSA.

Table 1.

Description of the diagnostic groups

Median (range) or mean (sd) variable	Total	Other	Dead from cancer	P for comparison, dead from cancer vs other*
No. of subjects	634	623	11
Age, 1st PSA	49.4 (20.4–92)	49.2 (20.4–92)	50.3 (38.9–70.1)
	50 (14.6)	49.8 (14.6)	52.9 (8.9)	0.496
Age, last PSA	68 (27.7–95.2)	68 (27.7–95.2)	69.5 (56.1–80)
	66.1 (14)	66 (14.1)	67.6 (7.8)	0.526
1st to last PSA, years	15.4 (1.7–38.8)	15.5 (1.7–38.8)	13.6 (5.8–23.2)
	16.2 (7.9)	16.2 (7.9)	14.8 (5.7)	0.545
Last PSA to censoring†	5.4 (0.1–33.5)	5.4 (0.1–33.5)	11.4 (3.5–20.2)
	7 (5.3)	6.9 (5.3)	10.8 (4.7)	0.014
No. of repeat PSA levels	6 (3–15)	6 (3–15)	7 (4–14)
	6.3 (2.5)	6.3 (2.5)	8 (3.4)	0.023
Years between PSA measures	2.1 (0.1–21)	2.1 (0.1–21)	1.9 (0.9–10.4)
	3.1 (2.2)	3.1 (2.2)	2.5 (1.6)	< 0.001
Time from 1st PSA to diagnosis of cancer
	21.7 (2.5–41.6)	21.7 (2.5–41.6)	18.8 (12.7–25.9)
	19.9 (8)	19.9(8.3)	19.7 (5.3)	0.913
Survival time‡	22.8 (4.5–44.3)	22.8 (4.5–44.3)	27.2 (18.1–34.7)
	23.1 (8.8)	23.1 (8.8)	25.6 (6.7)	0.347
Time from baseline to death (for dead subject)
	21.1 (4.5–41.6)	21.1 (4.5–41.6)	27.2 (18.1–34.7)
	21 (7.8)	20.7 (7.8)	25.6 (6.7)	0.046

^*Comparisons were by pooled t-tests in the case of equal variances and the Wilcoxon two-sample test in the case of unequal variances.

^†Last PSA to last visit or death for those without prostate cancer; or last visit to cancer death for those with prostate cancer.

^‡1st PSA to death for those who died or 1st PSA until last visit for those subjects who were alive.

Cause of death was determined from the BLSA death file, including cause-of-death information ascertained by intermittent telephone follow-up, correspondence from relatives, and searches of the National Death Index. For men who died, the cause of death was determined by consensus of three physicians reviewing all available information, including death certificates, letters from physicians and families, medical records, and autopsy reports.

Of 634 men, 88 (14%) were diagnosed with prostate cancer (53 alive, 35 dead). Of those who were dead, 11 died from prostate cancer and were considered events, whereas 24 with prostate cancer died from other causes. In the remaining 546 men (86%) with no diagnosis of prostate cancer, 406 were alive and 140 dead, including 20 with prostate cancer discovered at autopsy. We categorized autopsy-detected cancers as ‘non-cancers’ because autopsies were not routine in all men in the BLSA, and these men were unaware of a prostate cancer diagnosis during life. Thus, 1.8% of the cohort (11 of 634 subjects) died from prostate cancer at a median of 5.3 years after diagnosis (median age at death 79 years), similar to the ≈□1.0% probability of dying from prostate cancer by age 80 years for white men in the USA from birth [16].

The median (range) year of diagnosis was 1995 (1985–2003) for the 53 men with prostate cancer who were alive, 1990 (1979–1996) for the 24 with prostate cancer who died from another cause, and 1987 (1979–1994) for the 11 who died from prostate cancer. The median year of last PSA measurement for subjects with no diagnosis of prostate cancer was 1998 (1971–2002). Cancer stage and grade were not consistently available and thus were not included in analyses.

Statistical analyses

All PSA measurements were censored at prostate cancer diagnosis, at prostate surgery for benign disease, or at the last visit of the subject. The PSA distribution by age in the BLSA is similar to that in the National Health and Nutrition Examination Survey [17].

Five methods for estimating PSAV were investigated, including four extensively used in previous reports [1,3,7,16]. These five methods and their assumptions are described in Table 2. To identify the method for estimating PSAV that was most closely associated with death from prostate cancer, we evaluated the association between PSAV and death from prostate cancer during the 5–10 years before diagnosis/censorship. This restricted the cohort to men who had at least three PSA evaluations > 5 years before diagnosis, and at least one PSA estimate within the 5–10 years before diagnosis. The PSAV was determined using all PSA measurements before and including the one within the 5–10-year period before diagnosis, ending with the earliest measurement within the 5-year period if more than one was available. Of 405 men with a PSAV determination during the 5–10 years before diagnosis, 11 men died from prostate cancer.

Table 2.

Comparisons of different approaches to estimating PSAV at 5–10 years before diagnosis (retrospective analysis)

Methods/ref	Description	Limitations
Two-point approach [16]	Annualised change in PSA between first and last measure disregarding other PSA values	Ignores all PSA values except the first and last measures
Moving average [1]	Average rate of PSA change over three consecutive measures	PSAV determined from three PSA values ignoring other values
Linear regression (straight line fit) [3]	Slope of the regression of PSA on time using all PSA measures	Assumes PSA trajectory is linear
Velocity of logPSA [7]	Slope of regression of logPSA on time using all PSA values	Assumes that rate of change in logPSA is constant over time; result is velocity of logPSA not PSAV
Instantaneous velocity of PSA (exponential fit)*	PSA times slope of logPSA on time (derivative of linear regression of logPSA on time) using all PSA values*	Assumes exponential PSA trajectory

^*Derivation: Assuming an exponential fit of PSA trajectory, use linear regression of log(PSA) over time to fit the model log(PSA) = B ×□time + A to find the slope B. Differentiating both sides of this equation with respect to time gives 1/PSA × d(PSA)/d(time) = slope, where d(PSA)/d(time) is the derivative of PSA with respect to time, i.e. the instantaneous PSAV. Multiplying both sides by PSA yields PSAV = slope ×□PSA.

Cox proportional hazards regression was used to evaluate associations between these covariates: age at the visit 5–10 years before diagnosis, date of diagnosis, different approaches for PSAV calculation and the main outcome, death from prostate cancer. To compare hazard ratios, the PSAV values for each calculation technique were standardized by subtracting the mean and dividing the difference by the sd. The association between each PSAV calculation technique and death from cancer was compared using four criteria: (i) hazard ratio per unit increase of standardized velocity; (ii) model fit based on Akaike Information Criterion (AIC) [18]; (iii) overall improvement in sensitivity and specificity over a base model that includes age and date of diagnosis, as determined using net reclassification improvement (NRI) [19]; and (iv) the concordance index. We chose the approach to estimating PSAV that had the highest hazard ratio per unit increase of standardized velocity and the best model fit (lower AIC, higher concordance index). The NRI results shed further light on the nature of the improvements. The selected approach was then used to assess the PSA history of those subjects with a transition point. Linear regression was used to identify the point when the shape of the subject's PSA history curve transformed from linear to exponential (Appendix). For each subject's PSA history, R² was used to compare the fit of linear regression of PSA on time to the fit of linear regression of log(PSA) on time, the latter testing for exponential growth. For the regression we used only the first three PSA measurements, then repeated at consecutive PSA measurements until including all measurements. The fits were compared at each point in the PSA trajectory, starting with the third PSA measurement. If R² was greater for the regression of log(PSA) on time, the PSA history curve was considered to be exponential, otherwise it was considered to be linear. The first point at which a subject's PSA history better fitted an exponential model than a linear model was defined as the PSA transition point. An example is illustrated in the Appendix.

We evaluated both PSA and PSAV as biomarkers at the transition point for each subject to assess whether PSAV improves the prediction of death from prostate cancer. Note that PSA values after the transition point were not included in calculating PSAV at the transition point, as future PSA values are not available in clinical situations. The Wilcoxon two-sample test was used to compare PSA and PSAV separately between subjects with and without lethal prostate cancer at the transition point. The concordance index was evaluated as one of measures of model performance. Typically, the additional information in a useful new biomarker only generates a small increase in the concordance index.

Because it is well known that large changes in specificity and sensitivity of a biomarker can be masked by small changes in the area under the receiver operating characteristic curve, NRI [19] was used to compare improvements in sensitivity and specificity for death from, prostate cancer by adding PSA and PSAV separately at the transition point to the same base model containing age and date of diagnosis. The analysis was based on comparisons between Cox proportional hazards models examining risk for each man. The few events in this study preclude recommending a specific PSAV threshold. The probabilistic approach using NRI provides an overall measure of sensitivity and specificity improvements over the base model even with few events. To apply NRI, the two models to be compared must be nested. Because PSA and PSAV are highly correlated, nested models would have to account for their interactions. Therefore, a separate comparison for PSA and PSAV provided a more logical approach for this analysis [14].

Results

The follow-up from the last PSA test to censoring was longer for men who died from prostate cancer than those who did not, whereas the follow-up from first to last PSA measurement did not differ between groups (Table 1). Men who died from prostate cancer had more PSA evaluations before censoring and a shorter interval between measures than those who did not die from prostate cancer. The time from first PSA evaluation to death was longer for men who died from prostate cancer than for those who died from other causes.

Among the five methods tested, instantaneous PSAV (Table 2), which assumes an exponentially increasing PSA level, had the highest hazard ratio of prostate cancer death per standardized unit increase of velocity for the 5–10 years before diagnosis, adjusting for age and date of diagnosis (1.484, 95% CI 1.180–1.867, P < 0.001; Table 3). The model containing instantaneous PSAV also had the best model fit (AIC 97.1, Table 3). All PSAV methods yielded large improvements (P NRI < 0.015 for all models) in sensitivity compared to the base model. However, instantaneous PSAV improved the specificity by more than twice as much as all other methods examined. Also, instantaneous PSAV had the highest concordance index among all of the methods tested. Thus, instantaneous PSAV was used in subsequent analyses for predicting death from prostate cancer.

Table 3.

Comparisons of different approaches to estimating PSAV over 5-10 years before diagnosis (retrospective analysis)

Approach to estimating PSAV*	Hazard ratio (95% CI)†	P	AIC‡	Overall improvement, %§		Concordance index
				sensitivity	specificity
Moving average	1.399 (1.094–1.789)	0.008	100	82	9	0.7623
Instantaneous PSAV	1.484( 1.180–1.867)	0.001	97.1	82	21	0.7976
Two-point velocity	1.338 (1.071–1.671)	0.01	100.5	82	9	0.7677
Velocity of logPSA	1.243 (0.984–1.570)	0.068	102.3	64	10	0.7423
Linear regression	1.332 (1.068–1.663)	0.011	100.5	81	8	0.7668

^*Each approach for PSAV estimation was part of a separate multivariate Cox model adjusted for age and date of diagnosis. See Appendix for description of approaches.

^†For death from prostate cancer in multivariate Cox model adjusted for age and date of diagnosis. The assumptions of proportionality were satisfied. In this analysis, time 0 was the visit 5–10 years before diagnosis at which PSAV was determined. All variables were considered to be continuous. The P value corresponds to the PSAV in each of the Cox models.

^‡Lower value associated with best model fit.

^§Results from the NRI analysis based on comparison between Cox proportional hazards models involving examination of total risk for each individual. PSA and PSAV were added separately to a base model that included age and date of diagnosis.

Of 634 men, 522 (82%) had a transition point (change from linear to exponential trajectory) in their PSA history, including 82 (16%) who were diagnosed with prostate cancer, of whom 11 had lethal cancers. The mean (sd) number of repeat PSA measurements and follow-up (years) for the 522 men was 6.5 (2.5) and 16.8 (7.8), respectively. In comparison, of 112 men who did not have a transition point in their PSA history, six (5%) were diagnosed with prostate cancer and none were lethal. In this group, the mean (sd) number of repeat PSA measurements and follow-up (years) was 5.4 (2.4) and 13.5 (7.7), respectively.

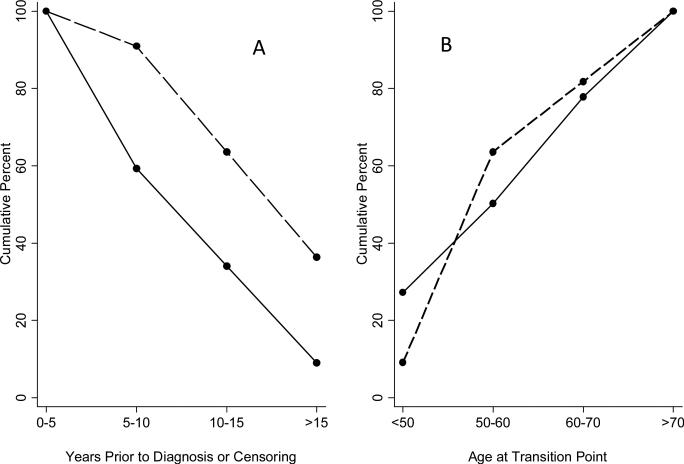
All men who died from prostate cancer had a transition point, with seven of the 11 having their transition point > 15 years before diagnosis (Fig. 2A). By contrast, a transition point occurred < 10 years from diagnosis or censoring in 60% of men who did not die from prostate cancer. The transition point was reached by age 60 years in the seven of 11 men who died from prostate cancer but in only 50% of men who did not (Fig. 2B).

Fig. 2.

Cumulative percentage of men with a PSA transition point: (a) by time before diagnosis; and (b) by age at the transition point. The solid line depicts men who did not and the dotted line depicts those who did die from prostate cancer.

The transition point identified by comparison of linear regression fits was extremely robust, based on the rarity of reversals. None of the men who died from prostate cancer had a change back to a linear shape (R² higher for linear fit than for exponential fit) after the transition point, and only one of 71 other men diagnosed with prostate cancer at any time during the study had such a reversal. Among 1544 PSA evaluations after the transition point in the entire dataset, including PSA values of men not diagnosed with cancer, 78 PSA evaluations resulted in a higher R² for a linear fit than exponential fit. These same men had 240 PSA evaluations at any time, including before transition point, which resulted in higher R² for linear fit than exponential fit. If the difference in R² between linear and exponential fits were randomly distributed among all visits, the probability is very small (Prob (number of reversals < 78) < 0.001) for having < 78 of the 1544 PSA evaluations after the transition point result in an R² higher for linear fit than for exponential fit.

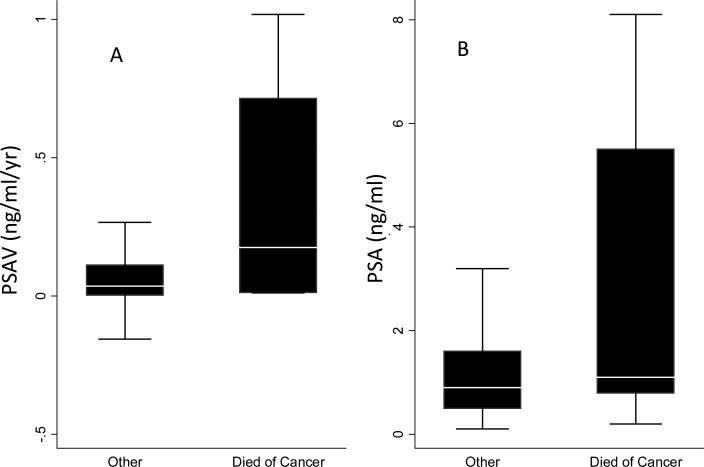
The distributions of PSA and PSAV at the transition point are shown in Fig. 3. Instantaneous PSAV was calculated using only the PSA history up to and including the measurements at the transition point. and did not include measurements after the transition point. The correlation of PSA and PSAV at the transition point was 0.76. The median (interquartile range, IQR) PSA (ng/mL) and PSAV (ng/mL/year) at the transition point for those who died from prostate cancer was 1.1 (0.8–5.5) and 0.17 (0.01–0.71), and for those who did not was 0.9 (0.5–1.6) and 0.03 (0.002–0.11), respectively. At the transition point, PSAV was significantly higher among men who died from prostate cancer than among men who did not (P = 0.021; Wilcoxon two-sample test) while the groups had similar PSA levels (P = 0.112).

Fig. 3.

Distributions of PSAV levels and PSA at the transition point for men who did and did not die from prostate cancer. (A) Distribution of PSAV; (B) Distribution of PSA levels. Boxes represent the 25th to 75th percentiles (IQR); horizontal lines within boxes are the median values; vertical lines are 1.5 times the IQR (outliers of > 1.5 times the IQR were removed from illustration).

Concordance indices are given in Table 4 comparing the addition of PSA to the base model and the addition of PSAV to the same base model. The concordance index was 6% higher for the model containing PSAV than for the model containing PSA. Further, the model containing PSA showed little improvement in concordance index over the base model alone, probably due to the transition point occurring at such low PSA values in most men (PSA of 1.6 ng/mL at the 75th percentile and 3.1 at the 90th percentile among all men whose PSA history contained a transition point). Due to the small values of PSA at the transition point in most men, the model containing PSAV at the transition point implicitly contains a narrow range of PSA level, analogous to having PSA as a latent variable in the model.

Table 4.

Comparison of predictive abilities of the models using PSA and PSAV at the transition point (prospective analysis)

	Cox model
Variable	Base + PSA	Base + PSAV
Overall improvement, %, in
sensitivity*	9	45
specificity*	9	13
P*	0.275	0.028
Concordance index†	0.8363	0.8872
Change in concordance index from base model†	0.0025	0.0534

^*Results from the NRI analysis based on comparison between Cox proportional hazards models involving examination of total risk of prostate cancer death for each individual. PSA and PSAV were added separately to a base model that included age and date of diagnosis. All models were examined at the transition point. We did not attempt to establish a threshold for PSA or PSAV to correctly classify subjects as there were too few events.

^†The concordance index measuring the capability of each model's predictions of death from prostate cancer.

PSA level at the transition point was a significant predictor of death from prostate cancer in the Cox proportional hazards model adjusted for age and date of diagnosis (P = 0.03). However, based on NRI analysis, adding PSA level at the transition point to the base model did not significantly improve the overall sensitivity and specificity (P NRI, = 0.275; Table 4). By contrast, adding PSAV at the transition point to the base model significantly improved overall sensitivity and specificity (P NRI, = 0.028).

Discussion

We found that most men (82%) in an unselected population had a transition point from linear to exponential in their PSA history when evaluated over one or two decades. The transition point in the PSA history of men with lethal cancer was found to occur early, > 15 years before diagnosis in more than half of those cases, while PSA values were still small, < 1.6 ng/mL in 75% of all men who had a transition point. At this transition point, PSAV, but not PSA, differed significantly between those who did and did not die from prostate cancer, and the concordance index showed a notable improvement for PSAV but barely detectable improvement for PSA. Furthermore, reclassification analysis indicated that PSAV (but not PSA) significantly improved the overall sensitivity and specificity for predicting prostate cancer.

Some investigators have suggested that PSAV adds no prognostic information beyond PSA, and that a PSA history that spans years can be disregarded in risk assessment [7,8]. The inability to show an independent association between PSAV and disease outcome might be due to numerous issues, including the PSAV calculation method, the time in a PSA history when that calculation is made, and the statistical methods used to compare closely related variables (PSA and PSAV). The results of our study suggest that PSAV might provide useful additional information especially at the time when PSA is still low.

Several studies have evaluated different methods for calculating PSAV [9–13]; no one method has been accepted as standard. We found that a method which assumes an exponential increase in PSA (the derivative of the linear regression of logPSA on time) applied at the point of PSA transition from linear to exponential, was associated with the highest hazard ratio per unit increase of velocity (and the best model fit), in predicting death from prostate cancer. Previous reports hypothesized that a transition point might be associated with the onset of malignancy [21]. If it is an indicator of biological activity, that might explain the robustness of our method for identifying the transition point. To our knowledge, this approach has not previously been used to study the relationship between PSAV and prostate cancer. By applying the instantaneous PSAV method at the point when a PSA history becomes exponential, we avoided applying an exponential-based method to the approximately linear portion of data. Previous studies using one PSAV technique to evaluate both linear and exponential changes in PSA might have had limited predictive ability.

Distinguishing between the independent predictive information from PSA and PSAV in the same model is complicated [14] by their co-linearity [2]. Instead, we assessed the separate improvements of PSA and PSAV over a common base model using the approach of Pencina et al. [19]. However, we also note that the preponderance of small PSA values at the time of the transition point is somewhat analogous to implicitly including PSA in the model which contains PSAV.

Our finding that at the transition point, PSAV, but not PSA, significantly improved sensitivity and specificity (Table 4), coupled with the difference in distributions of PSA and PSAV between men who died and did not die from prostate cancer (Fig. 3), strongly suggests that PSAV adds important clinical information beyond PSA alone during the early exponential phase of a man's PSA history.

Biomarker histories for other cancers might also have exponential shapes over time for an individual. It is possible that identifying a critical transition point in the shape of those biomarker histories might provide useful information for the early detection of cancer or of potentially lethal forms of cancer.

Our study has several limitations. First, given the few events, this is a proof-of-principle assessment and cannot establish thresholds for the use of PSA or PSAV. Second, the interval between PSA measurements in the BLSA is 2–3 years, and evaluation of more frequent PSA measurements could result in different findings. Third, the same assay was used for all PSA measures, which might not always occur in clinical practice. Fourth, we could not consistently assess cancer stage and grade in our cohort, and the type of treatment received was not known in all cases. Finally, our cohort was primarily white and our findings might not be applicable to other racial/ethnic groups.

In summary, at a time when PSA levels begin changing in an exponential fashion, PSAV could provide useful information about the presence of life-threatening cancer. If larger studies confirm these findings, the use of PSAV as a trigger for prostate biopsy at a time when a PSA history becomes exponential could reduce the detection of indolent disease and thus reduce prostate cancer over-diagnosis and over-treatment.

Abbreviations

BLSA

Baltimore Longitudinal Study of Aging

PSAV

PSA velocity

AIC

Akaike Information Criterion

NRI

net reclassification improvement

Appendix

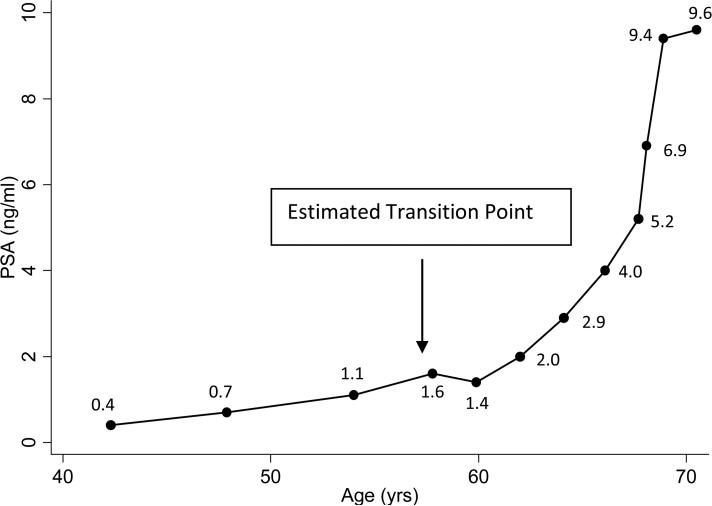
An example of estimating the transition point: For the subject with the PSA history depicted in Fig. 4, the R² statistic was compared for the linear regression of PSA and logPSA on time using the first three measures, and separately at each measure beyond the third PSA measure (using all previous data). The R² statistic for the linear regression of PSA on time and the linear regression of logPSA on time using the first 3 measures was 0.73 and 0.72, respectively, indicating that at the third PSA measure the best fit for the PSA history was linear (i.e. R² from the model of linear regression of PSA on time was ≥□R² from linear regression of logPSA on time). The R² statistic for the linear regression of PSA on time vs logPSA on time using the first four PSA measures was 0.79 and 0.81, respectively, indicating that at the fourth PSA measure the best model fit was exponential (i.e. R² from the model of linear regression of PSA on time was ≤□R² from linear regression of logPSA on time). Thus, the transition point was estimated to occur at the time of the fourth PSA measure.

Fig. 4.

An example of the estimated transition point.

Editorial comment

Ketterman et al. start their report by arguing that ‘there are conflicting data on whether or not [PSAV] adds to the predictive value of PSA alone’. In support of this statement they cite the systematic review [1] and a paper analysing data from the control arm of the Swedish randomized trial of radical prostatectomy [2]. The former study concluded ‘there is little evidence that calculation of PSA velocity ... provides predictive information beyond that provided by absolute PSA level alone’; the latter report states that ‘the rate of PSA change [is a] poor predictor of lethal prostate cancer’. It is hard to see these as conflicting data. Several more recent publications come to similar conclusions about the lack of benefit with PSAV: it failed to increase the accuracy of prediction models for either recurrence [3] or mortality [4] after radical prostatectomy; has little clinical role for predicting the outcome of biopsy [5–6]; does not aid the long-term prediction of cancer in unscreened men [7]; and is of no value for men on active surveillance [8].

Given this unequivocally negative picture, this report by Ketterman et al. constitutes the most sophisticated attempt yet to find a role for PSAV in men before treatment for prostate cancer. Certainly the idea of a transition point is an interesting one, although it is surely a concern that most men have one, even if they do not go on to develop cancer. What is the biological transition ‘to’ and ‘from’ in a man who remains cancer-free?

As the authors acknowledge, the study has an obvious problem; it is based on only 11 events. It is not hard to believe that the investigators are able to find an algorithm that will provide a good prediction for 11 men, especially as they tested five different definitions of PSAV and chose the best one. Critically, the few events entails that the investigators are unable to address the fundamental question of whether PSAV adds to the predictive power of PSA alone. Statisticians normally follow a guideline of ‘10 events per variable’, meaning that a suitable study would require a minimum of 20 deaths from prostate cancer.

A second problem concerns practical implementation. The suggestion appears to be that each time a PSA level is obtained, the physician would conduct a ‘linear regression of PSA and logPSA on time using the first three measures, and separately at each measure beyond the third PSA measure (using all previous data)’. Following this, the physician would compare R² statistics to determine if the patient has reached a transition point. If so, the physician would calculate the ‘derivative of the linear regression of logPSA on time to obtain the PSAV’. Then, and only then, could a decision be made about biopsy. It seems implausible that such an algorithm could ever be incorporated into clinical practice. In theory, these calculations could be automated, but implementing a suitable system seamlessly into the clinic is considerably more complex than it might appear, and would need to be well motivated.

The authors state that theirs is a ‘proof of principle’ study that requires confirmation. I agree that PSAV is of unproven value and, as such, it should not currently be used to assess risk.

Andrew Vickers, Memorial Sloan-Kettering Cancer Center, New York, NY, USA