A Comparison of Methods to Detect and Quantify the Markers of Antimalarial Drug Resistance

Abstract

We compare, contrast, and evaluate methods to quantify genetic markers of antimalarial drug resistance. Frequency estimates should be reported along with crude prevalence. There are four main potential methods to estimate frequencies in blood samples: simple counting of single nucleotide polymorphisms (SNPs) and haplotypes in samples with multiplicity of infection (MOI) = 1; SNP counting in samples with MOI ≤ 2; SNP and haplotypes counting in samples with unambiguous genotypes; statistical inference using SNP and MOI data from all samples. Large differences between the methods became apparent when analyzing field data with high MOI. Simple counting dramatically reduced sample size and estimate precision, and we show that analysis of unambiguous samples is biased, leaving maximum likelihood or similar statistical inference as the only practical option. It is essential to account for genotyping missing minor clones; ignoring this phenomenon resulted in a 2-fold underestimation of SNPs and haplotypes present at low frequencies.

Introduction

Malaria continues to kill and debilitate millions of people, despite the availability of effective drugs. Delayed treatment caused by its rather non-specific symptoms and rapid onset of severe disease is the main reason for this mortality, but there is increasing realization that drug resistance may play a major role. The gold-standard surveillance technique for detecting drug resistance is direct observation in vivo; patients are treated, and success or failure is observed. This approach is logistically difficult, because it requires extended follow-up periods that are difficult to achieve and consequently, sample sizes are small. An alternative approach is to monitor mutations associated with drug resistance.¹ These can be readily detected in the parasites contained in infected human blood samples, which are relatively easy and economical to collect and can be rapidly screened. These single nucleotide polymorphisms (SNPs) or molecular markers of drug resistance, therefore, have the potential to guide public-health policy in a timely manner.^2,3 Importantly, the optimal way of analyzing these data has never been fully explored, and therefore, it remains a subject of intense debate, particularly for samples originating from the areas of intense malaria transmission that characterize much of sub-Saharan Africa; these areas are where most malaria mortality occurs and where the need for informed drug policy choice is greatest. This manuscript considers the appropriate methods of analyzing and presenting molecular marker data from such areas by evaluating alternative methods of analysis.

A major problem in analyzing human blood samples is that humans in areas of moderate to high malaria transmission are often infected by several genetically distinct malaria clones; the number of clones is known as their multiplicity of infection (MOI). Consequently, many blood samples will have MOI > 1 and be genetically ambiguous; for example, if a sample has a MOI of 4 and is known to contain both wild-type and mutant SNPs, it is impossible to discern whether the ratio of wild-type to mutant clones in the sample is 3:1, 2:2, or 1:3. A second problem is that relatively low assay sensitivity seems to be an inherent property of polymerase chain reaction (PCR)-based genotyping methodology. Liu and others⁴ found it difficult to detect minor SNPs if they were present in less than around 10% of the parasites in the sample, even under idealized laboratory conditions, whereas Juliano and others⁵ assert, more realistically in our view, that the detection limit in most protocols is closer to 20%; there is also likely to be substantial variation in assay sensitivity between different laboratories.⁶ These inherent methodological limits are often augmented by assay protocol steps designed to eliminate false-positive SNP signals; in the genotyping results that we analyze herein, this was implemented as an instruction to ignore any signal that was less than 30% of the larger signal. This inability to detect minor SNPs leads to misclassification. For example, if MOI = 5 and contains one mutant clone and four wild types, then the marker will, on average (see Discussion), constitute around 1/5 (20%) of the total DNA and may be missed; this leads to the sample being incorrectly classified as containing only wild-type markers. The appropriate genotyping sensitivity limit (GSL) needs to be incorporated into analyses of human blood data in areas of high MOI.

Despite the interest in using molecular markers to guide policy,^1–3 there has been relatively little discussion about the most appropriate way to analyze human blood samples in the context of genetic ambiguity caused by high MOI and misclassification caused by low assay sensitivity. This manuscript addresses these issues. We first consider the implications of summarizing data by prevalence rather than frequency. Second, we critically evaluate four potential methods of estimating frequency. Third, we show the importance of allowing for assay sensitivity, quantified at its GSL, in analyses.

Materials and methods

Prevalence is defined as the proportion of human blood samples where the marker is present, implying that one or more clones in the sample carry the marker. Frequency is defined as the proportion of individual malaria clones that carries the marker. The theoretical relationship between the prevalence of markers and underlying mutation frequency depends on the distribution of MOI as follows:

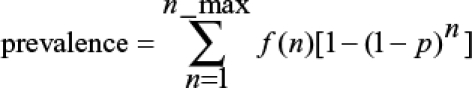where n is MOI, n_max is maximum observed MOI, f(n) is the frequency of samples with MOI = n, and p is the frequency of the mutation. This assumes perfect detection of mutations. If minor clones are missed (i.e., a GSL occurred), it is necessary to consider each SNP combination within each MOI class to test whether its presence would be detected. This is done using the binomial distribution as follows:

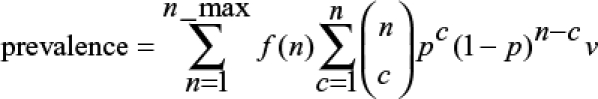where c is the number of mutant clones within the n clones of the sample and v is an indicator variable that takes a value of zero if c/n is less than the GSL and unity if c/n is equal or greater than the GSL.

We analyzed two real field datasets, one from a relatively low-transmission area of Papua New Guinea (PNG) and one from a high-transmission area of Tanzania; both were genotyped by the same person using the same protocol in the same laboratory. The PNG samples⁷ were obtained from patients (of all ages) attending the health center in the Wosera area during 2000 and 2001 with presumptive symptoms of malaria. Blood was collected by venipuncture or fingerprick into ethylenediaminetetraacetic acid (EDTA) microtainers and glass capillaries, respectively, and stored at −70°C. This dataset consisted of 100 malaria-infected blood samples containing a total of 173 clones. The Tanzanian samples were collected from the placebo group (ages 1–5 years) of the Spf66 vaccine trial⁸ in the Morogoro region of Tanzania during 1993 and 1994.⁷ Blood samples were collected by fingerprick into heparinized microtainers and stored at −70°C. This dataset consisted of 82 malaria-infected blood samples containing a total of 298 clones. DNA was extracted, and the parasites were genotyped at merozoites surface protein 2 (MSP2) to establish the MOI and at several loci implicated in drug resistance as described previously,^7,9 although only two resistance loci were analyzed here (i.e., dhfr in the PNG datasets and both dhfr and dhps in the more interesting Tanzanian dataset). Genotypic failures (entered as missing data in the analyses) were around 3% per SNP. Critically, the protocol explicitly stated that any SNP signals less than 30% of the major SNP genotype were ignored; hence, the GSL is 0.3. We chose these datasets, because both were genotyped in the same laboratory by the same person (Nsanzabana), maximizing their comparability, and they had a clearly stated assay GSL. We note that our Tanzanian datasets had relatively high MOI, and recent malaria-control efforts have tended to reduce the intensity of transmission (and hence, MOI) in many African settings. We similarly note that the GSL of 30% was relatively high. The biases and errors noted in the main text become accentuated at high MOI and low assay sensitivity, and therefore, it is likely that our analysis represents a near worst-case scenario, although this does have the advantage of clearly showing the dangers and biases that may be encountered in these types of molecular analysis.

We obtained SNP and haplotype frequencies in our field datasets using four methods of estimation, two of which can also allow for a missing minor clone, giving a total of six methods.

• (1)Direct counting of SNPs and haplotypes in samples with MOI = 1.
• (2)Direct counting of SNPs in samples with MOI ≤ 2. Haplotypes cannot be counted in such samples, because they may be ambiguous. For example, if MOI = 2, the haplotype is defined at two codons (e.g., 108 and 59 in pfdhfr) and the sample is mixed wild type/mutant at both codons: it is impossible to discern the linkage phase¹⁰ (i.e., whether the two constituent haplotypes are ++ with −− or +− with −+ (where + represents the mutation and – represents the wild type).
• (3)Direct counting of SNPs and haplotypes in unambiguous samples. Obviously, not all blood samples are ambiguous. For example, if MOI is 4 and contains only wild-type markers, then we can directly count four wild-type clones; similarly, if MOI is 2 and contains only mutants at two SNPs, then we can directly count two ++ haplotypes. These unambiguous samples allow simple counting, even when MOI > 2.
• (4)Direct counting of SNPs and haplotypes in unambiguous samples allowing for GSL. Samples where, in principle, one SNP may be present but not detected are classed as ambiguous and ignored. For example, if MOI is 4 and the GSL is 30%, then any samples with MOI ≥ 4 should be ignored, because if the SNP was present in only a single clone, its contribution would be on average 1/4 (25%; see Discussion), which is less than 30% and may not be detected.
• (5)Maximum likelihood (ML) estimation of SNPs and haplotypes frequencies, assuming that all clones are detected.
• (6)ML estimation of SNPs and haplotypes frequencies allowing for GSL.

An revised version of MalHaploFreq¹¹ was written to incorporate all methods of analysis (i.e., MOI = 1, MOI = 2, unambiguous samples, and ML). This version (v2.1) is freely available for download at http://pcwww.liv.ac.uk/hastings/MalHaploFreq; 95% confidence intervals (CI) around the frequency estimates obtained by all methods, including counting, were obtained by maximum likelihood, where the CI limits are defined as 2 log units less than the maximum log likelihood. This may lead to underestimates of the width of CI when frequencies are close to 0% or 100%¹² but allows for direct comparison across analyses using different methods and different frequency estimates. MalHaploFreq outputs the SNP and haplotype counts (and their denominators) so that users can, if they wish, generate their own CI around count data, using methods described elsewhere.¹²

MalHaploFreq was run with level of precision set to 8 for frequency estimation and 3 for generation of CIs. The GSL, where invoked, was set at 30%. Haplotype frequencies for pfdhfr were estimated using MalHaploFreq option 4, which assumes that the following three haplotypes do not exist: pfdhfr 51 mutant alone, pfdhfr 59 mutant alone, and the double mutant haplotype pfdhfr 51 mutant + pfdhfr 59 mutant.

The internal simulation facility in MalHaploFreq was invoked to investigate how GSL affects the width of the CIs around frequency estimates. Artificial datasets, each of 100 individuals with MOI frequencies observed in Tanzania, were generated, assuming GSL of 0.0, 0.1. 0.2, 0.3, and 0.4. Five artificial datasets were analyzed, and the mean width of the CI was recorded.

The assumptions inherent in this and similar ML analyses have been described elsewhere,^11,13,14 but we include them in Appendix S1 in the interest of transparency. It has also become clear that this ML technique is unfamiliar to a substantial proportion of readers, and therefore we add points of clarification in Appendix S1.

Prevalences of SNPs and multilocus genotypes in the PNG and Tanzanian datasets were obtained by direct counting and 95% CIs around these proportions obtained using the Wald method from the GraphPad website (http://www.graphpad.com/quickcalcs/ConfInterval1.cfm). Note that prevalences do not sum to 100%, because many samples are ambiguous (e.g., a sample containing both wild-type and mutant SNPs will be counted two times, one time in counting the prevalence of the wild type and one time in counting the prevalence of the mutation). Similarly, if a sample is mixed at two loci, it will be included in four multilocus counts: −−, −+, +−, and ++ where − represents wild type and + represents the mutation; note that the linkage phase is not considered in this counting, and therefore, the estimates of multilocus genotype prevalence should not be confused with prevalence of haplotypes.

Results

The two study sites showed very different distributions of MOI (Figure 1), with the Tanzania dataset having much higher MOI. These observed MOI distributions were used to investigate the theoretical relationship between prevalence and mutation frequency in the two sites. As expected, predicted prevalence differed substantially between the two sites, even when resistance was present at the same frequency (Figure 1C) because of their differing MOIs (Equations 1 and 2). Importantly, the presence of a GSL meant that observed prevalence should theoretically be substantially lower than true prevalence (Figure 1C) in the Tanzanian dataset.

Figure 1.

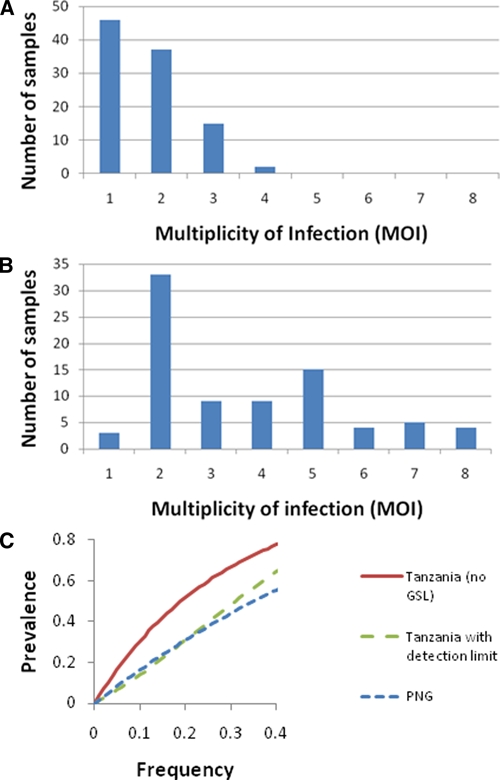
(A and B) Observed distribution of MOI from Papua New Guinea (PNG) and Tanzanian datasets. (C) The theoretical relationship between prevalence and mutation frequency given the observed MOI; prevalence in the Tanzanian data is shown assuming no genotyping sensitivity limit (GSL) or assuming a GSL of 0.3. This figure appears in color at www.ajtmh.org.

The results of SNP and haplotype frequency estimates from field data from PNG were fairly consistent between the different analyses (Table 1). For SNP frequency estimation, there were 45 clones among the samples with MOI = 1, and 117 clones in the samples with MOI ≤ 2, whereas ML analysis included ~170 clones in the analyses and the width of the CIs fell as more clones entered the analysis. It is not possible to use the MOI ≤ 2 approach in haplotype analysis (see Materials and Methods), and therefore, the choice was between MOI = 1 (45 clones) and ML analysis (167 clones), with the latter giving smaller CIs. Interestingly, there was a discrepancy in the dhfr −+ frequency estimates: it was 0.022 by direct counting in MOI = 1 class and around 0.1 in other methods; we are unable to explain this other than purely because of chance. Incorporating the GSL gave a significantly better fit to the data in both SNP and haplotype analyses (Table 1) (a 2-unit change in log likelihood (LL) is conventionally regarded as statistically significant), although it made no appreciable difference to the frequency estimates or their associated CIs.

Table 1.

SNP and haplotype estimates from Papua New Guinea (PNG) and Tanzanian (TNZ) datasets

SNP/haplotype	Data	Prevalence	MOI = 1	MOI ≤ 2	Unambiguous (no GSL)	Unambiguous (no GSL)	ML (no GSL)	ML (with GSL)
dhfr SNP C59R	PNG	0.58 (0.48–0.67)	0.53 (0.39–0.68)N = 45	0.56 (0.46–0.65) N = 117	0.56 (0.48–0.64) N = 167	0.54 (0.46–0.62) N = 159	0.56 (0.48–0.63) N = 170; LL = −39.5	0.55 (0.47–0.6) N = 170; LL = −36.6
dhfr SNP S108N	PNG	0.64 (0.54–0.73)	0.56 (0.41–0.70)N = 45	0.64 (0.55–0.73) N = 117	0.66 (0.58–0.73) N = 167	0.64 (0.56–0.72) N = 159	0.66 (0.58–0.73) N = 167; LL = −44.3	0.65 (0.57–0.72) N = 167; LL = −42.0
dhfr 2C hap (– –)	PNG	0.38 (0.29–0.48)	0.44 (0.30–0.59)N = 45	na	0.35 (0.27–0.42) N = 162	0.36 (0.28–0.44) N = 154	0.34 (0.27–0.42) N = 167; LL = −63.6	0.35 (0.27–0.42) N = 167; LL = −60.7
dhfr 2C hap (−+)	PNG	0.12 (0.07–0.21)	0.022 (0.0002–0.097)	na	0.10 (0.06–0.15)	0.10 (0.06–0.16)	0.10 (0.06–0.16)	0.10 (0.06–0.16)
dhfr 2C hap (++)	PNG	0.58 (0.48–0.67)	0.53 (0.38–0.68)	na	0.56 (0.48–0.63)	0.53 (0.45–0.61)	0.56 (0.48–0.63)	0.55 (0.47–0.622)
dhfr SNP N51L	TNZ	0.16 (0.10–0.26)	0.00 (0.00–0.49)N = 3	0.075 (0.027–0.15) N = 67	0.062 (0.036–0.097) N = 257	0.12 (0.066–0.21) N = 88	0.083 (0.053–0.12) N = 289; LL = −41	0.16 (0.11–0.22) N = 289; LL = −26.5
dhfr SNP C59R	TNZ	0.32 (0.23–0.43)	0.33 (0.020–0.85)N = 3	0.22 (0.13–0.34) N = 67	0.11 (0.076–0.16) N = 228	0.25 (0.16–0.35) N = 85	0.15 (0.11–0.20) N = 296; LL = −45	0.26 (0.20–0.31) N = 296; LL = −30
dhfr SNP S108N	TNZ	0.47 (0.36–0.59)	0.33 (0.020–0.85)N = 3	0.36 (0.24–0.49) N = 61	0.43 (0.36–0.49) N = 229	0.47 (0.36–0.58) N = 79	0.43 (0.37–0.50) N = 260; LL = −115	0.45 (0.39–0.52) N = 260; LL = −60
dhps SNP A437G	TNZ	0.10 (0.05–0.19)	0.00 (0.00–0.49)N = 3	0.10 (0.044–0.19) N = 67	0.054 (0.031–0.086) N = 278	0.11 (0.053–0.18) N = 94	0.060 (0.036–0.093) N = 289; LL = −39	0.12 (0.076–0.17) N = 289; LL = −25
dhps SNP K540E	TNZ	0.14 (0.08–0.23)	0.00 (0.00–0.49) N = 3	0.095 (0.03–0.19) N = 63	0.080 (0.050–0.12) N = 263	0.10 (0.048–0.18) N = 90	0.093 (0.062–0.13) N = 292; LL = −55	0.17 (0.12–0.22) N = 292; LL = −36
dhfr 3C hap (– – –)	TNZ	0.62 (0.51–0.73)	0.67 (0.15–0.98) N = 3	na	0.74 (0.67–0.80) N = 130	0.58 (0.46–0.69) N = 79	0.58 (0.5–0.64) N = 260; LL = −164	0.55 (0.48–0.61) N = 260; LL = −99
dhfr 3C hap (– – +)	TNZ	0.32 (0.22–0.43)	0.00 (0.00–0.63)	na	0.11 (0.067–0.16)	0.11 (0.052–0.20)	0.20 (0.14–0.26)	0.15 (0.097–0.21)
dhfr 3C hap (+−+)	TNZ	0.11 (0.05–0.21)	0.00 (0.00–0.63)	na	0.011 (0.001–0.035)	0.028 (0.004–0.086)	0.014 (0.002–0.041)	0.028 (0.004–0.072)
dhfr 3C hap (−++)	TNZ	0.31 (0.21–0.42)	0.33 (0.020–0.85)	na	0.09 (0.053–0.14	0.15 (0.082–0.25)	0.15 (0.097–0.21)	0.15 (0.10–0.22)
dhfr 3C hap (+++)	TNZ	0.15 (0.09–0.26)	0.00 (0.00–0.63)	na	0.05 (0.02–0.09)	0.13 (0.06–0.22)	0.065 (0.035–0.10)	0.12 (0.072–0.177)
dhps 2C hap (– –)	TNZ	0.94 (0.86–0.98)	1.00 (0.51–1.00) N = 3	na	0.94 (0.91–0.97) N = 256	0.89 (0.81–0.94) N = 90	0.93 (0.89–0.96) N = 285; LL = −50	0.85 (0.79–0.89) N = 285; LL = −39
dhps 2C hap (+−)	TNZ	0.04 (0.01–0.11)	0.00 (0.00–0.49)		0.0039 (0.000–0.018)	0.011 (0.000–0.049)	0.0036 (0.000–0.017)	0.0065 (0.000–0.029)
dhps 2C hap (−+)	TNZ	0.06 (0.02–0.14)	0.000 (0.000–0.49)	na	0.000 (0.000–0.0080)	0.000 (0.000–0.022)	0.011 (0.0021–0.030)	0.021 (0.0047–0.055)
dhps 2C hap (++)	TNZ	0.09 (0.04–0.18)	0.000 (0.000–0.49)	na	0.055 (0.031–0.089)	0.10 (0.048–0.18)	0.057 (0.033–0.089)	0.12 (0.081–0.18)

There are six methods of estimating frequency (see Text), noting that the MOI ≤ 2 approach cannot be used for haplotypes frequency estimate. Numbers in parentheses are the 95% CIs. SNP nomenclature is self-explanatory. The dhfr two-codon haplotypes (dhfr 2C hap) are defined at positions 59 and 108 with − indicating wild-type SNP and + indicating mutant, so that, for example, – – is wild type at both positions and −+ is wild type at 59 but mutant at 108. The three-codon dhfr haplotypes (dhfr 3C hap) are defined at positions 51, 59, and 108, and the two-codon dhps haplotypes (dhps 2C hap) are defined at positions 437 and 540, with − and + again indicating wild type and mutant at these codons. Mutations at dhfr codons 51 and 59 very rarely occur without the presence of a mutation at 108, and therefore, two-codon haplotype +− and three-codon haplotypes +–, −+−, and ++− are omitted. Note that prevalence is for multilocus genotypes and not for haplotypes, because prevalence estimates cannot distinguish linkage phase within a sample (see Materials and Methods). GSL = genotyping sensitivity limit; N = number of clones entering the analyses; LL = the maximum log likelihood obtained in the ML analyses. The same data are analyzed simultaneously when estimating frequencies of haplotypes, and therefore, N and LL are the same for each haplotype and consequently, are only given for the wild type.

The results from the Tanzania field dataset differed greatly between the six methods of analysis (Table 1). Direct counting when MOI = 1 only allowed three clones to enter the analyses, was uninformative. Counting SNPs in samples where MOI ≤ 2 increased sample size from 3 to > 60 (Table 1), but the CIs were wider than subsequent analyses and this approach could not be used to count haplotypes. Unambiguous samples assuming no GSL allowed a large number of clones to enter the analysis (200 + in SNP analysis), although this number fell dramatically when a GSL was recognized because all samples with MOI ≥ 4 were then excluded (because one minor clone among four could be present at < 25%, which is below the GSL of 0.3). ML analyses allowed > 260 clones to enter the analyses; the exact number varied depending on missing data. Allowing for the GSL had a large impact when SNP frequencies were less than around 25% (i.e., all SNPs except dhfrS108N on Table 1) or when haplotype frequencies were less than about 10% (dhfr haplotypes +−+ and +++ and all dhps haplotypes except wild type on Table 1). The magnitude of the effect was large: frequency estimates for these SNPs and haplotypes were consistently around 2-fold higher in analyses allowing for GSL. The likelihoods were substantially lower for analyses that allowed a GSL, indicating that these estimates provided a far better fit to the data. This shows that not allowing for a GSL leads to a 2-fold error in estimating SNPs and haplotypes present at low frequencies.

The presence of a GSL, therefore, has a large impact on frequency and prevalence estimates. We further investigated the value of GSL in our Tanzanian datasets by systematically varying its assumed value in the ML analysis. The reasoning was that, although the nominal GSL stated in the assay protocol was 0.3, its operational value in practice may have been higher or lower than this value. This operational GSL value was obtained by varying the GSL value to find the values (its ML estimator) that maximizes the likelihood of observing the data. Illustrative results for SNPs and haplotypes are given in Figure 2. There was a limit to increasing our assumed GSL, because mixed wild-type + mutant samples are not compatible with high GSL (clarification 5 in Supplemental Appendix S1, available at www.ajtmh.org). The likelihood increases with GSL, showing a better fit to data as GSL increases (Figure 2). This implies that, at least in these surveys, the effective GSL may, in practice, be much larger than the nominal value of 0.3 stated in the protocol. However, the impact on estimated frequencies was small. The dhfr allele frequency estimates did not alter, because the GSL could not be increased beyond 0.33, which gave identical results to those obtained at 0.3. There were slight changes in estimated frequencies at dhps: dhpsA437G increased from 0.12 to 0.14 and dhpsK540E increased from 0.17 to 0.19. Among the dhps437/540 haplotypes using + to indicate mutant, the – – haplotype frequency fell from 0.85 to 0.82, the +− frequency increased from 0.007 to 0.008, the −+ frequency increased from 0.021 to 0.025, and the ++ frequency increased from 0.12 to 0.14.

Figure 2.

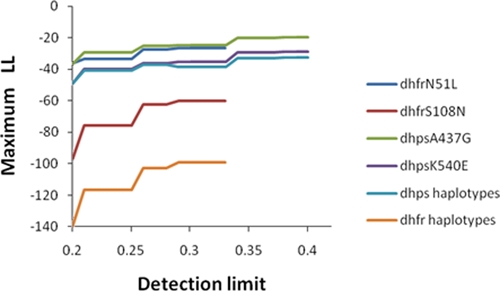
Changes in the observed maximum log likelihood with the assumed value of the detection limit (GSL) in the SNP and haplotype analyses on the Tanzania dataset. Increasing maximum LL indicates a better fit to the data. The curves have flat segments where changes in detection limit do not alter the likelihood, because the changes do not alter classification of mixed samples into all mutant or all wild type. Steps in the curves occur when the detection limit changes sufficiently to reclassify some of the mixed samples. This figure appears in color at www.ajtmh.org.

A surprising observation was that prevalences directly observed in our high MOI Tanzanian dataset were close to our best estimates of frequency (Table 1), despite the theoretical expectation that they would be much higher (Figure 1).

The size of GSL did slightly affect the precision of frequency estimates as measured by the width of CI. The effect was minimal when simulated frequencies were evenly distributed between 0% and 100% (results not shown). The effect of ambiguity introduced by increasing GSL did have an effect when frequencies were constrained to lie between 2% and 10%: the mean width of CI was 5.2% units when GSL was 0 or 0.1, rising to 5.5%, 6.7%, and 7.6% units when GSL was 0.2, 0.3, and 0.4, respectively (standard error of these widths was 0.06% units in each case).

Discussion

It was important to clearly define the difference between the prevalence and frequency of markers and haplotypes (see Results), because there is a tendency for researchers to regard them as synonymous. Equations 1 and 2 and Figure 1C clearly show the operational distinction: as transmission changes, so does MOI and consequently, so does prevalence. This occurs because each clone in the MOI has a chance of carrying the resistance marker; a useful approximation at low frequencies of the marker is that prevalence ~ frequency × MOI. This effect of MOI makes it impossible to use prevalence to compare the level of resistance at different sites or perhaps more importantly, to assess the impact of interventions on drug resistance. A relatively common conclusion from studies of malaria-control intervention (e.g., bed-net provision^15,16 or mosquito control¹⁷) is that the intervention reduces selection for resistance. The molecular components of such studies invariably base the pre- and post-intervention comparison on the prevalence of molecular markers of resistance: any effective intervention will tend to reduce MOI, and therefore, it will inevitably reduce prevalence, irrespective of its impact on frequency. The confounding factor of MOI together with other key features, such as immigration of sensitive malaria into the study sites, weaken these conclusions. Furthermore, Equation 2 and Figure 1C shows that, in areas of high transmission, the presence of a GSL may result in observed prevalence being substantially lower than true prevalence; this reduces the ability to compare results from surveys performed by different research groups whose assay sensitivities may vary. Moreover, there seems to be no obvious way to incorporate GSL into measurements of prevalence (Figure 1C). Frequency estimates, therefore, constitute a common scale, unaffected by malaria epidemiology and MOI, on which to compare levels of resistance. Despite these theoretical predictions, observed prevalences in our dataset seem relatively close to our best frequency estimates; the most likely reason is that the relatively high GSL (see Discussion) and fluctuations in clonal density (Supplemental Appendix S1) mean that only one or two numerical dominant clones are likely to enter the SNP genotyping.

Prevalence and frequency may have different clinical implications. If the intention is to clear all parasites, then the presence of even a single resistant clone may prevent this, leading to parasitological failure; this would be related to prevalence. If symptomatic disease is associated with a single pathogenic clone, then clinical failure (i.e., the inability to clear the pathogenic clone) depends on the probability that the single clone bears a resistance mutation(s) (i.e., on the frequency of the SNP or haplotype). Given the relative ease of including a marker of MOI in genetic analyses, the above arguments constitute a compelling argument that MOI be measured and frequencies calculated and reported along with any estimates of prevalence (although we do note that some inaccuracies may arise in estimating MOI; see assumption 1 in Supplemental Appendix S1).

Having established that frequency estimates of both SNPs and haplotypes are important, the obvious question is what is the best method to obtain these estimates? Unambiguous sample selection will be ignored in subsequent discussion, because it seems pointless to use a method that is demonstrably biased (see below). In our PNG dataset with low MOI, all methods gave similar frequency estimates; however, the ML methods incorporated all the data, and so, they tended to give narrow CIs and did not require data selection, reducing concerns about bias. These two factors suggest ML is superior to the other two methods, but in practice, it made little difference (Table 1). This conclusion accords with that of Anderson and others,¹⁸ who found little difference between three methods of frequency estimation (MOI = 1, ML estimation, and predominant allele counting) in relatively low-transmissions areas of southeast Asia. The situation was very different in areas of high transmission as illustrated by the results shown on Table 1 from the Tanzanian dataset: MOI = 1 analyses allowed only three clones to be counted, and MOI ≤ 2 could not be used for haplotype counting. This left ML (or similar inference techniques such as Markov Chain Monte Carlo (MCMC); Supplemental Appendix S1) as the only effective method to extract frequency estimates with reasonable CI from field samples.

The necessity of data selection in the first three methods (i.e., analyses restricted to MOI = 1, MOI ≤ 2, or unambiguous samples) immediately raises the prospect of introducing bias into the analyses. There are at least two potential sources of bias in the analyses restricted to MOI = 1 and MOI ≤ 2. First, Schoepflin and others¹⁹ noted that mutant SNP frequencies may be higher in newly acquired infections and suggested that this may be caused by putative fitness effects associated with the mutations being less deleterious when there are no competing coinfecting clones. Second, low MOI infections may reflect recent drug use; most antimalarial drugs have long half-lives, and the first clones to recolonize treated individuals tend to be those that are more resistant to the drug,^20–22 making resistance mutations likely to be overrepresented in infections with low MOI. An important bias arises in analyses counting unambiguous samples, because low-frequency SNPs and haplotypes will be systematically underrepresented. As an example, imagine a fictitious situation where all samples have an MOI = 3 and a mutant SNP is present at a frequency of 10%. Assuming independent acquisition of clones, the probability of a sample being unambiguously all mutant is 0.1³ (i.e., 1 in 1,000). Most mutant SNPs will, therefore, occur in samples that also contain wild types, and all such samples will be excluded on the basis of ambiguity. This results in underestimating the frequency of the less frequent SNP. The bias does not seem to be huge (Table 1), but it is noticeable that the unambiguous samples consistently gave lower frequency estimates (for low-frequency SNPs) and higher frequency estimates (for higher frequency SNPs and haplotypes) than their ML equivalent, providing good empirical evidence that the bias does occur in practice. Anderson and others¹⁸ suggested a method of SNP frequency estimation based on counting the dominant allele signal in a sample. This is likely to be biased for the same reason as analyses based on unambiguous samples: low-frequency SNPs are likely to be minor, non-dominant clones in high-MOI mixed infections (because other clones in the sample bearing the alternative high-frequency SNP will combine to provide the dominant SNP signal) and therefore, will not enter the analysis. This leads to systematic underestimation of low-frequency SNPs.

The results shown in Table 1 show the importance of incorporating GSL when estimating SNP and haplotype frequencies in areas with high MOIs; failure to do so may result in a 2-fold underestimate of SNPs and haplotypes present at low frequency. Most surveillance surveys are explicitly designed to detect resistance markers as they spread from low frequencies, and therefore, incorporating GSL is an important facet of molecular surveillance analysis. It is straightforward to incorporate GSL into MalHaploFreq, although this software necessarily implements this in a rather crude manner (Supplemental Appendix S1). It is essential that researchers report their likely GSL in publications, because its value may vary substantially; for example, GSL was 30% in our analysis,^7,9 whereas Anderson and others¹⁸ used 10%. It also seems that some laboratories do not use a formal definition of what constitutes a minor peak and rely on individuals to make a subjective decision as to whether a minor peak represents a minor clone or is an artefact. In the absence of such information, we would tend to agree with Liu and others⁴ and suggest a GSL of 20% in PCR-based analyses with the recommendation that values 10%, 15%, and 25% also be tested to assess whether they provide a much better fit to the data (Figure 2). This is important because our analyses suggest that the effective GSL may differ from that stated in the protocol (Figure 2). The lack of assay sensitivity meant that true prevalence was underestimated to the extent that it became similar to estimated frequency (Figure 1C and Table 1); this observation together with the analysis shown on Figure 2 suggest operational assay sensitivity may be much lower than anticipated. It is ironic, given the limitations of prevalences (see Results), that they end up with similar values to frequencies. As assay sensitivity improves, it is inevitable that prevalence will be better estimated and that frequency and prevalence estimates will diverge (Figure 1C). The impact of GSL serves as an impetus driving attempts to increase assay sensitivity through novel protocols²³; in particular, it increases the precision of frequency estimates in the early stages of mutation spread when their frequencies are low. Simulations indicate that, in the Tanzanian dataset, the width of the CI would fall from 7.5% units to 5.2% units as GSL fell from 0.4 to < 0.1.

To summarize, we strongly urge researchers to estimate and report frequencies as well as prevalences: the former constitutes a common scale of measurements unaffected by different malaria epidemiology (MOIs) and different laboratory practices (which determine GSL). Many malaria endemic areas have recently reported rapid reductions in transmission intensity. This is reflected in reductions in MOI and hence, decreases in the prevalence of resistance SNPs, even when there is no change in the frequency of genetic resistance. Frequency estimates are, therefore, essential to gauge the impact of interventions on antimalarial drug resistance. It is also important to present haplotype frequencies as well as individual constituent SNPs, because SNPs rarely act independently and their combination in haplotypes is often more important than their individual frequencies and prevalences.²⁴ Researchers should also consider, report, and incorporate the likely GSL of their protocols. Here, we have attempted to describe the best ways to obtain good-quality, unbiased genetic data from surveys attempting to monitor the spread of antimalarial drug resistance and have updated, and provide, freely available software to achieve this. The future success of molecular markers to guide antimalarial drug-deployment policy lies in providing consistent, comparable, quality data on which rational decisions can be based. The analyses described above constitute an important first step in developing and describing a framework for achieving this.

Note: Supplemental appendix is available at www.ajtmh.org.