Pigeons' Discounting of Probabilistic and Delayed Reinforcers

Abstract

Pigeons' discounting of probabilistic and delayed food reinforcers was studied using adjusting-amount procedures. In the probability discounting conditions, pigeons chose between an adjusting number of food pellets contingent on a single key peck and a larger, fixed number of pellets contingent on completion of a variable-ratio schedule. In the delay discounting conditions, pigeons chose between an adjusting number of pellets delivered immediately and a larger, fixed number of pellets delivered after a delay. Probability discounting (i.e., subjective value as a function of the odds against reinforcement) was as well described by a hyperboloid function as delay discounting was (i.e., subjective value as a function of the time until reinforcement). As in humans, the exponents of the hyperboloid function when it was fitted to the probability discounting data were lower than the exponents of the hyperboloid function when it was fitted to the delay discounting data. The subjective values of probabilistic reinforcers were strongly correlated with predictions based on simply substituting the average delay to their receipt in each probabilistic reinforcement condition into the hyperboloid discounting function. However, the subjective values were systematically underestimated using this approach. Using the discounting function proposed by Mazur (1989), which takes into account the variability in the delay to the probabilistic reinforcers, the accuracy with which their subjective values could be predicted was increased. Taken together, the present findings are consistent with Rachlin's (Rachlin, 1990; Rachlin, Logue, Gibbon, & Frankel, 1986) hypothesis that choice involving repeated gambles may be interpreted in terms of the delays to the probabilistic reinforcers.

Human and nonhuman animals often must choose among outcomes that differ in terms of quantity, quality, delay, and their probability of occurrence. For foragers, these decisions affect the likelihood of obtaining sufficient food, finding a mate, avoiding predation, and producing viable offspring. For humans, the choices involved in purchasing, career, investment, and health decisions also are influenced by the quantity, quality, delay, and probability of occurrence of the alternatives. Although individuals typically prefer larger to smaller, sooner to later, and certain to uncertain reinforcers, predicting choice becomes more complicated when outcomes differ along more than one dimension. For example, although individuals usually prefer larger reinforcers when other outcome dimensions are held constant, a smaller reinforcer may be preferred if it is available immediately and/or its receipt is certain and the larger reinforcer is only available after a delay and/or its receipt is less probable. The discounting framework provides an approach to understanding such multidimensional decisions (for a review, see Green & Myerson, 2004).

Discounting curves describe the relation between the subjective value of an outcome and some dimension of that outcome such as the delay to, or odds against, its receipt (Rachlin, 2006). For positive outcomes, subjective value decreases as the delay to (delay discounting) or the odds against (probability discounting) their receipt increases. A hyperboloid function of the following form describes the relation between subjective value and delay to or odds against receipt (Green & Myerson, 2004):

where V is subjective value, A is amount, and X is delay to or odds against receipt. The parameters b and s index the rate of discounting and the nonlinear scaling of the outcome dimensions, respectively. When s  =  1.0, the function reduces to a simple hyperbola (Mazur, 1987; Rachlin, Raineri & Cross, 1991).

Equation 1 has been shown to provide an excellent description of the discounting of both delayed and probabilistic outcomes in humans (for a review, see Green & Myerson, 2004). A number of studies have examined the delay discounting function in nonhuman animals, and in each of these studies the data also were well described by Equation 1 (Calvert, Green, & Myerson, 2010; Green, Myerson, Holt, Slevin, & Estle, 2004; Mazur, 1987, 2000; Richards, Mitchell, de Wit, & Seiden, 1997; Woolverton, Myerson, & Green, 2007). Few studies, however, have examined the discounting function for probabilistic reinforcers by nonhumans (e.g., Mobini et al., 2002; Mobini, Chiang, Ho, Bradshaw, & Szabadi, 2000). Perhaps one reason why probability discounting in nonhumans has received so little attention is because of the problem of instantiating probability in a way similar to that used in human studies. Whereas humans can be told the probability of an outcome, this approach is obviously inappropriate with nonhumans.

In the real world, humans experience probabilities in the form of both one-shot decisions and repeated gambles. Rachlin (Rachlin, 1990; Rachlin, Logue, Gibbon, & Frankel, 1986) has suggested that the time to obtain rewards in choices involving repeated gambles controls behavior in the same way that time controls behavior in delay discounting. In an effort to test Rachlin's hypothesis that probabilistic rewards function as delayed rewards, Mazur (1989, 1991, 2005, 2007) examined the interaction between delay and probability of reinforcement in pigeons and rats. Mazur first tested this hypothesis using an equation proposed by Rachlin et al. (1986) for converting the probability of reinforcement to the average delay to reinforcement. However, this equation led to systematic underestimation of the subjective value of probabilistic reinforcers.

Mazur (1989) noted that Rachlin's equation implicitly treats probabilistic reinforcers as occurring after fixed delays, when in fact they occur after variable delays. He proposed using a discounting function that is an extension of Equation 1 and that applies when the delay to a reinforcer varies from trial to trial (Mazur, 1984). According to Mazur's equation, the value of a probabilistic reinforcer is given by:

where P_i is the probability that a delay of D_i seconds to that probabilistic reinforcer will occur on any given trial, and the parameter k (which corresponds to b in Eq. 1) is an index of discounting rate. (An analogous equation in which the denominator, [1+k D_i], is raised to a power, s, would be appropriate in cases where s differed significantly from 1.0.) Using Equation 2, Mazur (1989, 1991, 2005, 2007) reported results that were consistent with Rachlin's hypothesis that probabilistic rewards function as delayed rewards. The choices in these studies involved both delayed and probabilistic outcomes, and adjusting-delay procedures (Mazur, 1987) were used. Thus, there is a need for research with nonhumans that uses an adjusting-amount procedure and focuses specifically on choices between immediate, certain and probabilistic reinforcers, as is typically the case in studies of probability discounting in humans (e.g., Green & Myerson, 2004).

Accordingly, the present study used an adjusting-amount procedure to examine pigeons' choice between a smaller, certain reinforcer and a larger reinforcer obtained on a variable-ratio (VR) schedule. On a VR schedule, the probability of reinforcement for a single response is simply the reciprocal of the size of the ratio. The primary issue in the present study was whether pigeons' discounting of probabilistic reinforcers would be well described by a hyperboloid discounting function, Equation 1 and/or Equation 2.

A second issue concerns the relation between delay discounting and probability discounting. To address this issue, pigeons in the present study were tested on both probability and delay discounting tasks. More specifically, if probability is convertible to delay, then pigeons' performance on the probability discounting task should be predictable from the observed delays to the probabilistic reinforcers using the same equation that described their performance on the delay discounting task. Therefore, the present study examined the extent to which the subjective values of probabilistic reinforcers were predicted by the best fitting delay discounting function.

A final issue concerns the value of the exponent, s, in Equation 1. With humans, the exponent is often significantly less than 1.0 when Equation 1 is used to describe delay discounting data; with nonhumans, however, the exponent of the delay discounting function is rarely significantly less than 1.0 (e.g., Green et al., 2004). When Equation 1 is used to describe human probability discounting, the exponent is even lower than for human delay discounting (Green & Myerson, 2004). Therefore, the present study also examined whether the exponent in the probability discounting function for pigeons is lower than the exponent in their delay discounting function.

METHOD

Subjects

Eight female White Carneau pigeons served as subjects. They were maintained at 80–85% of their individual free-feeding weights (507–615 g) by providing supplemental feeding (Purina Pigeon Checkers) after experimental sessions. They were housed in individual home cages where they had continuous access to water and health grit and were maintained on a 12∶12 hr light∶dark cycle.

The delay discounting data from pigeons 81–84 were previously reported in Green et al. (2004). Between the delay discounting task and the probability discounting task in the present experiment, all of the pigeons participated in an experiment comparing adjusting-amount and adjusting-delay procedures (Green, Myerson, Shah, Estle, & Holt, 2007), although one pigeon (94) did not complete that experiment.

Apparatus

Two experimental chambers (Coulbourn Instruments, Inc.), each measuring 28 cm long by 23 cm wide by 30.5 cm high, were located within sound- and light-attenuating enclosures equipped with ventilation fans. Three response keys, spaced 8 cm apart center to center, were mounted on the front panel of the experimental chamber. The right- and left-most (choice) keys, located 25 cm above the grid floor and 3.5 cm from the side walls of the chamber, could be transilluminated with green and red light, respectively. The center key, located 21 cm above the floor, could be transilluminated with yellow light, and a triple-cue light, located 6 cm above the center key, was equipped with green, yellow, and red light bulbs. Two food magazines, mounted directly below the right and left keys and 4 cm above the grid floor, were illuminated with a 7-W light during reinforcement. A 7-W houselight was mounted centrally on the ceiling of the chamber.

Experimental events were controlled and responses were recorded using a personal computer operating with Med-PC™ software (Med-Associates, Inc.) located in an adjacent room.

Procedure

Pigeons were trained to peck the response keys, and experimental sessions began immediately after pecking was established. Experimental sessions were conducted daily and ended after 10 blocks of trials were completed or 90 min had elapsed, whichever occurred first. Four of the pigeons (81, 82, 83, and 84) were run on the delay discounting task before the probability discounting task, and the others (91, 92, 93, and 94) were run on the delay and probability discounting tasks in the reverse order.

On both the delay and probability discounting tasks, the left (red) key was always associated with the standard amount of pellets (i.e., twenty 20-mg food pellets). The right (green) key was always associated with an adjusting number of 20-mg food pellets, the number of which depended on a pigeon's previous choices (see Adjusting-amount procedure, below). Pellets were delivered at a rate of one pellet every 0.3 s.

Delay discounting task

The beginning of a trial was signaled by the illumination of the center yellow response key and the yellow cue light. On free-choice trials, a response on the yellow key resulted in the illumination of the red (standard) and green (adjusting) side keys as well as the red and green cue lights. (On forced-choice trials, only one side key and the associated cue light were illuminated.) A single response on the red (standard) key darkened the side keys, the green cue light, and the houselight, and initiated the delay to reinforcement, during which the red cue light remained illuminated. After the delay interval had elapsed, the cue light was extinguished, the left magazine light was illuminated, and 20 pellets were delivered. A single response on the green (adjusting) key darkened the side keys, the red cue light, and the houselight. The green cue light remained illuminated for 0.5 s, after which the cue light was extinguished, the right magazine light was illuminated, and an adjusting number of pellets was delivered. In different conditions, the delay to the standard reinforcer was 1, 2, 4, 8, 16, and 32 s. Each pigeon experienced the delay conditions in a different order.

Probability discounting task

The procedure for the probability discounting task was similar to the delay discounting procedure. The beginning of a trial was signaled by the illumination of the center yellow response key and the yellow cue light. On free-choice trials, a response on the yellow key resulted in the illumination of the red (standard) and green (adjusting) side keys, as well as the red and green cue lights. (On forced-choice trials, only one side key and the associated cue light were illuminated.) A response on the red (standard) key darkened the side keys, the green cue light, and the houselight, and a variable number of responses, determined by a constant-probability VR schedule, was required before the 20-pellet reinforcer was delivered. Each key peck extinguished the red key light for 0.75 s, but the red cue light remained illuminated until the response requirement was fulfilled; a response to the extinguished key light had no consequence.

Once the response requirement was completed, the red key, red cue light, and houselight were extinguished, the left magazine light was illuminated, and 20 pellets were delivered. A single response on the green (adjusting) key darkened the side keys, the red cue light, and the houselight. The green cue light remained illuminated for 0.5 s, after which the cue light was extinguished, the right magazine light was illuminated, and an adjusting number of pellets was delivered. In different conditions, the VR for the standard reinforcer was 1, 2, 4, 8, and 16. Each pigeon experienced the VR conditions in a different order.

Following food delivery on all trials of the delay and probability discounting tasks, the magazine light remained illuminated until 3 s had elapsed since the pigeon removed its head from the magazine. After the magazine light was extinguished, the houselight was re-illuminated. The next trial (signaled by illumination of the center key) began 70 s after the pigeon made its choice response on the preceding trial.

Adjusting-amount procedure

On both the delay and probability discounting tasks, experimental trials were arranged in blocks of four trials each. The first two trials in each block were forced-choice trials. One of these forced-choice trials was for the larger, delayed/probabilistic reinforcer, and the other was for the adjusting, immediate/certain reinforcer. The order in which the alternatives were presented varied randomly across blocks. Forced-choice trials were included to give pigeons experience with both of the alternatives prior to the free-choice trials. The last two trials in each block were free-choice trials.

If a pigeon chose the adjusting immediate/certain reinforcer on both free-choice trials in a block, then the number of pellets received for the adjusting alternative was decreased by one pellet on the next block of trials. If the pigeon chose the 20-pellet delayed/probabilistic reinforcer on both free-choice trials, then the number of pellets received for the adjusting alternative was increased by one pellet on the next block of trials. For the first block of trials in a condition, choice of the adjusting immediate/certain reinforcer produced a single pellet and choice of the standard delayed/probabilistic reinforcer produced 20 pellets. After the first session in each condition, the starting value (i.e., the number of pellets) for the adjusting alternative in subsequent sessions was determined based on the choices in the final block of the preceding session.

Stability

Each condition remained in effect until at least 20 sessions had been completed and choice was stable. Stability was defined as five consecutive sessions in which: 1) there was no visual trend in the number of immediate/certain pellets obtained, and 2) when each of the 5 sessions was divided in half, none of the resulting 10 means differed by more than 2 pellets from the overall mean number of immediate/certain pellets obtained. The subjective value of the delayed/probabilistic 20-pellet reinforcer for each delay and VR schedule was operationally defined as the mean number of immediate/certain pellets obtained at stability. Across pigeons, the mean number of sessions to stability in the delay conditions ranged from 26.3 to 55.7, and the mean number in the VR conditions ranged from 25.2 to 102.2.

RESULTS

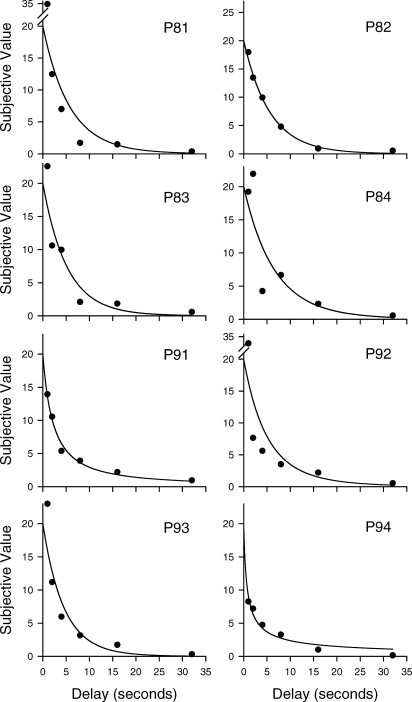
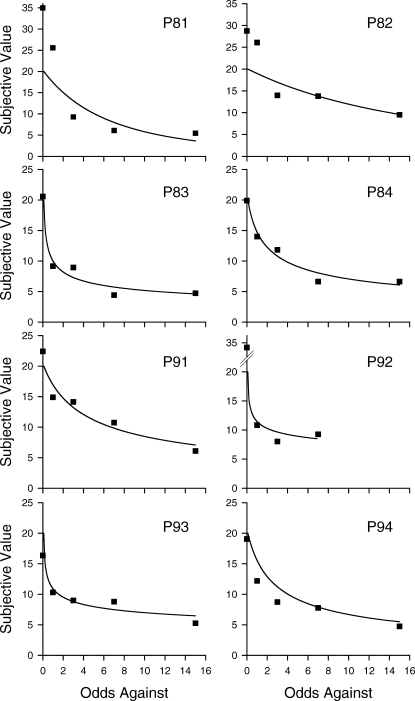
Figure 1 shows subjective value plotted as a function of the delay to the 20-pellet reinforcer in the delay discounting task, and Figure 2 shows subjective value plotted as a function of the odds against receipt of the 20-pellet reinforcer in the probability discounting task. (Note that P92 did not complete the VR 16 condition.) For each pigeon, subjective value decreased systematically with delay and with odds against, and the fits of Equation 1 to the delay and probability discounting data were equally good: For delay discounting, the median R² was .84, and for probability discounting, the median R² was .83.

Fig 1.

Subjective value as a function of delay to reinforcement for each pigeon on the delay discounting task. Circles represent subjective values of the delayed 20-pellet reinforcer; the curves are the best-fitting discounting functions (Eq.1). Note the differences in scaling on the y-axes.

Fig 2.

Subjective value as a function of odds against reinforcement for each pigeon on the probability discounting task. Squares represent subjective values of the probabilistic 20-pellet reinforcer; the curves are the best-fitting discounting functions (Eq.1). Note the differences in scaling on the y-axes.

For both delay and probability discounting, we tested whether the exponent of the hyperboloid discounting function (s in Eq. 1) that best fit each pigeon's data differed significantly from 1.0 by dividing the observed difference by the standard error to obtain a value of the t statistic. (This t value has n − p degrees of freedom, where n is the number of data points, and p is the number of free parameters.)

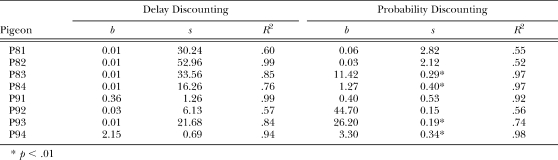
For the delay discounting task, the exponent, s, was not significantly different from 1.0 for any pigeon, indicating that a simple hyperbola (Eq. 1 with s  =  1.0) would suffice to describe the data. For the probability discounting task, in contrast, the exponent was less than 1.0 for 6 of the 8 pigeons, and significantly so for 4 of them (P83, P84, P93, P94). Table 1 presents the R²s and the parameter estimates for each pigeon. It may be noted that there is considerable variability in the parameter estimates, but in every case the exponent of each pigeon's probability discounting function was lower than the exponent of its delay discounting function. This difference between the exponents of the delay and probability discounting functions was statistically significant; t (7)  =  2.97, p < .05.

Table 1.

Estimated b and s parameters and the proportion of variance accounted for (R²) by Equation 1 for delay and probability discounting for each pigeon.

In order to examine the relation between delay and probability discounting, we compared the subjective values of the probabilistic reinforcers with what would be predicted if their subjective value were determined by the delays until those reinforcers were received. If delay and probability discounting are equivalent, then for a given repeated gamble (VR schedule), substituting the average delay until a pigeon received a reinforcer into that pigeon's delay discounting function should predict the subjective value of the probabilistic reinforcer to that pigeon. This procedure was followed for each pigeon in each probabilistic reinforcement condition (i.e., the VR 2, 4, 8, 16 schedules). Because the exponent, s, did not differ significantly from 1.0 for any pigeon on the delay discounting task, the best fitting simple hyperbola (Eq. 1 with s  =  1.0) was used for each pigeon's delay discounting function.

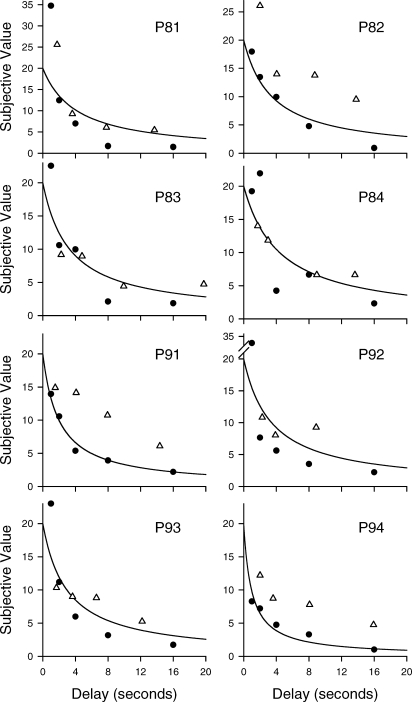
The subjective values of the reinforcers obtained on the probability discounting task, plotted as a function of the mean of the actual delays until they were received, are represented in Figure 3 by unfilled triangles. Also shown are the subjective values of the reinforcers on the delay discounting task, represented by filled circles (replotted from Fig. 1). The discounting functions (curved lines) represent the fits of the simple hyperbola (Eq. 1 with s  =  1.0) to all of the delay discounting data, although only the data from the first five delays, which spanned a range similar to that of the delays to the probabilistic reinforcers, are presented.

Fig 3.

Subjective value as a function of delay to reinforcement for each pigeon. Triangles represent subjective values of the 20-pellet reinforcer on the probability discounting task plotted as a function of the mean of the delays to reinforcement for each VR condition except for the VR 1. Circles represent subjective values of the 20-pellet reinforcer on the delay discounting task, replotted from Figure 1. The delay discounting functions (solid curves) represent fits of Equation 1 with s  =  1.0 to the data from all six delay conditions, although the data from the longest (32 s) delay condition are not shown. Note the differences in scaling on the y-axes.

As may be seen in Figure 3, for 5 pigeons (P81, P83, P84, P92, and P93), the subjective values of the probabilistic reinforcers were reasonably well predicted by the discounting function that best described the delay discounting data. For the other 3 pigeons (P82, P91, and P94), the subjective values of the probabilistic reinforcers all fell above the delay discounting function. Importantly, for all 8 pigeons, in those cases where the delay to a reinforcer obtained on the probability discounting task was approximately equal to the delay to a reinforcer obtained on the delay discounting task, there was a strong tendency for the subjective value of the former (unfilled triangles) to be higher than the subjective value of the latter (filled circles).

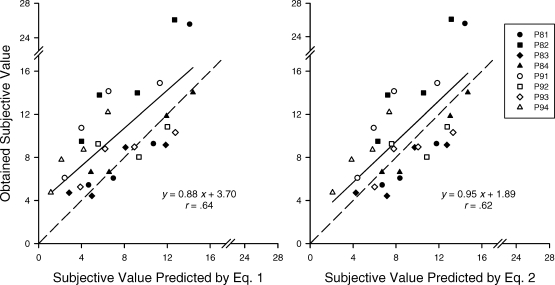
The tendency of the simple hyperbola, Equation 1 with X equal to the mean delays to the probabilistic reinforcers and s  =  1.0, to underestimate the obtained subjective values of these reinforcers also may be seen in the left panel of Figure 4. The obtained subjective values of the probabilistic reinforcers are replotted here as a function of the subjective values predicted by Equation 1 based on their mean delays. Results for each pigeon in each VR condition are shown, as well as the regression line fitted to all of the data. If the obtained subjective values equaled the predicted values, all data points would fall along the dashed line. There was a strong correlation between obtained and predicted values, and the slope of the regression line did not differ significantly from 1.0; t (29) < 1.0. However, the intercept was significantly greater than 0.0, reflecting a systematic bias, that is, a general tendency for the obtained subjective values to be greater than those predicted by Equation1; t (29)  =  2.33, p < .05.

Fig 4.

Obtained subjective values of probabilistic reinforcers for individual pigeons plotted as a function of the subjective values predicted based on Equation 1 with s  =  1.0 (left panel) and Equation 2 (right panel). The solid lines represent the regression lines. If the obtained values were equal to the predicted values, the symbols would fall along the dashed lines.

Finally, the right panel of Figure 4 shows the same subjective values of the probabilistic reinforcers now plotted as a function of the subjective values predicted by Mazur's (1984) discounting function for variable delays (Eq. 2). To obtain the predicted value for each pigeon on each VR, the actual delays until the reinforcers obtained on that VR were divided into 20 bins. The width of each bin was one-twentieth of the difference between the shortest and longest delays for that pigeon on that VR. The delay (D_i) in Equation 2 corresponded to the midpoint of each bin, and P_i corresponded to the proportion of delays in the bin.

With the exception of two highest obtained subjective values (corresponding to the VR 2 conditions for P81 and P82), which were also poorly predicted by Equation 1 based on the mean delays to the probabilistic reinforcers, Equation 2 predicted the probability discounting data fairly well. This is reflected in the strong correlation between obtained and predicted values, as well as the finding that the slope of the regression line did not differ significantly from 1.0, t (29) < 1.0, and the intercept did not differ significantly from 0.0, t (29) < 1.0. Thus, use of Equation 2 eliminated the systematic bias associated with predicting the subjective values of probabilistic reinforcers using Equation 1.

DISCUSSION

The primary goal of the present study was to determine whether the hyperboloid discounting function describes the discounting of probabilistic reinforcers in pigeons. This question is of interest in part because in humans, both probability and delay discounting are well described by a hyperboloid function (Green & Myerson, 2004). Consistent with the results of previous studies with nonhumans (Green et al., 2004; Mazur, 1987, 2000; Richards et al., 1997; Woolverton et al., 2007), the hyperboloid discounting function (Eq. 1) provided good fits to the delay discounting data from individual pigeons in the present study. More importantly, the present results are the first to show that the hyperboloid function, with odds against receipt of a reinforcer as the independent variable, also fits individual pigeon's probability discounting data.

As in previous studies with nonhuman animals, the exponents of the hyperboloid delay discounting function did not differ significantly from 1.0. With respect to the probability discounting function, the exponent was less than 1.0 for 6 of the 8 pigeons, significantly so for 4 of them. In all cases, the exponent of an individual pigeon's probability discounting function was lower than the exponent of its corresponding delay discounting function. This finding is consistent with the results of human discounting studies which have consistently shown that probability discounting functions have lower exponents than delay discounting functions (Green & Myerson, 2004).

The present results bear on Rachlin's (1990; Rachlin et al., 1986; Rachlin et al., 1991) hypothesis that probability of reinforcement is convertible to delay of reinforcement. When the delays to probabilistic reinforcers were substituted into the hyperboloid discounting function (Eq. 1), this equation provided a reasonably good fit to the data. However, there was evidence that the equation tended to underestimate the subjective values of the probabilistic reinforcers. Because this bias may have been due to the fact that the delays to reinforcement on the probability discounting task were variable, we used the discounting function (Eq. 2) proposed by Mazur (1984) to deal with such variation. Using Mazur's equation, the bias observed with Equation 1 was no longer significant, and the subjective values of probabilistic reinforcers could be estimated using no free parameters, just the observed delays to probabilistic reinforcers and the rate parameter estimated from the delay discounting data (i.e., in predicting the subjective values of the probabilistic reinforcers, k was an empirical constant, not a free parameter).

This finding is consistent with Rachlin's (1990; Rachlin et al., 1986) contention that choice involving repeated gambles may be interpreted in terms of the delay to the delivery of probabilistic reinforcers, and supports Mazur's (1989) claim that the variability in delay to probabilistic reinforcers needs to be taken into account. However, we believe that Mazur's equation (Eq. 2) represents more than just a better way of averaging the data; it is a significant theoretical statement about the process underlying the discounting function, at least in pigeons. That is, the finding that in a condition involving variable delays, the subjective value for that condition is best predicted by averaging the subjective values of each individual reinforcer obtained in that condition, rather than by averaging the delays and then substituting the average delay into the hyperboloid discounting function, suggests that the discounting function is not just a rule describing the molar relation between subjective value and delay. Rather, it may describe the reinforcing value of the outcome received on each trial, and Mazur's equation represents the average of these reinforcing values, weighted by the frequency of their occurrence. According to this interpretation, which is implicit in Mazur's use of Equation 2, the hyperboloid discounting function accurately reflects the molecular process that occurs on every single trial.

With respect to Rachlin's (1990; Rachlin et al., 1986) hypothesis regarding repeated gambles, it might be argued, of course, that a more rigorous test of the equivalence of delay and probability discounting would use a delay discounting task that, like the probability discounting task used here, involved variable delays to the larger reinforcer. Alternatively, one could use fixed delays in the delay discounting task and one-shot decisions, rather than repeated gambles, in the probability discounting task. Nevertheless, the present results obtained using adjusting-amount procedures, taken together with those of Mazur (e.g., 1989) obtained using adjusting-delay procedures, are consistent with the hypothesis that repeated gambles are functionally equivalent to variable delays to reinforcement, at least in nonhuman animals.

In humans, however, comparisons of delay and probability discounting suggest nonequivalence, as exemplified by the opposite effects that amount has on human delay and probability discounting (Green & Myerson, 2004). Nevertheless, it is possible that a comparison of delay and probability discounting using repeated gambles and real rewards, rather than the one-shot choices between hypothetical certain and probabilistic rewards that are typically studied, would reveal results more consistent with those of the present study of delay and probability discounting in pigeons.