Testing Model Nesting and Equivalence

Abstract

Using existing technology, it can be hard or impossible to determine whether two structural equation models that are being considered may be nested. There is also no routine technology for evaluating whether two very different structural models may be equivalent. A simple nesting and equivalence testing (NET) procedure is proposed that uses random sample and model-reproduced moment matrices to evaluate both model nesting and equivalence. The analysis is “local” rather than “global” in nature, but its use with simulation or bootstrapping can imply global conclusions. Two standard applications of NET are to verify whether or not two proposed models are equivalent, and whether a baseline model used in an incremental fit index is appropriately nested.

The basic ideas of model nesting and model equivalence in structural equation modeling (SEM) are widely known, already discussed in introductory texts (Byrne, 2006; Kline, 2005; Mulaik, 2009; Raykov & Marcoulides, 2006). Most SEM practitioners know that fixing one or more free parameters to yield a more restricted model will yield a nested model, and that changing the direction of one or more paths in a simple model may yield an equivalent structural equation model.

Model nesting is the easier concept. It is facilitated by SEM programs that allow a researcher to run any two models, whose test statistics output can then be used to compute a chi-square difference test. However, the difference test also can be computed when the models are not nested and such a test is meaningless. Although no researcher would do this on purpose, such a meaningless comparison sometimes is made in the context of widely used fit indices such as the comparative fit index (CFI, Bentler, 1990). To compute such an index, a SEM program may automatically generate the standard baseline or null model of uncorrelated variables and compute the fit index by comparing the fit of the current substantive model to that of this null model. However, as noted by Widaman and Thompson (2003), the model of uncorrelated variables often is not a nested subset of the model of interest, so the resulting fit index is inappropriate and meaningless. SEM programs, however, provide no information on the appropriateness of the model comparison used in computing incremental fit indices. A simple and automated method for evaluating model nesting would eliminate this problem.

Model equivalence is harder to evaluate, and tends to be overlooked in practice (e.g., Henley, Shook, & Peterson, 2006). Moment equivalent models are those “that, regardless of the data, yield identical (a) implied covariance, correlation, and other moment matrices when fit to the same data, which in turn imply identical (b) residuals and fitted moment matrices, (c) fit functions and chi-square values, and (d) goodness-of-fit indices based on fit functions and chi-square” (Hershberger, 2006, p. 15). What is especially hard for a practitioner to do is to evaluate whether models are nested or equivalent when, for example, the structures of the models being compared are very different or if the models are so large as to make overview difficult. SEM programs provide no help in evaluating equivalent models, and researchers are left to study the complicated rules of path replacement, recently summarized by Hershberger (2006), to see if models are equivalent.

This paper describes simple computations that can be added to any SEM program to obtain evidence on nesting or equivalence. Similarly, a researcher can perform their own nesting and equivalence tests using two SEM modeling runs. The first run fits the presumed more restricted model. The resulting implied moment matrix is fit in the second run by the presumed equal or more general model. Our proposed decision rules are then applied to standard output to yield the required conclusions.

We use the following notation. Let two models be designated as M₁ and M₂, where, if the models have different degrees of freedom (df), M₁ is the model with the larger df. This implies that when models are nested, M₁ is the more restricted model; or, if the df are equal, it may be equivalent to M₂. When neither nesting nor equivalence holds, M₁ and M₂ are just two models of interest.

Methodology

Bentler and Bonett (1980) introduced the concepts of parameter nesting and covariance matrix nesting. The type of nesting typically considered is parameter nesting, where a free parameter in M₂ is fixed in the more restricted model M₁ or a free parameter is added into a constraint equation that reduces the effective number of free parameters. A result is that the df in M₁ must be larger than those in M₂. Parameter nesting is relatively easy to evaluate, especially in simple models, and hence a special technology to evaluate parameter nesting is typically not needed. However, verifying parameter nesting also can be difficult, or at least, subject to human error, and computerized assistance may be helpful.

Covariance matrix nesting, or, allowing mean structures as well, moment matrix nesting, is more difficult to verify. In such models, the mapping from parameters to mean and covariances matrices may take completely different forms in the two models being compared, and yet the set of possible moment matrices under M₁ remains a subset of the set of possible mean and covariance matrices under M₂. Consider for example the two models in Figure 1. These models look completely different -- they have a different number of equations; they have a different number of independent variables; and only one has latent variables. Yet, under standard identification conditions, they are nested. This can be seen easily since model M₂ is a saturated model, and M₁ is just some structural model. In more complicated models it can be even more difficult to establish moment matrix nesting. Computerized assistance would definitely be helpful.

Figure 1.

Two Nested Models

We will define model equivalence in terms of nesting. We will see that equivalent models are those with equal df in which M₁ is nested in M₂, and simultaneously, M₂ is nested in M₁. In terms of methodology, our approach is quite different from that of previous authors. The typical approach is based on abstract algebra (including computer algebra programs) associated with parameters, functions, and population model structures (e.g., Bekker, Merckens, & Wansbeek, 1994; Raykov & Penev, 1999), which is elegant but essentially impossible for an empirical scientist to implement. In contrast, the proposed approach uses sample data to investigate population nesting and equivalence. In order to assure that this methodology is statistically sound, we make several assumptions. First, nesting and equivalence are defined with regard to a given population with means μ and full rank covariance matrix Σ. Second, an empirical or simulated random sample from this population has been obtained, yielding sample means $\stackrel{‒}{X}$ and full rank covariance matrix S. Third, it is assumed that the asymptotic variance matrix of the vector of sample moments is nonsingular. Fourth, the models M_i [Σ_i(θ_i) and μ_i(θ_i) if relevant] being considered are identified, and the vector-valued function that expresses the moments as a function of the free unconstrained parameters is continuously differentiable with Jacobian of full column rank in a neighborhood of population values. Fifth, no inequality constraints are involved in the definition of the models considered. These conditions¹ are adopted to rule out pathological cases that can be devised to make standard methods break down, as further discussed below. At this point, we describe our method. A detailed rationale is provided subsequently.

Nesting and Equivalence Test (NET)

The sample means $\stackrel{‒}{X}$ and covariance matrix S are used in the following.

• Step 1. Do a normal SEM run on model M₁. Save the df and the model reproduced covariances (and means, in a mean structure). Call these df₁, ${\widehat{\Sigma }}_1$ (and ${\widehat{\mu }}_1$ if needed).

• Step 2. Read in the ${\widehat{\Sigma }}_1$ (and ${\widehat{\mu }}_1$ if needed) as data to be analyzed in a SEM run with model M₂ using the same estimation method. The output needed from this run is the df, say df₂, and the minimum of the fit function $\widehat{F}$ (or the associated chi-square statistic).

• Step 3. Compute d = df₁−df₂, and set ε, a small criterion value for $\widehat{F}$ (e.g., ε = .001).

• Step 4.

  1. If d > 0 and $\widehat{F}⟨\epsilon$, the models are nested.
  2. If d = 0 and $\widehat{F}⟨\epsilon$, the models are equivalent.
  3. If d < 0 or $\widehat{F}\ge \epsilon$, M₁ is not nested in, or equivalent to, M₂.

The key idea is that when $\widehat{F}⟨\epsilon$, the M₁ model-reproduced means and covariance matrix can be precisely reproduced by model M₂. With nonnegative d, as in (a), this implies the models are nested. With d = 0, as in (b), this implies the models are equivalent. Negative degrees of freedom, as in (c), imply non-nesting of M₁ in M₂ and non-equivalence of the models. Note that if $\widehat{F}\ge \epsilon$, i.e., if the restricted model reproduced means and covariances cannot be fit exactly by an equal or more general model, the models are neither nested or equivalent. The reason for picking some small ε as a criterion is that computations always involve some numerical approximations -- terminating computations by a convergence criterion depends on the specific choice of criterion, the computational accuracy of the computer, and so on. As computer precision improves, ε can be made very small indeed.²

In some situations, sample data may not be available. In such a case, we can create an artificial population and sample from it so that the moment matrix to be analyzed in NET corresponds to a true random matrix. We may do this in many ways; we mention three: (1) Choose some specific unstructured Σ (and μ when means are in included in the model) and draw a random sample from the corresponding multivariate normal distribution, obtaining the sample covariance matrix S (and sample means $\stackrel{‒}{X}$ when means are included) and use NET as before. (2) As a variant of (1), instead of choosing a saturated model, use a restricted model with added random sampling. This can be done in two ways, (2a) choose values of the parameters in the equation/covariance specification of the model under consideration, generate the implied $\widehat{\mu }$, $\widehat{\Sigma }$ and use this to define the artificial population, then proceed as in (1); or (2b) sample from a multinormal distribution to obtain sample values for the independent variables of the model, and use these with chosen values of the parameters in the model equations to obtain the values of the dependent variables. Obtain S (and $\stackrel{‒}{X}$ if needed) from the full sample and proceed with Step 1. (3) Assign randomly chosen proper parameter values to the restricted model M₁, generate the implied $\widehat{\mu }$, $\widehat{\Sigma }$, use these as ${\widehat{\mu }}_1$, ${\widehat{\Sigma }}_1$ (with df₁) in Step 1 of NET, then proceed directly to Step 2 and continue as above. The validity of each of these methods hinges on the randomness of its specified random aspect, either of the sample data from which S and $\stackrel{‒}{X}$ are obtained, or the random choice of parameter values to obtain a moment matrix and vectors under the more restricted model. If the samples so generated create problems in model estimation, the simulation sample size can be increased to generate a tighter neighborhood in which these model comparisons are undertaken (see Appendix A). In a sense, these simulation methods are counterparts and extensions to standard SEM practice, in which the empirical rank of a Jacobian or information matrix is evaluated at some set of parameter estimates to determine local identification.

Next we illustrate how to do our nesting test with several small examples from the literature. Theoretical rationales are presented subsequently.

Illustrations

Nested Models

The first example involves the two models M₁ and M₂ of Figure 1. The sample covariance matrix S is the 3 by 3 covariance matrix given by Hershberger (2006, p. 15), namely,

$$S=\left[\begin{array}{ccc}\hfill 2.00\hfill & \hfill \hfill & \hfill \hfill \\ \hfill .94\hfill & \hfill 1.80\hfill & \hfill \hfill \\ \hfill 1.03\hfill & \hfill .65\hfill & \hfill 1.50\hfill \end{array}\right].$$

Hershberger does not give the sample size, and we take it as N=100. Model M₁ is his Model 1 (p. 17), which has 1 df (df₁=1). In Step 1, we use maximum likelihood (ML) estimation, and obtain the model-reproduced covariance matrix based on the ML estimates as

$${\widehat{\Sigma }}_1=\left[\begin{array}{ccc}\hfill 2.00\hfill & \hfill \hfill & \hfill \hfill \\ \hfill .94\hfill & \hfill 1.80\hfill & \hfill \hfill \\ \hfill .339\hfill & \hfill .651\hfill & \hfill 1.50\hfill \end{array}\right].$$

This is identical to that reported by Hershberger (2^nd matrix, top of p. 16). Next, we do Step 2, using ${\widehat{\Sigma }}_1$ as data to be analyzed using model M₂ of Figure 1. The output from this run provides the df (df₂=0) and the minimum of the ML fit function, $\widehat{F}=.00000$. In step 3, we compute the difference in degrees of freedom as d = df₁ − df₂ = 1 − 0 = 1, and choose the default ε = .001. We see that the results favor part (a) of Step 4, that is, d > 0 and $\widehat{F}⟨\epsilon$ and hence we conclude that the models are nested, which is not surprising since M₂ is a saturated model.

Model Equivalence

Figure 2 shows a model that Hershberger has shown to be equivalent to model M₁ of Figure 1; it is his Model 3 (p. 17). We now use our NET procedures to evaluate the equivalence hypothesis. Step 1 gives the same results as previously. Using the output of Step 1 (${\widehat{\Sigma }}_1$ as shown above) as input to Step 2, we now run the model of Figure 2. The results show the df (df₂=1) and the minimum of the ML fit function, $\widehat{F}=.00000$. In step 3, difference in df is given as d = df₁ − df₂ = 1 − 1 = 0. With the same default ε as before, the results are consistent with part (b) of Step 4. Since d = 0 and $\widehat{F}⟨\epsilon$, the models are equivalent.

Figure 2.

An Equivalent Model to Model M₁ of Figure 1

Appropriateness of Fit Indices

Next we consider one of the examples provided by Widaman and Thompson (2003) on appropriate and inappropriate null models for fit indices. An inappropriate model is one in which the baseline model, typically taken by default as the model of uncorrelated variables, is not nested in the model of interest. They analyzed several psychometric test theory models on 4 variables taken from Votaw (1948). Based on 126 subjects, the means of these variables are 14.905, 15.484, 14.444, 15.123, and the covariance matrix is

$$S=\left[\begin{array}{cccc}\hfill 25.070\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill 12.436\hfill & \hfill 28.202\hfill & \hfill \hfill & \hfill \hfill \\ \hfill 11.726\hfill & \hfill 9.228\hfill & \hfill 22.739\hfill & \hfill \hfill \\ \hfill 20.751\hfill & \hfill 11.973\hfill & \hfill 12.069\hfill & \hfill 21.871\hfill \end{array}\right].$$

Among the several models they considered is a restricted one-factor model with equal factor loadings, equal unique variances, and equal means (their model 1A). The ML test statistic T_ML of this substantive model, based on df=11, is T_ML = 115.266. Their standard baseline model (model 0C) had no factors, freely estimated unique variances, and freely estimated means. This model is clearly not nested in the substantive model since it frees up parameters rather than restricting them further. It yielded T_ML = 272.492 with 6 df. In this example, the smaller rather than greater number of df should clearly warn the user about the inappropriateness of this baseline model, and hence the inappropriateness of all incremental fit indices. Widaman and Thompson suggested that an acceptable baseline model for their substantive model would be a model that has no factors, equal unique variances, and equal means (model 0A). This yielded T_ML = 277.826 with 12 df. We now show how our NET methodology verifies that model 0C is not nested in the substantive model, while model 0A is appropriately nested. We use the χ² statistics for this evaluation, rather than the minima of the fit function as before.

Our Step 1 model M₁ for model 0C showed T_ML = 272.492 with 6 df (=df₁). The model reproduced means are 14.905, 15.484, 14.444, and 15.123 and the unique variances are 25.070, 28.202, 22.739, and 21.871, i.e., these estimates correspond to the sample means and variances as would be expected. In Step 2, these are input into a new run with analysis based on M₂, which is their model 1A (see above). The resulting T_ML = 5.334 with 11 df (=df₂). In Step 3, we compute d = df₁ − df₂ = 6 − 11 = −5 and choose ε = .001 as before. In Step 4, since d < 0 and T_ML = 5.334 > ε, neither conditions (a) or (b) are met, while (c) is met, attesting to the conclusion that the models are not nested as hypothesized or equivalent. Repeating this procedure for model 0A, in Step 1, as noted T_ML = 277.826 with 12 df (=df₁). The corresponding model reproduced means are 14.989, 14.989, 14.989, and 14.989, and the unique variances are 24.612, 24.612, 24.612, and 24.612. In Step 2, these are input into a new run with analysis based on model M₂(model 1A), yielding T_ML = 0.000 with 11 df (=df₁). In Step 3, d = df₁ − df₂ = 12 − 11 = 1, and we choose ε = .001. Using the results of Steps 2 and 3 in Step 4, we have d > 0 and T_ML < ε, and hence we conclude, correctly, that model 0A is nested in model 1A. Hence, incremental fit indices can be based on it.

Model Comparison without Data

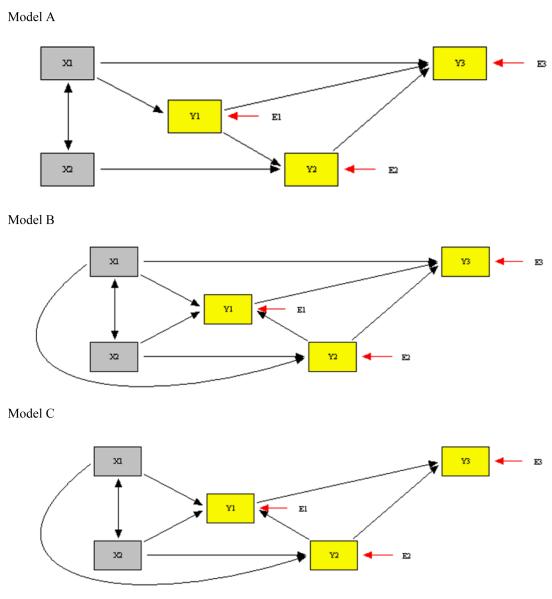
Next we show how to use the NET procedure when no sample data is available. We use the third method described above. The specific illustration is based on a model taken from educational psychology (Meece, Blumenfeld, & Hoyle, 1988) that was studied by MacCallum, Wegener, Uchino, and Fabrigar (1993) and shown by them to be equivalent to three further models as given in their figure 2. While we could demonstrate our method to evaluate model equivalence with the MacCallum et al. models, we consider nesting tests on models derived from two of the equivalent models: their “original model” and their model 2C. To achieve this, we suppress two paths of their original model, yielding our Model A as shown in the top part of Figure 3. We keep intact their model 2C and make it our Model B, shown in the middle of Figure 3. Finally, we suppress one path of model B (their 2C) to obtain our Model C, the bottom part of Figure 3. The three models are defined by equations as follows.³

• Model A

  $$\begin{array}{cc}\hfill Y_1& ={\gamma }_{11}{X}_1+E_1\hfill \\ \hfill Y_2& ={\beta }_{21}{Y}_1+{\gamma }_{22}{X}_2+E_2\hfill \\ \hfill Y_3& ={\beta }_{31}{Y}_1+{\beta }_{32}{Y}_2+{\gamma }_{31}{X}_1+E_3\hfill \end{array}$$
• Model B

  $$\begin{array}{cc}\hfill Y_1& ={\beta }_{12}{Y}_2+{\gamma }_{11}{X}_1+{\gamma }_{12}{X}_2+E_1\hfill \\ \hfill Y_2& ={\gamma }_{21}{X}_1+{\gamma }_{22}{X}_2+E_2\hfill \\ \hfill Y_3& ={\beta }_{31}{Y}_1+{\beta }_{32}{Y}_2+{\gamma }_{31}{X}_1+E_3\hfill \end{array}$$
• Model C

  $$\begin{array}{cc}\hfill Y_1& ={\beta }_{12}{Y}_2+{\gamma }_{11}{X}_1+{\gamma }_{12}{X}_2+E_1\hfill \\ \hfill Y_2& ={\gamma }_{21}{X}_1+{\gamma }_{22}{X}_2+E_2\hfill \\ \hfill Y_3& ={\beta }_{31}{Y}_1+{\beta }_{32}{Y}_2+E_3\hfill \end{array}$$

In all models, the variances and covariances of the exogenous X₁ and X₂, and the variances of the residuals E₁, E₂, E₃ are unrestricted parameters of the model, with the E_i specified as uncorrelated. The df of models A, B and C are respectively 3, 1 and 2, implying that none of the models are equivalent. But are they nested?

Figure 3.

Models to Illustrate Nesting or Nonnesting with Artificial Data

If Models A and B are nested, Model A must be the more restricted model since Model B has fewer df, i.e., more free parameters. In fact, we know from MacCallum et al. that Model A must be nested in Model B, since model A is just one of their equivalent models with some paths suppressed. Yet nesting is not obvious from the figures. Comparing the figures, or equivalently, the equations, it is easy to see that the paths X₁ to Y₂(γ₂₁) and X₂ to Y₁(γ₁₂) in Model B are set to zero to yield Model A, implying nesting. However, at the same time, the path from Y₂ to Y₁ also is reversed, implying non-nesting. To avoid the extensive required algebra to see if the models are nested, let us apply NET.

Using the above third-mentioned method for dealing with absence of empirical data, we used an integer-based uniform random number generator to obtain random parameter values for Model A, the more restricted model in both comparisons. For greater plausibility when compared with real data, the generated random parameters were limited to appropriate ranges for coefficients, variances, and covariances. Distributions also could be specified, but we did not do so. For coefficients, we limited the random numbers $\mathfrak{R}$ to the range 1-200 and computed γ_ij or β_ij as $.6(\mathfrak{R}-100)∕100$. To keep the correlation among independent variables from being too large, we limited random $\mathfrak{R}$ to the range 1-150 and computed it as $(\mathfrak{R}-75)∕100$. To keep variances in a small range around 1, we use $\mathfrak{R}$ in the range 80-120 and computed them as $\mathfrak{R}∕100$. Standard deviations were taken as square roots of variances; together with a correlation, they yielded a covariance. The implied model covariance matrix from this procedure was

$$\widehat{\Sigma }=\left[\begin{array}{ccccc}\hfill .840\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill .589\hfill & \hfill .920\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill -.217\hfill & \hfill -.154\hfill & \hfill 1.006\hfill & \hfill \hfill & \hfill \hfill \\ \hfill .190\hfill & \hfill .260\hfill & \hfill -.220\hfill & \hfill 1.105\hfill & \hfill \hfill \\ \hfill -2.76\hfill & \hfill -.141\hfill & \hfill -.438\hfill & \hfill .487\hfill & \hfill 1.487\hfill \end{array}\right].$$

Applying NET, the minimum $\widehat{F}$ when Model B is fit to this matrix was .00000, indicating that Model A is nested in Model B. With Model C, minimum $\widehat{F}=.224$, indicating that A is not nested in C. This methodology was repeated several times to generate different random $\widehat{\Sigma }$, and the nesting conclusions were identical each time. A formal simulation was not undertaken since it would just verify our derivations.

In this example, we could anticipate the conclusions. Without MacCallum et al., we would have had to do tedious algebra to obtain the results; with NET, the conclusions were reached with a few computer runs. The R code in Appendix C can be used to do these runs.

Rationale for NET Methodology

Consider a situation in which the set of possible mean and covariance matrices under M₁ is equal to, or is a subset of, the set of possible mean and covariance matrices under M₂. This moment matrix nesting requires that all possible sets of parameters θ₁ that could generate means μ₁(θ₁) and covariance matrices Σ₁(θ₁) must generate sets of means and covariances that also are found among the means μ₂(θ₂) and covariance matrices Σ₂(θ₂). As a consequence, fitting the more general model {μ₂(θ₂), Σ₂(θ₂)} to the restricted means and covariances {μ₁(θ₁), Σ₁(θ₁)} must yield a perfect fit. In practice, the restricted model is estimated to obtain $\left\{{\mu }_1\right({\widehat{\theta }}_1),{\Sigma }_1({\widehat{\theta }}_1\left)\right\}$, and the more general model {μ₂(θ₂), Σ₂(θ₂)} is then fit to $\left\{{\mu }_1\right({\widehat{\theta }}_1),{\Sigma }_1({\widehat{\theta }}_1\left)\right\}$ with some estimation methodology. If the fit is perfect and the fitted moments under the more restricted model are based on a random sample, or on a random choice of parameter values under the null hypothesis, the models are nested. Furthermore, if both models have the same degrees of freedom, they are equivalent. The mathematical and statistical basis for this methodology is given in Appendix B.

The Role of Random Sampling

The importance random sampling in our NET methodology can be visualized in a simple example. Consider the following three models for two variables X and Y

$$\begin{array}{cc}\hfill & \left(\mathrm{a}\right)M:\sigma (a,b,c)=\{{\sigma }_{xx}=a,{\sigma }_{xy}=b,{\sigma }_{yy}=c\}\hfill \\ \hfill & \left(\mathrm{b}\right)M_1:{\sigma }_1(1,b,c)=\{{\sigma }_{xx}=1,{\sigma }_{xy}=b,{\sigma }_{yy}=c\}\hfill \\ \hfill & \left(\mathrm{c}\right)M_2:{\sigma }_2(a,b,1)=\{{\sigma }_{xx}=a,{\sigma }_{xy}=b,{\sigma }_{yy}=1\}\hfill \end{array}$$

where a, b, and c are labels for free parameters. Note that M is a saturated model. We associate the names of the model with the set of covariance matrices reproduced when varying the parameters of the model, e.g., M₁ is the set of covariance matrices σ₁ reproduced as σ_xx = 1 and only b and c are varied.

In Figure 4 we represent M by unrestricted points in three-dimensional Euclidean space (a cone, if we restrict the covariance matrix to be non-negative definite); M₁ is the plane defined by a = 1; M₂ is the plane defined by c = 1. Note that both planes intersect on a line, say M₁₂ = M₁ ⋂ M₂, which is a proper subset of both M₁ and M₂ where this intersection M₁₂ is a non-empty set. Here it is clearly visible that M₁ is not nested within M₂, and that both M₁ and M₂ are nested within M. We denote nesting of A within B by A<B.

Figure 4.

M₁ and M₂ as Planes with Intersection M₁₂

It is clear that NET will yield incorrect conclusions on global equivalence of M₁ and M₂ if a sample covariance matrix S happens to contain variances s_xx = s_yy = 1. Although this is true, it does not impair NET because, as we have noted, NET must be evaluated on a sample moment matrix, not on a given matrix. That is, we are not allowed to choose S, which must be obtained randomly, and when it is, NET will yield the correct conclusion even if σ_xx =σ_yy = 1 are common points in both M₁ and M₂.

To verify that NET does not break down, suppose that we have a true random sample S from M. In Step 1 of NET, we fit M₁ :σ₁(1,b,c) = {σ_xx =1,σ_xy = b,σ_yy = c} to S and obtain ${\widehat{\sigma }}_1=(1,s_{xy},s_{yy})$ with df₁ = 1. Because the sampling variability of each element of S is absolutely continuous, and any single point has probability mass zero, the probability that s_yy = 1 is equal to zero. In Step 2, we fit M₂ :σ₂(a,b,1) = {σ_xx = a, σ_xy = b, σ_yy =1} to ${\widehat{\sigma }}_1=(1,s_{xy},s_{yy})$ with df₂ =1. Since s is not equal to 1, we will obtain $\widehat{F}⟩\epsilon$. In Step 3 of NET we compute d = df₁−df₂=0. In Step 4, we see that since $\widehat{F}\ge \epsilon$, we conclude that M₁ is not nested in, or equivalent to, M₂. Next assume that we have no sample S. To proceed, we first have to define the population M :σ(a,b,c) = {σ_xx = a,σ_xy = b,σ_yy = c}. To make this more challenging, we choose σ_xx = σ_yy = 1 and σ_xy = .4, conceivably hastening the breakdown of NET. We choose a sample of size 100, and use method (1) to draw a random sample and obtain

$$S=\left[\begin{array}{cc}\hfill 1.1827\hfill & \hfill .6156\hfill \\ \hfill .6156\hfill & \hfill 1.7959\hfill \end{array}\right].$$

In Step 1 of NET, we fit model M₁ to S and obtain ${\chi }_1^2=9.82$ with

$${\widehat{\Sigma }}_1=\left[\begin{array}{cc}\hfill 1.0000\hfill & \hfill .2964\hfill \\ \hfill .2964\hfill & \hfill .9758\hfill \end{array}\right].$$

In Step 2 of NET, we fit M₂ to ${\widehat{\Sigma }}_1$ and obtain ${\chi }_1^2=.2842$. In step 3 of NET, we compute d = df₁−df₂=0. In Step 4, we see again that since $\widehat{F}\ge \epsilon$, M₁ is not nested in, or equivalent to, M₂. This procedure was repeated many times, and the NET conclusion was identical each time. Notice that the correct conclusion is reached by NET whether or not we have a sample S at hand and even when sampling from a population which is in the intersection of the two models.

With regard to M₁ < M₂, clearly, only if ${\widehat{\Sigma }}_1$ is in M₁₂ = M₁ ⋂ M₂ will χ² ≤ ε. This would require that ${\widehat{\Sigma }}_1$ contains the free parameter c whose sample estimate happens to be precisely 1.0. The probability of this occurring, when S is an empirical random sample, is zero! As Appendix B shows, the set M₁₂ = M₁ ⋂ M₂ has Lebesgue measure zero in M₁ and thus, when using a random sample, there is zero probability that ${\widehat{\Sigma }}_1$ falls into M₁₂ = M₁ ⋂ M₂.

Roles of Parameter and Moment Structure Nesting

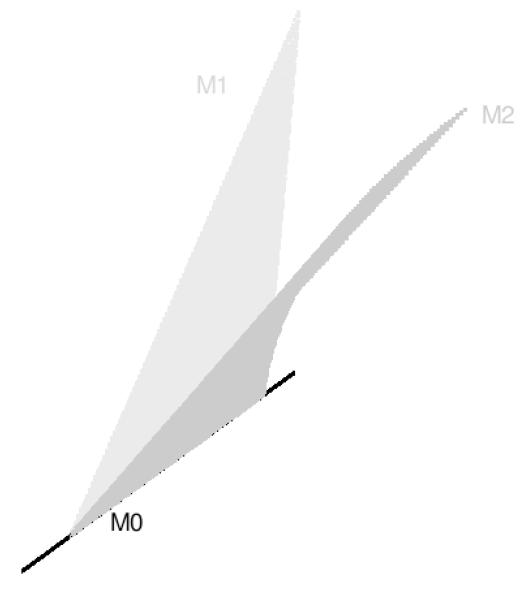
Parameter nesting is usually an obvious feature when comparing models, while moment nesting, the method used in NET, can be difficult to understand since, as a reviewer noted, it is not widely discussed in the SEM literature. We use a simple example that allows a graphical view to illustrate these types of nesting. Consider three restricted regression models M₁, M₂ and M₀ involving just two observable variables X and Y which, for simplicity of exposition, are considered to be centered. (1) M₁ is Y = γX + e_y, where e_y is the residual in the regression with E(Xe_y) = 0, γ, ϕ_xx = E(X²) and ${\psi }_y=E_y\left(e_y^2\right)$ are scalar parameters, and E is the expectation operator. We restrict the regression so that ϕ_xx = ψ_yy. (2) M₂ is X = βY + e_x, where e_x is the residual in the regression with E(Ye_x) = 0, and β, ϕ_yy = E(Y²) and ${\psi }_x=E_x\left(e_x^2\right)$ are scalar parameters. We restrict the regression so that ϕ_yy=ψ_xx. (3) The final model M₀ is X = e_x, with E(Ye_x) = 0.

Model M₀ clearly is parameter nested in M₂, since it can be obtained by setting β = 0. More difficult tasks are to see whether M₁ and M₂ are nested or equivalent and whether M₀ is also nested in M₁. Using the NET procedure outlined above without data, we generate random data of sample size n = 500 from a 2 -variate standard normal distribution with arbitrary correlation .36. Its sample covariance matrix S had variances 1.017 and 1.029 and covariance .374 (to 3 decimals). When M₁ was fitted to S, we obtained ${\widehat{\chi }}_1^2=2.991$ and the fitted covariance matrix ${\widehat{\Sigma }}_1$ with variances 1.081 and .955 and covariance .347. We then fitted M₂ to ${\widehat{\Sigma }}_1$ and obtained ${\widehat{\chi }}_1^2=7.648$. So, according to NET, M₁ is not nested in M₂.

To assess whether M₀ is nested in M₁, we repeated the process of generating a sample moment matrix S. M₀ was then fitted to this S, yielding a fitted ${\widehat{\Sigma }}_1$ and ${\widehat{\chi }}_2^2=52.658$. Fitting M₂ to ${\widehat{\Sigma }}_1$ yielded a perfect fit with ${\widehat{\chi }}_1^2=0.000$. Hence, according to NET, M₀ is nested in M₁. Finally, we repeated the same process but now with respect to M₂, and, as we would require from parameter nesting, NET also concluded that M₀ is nested in M₂.

Covariance algebra can be given to verify these NET results. A picture may be even more informative. Figure 5 shows the two models M₁ and M₂ as two manifolds, and well as the model M₀. Clearly, M₀ is in the intersection of the two manifolds, meaning that it is moment nested in both M₁ and M₂ as NET had shown. The figure also shows that M₁ is not nested in M₂, and similarly, M₂ is not nested in M₁.

Figure 5.

Nesting Relations Among Three Models

In this case, the nesting results are global, as we verified empirically by obtaining identical results from NET analysis regardless of a wide variation of the population covariance matrix used to generate the sample matrix S. We discuss this general issue more fully next.

Local vs Global NET

Although the requirements for NET are described above and in Appendix B, their implications may not be obvious and so we discuss further one key issue: Are NET results guaranteed to hold globally for all conceivable sets of parameters and moment matrices, or do they hold only locally in some small neighborhood of the current randomly drawn data from μ, Σ ? In general, the topological structure (on a p-dimensional Euclidean space) of matrices reproduced by variation on the parameters of the model can be too complex for addressing results of global equivalence and nesting. Thus NET gives results that apply to model equivalence and nesting on a neighborhood of the sample covariance matrix (and sample means where relevant). This requirement is not unusual, since it is, in fact, within such a neighborhood that standard statistical inference and χ² difference testing operates (see e.g., Satorra, 1989).

The issue of nesting and equivalence in the pathological case of set of Lebesgue measure zero has a parallel in the area of model identification. For example, the four variable 2-factor confirmatory factor (CFA) model with factor loadings (λ₁,λ₂,0,0) for factor 1, loadings of (0,0,λ₃,λ₄) for factor 2, factor variances of 1, and factor correlation ϕ₁₂ is identified almost everywhere. But there are special situations where it is not identified, e.g., when ϕ₁₂ = 0. This limitation is far less serious than it might seem. In contrast to traditional theoretical discussions of equivalence and nesting that utilize only sets of population moment matrices and their relations, we make use of the properties of simple random sampling from a continuous population to almost always rule out pathological cases.⁴ We assume that researchers know the neighborhood where testing is to be done, after all, they should be able to at least conceptually specify the population μ, Σ from which the random sample $\stackrel{‒}{X}$, S is drawn. While a pathological sample, e.g., a sample where identification breaks down, is possible, this will occur with probability zero. For example, in the 4-variable CFA model just discussed, if the population ϕ₁₂ ≠ 0, the probability is zero that a random sample S has exactly 0.0 values for all four cross-covariances of variables {1,2} with {3,4}, or values where ${\widehat{\varphi }}_{12}=0.0$. This is not to say that it is impossible to observe a sample from such a pathological set of Lebesgue measure zero, but it will occur with probability zero since we require S to be randomly drawn from the relevant population.

There are indeed situations where global and local results will differ depending on regions of the parameter or data space considered. An example is with three variables X, Y, and Z, and two models M₁ and M₂. The equations for M₁ are Z = X + e, Y = γX + ε, with uncorrelated independent variables with variances ${\sigma }_X^2$, ${\sigma }_e^2$, ${\sigma }_{\epsilon }^2$. M₂ contains a phantom variable F (Rindskopf, 1984) and has equations Z = αX + d, F = βX, Y =βF + δ with uncorrelated independent variables with variances ${\sigma }_X^2$, ${\sigma }_d^2$, ${\sigma }_{\delta }^2$. Is M₁ is nested in M₂ ? Suppose we consider the parameter space under the data restriction σ_xy ≥ 0. This covariance is reproduced by γ in M₁ and by β² in M₂, so the data restriction implies the parameter inequality γ > 0. This inequality can be met. We can set γ = β², 1 = α, ${\sigma }_e^2={\sigma }_d^2$, ${\sigma }_{\epsilon }^2={\sigma }_{\delta }^2$ and model M₁ is nested in M₂ because the free parameter α in M₂ is restricted to 1.0 in M₁. However, if we consider the parameter space where σ_xy < 0, in M₁ we have γ = σ_xy while in M₂ we have the imaginary number $\beta =\sqrt{{\sigma }_{xy}}$ (now the square root of a negative number!). Model M₂ with nonimaginary parameters will not reproduce the population covariances. So we can conclude that (a) with real parameters, the models are not nested; (b) with σ_xy ≥ 0 and real parameters, the models are nested; (c) with σ_xy < 0 and real parameters, the models are not nested; and (d) allowing imaginary parameters, the models are nested. For the typical case of real parameters, the global conclusion is that the models are not nested. The local conclusion depends on the sign of σ_xy and, in a sample, on the sign of its sample equivalent s_xy. Note that even though this example with its inequality constraints contradicts one of the requirements of our method, NET asymptotically will yield the correct local answer (b) or(c), depending on the sign of σ_xy.

Bootstrap Net

Conclusions from NET will represent nesting and equivalence in the neighborhood of the population μ, Σ if the sample size is large enough, e.g., in the example above, if the sign of s_xy is the same as the sign of σ_xy. If there is a question on whether NET might yield different results for different samples, NET can be applied repeatedly to bootstrap resamples from the data (see e.g., Yung & Bentler, 1996). Varying results would imply that conclusions are not invariant across regions of the sample space; we would expect this to occur rarely with standard models.

An Equivalence Example with Non-regular Points

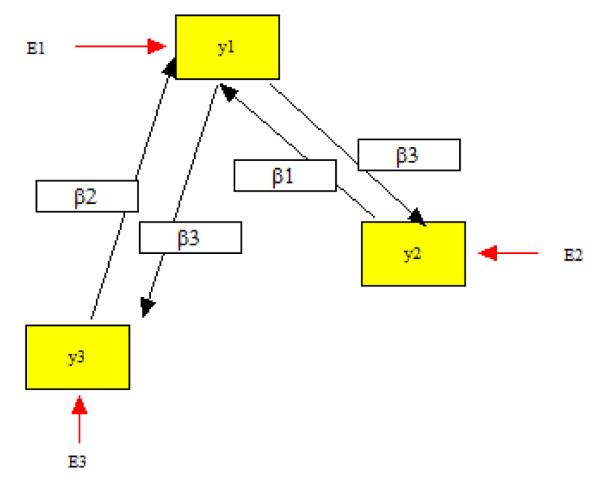
An important question is whether an empirical methodology such as NET can handle models that are evaluated at points close to empirical nonidentification.⁵ This example shows that NET can draw correct conclusions in such a case. We use a nonrecursive model that was analyzed in mathematical detail by Bekker, Merckens and Wansbeek (1994, p. 163, eq. 7.3.1), using the rank of elaborated Jacobian matrices in symbolic form. The model is

$$\begin{array}{cc}\hfill Y_1& ={\beta }_1{Y}_2+{\beta }_2{Y}_3+E_1\hfill \\ \hfill Y_2& ={\beta }_3{Y}_1+E_2,\hfill \\ \hfill Y_3& ={\beta }_3{Y}_1+E_3\hfill \end{array}$$

where the disturbances E₁, E₂, E₃ are uncorrelated with zero expectations and variances ${\sigma }_{E1}^2$, ${\sigma }_{E2}^2$, ${\sigma }_{E3}^2$. A path diagram is given in Figure 6. The model has six parameters and zero df. Bekker et al. show that although this model is identified in general, at the point {β₁ = β₂ = 0} the Jacobian is singular and the parameters are not identified. We use this knowledge to generate a multivariate normal population with {β₁ = β₂ = 0, β₃ = 0.5, ${\sigma }_{E1}^2={\sigma }_{E2}^2={\sigma }_{E3}^2=1$}, and draw a sample of N=300 from it using our method (2a) to deal with absence of a sample covariance matrix, namely, we choose parameter values and then sample from the corresponding model (see also Appendix A).⁶ This sample is used to evaluate the equivalence of two submodels A and B, where Model A is defined by β₂ = 0 and β₁, β₃, ${\sigma }_{E1}^2$, ${\sigma }_{E2}^2$, ${\sigma }_{E3}^2$ as free parameters, and Model B is defined by β₁ = 0 and β₂, β₃, ${\sigma }_{E1}^2$, ${\sigma }_{E2}^2$, ${\sigma }_{E3}^2$ free. Note that it is not at all obvious from Figure 6 that these are equivalent models, although Bekker et al. prove that they are locally equivalent. The question is whether the results from NET agree with the technical mathematical proof, even when sampling from a point that is not regular for this model with zero df (i.e., a point where the model is not identified).

Figure 6.

A Nonrecursive Model

The sample covariance matrix we obtained is given by

$$\left[\begin{array}{ccc}\hfill .9652\hfill & \hfill \hfill & \hfill \hfill \\ \hfill .5269\hfill & \hfill 1.7761\hfill & \hfill \hfill \\ \hfill .4659\hfill & \hfill .2992\hfill & \hfill 1.3097\hfill \end{array}\right].$$

In Step 1 of NET, Model A was fit to this matrix with ML, yielding the goodness-of-fit ${\widehat{\chi }}_{1\left(A\right)}^2=.374$. The parameter estimates {${\widehat{\beta }}_1=.040$, ${\widehat{\beta }}_3=.483$, ${\widehat{\sigma }}_{E1}^2=.926$, ${\widehat{\sigma }}_{E2}^2=1.492$, ${\widehat{\sigma }}_{E3}^2=1.085$} were used to obtain ${\widehat{\Sigma }}_A$, which was then used in Step 2 of NET as the input covariance matrix to be analyzed by Model B. Model B yielded ${\widehat{\chi }}_{1\left(B\right)}^2=0.00000$. Applying Steps 3 and 4 of NET, the difference in d = 1−1 = 0 and ${\widehat{\chi }}_{1\left(B\right)}^2⟨\epsilon$, so Models A and B are locally equivalent. This example is a small model but it illustrates the type of complexities that may arise in practice. Even when starting with a non-regular population, NET yields the same conclusions as the elaborate mathematics of Bekker et al.

Discussion

In principle, the approach outlined here for evaluating model nesting and equivalence applies to a wide variety of related modeling situations such as multiple group models or higher moment structures in SEM, log-linear models in categorical data situations, and so on. Since incremental fit indices are almost universally reported in SEM, one of the simplest yet most important areas of application is that of verifying the nestedness of a baseline or null model for the computation of incremental fit indices. Although Bentler and Bonett (1980) had emphasized that an appropriate null model for such indices must be a nested model relative to the substantive model of interest, they also noted that “there are cases when it is not a simple matter to verify that M₀ [the null model] is a special case of M_k, M_l [substantive models], or M_s [the saturated model]. Nonetheless, this is a fundamental requirement of M₀” (p. 596). Such a difficulty may be inevitable when the researcher uses prior results (Sobel & Bohrnstedt, 1985), an equal-correlation baseline model (Rigdon, 1998), or some untested ideas to specify the null model. The only standard default used in SEM programs that we know about is the uncorrelated variables model as the baseline model, yet, as Widaman and Thompson (2003) show, this can be an inappropriate model choice when it is not nested in the model of interest. As illustrated in our example, the methodology provided here can be easily implemented to routinely evaluate nesting for incremental fit indices, especially when the null model is provided by a program default.

It may seem that missing data could provide difficulties for NET, but any methodology that permits a stochastically derived empirical covariance matrix S (and a vector of means $\stackrel{‒}{X}$ when needed) can be used in the step 1 of NET. For example, the two-stage maximum likelihood method described by Yuan and Bentler (2000), Savalei and Bentler (2009), Cai (2008), and Yuan and Lu (2008) can be used with the proposed NET framework. In the two-stage approach, a saturated model (sometimes called the EM means and covariance matrix) is first estimated. These saturated means and covariances are then taken as the sample means and covariances to be modeled in the subsequent step. For the NET procedure, the saturated moments are taken as the data to be analyzed in Step 1 above, and model M₁ is fit to it. Then Steps 2-4 are completed as usual.

A useful application is to evaluate nestedness to determine whether a χ² difference test is appropriate when nesting is not obvious. For example, consider the 4-variable CFA model M₂ with two factors F1 and F2. Suppose the F1 loadings are (1,λ₂,0,0) and the F2 loadings are (0,0,1,λ₄), with λ_i, ${\sigma }_{F1}^2$, ${\sigma }_{F2}^2$, and covariance ϕ₁₂ as free parameters. Compare this to the 1-factor model M₁ with free loadings (λ₁,λ₂,λ₃,λ₄) and ${\sigma }_{F1}^2=1$. The 1-factor model can not be obtained by simply fixing some free parameters in the 2-factor model, i.e., the models are not parameter-nested. They are covariance-matrix nested; after all, M₁ can be obtained from a new model $M_2^{\ast }$ by parameter nesting, where $M_2^{\ast }$ is the equivalent model to M₂ obtained by freeing its loadings of 1 and fixing the factor variances at 1. Setting ϕ₁₂ =1 in $M_2^{\ast }$ leads to M₁. NET would prove this directly by fitting M₁ to a random S, and generating ${\widehat{\Sigma }}_1$. A fit of M₂ to ${\widehat{\Sigma }}_1$ would yield $\widehat{F}⟨\epsilon$.⁷

NET can also provide a theoretical justification of the typical method for determining whether a given model M_k is a saturated model. It is well-known that a saturated model is one with 0 df that perfectly reproduces any sample covariance matrix S. Hence, running M_k and getting a perfect fit with 0 df implies saturation. NET justifies this conclusion, since all saturated models are equivalent, and a well-known saturated model model M_s is the one whose free parameters are the components of the moment vector. In the language of NET, M_k will be saturated if M_s is nested or equivalent to M_k. Step 1 of NET is not needed, as the fitted moment matrix is the same as S ; Step 2 fits M_k to S, concluding nesting (i.e., saturation) or not as in standard NET practice.

Traditional approaches to nesting and equivalence do not use data at all; they are concerned with algebraic and set-theoretic relations holding among classes of population means and covariance matrices. Our approach is unique in that nesting and equivalence are evaluated on a random sample of data from the population. We substitute probability theory for mathematical certainty. As a result, the NET methodology theoretically can fail when a truly bizarre sample is chosen. However, the theorem given in Appendix B verifies that this will occur with a probability approaching zero. If there is suspicion about the results, simulated random samples from the population or bootstrap resamples from a given sample can be drawn and the NET methodology applied as a verification. Although it may be tempting to create an artificial example where the NET methodology breaks down, it should be remembered that NET cannot be used on an artificial covariance matrix. It should only be applied to a sample covariance matrix.

An immediate question, then, is how to apply the proposed NET procedure when there are no data at hand, i.e., when no sample covariance matrix S (and means, when relevant) is available for Step 1 of our method. The solution is to generate a randomly simulated sample covariance matrix S or a model-implied covariance matrix ${\widehat{\Sigma }}_1$. This can be done in various ways using simulation and random data generation as was discussed and illustrated earlier and in Appendix A. While our NET procedure suggests sampling from the true population Σ, we have found that drawing a random sample near Σ works as well. Surprisingly, and though we do not recommend it, we have found that it often works when data is randomly drawn from a possibly widely different population, such as one with covariance matrix Σ = I. Clearly, further research is needed to understand the boundaries of NET.

An important theoretical point, and one that implies further research, is the local nature of our NET procedure. As is made precise in Appendix B, by “local” we mean that we restrict attention to moment matrices in a neighborhood of a given moment matrix σ₀ that has non-null intersection with model M₁. NET provides results that are valid in a local sense, based on assumptions parallel to those that underlie the usual χ² difference test. Of course, we concentrate on a region of the parameter space where it is likely that the true population value lies, which justifies taking a sample covariance matrix in this region. Even though the results hold locally, depending on the class of models, the topological local structure is often the same as the global one, in which case local nesting or equivalence implies the global one. Yet this is not always true, as our example with an inequality constraint demonstrates. It is a matter of further research to investigate the topological local versus global nature of moment spaces for different families of SEM models, which will have implications for model identification as well as nesting and equivalence. Even abstract studies on identification and equivalent models have focused primarily on local identification and only occasionally on global identification (Bekker et al., 1994, p. 19).

Throughout this paper, we emphasized the importance of using random matrices to ensure that NET results apply almost everywhere on a neighborhood of a chosen point. Points of the parameter space that are NET non-regular (in the sense that nesting or equivalence relations differ from what applies almost everywhere in its neighborhood) will thus not be captured, since such points arise with probability zero when the input to Step 1 is indeed a true random matrix. This is similar as in the 2-factor, 2-indicator model that is identified almost everywhere except on the set of points where the correlation between factors is exactly zero. We now note that NET can indeed also be used to address results of nesting or equivalence at a particular point, such as the non-regular points that may exist in the parameter space. However, when we choose a specific moment matrix in Step 1, we have to be clear that NET conclusions then no longer apply almost everywhere in the neighborhood of the chosen matrix. In some instances, this non-standard use of NET may provide interesting information.

With regard to model equivalence, we should note that our goals have been modest. We proposed a way to evaluate whether any two models that a researcher nominates might be equivalent moment structure models. Making such a comparison is critical to ruling out potentially competing explanations of a phenomenon (MacCallum, Wegener, Uchino, & Fabrigar, 1993; Stelzl, 1986). However, our methods do not address the more complicated problem of starting with only one model and generating an entire class of models that might be equivalent to a given model. Rules for specifying some equivalent models have been developing for over two decades since Stelzl (1986) first pointed out that alternative causal hypotheses could yield identical indices of model fit (e.g., Lee & Hershberger, 1990; Luijben, 1991; Hershberger, 1994, 2006). These rules can be complex and difficult to implement with complete accuracy, so our NET procedure can make a contribution by providing a method for evaluating models that are considered to be candidates for equivalence through use of these rules. Since there may be a lot of equivalent models (Raykov & Marcoulides, 2001, 2007; Markus, 2002), a computer algebra surely will need to be incorporated into SEM programs to help the researcher generate and evaluate such candidates. Our methods also do not address the complicated issue of whether models might be equivalent in the broader sense of observational equivalence, implying that their generating probability distributions are equivalent. This topic may require studying individual case scores and residuals (e.g., Raykov & Penev, 2001).

Appendix A

NET requires convergence in model fit of the algorithms used. This may be a limitation in some cases, where the model is very complex and/or large deviations of sample moments from the hypothesized model arise. Such a problem frequently occurs, for example, with non-recursive structural equation models. A practical solution is to tighten up the neighborhood where NET applies. One approach to doing this is to assure that the specified population moment vector σ₀ is in M₁ and the analyzed moment vector s is close enough to σ₀. This can be done by using methods (2a) or (2b) described in the text. In both of these methods, enlarging the sample size will tighten the neighborhood around σ₀ as much as is needed for reaching convergence in computations required for the NET procedure. At some large enough sample size, the models will be locally identified, the algorithm will converge, and NET will give a Yes/No answer regarding nesting and equivalence. If doubts remain, alternative sample input covariance matrices based on various sample sizes can be studied to determine if they yield identical conclusions.

Appendix B

Let σ ≡ [μ’,vech(Σ)’]’ and consider two moment structural models M₁ :σ = σ₁(θ₁), θ₁ ∈ Θ₁ and M₂ :σ = σ₂(θ₂), θ₂ ∈ Θ₂ defined on the space of unconstrained moments C = {σ ∈ R^p |σ ∈ Θ}, where Θ₁ ⊂ R^q₁, Θ₂ ⊂ R^p are open sets, and σ₁(.) and σ₂(.) are continuously differentiable functions.⁸ Consider the subsets C₁ and C₂ of C associated to the two models, and their intersection C₁₂ = C₁ ⋂ C₂. It holds that (see, e.g., Satorra, 1989)

Result 1. For any σ₀ ∈C_j locally⁹ around σ₀ there is a differentiable vector-valued function h_j of full row rank where C_j = {σ ∈ R^p | h_j(σ) = 0}.

Assume that s is a sample realization from an absolutely continuous distribution in the set C .¹⁰ Consider the fit of M₁ to s and let ${\widehat{\sigma }}_1$ be the fitted moment vector. Consider the fit of M₂ to ${\widehat{\sigma }}_1$ and let F₁₂ be the minimum of the fitting function. Assume that the Jacobians of h₁ and of h = (h₁’, h₂’)’ are regular at ${\widehat{\sigma }}_1$. Under this set-up, we have the following theorem.

Theorem. Let s be a sample moment vector and F₁₂ the associated fit value of Step 3 of NET. Then locally at ${\widehat{\sigma }}_1$

1. F₁₂ = 0 implies with probability one that M₁ is nested in M₂

2. F₁₂ > 0 implies with probability one that M₁ is not nested in M₂.

Proof: Current assumptions and Result 1 imply that C₁ , C₂ and C₁₂ are manifolds, with the dimension of C₁₂ smaller than or equal to the dimensions of C₁ . If the dimension of C₁₂ is strictly smaller than the dimension of C₁ then Sard’s Theorem¹¹ implies that C₁₂ is of Lebesgue measure zero in C₁ and thus there is probability zero of ${\widehat{\sigma }}_1\in C_{12}$, hence of F₁₂ = 0 .¹² Note that the distribution of ${\widehat{\sigma }}_1$ is absolutely continuous in C₁ with nonsingular covariance matrix, since the Jacobian of h₁ is of full row rank. So, if we observe F₁₂ = 0 , with probability one the dimension ofC₁₂ equals the dimension of C₁ , and thus the two models are nested. Clearly, if M₁ is locally nested in M₂ , necessarily F₁₂ = 0 ; so, F₁₂ > 0 implies that M₁ is not locally nested in M₂ . Q.E.D.

This theorem can be illustrated with a graph such as the one in Figure B1. The graph shows model M₂ of dimension 2, and two models M₁ (models M_1a and M_1b) both of dimension 1. With regard to the intersection M₁₂ of the two models, we have the following situation: when M₁ = M_1a , M₁₂ is of dimension one less than M₁ ( M₁₂ is a point); when M₁ = M_1b , M₁₂ is of dimension equal to the dimension of M₁ ( M₁₂ equals M₁). Thus, M₁ = M_1a is a case of M₁ non-nested in M₂ , and M₁ = M_1b is a case of M₁ nested in M₂ . Note that a sample moment s would be standing in the tridimensional space with probability one deviating from the manifolds. Step 1 of NET projects s into M₁ obtaining ${\widehat{\sigma }}_1$; clearly, in the case of M₁ = M_1a , the projected point ${\widehat{\sigma }}_1$ has probability zero of standing also in M₂ (since the intersection of M₁₂ is a point), and so F₁₂ > ò); while in the case of M₁ = M_1b , ${\widehat{\sigma }}_1$ also would be standing in M₂ , and so F₁₂ < ò .

Figure B1.

Model M₂ and Two Different Nested Models M_1a and M_1b

This result suggests the procedure of the Nesting and Equivalence Test given in the text, where F₁₂ is designated as $\widehat{F}$, concluding that M₁ < M₂ when F₁₂ < ò , for ò a small constant; model equivalence when in addition to F₁₂ < ò , the two models have the same number of degrees of freedom ( d = 0 ) ; or non-equivalence and non- nesting of M₁ in M₂ when F₁₂ > ò.

Appendix C

A NET analysis can be undertaken using the R function net1.R given below. This makes use of the R interface REQS (Mair, Wu, & Bentler, in press) between R (Development Core Team, 2009) and EQS (Bentler, 2006)¹³ that contains functions to read EQS script files and import the results into R, call EQS script files from R, run EQS script files from R, and import the results after computation.

An illustration is the NET evaluation of models A and B of Figure 3. Models have to be specified in *.eqs files along with the number of variables p . The function call net(“MA.eqs”,“MB.eqs”, p= 5) implies that “MA.eqs” (any name with extension .eqs) is the EQS file for M₁ and “MB.eqs“ is the EQS file for M₂ , and p = 5 . Based on the appropriate *.eqs input files, R produces the result

[1] “M1 is nested to M2”
$FitToModel1
[1] 80.442 3.000
$FitToModel2
[1] 0 1

This reports the conclusion first, here, that model A is nested in model B, or more generally, whether or not the model in the first *.eqs file (MA.eqs) is nested in the model of the second *.eqs file (MB.eqs). The numerical output then gives the χ² and df for the fit of M₁ to a randomly generated s , and finally provides the results of the fit of M₂ to the fitted matrix ${\widehat{\sigma }}_1$. In this case, ${\widehat{F}}_{12}=0$ with 1 df.

The analysis implemented in net1.r does not require a data matrix. It generates simulated data from a spherical normal distribution. An R user can easily modify this function to accommodate other simulation options as described in the text.

Function net1.R for NET Computations in R and EQS
library(“gtools”)
library(“REQS”)
library(“mvtnorm”)
net= function(model1,model2, p){
setwd(“/A/UCLA2008research/NestingSEM/Revisions/Revision_II/REQSrunsNET/RNET”)
#----------------------- begin NET -------------------------------
### machine accuracy parameter
epsilon= .00001
n <- 500                #total sample size
Sigma1 <- matrix(0, p, p) #VC matrix component 1 (3 variables)
diag(Sigma1) <- 1
X1 <- rmvnorm(n, mean = rep(0, p), sigma = Sigma1)
S1 = cov(X1)
write.table(S1, file = “factorcov.dat”, col.names = FALSE, row.names = FALSE)
###EQS under M1
res.F1 <- run.eqs(EQSpgm = “/A/MACEQS/maceqs”, EQSmodel = model1, serial = “1234”)
Fit1 <- res.F1$fit.indices[c(“CHI”),]; DF1=res.F1$model.info[5,]
 ‘Fit and DF of S under M1’
FITM1= c(round(Fit1,3),round(DF1))
FITM1
FS1 = res.F1$sigma.hat
###EQS under M2
write.table(FS1, file = “factorcov.dat“, col.names = FALSE, row.names = FALSE)
### un EQS under M1
res.F1 <- run.eqs(EQSpgm = “/A/MACEQS/maceqs”, EQSmodel = model2, serial = “1234”)
### end EQS under M2
Fit1 <- res.F1$fit.indices[c(“CHI”),]; DF1=res.F1$model.info[5,]
 ‘Fit and DF of S1 under M2’
FITM2= c(round(Fit1,3),round(DF1))
FITM2
if (Fit1 < epsilon){ print(“M1 is nested into M2”)}
if (Fit1 > epsilon){ print(“M1 is NOT nested into M2”)}
list(FitToModel1 = FITM1 ,FitToModel2= FITM2)
#-----------------------end NET -------------------------------
}