From genes to neural tube defects (NTDs): insights from multiscale computational modeling

Abstract

The morphogenetic movements, and the embryonic phenotypes they ultimately produce, are the consequence of a series of events that involve signaling pathways, cytoskeletal components, and cell- and tissue-level mechanical interactions. In order to better understand how these events work together in the context of amphibian neurulation, an existing multiscale computational model was augmented. Geometric data for this finite element-based mechanical model were obtained from 3D surface reconstructions of live axolotl embryos and serial sections of fixed specimens. Tissue mechanical properties were modeled using cell-based constitutive equations that include internal force generation and cell rearrangement, and equation parameters were adjusted manually to reflect biochemical changes including alterations in Shroom or the planar-cell-polarity pathway. The model indicates that neural tube defects can arise when convergent extension of the neural plate is reduced by as little as 20%, when it is eliminated on one side of the embryo, when neural ridge elevation is disrupted, when tension in the non-neural ectoderm is increased, or when the ectoderm thickness is increased. Where comparable conditions could be induced in Xenopus embryos, good agreement was found, an important step in model validation. The model reveals the neurulating embryo to be a finely tuned biomechanical system.

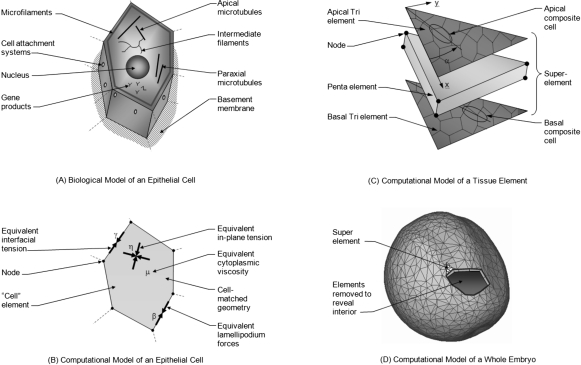
During early embryo development, cells and tissues must undergo specific changes of shape in order to form organs and other critical structures (Pilot and Lecuit, 2005). The molecular pathways responsible for these morphogenetic movements are encoded in the genome but they can be affected by extrinsic environmental and nutritional conditions (Boyles et al., 2005; Colas and Schoenwolf, 2001; Detrait et al., 2005; Kappen, 2005; Kibar et al., 2007; Koren, 1999). These pathways govern the assembly of the cytoskeleton and other force-generating systems [Fig. 1A], as well as the strengths of their actions (Keller, 2004; Patwari and Lee, 2008). The spatially distributed forces they ultimately produce at the cellular and tissue levels, together with mechanical interactions between adjacent tissues, then determine the morphogenetic movements that occur (Chen and Brodland, 2008). Irregularities in these movements can give rise to serious developmental anomalies, which in humans, include cranio-facial, cardiac and neural tube defects (NTDs) (Detrait et al., 2005; Moore and Persaud, 1998).

Figure 1. The multiscale computational model.

(A) Shown are primary components associated directly or indirectly with force generation. (B) In the corresponding cell-matched computational model, equivalent forces are calculated using equivalent joint loads and other engineering principles. Thousands of cell-level simulations involving tens to hundreds of cells such as the one shown were used to investigate the mechanics of embryonic epithelia. Ultimately, these studies provided sufficient understanding that cell-level constitutive equations relating stress, strain, cellular fabric, lamellipodium action and other relevant factors could be constructed. (C) These equations can be incorporated into “superelements” that can accurately represent the mechanics of a triangular piece of tissue. To model a whole embryo [Fig. 1D], its surface epithelium is broken into triangular regions consisting of several tens of cells. Each of these regions is represented by a superelement in which tri elements along the apical and basal surfaces of the monolayer tissue replicate the active forces produced by its cells. The angle α is measured as shown from an arbitrary reference edge. The penta element represents the passive forces generated by the cytoplasm and its contents (Chen and Brodland, 2008). (D) The initial geometry of the whole-embryo model was built by extruding triangles from a three-dimensional surface reconstruction of a live embryo, toward the centroid of the reconstruction a distance corresponding to the thickness of the ectoderm (surface layer) as seen in serial section sets. See text for details.

The aim of the present study is to use a multiscale computational model to investigate the mechanics of neural plate morphogenesis, including how changes to the properties of individual tissues affects the phenotypes produced. In the present study, a conceptual model is used to systematize the forces generated by the cytoskeleton and other subcellular structures in the cell, a cell-based computational model then relates these forces to cell and tissue behavior, and finally a tissue-based model predicts how these tissues would interact, produce specific morphogenetic movements, and ultimately, give rise to specific phenotypes. The present work builds on previous studies, which showed that computational modeling can be used to relate factors at one length scale to biological behavior at another and that suitable cell- and tissue-level models can predict morphogenetic movements (Brodland, 2004; Brodland et al., 2006; Chen and Brodland, 2008; Conte et al., 2008, 2009; Davidson et al., 1995; Jacobson and Gordon, 1976; Ramasubramanian et al., 2006; Taber, 2006).

The modeling of morphogenetic movements in embryos is challenging because interactions of multiple types spanning a range of length scales must be brought together into a unified framework. In addition, the requisite quantitative geometric and material property data are often not available, and it is not always clear, which tissues and other structures need to be included in the model.

The morphogenetic movements of neurulation (Fig. 2), a process during which the neural plate becomes a closed tube, have received much attention because they are similar in most vertebrates, they occur on the outside surface of the embryo, where they are relatively easy to observe, and irregularities in these movements give rise to NTDs. These movements, specifically the ones that occur in amphibians, will be the focus of the present work. Neurulation in vertebrates typically involves highly coordinated movements of the neural plate, the surrounding ectoderm and the subjacent notochord and mesoderm. Within the neural plate, cells move, change shape, and divide, resulting in the elevation, medial migration, and fusion of the neural folds. Recent evidence suggests that neural fold elevation, movement, and fusion are distinct morphogenetic events controlled independently. Neural fold elevation requires the actin-binding protein Shroom (Hagens et al., 2006; Hildebrand and Soriano, 1999; Martin, 2004). Shroom is responsible for cytoskeletal rearrangements that polarize cells resulting in radial elongation and eventual bending of the neural plate at hinge points (Hildebrand, 2005). Following neural fold elevation one of the prominent cell rearrangements in the neural plate is convergent extension, the narrowing and elongation of a field of cells (Keller et al., 2000). In vertebrates, neural plate convergent-extension requires polarized cell movements (Elul and Keller, 2000; Shih and Keller, 1992) controlled via the planar-cell-polarity (PCP) cascade (Kinoshita et al., 2008; Tada and Smith, 2000; Wallingford et al., 2000). The PCP cascade is essential for the medial movement and consequently the closure of neural folds late in neurulation (Wallingford and Harland, 2002). Cells at the midline of the neural plate do not undergo convergent extension and during neural tube morphogenesis this tissue extends in conjunction with the closely adherent underlying notochord (Ezin et al., 2003, 2006). Recent evidence suggests that the mesoderm is a primary force-producing tissue during neurulation (Zhou et al., 2009). However, Xenopus explants lacking notochords can converge and extend (Malacinski and Youn, 1981), indicating that neural morphogenesis likely stems from morphogenetic movements occurring in both the mesoderm and overlying neural plate.

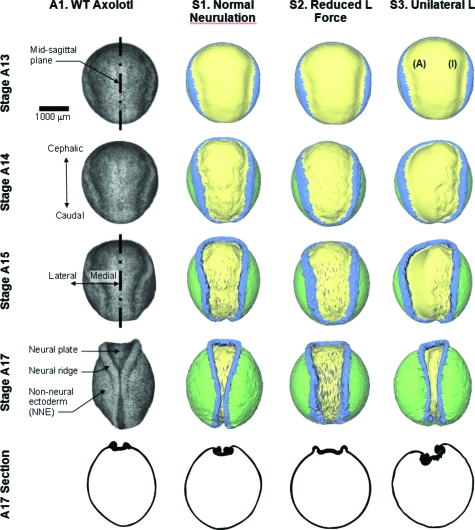
Figure 2. Comparison of model output with an axolotl embryo.

Column A1 shows photographs taken from a single live axolotl embryo, and a stage 17 cross-section from a different embryo. Stages in the figure are labeled with the letter A to denote them as axolotl stage numbers. Column S1 shows a simulation of normal neurulation. For the simulation shown in column S2, the strength of the lamellipodium action L was reduced to 80% of its normal value. Not only are the morphogenetic movements delayed but the tube does not close. When L forces are turned off on one side of the embryo (the side labeled with an I, for inactive, as opposed to the active side A), an asymmetric phenotype results (column S3), and closure fails. See Supplementary Material, for corresponding videos.

Although modern biological methods have revealed much about the genes, biochemistry and cytoskeletal components involved in neurulation, they are unable to address some of its mechanical aspects. For example, if all of the forces implicated by these biological experiments are put into a single mechanical model, are they sufficient to produce neural tube closure? The answer to this question is not obvious since the tissues involved have nonlinear mechanical properties, force interactions occur simultaneously at the cell, tissue and whole embryo-level, and relatively complex three-dimensional geometries are involved. A recent computational model answered this question in the affirmative (Chen and Brodland, 2008) but other important questions remain: to what extent do the forces generated by convergent extension contribute to neural tube formation? How much must these forces be reduced to produce a NTD? Can experiments in which Shroom is knocked down be explained entirely by known cytoskeletal changes or must adjacent tissues be affected as well, perhaps through other signaling pathways?

Early two-dimensional models provided a number of insights into the mechanics of neurulation (Brodland and Clausi, 1995; Clausi and Brodland, 1993; Dunnett et al., 1991; Jacobson and Gordon, 1976; Odell et al., 1981) but attempts to extend these models to three-dimensions so that the full range of mechanical interactions could be included, were fraught with difficulty. Eventually, cell-level finite element studies [Fig. 1B] showed that embryonic epithelia are more labile in-plane than was previously realized and that only when specialized constitutive equations are used to model them (Brodland et al., 2006) could realistic 3D computational models be built (Chen and Brodland, 2008). These studies showed that multiscale modeling was crucial to understanding the mechanics of morphogenesis and that suitable mathematical descriptions (constitutive equations) for these cellular materials could be used to carry the knowledge gained through cell-level models to tissue- and whole embryo-level models.

The present study builds on a multiscale 3D finite element model (Chen and Brodland, 2008) used recently to investigate neurulation in the axolotl (Ambystoma mexicanum). Axolotls were used because although neurulation has been studied in a wide range of animal systems—including amphibians (Burnside and Jacobson, 1968; Jacobson, 1962; Lee et al., 2007; Pohl and Knöchel, 2001; Rolo et al., 2009; Veldhuis et al., 2005; Wallingford et al., 2000; Wallingford and Harland, 2002; Wiebe and Brodland, 2005; Zhou et al., 2009), chick (Colas and Schoenwolf, 2001), quail (Zamir et al., 2005), mouse (Copp, 2005), and zebrafish (Hong and Brewster, 2006)—the full range of geometric and mechanical data needed for the model are available only in axolotl. As necessary, axolotl data are supplemented by the data from Xenopus laevis literature under the assumption that the mechanical properties of biological tissues are conserved across species. Where possible, in silico predictions were tested in vivo using Xenopus.

THE MULTISCALE MODEL

Model of a single cell

A wide variety of structural components are associated with embryonic cells. In the case of epithelia [Fig. 1A], these include a basement membrane and specialized cell-cell attachment sites. Components that can drive cell and tissue reshaping include microfilaments, microtubules, and cell membrane with its associated proteins. We have argued elsewhere that the forces generated by these components can be resolved into equivalent forces along the edges of the cells (Chen and Brodland, 2000, 2009). In the case of forces associated with cortical actin, membrane contraction and cell-cell adhesions, the equivalent force calculations are mathematically exact, whereas for paraxial and apical microtubules, they are approximate. The net equivalent edge forces (interfacial tensions) that they generate [Fig. 1B] can be cell- or edge-specific. When a lamellipodium acts along an edge, the net force there is assumed to be increased to a value β, typically twice as large as γ (Brodland and Veldhuis, 2006).

The values of the equivalent driving forces γ and β depend on the cytoskeletal components present, their arrangement within the cell and the strengths of the forces they generate. Interestingly, the interfacial tensions γ are reduced by the action of cell-cell adhesions (Brodland, 2002; Lecuit and Lenne, 2007). Extracellular matrix (ECM) was assumed to move with the cells and tissues and to not provide a meaningful contribution to the forces acting along the cell edges (Zhou et al., 2009). If gene expression affects any of these subcellular structural components, then the values of the associated driving forces will change. In the case of cytoskeletal components present at only one surface of the cell, such as circumferential microfilament bundles at the apical ends of cells, their contributions can be apportioned to equivalent forces specific to the apical and basal surfaces of the cell, as appropriate (Chen and Brodland, 2009). A consequence of an asymmetrical distribution is that it can give rise to bending of the cell sheet, a factor important in the present study.

Previous epithelium models have focused on in-plane forces arising from tensions γ along the cell-cell interfaces. Recent studies (Ma et al., 2009), however, have revealed that tensions along the apical and basal surfaces provide another significant source of in-plane tension. Because the cells in the tissues of interest here remain nearly isotropic and their density does not change substantially during neurulation, the net in-plane force they generate is essentially isotropic and sensibly constant. At the strain rates common to morphogenetic movements, one would expect the total apical and basal tensions η [Fig. 1B] to behave similarly and, thus, not to be distinguishable from γ-generated forces. Since the material parameters γ used in the present study were calibrated using experiments on epithelia in which these apical and basal forces were presumably acting in concert with γ forces, the simulations can be interpreted as including these forces even though, for simplicity, from this point onwards the in-plane forces are reported as though they arise exclusively from γ forces.

In addition, we assume that the cells have a nonzero equivalent viscosity μ that arises from the mechanical properties of the cell cytoplasm. Unlike the “active” forces discussed in the previous paragraphs, these are considered “passive” and, by themselves, they would not be able to drive morphogenetic movements. At the strain rates typical of morphogenetic movements, forces caused by deformation of the cytosol, organelles, intermediate filament network, basement membrane, and other components can be represented well by an equivalent viscosity (Brodland et al., 2006).

Model of a sheet of cells

Next, to determine how the mechanical characteristics of cell sheets derive from the properties of their cells, a series of studies were carried out using a cell-based computational model (Brodland et al., 2006; Brodland and Veldhuis, 2006). In those studies, synthetic (model) cell sheets were assigned various combinations of input properties and subjected to various loads and deformations. Edge tensions γ and β were resolved into equivalent nodal loads and finite element methods were used to determine mathematically correct damping matrices for each cell-based on μ and the current geometry of the cell. Proper calculation of these viscous forces is necessary if the temporal scale of the simulation is to be meaningful.

The thousands of individual simulations run as part of those studies led to a detailed understanding of how the properties of an embryonic epithelium are related to cell-level properties such as γ and μ. The mechanical properties of an epithelium were found to depend on the average in-plane area of its cells (or conversely their density) and, if its cells are anisotropic, the aspect ratio of the cells and the average direction of their long axes. Ultimately, these relationships were distilled mathematically into constitutive equations (Brodland et al., 2006) that relate the directional tensions and deformations in an epithelium to its driving forces γ and β and viscosity μ, and to its cellular fabric, as described by average (composite) cell density ζ aspect ratio κ and orientation α. Constitutive equations of this kind are crucial to construction of a 3D whole embryo model because noncontinuum effects arising from the cellular nature of its tissues can be captured but one can avoid the excessive run times that would be associated with modeling each cell. The simulations also showed that oriented lamellipodia generate an equivalent tension, called an “L force,” at a certain level in these equations. The contribution they make to the forces in a particular tissue at a given time, although, depends on a number of factors such as the strain rate in that tissue and the equations replicate these effects. The equations provide an advanced material characterization of the ectoderm and its associated tissues, and they allow specific tissues and their subregions [Fig. 1C] to be described at any given time with parameters (such as γ, L, and μ) estimated from experiments.

Numerically, the active forces in the constitutive equations are implemented through apical and basal triangular (tri) elements (Chen and Brodland, 2008) so that they can be asymmetrically apportioned and used to generate both in-plane tensions and bending moments. These tri elements sandwich a volumetric pentahedral (penta) element that is assigned viscosity μ and that models the mechanical response of the cytoplasm of the several tens of cells it contains.

Model of a whole embryo

The starting configuration for the whole-embryo model [Fig. 1D] was derived from a three-dimensional surface reconstruction of a live, late stage 13 (Bordzilovskaya et al., 1989) axolotl embryo. The reconstruction consisted of 1282 surface points and 2559 triangles and was made from images collected from 63 viewing angles (Bootsma and Brodland, 2005). To generate a surface tissue layer, these triangles were extruded h₀=50μm toward the centroid of the reconstructed volume. This was nominally the thickness of the surface epithelium, as determined from serial sections but the layer was intended to embody the mechanical properties of the surface epithelium, its basement membrane and its mechanically significant subjacent tissues, including the notochord and mesoderm.

As these surface triangles were extruded, they generated volumes of pentahedral shape, each of which was represented by a single superelement [Fig. 1C]. The superelements were assigned to one of three tissue types—neural plate (NP, shown in yellow in Fig. 2), neural ridge (NR, in blue) and non-neural ectoderm (NNE, in green)—based on their locations. Tissue- and region-specific mechanical parameters were then assigned to each superelement (Chen and Brodland, 2008) using code that read a master database of cellular fabric and mechanical property data and used interpolation algorithms to assign appropriate starting values to each superelement based on its tissue type and location. Depending on the biological state of specific tissues, such as the neural ridges, active properties were adjusted or apportioned differently between the apical and basal surfaces. The details of this process are given in the sections that describe the simulation cases.

The volume of each pentahedral element was assumed to remain constant, as was the total volume of the interior cells and fluid that the shell-like surface of superelements surrounds. Both constraint types were implemented numerically using Lagrange side conditions. Because the embryo was assumed to be neutrally buoyant, no external traction forces were applied. However, to prevent arbitrary free body motions, three suitable points in the model were selected and fully or partially constrained, as appropriate (Chen and Brodland, 2008).

The simulation runs by taking a series of small time increments of size Δt. Within each increment, it calculates the forces generated by active components in both of the tri elements of each superelement, and it vectorially adds together their contributions at each node to produce a set of net nodal forces f (Belytschko et al., 2000; Zienkiewicz and Taylor, 2005). It then calculates damping matrices for each penta element and assembles these into a global damping matrix C. Next, it solves the matrix equation

$$\frac{1}{\Delta t}\mathbf{C}\mathbf{\Delta }\mathbf{u}=\mathbf{f}$$ (1)

to determine the vector of incremental displacements Δu that occur during the interval Δt. Finally, it updates the geometry of the embryo and the fabric in each of its tri elements, and the process is repeated until sufficient simulation time has elapsed. In this way, the simulation determines the driving forces present at each time step and the incremental displacements that they would produce.

SIMULATIONS AND EXPERIMENTS

S1. Normal neurulation

The first column of Fig. 2 (labeled A1) shows the dorsal surface of a wild type axolotl embryo during the process of neurulation. The image labeled stage 13 is from the latter portion of that stage (Bordzilovskaya et al., 1989) and the embryo is spherical except for neural ridges that trace a ring encompassing approximately the cephalic three-quarters of its circumference. From a geometric perspective, neurulation produces neural ridges, which become increasingly well defined and move toward the midsagittal plane of the embryo. When viewed from the dorsal direction, as in Fig. 2, the neural plate acquires a distinctive keyhole shape by stage 15. As the ridges continue to move toward the embryo midline, they make contact midway along the dorsal aspect of the embryo by stage 17 and fuse completely by stage 19 (not shown). Videos matching each of the cases reported in Figs. 234 are included in the Supplemental Material, where their names match those used in the figures.

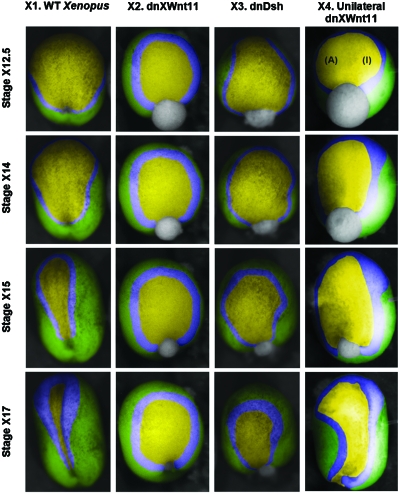
Figure 3. Experiments with Xenopus embryos.

Stage numbers are denoted with an X to distinguish them from the axolotl stage numbers shown in Fig. 2. Embryos injected with dnXWnt11 (column X2) or dnDsh constructs (column X3) or injected unilaterally with dnXWnt11 (column X4) are compared to controls (column X1) of the same clutch at developmental stages 12.5 (early neurulation), 14, 15, and 17 (late neurulation). Injected embryos show developmental defects including large and irregularly shaped neural plates, enlarged neural folds, and delayed neural fold migration. The manually overlaid colors correspond to those in Figs. 24.

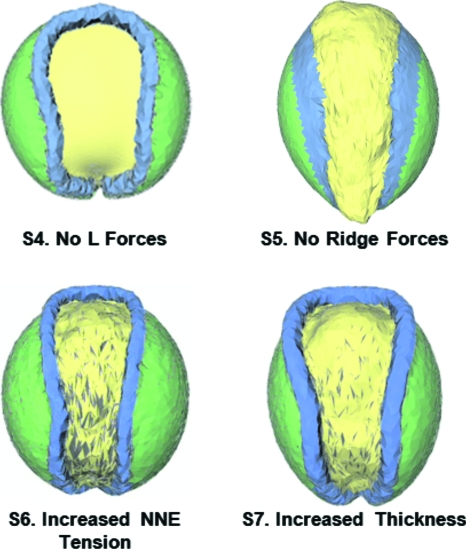
Figure 4. Additional simulations.

When lamellipodium action is totally disabled in the model (Case S4), the resulting NTD embryo has features very similar to those produced when microinjected mRNA is used to disrupt the PCP pathway (Wallingford and Harland, 2002). When forces in the neural ridges assumed to be produced by Shroom are turned off in the model (Case S5), it predicts a final geometry consistent with that produced in Xenopus embryos when Shroom3 is disabled using an antisense morpholino oligonucleotide (Haigo et al., 2003). Case S6 shows an embryo in which the tensions in the NNE have been doubled and Case S7 shows an embryo in which the thickness of the epidermis and mesoderm have been doubled. All of the cases shown in this figure were run for extended periods of time and all give rise to NTDs as their final configurations, illustrated here, show.

The corresponding model is shown in the column labeled S1. In this simulation, as in all of those reported here, the initial cell fabric was assumed to be isotropic (κ=1), the cell density was taken as ζ=0.012 cells∕μm² and μ was set to 2.67× 10⁻⁴ nN h∕μm². In this simulation, the γ values were all set to 9.1 nN, except for γ_apical in the neural plate, which was set to 61 nN (Table 1). Lamellipodia were assumed to generate an L force in the mediolateral direction under the control of components in the PCP pathway as well as other downstream effectors (Keller, 2004; Wallingford and Harland, 2002). Here, the L force is understood to include mechanical effects associated with notochord elongation and mesoderm deformation. The tension L was made to vary linearly from 20 nN∕μm at the midsagittal plane to zero at the lateral edge of the neural plate. These values and patterns were based on measurements of real tissues and on a previous computational study (Chen and Brodland, 2008). Model-experiment agreement in terms of morphogenetic movements, stresses, strains, and cellular fabric found in that study, after the parameters were set, provided support for them. As the cross-section in Fig. 2 shows, the model replicates the changes that occur in neural plate thickness but it does not fully capture the sharp fold (Colas and Schoenwolf, 2001) that arises at the edge of the neural plate.

Table 1.

Parameters used in the simulations. Values that are different from “Normal neurulation” are shown in boldface. The L force values are those acting along the midsagittal plane of the embryo and the pair of values shown in Case S3 correspond to the sides labeled A (active) and I (inactive).

Tissue and properties		Case
		S1 Normal neurulation	S2 Reduced L force	S3 Unilateral L	S4 No L forces	S5 No ridge forces	S6 Increased NNE tension	S7 Increased thickness
All tissues	Thickness	50	50	50	50	50	50	100
Neural plate	γapical (nN)	61	61	61	61	61	61	61
	γbasal (nN)	9.1	9.1	9.1	9.1	9.1	9.1	9.1
	L(nN∕μm)	20	16	20(A), 0(I)	0	20	20	20
Neural ridges	γapical (nN)	9.1	9.1	9.1	9.1	0	9.1	9.1
	γbasal (nN)	9.1	9.1	9.1	9.1	0	9.1	9.1
NNE	γapical (nN)	9.1	9.1	9.1	9.1	9.1	18.3	9.1
	γbasal (nN)	9.1	9.1	9.1	9.1	9.1	18.3	9.1

Contrary to previous two-dimensional models (Brodland and Clausi, 1994, 1995; Clausi and Brodland, 1993; Dunnett et al., 1991; Jacobson and Gordon, 1976; Odell et al., 1981), this model indicates that specialized forces must act in the neural ridge region for a normal ridge to form. Interestingly, the model shows that forces that are isotropic (the same in the cephalo-caudal direction as in the mediolateral direction) can produce a ridge that is highly curved in only the mediolateral direction. Thus, surprisingly, a locally anisotropic pattern of deformation is produced by isotropic driving forces along a strip (the presumptive neural ridges) whose material properties and geometry are otherwise isotropic. The force system needed to produce the distinctive keyhole shape of the neural plate is also unexpected. Regional strain histories in the neural plate do not vary significantly with mediolateral position but they do vary strongly with cephalo-caudal position (Brodland et al., 1996; Burnside and Jacobson, 1968; Jacobson and Gordon, 1976; Jacobson, 1962; Veldhuis et al., 2005). However, forces that vary strongly in the M-L direction but that do not vary in the C-C direction are needed to produce these patterns of deformation.

S2. Reduced L force

To test how robust closure is to changes in the strength of L—which might arise from reductions in lamellipodium frequency or force generation (Zhou et al., 2009) or traction behavior—tests were run in which L was adjusted in sequence to 60%, 70%, and 80% of its normal value. The case shown as S2. Reduced L force is for the run in which L was reduced to 80% of the normal value (Table 1). Differences between this case and the normal case are evident as early as stage 15. The simulations in each row of Fig. 2 correspond to the same amount of elapsed time, the basis on which the stage numbers were assigned to all but the normal case. When the model reached the configuration identified as stage 17, morphogenetic movements had essentially stopped and, as in cases where lesser L forces act, the neural tube remains open. The final cross sections produced in these cases are generally similar to those found in normal stage 15 axolotls. The model indicates that L reductions as modest as 20% are sufficient to prevent tube closure, suggesting that little excess force is normally available in real embryos. Given the range of natural variability in embryos (often 30%), one might wonder why NTDs are not much more frequent if this were the case. It is possible that properties found in a typical experiment do not reveal harmonious patterns of mechanically balanced global offsets that may be present throughout that embryo.

The morphogenesis of the Xenopus laevis neural plate has been well characterized (Ezin et al., 2003, 2006) and we tested the ability of the simulations to predict phenotypes in embryos with disrupted signaling pathways. The regulatory pathways associated with convergent extension of the neural plate have been studied extensively in Xenopus. Those experiments show that the PCP pathway is crucial for neural tube closure (Wallingford and Harland, 2002). Details of the pathway are highly conserved in diverse animal models, and a common picture is starting to arise. Key components of this system include the soluble ligand Wnt, its receptor frizzled, dishevelled (Dsh in Drosophila and Dv1 in vertebrates) and prickle (Kibar et al., 2007; Wallingford et al., 2000; Wallingford and Harland, 2002). Downstream of Dsh the small GTPases Rac and Rho act to regulate cytoskeletal dynamics effecting lamellipodial activity (Davidson et al., 2006; Ehrlich et al., 2002; Keller et al., 2000; Keller, 2005, 2006; Marsden and DeSimone, 2001). Disruption of any component in these pathways causes an abnormal phenotype.

When the PCP pathway is interrupted in Xenopus embryos outside the cell with dnXWnt11 (Tada and Smith, 2000) (column X2 in Fig. 3 and Supplementary Material), or in the cytoplasm with dnDsh (column X3) (Rothbächer et al., 2000) abnormal phenotypes result. Fertilized eggs were injected with in vitro transcribed mRNA derived from a mutated Dsh construct lacking the DIX domain (Wallingford and Harland, 2002) or a truncated Wnt11 (Tada and Smith, 2000) that acts as dominant negative. Control sibling embryos as well as injected embryos from the same clutch were cultured and staged according to (Nieuwkop and Faber, 1967). Embryos at the late blastula stage were imaged using a Zeiss Lumar stereoscope. Colored overlays were used to identify the ectoderm (green), neural folds (blue), and neural plate (yellow). Embryos injected with dominant-negatives exhibited developmental defects when compared to sibling controls at the same stage. Generally, injected embryos had larger and abnormally shaped neural plates with enlarged neural folds that exhibited delayed migration toward the midline suggesting failed convergence extension. At later stages, injected embryos were severely truncated and exhibited NTDs (see Supplementary Material). These findings are consistent with experiments in which the PCP pathway is disrupted by injecting mRNA encoding a DIX-deleted Dsh (Wallingford and Harland, 2002). CE is reduced and neural tube closure fails, a similar result to that obtained in previous computational models (Chen and Brodland, 2008) and other experiments (Kinoshita et al., 2008; Wallingford and Harland, 2002).

To evaluate the capacity of the model to predict phenotypes, we compared the neural plate phenotypes it predicts to those observed in wild type Xenopus embryos (Fig. 3, column X1). The morphogenesis of the Xenopus neural tube follows a slightly different time course form that of axolotl, however, there is a good correlation between the simulation and neural plate morphogenesis in vivo. The model predicts that a modest reduction in L forces would result in the failure of neural tube morphogenesis. We tested this in Xenopus by disrupting the PCP pathway with various dominant negative constructs. The PCP pathway regulates convergent extension in both the dorsal mesoderm as well as the neural plate. Disruptions of the pathway result in a failure of convergent extension that is thought to stem from a loss of cell polarity (Wallingford et al., 2000) as well as a reduction in cell-cell adhesion (Dzamba et al., 2009; Ulrich et al., 2005). In the simulations presented above this would be represented by a decrease in the L value. The model predicts that there would be a failure of neural fold medial migration and the neural plate would retain a more rounded shape (Fig. 2, column S2). When we follow neural plate morphogenesis in embryos that have been injected with a dnXWnt11 construct we observe phenotypes similar to those predicted by the model (Fig. 3, column X2). The neural plate remains open throughout neurulation and there is little medial migration of neural folds as predicted by the model. The neural plate in embryos expressing the dominant negative Wnt construct remains more rounded than predicted by the reduced L force simulation and looks to closer resemble the outcomes predicted by the no L force simulation (Fig. 4, column S4). It should be noted that we do not have a quantitative estimate of the forces disrupted by the dominant negative constructs. We used a second manipulation with a dnDsh construct (Xdd1) (Rothbächer et al., 2000) to confirm our observations. Dsh lies downstream of Wnt signaling in vertebrate PCP and we would expect similar phenotypes with the two dominant negative constructs. Indeed, dnDsh injected embryos closely resemble those injected with dnXWnt11 and again mimic the predictions of the simulation with reduced L forces (Fig. 3, column X3). The minor neural ridge profile differences between the model and our experiments occur primarily due to Xenopus embryos having substantially wider neural ridges than Ambystoma embryos. This difference does not detract from the predictive nature of the model.

S3. Unilateral L

Experiments in which the properties of one side of an embryo are modified are relatively common because the unaltered side can then serve as a control (Colas and Schoenwolf, 2001; Nagamoto and Hashimoto, 2007). In simulation S3, unilateral L, the L force has been deactivated on the side labeled I (inactive). The model embryo deforms in an asymmetric way and the neural tube does not close. The ridge on the normal side is not able to move past the embryo midline sufficiently to contact the ridge on the abnormal side. Strong cross-sectional asymmetries are also produced. The simulation is important from a developmental perspective because it suggests that the normal ridge is not able to move substantially past the midsagittal plane indicating that normally neural fold fusion requires bilateral forces.

We evaluated the simulation prediction by injecting embryos in one blastomere at the two cell stage. This limits expression of the dnXWnt11 construct to one side of the embryo and morphogenesis is only disrupted on the side that expresses the construct. The simulation predicts that the neural folds on the injected side will move medial as observed in wild type embryos (Fig. 2, column S3) while the side lacking L forces will not move enough to close the neural tube. In our embryo experiments, we see a result that closely resembles that predicted by the simulation. The uninjected side has robust neural folds that move toward but not across the embryo midline. The side of the embryo expressing the dominant negative construct remains open and while its neural fold moves medially it does not do so enough to close the neural tube (Fig. 3, column X4).

S4. No L forces

When the L forces are completely deactivated in the model—as opposed to partially, as in the S2 model—the phenotype shown in Fig. 4 (Case S4, no L forces) results (see Supplementary Material). This is the final configuration, further motions do not occur, even if the model is run for a protracted period. The stage 17 geometry it predicts is in good agreement with the experiments shown in columns X2 and X3 of Fig. 3. Quantitative estimates of the effects of the dominant negative constructs on L forces are not currently available but it could be that the reduction is severe enough that the situation is best represented by the S4 simulation.

S5. No ridge forces

To investigate whether the apically basally asymmetric forces needed to form the neural ridges affect the in-plane motions of the plate enough to prevent closure, simulations were run in which the neural ridge forces were set to zero (γ_apical=γ_basal=0). In this case, the plate deforms in-plane so as to form a keyhole shape (Fig. 4, Case S5) much like it does in the normal case but neural ridges do not form and the tube does not close.

A number of developmentally significant proteins are expressed selectively in the neural ridge area of neurulation-stage embryos. One of these proteins, Shroom3 (Hagens et al., 2006), has been shown to regulate microtubule architecture (Lee et al., 2007); to induce apical constriction in neural plate cells (Haigo et al., 2003; Hildebrand, 2005) and to be essential for neural tube closure (Haigo et al., 2003; Hildebrand and Soriano, 1999). The above simulation was created to model the mechanical consequences of experiments in which the actin-binding protein Shroom3 is disrupted. Experimentally, Shroom3 morphant embryos do not develop normal neural ridges (Lee et al., 2007) and they appear similar to those predicted by our model.

S6. Increased NNE tension

The model also was used to investigate how changes to the tension in the non-neural ectoderm might affect neurulation. When this tension is doubled but the neural plate tensions are unchanged (Table 1), neural ridges form, narrowing of the plate is substantially delayed and reduced (Fig. 4, Case S6), and the tube does not close. It is not difficult to envision corresponding biological experiments and one hopes that in time they will be carried out.

S7. Increased thickness

Previous 2D simulations showed that changing the thickness of a tissue can significantly change the morphogenetic movements it undergoes (Clausi and Brodland, 1993). To test whether a similar result is obtained when a 3D model is used, the thickness of the active surface layer (the ectoderm and mesoderm) was doubled. The model predicts (Fig. 4, Case S7) that the movements would be delayed compared to the normal case and that tube closure would fail, a finding not inconsistent with the 2D model, where a thinner neural plate deformed more quickly than normal. Biological experiments against which the model predictions can be compared are not currently available.

DISCUSSION AND CONCLUSIONS

Over time, our understanding of the process of neurulation has changed considerably and this has altered the role that computational models play. In the 1970s, when time-lapse movies and serial section represented the state-of-the-art (Jacobson and Lofberg, 1969) and computers were a ground-breaking research tool, the pioneering computational modellers addressed in-plane kinematics of neurulation (Jacobson and Gordon, 1976), something that could be modeled with the computers available at the time. Their studies showed that regional variations in properties were necessary to produce the observed tissue motions. As the cytoskeleton and its morphology became known and computational technology advanced (Burnside, 1973), simulations of neural plate cross-sections became popular (Brodland and Clausi, 1995; Clausi and Brodland, 1993; Dunnett et al., 1991; Odell et al., 1981). These models made reference to the cytoskeleton and often derived their material properties from it. They provided important insights into the mechanics of the neural plate and its surrounding tissues and confirmed the central role played by actomyosin contraction systems. Now, the primary signaling pathways associated with neurulation are becoming clear and multiscale mechanical models of the kind presented here can be built. These models can begin to relate the biochemical state of a tissue to the forces that it generates, the mechanical interactions that occur between the various tissues in the embryo and the phenotypes that are ultimately produced. The result is a deeper and more comprehensive understanding of the process of neurulation.

The simulations show that the final geometries produced during neurulation are sensitive to the forces at work in all of the tissues of the embryo (Simulations S2, S5, and S6). They also show that NTDs can be produced by a wide variety of mechanical factors (Simulations S2–S7). When the mechanical effects that specific signaling molecules are understood to induce were removed (Simulations S2–S5), the simulations produced morphogenetic movements and phenotypes that were in generally good agreement with companion experiments. Since phenotype is sensitive to the forces present, these correlations provide evidence in support of the claimed mechanical effects. As this line of reasoning demonstrates, another important role of simulations is to test current understanding of the mechanical roles of various signaling pathways.

The model has proven to be a surprisingly strong predictor of morphogenetic defects in Xenopus even though it is based on axolotl geometries and properties and may not adequately account for disruptions to morphogenetic movements in the underlying mesoderm introduced by the molecular interventions. The mesoderm is thought to be the primary source of the forces that result in axial extension (Zhou et al., 2009) and this likely accounts for the more rounded embryo shape seen in vivo versus in silico. The molecular manipulations we have used here are preliminary and are likely to cause diverse effects on neural tissue, possibly blocking cell polarity as well as the adhesive properties of cells. Further refinement of our experimental conditions would allow us to differentiate the roles played by the cytoskeleton, ECM, and various adhesion molecules. How the various components of biochemical signaling pathways impact mechanical properties is only now beginning to be understood (Rolo et al., 2009; Zhou et al., 2009) although the relationship between lamellipodium action and CE has been investigated using computational models (Brodland and Veldhuis, 2006). The change in L force can be viewed as resulting from a reduced lamellipodium generation rate due to irregularities in PCP signaling, a lack of polarized adhesion, a decrease in cell-cell adhesion, or a reduction in actin-myosin IIb contraction in the lamellipodia resulting in decreased force generation. If lamellipodium generation rates were known for a particular embryo and the average contraction strength were known, equations derived from cell-level computer models would allow L to be calculated. Alternatively, if the L value required to produce a particular NTD were known, those equations could be used to calculate the degree to which lamellipodium generation or contraction would have to be affected to produce that defect. Even considering these complex experimental issues, the robust predictive value of the model is clear.

Multiscale models can predict morphogenetic movements with much more precision than was previously possible but further advances could be made. Ideally, one would incorporate the effects of the PCP pathway, Shroom and other regulating factors at the cytoskeletal level and use the constitutive equations to propagate them through the various scale levels of the model. One might also build computational models of the relevant biochemical signaling pathways and run them in parallel with the mechanical models. One might then be able to better understand how genetic, environmental, and nutritional factors influence neurulation outcomes.

Validation, the process through which one demonstrated that a model faithfully duplicates the response of the physical system it aims to replicate, is an important element of model development and the present study offers an important step in that direction. Specifically, the model used here has inputs that allow a wide range of biological factors to be incorporated (Figs. 24). When simulations based on best current knowledge of how these factors affect mechanical properties are run, the predicted tissue motions and phenotypes are consistent with corresponding experiments. Large embryo-to-embryo variations are common in vivo, especially when molecular interventions are applied. Thus, next steps might include statistical characterizations of real embryos and quantitative comparisons of simulation predictions with those statistical descriptors.

As models of the type presented here mature and are better calibrated against experiments, they may provide insights of value in reducing the incidence of NTDs in humans. Important differences exist between human and amphibian embryos (Detrait et al., 2005; Tekkök, 2005) but conceivably, models of human neurulation could eventually be constructed and used to test, in silico, the effectiveness of proposed medical interventions.