The Importance of Identifying and Validating Prognostic Factors in Oncology

Abstract

Prognosis plays a vital role in patient management and decision making. The assessment of prognostic factors, which relate baseline clinical and experimental covariables to outcomes, is one of the major objectives in clinical research. Historically, the impetus for the identification of prognostic factors has been the need to accurately estimate the effect of treatment adjusting for these variables. In oncology, the variability in outcome may be related to prognostic factors rather than to differences in treatments. In this article, we begin with a brief review of prognostic factors, and then subsequently offer a general discussion of their importance. Next, we describe the significance of study design before presenting various modeling approaches for identifying these factors and discussing the relative values of the different approaches. We illustrate the concepts within the framework of published and ongoing phase III trials in oncology.

Prognosis plays a vital role in patient management and decision making. The assessment of prognostic factors is one of the major objectives in clinical research. In this article, we begin with a brief review of prognostic factors, and then subsequently offer a general discussion of their importance. Next, we describe the significance of study design before presenting various modeling approaches for identifying these factors and discussing the relative values of the different approaches. We illustrate the concepts within the framework of published and ongoing phase III trials in oncology.

STUDIES OF THE IMPORTANCE OF PROGNOSTIC FACTORS

There are several reasons why prognostic factors are important.^1–3 First, by determining which variables are prognostic of outcomes we gain insights on the biology and natural history of the disease. Second, appropriate treatment strategies may be optimized based on the prognostic factors of an individual patient.^1,2 Third, prognostic factors are often used in the design, conduct, and analysis of clinical trials.^4–7 Finally, patients and their families are informed about the risk of recurrence or death.

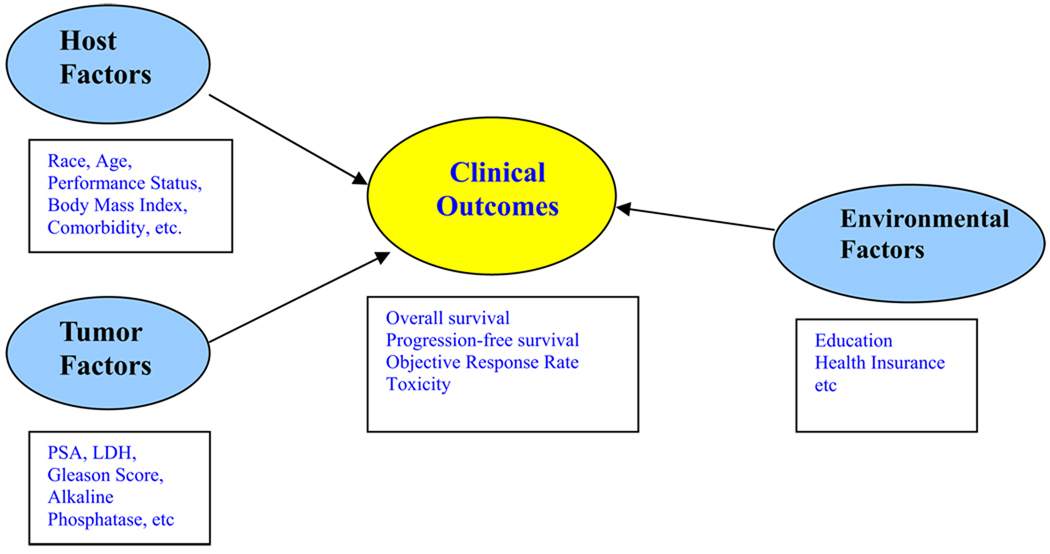
Within this context, what is of interest is to investigate the potential relationship between a set of host, tumor-related, environmental baseline explanatory variables and clinical outcomes. These factors, to be referred to as co-variables for notational brevity in this article, and those which are deemed to be important or useful are called prognostic. Figure 1 presents the potential relationship between host, tumor, environmental factors, and clinical outcomes. The reader is referred to Gospodarowicz et al for a more detailed discussion on the different types of prognostic factors.⁸ The focus in this article is on factors that are relevant at the time of diagnosis or initial treatment.

Figure 1.

Relationship between host, tumor, environmental and clinical outcomes.

There are several distinct but related concepts that we need to first consider. Statistical inference is performed to quantify the amount of statistical evidence of the association between co-variables and the outcome. Regression models are used to jointly model the relationship between a set of co-variables and outcomes. On the other hand, classification models are used to ascertain if patients can be classified into distinct risk groups on the basis of the co-variables. Although individual prognostic factors are useful in predicting outcomes, investigators may be interested in constructing classification schemes. Combining multiple prognostic variables to form a prognostic index or score is a powerful strategy that will allow for the identification of groups of patients with differing risks of progression or death.

Prognostic models have been widely used and will continue to be employed in trials in oncology. The following examples demonstrate the importance of prognostic factors and the applicability of such models in the design, conduct, and analysis of clinical trials in oncology.

In Cancer and Leukemia Group B (CALGB) 90203, a neoadjuvant phase III trial, 750 men with prostate cancer who are at high risk are randomized to either prostatectomy or docetaxel plus hormones followed by prostatectomy. ⁵ Using the Kattan nomogram, high-risk men are considered eligible to participate on this trial if their predicted probability of being disease-free 5 years after surgery is less than 60%.⁹

Researchers may employ prognostic models that are used in stratified randomized trials. As patient outcomes often depend on prognostic factors, randomization helps balance such factors by treatment assignments. Some imbalances may nevertheless occur by chance. One strategy to limit this effect is to use blocked randomization within predefined combinations of the prognostic factors (strata). In CALGB 90401, a recently completed phase III trial, 1,050 men with castrate-resistant prostate cancer (CRPC) were randomly assigned to receive either docetaxel or docetaxel plus bevacizumab.⁶ Randomization was stratified by the predicted survival probability at 24 months: <10%, 10%–29.9%, or ≥30%.¹⁰

Adjusting on prognostic factors to avoid bias in estimating the treatment effect is important even if the baseline factors are balanced between treatment groups. The need, though, to adjust on prognostic factors is more critical when the randomization is unbalanced. In a randomized phase III trial, 127 asymptomatic men with CRPC were randomized in a 2:1 ratio to either sipuleucel-T or placebo. The primary and secondary endpoints were time to progression and overall survival (OS), respectively. In the multivariable analysis of OS, Small et al identified five clinical variables (lactate dehydrogenase [LDH], prostate-specific antigen [PSA], number of bone metastases, body weight, and localization of disease) that were highly prognostic of OS in this study cohort. To correct for any potential imbalances in prognostic factors, the treatment effect of sipuleucel-T was adjusted using the above variables. The observed hazard ratio (HR) was estimated to be 2.12 (95% confidence interval [CI], 1.31– 3.44).⁷

STUDY DESIGN

The literature is rich in articles related to prognostic factors, but despite their abundance, results may conflict on the importance of certain markers in predicting outcomes. Accurate and reliable information based on the accessible literature with regard to prognostic factors needs to be consistent so that the two critical questions on “who to treat” and “how to treat each individual” can be addressed.¹¹ General principles and methods related to the assessment and evaluation of prognostic factors are not as well developed as the methodology for treatment trials. Recently, reporting recommendations for tumor marker prognostic studies guidelines (REMARK) have been developed and it is anticipated that the quality and reporting of results of prognostic factors in cancer will be greatly improved.¹²

Most prognostic factors studies are based on retrospective data analysis that have a small sample size or sparse data and as a result have poor data quality.¹ As with any scientific study, investigators planning a prognostic factor analysis should start with a primary hypothesis, the end point should be specified a priori and sample size or power computations should be justified. As suggested by Altman, the sample size should be large in order to account for the multitude of potential biases that may arise in conducting such analyses.¹ These issues may be related to multiple comparisons of variables, selection of variables, comparisons of different models, and missing data of the variables or outcomes.¹

Several papers in the literature have considered the sample size required for prognostic studies.^13–15 To examine the role of a prognostic factor, sample size needs to be justified. As for model building, a general ad hoc rule of thumb is to use 10 subjects per variable for a binary endpoint (such as objective response) and 15 events (such as deaths) per variable for time-to-event endpoints (such as OS).¹⁴ For predictive factors studies, sample size computation should be formally justified based on a test of interaction between the prognostic factor and the treatment.¹⁵ Usually, the sample size required for such studies is very large. For more discussions on this topic, see Simon and Altman¹⁶ and Schumacher et al³ who provide rigorous and thoughtful reviews of statistical aspects of prognostic factors studies in oncology.

IDENTIFICATION OF PROGNOSTIC FACTORS

Multiple strategies exist for the identification of prognostic factors among this set of co-variables. For illustration, we will describe three commonly used modeling approaches: the logistic regression for binary endpoints,¹⁷ the proportional hazards regression for censored time-to-event endpoints,¹⁸ and conditional tree models for both binary and time-to-event endpoints. ^19–21

Logistic Regression Model

The logistic regression model is a popular approach for modeling the relationship between a binary event outcome and a set of co-variables. A binary outcome, say D, assumes one of two possible values say 0 (failure) or 1 (success). Examples of binary endpoints are objective response, recurrence-free survival at 1 year, or OS at 5 years. For the logistic model, the probability of the occurrence of the event of interest given the co-variables, say X₁, …, X_K, is assumed to be of the form:

$$P[D=1|X_1,X_2,\dots ,X_K]=1/[1+e^{-z}]$$

where z = β₀ + β₁X₁ + β₂X₂ + … + β_KX_K and is known as the prognostic index or score. β₀ is the intercept and β_k, where k = 1, 2, … K, are the unknown regression coefficients corresponding to the K co-variables.

The logit transformation is essential to the use of the logistic model. The logistic model is a so called generalized linear model (GLM). Note that the conditional probability in the equation above is not a linear function of the model parameters. It is trivial to show that:

$$\mathit{\text{log}}[P(D=1|X_1,X_2,\dots X_K)/1-P(D=1|X_1,X_2,\dots X_K)]={\mathrm{\beta }}_0+{\mathrm{\beta }}_1{X}_1+{\mathrm{\beta }}_2{X}_2+\dots +{\mathrm{\beta }}_K{X}_K$$

where log is the natural logarithm (ie, to the base e). The function 1/(1 + exp(z)) is called the logistic function, from which the name of model is derived, and its inverse log(p/1−p) is called the logit function. It is noted that the logit function, commonly referred to as a link in the GLM literature, linearizes the model.¹⁷ This model is parametric in the sense that the probability of the occurrence of the event given the co-variables is assumed to be known up to a finite number of model parameters. The regression coefficients can be interpreted as follows. If we fix the values of X₂, …, X_K, then one unit increase in X₁ corresponds to a exp(β₁) increase in the odds of the event.

The logistic regression model implicitly makes certain assumptions on the relationship between the conditional mean and variance of the outcome. The variability based on the data may be below or above the level assumed by the model. This is often referred to as under- or over-dispersion. In this case, the inference drawn if the assumption does not hold may lead to wrong conclusions. The method of generalized estimating equations is a generalization of this model that aims to address this caveat.²²

The estimated regression coefficients can be used to estimate the predicted probability by inverting the regression model as demonstrated in the following example.

Example: Robain et al used a logistic regression model to predict objective response in 1,426 women with metastatic breast cancer. Objective response was defined as either the presence of a partial or complete response.²³ Fifteen baseline co-variables were examined as potential predictors of objective response. These were age, performance status (Karnofsky index), number of sites (1, ≥2), and location of metastases (bone, lung, pleura, liver, peritoneum, skin, lymph nodes), serum LDH, weight loss before treatment, menopausal status, disease-free interval from primary tumor diagnosis to metastases, year of inclusion in a metastatic trial, serum alkaline phosphatase, γ glutamyl transferase (γGT), aspartate aminotransferase (AST), serum albumin levels, and absolute lymphocyte count.

Forward stepwise regression was used to select the prognostic factors and the maximized log-likelihood was used for comparison of models based on selection of prognostic factors at each step. Prior chemotherapy (yes v no), low Karnofsky index (<60 v ≥60), high LDH (>1 × N v ≤1 × N), presence of lung metastases (yes v no), and pleural metastases (yes v no) were combined to form a predictive score. The estimated score was: −1.32 + 0.54 (no prior adjuvant chemotherapy) + 0.80 (low Karnofsky index) + 0.75 (elevated LDH) + 0.49 (lung metastases) + 0.51 (pleural metastases).

The estimated regression coefficients can be used to compute the predicted probability by inverting the regression model. For example, the predicted probability of not achieving objective response for a woman without prior adjuvant chemotherapy (coded as 0), low Karnofsky index (coded as 1), high LDH (coded as 1), presence of lung (coded as 1), and pleural metastases (coded as 1) is calculated to be:

$$\mathit{\text{exp}}(-1.32+0.54\times (0)+0.80\times (1)+0.75\times (1)+0.49\times (1)+0.51\times (1))=/[1+\mathit{\text{exp}}(-1.32+0.54\times (0)+0.80\times (1)+0.75\times (1)+0.49\times (1)+0.51\times (1))]=0.774.$$

Proportional Hazards Model

Often, an investigator seeks to assess the prognostic importance of several independent variables on a time-to-event endpoint. In phase III trials, time-to-event endpoints refer to outcomes where time is measured from randomization until occurrence of an event of interest. The time variable is referred to as the failure time and is measured in years, or other unit of time. The event may be death, death due to a specific cause, or the development of metastases. In general, OS is the most common time-to-event end point in phase III trials in oncology. Most time-to-event end points must consider a basic analytical element known as censoring. Censoring arises when information about individual failure time is unknown and it occurs when patients either do not experience the event before the study ends or patients are lost during the follow-up period.

Two quantitative terms are fundamental in any survival analysis. These are survivor function, denoted by S(t), and hazard function, denoted by λ(t).²⁴ The survivor function is the probability that a person survives longer than some specified time t. The hazard function λ(t), is the instantaneous potential per unit time for an event to occur, given that the individual survived until time t. There is a clearly defined relationship between these two functions, but it is simpler to mathematically model the hazard function than the survival function when an investigator is interested in assessing prognostic factors of time-to-event endpoints.

One of the most common approaches in the medical literature is the use of the regression proportional hazards model.¹⁸ This model is used to analyze time-to-event data and it is a popular method because it can incorporate both baseline and time-varying factors. A proportional hazards model with a hazard function is given by:

$$\mathrm{\lambda }(t|X_1,X_2,\cdots ,X_K)={\mathrm{\lambda }}_0(t)\mathit{\text{exp}}({\mathrm{\beta }}_1{X}_1+{\mathrm{\beta }}_2{X}_2+\dots +{\mathrm{\beta }}_K{X}_K)$$

where X₁, X₂, … X_K represent the baseline co-variables, β̲ are the regression or the log-HR parameters. λ₀(t) is the baseline hazard which is a function of time and is equal to the overall hazard function when all the values of co-variables are zero. The proportional hazards model is semi-parametric as it does not specify the form of λ₀(t). The co-variables are assumed to be linearly related to the log-hazard function. The parameter β can be estimated by maximizing the partial likelihood function as described by Cox.¹⁸ By estimating β̲ it will allow one to quantify the relative rate of failure for an individual with one set of co-variables compared to another individual with another set of co-variables. From the proportional hazards model, the estimated HR for death and 95% CIs are usually summarized.

The proportional hazards model specifies multiplicative relationship between the underlying hazard function and the log-linear function of the co-variables. This assumption is also known as the proportional hazards assumption.¹⁸ In other words, if we consider two subjects with different values for the co-variables, the ratio of the hazard functions for those two subjects is independent of time. The proportional hazards model is a powerful tool as it can be extended to include stratification and time-dependent co-variables, those factors whose values change over time.

The proportional hazards model can be extended to allow for different strata and is written as:

$${\mathrm{\lambda }}_s(t)={\mathrm{\lambda }}_{0s}(t)\mathit{\text{exp}}({\mathrm{\beta }}_1{X}_1+{\mathrm{\beta }}_2{X}_2+\dots +{\mathrm{\beta }}_K{X}_K)$$

where λ _0s(t) is the baseline hazard function in the sth stratum, s = 1, 2, …, l. The stratified proportional hazards model assumes that patients within each stratum satisfy the proportional hazards assumption, but patients in different strata have different baseline hazard function and thus are allowed to have nonproportional hazards. It is important to note that β̲ does not depend on the strata.

Both graphical and test-based methods are used for assessing the proportional hazards assumption.^25,26 Some of the graphical approaches include plotting the log [−log S(t)] versus time or using the stratified proportional hazards model. There are several formal tests for assessing the proportionality hazards assumption. These tests are either based against a specified alternative or a general alternative hypothesis. An ominbus test against a general alternative test developed by Schoenfeld is a common and effective approach for testing the proportionality hazards assumption.²⁶

Example: In Halabi et al, we identified seven prognostic factors of OS in men with CRPC using clinical data from 1,100 patients enrolled on CALGB studies.¹⁰ The goal was to have at least 20 events (deaths) per variable. The data were split in two: two thirds (n = 760) for the learning set and one third (n = 341) of the data to be used for the testing set. All potential prognostic factors were identified a priori of the data analysis based on a thorough review of the literature. Schoenfeld residuals were used to check the proportional hazards assumption. PSA, LDH, and alkaline phosphatase were modeled using the log transformation as these variables were not normally distributed. The final model included the following factors: LDH, PSA, alkaline phosphatase, Gleason sum, Eastern Cooperative Oncology Group (ECOG) performance status, hemoglobin, and the presence of visceral disease (Table 1).

Table 1.

Multivariable Model Predicting Overall Survival Duration

Factors	Parameter Estimate	HR (95% CI)*	P Value
Performance status			<.0001
0 (0)		1.00 (referent)
1 (1)	0.392	1.48 (1.31–1.67)
2 (2)	0.784	2.19 (1.94–2.47)
Gleason sum			<.0001
<8 (0)		1.00 (referent)
8–10 (1)	0.335	1.40 (1.20–1.62)
log (LDH)	0.312	1.37 (1.21–1.55)	<.0001
log (Alkaline phosphatase)	0.211	1.23 (1.12–1.36)	<.0001
log (PSA)	0.093	1.10 (1.05–1.15)	<.0001
Visceral disease	0.161		.147
No (0)		1.00 (referent)
Yes (1)
Hemoglobin	−0.082	0.92 (0.87–0.97)	<.0001

Abbreviations: HR, hazard ratio; CI, confidence interval; LDH, lactate dehydrogenase; PSA, prostate-specific antigen.

Reprinted with permission. © 2003 American Society of Clinical Oncology. All rights reserved. Halabi S, et al. J Clin Oncol. 2003;21:1232–7.

Similar to the logistic regression, if the co-variable is binary and is coded as either 0 or 1 if we fix the values of X₂, …, X_K, then one unit increase in X₁ corresponds to a exp(β₁) increase in the risk of death. For example, the observed hazard ratio associated with Gleason sum can be computed as exp(0.335), which is 1.40 (Table 1). This means that men with high Gleason sum^8–10 had a 1.4-fold increased risk of death compared to men with Gleason sum <8 after adjustment for other co-variables in the model.

Classification Trees

A classification tree is a flexible nonparametric technique for attempting to classify patients with respect to the outcome on the basis of the covariables.^19–21 The objective is to split the patients into homogeneous subsets. In cancer, these subsets are typically called risk sets. The most common approach to create these risk sets recursively based on binary splits, on the basis of the co-variables, split the patients into two subgroups, and until it is no longer feasible to continue based on a pre-specified set of criteria.

For the logistic and proportional hazards models, a patient for whom any one of the co-variables is missing must be excluded from the analysis. Classification trees do not suffer from this caveat. This approach has been extended to combine elements of classification with statistical inference, and to allow using more complex outcomes such as right-censored time-to-event outcomes. Another caveat with using the logistic and proportional hazards models is that interactions among the co-variables need to be explicitly defined. On the other hand, classification tree models implicitly account for potential interactions.

One of the major disadvantages of tree models is that complicated structures may emerge making the interpretation of the data difficult, not using continuous variables effectively, the tree structures can be unstable and that of overfitting.²⁷ The latter caveat, of course, applies to the logistic and proportional hazards models as well.

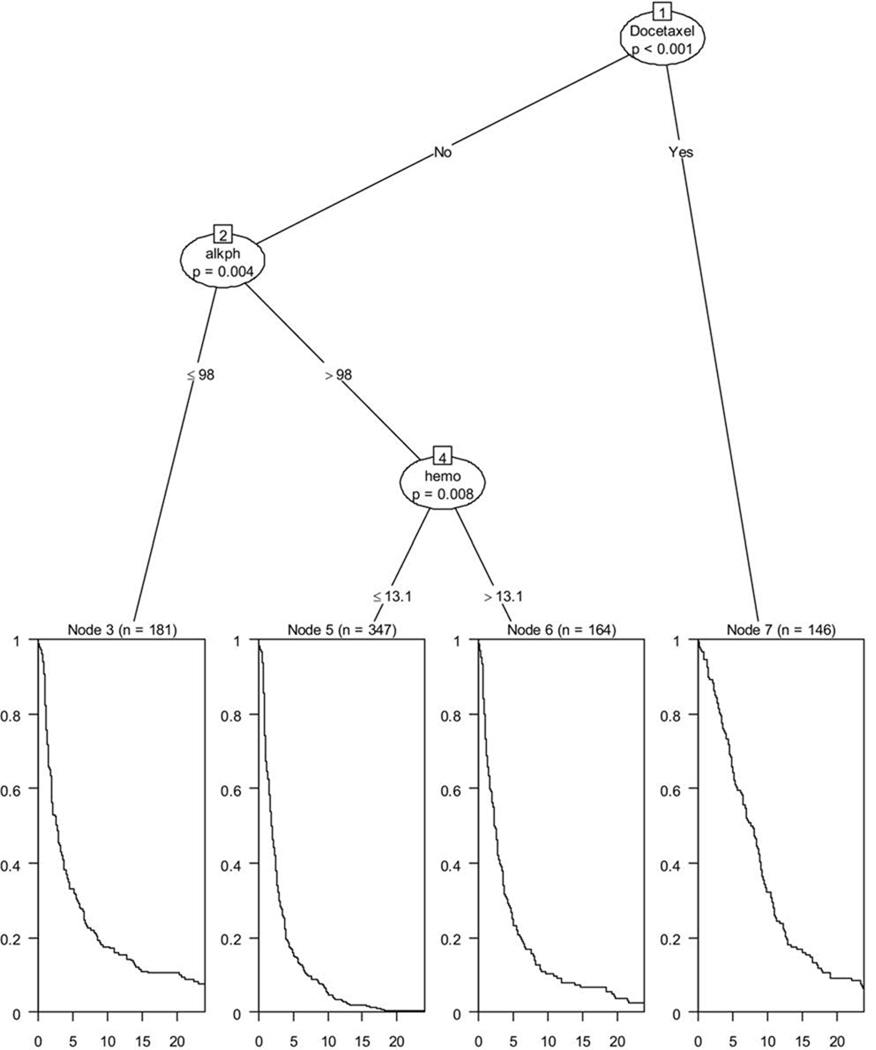
Figure 2 shows an example of a conditional inference tree²⁸ model fitted on data from 1,296 men with CRPC. Four prognostic groups were identified that were statistically significant, at a family-wise error rate of at most 0.05, for the primary endpoint progression-free survival (PFS). The three prognostic factors were treatment with docetaxel, alkaline phosphatase, and hemoglobin. The lowest risk group was comprised of men who were treated with docetaxel-based regimens. This group had a median PFS of 7.74 months, whereas risk group 2 was comprised of men with alkaline phosphatase levels ≤98 U/L and a median PFS of 2.64 months. The high-risk group had alkaline phosphatase >98 U/L and hemoglobin >13.1 g/dL with an observed median PFS of 1.40 months, whereas the highest risk group had alkaline phosphatase >98 U/L and hemoglobin of ≤13.1 and had a median PFS of 1.88 months.

Figure 2.

Regression tree for progression-free survival in men with CRPC.

Example: Banjeeree et al used data from 1,055 women with stages I–III breast cancer to identify recurrence-free survival, their primary endpoint, which is defined as the time between diagnosis and documented recurrence (local, regional, or distant recurrence), excluding new primary breast cancer.²⁹ The investigators considered 15 baseline variables, which were age, race, socioeconomic status, marital status, obesity, tumor size, number of positive lymph nodes, progesterone receptor (PR) status, estrogen receptor (ER) status, tumor differentiation, hypertension, heart disease, diabetes, cholesterol level, and stroke. Using recursive partitioning, four distinct risk groups were identified based on the prognostic factors: race, marital status, tumor size, number of positive nodes, progesterone status, and tumor differentiation.

COMMON PROBLEMS WITH MODELING

In this section, we discuss common pitfalls in building models so that they can be avoided.

Categorizing a continuous prognostic factor as a binary variable based on the sample median is a common practice in the medical literature.^1–3 In the proportional hazards model, it is assumed that continuous variables have a log-linear relation with the hazard function. While many researchers cannot make this assumption, dichotomizing a continuous variable may result in substantial loss of information.

Royston et al suggested another alternative, which is to use several categories for quantifying the relationship of continuous variable to the hazard of death.³⁰ Other approaches such as cubic splines or fractional polynomial have been effectively applied in assessing the relationship between continuous variables and hazard function.^2,31

Identification of a prognostic factor based on the optimal cut point is often applied in prognostic studies, but this approach is based on identifying the cut point that yields the minimal P value.³² The approach is problematic as it does not correct for the multiplicity of comparisons and is rightly criticized due to the subjectivity and arbitrariness of the cut point. There are new algorithms that adjust for multiple comparisons, but even if this approach is employed the analysis should be considered only as exploratory. A confirmatory study of this prognostic factor should be undertaken and the sample size needs to be large in order to increase the precision of the estimate.

As an example, exploratory statistical methods were used to find different cut points for the association between vascular endothelial growth factor (VEGF) levels and OS in men with CRPC.²⁸ Several cut points above and below the median showed an association between high VEGF levels and decreased duration of survival. At a cut point of 260 pg/mL, differences in median survival were 17 months (95% CI, 14–18) versus 11 months (95% CI, 6–13; P <.0005) for patients below and above the cut point, respectively.³³ The multivariable HR associated with a VEGF levels ≥260 pg/ml was 2.42, demonstrating the strongest association between VEGF levels and survival time.³³ This analysis is deemed as exploratory and this cut point is being validated prospectively in an ongoing CALGB phase III trial in men with CRPC.

Variable selection is a critical step of model building. Some investigators have used the stepwise methods for selecting prognostic factors. However, this type of variable selection approach may produce overoptimistic regression estimates that will yield a low predictive ability.^1,10 Backward elimination is considered by many as advantageous compared to stepwise variable selection procedures.^2,3,34

As with any regression method, one needs to understand and verify the assumptions of the model.² If these assumptions are not held, then interpreting the results of the fitted model may be difficult. Assessing the proportional hazards assumption in the proportional hazards model is often overlooked. The reader is referred to an excellent review of strategies involved in model building that is provided by Harrell et al.²

Example: In Smaletz et al, a proportional regression model was initially used to fit the baseline co-variables. ³⁵ However, several variables violated the proportional hazards assumption of a constant hazard over time. Consequently, an accelerated failure time model was used to fit the data.

MODEL VALIDATION

The primary goal of a prognostic model is to minimize uncertainty in predicting outcome in new patients. ² Validation is a critical step in developing a prognostic model. Assessing predictive accuracy is the next important step for model validation.^1,2 As described by Harrell et al,² calibration or reliability refers to the extent of the bias or match between prediction and outcome. Discrimination, on the other hand, measures a model or predictor’s ability to classify or separate patients with different responses.² One of the main caveats with model developing is overfitting or over-learning. Overfitting refers to a situation in which a model has been fit with random noise and the associations between the co-variables and the outcomes will be spurious.

A critical component in any validation procedure is to decide on a measure to quantify the accuracy of the prediction. If the outcome and predictions are both binary, a simple tabulation of the observed versus the predicted outcomes may suffice. Note that most predictive algorithms do not produce a binary result. Rather, they produce a quantitative prediction, such as a probability. A subject with a large predicted probability would be classified as a responder. One may want to assess the performance of the model by constructing the receiver operating curve (ROC) using the observed outcomes as the gold standard rather than using simple cross-tabulations.

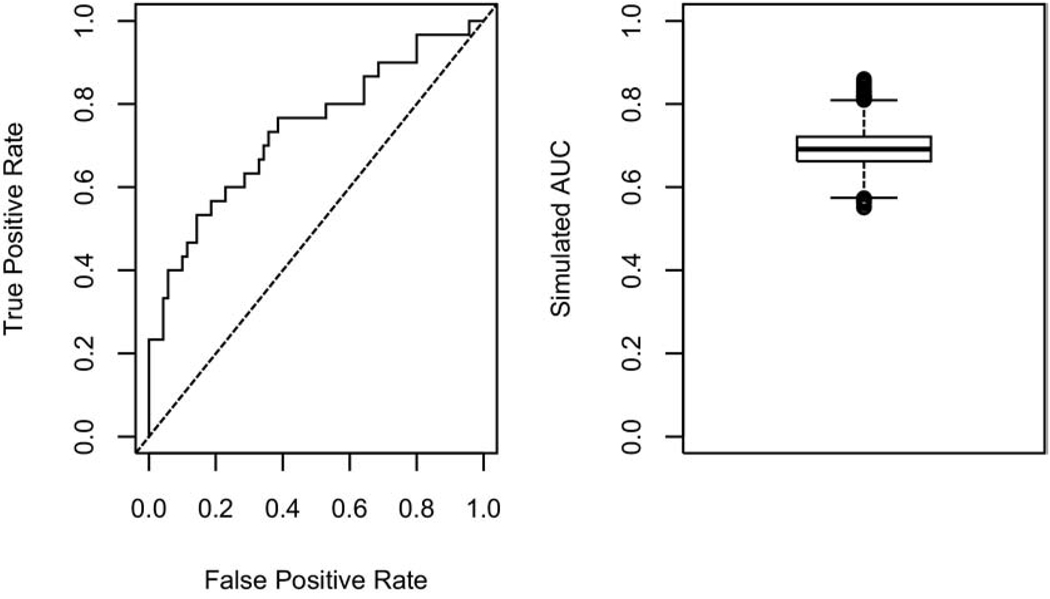
We illustrate the concept of overfitting, within the framework of studies with small sample size and large number of co-variables, to emphasize the importance of proper model validation. Let us consider a binary outcome (eg, tumor response) with a relative frequency of 0.3. In other words, 30% of the patients in the target population are expected to be responders. Suppose that this outcome has been observed for 100 patients along with K = 50 baseline co-variables. The primary objective is to build a prognostic model based on a subset of the K co-variables. We arbitrarily, assign the first 30 patients as responders and the remaining 70 as nonresponders. It is noted that by design, there is absolutely no relationship between the outcome and any of the co-variables. Any model developed based on these data would be a case of noise-discovery. It is neither practical nor advisable to build the model based on all K co-variables. A common approach is to carry out variable selection after reducing the number of co-variables and then build the model based on this subset. A standard feature selection approach is to establish the marginal significance of each co-variable and then build the model based on the top important variables. We will rank the co-variables based on the absolute value of the two-sample t statistic and select the top 10 among K = 50 co-variables to build a model using logistic regression. We carry out this simulation analysis once and establish the performance of the resulting model using the ROC based on the predicted probabilities from the logistic model (left panel in Figure 3). The corresponding area under the curve is 0.74. As this area exceeds 0.5, this may suggest that we have come up with a potentially prognostic model. To investigate this further, we repeat this simulation 10,000 times and summarize the corresponding 10,000 areas under the curve using a boxplot (right panel in Figure 3). This confirms the previous observation. As we have trained these models on noise, we know that these observations should be rejected. What went wrong? Given the large number of potential co-variables, just by chance it is likely that some of the simulated variables will be able to discriminate the responders from the nonresponders. Although each model provided a reasonable fit to the data it was trained on, it will unlikely provide a good fit to an independent data set. To reduce the likelihood of overfitting, cross-validation applied to the variable selection process and the logistic model, needs to be employed.

Figure 3.

An illustration of noise discovery due to overfitting using the logistic regression model.

There are two types of validation: external and internal. External validation is the most rigorous approach where the frozen model trained on the study data is applied to an independent data set.^36,37 Ideally, investigators would have an independent data set available for validation purposes, although this is rarely available.²⁷ Other types of internal validation such split-sample, cross-validation, and bootstrapping are used to obtain an unbiased estimate of predictive accuracy.³⁷

In split-sample validation, the data set is randomly divided into two groups: a learning dataset where the model is developed, and a testing set where the model performance is evaluated. This is a critical process as improperly distributed imbalances by outcomes or predictors may occur and produce unreliable estimate of model performance.

Cross-validation is a generalization and thus similar to data splitting. With this approach one fits a model based on a random sample before subsequently testing it on the sample that was omitted. For example, in 10-fold cross validation, 90% of the original sample is used to train the model and 10% of the sample is used to test it. This procedure is repeated 10 times, such that all subjects have once served to test the model. To obtain accurate estimates using cross-validation, more than 200 models need to be fitted and tested with the results averaged over the 200 repetitions. The major advantage of cross-validation over data-splitting is that the former reduces variability by not relying on a single sample split.

Bootstrapping is a very effective technique of deriving reliable estimates without making any assumptions about the distribution of the data.³⁸ The bootstrap does with a computer what the experimenter would do in practice if it were possible: he/she would repeat the experiment. In bootstrap, the observations are randomly drawn with replacement and reassigned, and estimates are recomputed.

Bootstrapping reflects the process of sampling from the underlying population. Bootstrap samples are drawn with replacement from the original sample. They are of the same size as the original sample. For example, when 500 patients are available for model development, bootstrap samples also contain 500 patients, but some patients may not be included, others once, others twice, others three times, etc. As with cross-validation, the drawing of bootstrap samples needs to be repeated many times to obtain stable estimates.

We have reviewed a number of re-sampling approaches for validating the predictive ability of a prognostic model. It should be noted that these approaches may not be sensitive enough to reveal noise-discovery. Consider, for example, a rare outcome. As the number of cases, compared to the number of controls, is relatively small, the cross-validation procedure may produce results that are overly optimistic. Another layer of re-sampling may be needed to further investigate the result from the validation study. One approach is to randomly permute the outcome and then repeat the validation process.³⁹ Note that by virtue of shuffling the outcome, we break any potential relationship between the outcome and the co-variables. As such, we would anticipate that any model trained on these random outcomes would not display good predictive ability. To carry out the analysis, the predictive performance of the noisy data is compared to that of the observed data by repeating the permutation process several times. If the performance under the noisy data is comparable to that of the observed data, noise discovery should be suspected.

In summary, prognostic studies can address important questions that are relevant to patient outcomes, however they must be rigorously and carefully designed to ensure that we obtain reliable results. Such studies should begin with a hypothesis, defining a priori the endpoint, justifying the sample size, specifying appropriate variable selection approaches, testing robustness of the models applied, and using the REMARK guidelines to report on the results. It is vital to validate prognostic factors so that we understand prognosis and minimize uncertainty in predicting outcome in future patients.