Abstract
The projected height of an object in a scene relative to a ground surface influences its perceived size and distance, but the effect of height should change when the object is moved above the horizon. In four experiments, observers judged relative size or relative distance for pairs of objects varying in height with respect to the horizon. Higher objects equal in projected size were judged larger below the horizon, but the relative size effect was reversed either when one object was on the horizon and one was above the horizon or when both objects were above the horizon. With the real horizon not explicitly present in the display, relative size judgments were affected both by the boundary of the visible surface and the vanishing point implied by the converging lines. For relative distance judgments, the higher object was judged more distant regardless of the height of the objects relative to the perceptual horizon, resulting in a reversal of the relation between size and distance judgments for objects above the horizon.
The role of background surfaces in determining the perceived layout of objects was a major component of Alhazen’s (c. 1039/1989) theory of depth perception. Gibson (1950) highlighted the role of ground surfaces in the perception of the visual world, presenting ground theory as an alternative to “air theories,” which considered only distances between the eyes and objects in empty space as an account of depth perception. He showed how the perceived position of an object in a scene could be determined by optical contact — the location at which the image of the object contacted the image of the ground surface. He also showed how optical contact could be misleading if the object was not in physical contact with the ground surface.
Recent research extending Gibson’s ideas has confirmed that a background surface, especially a ground surface, provides crucial information about the position of an object in a 3-D scene. Meng and Sedgwick (2001, 2002) showed that the positions of objects that were not in physical contact with the ground could be perceived through mediated contact relations, that is, information about an object’s position on an intermediate surface and about the position of the intermediate surface relative to the ground. Ni, Braunstein and Andersen (2004, 2005, 2007) showed that the positions of floating objects can be determined from a combination of optical contact with a ground surface and other distance information, including motion parallax, shadow and occlusion.
The ground surface does not typically extend throughout a natural 3-D scene, but terminates at the horizon, or below the horizon if the horizon is obscured. The importance of the horizon has been demonstated in studies of perceived distance and perceived size of objects on a ground plane. As an indicator of eye level, the horizon may have a role in the perception of absolute distance to objects displayed against a ground plane. For example, the distance on an object along a continuous, level ground surface can be computed using eyeheight and angular declination — the angle between a horizontal line of sight and a line of sight to the object (Sedgwick, 1983; Ooi, Wu & He, 2001). Use of angular declination to recover absolute distance requires accurate perception of eye level, that is, the line of sight to the horizon, although there are other indicators of eye level available in the absence of a visible horizon (Matin & Li 1994, 1995; Sedgwick 1983, 1986; Stoper & Cohen 1986). Recently, linear perspective information on ground surfaces (Wu, He, & Ooi, 2007) and the focus of expansion of the optic flow (Wu, He, & Ooi, 2005) also have been found to influence perceived eye level.
The depth cue of height in the visual field (Epstein, 1966; Gardner & Mon-Williams, 2001; Gibson, 1950; Philbeck & Loomis, 1997; Sedgwick, 1986; Wallach & O’Leary, 1982) is closely related to, and sometimes equated with, angular declination (Wu, 2004 ) and may be based on the presence of an implicit or explicit horizon. For example, Epstein (1966) demonstrated that the interpretation of height in the field information depends on the type of background surface against which objects were presented: With a ground surface the higher object appeared to be further away, but with a ceiling surface the lower object appeared to be further.
The position of the horizon is also relevant to the Sequential-Surface-Integration-Process (SSIP) proposed by He et al (2004) to explain the reduction in perceived distance on discontinuous surfaces. The SSIP hypothesis is based on two assumptions: (1) Ground surfaces are perceived as having 90° degree slant1 only when sufficient depth cues are available at near distances, and (2) the perceptual system has an intrinsic bias to perceive a ground surface as slanted with its far end upward. According to the SSIP hypothesis (He et al., 2004; Wu, Ooi & He, 2004), the visual system constructs the representation of the near ground surface (no more than 2 to 3 m) by using the reliable near depth cues (e.g., vergence, binocular disparity, etc.), and then uses the near surface patch as a template to integrate adjacent patches into a holistic representation of the ground surface. If there is a discontinuity in the texture, the template based on near depth cues cannot be applied to more distant surfaces and the visual system relies more on the intrinsic bias, which leads to a representation of far surfaces as slanted and an underestimation of distances (Sinai, Ooi, & He, 1998; Feria, Braunstein, & Andersen, 2003). The perception of the ground plane as slanted upward would place the perceptual horizon2 for that plane closer than the actual horizon for the ground surface.
The horizon may be used also in the perception of the size of objects on the ground surface. The horizon-ratio, which is the ratio of the distance from the base of an object to its top to the distance from the base of the object to the horizon, has been shown to be a source of information for the perception of spatial relations in pictures (Sedgwick, 1973, 1980, 1986; Rogers, 1996). Rogers (1996) reported that the horizon-ratio provides information for relative size judgments when the horizon line is explicitly present and that the judgments can also be based on an implicit horizon, which is defined either by the eye height of the observer or the content of a picture. Sedgwick (1980) also noted that an imaginary horizon might allow the estimation of relative size and relative layout of objects. If the visible ground surface terminates below the actual horizon, because of a barrier blocking the observer’s view of the horizon for example, the observer might use the termination of the ground surface as an approximation to the horizon. Use of such an approximation in the horizon-ratio computation will result in a larger perceived size, with the extent of the error dependent on the distance of the actual horizon from the horizon used in the computation (Sedgwick, 1983, 1986).
The perspective information in a scene can potentially be used by the visual system to derive an implicit horizon when the actual horizon is not visible. In a 2-D projection of a 3-D scene, parallel lines present in the physical world converge at an infinitely distant point called the vanishing point. The vanishing point of parallel lines determines the height of the horizon. It has been proposed that when the vanishing point is not explicit in a scene, the observer can locate the horizon by extrapolating converging lines in the image which are parallel lines in the physical world (Gibson, 1979; Sedgwick, 1986; Wu, Ooi, & He, 2003).
The present study will consider the effects of the location of the perceptual horizon on judgments of object size and judgments of object distance. According to the size-distance invariance hypothesis (SDIH; e.g., Kilpatrick & Ittelson, 1953), perceived size is determined by a combination of retinal size and information specifying distance. Although both size and distance judgments have been shown to be influenced by the perceptual horizon, the relation between size and distance judgments is not always consistent with the predictions of SDIH (Ono, Muter, & Mitson, 1974; Mon-Williams, & Tresilian, 1999). Information indicating increasing distance may result in an increase in judged size but a decrease in judged distance. This “paradox” has been explained by a cognitive bias to judge objects that appear larger to be closer, even though perceptual information for distance indicates that the object is more distant (Epstein, Park & Casey, 1961; Gogel, 1978; Heinemann, Tulving & Nachmias, 1959). An alternative explanation for the failure of the SDIH to account for the results of studies involving size and distance judgments is that each judgment uses different perceptual processes. The judgments may be correlated when the information used by each process is similar, but the two types of judgments can be made independently. Use of the horizon-ratio in the perception of size, for example, does not require information specifying distance (Sedgwick 1973).
The purpose of the present study was to determine how the perception of objects in a scene is altered as the objects are moved from positions below the horizon, where they have ground contact, to positions above the horizon. We considered two related factors that might affect this change: whether the horizon is explicit in the scene, and where the visible surface terminates, if the horizon is not explicit. We hypothesized that the perceived extent of a background surface is affected both by the location at which the visible surface terminates and also by the implicit height of the horizon derived by extrapolating converging lines. The perceived extent of the surface, derived from both sources of information, should affect both the perceived size and the perceived distance of objects.
In the first experiment we examined the effect on relative size judgments of placing a pair of vertically separated objects below, at or above the horizon in a scene containing either a ground surface, a ceiling surface, or both surfaces represented by patterns of converging lines. The second experiment replicated the ground surface conditions using photographs of actual scenes. Conditions in which the horizon was specified by an implicit or explicit vanishing point were compared in the third experiment. In the fourth experiment we compared relative distance judgments to relative size judgments using real scene backgrounds.
EXPERIMENT 1: GROUND AND CEILING PLANES
Experiment 1 considered the effect of the location of objects with respect to the horizon on relative size judgments. Our primary interest was in positions relative to the ground surface horizon, based on several recent studies showing the superiority of ground planes to ceilings in the perceptual representation of the 3-D world (for example, Bian, Braunstein, & Andersen, 2005; McCarley & He, 2000, 2001). Ceiling surfaces, and a no-background condition, were included in the first experiment for comparison.
Method
Observers
The observers were 4 undergraduate students at the University of California, Irvine. They were naïve regarding the purpose of the experiment, and all had normal or corrected to normal visual acuity (20/40 measured with a Snellen eye chart). All received course credit for their participation.
Stimuli
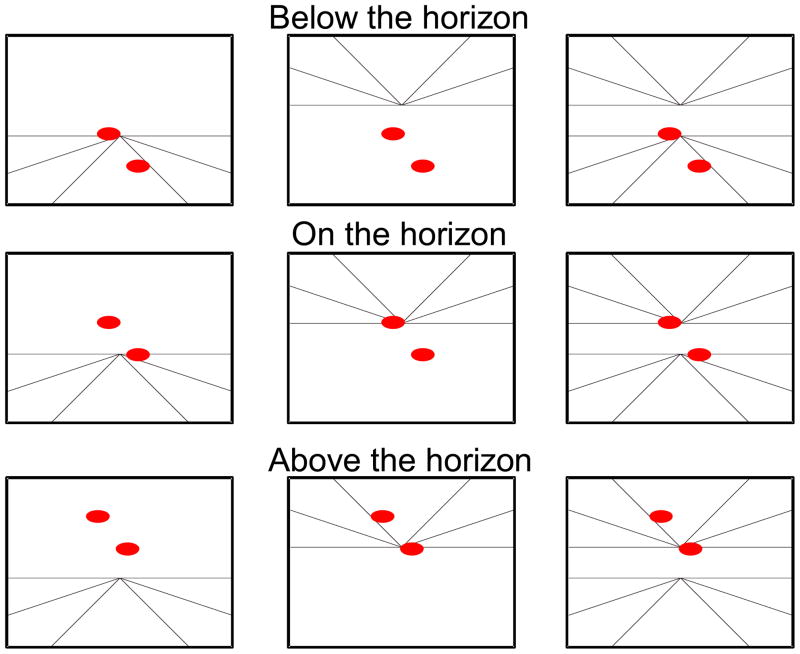
The stimuli were computer-generated line drawings that represented ground and ceiling planes and two wireframe ellipses, with horizontal major axes, that were equal in projected size (see Figure 1). Ground and ceiling surfaces were drawn by projecting a set of parallel lines onto a projection plane as lines converging toward a single vanishing point. In both surfaces, the vanishing point was explicit and represented the location of the horizon for that surface, which corresponded to the furthest visible point on the surface. In order to examine the effects of the ellipse positions relative to the ground and ceiling surfaces separately, non-overlapping horizon lines were drawn for the two surfaces, centered about the observer’s eyeheight at 12.6 cm and 18.4 cm from the bottom of the display. Taking into account the lens magnification, this resulted in simulated surface slants of 95.7° for the ground surface and −95.7° for the ceiling surface. The stimulated distance from the observer to the closest point on both the ground and ceiling surfaces was 298 cm. The simulated distance of the farthest point on each surface, the vanishing point, corresponded to infinity. The calculations of the scene dimensions were based on the eye-height of the seated observer, which was 120 cm.
Figure 1.
Displays used in Experiment 1. In the actual displays the lines were black, the ellipses were light green and the background was a medium green. The labels refer to the position of the lower ellipse relative to the height of the ground horizon.
The dimensions of each surface (ground and ceiling measured separately) on the monitor were 48 cm (W) X 12 cm (H), subtending a visual angle of 68.9° X 19.4°. The major and minor axes of the ellipses were 2.5 cm and 0.6 cm, subtending visual angles of 4.1° and 0.98°, respectively. The calculations of the visual angles are based on a viewing distance of 42 cm and take into account a 20 % magnification by the collimating lens which was placed between the observer and the displays.
Design
There were two independent variables in the first experiment: (1) the background condition (ground only, ceiling only, ground and ceiling and no background), and (2) the height of the ellipse pairs. Two ellipses appeared in each scene with the horizontal major axes positioned either both below the ground horizon, both above the ceiling horizon, or one at the ground horizon and one at the ceiling horizon. In these three ellipse height conditions, the centers of the ellipses, measured from the bottom of the image, were 5.1 and 10.9, 12.6 and 18.4, or 20.1 and 25.9 cm.3 Objects labeled “on the horizon” were centered vertically on the horizon line. The simulated distances to the bottoms of the ellipses, relative to the ground surface, or to the tops of the ellipses relative to the ceiling surface, were 550 cm for the 5.1 and 25.9 cm heights, 1467 cm for the 10.9 and 20.1 cm heights, and 7339 cm for the 12.6 and 18.4 cm heights. The vertical separation of the ellipses was 5.8 cm. Which of the two ellipses, either the left ellipse or the right ellipse, was presented in the higher position on the screen was counterbalanced across trials.
Apparatus
The displays were presented on a 21-in. (53-cm) flat screen Sony CRT monitor with pixel resolution of 1024 X 768. Observers viewed the displays monocularly through a viewing tube with a collimating lens which magnified the images by approximately 20%. The distance between the observer’s eye and the lens was 5 cm, and the distance from the eye to the monitor was 42 cm. The center of the viewing tube was aligned with the center of the display and was 120 cm above the floor and 15.5 cm above the bottom of the image. The observer’s eye was aligned with the center of the viewing tube. The viewing tube between the observer and the monitor maintained the appropriate viewing distance and prevented the observer from seeing the borders of the screen in order to increase the perceived depth of the images. The purpose of the collimating lens was to remove accommodation as a flatness cue and thus increase perceived depth in the 2-D projections of the 3-D scenes.
Procedure
The experiment was run in a dark room. The observers were requested to use the eye with which they felt more comfortable in looking through the viewing tube and instructed to use the same eye throughout the experiment. In each trial, a scene with two ellipses was presented continuously until the observer responded. The task of the observers was to determine which of the two ellipses appeared to be larger. They were instructed to base their judgments “on 3-D appearances” and not to “try to use knowledge about the physical layout or any type of deliberate computations.” They pressed either the right or left button of a mouse to indicate whether the left or the right ellipse appeared larger. After the observer responded, a blank green screen appeared for 1 second prior to the next trial.
Each of the 12 conditions (4 backgrounds X 3 heights) was repeated 10 times, for a total of 120 trials. Trials were presented in two equal blocks, with a rest period between blocks. Each block started with 12 practice trials. The order of the trials within a block was randomized.
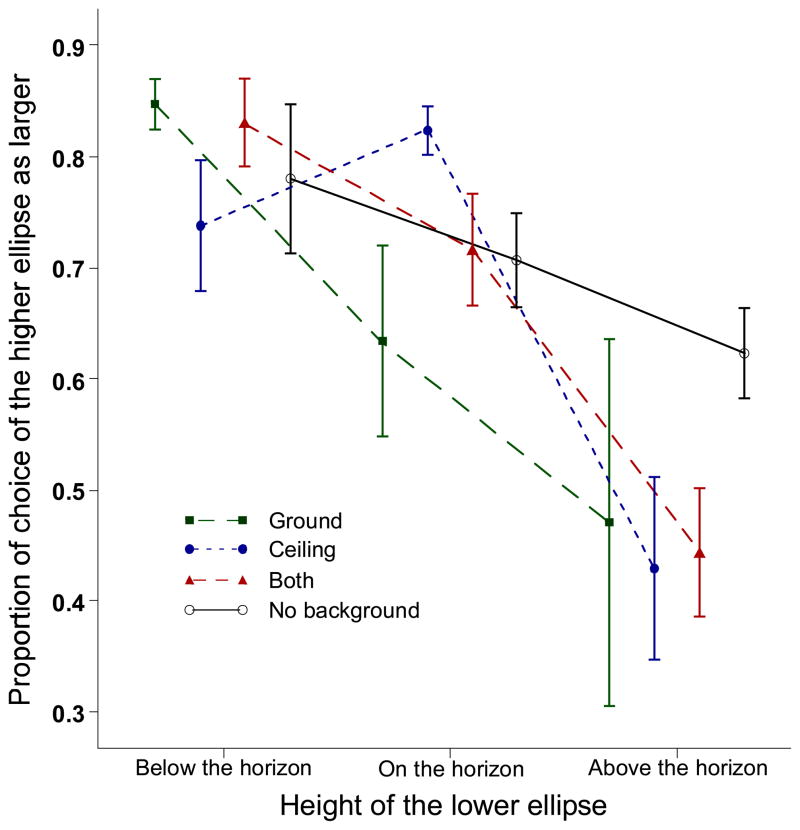
Results and Discussion
The proportion of trials in each condition in which the higher ellipse was selected as appearing larger was determined for each observer. As shown in Figure 2, for the ground surfaces the higher of the two ellipses was judged to be larger when the lower ellipse was below the horizon (see Figure 1, upper left panel), but judged to be smaller when the lower ellipse was above the horizon (see Figure 1, lower left panel). This effect of horizon location was also found for ceiling surfaces, but in a reversed order: The higher ellipse was judged to be smaller when it was above the ceiling horizon, but judged to be larger when it was below the ceiling horizon.
Figure 2.
Effect of the location of objects relative to the ground horizon on the proportions of choice of the higher object as larger for the four background conditions in Experiment 1. Error bars represent ±1 standard error.
A two-way analysis of variance (ANOVA), using an arcsine square-root transformation of the proportions, showed a significant main effect for height [F (2, 6) = 10.51, MSE = 0.039, p < .05, η2 = 0.79] and a significant interaction effect between height and background surface, [F (6, 18) = 4.31, MSE = 0.007, p < .01, η2 = 0.59]. For ground only conditions, a Tukey HSD post hoc test found a significant difference between height conditions above and below the horizon (p < .01), and also between below and on the horizon conditions (p < .05). For ceiling only conditions, a Tukey HSD test found a significant difference between height conditions below and above the horizon (p < .01) and also between on and above the horizon conditions (p < .01). For conditions with both ceiling and ground surfaces, significant differences between conditions below and above the horizon (p < .01), and also between on and above the horizon (p < .01) were found. No significant differences were found for conditions without a background surface. The main effect for the background surface was not significant [F (3, 9) = 0.33, MSE = 0.019, p > .05].
These results indicate that the perceived relative size of objects in a scene depends on both the position of objects relative to the background surface and on their location relative to the horizon. This suggests that perceived layout of objects in a scene is influenced by the location of the objects relative to the horizon.
EXPERIMENT 2: SIZE JUDGMENTS WITH REAL SCENE BACKGROUNDS
In the first experiment, using line drawings that represented ground and ceiling surfaces, we found that the location of objects in relation to the horizon significantly affects relative size judgments. The purpose of the second experiment was to determine whether this effect would generalize to real scene backgrounds.
Method
Observers
The observers were 4 undergraduate students at the University of California, Irvine. All met the same visual-acuity requirements as in Experiment 1 and were naïve to the purpose of the experiment. They received course credit for their participation.
Stimuli
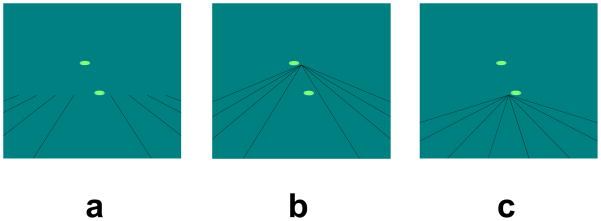
The stimuli were two real scene images with visible horizons (Figure 3) selected from the NOAA image database (http://www.photolib.noaa.gov). Two computer-generated cylinders were superimposed on each scene with varying heights relative to the horizon. The projected height and width of the cylinder were 3 cm and 4.7 cm, subtending visual angles of 4.9o and 7.6o, respectively. The height of the center of the lower cylinder above the bottom of the image was 10.8, 15.3, 19.8 or 24.3 cm. The center of the higher cylinder was 4.5 cm above that of the lower cylinder. The horizon was approximately 19.8 cm above the bottom of the image.
Figure 3.

Examples of the stimuli in Experiment 2: (a) objects on and below the horizon, (b) objects on and above the horizon.
Design
There were two independent variables: the background scene and the height of the cylinders. Two different real scene images were used to control for effects of scene specific variations. The cylinders were either both below the horizon (height 1), one below and one on the horizon (height 2), one on and one above the horizon (height 3) or both above the horizon (height 4). As in the Experiment 1, the vertical separation between the cylinders was constant. In each trial, either the left or the right cylinder was higher and this was counterbalanced across trials.
Apparatus
The apparatus was the same as in Experiment 1.
Procedure
The procedure was the same as in Experiment 1. The task of the observers was to indicate which of the two cylinders appeared to be larger.
Each of the 8 conditions (2 scenes X 4 heights) was repeated 10 times, for a total of 80 trials. Trials were presented in two blocks with an equal number of trials in each block and a rest period between blocks. Each block was preceded by 8 practice trials.
Results and Discussion
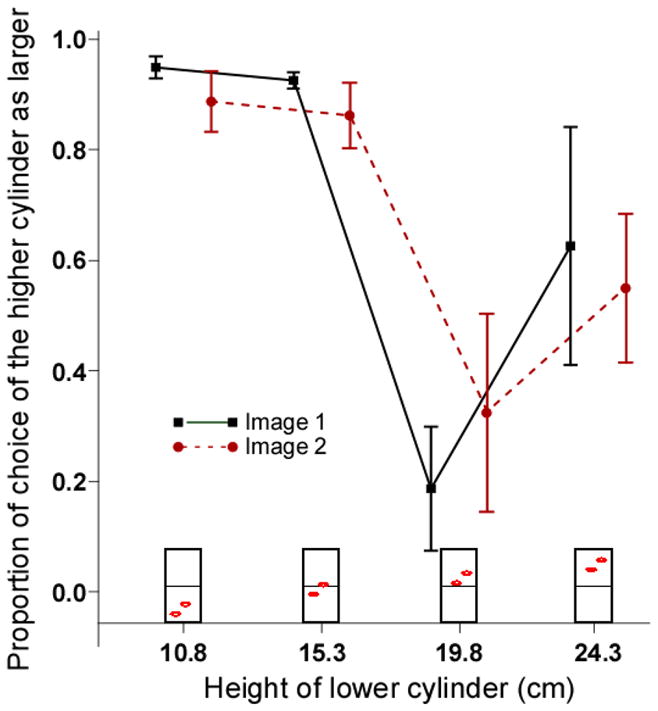
As in the first experiment, the proportion of trials in each condition in which the higher ellipse was selected as appearing larger was determined for each observer. As shown in Figure 4, the higher of the two cylinders was judged to be larger when both were below the horizon. When the lower cylinder was at or above the horizon, however, the higher cylinder was most often judged to be smaller than the lower cylinder. When both cylinders were above the horizon, the lower cylinder was again judged to be smaller more often, but the proportions were close to chance. The effects were the same for both scene backgrounds.
Figure 4.
The effect of the location of objects relative to the horizon on the proportions of choice of the higher object as larger in real scene backgrounds in Experiment 2. Error bars represent ± 1 standard error.
The proportions of larger judgments were subjected to an arcsine square-root transformation. A two-way analysis of variance (ANOVA) of the transformed proportions showed a significant main effect of height [F (3, 9) = 9.62, MSE = 0.08, p < .01, η2 = 0.76]. A Tukey HSD post hoc test found a significant difference between height 1 and height 3 (p < .01) and between height 2 and height 3 (p < .01) for both images. The main effect of the two different real scene backgrounds and the interaction of scene background with cylinder height were not significant.
These results with real scene images were in accordance with the results found with line drawings of planes in Experiment 1. These two experiments together confirm the importance of the horizon location in determining perceived layout. The perceived layout of objects in a scene, inferred from relative size judgments, depends on the location of objects relative to the horizon as well as their height in the image.
Control Experiment
In Experiment 2, the cylindrical objects were kept constant in projected shape, regardless of their simulated height in the scene. The perspective was consistent with that of a cylinder on the ground, but not with a cylinder above the line of sight. To be sure that the relation between height in the image and the appropriateness of the projected shape did not influence the results of Experiment 2, we replicated this experiment using spherical objects. The projected shape of these objects, which was again constant across height conditions, was equally consistent with locations above and below the horizon.
The observers were four undergraduate students at the University of California, Irvine. They were naïve regarding the purpose of the experiment and none had participated in any other experiment in this study. All had visual acuity of 20/40 or better (measured with a Snellen eye chart) and all received course credit for their participation. Informed consent was obtained from all observers prior to the experiment. The stimuli were similar to those in Experiment 2, except that spheres instead of cylinders were inserted into the scenes and only the second background image from Experiment 2 was used.
The mean proportions of trials on which the higher sphere was judged larger were 0.70, 0.725, 0.275 and 0.225, for the four height levels (both spheres below the horizon, the higher sphere on the horizon, the lower sphere on the horizon and both spheres above the horizon). An ANOVA using an arsine transformation of the proportions showed a significant main effect of height [F (3, 9) = 6.44, p < .05 ]. The higher of the two spheres was judged to be larger when both were below the horizon. However, when the lower sphere was at or above the horizon, the higher sphere was judged to be smaller. These results replicated those of Experiment 2, indicating that the results of Experiment 2 cannot be attributed to the use of cylinders that did not change in their projected shape.
EXPERIMENT 3: EXPLICIT VS. IMPLICIT HORIZON LOCATIONS
The horizon defines the perceivable depth limit of a ground plane. It is a feature of the optic array, not of the physical environment (Rogers, 1996). What information in the optic array determines the perceived position of the horizon is still an open question. Sedgwick (1980, 1989) proposed that an implicit horizon might be recovered by extrapolating converging lines when the location of the horizon is not explicit in a scene. Sedgwick (1980) also suggested that the horizon location might be derived by just using the eye height, even when the horizon is not explicitly identified in the scene. Another possibility is that when the horizon is not explicitly present in a scene, the perceptual horizon might be determined by where the visible background surface terminates in the image (Sedgwick, 1983, 1986).
In the first two experiments, we found that for objects presented with a ground plane, the higher object was judged larger when the lower object was below the horizon, but when the lower object was at or above the horizon, the proportion of judgments of the higher object as larger was reduced, in some conditions falling below .5. In the present experiment, we considered whether the reduction in judgments of the higher object as larger for displays in which an explicit horizon was not present would be related to the height of the implicit horizon derived by extrapolating converging lines or the height at which the ground surface terminated. This will allow us to determine which information the perceptual system uses in perceiving the location of the horizon when it is not explicitly present in the optic array.
Method
Observers
The observers were 6 undergraduate students at the University of California, Irvine. All met the same visual-acuity requirements as in the first two experiments and received course credit for their participation.
Stimuli
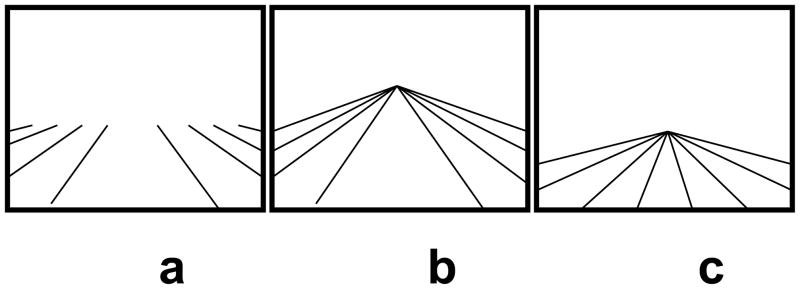
The stimuli were computer-generated line drawings that represented three different scene backgrounds, each with two wireframe ellipses similar to those in the first experiment (see Figure 5). For two of the background conditions (Figure 5a and Figure 5b), the simulated distance to the near point on the surface was 211 cm and the simulated slant was 86.1o. In these two conditions, the lines converged toward the same vanishing point (18.4 cm from the bottom of the image), but in one condition (Figure 5a) the lines were cut off at a distance of 12.6 cm from the bottom of the image (a simulated distance of 742 cm) and in the other (Figure 5b) the lines continued to the vanishing point. In these two background conditions, the simulated distances to ellipses at heights 1.2, 7.0, 12.8, 18.6 and 24.4 cm were 241 cm, 370 cm, 792 cm, 5538 cm and unspecified (above the horizon).
Figure 5.
Illustration of line drawing scenes used in Experiment 3: (a) Background 1 with the lines cut off below the vanishing point, (b) background 2 with the lines converging to a visible point, (c) Background 3 with the lines converging to a point at the Background 1 cut-off height.
In the third background condition (Figure 5c), the lines converged to an explicit vanishing point matched to the cut-off point of the lines in the first background condition. The simulated distance to the nearest visible point on the surface in this condition was 298 cm and the simulated slant was 93.9°. The simulated distances to ellipses at heights 1.2, 7.0, and 12.8 were 571 cm, 3350 cm and 8270 cm. Ellipses at heights 18.6 and 24.4 cm were above the horizon.
The dimensions on the monitor of the region of the background surface containing visible lines on the monitor were 48 cm (W) X 12.6 cm (H), subtending a visual angle of 68.9° X 20.4o for the two backgrounds for which the cut-off point and vanishing point heights were matched (Figures 5a and 5c). For the background with the higher visible vanishing point (Figure 5b), these dimensions were 48 cm (W) X 18.4 cm (H), subtending a visual angle of 68.9° X 29.5°. The calculations of the visual angle are based on a viewing distance of 42 cm and take into account a 20 % magnification by the collimating lens. The major and minor axes of the ellipses were the same as in the first experiment.
Design
There were two independent variables: background condition (3 levels) and height of the ellipses (4 levels). The background conditions were: (1) a ground plane without an explicit vanishing point (converging lines were cut off before reaching the vanishing point) (Figure 5a), (2) a ground plane with the lines converging to the same vanishing point as in the first condition, but with the vanishing point explicit (Figure 5b), and (3) a ground plane with an explicit vanishing point at the height at which the visible surface was cut off in the first condition (Figure 5c).
The height of the center of the lower ellipses above the bottom of the image was 1.2, 7.0, 12.8 or 18.6. The center of the higher ellipse was 5.8 cm above that of the lower ellipse. In height condition 1, both ellipses were on the ground surface. In height condition 2, the lower ellipse was on the ground surface and the higher ellipse was at the cut-off point (background 1), on the ground surface (background 2) or at the vanishing point (background 3). In height condition 3, the lower ellipse was at the cut-off point (background 1), on the ground surface (background 2), or at the vanishing point (background 3) and the higher ellipse was at the implicit or explicit vanishing point (backgrounds 1 and 2) or above the vanishing point (background 3). In height condition 4, the lower ellipse was at the implicit or explicit vanishing point (backgrounds 1 and 2) or at the vanishing point (background 3) and the higher ellipse was above the vanishing point in all background conditions. The vertical centers of objects “at the vanishing point” were 0.2 cm above the vanishing point (or equivalently, 0.2 cm above the implied horizon). Which of the two ellipses, either the left ellipse or the right ellipse, was presented in the higher position on the screen was counterbalanced across trials.
Apparatus
The apparatus was the same as in the previous experiments.
Procedure
The procedure was the same as in Experiment 1. On each trial, observers viewed the display monocularly through the viewing hood and a scene consisting of computer-generated line drawings with two ellipses was presented continuously until the observer responded. The observer’s task was to indicate which of the two ellipses appeared to be larger.
Each of the 12 conditions (3 different backgrounds X 4 heights) was repeated 10 times, for a total of 120 trials. Trials were presented in two equal blocks, each starting with 24 practice trials, with a rest period between blocks. The order of the trials within a block was randomized.
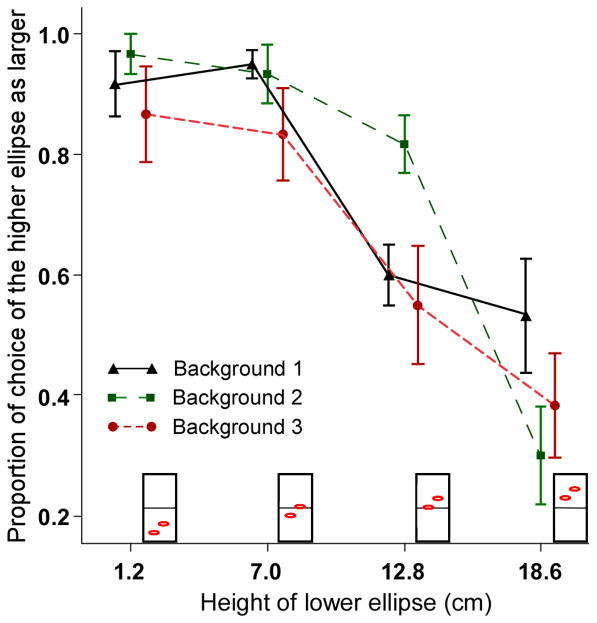
Results and Discussion
Figure 6 shows the proportion of trials on which the higher ellipse was selected as larger, averaged across observers, for the three background and four height conditions. A within-subjects ANOVA using an arcsine square-root transformation of the proportions for each observer revealed a significant main effect of height, [F (3, 15) = 10.49, MSE = 0.032, p < .01, η2 = 0.67]. The ANOVA also revealed a significant main effect of background surface, [F (2, 10) = 6.95, MSE = 0.004, p < .05, η2 = 0.58], but the interaction between the background surface and the height of the ellipse pair was not significant [F (6, 30) = 2.05, MSE = 0.009, p>.05]. As in the first two experiments, the proportion of trials on which the higher ellipse was selected as appearing larger varied with the height of the ellipse pairs.
Figure 6.
Proportion of choice of the higher object as larger for three background and four height conditions in Experiment 3. Error bars represent ± 1 standard error.
In this experiment, our main concern was with the differences between the ground surfaces. We wanted to see whether the relation between the height of the objects in the image and judgments of relative size with an implicit vanishing point implied by converging lines was similar to that found with a visible vanishing point at the height that the texture was cut off or to that found with a visible vanishing point at the height of the implied vanishing point. This would help us understand whether observers extrapolate the converging lines and perceive the horizon at the vanishing point or perceive the horizon where the visible surface ends. The critical ellipse height level for comparing the effects of the height of the vanishing point and the effects of the height of the visible boundary of the surface is level 3. Figure 7 shows this ellipse height condition for each of the three backgrounds. For Background 1, one ellipse is at the height at which the ground plane terminates and the other ellipse is at the implicit horizon. For Background 2, one ellipse is on the ground surface and the other is at the higher vanishing point. For Background 3, one ellipse is at the vanishing point and the other is above the horizon. If observers derived the horizon location by extrapolating the converging lines to a vanishing point, we would expect judgments for Background 2 to be similar to those for Background 1. On the other hand, if the perceived horizon is at the end point of the visible ground surface and observers fail to extrapolate the converging lines accurately, then Background 2 and Background 3 should have similar judgments. As seen in Figure 6, the results for Background 1 and Background 3 for ellipse height level 3 were closer to each other than to the Background 2 results. Planned pairwise comparisons with Bonferroni correction were computed for the three background conditions at height 3. The only significant difference was between Backgrounds 2 and 3, the conditions with visible vanishing points at different heights (t (5) = 3.99, p < .016). Planned comparisons between Backgrounds 1 and 2 (t (5) = 0.54, p > .016) and between Backgrounds 1 and 3 (t (5) = 2.33, p > .016) did not show significant differences.
Figure 7.
Positions of ellipses at height 3 for three different background surfaces in Experiment 3. If the perceptual horizon is at the implied vanishing point, then relative size judgments should be similar for Backgrounds 1 and 2. However, if the perceptual horizon is at the cutoff level of surfaces, then Backgrounds 1 and 3 should reveal similar relative size judgments.
The finding that the mean proportions for Background 2 and Background 3 are significantly different from each other, but that the mean proportion for Background 1 is in between those values, suggests that the location of the perceptual horizon may not be solely determined either by the implicit vanishing point or by the point at which the ground surface terminates, but may be affected by both factors (Sedgwick, 1983, 1986). The greater proximity of the Background 1 results to those of Background 3, rather than Background 2, suggests that the height of the visible texture may be more important in determining the location of the perceptual horizon than the height of the vanishing point indicated by the converging lines. Consequently, recovering the horizon location by extrapolating converging lines to locate the vanishing point, as suggested by most of the previous studies (e.g., Gibson, 1979; Sedgwick, 1983; 1986; Wu, Ooi & He, 2003), does not completely explain the recovery of a horizon location for scenes in which the horizon is not visible.
EXPERIMENT 4: COMPARISON OF SIZE AND DISTANCE JUDGMENTS IN REAL SCENE IMAGES
The previous experiments demonstrate that relative size judgments are affected by the positions of objects in relation to a visible or implied horizon. For the real scenes in Experiment 2, with the lower object positioned on the horizon, the upper object was more likely to be judged as larger than when both objects were below the horizon. The present experiment considers whether a similar effect of the position of objects relative to the horizon occurs for distance judgments, using the real scene backgrounds that were studied in the second experiment.
Method
Observers
The observers were 9 undergraduate students at the University of California, Irvine. All met the same visual-acuity requirements as in the previous experiments and were naïve to the purpose of the experiment. They received course credit for their participation.
Stimuli
The stimuli were the same as in Experiment 2.
Design
The design of this experiment was similar to that of Experiment 2. There were two independent variables: the background image (the same two images as in Experiment 2) and the height of the cylinders (the same 4 heights as in Experiment 2: the center of the lower ellipse was 10.8, 15.3, 19.8 or 24.3 cm above the bottom of the image; the center of the higher ellipse was 4.5 cm above that of the lower ellipse). The present experiment differs from Experiment 2 in that there were two dependent variables: size judgments and distance judgments.
Apparatus
The apparatus was the same as in the previous experiments.
Procedure
The procedure was similar to that used in Experiment 2, except that observers performed two tasks. One task was to determine which of the ellipses appeared to be larger as in the previous experiments. The other task was to determine which of the two ellipses appeared closer. The instructions for that task were the same, except that observers were asked to judge which object appeared “closer” instead of which object appeared “bigger.”
Observers judged the relative size or distance of cylinders in separate blocks. Each of the 8 conditions was repeated 10 times for both size and distance tasks, making a total of 160 experiment trials. The size and distance blocks each started with 16 practice trials. The order of the tasks was counterbalanced among observers.
Results and Discussion
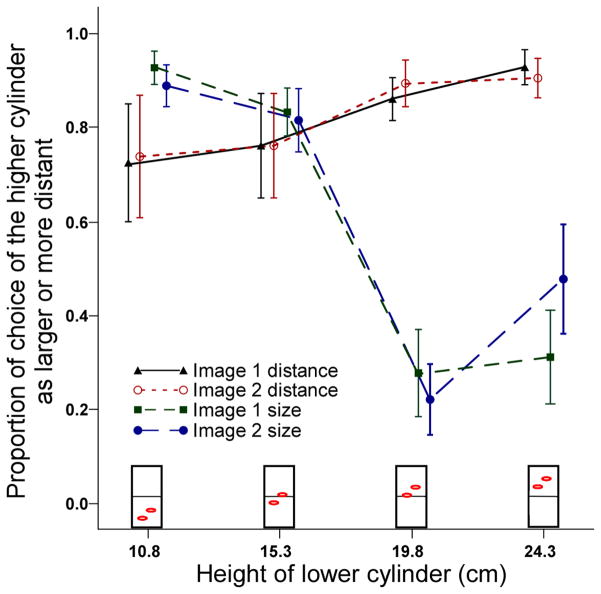
The proportion of trials on which the higher cylinder was judged as larger or closer, averaged across observers, is shown in Figure 8 for the two scenes and four object heights. A within subjects analysis of variance (ANOVA) using an arcsine square root transformation of the proportions for each observer in each condition in the size judgment block revealed a significant main effect of height, [F (3, 24) = 24.76, MSE = 0.075, p < .01, η2 = 0.76]. The main effect of scene type and the interaction were not significant. These results are in accordance with the findings from Experiment 2, showing that relative size judgments reverse according to the height of the objects relative to the horizon.
Figure 8.
Proportions of trials in which the higher object was judged to be larger in the size judgments or more distant in the distance judgments in Experiment 4. Error bars represent ± 1 standard error.
In the distance block, the observers always judged the lower disk as closer. The proportions of choosing the higher ellipse as more distant for all 8 conditions were above .5, ranging from 0.72 to 0.93 (M=0.82, SD=0.08). The main effects of image type, F(1, 8) = 0.22, and of height, F(3, 24) = 1.55, and the interaction, F(3, 24) = 0.5, were not significant (p > .05). The relation between the size and distance judgments reversed depending on the positions of the objects relative to the horizon. When both objects were below the horizon, the higher object was judged to be further back and judged to be larger, but when the lower object was presented on the horizon, the higher object was judged to be further back and judged to be smaller (see Figure 8).
GENERAL DISCUSSION
In a series of experiments, we examined the effect of information specifying the location of the horizon on judgments of relative size and distance for objects displayed against scene backgrounds. We found that size judgments appear to be determined by the location of the objects relative to the perceptual horizon, whereas distance judgments appear to be determined by height in the image. When two objects equal in projected size were presented in a scene with a ground plane, the higher of the two objects was judged to be larger if the lower object was below the horizon. The higher object was judged to be smaller, however, when the lower object was at the horizon. This was true for both real scene images and line drawing scenes. This effect of the height of objects relative to the horizon was also found with a ceiling surface, but in a reversed order. With both objects above the horizon, the proportion of choice of the higher object as smaller was reduced in most conditions, sometimes falling below .5, especially with real scene backgrounds.
The perceived position of objects displayed against a background surface can be determined by optical contact (Gibson, 1950, 1979), by mediated optical contact (Meng & Sedgwick, 2001, 2002) or by optical contact in combination with motion parallax, shadow and occlusion (Ni et al., 2004, 2005, 2007). When one or more objects is located above the horizon of a ground plane or below the horizon of a ceiling plane, optical contact information relative to a background plane is not available. This creates an infinite number of possible layouts for the objects. In our experiments, when the higher of two objects was presented above the horizon and the lower one was on the horizon, observers judged the higher object to be smaller than the lower one. Under the SDIH, this would indicate that visual system associates objects above the horizon with a position along the ground surface that is closer than the perceptual horizon.
We suggest two possible reasons for associating an object above the perceptual horizon with a closer position. The first possibility is that the visual system could be creating an optical contact relation between the floating object and the ground plane, for example, by drawing imaginary lines that connects the objects with the available surface. Where the floating objects are associated with the ground plane may be based on an assumption of symmetry — an assumption that the height above the horizon represents the same shift in depth as the height below the horizon, but with reversed sign. The other possibility is that the visual system could be assuming the presence of a ceiling plane and using optical contact with this implicit ceiling plane to determine the position of the objects. Epstein (1966) demonstrated that the interpretation of height in the field information depends on the type of background surface against which objects are presented. The higher object appears to be further back with a ground plane, but with a ceiling plane it is the lower object that appears more distant. Both explanations result in the same predictions if the ceiling plane is assumed to be symmetrical with the ground plane. Although objects presented above the perceptual horizon may be associated with positions along the ground surface that are closer than the horizon, there is likely to be more ambiguity in the perceived location of such objects than those presented at or below the horizon. These objects do not have ground contact with a visible or extrapolated ground plane. Our results with both objects above the horizon, especially with real scene backgrounds, reflect this ambiguity.
The possibility that objects above the horizon are associated with a surface — either the ground or an assumed ceiling — is suggested by studies supporting the importance of a surface representation in a variety of contexts, including visual search (He & Nakayama, 1992), motion perception (He & Nakayama, 1994a) and visual texture segregation (He & Nakayama, 1994b). . The importance of a background surface also has been demonstrated for the perception of the layout of objects in 3-D space (Meng & Sedgwick, 2001, 2002), which depends on optical contact or mediated optical contact with a background surface.
Where is the perceptual horizon?
The existence of an implicit horizon in the absence of visual information has been mentioned in previous studies (Sedgwick, 1980, 1986; Rogers, 1996). Rogers (1996) noted that the eye height of the observer could be used to determine an implicit horizon and that this implicit horizon could affect the perceived layout of objects in a scene. The angular declination rule (Ooi, Wu, & He, 2001) suggests that the visual system uses the angular declination below the horizon to judge the distance of objects and this rule also depends on using eye height to find the horizon and then locating objects in a scene relative to the horizon. Other evidence suggests that an implicit horizon can be constructed by extrapolating converging lines which are assumed to be parallel in the physical world to find the vanishing point (Gibson, 1979; Sedgwick, 1986; Wu, Ooi, & He, 2003). In the present study, we used the point at which relative size judgments reversed to estimate the location of the perceptual horizon. This was based on our finding that these judgments reversed when the higher of two objects was placed above a visible horizon.
In Experiment 3, using computer generated line-drawing scenes, we addressed the question of whether relative size judgments for a surface displayed with converging lines that were cut-off below the vanishing point would be more similar to judgments with an explicit vanishing point at the same height as the implied vanishing point or to judgments for a surface with an explicit vanishing point at the height at which the ground surface terminated. Our results suggest that the location of the perceptual horizon is affected both by the implied vanishing point and by the point where the ground surface terminates, but with greater emphasis given to the height at which the surface terminates.
Wu, He and Ooi (2007) identified two rules used by the visual system to represent scenes: (1) the visual systems assumes converging lines in the retinal image to be parallel lines in 3-D (the parallel line rule), and (2) the visual system uses the vanishing point of converging lines to locate the horizon which in turn determines the perceived eye level (the horizon rule). Wu et. al. (2007) showed that a parallel-line background significantly affects the perceived eye level, concluding that the parallel-line rule is an intrinsic rule which helps to sustain an accurate representation of background surfaces. The present results indicate that constructing the representation of scenes occurs as a result of a combination of an intrinsic rule (the horizon rule) and the external depth information (extent of the visible surface). We suggest that the use of the visible boundary by the visual system to locate the perceptual horizon may be regarded a decoding principle (Johansson, 1970) or a heuristic process (Braunstein, 1976, 1983, 1994) because it is theoretically possible to locate the horizon precisely using the horizon rule. Heuristic processes in perception are similar to heuristics in decision-making and are used to gain efficiency even though they do not provide a veridical percept all the time (Braunstein, 1994).
Size-Distance Invariance
According to the size-distance invariance hypothesis, when two objects at different distances subtend the same visual angle, the visual system perceives the closer object as smaller and the more distant object as larger. It has been suggested, however, that this perceived difference in size may cause observers to report that the more distant object is closer, a phenomenon known as a size-distance paradox (Gruber, 1954; Ono, Muter & Mitson, 1974). In Experiment 4, we compared size and distance judgments for objects displayed against real scene backgrounds. Our results showed that when the higher object was at or below the horizon, it was judged larger and more distant, consistent with the size-distance invariance hypothesis. This suggests that in the presence of a background surface, distance judgments are based on optical contact information. When the lower objects was on the horizon and the higher objects was above the horizon, however, the higher object was judged smaller but still more distant than the lower object, resulting in a paradoxical size-distance relation of the type found in the moon illusion.
Recent studies show that the variance in size-distance judgments, as well as the paradoxical size-distance judgments in the moon illusion, may be an instance of a response bias (Kaufman & Kaufman, 2000; Kaufman et al., 2006, 2007). Kaufman and Kaufman (2000) showed that the visual system responds as if the horizon moon is at a greater distance than the elevated moon, supporting the apparent distance theories of the moon illusion. Kaufman et al. (2007) developed an unbiased sensitivity measure for size and distance which showed that the sensitivity to illusory differences in the size and distance of the moon is in fact consistent with the size-distance invariance hypothesis. They suggested using the term “perceptual distance” instead of perceived distance to refer to an unbiased estimate of psychological distance, and to avoid the implication that one perception leads to another. For similar reasons, we use “perceptual horizon” rather than perceived horizon to refer to an estimate of a horizon position inferred from size or distance judgments.
The explanation for the paradoxical relation between size and distance judgments presented above may be regarded as unnecessarily indirect in suggesting that size judgments are based on a perceptual distance and explicit distance judgments may be based on a perceived size determined by that perceptual distance. An alternative explanation is that size and distance judgments, although they may use the same information, involve difference perceptual processes. In the present context, size judgments may be affected by the texture gradient on the ground surface, with a converging texture associated with increasing perceived size for objects that have the same projected size. Objects above the horizon may be associated with positions along the ground plane under an assumption of symmetry, as described above. For distance judgments, on the other hand, there may be a direct association of height in the visual field with greater distance, unless contradictory information is present. Size and distance judgments would thus correlate positively below the horizon, but could correlate negatively above the horizon. The present study does not distinguish between these two types of explanations. A similar discrepancy between perceived extent and perceived location has been reported by Foley, Ribeiro-Filho & Da Silva, 2004.
Overall, our results show that judgments of relative size for objects in a scene are affected by their locations relative to the perceptual horizon. The location of the perceptual horizon appears to be based on a combination of two sources of information: (1) the implied vanishing point, derived by the horizon rule and (2) the boundary of the visible surface. Finally, our results from the last experiment suggest that the height of the horizon affects size judgments, but distance judgments appear to be affected only by height in the image. Consequently, the relation between size and distance judgments for objects below the horizon is different from that found for objects above the horizon.
Acknowledgments
This research was supported by NIH grant EY18334. Portions of this research were presented at the 2006 and 2007 meetings of the Vision Sciences Society.
Footnotes
Stevens (1983) defines the slant of a surface as the angle between the line of sight and the surface normal. For a horizontal line of sight, a ground surface would have a slant of 90°. He et al. use an alternative definition, referred to as geographical slant (Sedgwick, 1986), according to which a ground surface would have a slant of 0°.
We use the term “perceptual horizon” rather than “perceived horizon” to avoid an implication of percept-percept coupling when referring to a subjective horizon location inferred from other perceptual judgments.
The projected size of the ellipses and their separation did not vary across trials. This could have reduced the effects of the independent variables if observers were attempting to make judgments based on the projected sizes and separations, but the systematic effects of height in the image in all conditions suggest that judgments were not based only on the projected sizes and separations of the ellipses in the images.
References
- Alhazen I. Book of optics. In: Sabra AI, translator. The optics of Ibn-Haytham. Vol. 1. London: University of London, Warburg Institute; 1039/1989. (Exact date is unknown. Alhazen died about 1039 C. E.) [Google Scholar]
- Bian Z, Braunstein ML, Andersen GJ. The ground dominance effect in the perception of 3-D layout. Perception & Psychophysics. 2005;67:815–828. doi: 10.3758/bf03193534. [DOI] [PubMed] [Google Scholar]
- Braunstein ML. Depth perception through motion. New York: Academic Press; 1976. [Google Scholar]
- Braunstein ML. Contrasts between human and machine vision: Should technology recapitulate phylogeny? In: Beck J, Hope B, Rosenfeld A, editors. Human and machine vision. New York: Academic Press; 1983. pp. 85–96. [Google Scholar]
- Braunstein ML. Decoding principles, heuristics and inference in visual perception. In: Jansson G, Bergstrom SS, Epstein W, editors. Perceiving Events and Objects. Hillsdale, NJ: Erlbaum; 1994. pp. 436–446. [Google Scholar]
- Epstein W. Perceived depth as a function of relative height under three background conditions. Journal of Experimental Psychology. 1966;72:335–338. doi: 10.1037/h0023630. [DOI] [PubMed] [Google Scholar]
- Epstein W, Park J, Casey A. The current status of size-distance hypothesis. Psychological Bulletin. 1961;58:491–514. doi: 10.1037/h0042260. [DOI] [PubMed] [Google Scholar]
- Feria CS, Braunstein ML, Andersen GJ. Judging distance across texture discontinuities. Perception. 2003;32:1423–1440. doi: 10.1068/p5019. [DOI] [PubMed] [Google Scholar]
- Foley JM, Ribeiro-Filho NP, Da Silva JA. Visual perception of extent and the geometry of visual space. Vision Research. 2004;44:147–156. doi: 10.1016/j.visres.2003.09.004. [DOI] [PubMed] [Google Scholar]
- Gardner PL, Mon-Williams M. Vertical gaze angle: absolute height-in-scene information for the programming of prehension. Experimental Brain Research. 2001;136:379–385. doi: 10.1007/s002210000590. [DOI] [PubMed] [Google Scholar]
- Gibson JJ. The perception of the visual world. Boston: Houghton-Mifflin; 1950. [Google Scholar]
- Gibson JJ. The Ecological Approach to Visual Perception. Hillsdale, NJ: Lawrence Erlbaum Associates; 1979. [Google Scholar]
- Gogel WC. The adjacency principle in visual perception. Scientific American. 1978;238:126–139. doi: 10.1038/scientificamerican0578-126. [DOI] [PubMed] [Google Scholar]
- Gruber HE. The relation between perceived size and perceived distance. American Journal of Psychology. 1954;67:411–426. [PubMed] [Google Scholar]
- He ZJ, Nakayama K. Surfaces versus features in visual search. Nature. 1992;359:231–233. doi: 10.1038/359231a0. [DOI] [PubMed] [Google Scholar]
- He ZJ, Nakayama K. Apparent motion determined by surface layout not by disparity or 3-dimensional distance. Nature. 1994a;367:173–175. doi: 10.1038/367173a0. [DOI] [PubMed] [Google Scholar]
- He ZJ, Nakayama K. Perceiving textures: Beyond filtering. Vision Research. 1994b;34:151–162. doi: 10.1016/0042-6989(94)90328-x. [DOI] [PubMed] [Google Scholar]
- He ZJ, Wu B, Ooi TL, Yarbrough G, Wu J. Judging egocentric distance on the ground: Occlusion and surface integration. Perception. 2004;33:789–806. doi: 10.1068/p5256a. [DOI] [PubMed] [Google Scholar]
- Heinemann EG, Tulving E, Nachmias J. The effect of oculomotor adjustments on apparent size. American Journal of Psychology. 1959;72:32–45. [Google Scholar]
- Johansson G. On theories for visual space perception: A letter to Gibson. Scandinavian Journal of Psychology. 1970;11:67–74. doi: 10.1111/j.1467-9450.1970.tb00719.x. [DOI] [PubMed] [Google Scholar]
- Kaufman L, Kaufman JH. Explaining the moon illusion. Proceedings of National Academy of Sciences USA. 2000;97:500–505. doi: 10.1073/pnas.97.1.500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman L, Kaufman JH, Noble R, Edlund S, Bai S, King T. Perceptual distance and the constancy of size and stereoscopic depth. Spatial Vision. 2006;19:439–457. doi: 10.1163/156856806778457377. [DOI] [PubMed] [Google Scholar]
- Kaufman L, Vassiliades V, Noble R, Alexander R, Kaufman J, Edlund S. Perceptual distance and the moon illusion. Spatial Vision. 2007;20:155–175. doi: 10.1163/156856807779369698. [DOI] [PubMed] [Google Scholar]
- Kilpatrick FP, Ittelson WH. The size-distance invariance hypothesis. Psychological Review. 1953;60:223–231. doi: 10.1037/h0060882. [DOI] [PubMed] [Google Scholar]
- Matin L, Li W. Spatial summation among coextensive and parallel line segments across wide separations (50°): Egocentric localization and the great circle model. Vision Research. 1994;34:2577–2598. doi: 10.1016/0042-6989(94)90244-5. [DOI] [PubMed] [Google Scholar]
- Matin L, Li W. Multimodal basis for egocentric spatial localization and orientation. Journal of Vestibular Research: Equilibrium & Orientation Special Issue: Spatial Orientation (AFOSR) 1995;5:499–518. [PubMed] [Google Scholar]
- McCarley JS, He ZJ. Asymmetry in 3-D perceptual organization: Ground-like surface superior to ceiling-like surface. Perception & Psychophysics. 2000;62:540–549. doi: 10.3758/bf03212105. [DOI] [PubMed] [Google Scholar]
- McCarley JS, He ZJ. Sequential priming of 3-D perceptual organization. Perception & Psychophysics. 2001;63:195–208. doi: 10.3758/bf03194462. [DOI] [PubMed] [Google Scholar]
- Meng JC, Sedgwick HA. Distance perception mediated through nested contact relations among surfaces. Perception & Psychophysics. 2001;63:1–15. doi: 10.3758/bf03200497. [DOI] [PubMed] [Google Scholar]
- Meng JC, Sedgwick HA. Distance perception across spatial discontinuities. Perception & Psychophysics. 2002;64:1–14. doi: 10.3758/bf03194553. [DOI] [PubMed] [Google Scholar]
- Mon-Williams M, Tresilian JR. The size-distance paradox is a cognitive phenomenon. Experimental Brain Research. 1999;126:578–582. doi: 10.1007/s002210050766. [DOI] [PubMed] [Google Scholar]
- Ni R, Braunstein ML, Andersen GJ. Perception of scene layout from optical contact, shadows, and motion. Perception. 2004;33:1305–1318. doi: 10.1068/p5288. [DOI] [PubMed] [Google Scholar]
- Ni R, Braunstein ML, Andersen GJ. Distance perception from motion parallax and ground contact. Visual Cognition. 2005;12:1235–1254. [Google Scholar]
- Ni R, Braunstein ML, Andersen GJ. Perception of scene layout from ground contact, occlusion and motion parallax. Visual Cognition. 2007;15:48–68. [Google Scholar]
- Ono H, Muter P, Mitson L. Size-distance paradox with accommodative micropsia. Perception & Psychophysics. 1974;15:301–307. [Google Scholar]
- Ooi TL, Wu B, He ZJ. Distance determined by the angular declination below the horizon. Nature. 2001;414:197–200. doi: 10.1038/35102562. [DOI] [PubMed] [Google Scholar]
- Philbeck JW, Loomis JM. Comparison of two indicators of perceived egocentric distance under full-cue and reduced-cue conditions. Journal of Experimental Psychology: Human Perception and Performance. 1997;23:72–85. doi: 10.1037//0096-1523.23.1.72. [DOI] [PubMed] [Google Scholar]
- Rogers S. The horizon-ratio relation as information for relative size in picture. Perception & Psychophysics. 1996;58:142–152. doi: 10.3758/bf03205483. [DOI] [PubMed] [Google Scholar]
- Sedgwick HA. The visible horizon: A potential source of visual information for the perception of size and distance. Dissertation Abstracts International. 1973;34:1301B–1302B. (University Microfilms No. 73-22530) [Google Scholar]
- Sedgwick HA. The geometry of spatial layout in pictorial representation. In: Hagen MA, editor. The perception of pictures. Vol. 1. New York: Academic Press; 1980. pp. 33–90. [Google Scholar]
- Sedgwick HA. Environment-centered representation of spatial layout: Available visual information from texture and perspective. In: Beck J, Hope B, Rosenfeld A, editors. Human and Machine Vision. New York: Academic Press; 1983. pp. 425–458. [Google Scholar]
- Sedgwick HA. Space perception. In: Boff KR, Kaufman L, Thomas JT, editors. Handbook of Perception and Human Performance. New York: John Wiley; 1986. pp. 21–1.pp. 21–57. [Google Scholar]
- Sinai MJ, Ooi TL, He ZJ. Terrain influences the accurate judgment of distance. Nature. 1998;395:497–500. doi: 10.1038/26747. [DOI] [PubMed] [Google Scholar]
- Stevens KA. Slant-tilt: The visual encoding of surface orientation. Biological Cybernetics. 1983;46:183–195. doi: 10.1007/BF00336800. [DOI] [PubMed] [Google Scholar]
- Stoper AE, Cohen MM. Judgments of eye level in light and in darkness. Perception & Psychophysics. 1986;40:311–316. doi: 10.3758/bf03203022. [DOI] [PubMed] [Google Scholar]
- Wallach H, O’Leary A. Slope of regard as a distance cue. Perception & Psychophysics. 1982;31:145–148. doi: 10.3758/bf03206214. [DOI] [PubMed] [Google Scholar]
- Wu J, He ZJ, Ooi TL. Vertical and horizontal references determined by linear perspective and optic flow information'. Journal of Vision. 2003;3(9):499a. (abstract), http://journalofvision.org/3/9/499/
- Wu J, He ZJ, Ooi TL. Visually perceived eye level and horizontal midline of the body trunk influenced by optic. Perception. 2005;34:1045–1060. doi: 10.1068/p5416. [DOI] [PubMed] [Google Scholar]
- Wu J, He ZJ, Ooi TL. The Linear perspective information in ground surface representation and distance judgment. Perception & Psychophysics. 2007;69:654–672. doi: 10.3758/bf03193769. [DOI] [PubMed] [Google Scholar]
- Wu B, Ooi TL, He ZJ. Perceiving distance accurately by a directional process of integrating ground information. Nature. 2004;428:73–77. doi: 10.1038/nature02350. [DOI] [PubMed] [Google Scholar]