Evolutionary dynamics of tumor progression with random fitness values

Abstract

Most human tumors result from the accumulation of multiple genetic and epigenetic alterations in a single cell. Mutations that confer a fitness advantage to the cell are known as driver mutations and are causally related to tumorigenesis. Other mutations, however, do not change the phenotype of the cell or even decrease cellular fitness. While much experimental effort is being devoted to the identification of the functional effects of individual mutations, mathematical modeling of tumor progression generally considers constant fitness increments as mutations are accumulated. In this paper we study a mathematical model of tumor progression with random fitness increments. We analyze a multi-type branching process in which cells accumulate mutations whose fitness effects are chosen from a distribution. We determine the effect of the fitness distribution on the growth kinetics of the tumor. This work contributes to a quantitative understanding of the accumulation of mutations leading to cancer.

1 Introduction

Tumors result from an evolutionary process occurring within a tissue (Nowell, 1976). From an evolutionary point of view, tumors can be considered as collections of cells that accumulate genetic and epigenetic alterations. The phenotypic changes that these alterations confer to cells are subjected to the selection pressures within the tissue and lead to adaptations such as the evolution of more aggressive cell types, the emergence of resistance, induction of angiogenesis, evasion of the immune system, and colonization of distant organs with metastatic growth. Advantageous heritable alterations can cause a rapid expansion of the cell clone harboring such changes, since these cells are capable of outcompeting cells that have not evolved similar adaptations. The investigation of the dynamics of cell growth, the speed of accumulating mutations, and the distribution of different cell types at various timepoints during tumorigenesis is important for an understanding of the natural history of tumors. Further, such knowledge aids in the prognosis of newly diagnosed tumors, since the presence of cell clones with aggressive phenotypes lead to less optimistic predictions for tumor progression. Finally, a knowledge of the composition of tumors allows for the choice of optimum therapeutic interventions, as tumors harboring pre-existing resistant clones should be treated differently than drug-sensitive cell populations.

Mathematical models have led to many important insights into the dynamics of tumor progression and the evolution of resistance (Goldie and Coldman, 1983 and 1984; Bodmer and Tomlinson, 1995; Coldman and Murray, 2000; Knudson, 2001; Maley and Forrest, 2001; Michor et al., 2004; Iwasa et al., 2005; Komarova and Wodarz, 2005; Michor et al., 2006; Michor and Iwasa, 2006; Frank 2007; Wodarz and Komarova, 2007; Schweinsberg, 2008; Durrett, Schmidt, and Schweinsberg, 2009). These mathematical models generally fall into one of two classes: (i) constant population size models, and (ii) models describing exponentially growing populations. Many theoretical investigations of exponentially growing populations employ multi-type branching process models (e.g., Iwasa et al., 2006; Haeno et al., 2007; Durrett and Moseley, 2009), while others use population genetic models for homogeneously mixing exponentially growing populations (e.g., Beerenwinkel et al., 2007; Durrett and Mayberry, 2010). In this paper, we focus on branching process models. In these models, cells with i ≥ 0 mutations are denoted as type-i cells, and Z_i(t) specifies the number of type-i cells at time t. Type-i cells die at rate b_i, give birth to one new type-i cell at rate a_i, and give birth to one new type-(i + 1) cell at rate u_i+1. Some authors (e.g., Haeno et al., 2007) consider an alternate version of our model in which mutations occur with probability μ_i+1 during birth events which occur at rate α_i, but the two versions are equivalent provided u_i+1 = α_iμ_i+1 and a_i = α_i (1 − μ_i+1). This relationship between the parameters must be kept in mind when comparing results across papers.

One biologically unrealistic aspect of this model as presented in the literature is that all type-i cells are assumed to have the same birth and death rates. This assumption describes situations during tumorigenesis in which the order of mutations is predetermined, i.e. the genetic changes can only be accumulated in a particular sequence and all other combinations of mutations lead to lethality. Furthermore, in this interpretation of the model, there cannot be any variability in phenotype among cells with the same number of mutations. In many situations arising in biology there is marked heterogeneity in phenotype even if genetically, the cells are identical (Elowitz et al., 2002; Becskei et al., 2005; Kaern et al., 2005; Feinerman et al., 2008). This variability may be driven by stochasticity in gene expression or in post-transcriptional or post-translational modifications. In this paper, we modify the branching process model so that mutations alter cell birth rates by a random amount.

An important consideration for this endeavor is the choice of the mutational fitness distribution. The exponential distribution has become the preferred candidate in theoretical studies of the genetics of adaptation. The first theoretical justification of this choice was given by Gillespie (1983, 1984), who argued that if the number of possible alleles is large and the current allele is close to the top of the rank ordering in fitness values, then extreme value theory should provide insight into the distribution of the fitness values of mutations. For many distributions including the normal, Gamma, and lognormal distributions, the maximum of n independent draws, when properly scaled, converges to the Gumbel or double exponential distribution, Λ(x) = exp(−e^−x). In the biological literature, it is generally noted that this class of distributions only excludes exotic distributions like the Cauchy distribution, which has no moments. However, in reality, it eliminates all distributions with P(X > x) ~ Cx^−α. For distributions in the domain of attraction of the Gumbel distribution, and if Y₁ > Y₂ ··· >Y_k are the k largest observations in a sample of size n, then there is a sequence of constants b_n so that the spacings Z_i = i(Y_i−Y_i+1)/b_n converge to independent exponentials with mean 1, see e.g., Weissman (1978). Following up on Gillespie’s work, Orr (2003) added the observation that in this setting, the distribution of the fitness increases due to beneficial mutations has the same distribution as Z₁ independent of the rank i of the wild type cell.

To infer the distribution of fitness effects of newly emerged beneficial mutations, several experimental studies were performed; for examples, see Imhoff and Schlotterer (2001), Sanjuan et al. (2004), and Kassen and Bataillon (2006). The data from these experiments is generally consistent with an exponential distribution of fitness effects. However, there is an experimental caveat that cannot be neglected (Rozen et al., 2002): if only those mutations are considered that reach 100% frequency in the population, then the exponential distribution is multiplied by the fixation probability. By this operation, a distribution with a mode at a positive value develops. In a study of a quasi-empirical model of RNA evolution in which fitness was based on secondary structures, Cowperthwaite et al. (2005) found that fitnesses of randomly selected genotypes appeared to follow a Gumbel-type distribution. They also discovered that the fitness distribution of beneficial mutations appeared exponential only when the vast majority of small-effect mutations were ignored. Furthermore, it was determined that the distribution of beneficial mutations depends on the fitness of the parental genotype (Cowperthwaite et al., 2005; MacLean and Buckling, 2009). However, since the exceptions to this conclusion arise when the fitness of the wild type cell is low, these findings do not contradict the picture based on extreme value theory.

In contrast to the evidence above, recent work of Rokyta et al. (2008) has shown that in two sets of beneficial mutations arising in the bacteriophage ID11 and in the phage φ6 – for which the mutations were identified by sequencing – beneficial fitness effects are not exponential. Using a statistical method developed by Biesal et al. (2007), they tested the null hypothesis that the fitness distribution has an exponential tail. They found that the null hypothesis could be rejected in favor of a distribution with a right truncated tail. Their data also violated the common assumption that small-effect mutations greatly outnumber those of large effect, as they were consistent with a uniform distribution of beneficial effects. A possible explanation for the bounded fitness distribution may be found in the culture conditions utilized in the experiments: they evolved ID11 on E. coli at an elevated temperature (37° C instead of 33° C). There may be a limited number of mutations that will enable ID11 to survive in increased temperatures. The latter situation may be similar to scenarios arising during tumorigenesis, where, in order to develop resistance to a drug or to progress to a more aggressive stage, the conformation of a particular protein must be changed or a certain regulatory network must be disrupted. If there is a finite, but large, number of possible beneficial mutations, then it is convenient to use a continuous distribution as an approximation.

In this paper, we consider both bounded distributions and unbounded distributions for the fitness advance and derive asymptotic results for the number of type-k individuals at time t. We determine the effects of the fitness distribution on the growth kinetics of the population, and investigate the rates of expansion for both bounded and unbounded fitness distributions. This model provides a framework to investigate the accumulation of mutations with random fitness effects.

The remainder of this section is dedicated to statements and discussion of our main results. Proofs of these results can be found in Sections 2–5.

1.1 Bounded distributions

The model we consider is a multi-type branching process in which type-i cells have accumulated i ≥ 0 advantageous mutations. All cells in the population die at rate b₀. The initial population consists entirely of type-0 cells that give birth at rate a₀ > b₀ to new type-0 cells and produce type-1 cells at rate u₁. We assume that the population of type-0 cells starts at a sufficiently large population V₀ so that we can approximate its size by Z₀(t) = V₀e^λ₀t, where λ₀ = a₀ − b₀. When a type-0 cell produces a type-1 cell, the new cell gives birth to type-1 cells at rate a₀ + x, where x ≥ 0 is drawn according to a probability distribution ν and produces type-2 cells at rate u₂. In general, a type-k cell with birth rate a produces a new type-(k + 1) cell at rate u_k and the new type-(k + 1) cell assumes an increased birth rate a + x where x ≥ 0 is drawn according to ν. We let Z_k(t) denote the total number of type-k cells in the population at time t. When we refer to the kth generation of mutants, we mean the set of all type-k cells.

We begin by considering situations in which the distribution of the increase in the birth rate is concentrated on [0, b]. In particular, suppose that ν has density g with support in [0, b] and assume that g satisfies:

$$g\text{is}\text{continuous}\text{at}b,g(b)>0,g(x)\le G\text{for}x\in [0,b]$$ (*)

Our first result describes the mean number of first generation mutants at time t, EZ₁(t).

Theorem 1

If (*) holds, then

$${EZ}_1(t)\sim \frac{V_0{u}_{1}g(b)}{bt}{e}^{({\lambda }_0+b)t}$$

where a(t) ~ b(t) means a(t)/b(t) → 1.

The next result shows that the actual growth rate of type-1 cells is slower than the mean. Here, and in what follows, we use ⇒ to indicate convergence in distribution.

Theorem 2

If (*) holds and p = b/λ₀, then for θ ≥ 0,

$$Eexp(-\theta t^{1+p}{e}^{-({\lambda }_0+b)t}{Z}_1(t))\to exp(-V_0{u}_1{\theta }^{{\lambda }_0/({\lambda }_0+b)}{c}_1({\lambda }_0,b)),$$ (1.1)

where c₁(λ₀, b) is a constant whose value will be given in (3.8). In particular, we have

$$t^{1+p}{e}^{-({\lambda }_0+b)t}{Z}_{1}t)\Rightarrow V_1,$$

where V₁ has Laplace transform given by the righthand side of (1.1).

Theorem 2 is similar to Theorem 3 in Durrett and Moseley (2009) which assumes a deterministic fitness distribution so that all type-1 cells have growth rate λ₁ = λ₀ + b. There, the asymptotic growth rate of the first generation is exp(λ₁t). In contrast, the continuous fitness distribution we consider here has the effect of slowing down the growth rate of the first generation by the polynomial factor t^1+p. To explain this difference, we note that the calculation of the mean given in Section 3 shows that the dominant contribution to Z₁(t) comes from growth rates x = b − O(1/t). However, mutations with this growth rate are unlikely until the number of type-0 cells is O(t), i.e., roughly at time r₁ = (1/λ₀) log t. Thus at time t, the number of type-1 cells will be roughly exp((λ₀+b)(t − r₁)) = exp((λ₀ +b)t)/t^1+p.

To prove Theorem 2, we look at mutations as a point process in [0, t] × [0, b]: there is a point at (s, x) if there was a mutant with birth rate a₀ + x at time s. This allows us to derive the following explicit expression for the Laplace transform of Z₁(t):

$$E(e^{-\theta Z_1(t)})=exp\left(-u_1{\int }_0^{b}dxg(x){\int }_0^{t}ds{V}_0{e}^{{\lambda }_{0}s}(1-{\stackrel{\sim }{\phi }}_{x,t-s}(\theta ))\right)$$

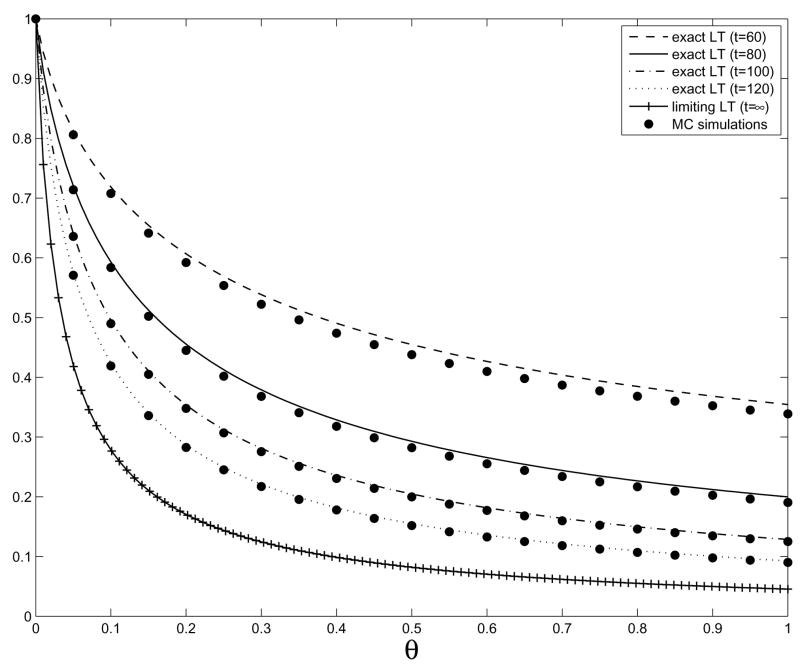
where ${\stackrel{\sim }{\phi }}_{x,r}(\theta )={Ee}^{-\theta {\stackrel{\sim }{Z}}_r^x}$ and ${\stackrel{\sim }{Z}}_r^x$ is a continuous-time branching process with birth rate a₀+x, death rate b₀, and initial population ${\stackrel{\sim }{Z}}_0^x=1$. In Figure 1, we compare the exact Laplace transform of t^1+p exp(−(λ₀+b)t)Z₁(t) with the results of simulations and the limiting Laplace transform from Theorem 2, illustrating the convergence as t → ∞.

Figure 1.

Plot of the exact Laplace transform (LT) for t^(1+p) e^{−(λ₀+b)t} Z₁ (t) at times t = 60, 80,100,120, the approximations from Monte Carlo (MC) simulations at the corresponding times, and the asymptotic Laplace transform from Theorem 2. Parameter values: a₀ = 0.2, b₀ = 0.1, b = 0.01, and u₁ = 10⁻³. g is uniform on [0, .01].

Notice that the Laplace transform of V₁ has the form exp(C θ^α) where α = λ₀/(λ₀ + b) which implies that P(V₁ > v) ~ v^−α as v → ∞ (see, for example, the argument in Section 3 of Durrett and Moseley (2009)). To gain some insight into how this limit comes about, we give a second proof of the convergence that tells us the limit is the sum of points in a nonhomogeneous Poisson process. Each point in the limiting process represents the contribution of a different mutant lineage to Z₁(t). More precisely, we define a three dimensional point process 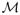(t) on [0, t] × [0, b] × (0, ∞) by the following rule: there is a point at (s, x, v) if there was a type-1 mutant with birth rate a₀ + x at time s and the number of its type-1 descendants at time t, $Z_1^{s,x}(t)$, has $e^{-({\lambda }_0+x)(t-s)}{Z}_1^{s,x}(t)\to v$ as t → ∞ with v > 0. We define F : [0, ∞)³ → [0, ∞) by

$$F(s,x,v)=v{t}^{1+p}{e}^{-({\lambda }_0+b)t}{e}^{({\lambda }_0+x)(t-s)}$$

i.e. F maps a point in 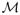(t) onto its contribution to V₁ = lim_t→∞ t^1+pe^{−(λ₀+b)t}Z₁(t).

Theorem 3

As t → ∞, F(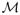(t)) ⇒ Λ where Λ is a Poisson process on (0, ∞) with mean measure μ(z, ∞) = A₁(λ₀, b)u₁V₀z^{−λ₀/(λ₀+b)} and A₁(λ₀, b) is a constant whose value is given in (3.9). In particular, V₁ = lim_t→∞ t^1+pe^{−(λ₀+b)t}Z₁(t) is the sum of the points in Λ.

A similar result can be obtained for deterministic fitness distributions, see the Corollary to Theorem 3 in Durrett and Moseley (2009). However, the new result shows that the point process limit is not an artifact of assuming that all first generation mutants have the same growth rate. Even when the fitness advances are random, different mutant lines contribute to the limit. This result is consistent with observations of Maley et al. (2006) and Shah et al. (2009) that tumors contain cells with different mutational haplotypes. Theorem 3 also gives quantitative predictions about the relative contribution of different mutations to the total population. These implications will be explored further in a follow-up paper currently in progress.

With the behavior of the type-1 individuals analyzed, we are ready to proceed to the study of type-k individuals. The computation of the mean is straightforward.

Theorem 4

If (*) holds, then

$${EZ}_k(t)\sim \frac{V_0·u_1\cdots u_k·g{(b)}^k}{t^k{b}^{k}k!}{e}^{({\lambda }_0+kb)t}$$

As in the k = 1 case, the mean involves a polynomial correction to the exponential growth and again, does not give the correct growth rate for the number of type-k cells. To state the correct limit theorem describing the growth rate of Z_k(t), we will define p_k and u_1,k by

$$k+p_k=\sum _{j=0}^{k-1}\frac{{\lambda }_0+kb}{{\lambda }_0+jb}\text{and}{u}_{1,k}=\prod _{j=1}^k{u}_j^{{\lambda }_0/({\lambda }_0+(j-1)b)}$$

for all k ≥ 1.

Theorem 5

If (*) holds, then for θ ≥ 0

$$Eexp(-\theta t^{k+p_k}{e}^{-({\lambda }_0+kb)t}{Z}_k(t))\to exp(-c_k({\lambda }_0,b)V_0{u}_{1,k}{\theta }^{{\lambda }_0/({\lambda }_0+kb)})$$ (1.2)

where c_k(λ₀, b) is a constant whose value will be given in (4.9). In particular, we have

$$t^{k+p_k}{e}^{-({\lambda }_0+kb)t}{Z}_k(t)\Rightarrow V_k,$$

where V_k has Laplace transform given by the righthand side of (1.2).

If we let $Z_k^{s,x,v}(t)$ be the number of type-k descendants at time t of the 1 mutant at (s, x, v) ∈ 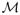(t) where 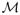(t) is the three dimensional point process described in the paragraph preceding Theorem 3, then $Z_k^{s,x,v}$ is the same as a process in which the initial type (here type-1 cells) behaves like ve^{(λ₀ + x)(t − s)} instead of Z₀(t) = V₀e^λ₀t. Therefore, Theorem 5 can be proved by induction. To explain the form of the result we consider the case k = 2. Breaking things down according to the times and the sizes of the mutational changes, we have

$${EZ}_2(t)={\int }_0^{b}d{x}_{1}g(x_1){\int }_0^{b}d{x}_{2}g(x_2){\int }_0^{t}d{s}_1{\int }_{s_1}^{t}d{s}_2{V}_0{e}^{{\lambda }_0{s}_1}{u}_1{e}^{({\lambda }_0+x_1)(s_2-s_1)}{u}_2{e}^{({\lambda }_0+x_1+x_2)(t-s_2)}$$

As in the result for Z₁(t) the dominant contribution comes from x₁, x₂ = b − O(1/t) and as in the discussion preceding the statement of Theorem 2, the time of the first mutation to b − O(1/t) is ≈ r₁ = (log t)/λ₀. The descendants of this mutation grow at exponential rate λ₀ + b − O(1/t), so the time of the first mutation to 2b − O(1/t) is ≈ r₂ = r₁ + (log t)/(λ₀ + b). Noticing that

$$exp(({\lambda }_0+2b)(t-r_1-r_2))=exp(({\lambda }_0+2b)t)t^{-({\lambda }_0+2b)/{\lambda }_0-({\lambda }_0+2b)/({\lambda }_0+b)}$$

tells us what to guess for the polynomial term: t^−(2+p₂) where

$$2+p_2=\frac{{\lambda }_0+2b}{{\lambda }_0}+\frac{{\lambda }_0+2b}{{\lambda }_0+b}$$

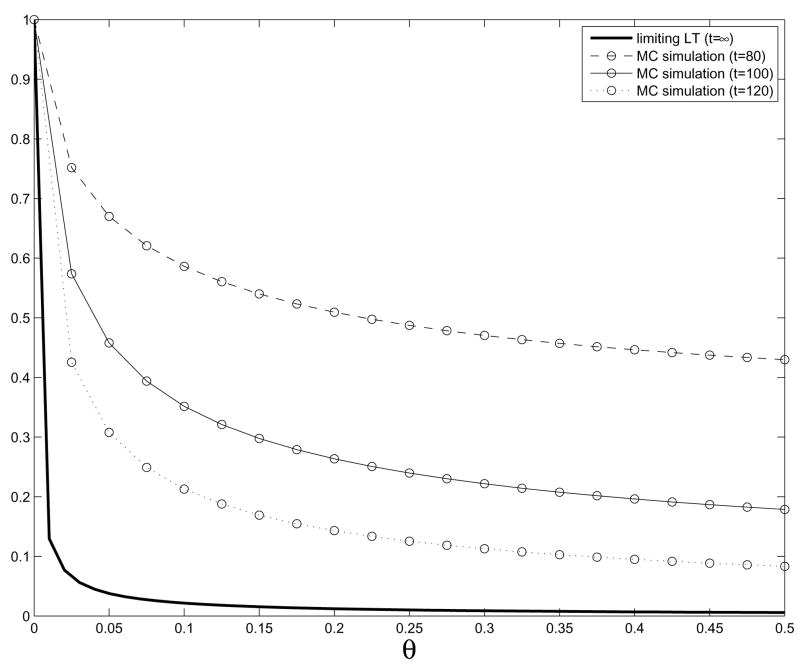
In Figure 2, we compare the asymptotic Laplace transform from Theorem 5 with the results of simulations in the case k = 2. To explain the slow convergence to the limit, we note that if we take account of the mutation rates u₁, u₂ in the heuristic from the previous paragraph (which becomes important when u₁, u₂ are small), then the first time we see a type-1 cell with growth rate b − O(1/t) will not occur until time ${\lambda }_0^{-1}log(t/u_1)$ when the type-0 cells reach O(t/u₁) and so the first type-2 cell with growth rate 2b − O(1/t) will not be born until time $r={\lambda }_0^{-1}log(t/u_1)+{({\lambda }_0+b)}^{-1}log(t/u_2)$ when the descendants of the type-1 cells with growth rate b − O(1/t) reach size O(t/u₂). When u₁ = u₂ = 10⁻³, λ₀ = .1, and b = .01, r ≈ 223. The mutations created at this point will need some time to grow and become dominant in the population. It would be interesting to compare simulations at time 300, but we have not been able to do this due to the large number of different growth rates in generation 1.

Figure 2.

Plot of the approximations to the Laplace transform of t^2+p₂e^{−(λ₀+2b)t} Z₂(t) from Monte Carlo (MC) simulations at times t = 80,100,120 along with the asymptotic Laplace transform from Theorem 5. Parameter values: a₀ = 0.2, b₀ = 0.1, b = 0.01, and u₁ = u₂ = 10⁻³. g is uniform on [0, 0.01].

1.2 Unbounded distributions

In this section, we consider situations in which the fitness distribution is unbounded. We will suppose that the fitness distribution ν has tail

$$\nu (x,\infty )\sim K{x}^{\beta }exp(-\gamma x^{\alpha })$$ (1.3)

as x → ∞ for some α, γ, K > 0, and β ∈ ℝ. Our assumption (1.3) on the tail of ν is satisfied by a number of natural distributions including the gamma(β +1, γ) distribution which has α = 1 (and includes the exponential distribution as the special case β = 0) and the normal distribution which has α = 2, β = −1.

To analyze this situation, we will again take a Poisson process viewpoint and look at the contribution from a mutation at time s with increased growth rate x. A mutation that increases the growth rate by x at time s will, if it does not die out, grow to e^{(λ₀ + x)(t − s)} ζ at time t where ζ has an exponential distribution. The growth rate (λ₀ + x)(t − s) ≥ z when

$$x\ge \frac{z}{t-s}-{\lambda }_0.$$

Therefore,

$$\begin{array}{l}\mu (z,\infty )\equiv E(\#\text{mutations}\text{with}({\lambda }_0+x)(t-s)\ge z)\\ =V_0{u}_1{\int }_0^t{e}^{{\lambda }_{0}s}\nu (z/(t-s)-{\lambda }_0,\infty )ds\\ =K{V}_0{u}_1{\int }_0^t{e}^{{\lambda }_{0}s}q(z/(t-s)-{\lambda }_0){\left(\frac{z}{t-s}-{\lambda }_0\right)}^{\beta }exp\left(-\gamma {\left(\frac{z}{t-s}-{\lambda }_0\right)}^{\alpha }\right)ds\\ =K{V}_0{u}_1{\int }_0^{t}q(z/(t-s)-{\lambda }_0){\left(\frac{z}{t-s}-{\lambda }_0\right)}^{\beta }exp(\phi (s,z))ds\end{array}$$

where

$$q(x)=\frac{\nu (x,\infty )}{K{x}^{\beta }exp(-\gamma x^{\alpha })}\to 1$$ (1.4)

as x → ∞ and

$$\phi (s,z)={\lambda }_{0}s-\gamma {\left(\frac{z}{t-s}-{\lambda }_0\right)}^{\alpha }.$$ (1.5)

The size of this integral can be found by maximizing the exponent φ over s for fixed z. Since

$$\frac{\partial \phi }{\partial s}(s,z)={\lambda }_0-\alpha \gamma {\left(\frac{z}{t-s}-{\lambda }_0\right)}^{\alpha -1}\frac{z}{{(t-s)}^2}$$ (1.6)

and

$$\frac{{\partial }^2\phi }{\partial s^2}(s,z)=-\alpha (\alpha -1)\gamma {\left(\frac{z}{t-s}-{\lambda }_0\right)}^{\alpha -2}\frac{z^2}{{(t-s)}^4}-\alpha \gamma {\left(\frac{z}{t-s}-{\lambda }_0\right)}^{\alpha -1}\frac{2z}{{(t-s)}^3}$$ (1.7)

we can see that ∂² φ/∂s²(s, z) < 0 when αz > λ₀(t − s) so that for all z in this range, φ(s, z) is concave as a function of s and achieves its maximum at a unique value s_z.

When α = 1, it is easy to set (1.6) to 0 and solve for s_z. This in turn leads to an asymptotic formula for μ(z, ∞) and allows us to derive the following limit theorem for Z₁(t).

Theorem 6

Suppose α = 1 and let c₀ = λ₀/4γ. Then t⁻² log Z₁(t) → c₀ and

$$\frac{1}{t}\left[log{Z}_1(t)-c_0{t}^2\left(1+\frac{(2\beta +1)logt}{{\lambda }_{0}t}\right)\right]\Rightarrow y^{\ast }$$

where y* is the rightmost point in the point process with intensity given by

$${(2c_0)}^{\beta }{(\pi /{\lambda }_0)}^{1/2}K{V}_0{u}_{1}exp(\gamma {\lambda }_0-{\lambda }_{0}y/2c_0).$$ (1.8)

When α ≠ 1, solving for s_z becomes more difficult, but we are still able to prove the following limit theorem for Z₁(t).

Theorem 7

For any integer α > 1, there exist explicitly calculable constants c_k = c_k(α, γ), 0 ≤ k < α, and κ = κ(β, α, γ) so that t^−(α+1)/α log Z₁(t) → c₀ and

$$\frac{1}{t^{1/\alpha }}\left[log{Z}_1(t)-c_0{t}^{(\alpha +1)/\alpha }\left(1+\sum _{1\le k<\alpha }{c}_k{t}^{-k/\alpha }+\kappa \frac{logt}{t}\right)\right]\Rightarrow y^{\ast }$$

where y* is the rightmost particle in a point process with explicitly calculable intensity.

The complicated form of the result is due to the fact that the fluctuations are only of order t^1/α so we have to be very precise in locating the maximum. The explicit formulas for the constants and the intensity of the point process are given in (5.11) and (5.12). With more work this result could be proved for general α > 1, but we have not tried to do this or prove Conjecture 1 below because the super-exponential growth rates in the unbounded case are too fast to be realistic.

We conclude this section with two comments. First, the proof of Theorem 7 shows that in contrast to the bounded case, in the unbounded case, most type-1 individuals are descendants of a single mutant. Second, the proof shows that the distribution of the mutant with the largest growth rate is born at time s ~ t/(α + 1) (see Remark 1 at the end of Section 5) and has growth rate z = O(t^(α+1)/α). The intuition behind this is that since the type-0 cells have growth rate e^λ₀s and the distribution of the increase in fitness has tail ≈ e^−γxα, the largest advance x attained by time t should occur when s = O(t) and satisfy

$$e^{C{\lambda }_{0}t}{e}^{-\gamma x^{\alpha }}=O(1)\text{or}x=O(t^{1/\alpha }).$$

The growth rate of its family is then (λ₀ + x)(t − s) = O(t^(α+1)/α).

Since the type-1 cells grow at exponential rate c₁t^(α+1)/α, if we apply this same reasoning to type-2 mutants, then the largest additional fitness advance x attained by type-2 individuals should satisfy

$$e^{c_{1}t(\alpha +1)/\alpha }{e}^{-\gamma x^{\alpha }}=O(1)\text{or}x=O(t^{1/\alpha +1/{\alpha }^2}).$$

and the growth rate of its family will be O(t^1+1/α+1/α2). Extrapolating from the first two generations, we make the following

Conjecture 1

Let $q(k)={\sum }_{j=0}^k{\alpha }^{-j}$. As t → ∞,

$$\frac{1}{t^{q(k)}}log{Z}_k(t)\to c_k$$

Note that in the case of the exponential distribution, q(k) = k + 1.

The rest of the paper is organized as follows. Sections 2–5 are devoted to proofs of our main results. After some preliminary notation and definitions in Section 2, Theorems 1–3 are proved in Section 3, Theorems 4–5 in Section 4, and Theorems 6–7 in Section 5. We conclude with a discussion of our results in Section 6.

2 Preliminaries

This section contains some preliminary notation and definitions which we will need for the proofs of our main results. We denote by 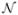(t) the points in a two-dimensional Poisson process on [0, t] × [0, ∞) with mean measure

$$V_0{e}^{{\lambda }_{0}s}ds\nu (dx),$$

where in Sections 3–4, ν(dx) = g(x)dx with g satisfying (*) and in Section 5, ν has tail satisfying (1.3). In other words, we have a point at (s, x) if there was a mutant with birth rate a₀ + x at time s. Define a collection of independent birth/death branching processes $Z_1^{s,x}(t)$ indexed by (s, x) ∈ 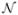(t) with $Z_1^{s,x}(s)=1$, individual birth rate a₀ + x, and death rate b. $Z_1^{s,x}(t)$ is the contribution of the mutation at (s, x) and

$$Z_1(t)=\sum _{(s,x)\in \mathcal{N}(t)}{Z}_1^{s,x}(t).$$

It is well known that

$$e^{-({\lambda }_0+x)(t-s)}{Z}_1^{s,x}(t)\to \frac{b}{a_0+x}{\delta }_0+\frac{{\lambda }_0+x}{a_0+x}\zeta ,$$

where ζ ~ exp((λ₀ + x)/(a₀ + x)) (see, for example, equation (1) in Durrett and Moseley (2009)). In several results, we shall make use of the three-dimensional Poisson process 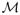(t) on [0, t] × [0, ∞) × (0, ∞) with intensity

$$V_0{e}^{{\lambda }_{0}s}\nu (dx){\left(\frac{{\lambda }_0+x}{a_0+x}\right)}^2{e}^{-v({\lambda }_0+x)/(a_0+x)}dv.$$

In words, (s, x, v) ∈ 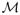(t) if there was a mutant with birth rate a₀ + x at time s and the number of its descendants at time t, $Z_1^{s,x}(t)$, has $Z_1^{s,x}(t)\sim v{e}^{({\lambda }_0+x)(t-s)}$. It is also convenient to define the mapping z: [0, ∞) × [0, t] → [0, ∞) which maps a point (s, x) ∈ 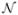(t) to the growth rate of the induced branching process if it survives: z(s, x) = (λ₀ + x)(t − s) and let

$$\mu (A)=E\mid \{(s,x)\in \mathcal{N}(t):z(s,x)\in A\}\mid$$

for A ⊂ [0, ∞).

We shall use C to denote a generic constant whose value may change from line to line. We write f(t) ~ g(t) if f(t)/g(t) → 1 as t → ∞ and f(t) = o(g(t)) is f(t)/g(t) → 0. f(t) ≫ (≪)g(t) means that f(t)/g(t) → ∞ (resp. 0) as t → ∞ and f(t) = O(g(t)) means |f(t)| ≤ Cg(t) for all t > 0. We also shall use the notation f(t) ≃ g(t) if f(t) − g(t) → 0 as t → ∞.

3 Bounded distributions, Z₁

In this section, we prove Theorems 1–3.

Proof of Theorem 1

Mutations to type-1 cells occur at rate V₀u₁e^λ₀s so

$$\begin{array}{l}{EZ}_1(t)=u_1{\int }_0^t{\int }_0^b{e}^{(t-s)({\lambda }_0+x)}g(x)dx{V}_0{e}^{{\lambda }_{0}s}ds\\ =u_1{V}_0{e}^{{\lambda }_{0}t}{\int }_0^{b}dxg(x){\int }_0^t{e}^{(t-s)x}ds\\ =u_1{V}_0{e}^{{\lambda }_{0}t}{\int }_0^{b}dxg(x)\frac{e^{tx}-1}{x}.\end{array}$$ (3.1)

We begin by showing that the contribution from x ∈ [0, b − (1 + k) (log t)/t] can be ignored for any k ∈ [0, ∞). The Mean Value theorem implies that

$$\frac{e^{tx}-1}{x}\le t{e}^{tx}.$$ (3.2)

Using this and the fact that ${\int }_c^{d}t{e}^{tx}dx\le e^{td}$ for any c < d, we can see that

$$t^k{e}^{-bt}{\int }_0^{b-(1+k)(logt)/t}dxg(x)\frac{e^{tx}-1}{x}·\le G{t}^k{e}^{-(1+k)logt}\to 0$$ (3.3)

To handle the other piece of the integral, we take k = 1 and note that

$${\int }_{b-(2logt)/t}^{b}dxg(x)\frac{e^{tx}-1}{x}\sim \frac{g(b)}{b}{e}^{bt}{\int }_{b-2logt/t}^b{e}^{t(x-b)}dx.$$

After changing variables y = (b − x)t, dx = −dy/t, the last integral

$$=\frac{1}{t}{\int }_0^{2logt}{e}^{-y}dy\sim 1/t,$$

which proves the result.

The above proof tells us that the dominant contribution to the type-1 cells comes from mutations with fitness increase x ≥ b_t = b − 2log t/t. To describe the times at which the dominant contributions occur, let S(t) = (2/b) log log t. Then the contribution to the mean from x ∈ [b_t, b] and s ≥ S(t) is by (3.1)

$$\begin{array}{l}\le G{u}_1{V}_0{e}^{({\lambda }_0+b)t}\frac{2(logt)}{t}{\int }_{S(t)}^{\infty }{e}^{-s{b}_t}ds\\ \le G{u}_1{V}_0{e}^{({\lambda }_0+b)t}\frac{2(logt)}{t{b}_t}{e}^{-b_{t}S(t)}.\end{array}$$

Since b_tS(t) ≥ (3/2) log log t for all t sufficiently large, this quantity is o(t⁻¹e^(λ₀+b)t). In words, the dominant contribution to the mean comes from points close to (0, b) or more precisely from [0, (2/b) log log t] × [b − (2 log t)/t, b].

Proof of Theorem 2

It suffices to prove (1.1). The computation in (3.3) with k = 2 + p implies that the contribution from mutations with x ≤ b_t = b − (3 + p)(log t)/t can be ignored. Therefore, we have

$$Eexp(-\theta Z_1(t)e^{-t({\lambda }_0+b)}{t}^{1+p})\simeq E(exp(-\theta Z_1(t)e^{-t({\lambda }_0+b)}{t}^{1+p});A_t)$$

where A_t = {(s, x) ∈ 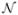(t): x > b_t}. Lemma 2 of Durrett and Moseley (2009) implies that

$$E(e^{-\theta Z_1(t)};A_t)=exp\left(-u_1{\int }_{b_t}^{b}dxg(x){\int }_0^{t}ds{V}_0{e}^{{\lambda }_{0}s}(1-{\stackrel{\sim }{\phi }}_{x,t-s}(\theta ))\right)$$

where ${\stackrel{\sim }{\phi }}_{x,r}(\theta )={Ee}^{-\theta {\stackrel{\sim }{Z}}_r^x}$ and ${\stackrel{\sim }{Z}}_r^x$ is a birth/death branching process with birth rate a₀ + x, death rate b₀, and initial population ${\stackrel{\sim }{Z}}_0^x=1$. Using

$$e^{-({\lambda }_0+b)t}=e^{-({\lambda }_0+x)(t-s)}{e}^{-({\lambda }_0+x)s}{e}^{-(b-x)t}$$ (3.4)

we have

$$E(exp(-\theta Z_1(t)e^{-t({\lambda }_0+b)}{t}^{1+p});A_t)=exp\left(-u_1{V}_0{\int }_{b_t}^{b}dxg(x){\int }_0^{t}ds{e}^{{\lambda }_{0}s}\{1-{\stackrel{\sim }{\phi }}_{x,t-s}(\theta e^{-({\lambda }_0+x)(t-s)}{e}^{-({\lambda }_0+x)s}{e}^{-(b-x)t}{t}^{1+p})\}\right)$$

Changing variables s = r_x + r where $r_x=\frac{1}{{\lambda }_0+x}log(t^{1+p})$ on the inside integral, y = (b − x)t, dy/t = −dx on the outside, and continuing to write x as short hand for b − y/t, the above

$$=exp\left(-u_1{V}_0{\int }_0^{(3+p)logt}\frac{dy}{t}g(x)t^{(1+p){\lambda }_0/({\lambda }_0+x)}{\int }_{-r_x}^{t-r_x}dr{e}^{{\lambda }_{0}r}\{1-{\stackrel{\sim }{\phi }}_{x,t-r-r_x}(\theta e^{-({\lambda }_0+x)(t-r-r_x)}{e}^{-({\lambda }_0+x)r}{e}^{-y})\}\right)$$ (3.5)

Formula (20) in Durrett and Moseley (2009) implies that as u → ∞,

$$1-{\stackrel{\sim }{\phi }}_{x,u}(\theta e^{-({\lambda }_0+x)u})\to \frac{{\lambda }_0+x}{a_0+x}·\frac{\theta }{\theta +\frac{{\lambda }_0+x}{a_0+x}}$$ (3.6)

and therefore, letting t → ∞ and using (1 + p) λ₀/(λ₀ + b) = 1, we can see that the expression in (3.5)

$$\to exp\left(-u_1{V}_{0}g(b){\int }_0^{\infty }dy\frac{{\lambda }_0+b}{a_0+b}{\int }_{-\infty }^{\infty }dr{e}^{{\lambda }_{0}r}\frac{\theta e^{-({\lambda }_0+b)r}{e}^{-y}}{\theta e^{-({\lambda }_0+b)r}{e}^{-y}+\frac{{\lambda }_0+b}{a_0+b}}\right)$$

Changing variables $r=\frac{1}{{\lambda }_0+b}\{q+log[\theta e^{-y}(a_0+b)/({\lambda }_0+b)]\}$, dr = dq/(λ₀ + b) gives

$$=exp\left(-u_1{V}_{0}g(b){\theta }^{{\lambda }_0/({\lambda }_0+b)}{\left(\frac{{\lambda }_0+b}{a_0+b}\right)}^{b/({\lambda }_0+b)}{\int }_0^{\infty }dy{e}^{-y{\lambda }_0/({\lambda }_0+b)}{\int }_{-\infty }^{\infty }\frac{dq}{{\lambda }_0+b}{e}^{q{\lambda }_0/({\lambda }_0+b)}\frac{e^{-q}}{e^{-q}+1}\right)$$

To simplify the first integral we note that

$${\int }_0^{\infty }dy{e}^{-y{\lambda }_0/({\lambda }_0+b)}=\frac{{\lambda }_0+b}{{\lambda }_0}$$

For the second integral, we prove

Lemma 1

If 0 < c < 1

$${\int }_{-\infty }^{\infty }dq{e}^{qc}\frac{e^{-q}}{e^{-q}+1}=\mathrm{\Gamma }(c)\mathrm{\Gamma }(1-c)$$ (3.7)

Proof

We can rewrite the integral as

$${\int }_{-\infty }^{\infty }dq{e}^{qc}{\int }_0^{\infty }dx{e}^{-x}{e}^{-q}exp(-e^{-q}x)$$

so that after interchanging the order of integration and changing variables w = e^−qx, dw = −dqe^−qx so that w/x = e^−q, dw/x = −dqe^−q, we have

$$={\int }_0^{\infty }dx{\int }_0^{\infty }\frac{dw}{x}{(w/x)}^{-c}{e}^{-x}{e}^{-w}={\int }_0^{\infty }dx{x}^{-1+c}{e}^{-x}{\int }_0^{\infty }dw{w}^{-c}{e}^{-w}$$

which is = Γ(c)Γ(1 − c).

Taking c = λ₀/(λ₀ + b) and letting

$$c_1({\lambda }_0,b)=g(b)\frac{{\lambda }_0+b}{{\lambda }_0}·\frac{1}{{\lambda }_0+b}{\left(\frac{a_0+b}{{\lambda }_0+b}\right)}^{-b/({\lambda }_0+b)}\mathrm{\Gamma }({\lambda }_0/({\lambda }_0+b))\mathrm{\Gamma }(1-{\lambda }_0/({\lambda }_0+b))$$ (3.8)

we have proved Theorem 2.

Recall that we have assumed Z₀(t) = V₀e^λ₀t is deterministic. This assumption can be relaxed to obtain the following generalization of Theorem 2 which is used in Section 4.

Lemma 2

Suppose that Z₀(t) is a stochastic process with Z₀(t) ~ e^λ₀tV₀ for some constant V₀ as t → ∞. Then the conclusions of Theorem 2 remain valid.

To see why this is true, we can use a variant of Lemma 2 from Durrett and Moseley (2009) to conclude that

$$E\left(e^{-\theta Z_1(t)}\mid {\mathcal{F}}_t^0\right)=exp\left(-u_1{\int }_0^{b}dxg(x){\int }_0^{t}ds{Z}_0(s)\left(1-{\stackrel{\sim }{\phi }}_{x,t-s}(\theta )\right)\right),$$

where ${\mathcal{F}}_t^0$ is the σ-field generated by Z₀(s) for s ≤ t. Therefore,

$$E\left(e^{-\theta Z_1(t)}\right)=Eexp\left(-u_1{\int }_0^{b}dxg(x){\int }_0^{t}ds{Z}_0(s)\left(1-{\stackrel{\sim }{\phi }}_{x,t-s}(\theta )\right)\right),$$

Given ε > 0, we can choose t_ε > 0 so that

$$\left|\frac{Z_0(t)}{V_{0}exp({\lambda }_{0}t)}-1\right|<\epsilon$$

for all t > t_ε. Since the contribution from t ≤ t_ε will not affect the limit and the term inside the expectation is bounded, the rest of the proof can be completed in the same manner as the proof of Theorem 2.

We conclude this section with the

Proof of Theorem 3

Let 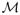(t) be the three dimensional Poisson process defined in Section 2. Recall that

$$F(s,x,v)=v{t}^{1+p}{e}^{-({\lambda }_0+b)t}{e}^{({\lambda }_0+x)(t-s)}$$

i.e. F maps a point in 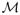(t) to its contribution to the limit t^1+pe^{−(λ₀+b)t}Z₁(t). Using (3.4), we see that in order to have F(s, x, v) > z we need

$$v>z{t}^{-(1+p)}{e}^{(b-x)t}{e}^{({\lambda }_0+x)s}$$

Therefore, the expected number of mutations that contribute more than z to the limit is

$$u_1{V}_0{\int }_0^{b}dxg(x){\int }_0^{t}ds{e}^{{\lambda }_{0}s}\frac{{\lambda }_0+x}{a_0+x}exp\left(-\frac{{\lambda }_0+x}{a_0+x}·z{t}^{-(1+p)}{e}^{(b-x)t}{e}^{({\lambda }_0+x)s}\right)$$

The exponential term can be simplified by making the change of variables

$$s=\frac{1}{{\lambda }_0+x}log\left(\frac{r}{z{t}^{-(1+p)}{e}^{(b-x)t}\frac{{\lambda }_0+x}{a_0+x}}\right),$$

ds = dr/r(λ₀ + x) yielding the equivalent expression

$$u_1{V}_0{\int }_0^{b}dxg(x)z^{-{\lambda }_0/({\lambda }_0+x)}{\left(\frac{{\lambda }_0+x}{a_0+x}\right)}^{x/({\lambda }_0+x)}·t^{(1+p){\lambda }_0/({\lambda }_0+x)}{e}^{-(b-x)t{\lambda }_0/({\lambda }_0+x)}{\int }_{\alpha (x,t)}^{\beta (x,t)}\frac{dr}{{\lambda }_0+x}{r}^{-x/({\lambda }_0+x)}{e}^{-r}$$

where α(x, t) = zt^−(1+p)e^(b−x)t(λ₀ + x)/(a₀ + x) and β(x, t) = α(x, t) e^(λ₀+x)t. As in the previous proof, the main contribution comes from x ∈ [b_t, b] so when we change variables y = (b − x)t, dx = −dy/t, replace the x’s by b’s and use 1 = (1 + p)λ₀/(λ₀ + b) we convert the above into

$$g(b)z^{-{\lambda }_0/({\lambda }_0+b)}\frac{u_1{V}_0}{{\lambda }_0+b}{\left(\frac{{\lambda }_0+b}{a_0+b}\right)}^{b/({\lambda }_0+b)}{\int }_0^{\infty }dy{e}^{-y{\lambda }_0/({\lambda }_0+b)}{\int }_0^{\infty }{r}^{-b/({\lambda }_0+b)}{e}^{-r}dr$$

Performing the integrals gives the result with

$$A_1({\lambda }_0,b)=g(b)\frac{1}{{\lambda }_0}{\left(\frac{{\lambda }_0+b}{a_0+b}\right)}^{b/({\lambda }_0+b)}\mathrm{\Gamma }({\lambda }_0/({\lambda }_0+b))$$ (3.9)

4 Bounded distributions, Z_k

We now move on to the proofs of Theorems 4 and 5. Recall that we have defined p_k by the relation

$$k+p_k=\sum _{j=0}^{k-1}\frac{{\lambda }_0+kb}{{\lambda }_0+jb}.$$

Proof of Theorem 4

Breaking things down according to the times and the sizes of the mutational changes we have

$$\begin{array}{l}{EZ}_k(t)={\int }_0^{b}d{x}_{1}g(x_1)\cdots {\int }_0^{b}d{x}_{k}g(x_k){\int }_0^{t}d{s}_1\cdots {\int }_{s_{k-1}}^{t}d{s}_k{V}_0{e}^{{\lambda }_0{s}_1}{u}_1{e}^{({\lambda }_0+x_1)(s_2-s_1)}\cdots u_k{e}^{({\lambda }_0+x_1+\cdots +x_k)(t-s_k)}\\ ={\int }_0^{b}d{x}_{1}g(x_1)\cdots {\int }_0^{b}d{x}_{k}g(x_k){\int }_0^{t}d{s}_1\cdots {\int }_{s_{k-1}}^{t}d{s}_k{V}_0{u}_1\cdots u_k{e}^{{\lambda }_{0}t}{e}^{x_1(t-s_1)}\cdots e^{x_k(t-s_k)}.\end{array}$$ (4.1)

The first step is to show

Lemma 3

Let b_t = b − (2k + 1)(log t)/t. The contribution to EZ_k(t) from points (x₁,…x_k) with some xi ≤ b_t is o(t^−2ke^(λ₀+kb)t).

Proof

(3.2) implies that

$${\int }_{s_{j-1}}^{t}d{s}_j{e}^{(x_j+\cdots +x_k)(t-s_j)}=\frac{e^{(x_j+\cdots +x_k)(t-s_{j-1})}-1}{x_j+\cdots +x_k}\le t{e}^{(x_j+\cdots +x_k)(t-s_{j-1})}.$$

Applying this and working backwards in the above expression for EZ_k(t), we get

$${EZ}_k(t)\le t^k{V}_0{u}_1\cdots u_k{\int }_0^{b}d{x}_{1}g(x_1)\cdots {\int }_0^{b}d{x}_{k}g(x_k)e^{({\lambda }_0+x_1+\cdots +x_k)t}$$

and the desired result follows.

With the Lemma established, when we work backwards

$${\int }_{s_{j-1}}^{t}d{s}_j{e}^{(x_j+\cdots +x_k)(t-s_j)}=\frac{e^{(x_j+\cdots +x_k)(t-s_{j-1})}-1}{x_j+\cdots +x_k}\sim \frac{e^{(x_j+\cdots +x_k)(t-s_{j-1})}}{(k-j+1)b}$$

From this and induction, we see that the contribution from points {x_1, … x_k) with x_i ∈ [b_t, b] for all i is

$$\sim \frac{V_0{u}_1\cdots u_k}{b^{k}k!}g{(b)}^k{\int }_{b_t}^{b}d{x}_1\cdots {\int }_{b_t}^{b}d{x}_k{e}^{({\lambda }_0+x_1+\cdots +x_k)t}$$

Changing variables y_i = t(b − x_i) the above

$$\sim \frac{V_0{u}_1\cdots u_{k}g{(b)}^k}{b^k{t}^{k}k!}{e}^{({\lambda }_0+kb)t}$$

which proves the desired result.

In the proof of the last result, we showed that the dominant contribution comes from mutations with x_i > b_t. To prove our limit theorem we will also need a result regarding the times at which the mutations to the dominant types occur.

Lemma 4

Let ${\alpha }_k=\frac{2k+1}{kb}$. The contribution to EZ_k{t) from points with s₁ ≥ α_k log t is o(t^−2ke^(λ₀+kb)t).

Proof

Replace the X_i’s in the exponents by b’s, we can see from (4.1) that the expected contribution from points with s₁ ≥ α_k log t is

$$\begin{array}{l}\le b^k{G}^k{V}_0{u}_1\cdots u_k{\int }_{{\alpha }_{k}logt}^{t}d{s}_1{\int }_{s_1}^{t}d{s}_2\cdots {\int }_{s_{k-1}}^{t}d{s}_k{e}^{{\lambda }_{0}t}{e}^{b(t-s_1)}\cdots e^{b(t-s_k)}\\ \le C{e}^{{\lambda }_{0}t}{\int }_{{\alpha }_{k}logt}^t{e}^{kb(t-s_1)}d{s}_1\\ \le C{e}^{({\lambda }_0+kb)t}{t}^{-{\alpha }_{k}kb}\end{array}$$

and the desired result follows.

Recall that

$$k+p_k=\sum _{j=0}^{k-1}\frac{{\lambda }_0+kb}{{\lambda }_0+jb}.$$

For the induction used in the next proof, we will also need the corresponding quantity with λ₀ replaced by λ₀ + x and k by k − 1

$$k-1+p_{k-1}(x)=\sum _{j=0}^{k-2}\frac{{\lambda }_0+x+(k-1)b}{{\lambda }_0+x+jb}$$

which means

$$p_{k-1}(x)=\sum _{j=0}^{k-2}\frac{(k-1-j)b}{{\lambda }_0+x+jb}$$

The limit will depend on the mutation rates through

$$u_{1,k}=\prod _{j=1}^k{u}_j^{{\lambda }_0/({\lambda }_0+(j-1)b)}$$

Again we will need the corresponding quantity with k − 1 terms

$$u_{2,k}(x)=\prod _{j=1}^{k-1}{u}_{j+1}^{({\lambda }_0+x)/({\lambda }_0+x+(j-1)b)}.$$

We shall write u_2,k = u_2,k(b) and note that

$$u_{1,k}=u_1{u}_{2,k}^{{\lambda }_0/({\lambda }_0+b)}$$ (4.2)

Proof of Theorem 5

We shall prove the result under the more general assumption that Z₀(t) ~ V₀e^λ₀t for some constant V₀. The result then holds for k = 1 by Lemma 2. We shall prove the general result by induction on k. To this end, suppose the result holds for k −1. Let $Z_k^{s,x,v}(t)$ be the type-k descendants at time t of the 1 mutant at (s,x,v) ∈ 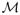(t). Since $Z_1^{s,x}(t)\sim v{e}^{({\lambda }_0+x)(t-s)}$ compared to Z₀(t) ~ V₀e^λ₀t, it follows from the induction hypothesis that

$$Eexp(-\theta {(t-s)}^{k-1+p_{k-1}(x)}{e}^{-({\lambda }_0+x+(k-1)b)(t-s)}{Z}_k^{s,x,v}(t))\to exp(-c_{k-1}({\lambda }_0+x,b)v{u}_{2,k}(x){\theta }^{({\lambda }_0+x)/({\lambda }_0+x+(k-1)b)})$$ (4.3)

Integrating over the contributions from the three-dimensional point process we have

$$Eexp(-\theta Z_k(t))=exp\left(-{\int }_0^{b}dxg(x){\int }_0^{t}ds{u}_1{V}_0{e}^{{\lambda }_{0}s}{\int }_0^{\infty }dv{\left(\frac{{\lambda }_0+x}{a_0+x}\right)}^{2}exp\left(-\frac{{\lambda }_0+x}{a_0+x}v\right)(1-{\phi }_{x,v,t-s}^{k-1}(\theta ))\right)$$

where ${\phi }_{x,v,t-s}^{k-1}(\theta )=Eexp(-\theta Z_k^{0,x,v}(t-s))$. To prove the desired result we need to replace θ by θt^k+pke^{−(λ₀+kb)t}. Doing this with (4.3) in mind we have

$$Eexp(-\theta t^{k+p_k}{e}^{-({\lambda }_0+kb)t}{Z}_k(t))=exp\left(-{\int }_0^{b}dxg(x){\int }_0^{t}ds{u}_1{V}_0{e}^{{\lambda }_{0}s}{\int }_0^{\infty }dv{\left(\frac{{\lambda }_0+x}{a_0+x}\right)}^{2}exp\left(-\frac{{\lambda }_0+x}{a_0+x}v\right)\{1-{\phi }_{x,v,t-s}^{k-1}(\theta t^{k+p_k}{e}^{-({\lambda }_0+x+(k-1)b)(t-s)}{e}^{-(b-x)t}{e}^{-({\lambda }_0+x+b(k-1))s})\}\right)$$ (4.4)

By Lemmas 3 and 4, we can restrict attention to x ∈ [b_t, b] and s ≤ α_k log t. The first restriction implies that all of the x’s except the one in (b − x) can be set equal to b and the second that we can replace t by t − s. Since (k + p_k) −(k − 1 + p_k−1 (b)) = (λ₀ + kb)/λ_0, the term in the exponential on the righthand side of (4.4) is

$$\simeq -{\int }_{b_t}^{b}dxg(x){\int }_0^{{\alpha }_{k}logt}ds{u}_1{V}_0{e}^{{\lambda }_{0}s}{\int }_0^{\infty }dv{\left(\frac{{\lambda }_0+b}{a_0+b}\right)}^{2}exp\left(-\frac{{\lambda }_0+b}{a_0+b}v\right)(1-{\phi }_{x,v,t-s}^{k-1}(\theta {(t-s)}^{k-1+p_{k-1}(b)}{e}^{-({\lambda }_0+kb)(t-s)}{t}^{({\lambda }_0+kb)/{\lambda }_0}{e}^{-(b-x)t}{e}^{-({\lambda }_0+kb)s}))$$

Changing variables s = R(t) + r where R(t) = (1/λ₀)(log t), and y = (b − x)t, dy = −tdx the above becomes

$$=-g(b){\int }_0^{(2k+1)logt}dy{\int }_0^{\infty }dy{\left(\frac{{\lambda }_0+b}{a_0+b}\right)}^{2}exp\left(-\frac{{\lambda }_0+b}{a_0+b}v\right){\int }_{-R(t)}^{{\alpha }_{k}logt-R(t)}dr{u}_1{V}_0{e}^{{\lambda }_{0}r}(1-{\phi }_{x,v,t-s}^{k-1}(\theta {(t-s)}^{k-1+p_{k-1}(b)}{e}^{-({\lambda }_0+kb)(t-s)}{e}^{-y}{e}^{-({\lambda }_0+kb)r}))$$

Using (4.3) now we have that the 1 − φ term converges to

$$1-exp(-c_{k-1}({\lambda }_0+b,b)v{u}_{2,k}{[\theta e^{-y}]}^{({\lambda }_0+b)/({\lambda }_0+kb)}{e}^{-({\lambda }_0+b)r})$$

To simplify this expression, we let

$$r=\frac{1}{{\lambda }_0+b}(q+Q(v,y))\text{where}Q(v,y)=log\{c_{k-1}({\lambda }_0+b,b)v{u}_{2,k}{[\theta e^{-y}]}^{({\lambda }_0+b)/({\lambda }_0+kb)}\}$$

dr = dq/(λ₀ + b). Plugging this into e^λ₀r results in

$$e^{q{\lambda }_0/({\lambda }_0+b)}{(c_{k-1}({\lambda }_0+b,b)v{u}_{2,k})}^{{\lambda }_0/({\lambda }_0+b)}{\theta }^{{\lambda }_0/({\lambda }_0+kb)}{e}^{-y{\lambda }_0/({\lambda }_0+kb)}$$

so we conclude that the term in the exponential on the righthand side of (4.4) converges to

$$-g(b)\frac{c_{k-1}{({\lambda }_0+b,b)}^{{\lambda }_0/({\lambda }_0+b)}}{{\lambda }_0+b}{V}_0{u}_1{u}_{2,k}^{{\lambda }_0/({\lambda }_0+b)}{\theta }^{{\lambda }_0/({\lambda }_0+kb)}{\int }_0^{\infty }dv{\left(\frac{{\lambda }_0+b}{a_0+b}\right)}^2{v}^{{\lambda }_0/({\lambda }_0+b)}exp\left(-\frac{{\lambda }_0+b}{a_0+b}v\right){\int }_0^{\infty }dy{e}^{-y{\lambda }_0/({\lambda }_0+kb)}{\int }_{-\infty }^{\infty }\frac{dq}{{\lambda }_0+b}{e}^{q{\lambda }_0/({\lambda }_0+b)}(1-exp(-e^{-q}))$$ (4.5)

To obtain a cleaner expression for the constants, we begin by noting that the change of variables w = v (λ₀ + b)/(a₀ + b), dw = dv(λ₀ + b)/(a₀ + b) implies that

$${\int }_0^{\infty }dv{\left(\frac{{\lambda }_0+b}{a_0+b}\right)}^2{v}^{{\lambda }_0/({\lambda }_0+b)}exp\left(-\frac{{\lambda }_0+b}{a_0+b}v\right)={\left(\frac{a_0+b}{{\lambda }_0+b}\right)}^{-1+{\lambda }_0/({\lambda }_0+b)}\mathrm{\Gamma }(1+{\lambda }_0/({\lambda }_0+b))$$ (4.6)

Furthermore, we also have

$${\int }_0^{\infty }dy{e}^{-y{\lambda }_0/({\lambda }_0+kb)}=\frac{{\lambda }_0+kb}{{\lambda }_0}$$ (4.7)

Finally, to evaluate the third integral in (4.5), we make the change of variables x = e^−q, dx = −e^−q dq, or dq = −dx/x to show that it is

$$={\int }_0^{\infty }dx{x}^{-1-{\lambda }_0/({\lambda }_0+b)}(1-e^{-x})dx.$$

Integrating by parts f (x) = 1−e^−x, g′(x) = x^{−1−λ₀/(λ₀+b)}, f′ (x) = e^−x, g(x) = x^{−λ₀/(λ₀+b)} (λ₀+ b)/λ₀ shows that the previous expression is

$$\frac{{\lambda }_0+b}{{\lambda }_0}\mathrm{\Gamma }(1-{\lambda }_0/({\lambda }_0+b))$$ (4.8)

Combining (4.6) – (4.8) and using (4.2), we conclude that the expression in (4.5) is

$$=c_{k-1}{({\lambda }_0+b,b)}^{{\lambda }_0/({\lambda }_0+b)}·g(b)\frac{{\lambda }_0+kb}{{\lambda }_0}·V_0{u}_{1,k}{\theta }^{{\lambda }_0/({\lambda }_0+kb)}·\frac{1}{{\lambda }_0}{\left(\frac{a_0+b}{{\lambda }_0+b}\right)}^{-1+{\lambda }_0/({\lambda }_0+b)}\mathrm{\Gamma }(1+{\lambda }_0/({\lambda }_0+b))\mathrm{\Gamma }(1-{\lambda }_0/({\lambda }_0+b))$$ (4.9)

Setting c_k(λ₀,b) equal to the quantity in (4.9) divided by V₀u_1,kθ^{λ₀/(λ₀+kb)} we have proved the result.

To work out an explicit formula for the constant and to compare with Durrett and Moseley (2009), it is useful to let λ_j = λ₀ + jb, a_j = a₀ + jb and

$$c_{h,j}=\frac{1}{{\lambda }_{j-1}}{\left(\frac{a_j}{{\lambda }_j}\right)}^{-1+{\lambda }_{j-1}/{\lambda }_j}\mathrm{\Gamma }(1+{\lambda }_{j-1}/{\lambda }_j)\mathrm{\Gamma }(1-{\lambda }_{j-1}/{\lambda }_j)$$

From this we see that

$$\begin{array}{l}{c}_k({\lambda }_0,b)=c_{k-1}{({\lambda }_1,b)}^{{\lambda }_0/{\lambda }_1}g(b)\frac{{\lambda }_k}{{\lambda }_0}{c}_{h,1}\\ =c_{k-2}{({\lambda }_2,b)}^{{\lambda }_0/{\lambda }_2}·{\left(g(b)\frac{{\lambda }_{k-1}}{{\lambda }_0}{c}_{h,2}\right)}^{{\lambda }_0/{\lambda }_1}·g(b)\frac{{\lambda }_k}{{\lambda }_0}{c}_{h,1}\end{array}$$

and hence

$$c_k({\lambda }_0,b)=\prod _{j=1}^k{\left(g(b)\frac{{\lambda }_{k-j+1}}{{\lambda }_0}{c}_{h,j}\right)}^{{\lambda }_0/{\lambda }_{j-1}}$$

In Durrett and Moseley (2009) if we let 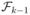be the σ-field generated by Z_j(t) for j ≤ k and all t ≥ 0 then

$$E(e^{-\theta V_k}\mid {\mathcal{F}}_{k-1})=exp(-u_k{V}_{k-1}{c}_{h,k}{\theta }^{{\lambda }_{k-1}/{\lambda }_k})$$

Iterating we have

$$\begin{array}{l}E(e^{-\theta V_k}\mid {\mathcal{F}}_{k-2})=E(exp(-u_k{V}_{k-1}{c}_{h,k}{\theta }^{{\lambda }_{k-1}/{\lambda }_k})\mid {\mathcal{F}}_{k-2})\\ =exp\left(-u_{k-1}{u}_k^{{\lambda }_{k-2}/{\lambda }_{k-1}}{V}_{k-2}{c}_{h,k-1}{c}_{h,k}^{{\lambda }_{k-2}/{\lambda }_{k-1}}{\theta }^{{\lambda }_{k-2}/{\lambda }_k}\right)\end{array}$$

and hence

$$E(e^{-\theta V_k}\mid V_0)=exp(-c_{\theta ,k}{V}_0{u}_{1,k}{\theta }^{{\lambda }_0/{\lambda }_k})$$

where $c_{\theta ,k}={\prod }_{j=1}^k{c}_{h,j}^{{\lambda }_0/{\lambda }_{j-1}}$.

5 Proofs for unbounded distributions

In this Section, we prove Theorems 6 and 7. The first step is to show that unlike in the case of bounded mutational advances, for unbounded distributions, the main contribution to the limit is given by the descendants of a single mutation. We will later show that the largest growth rate will come from z = O(t^(α+1)/α) so the next result is enough. Recall that z(s, x) = (λ₀ + x) (t − s) is the growth rate of the family descended from a mutant at (s, x).

Lemma 5

For any z̄, t > 0, we have

$$E\left(\sum _{(s,x):z(s,x)\le \overline{z}}{Z}_1^{s,x}(t)\right)\le V_0{u}_{1}t{e}^{{\lambda }_{0}t+\overline{z}}$$

Proof

z(s, y) ≤ z̄ if and only if we have a mutation at time s which increases fitness by y ≤ z̄/(t − s) − λ₀ and hence, the expected number of individuals produced by mutations with growth rates ≤ z̄ is

$$V_0{u}_1{\int }_0^t{\int }_0^{\frac{\overline{z}}{t-s}-{\lambda }_0}{e}^{{\lambda }_{0}s}·e^{z(s,y)}\nu (dy)ds\le V_0{u}_{1}t{e}^{{\lambda }_{0}t+\overline{z}}$$

since ${\int }_0^{\infty }\nu (dy)=1$.

To motivate the proof of the general result, we begin with the case when α = 1. Recall that the mean number of mutations with growth rate larger than z has

$$\mu (z,\infty )=K{V}_0{u}_1{\int }_0^{t}q(z/(t-s)-{\lambda }_0){\left(\frac{z}{t-s}-{\lambda }_0\right)}^{\beta }exp(\phi (s,z))ds$$

where q, φ are as in (1.4), (1.5).

Proof of Theorem 6

Since

$$Z_1(t)=\sum _{(s,x)\in \mathcal{N}(t)}{Z}_1^{s,x}(t)=\sum _{(s,x):z(s,x)\le z}{Z}_1^{s,x}(t)+\sum _{(s,x):z(s,x)>z}{Z}_1^{s,x}(t)$$

for any z > 0, we have

$$\frac{1}{t}log{Z}_1(t)\sim \frac{1}{t}\left[log\left(\sum _{(s,x):z(s,x)\le z}{Z}_1^{s,x}(t)\right)\vee log\left(\sum _{(s,x):z(s,x)>z}{Z}_1^{s,x}(t)\right)\right]$$

as t → ∞. Lemma 5 tells us that if there is a mutation with growth rate z = O(t²), then the contribution from mutations with growth rates smaller than z − ε can be ignored so it suffices to describe the distribution of the largest growth rates. We will show that if

$$z_t=c_0{t}^2\left(1+\frac{(2\beta +1)logt}{{\lambda }_{0}t}+f(t)\right)$$

then

$$\mu (z_t,\infty )\to \{\begin{array}{lll}4c_0^{\beta }{(\pi /{\lambda }_0)}^{1/2}{V}_0{u}_{1}exp(\gamma {\lambda }_0-2{\lambda }_{0}x/2c_0)\hfill & \text{if}\hfill & tf(t)\to \frac{x}{c_0},x\ge 0\hfill \\ 0\hfill & \text{if}\hfill & tf(t)\to \infty \hfill \end{array}$$ (5.1)

so that the largest growth rate is O(t²) and comes from the rightmost particle in the point process with intensity given by (1.8).

To prove (5.1), we first need to locate the maximum of φ. Let z > λ₀t so that there exists a unique maximum s_z. Solving φ_s(s, z) = 0 and using the expression for φ_s in (1.6) yields

$$s_z=t-a_0{z}^{1/2}$$

where a₀ = (γ/λ₀)^1/2 = (4c₀)^−1/2 which leads to the expression

$$\begin{array}{l}\phi (s_z,z)={\lambda }_{0}t-{\lambda }_0(t-s_z)-\gamma \left(\frac{z}{t-s}-{\lambda }_0\right)\\ ={\lambda }_{0}t-{\lambda }_0{a}_0{z}^{1/2}-\gamma z^{1/2}/a_0+\gamma {\lambda }_0\\ ={\lambda }_0(t-2a_0{z}^{1/2})+\gamma {\lambda }_0.\end{array}$$ (5.2)

If we take

$$z_t=c_0{t}^2\left(1+\frac{(2\beta +1)logt}{{\lambda }_{0}t}+f(t)\right)={\left(\frac{t}{2a_0}\right)}^2\left(1+\frac{(2\beta +1)logt}{{\lambda }_{0}t}+f(t)\right)$$

in (5.2) and use (1 + y)^1/2 = 1 + y/2 + O(y²), we obtain

$$\phi (s_{z_t},z_t)=-\frac{(2\beta +1)logt}{2}-{\lambda }_{0}tf(t)+\gamma {\lambda }_0+o(1)$$ (5.3)

as t → ∞. Furthermore, (1.7) implies that

$$\begin{array}{l}{\phi }_{ss}(s_{z_t},z_t)=-\frac{2\gamma z_t}{{(t-s_{z_t})}^3}=-\frac{2\gamma }{a_0^3{z}_t^{1/2}}=-\frac{a}{t}+o(1)\\ {\phi }_{\mathit{sss}}(s_{z_t},z_t)=-\frac{6\gamma z_t}{{(t-s_{z_t})}^4}=-\frac{6\gamma }{a_0^4{z}_t}=-\frac{24\gamma }{a_0^t{t}^2}+o(1)\end{array}$$

as t → ∞ with $a=4\gamma /a_0^2$. Since φ_s(s_z, z) = 0, taking a Taylor expansion around s_z yields

$$\phi (s,z_t)=\phi (s_{z_t},z_t)-\frac{a}{2t}{(s-s_{z_t})}^2+g(s,z_t)$$ (5.4)

where |g(s, z)| ≤ C|s − s_z|³/t² for all s. Also note that letting

$$\psi (s,z)=q(z/(t-s)-{\lambda }_0){\left(\frac{z}{t-s}-{\lambda }_0\right)}^{\beta }$$

and recalling (1.4), we have

$$\begin{array}{l}\psi (s_{z_t},z_t)=q(z_t/(t-s_{z_t})-{\lambda }_0){\left(\frac{z}{t-s_{z_t}}-{\lambda }_0\right)}^{\beta }\\ =c_t{z}_t^{\beta /2}/a_0^{\beta }+o(z_t^{\beta /2})\\ =c_t{(2c_0)}^{\beta }{t}^{\beta }+o(t^{\beta })\end{array}$$

where c_t → 1 as t → ∞ so that

$$\psi (s,z_t)=c_t{(2c_0)}^{\beta }{t}^{\beta }+g_2(s,z_t)$$

where |g₂(s, z)||s − s_z|⁻¹t^−β = o(1).

Write

$${\int }_0^t\psi (s,z_t)e^{\phi (s,z_t)}ds={\int }_A\psi (s,z_t)e^{\phi (s,z_t)}ds+{\int }_{A^c}\psi (s,z_t)e^{\phi (s,z_t)}ds$$

where A = {s: |s − s_zt| ≤ C(t log t)^1/2} ∩ [0, t]. Since concavity implies that for s ∈ A^c and C sufficiently large, we have

$$exp(\phi (s,z_t))\le \frac{1}{t^{2+\beta }}exp(\phi (s_{z_t},z_t))$$

the contribution of the second integral is negligible. After the change of variables s = s_zt + (t/a)^1/2r, when t is large, the first integral becomes

$${\int }_A\psi (s,z_t)e^{\phi (s,z_t)}ds=(c_t{(2c_0)}^{\beta }{t}^{\beta }+o(1))e^{\phi (s_{z_t,}{z}_t)}{\int }_{-C{(logt)}^{1/2}}^{C{(logt)}^{1/2}}{e}^{g(s,z_t)}{e}^{-r^2/2}{(t/a)}^{1/2}dr.$$

and therefore since |g(s, z_t)| ≤ C(t log t)^3/2/t² when s ∈ A, we have

$$\mu (z_t,\infty )=K{V}_0{u}_1{\int }_0^t\psi (s,z_t)e^{\phi (s,z_t)}ds\sim K{V}_0{u}_{1}b{t}^{\beta +1/2}{e}^{\phi (s_{z_t},z_t)}$$ (5.5)

where $b={(2c_0)}^{\beta }\sqrt{2\pi /a}={(2c_0)}^{\beta }{(\pi /{\lambda }_0)}^{1/2}$. Since

$$\phi (s_{z_t},z_t)=-\frac{(2\beta +1){\lambda }_{0}logt}{2}-{\lambda }_{0}tf(t)+\gamma {\lambda }_0$$

we can conclude that

$$\mu (z_t,\infty )\to \{\begin{array}{lll}K{V}_0{u}_{1}bexp(\gamma {\lambda }_0-2{\lambda }_0{a}_0^{2}x)=V_0{u}_{1}bexp(\gamma {\lambda }_0-2{\lambda }_{0}x/2c_0)\hfill & \text{if}\hfill & tf(t)\to \frac{x}{c_0}\hfill \\ 0\hfill & \text{if}\hfill & tf(t)\to \infty \hfill \end{array}$$

which proves (5.1).

When α ≠ 1, we no longer have an explicit formula for the maximum value s_z which complicates the process of identifying the largest growth rate. We shall assume for convenience that α > 1 is an integer.

Proof of Theorem 7

As in the proof of Theorem 6, it suffices to describe the distribution for the largest growth rates. Let z > λ₀t so the maximum s_z exists. To find a useful expression for the value of φ(s_z, z), we write

$$\phi (s,z)={\lambda }_{0}t-{\lambda }_0(t-s)-\gamma {\left(\frac{z}{t-s}-{\lambda }_0\right)}^{\alpha }.$$

Using the definition of s_z as the solution to φ_s(s_z, z) = 0 yields the condition that

$${(t-s_z)}^{\alpha +1}=\frac{\alpha \gamma }{{\lambda }_0}{z}^{\alpha }{(1-{\lambda }_0\frac{t-s_z}{z})}^{\alpha -1}$$

i.e.,

$$t-s_z={\left(\frac{\alpha \gamma }{{\lambda }_0}\right)}^{1/(\alpha +1)}{z}^{\alpha /(\alpha +1)}{\left(1-{\lambda }_0\frac{t-s_z}{z}\right)}^{(\alpha -1)/(\alpha +1)}.$$

If we substitute the right side of this equation back in for t − s_z in the parenthesis, then writing a₀ = (αγ/λ₀)^1/(α+1) we have

$$\begin{array}{l}t-s_z=a_0{z}^{\alpha /(\alpha +1)}{\left(1-{\lambda }_0{a}_0{z}^{-1/(\alpha +1)}{\left(1-\frac{{\lambda }_0(t-s_z)}{z}\right)}^{\frac{\alpha -1}{\alpha +1}}\right)}^{\frac{\alpha -1}{\alpha +1}}\\ =a_0{z}^{\alpha /(\alpha +1)}{\left(1-{\lambda }_0{a}_0{z}^{-1/(\alpha +1)}{\left(1-{\lambda }_0{a}_0{z}^{-1/(\alpha +1)}{\left(1-\frac{{\lambda }_0(t-s_z)}{z}\right)}^{\frac{\alpha -1}{\alpha +1}}\right)}^{\frac{\alpha -1}{\alpha +1}}\right)}^{\frac{\alpha -1}{\alpha +1}}\end{array}$$

Repeating this α times and then using the approximation (1 − x)ⁿ = 1 − nx + O(x²) with n = (α − 1)/(α + 1) yields

$$t-s_z=z^{\alpha /(\alpha +1)}\left(\sum _{j=0}^{\alpha }{a}_j{z}^{-j/(\alpha +1)}+O(z^{-1})\right)$$ (5.6)

where

$$a_j=a_0{\left(\frac{{\lambda }_0{a}_0(\alpha -1)}{\alpha +1}\right)}^j$$

for j ≥ 1. The error term is O(z⁻¹) because

$$0<(1-{\lambda }_0(t-s)/z)\le 1$$

for all z > λ₀t and s ≤ t. Factoring out a₀ in (5.6) and using (1 + x)⁻¹ = Σ(−x)^j when |x| < 1, we have that

$$\begin{array}{l}\frac{z}{t-s}-{\lambda }_0=a_0^{-1}{z}^{1/(\alpha +1)}\left(1-\sum _{i_1=1}^{\alpha }{a}_0^{-1}{a}_{i_1}{z}^{-i_1/(\alpha +1)}+\sum _{i_1,i_2=1}^{\alpha }{a}_0^{-2}{a}_{i_1}{z}^{-(i_1+i_2)/(\alpha +1)}-\cdots +{(-1)}^{\alpha }\sum _{i_1,\dots ,i_{\alpha }=1}^{\alpha }{a}_0^{-\alpha }\prod _{j=1}^{\alpha }{a}_{i_j}{z}^{-{\sum }_{j=1}^{\alpha }{i}_j/(\alpha +1)}+O(z^{-1})\right)-{\lambda }_0{z}^{1/(\alpha +1)}{z}^{-1/(\alpha +1)}\\ =z^{1/(\alpha +1)}\left(\sum _{j=0}^{\alpha }{b}_j{z}^{-j/(\alpha +1)}+O(z^{-1})\right)\end{array}$$ (5.7)

for large z where the b_j are given by

$$\begin{array}{l}{b}_0=1/a_0\\ b_1=-a_1/a_0^2-{\lambda }_0\\ b_2=-(a_2-a_1^2)/a_0^3\\ b_3=-(a_4-2a_1{a}_3-a_2^2-3a_1^2{a}_2+a_1^4)/a_0^4\end{array}$$

and in general,

$$b_i=\sum _{k=1}^{\alpha }\sum _{\begin{array}{c}{i}_1,\dots ,i_k=1\\ i_1+\cdots +i_k=i\end{array}}^{\alpha }{(-a_0)}^{-(k+1)}\prod _{j=1}^k{a}_{i_j}.$$

(5.7) implies that

$$-\gamma {\left(\frac{z}{t-s}-{\lambda }_0\right)}^{\alpha }=-\gamma z^{\alpha /(\alpha +1)}(b_0^{\alpha }+\alpha b_0^{\alpha -1}{b}_1{z}^{-1/(\alpha +1)}+\left(\alpha b_0^{\alpha -1}{b}_2+\left(\begin{array}{c}\alpha \\ 2\end{array}\right)b_0^{\alpha -2}{b}_1^2\right)z^{-2/(\alpha +1)}+\cdots +(\alpha b_0^{\alpha -1}{b}_{\alpha }+\cdots +b_1^{\alpha })z^{\alpha /(\alpha +1)}+O(z^{-1}))$$

and therefore,

$$\begin{array}{l}\phi (s_z,z)={\lambda }_{0}t+{\lambda }_0(t-s)-\gamma {\left(\frac{z}{t-s}-{\lambda }_0\right)}^{\alpha }\\ ={\lambda }_{0}t+\sum _{j=0}^{\alpha }{d}_j{z}^{\frac{\alpha -j}{\alpha +1}}+O(z^{-1/(\alpha +1)})\end{array}$$ (5.8)

where the d_j can be calculated explicitly, for example:

$$\begin{array}{l}{d}_0=-{\lambda }_0{a}_0-\gamma b_0^{\alpha }\\ d_1=-{\lambda }_0{a}_1-\gamma \alpha b_0^{\alpha -1}{c}_1\\ d_2=-{\lambda }_0{a}_2-\gamma \left(\alpha b_0^{\alpha -1}{b}_2+\left(\begin{array}{c}\alpha \\ 2\end{array}\right)b_0^{\alpha -2}{b}_1^2\right)\\ d_3=-\lambda a_3-\gamma \left(\alpha b_0^{\alpha -1}{b}_3+\left(\begin{array}{c}\alpha \\ 2\end{array}\right)b_0^{\alpha -2}{b}_1{b}_2+\left(\begin{array}{c}\alpha \\ 3\end{array}\right)b_0^{\alpha -3}{b}_1^3\right).\end{array}$$

To figure out the distribution of the growth rate for the largest mutant, we let c₀ = (−λ₀/d₀)^(α+1)/α and then search for κ_j, j = 1, …, α − 1 and κ so that plugging

$$z_t=c_0{t}^{(\alpha +1)/\alpha }\left(1+\sum _{j=1}^{\alpha -1}{\kappa }_j{t}^{-j/\alpha }+\frac{\kappa logt}{t}+f(t)\right)$$

into (5.8) yields

$$\phi (s_{z_t},z_t)=k_1-k_{2}tf(t)-k_{3}logt$$ (5.9)

for some constants k₁, k₂, k₃. Substituting z_t into (5.8) and writing κ₀ = 1, κ_α = x/c₀ to ease the notation we obtain

$$\phi (s_{z_t},z_t)={\lambda }_{0}t+\sum _{j=0}^{\alpha }{d}_j{\left(-\frac{{\lambda }_{0}t}{d_0}\right)}^{(\alpha -j)/\alpha }{\left(\sum _{j=0}^{\alpha }{\kappa }_j{t}^{-j/\alpha }+\kappa t^{-1}logt\right)}^{(\alpha -j)/(\alpha +1)}+O(t^{-1/\alpha }).$$

Since λ₀t + d₀(−λ₀t/d₀) = 0, the first order terms in this expansion is t^(α−1)/α and after using the Taylor series expansion

$${(1+x)}^p=1+px+p(p-1)x^2/2+\cdots +p(p-1)\cdots (p-\alpha +1)x^{\alpha }/\alpha !+O(x^{\alpha +1})$$

we obtain

$$\phi (s_{z_0},z_0)=\sum _{j=1}^{\alpha }{\rho }_j{t}^{(\alpha -j)/\alpha }+\rho logt+O(t^{-1/\alpha }logt)$$ (5.10)

where

$$\begin{array}{l}\rho =d_0\left(-\frac{{\lambda }_0}{d_0}\right)\left(\frac{\alpha }{\alpha +1}\right)\kappa =-\frac{\alpha {\lambda }_0}{\alpha +1}\kappa \\ {\rho }_1=d_0\left(-\frac{{\lambda }_0}{d_0}\right)\left(\frac{\alpha }{\alpha +1}\right)c_1+d_1{\left(-\frac{{\lambda }_0}{d_0}\right)}^{(\alpha -1)/\alpha }\\ {\rho }_2=d_0\left(-\frac{{\lambda }_0}{d_0}\right)\left[\frac{\alpha }{\alpha +1}{c}_2+\frac{\alpha }{\alpha +1}\left(\frac{\alpha }{\alpha +1}-1\right)c_1^2\right]+d_1{\left(-\frac{{\lambda }_0}{d_0}\right)}^{(\alpha -1)/\alpha }\left(\frac{\alpha -1}{\alpha }\right)c_1+d_2{\left(-\frac{{\lambda }_0}{d_0}\right)}^{(\alpha -2)/\alpha }\end{array}$$

and in general

$${\rho }_j=\sum _{i=0}^j{d}_i{\left(-\frac{{\lambda }_0}{d_0}\right)}^{(\alpha -i)/\alpha }\sum _{k=1}^{j-i}\prod _{\ell =1}^k\left(\frac{\alpha -i}{\alpha +1}-\ell +1\right){\kappa }_{i_{\ell }}$$

j = 1, 1, …, α where for each i and k, in the inner product, i₁, …, i_k are always chosen to satisfy i₁ + i₂ + ··· + i_k = j − i. Since ρ_j depends only on κ_i, i ≤ j, then after noting that the coefficient of κ_j in ρ_j is −αλ₀/(α + 1), we can use forward substitution to solve the system ρ_j = 0, j = 1, 2, …, α − 1 for κ_j to obtain the recursive formulas

$$c_j\equiv {\kappa }_j=-\frac{\alpha +1}{\alpha {\lambda }_0}\left({\rho }_j-\frac{-\alpha {\lambda }_0}{\alpha +1}{\kappa }_j\right)$$ (5.11)

for i = 1, 2, …, α − 1. Setting ρ = −k₃ yields

$$\kappa =\frac{(\alpha +1)k_3}{\alpha {\lambda }_0}$$

and for this choice of c_j, κ, we obtain (5.9) with

$$k_2=-\frac{\alpha }{\alpha +1}\frac{d_0}{c_0}\left(-\frac{{\lambda }_0}{d_0}\right)=\frac{\alpha {\lambda }_0}{(\alpha +1)c_0}$$

and k₁ = −(ρ_α − k₂x). Since

$$\begin{array}{l}{\left(\frac{z_t}{t-s_{z_t}}-{\lambda }_0\right)}^{\beta }=z_t^{\beta /(\alpha +1)}/a_0^{\beta }+o(z_t^{\beta /(\alpha +1)})\\ ={\left(\frac{c_0^{1/(\alpha +1)}}{a_0}\right)}^{\beta }{t}^{\beta /\alpha }+o(z_t^{\beta /(\alpha +1)})\end{array}$$

choosing k₃ = (2β/α + 1)/2 replaces (5.3) in the proof of Theorem 6.

Now substituting (5.6) and (5.7) in (1.7) yields

$$\begin{array}{l}{\phi }_{ss}(s_z,z)=-\alpha (\alpha -1)\gamma z^{\frac{\alpha -2}{\alpha +1}}{\left(\sum _{j=0}^{\alpha }{b}_j{z}^{-j/(\alpha +1)}+O(z^{-1})\right)}^{\alpha -2}\times \frac{z^2}{z^{4\alpha /(\alpha +1)}{\left({\sum }_{j=0}^{\alpha }{a}_j{z}^{-j/(\alpha +1)}+O(z^{-1})\right)}^4}-\alpha \gamma z^{\frac{\alpha -1}{\alpha +1}}{\left(\sum _{j=0}^{\alpha }{b}_j{z}^{-j/(\alpha +1)}+O(z^{-1})\right)}^{\alpha -1}\times \frac{2z}{z^{3\alpha /(\alpha +1)}{\left({\sum }_{j=0}^{\alpha }{a}_j{z}^{-j/(\alpha +1)}+O(z^{-1})\right)}^3}\\ =[-\alpha (\alpha -1)\gamma b_0^{\alpha -2}/a_0^4-\alpha \gamma b_0^{\alpha -1}/a_0^3]z^{-\alpha /(\alpha +1)}+o(z^{-\alpha /(\alpha +1)})\\ =-\frac{{\alpha }^2\gamma }{a_0^{\alpha +2}}{z}^{-\alpha /(\alpha +1)}+o(z^{-\alpha /(\alpha +1)})\end{array}$$

where in the second to last line we have used the fact that $b_0=a_0^{-1}$. When z = z_t, this becomes

$${\phi }_{ss}(s_{z_t},z_t)=-\frac{a}{t}+o(t^{-1})$$

where

$$a=\frac{{\alpha }^2\gamma }{a_0^{\alpha +2}{c}_0^{\alpha /(\alpha +1)}}.$$

Since φ_s(s_z, z) = 0 and a calculation similar to the one above shows that φ_sss(s_zt, z_t) = O(t⁻²), we have

$$\phi (s,z_t)=\phi (s_{z_t},z_t)-\frac{a}{2}{(s-s_{z_t})}^2+g(s_{z_t},z_t)$$

where |g(s,z)| ≤ C|s − s_z|³/t² for all s. This replaces (5.4) from the α = 1 proof and the rest of the proof is the same. Note that the intensity for the limiting point process is given by

$$K{V}_0{u}_1{\left(\frac{c_0^{1/(\alpha +1)}}{a_0}\right)}^{\beta }\sqrt{2\pi /a}exp(k_1-k_{2}x).$$ (5.12)

Remark 1

From (5.6), we have

$$t-s_{z_t}\sim a_0{(c_0{t}^{(\alpha +1)/\alpha })}^{(\alpha +1)/\alpha }=\frac{\alpha t}{\alpha +1}$$

which tells us that the time at which the mutant with largest growth rate is born is ~ t/(α + 1).

6 Discussion

In this paper, we have analyzed a multi-type branching process model of tumor progression in which mutations increase the birth rates of cells by a random amount. We studied both bounded and unbounded distributions for the random fitness advances and calculated the asymptotic rate of expansion for the kth generation of mutants.

In the bounded setting, we found that there are only two parameters of the distribution that affect the limiting growth rate of the kth generation (see Theorems 1, 2, 4, and 5): the upper bound for the support of the distribution and the value of its density at the upper bound. This is a rather intuitive result since one would expect that in the long run, the kth generation will be dominated by mutants with the maximum possible fitness. In addition, we found that there is a polynomial correction to the exponential growth of the kth generation. This correction is not present in the case where the fitness advances are deterministic. We have discussed this point in further detail in Section 1.1 and after the proof of Theorem 5 in Section 4. Finally, we showed that the limiting population is descended from several different mutations (see Theorem 3).

In the unbounded setting, we assumed that the distribution of the fitness advance has tail

$$\nu (x,\infty )\sim K{x}^{\beta }{e}^{-\gamma x^{\alpha }}$$ (6.1)

where α, β, γ, and K are parameters. We found that the population of cells with a single mutation grows asymptotically at a super-exponential rate exp(t^(α+1)/α) (see Theorems 6 and 7) and at large times, most of the first generation is derived from a single mutation (see Lemma 5 and the preceding paragraph). The super-exponential growth rate suggests that distributions of the form (6.1), which includes the exponential distribution that is often used to model fitness advances of organisms under selective pressure, is not a good choice for modeling the mutational advances in the progression to cancer where there is very little evidence for populations growing at a super-exponential rate.

These conclusions provide several interesting contributions to the existing literature on evolutionary models of cancer progression. First, our model generalizes previous multi-type branching models of tumor progression by allowing for random fitness advances as mutations are accumulated and provides a mathematical framework for further investigations into the role played by the fitness distribution of mutational advances in driving tumorigenesis. Second, we have discovered that bounded distributions lead to exponential growth whereas unbounded distributions lead to super-exponential growth. This dichotomy might provide a new method for testing whether a tumor population has evolved with an unbounded distribution of mutational advances. Third, we observe that in the case of bounded distributions, the growth rate of the tumor is somewhat ‘robust’ with respect to the mutational fitness distribution and depends only on its upper endpoint. Finally, our calculations of the growth rates for the kth generation of mutants serve as a groundwork for studying the evolution and role of heterogeneity in tumorigenesis. These implications will be explored further in future work.